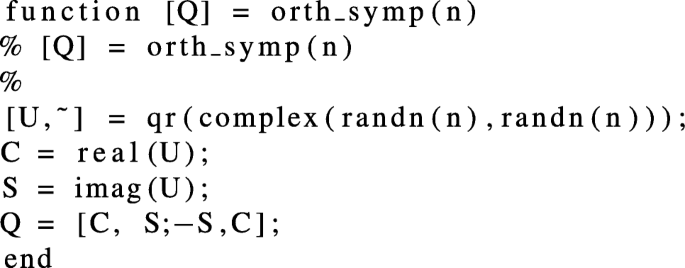On computing the symplectic LL^T factorization

Abstract

We analyze two algorithms for computing the symplectic factorization A = LL^T of a given symmetric positive definite symplectic matrix A. The first algorithm W₁ is an implementation of the HH^T factorization from Dopico and Johnson (SIAM J. Matrix Anal. Appl. 31(2):650–673, 2009), see Theorem 5.2. The second one is a new algorithm W₂ that uses both Cholesky and Reverse Cholesky decompositions of symmetric positive definite matrices. We present a comparison of these algorithms and illustrate their properties by numerical experiments in MATLAB. A particular emphasis is given on symplecticity properties of the computed matrices in floating-point arithmetic.

1 Introduction

We study numerical properties of two algorithms for computing symplectic LL^T factorization of a given symmetric positive definite symplectic matrix $A \in \mathbb {R}^{2n \times 2n}$. A symplectic factorization is the factorization A = LL^T, where $L \in \mathbb {R}^{2n \times 2n}$ is block lower triangular and is symplectic.

Let

$$ J_{n}=\left( \begin{array}{cc} 0 & I_{n} \\ -I_{n} & 0 \end{array} \right), $$

(1)

where I_n denotes the n × n identity matrix.

We will write J and I instead of J_n and I_n when the sizes are clear from the context.

Definition 1

A matrix $A \in \mathbb {R}^{2n \times 2n}$ is symplectic if and only if A^TJA = J.

We can use the symplectic LL^T factorization to compute the symplectic QR factorization and the Iwasawa decomposition of a given symplectic matrix via Cholesky decomposition. We can modify Tam’s method, see [1, 7]. Symplectic matrices arise in several applications, among which symplectic formulation of classical mechanics and quantum mechanic, quantum optics, various aspects of mathematical physics, including the application of symplectic block matrices to special relativity, optimal control theory. For more details we refer the reader to [1, 3], and [8].

Partition $A \in \mathbb {R}^{2n \times 2n}$ conformally with J_n defined by (1) as

$$ A=\left( \begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array} \right), $$

(2)

in which $A_{ij} \in \mathbb {R}^{n \times n}$ for i,j = 1,2.

An immediate consequence of Definition 1 is that the matrix A, partitioned as in (2), is symplectic if and only if $A_{11}^{T} A_{21}$ and $A_{12}^{T} A_{22}$ are symmetric and $A_{11}^{T} A_{22}-A_{21}^{T} A_{12}=I$.

Symplectic matrices form a Lie group under matrix multiplications. The product A₁A₂ of two symplectic matrices $A_{1}, A_{2} \in \mathbb {R}^{2n \times 2n}$ is also a symplectic matrix. The symplectic group is closed under transposition. If A is symplectic then the inverse of A equals A^− 1 = J^TA^TJ, and A^− 1 is also symplectic.

Lemmas 1–5 will be helpful in the construction and for testing of some herein proposed algorithms.

Lemma 1

A nonsingular block lower triangular matrix $L\in \mathbb {R}^{2n \times 2n}$, partitioned as

$$ L=\left( \begin{array}{cc} L_{11} & 0 \\ L_{21} & L_{22} \end{array} \right), $$

(3)

is symplectic if and only if $L_{22}=L_{11}^{-T}$ and $L_{21}^{T} L_{11}=L_{11}^{T} L_{21}$.

Lemma 2

A matrix $Q \in \mathbb {R}^{2n \times 2n}$ is orthogonal symplectic (i.e., Q is both symplectic and orthogonal) if and only if Q has a form

$$ Q=\left( \begin{array}{cc} C & S \\ -S & C \end{array}\right), $$

(4)

where $C, S \in \mathbb {R}^{n \times n}$ and U = C + iS is unitary.

Next, we use the following result from [9], Theorem 2.

Lemma 3

Every symmetric positive definite symplectic matrix $A \in \mathbb {R}^{2n \times 2n}$ has a spectral decomposition A = Q diag(D,D^− 1)Q^T, where $Q \in \mathbb {R}^{2n \times 2n}$ is orthogonal symplectic, and D = diag(d_i), with d₁ ≥ d₂ ≥… ≥ d_n ≥ 1.

In order to create examples of symmetric positive definite symplectic matrices we can use the following result from [3], Theorem 5.2.

Lemma 4

Every symmetric positive definite symplectic matrix $A \in \mathbb {R}^{2n \times 2n}$ can be written as

$$ A=\left( \begin{array}{cc} I_{n} & 0 \\ C & I_{n} \end{array} \right) \quad \left( \begin{array}{cc} G & 0 \\ 0 & G^{-1} \end{array} \right) \quad \left( \begin{array}{cc} I_{n} & C\\ 0 & I_{n} \end{array} \right), $$

(5)

where G is symmetric positive definite and C is symmetric.

Lemma 5

Let $A \in \mathbb {R}^{2n \times 2n}$ be a symmetric positive definite symplectic matrix, partitioned as in (2). Let S be the Schur complement of A₁₁ in A:

$$ S=A_{22}-A_{12}^{T}A_{11}^{-1}A_{12}. $$

(6)

Then S is symmetric positive definite and we have

$$ S=A_{11}^{-1}. $$

(7)

Proof

The property (7) was proved in a more general setting in [3], see Corollary 2.3. We propose an alternative proof for completeness.

It is well known that if A is a symmetric positive definite matrix then the Schur complement S is also symmetric positive definite. We only need to prove (7). Let A be a symmetric positive definite matrix. Then A is symplectic if and only if AJA = J, which is equivalent to the three following conditions:

$$ A_{11} A_{22}-A_{12}^{2}=I, $$

(8)

$$ A_{11} A_{12}^{T}=A_{12} A_{11}, $$

(9)

$$ A_{12}^{T} A_{22}=A_{22} A_{12}. $$

(10)

From (8) we get $A_{22}=A_{11}^{-1}+ \left (A_{11}^{-1} A_{12}\right ) A_{12}$. We can rewrite (9) as $A_{12}^{T} A_{11}^{-1}=A_{11}^{-1} A_{12}$. Thus, we have $A_{22}=A_{11}^{-1}+ A_{12}^{T}A_{11}^{-1}A_{12}$, which together with (6) leads to (7). □

We propose methods for computing symplectic LL^T factorization of a given symmetric positive definite symplectic matrix A, where L is symplectic and partitioned as in (3). We apply the Cholesky and the Reverse Cholesky decompositions. Practical algorithm for the Reverse Cholesky decomposition is described in Section 2, see Remark 1.

Theorem 6

Let $M \in \mathbb {R}^{m \times m}$ be a symmetric positive definite matrix.

(i):

Then there exists a unique lower triangular matrix $L \in \mathbb {R}^{m \times m}$ with positive diagonal entries such that M = LL^T (Cholesky decomposition).

(ii):

Then there exists a unique upper triangular matrix $U \in \mathbb {R}^{m \times m}$ with positive diagonal entries such that M = UU^T (Reverse Cholesky decomposition).

Proof

We only need to prove (ii). Using the fact (i) for the inverse of M, we get $M^{-1}=\hat {L} \hat {L}^{T}$, where $\hat {L}$ is a lower triangular matrix with positive diagonal entries. Then $M=(\hat {L} \hat {L}^{T})^{-1}=U U^{T}$ where $U=\hat {L}^{-T}$. Clearly, U is upper triangular with positive entries, and U is unique. □

Based on Theorem 6, we prove the following result on symplectic LL^T factorization (see [3], Theorem 5.2).

Theorem 7

Let $A \in \mathbb {R}^{2n \times 2n}$ be a symmetric positive definite symplectic matrix of the form

$$ A=\left( \begin{array}{cc} A_{11} & A_{12} \\ A_{12}^{T} & A_{22} \end{array} \right). $$

(11)

If $A_{11}=L_{11} L_{11}^{T}$ is the Cholesky decomposition of A₁₁, then A = LL^T, in which

$$ L=\left( \begin{array}{cc} L_{11} & 0 \\ L_{21} & L_{22} \end{array} \right)= \left( \begin{array}{cc} L_{11} & 0 \\ (L_{11}^{-1} A_{12})^{T} & L_{11}^{-T} \end{array} \right) $$

(12)

is symplectic.

If S is the Schur complement of A₁₁ in A, defined in (6), and S = UU^T is the Reverse Cholesky decomposition of S, then $L_{22}= L_{11}^{-T} = U$.

Proof

We can write

$$ L L^{T}= \left( \begin{array}{cc} L_{11} L_{11}^{T} & L_{11} L_{21}^{T} \\ \left( L_{11} L_{21}^{T}\right)^{T} & L_{21} L_{21}^{T} + L_{22} L_{22}^{T} \end{array} \right). $$

This gives the identities

$$ A_{11}= L_{11} L_{11}^{T}, \quad A_{12}= L_{11} L_{21}^{T}, \quad A_{22}=L_{21} L_{21}^{T}+L_{22} L_{22}^{T}. $$

Clearly, $L_{21}^{T}=L_{11}^{-1} A_{12}$, and $S=A_{22}-L_{21} L_{21}^{T}$ is the Schur complement of A₁₁ in A. Moreover, $S=L_{22} L_{22}^{T}$. If S = UU^T is the Reverse Cholesky decomposition of S and L₂₂ is upper triangular, then L₂₂ = U, by Theorem 6. From Lemma 5 we have $S=A_{11}^{-1}$, hence $S= L_{11}^{-T} L_{11}^{-1}$. Notice that $L_{11}^{-T}$ is upper triangular, so $U=L_{11}^{-T}$.

It is easy to prove that L in (12) is symplectic. It follows from Lemma 1 and (9). □

The paper is organized as follows. Section 2 describes Algorithms W₁ and W₂. Section 3 presents both theoretical and practical computational issues. Section 4 is devoted to numerical experiments and comparisons of the methods. Conclusions are given in Section 5.

2 Algorithms

We apply Theorem 7 to develop two algorithms for finding the symplectic LL^T factorization. They differ only in a way of computing the matrix L₂₂. Algorithm W₁ is based on Theorem 5.2 from [3]. We propose Algorithm W₂, which can be used for symmetric positive definite matrix A, not necessarily symplectic. However, if A is additionally symplectic then the factor L is also symplectic.

• Algorithm W₁

  Given a symmetric positive definite symplectic matrix $A \in \mathbb {R}^{2n \times 2n}$. This algorithm computes the symplectic LL^T factorization A = LL^T, where L is symplectic and has a form

  $$ L=\left( \begin{array}{cc} L_{11} & 0 \\ L_{21} & L_{22} \end{array} \right). $$

  • Find the Cholesky decomposition $A_{11}=L_{11}L_{11}^{T}$.

  • Solve the multiple lower triangular system $L_{11} L_{21}^{T}=A_{12}$ by forward substitution.

  • Solve the lower triangular system L₁₁X = I by forward substitution, i.e., computing each column of $X=L_{11}^{-1}$ independently, using forward substitution.

  • Take L₂₂ = X^T.

  Cost: $\frac {5}{3} n^{3}$ flops.

• Algorithm W₂

  Given a symmetric positive definite symplectic matrix $A \in \mathbb {R}^{2n \times 2n}$. This algorithm computes the symplectic LL^T factorization A = LL^T, where L is symplectic and has a form

  $$ L=\left( \begin{array}{cc} L_{11} & 0 \\ L_{21} & L_{22} \end{array} \right). $$

  • Find the Cholesky factorization $A_{11}=L_{11}L_{11}^{T}$.

  • Solve the multiple lower triangular system $L_{11} L_{21}^{T}=A_{12}$ by forward substitution.

  • Compute the Schur complement $S=A_{22}- L_{21} L_{21}^{T}$.

  • Find the Reverse Cholesky decomposition $S=L_{22} L_{22}^{T}$, where L₂₂ is upper triangular matrix with positive diagonal entries.

Cost: $\frac {8}{3} n^{3}$ flops.

Remark 1

The Reverse Cholesky decomposition M = UU^T of a symmetric positive definite matrix $M \in \mathbb {R}^{m \times m}$ can be treated as the Cholesky decomposition of the matrix M_new = P^TMP, where P is the permutation matrix comprising the identity matrix with its column in reverse order. If M_new = LL^T, where L is lower triangular (with positive diagonal entries), then M = UU^T, with U = PLP^T being upper triangular (with positive diagonal entries).

For example, for m = 3 we have

$$ P=\left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{array} \right), \quad P^{T} M P= \left( \begin{array}{ccc} m_{33} & m_{32} & m_{31} \\ m_{23} & m_{22} & m_{21} \\ m_{13} & m_{12} & m_{11} \end{array} \right), $$

and

$$ L=\left( \begin{array}{ccc} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \end{array} \right), \quad U=\left( \begin{array}{ccc} l_{33} & l_{32} & l_{31} \\ 0 & l_{22} & l_{21} \\ 0 & 0 & l_{11} \end{array} \right). $$

We use the following MATLAB code:

3 Theoretical and practical computational issues

In this work, for any matrix $X \in \mathbb {R}^{m \times m}$, ∥X∥₂ denotes the 2-norm (the spectral norm) of A, and κ₂(X) = ∥X^− 1∥₂ ⋅∥X∥₂ is the condition number of a nonsingular matrix X.

This section mainly addresses the problem of measuring the departure of a given matrix from symplecticity. We also touch a few aspects of numerical stability of Algorithms W₁ and W₂. However, this topic exceeds the scope of this paper.

First we introduce the loss of symplecticity (absolute error) of $X \in \mathbb {R}^{2n \times 2n}$ as

$$ {\Delta} (X) = \left\|{X^{T}JX-J}\right\|_{2}. $$

(13)

Clearly, Δ(X) = 0 if and only if X is symplectic. If $X \in \mathbb {R}^{2n \times 2n}$ is symplectic then X^− 1 = J^TX^TJ, and the condition number of X equals $\kappa _{2}(X)=\Vert {X}\Vert _{2}^{2}$. However, in practice Δ(X) hardly ever equals 0.

Lemma 8

Let $X \in \mathbb {R}^{2n \times 2n}$ satisfy Δ(X) < 1. Then X is nonsingular and we have

$$ \kappa_{2} (X) \leq \frac{\Vert{X}\Vert_{2}^{2}}{1-{\Delta} (X)}. $$

(14)

Proof

Assume that Δ(X) < 1. We first prove that $\det X \neq 0$.

Define F = X^TJX − J. Since J^T = −J and J² = −I_2n, we have the identity

$$ X^{T}JX=J \left( I_{2n}-JF\right). $$

(15)

Since J is orthogonal, we get ∥JF∥₂ = ∥F∥₂ = Δ(X) < 1, hence the matrix I_2n − JF is nonsingular. Then (15) and the property $\det J=1$ leads to $(\det X)^{2}=\det (X^{T}JX)=\det (I_{2n}-JF) \neq 0$. Therefore, $\det X \neq 0$.

To estimate κ₂(X), we rewrite (15) as

$$ X^{-1}= (I_{2n}-JF)^{-1} (J^{T}X^{T}J). $$

(16)

Taking norms we obtain

$$ \left\Vert{X^{-1}}\right\Vert_{2}\leq \left\Vert{(I_{2n}-JF)^{-1}}\right\Vert_{2} \left\Vert{J^{T}X^{T}J}\right\Vert_{2} \leq \frac{\Vert{X}\Vert_{2}}{1-\Vert{JF}\Vert_{2}}. $$

This together with ∥JF∥₂ = Δ(X) establishes the formula (14). The proof is complete. □

Now we show that the assumption Δ(X) < 1 of Lemma 8 is crucial.

Lemma 9

For every t ≥ 1 and every natural number n there exists a singular matrix $X \in \mathbb {R}^{2n \times 2n}$ such that Δ(X) = t.

Proof

The proof gives a construction of such matrix X.

Define

$$ X=\left( \begin{array}{cc} D & 0 \\ 0 & -D \end{array} \right), $$

where $D=\sqrt {t-1} diag(1,0, \ldots ,0)$. Clearly, $\det X=\det D \det (-D)=0$.

Then we have

$$ X^{T}JX-J=\left( \begin{array}{cc} 0 & -\left( D^{2}+I_{n}\right) \\ D^{2}+I_{n} & 0 \end{array} \right). $$

Therefore, Δ(X) = ∥D² + I_n∥₂ = ∥diag(t,1,…,1)∥₂ = t. This completes the proof. □

Lemma 10

Let $A \in \mathbb {R}^{2n \times 2n}$ be a symplectic matrix. Suppose that the perturbed matrix $\hat {A}=A+E$ satisfies

$$ \Vert{E}\Vert_{2}\leq \epsilon \Vert{A}\Vert_{2}, \quad 0<\epsilon<1. $$

(17)

Then $\hat {A} \neq 0$ and

$$ {\Delta} \left( \hat{A}\right) \leq \Vert{\hat{A}}\Vert_{2}^{2} \left( 2 \epsilon+{\mathcal{O}}\left( \epsilon^{2}\right)\right). $$

(18)

Proof

We begin by proving that $\Vert {\hat {A}}\Vert _{2}>0$ for 0 < 𝜖 < 1. Note that ∥A + E∥₂ ≥∥A∥₂ −∥E∥₂. This together with (17) leads to

$$ \Vert{\hat{A}}\Vert_{2} \ge (1-\epsilon) \Vert{A}\Vert_{2}>0, $$

(19)

hence $\hat {A} \neq 0$.

It remains to estimate ${\Delta } (\hat {A})$. For simplicity of notation, we define

$$ F=(A+E)^{T} J (A+E)-J. $$

Since A is symplectic, we get A^TJA − J = 0, hence F = A^TJE + E^TJA + E^TJE. Taking norms we obtain

$$ {\Delta} (\hat{A})=\Vert{F}\Vert_{2} \leq 2 \Vert{A}\Vert_{2} \Vert{E}\Vert_{2} + {\Vert{E}\Vert_{2}}^{2}. $$

Applying (17) yields

$$ {\Delta} (\hat{A}) \leq \Vert{A}\Vert_{2}^{2} \left( 2 \epsilon+\epsilon^{2}\right). $$

(20)

From (17) we deduce that $\Vert {\hat {A}}\Vert _{2}=\Vert {A}\Vert _{2} (1+\beta )$, where ∣β∣ ≤ 𝜖. This together with (17) and (20) gives

$$ {\Delta} (\hat{A}) \leq \Vert{\hat{A}}\Vert_{2}^{2} \frac{\left( 2 \epsilon+\epsilon^{2}\right)}{(1-\epsilon)^{2}}, $$

which completes the proof. □

According to (18) we introduce the loss of symplecticity (relative error) of nonzero matrix $A \in \mathbb {R}^{2n \times 2n}$ as

$$ sympA = \frac{\left\Vert{A^{T}JA-J}\right\Vert_{2}}{\Vert{A}\Vert_{2}^{2}}. $$

(21)

Remark 2

Assume that A is symplectic. Then we have A^TJA = J, so taking norms we obtain

$$ 1=\Vert{J}\Vert_{2} \leq \Vert{A^{T}}\Vert_{2} \Vert{J}\Vert_{2} \Vert{A}\Vert_{2} ={\Vert{A}\Vert_{2}}^{2}. $$

We see that ∥A∥₂ ≥ 1 for every symplectic matrix A. Therefore, under the hypotheses of Lemma 10 and applying (19) we get the inequality

$$ {\Delta} (\hat{A}) \ge (1-\epsilon)^{2} {\Vert{A}\Vert_{2}}^{2} symp {\hat{A}}. $$

(22)

If ∥A∥₂ is large and $\hat {A}$ is close to A, then $symp {\hat {A}} << {\Delta } (\hat {A})$. This property is highlighted in our numerical experiments in Section 4.

Proposition 11

Let $\tilde {L} \in \mathbb {R}^{2n \times 2n}$ be the computed factor of the symplectic factorization A = LL^T, where $A \in \mathbb {R}^{2n \times 2n}$ is a symmetric positive definite symplectic matrix.

Define

$$ F={\tilde{L}}^{T} J \tilde{L} - J. $$

(23)

Partition $\tilde {L}$ and F conformally with J as

$$ \tilde{L}=\left( \begin{array}{cc} \tilde{L}_{11} & 0 \\ \tilde{L}_{21} & \tilde{L}_{22} \end{array} \right), \quad F=\left( \begin{array}{cc} F_{11} & F_{12} \\ F_{21} & F_{22} \end{array} \right). $$

(24)

Then $F_{21}=-{F_{12}}^{T}$, F₂₂ = 0 and

$$ F_{11}= {\tilde{L}_{11}}^{T} \tilde{L}_{21}-{\tilde{L}_{21}}^{T} \tilde{L}_{11}, \quad F_{12}={\tilde{L}_{11}}^{T} \tilde{L}_{22}-I_{n}. $$

(25)

Moreover, the loss of symplecticity ${\Delta } (\tilde {L})$ can be bounded as follows

$$ \max \left\{\Vert{F_{11}\Vert_{2}}, \Vert{F_{12}}\Vert_{2} \right\} \leq {\Delta} (\tilde{L}) \leq 2 \max \left\{\Vert{F_{11}}\Vert_{2}, \Vert{F_{12}}\Vert_{2}\right\}. $$

(26)

Proof

It is easy to check that F is a skew-symmetric matrix satisfying (25), with F₂₂ = 0. Notice that ${\Delta } (\tilde {L})= \Vert {F}\Vert _{2}$. It remains to prove (26).

Write F in a form F = F₁ + F₂, where

$$ F_{1}=\left( \begin{array}{cc} F_{11} & 0 \\ 0 & 0 \end{array} \right), \quad F_{2}=\left( \begin{array}{cc} 0 & F_{12} \\ -{F_{12}}^{T} & 0 \end{array} \right). $$

It is obvious that ∥F₁∥₂ = ∥F₁₁∥₂ and ∥F₂∥₂ = ∥F₁₂∥₂, so

$$ \Vert{F}\Vert_{2} \leq \Vert{F_{1}}\Vert_{2}+\Vert{F_{2}}\Vert_{2} \leq 2 \max \{\Vert{F_{1}}\Vert_{2}, \Vert{F_{2}}\Vert_{2}\}. $$

. By property of 2-norm, it follows that ∥F_ij∥₂ ≤∥F∥₂ for all i,j = 1,2.

This completes the proof. □

Remark 3

If Algorithm W₁ runs to completion in floating-point arithmetic, then $\tilde {L}_{22}={\tilde {L}_{11}}^{-T} + \mathcal {O}(\varepsilon _{M})$, where ε_M is machine precision. See [5], pp. 263–264, where the detailed error analysis of methods for inverting triangular matrix was given. Notice that ∥F₁₂∥₂ defined by (25) depends only on conditioning of A₁₁, the submatrix of A. Since A is symmetric positive definite it follows that κ₂(A₁₁) ≤ κ₂(A). However, the loss of symplecticity of $\tilde {L}$ from Algorithm W₂ can be much larger than for Algorithm W₁, see our examples presented in Section 4.

Notice that F₁₁ defined by (25) remains the same for both Algorithms W₁ and W₂.

Now we explain what we mean by numerical stability of algorithms for computing LL^T factorization.

The precise definition is the following.

Definition 2

An algorithm W for computing the LL^T factorization of a given symmetric positive definite matrix $A \in \mathbb {R}^{2n \times 2n}$ is numerically stable, if the computed matrix $\tilde {L} \in \mathbb {R}^{2n \times 2n}$, partitioned as in (24), is the exact factor of the LL^T factorization of a slightly perturbed matrix A + δA, with ∥δA∥₂ ≤ ε_Mc∥A∥₂, where c is a small constant depending upon n, and ε_M is machine precision.

In practice, we can compute the decomposition error

$$ {dec}= \frac{\left\Vert{A-\tilde{L} {\tilde{L}}^{T}}\right\Vert_{2}}{\Vert{A}\Vert_{2}}. $$

(27)

If dec is of order ε_M then this is the best result we can achieve in floating-point arithmetic. We emphasize that here we apply numerically stable Cholesky decomposition of symmetric positive definite matrix A₁₁ (see Theorem 10.3 in [5], p. 197), and also numerically stable Reverse Cholesky decomposition of the Schur complement S (defined by (6)) applied in Algorithm W₂. Notice that Lemma 5 implies that κ₂(S) = κ₂(A₁₁). For general symmetric positive definite matrix A we have a weaker bound: κ₂(S) ≤ κ₂(A), see [2].

4 Numerical experiments

In this section we present numerical tests that show the comparison of Algorithms W₁ and W₂. All tests were performed in MATLAB ver. R2021a, with machine precision ε_M ≈ 2.2 ⋅ 10^− 16.

We report the following statistics:

• Δ(A) = ∥A^TJA − J∥₂ (loss of symplecticity (absolute error) of A),

• ${sympA}= \frac {\Vert {A^{T}JA-J}\Vert _{2}}{\Vert {A}\Vert _{2}^{2}}$ (loss of symplecticity (relative error) of A),

• ${dec}_{Algorithm}= \frac {\Vert {A-\tilde {L} {\tilde {L}}^{T}}\Vert _{2}}{\Vert {A}\Vert _{2}}$ (decomposition error),

• ${\Delta L}_{Algorithm}= \Vert {\tilde {L}^{T}J \tilde {L}-J}\Vert _{2}$ (loss of symplecticity (absolute error) of $\tilde {L}$),

• ${sympL}_{Algorithm}= \frac {\Vert {{\tilde {L}}^{T}J\tilde {L}-J}\Vert _{2}}{\Vert {\tilde {L}}\Vert _{2}^{2}}$ (loss of symplecticity (relative error) of $\tilde {L}$),

• ∥F₁₁∥₂ and ∥F₁₂∥₂ defined by (23)–(25).

Example 1

In the first experiment we take A = S^TS, where S is a symplectic matrix, which was also used in [1] and [7]:

$$ S=S(t)=\left( \begin{array}{cccc} \cosh{t} & \sinh{t} & 0 & \sinh{t}\\ \sinh{t} & \cosh{t} & \sinh{t} & 0 \\ 0 & 0 & \cosh{t} & - \sinh{t} \\ 0 & 0 & -\sinh{t} & \cosh{t} \end{array} \right), \quad t \in \mathbb{R}. $$

(28)

The results are contained in Table 1. We see that Algorithm W₁ produces unstable result $\tilde {L}$, opposite to Algorithm W₂.

Table 1 The results for Example 1 and A = S^TS, where S is defined by (28)

Example 2

For comparison, in the second experiment we use the same matrix S and repeat the calculations for the inverse of A from Example 1. Since κ₂(A^− 1) = κ₂(A), we see that the condition numbers of A is the same in both Examples 1 and 2. However, here A₁₁ is perfectly well-conditioned, opposite to the previous Example 1. The results are contained in Table 2. Now Algorithm W₁ produces numerically stable result $\tilde {L}$, like Algorithm W₂. We observe that for large values of ΔA (in the last columns of Tables 1 and 2) the loss of symplecticity of computed $\tilde {L}$ is significant.

Table 2 The results for Example 2 and A = (S^TS)^− 1, where S is defined by (28)

Example 3

Here A(10 × 10) is generated as follows

Random matrices of entries are from the distribution N(0,1). They were generated by MATLAB function “randn”. Before each usage the random number generator was reset to its initial state.

Here we use Lemmas 2–3 to create the following MATLAB functions:

• function for generating orthogonal symplectic matrix Q(2n × 2n):

  

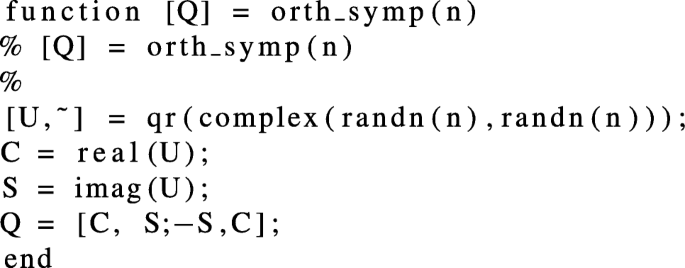
• and function for generating symmetric positive definite symplectic matrix S(2n × 2n) with prescribed condition number κ₂(S) = 10^2s

  

The results are contained in Table 3. However, the results of ∥F₁₂∥₂ from Algorithm W₂ are catastrophic in comparison with the values received from Algorithm W₁. Here A₁₁ is quite well-conditioned, but the departure of A from symplecticity conditions is very large.

Table 3 The results for Example 3

Example 4

Now we apply Lemma 4 for creating our test matrices. We take A = PDP^T, where

$$ P=\left( \begin{array}{cc} I_{n} & 0 \\ C & I_{n} \end{array} \right), \quad D=\left( \begin{array}{cc} \mathcal{B} & 0 \\ 0 & \mathcal{B}^{-1} \end{array} \right), $$

where C is the Hilbert matrix and ${\mathscr{B}}$ is beta matrix.

Here ${\mathscr{B}}=\left (\frac {1}{\beta (i,j)}\right )$, where β(⋅,⋅) is the β function.

By definition,

$$ \beta(i,j)=\frac{\Gamma(i){\Gamma}(j)}{\Gamma(i+j)}, $$

where Γ(⋅) is the Gamma function.

${\mathscr{B}}$ is symmetric totally positive matrix of integer. More detailed information related to beta matrix can be found in [4] and [6].

Note that generating A requires computing the inverse of the ill-conditioned Hilbert matrix. It influences significantly on the quality of computed results in floating-point arithmetic.

The results are contained in Table 4.

Table 4 The results for Example 4

Example 5

The matrices A(2n × 2n) are generated for n = 2 : 2 : 250 by the following MATLAB code:

We applied Lemma 3 for creating matrices of the form A = UGU^T, where G is a diagonal matrix, and U is an orthogonal symplectic matrix, generated by the same MATLAB function as in Example 3.

Figures 1, 2 and 3 illustrate the values of the statistics. We can see the differences between decomposition errors dec (in favor of Algorithm W₂) and between the values ΔL, in favor of Algorithm W₁.

Fig. 1

Condition numbers κ₂(A) and decomposition errors for Example 5

Fig. 2

The loss of symplecticity (relative errors) for Example 5

Fig. 3

The loss of symplecticity (absolute errors) for Example 5

5 Conclusions

• We analyzed two algorithms W₁ and W₂ for computing the symplectic LL^T factorization of a given symmetric positive definite matrix A(2n × 2n). To assess their practical behavior we performed numerical experiments.

• Algorithm W₁ is cheaper than Algorithm W₂. However, Algorithm W₁ is unstable for matrices not being exactly symplectic, although it works very well for many test matrices. The decomposition error (27) of the computed matrix $\tilde {L}$ via Algorithm W₁ can be very large. In opposite, in all our tests, Algorithm W₂ produces numerically stable resulting matrices $\tilde {L}$ in floating-point arithmetic (in sense of Definition 2). Numerical stability of Algorithms W₁ and W₂ remains a topic of future work.

• Numerical tests presented in Section 4 give indication that the loss of symplecticity of the computed matrix $\tilde {L}$ from Algorithm W₂ can be much larger than obtained from Algorithm W₁. We observe that the loss of symplecticity of $\tilde {L}$ for both Algorithms W₁ and W₂ strongly depends on the distance from the symplecticity properties (see Lemma 5), and also on conditioning of A and its submatrix A₁₁.