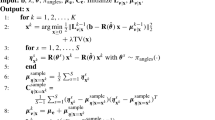Numerical methods for CT reconstruction with unknown geometry parameters

Abstract

Computed tomography (CT) techniques are well known for their ability to produce high-quality images needed for medical diagnostic purposes. Unfortunately, standard CT machines are extremely large, heavy, require careful and regular calibration, and are expensive, which can limit their availability in point-of-care situations. An alternative approach is to use portable machines, but parameters related to the geometry of these devices (e.g., distance between source and detector, orientation of source to detector) cannot always be precisely calibrated, and these parameters may change slightly when the machine is adjusted during the image acquisition process. In this work, we describe the non-linear inverse problem that models this situation, and discuss algorithms that can jointly estimate the geometry parameters and compute a reconstructed image. In particular, we propose a hybrid machine learning and block coordinate descent (ML-BCD) approach that uses an ML model to calibrate geometry parameters, and uses BCD to refine the predicted parameters and reconstruct the imaged object simultaneously. We show using numerical experiments that our new method can efficiently improve the accuracy of both the image and geometry parameters.

1 Introduction

In imaging applications, a typical inverse problem takes the form

$$ \boldsymbol A\boldsymbol x = \boldsymbol b, $$

(1)

where $\boldsymbol A\in \mathbb {R}^{M\times N}$ models the forward process, $\boldsymbol x\in \mathbb {R}^{N}$ is the image of interest, $\boldsymbol b\in \mathbb {R}^{M}$ is the observation that is usually contaminated with unknown noise $\boldsymbol \eta \in \mathbb {R}^{M}$, and b = b^ex + η. Here, b^ex = Ax^ex denotes the noise free data, and x^ex denotes the exact (true) solution. Note also that b and x are vectorized quantities of the observed data B and the solution image $\boldsymbol X\in \mathbb {R}^{n\times n}$, where N = n². It is typically assumed (see, e.g., [1,2,3]) that the forward model A is known exactly. In the image deblurring application, the forward model A is constructed using a point spread function (PSF), which can be formulated based on knowledge of the physical process, and can be obtained using a precise mathematical expression or through experimentation [4]. In imaging applications arising from computed tomography (CT), the matrix A models the Radon Transform [5] that outputs the projection data obtained from a tomographic scan. For CT, the observed data is a so-called “sinogram”, which stores the projection data.

Large-scale linear systems arising from inverse problems are usually very ill-conditioned, meaning that there might not be a unique solution, and a slight change in the data b can lead to a large change in the solution x. Hence, regularization is often needed in order to obtain a meaningful solution. Direct regularization methods add a penalty term to the least squares formulation of (1), i.e., $\min \limits _{\boldsymbol x} \|\boldsymbol A\boldsymbol x-\boldsymbol b\|_{2}^{2}$, so that we solve instead

$$ \min_{\boldsymbol x} \|\boldsymbol A\boldsymbol x - \boldsymbol b\|_{2}^{2} + \lambda\mathcal{R}(\boldsymbol x), $$

(2)

where λ > 0 is a regularization parameter, and $\mathcal {R}(\boldsymbol x)$ is a regularization term defined as a function of x (e.g., a vector norm). Popular choices for $\mathcal {R}(\boldsymbol x)$ include the ℓ₂ norm (Tikhonov regularization) and the ℓ₁ norm of x.

In this paper, we focus on a specific type of imaging inverse problem that arises from CT applications, where the forward model A is not known exactly. This scenario may arise, for example, in the diagnosis and management of infectious diseases such as Covid-19, where portable tomosynthesis machines are brought to the location of patients to help minimize the risk of cross-infection [6, 7], and more experimental errors such as inaccurate calibration of geometry parameters (e.g., source to object distance, source orientation) are introduced, making the image acquisition and reconstruction processes more challenging. Consider a fan-beam tomography set-up, in which we have a point source that emits fan beams, as can be seen in Fig. 1(a). Ideally, for each scan, the source should be of equal distance to the object and rotates a fixed angle. However, this may not be the case for portable CT machines that are subject to more experimental errors caused by machine transportation. In Fig. 1(b), the theoretical location of the center scanning position is shown in light green, but during the scanning process it may be shifted to the dark green location.

Fig. 1

Tomography illustration

Due to these uncertainties, forward models that describe the forward process only approximate the reality to some extent, and without proper model calibration, quality of the solutions will be degraded. Using mathematical language—when working on the corresponding inverse problem, we need to take into account an additional set of unknown parameters p that the forward operator A is dependent on. That is, when reconstructing the imaged object, we also need to perform geometry parameter calibration. So instead of (2), we need to solve the following problem:

$$ \min_{\boldsymbol x, \boldsymbol p} \|\boldsymbol A(\boldsymbol p)\boldsymbol x - \boldsymbol b\|_{2}^{2} + \lambda\mathcal{R}(\boldsymbol x). $$

(3)

Recall that b is the vectorized quantity of observed data, which, in this case, is the sinogram $\boldsymbol B\in \mathbb {R}^{N_{\tau }\times N_{\theta }}$ (where N_τ is the number of beams and N_𝜃 is the number of scanning angles). The true geometry parameters p in the image requisition process are unknown, but we know p₀, which are the theoretical (i.e., guessed or incorrectly assumed) values.

For this problem, we consider two types of uncertainties in the geometry parameters: source to object distances, and scanning angles. Hence, the unknown geometry parameters $\boldsymbol p\in \mathbb {R}^{2N_{p}}$ consist of two components r and d, i.e., p = [r; d], where $\boldsymbol r\in \mathbb {R}^{N_{p}} = [r_{1};\cdots ; r_{N_{p}}]$ are source to object distances with theoretical constant value (which we assume to be 2n in our experiments), and $\boldsymbol d\in \mathbb {R}^{N_{p}} = [\delta ^{\theta }_{1}; \cdots ; \delta ^{\theta }_{N_{p}}]$ are perturbation in scanning angles with theoretical value 0. We assume that r_i ∈ [1.5n,2.5n] (n is dimension of image) and $\delta ^{\theta }_{i} \in [-0.5, 0.5]$. Note that technically, N_p could be equal to the total number of scanning angles and can be as large as 180 or 360. For simplification purposes, we start by choosing N_p much smaller than the total number of scanning angles (e.g., N_p = 3 or N_p = 6). For instance, if we use N_𝜃 = 180 scanning angles 0:2:359 and N_p = 3, then $\boldsymbol p\in \mathbb {R}^{6}$, $\boldsymbol r,\ \boldsymbol d\in \mathbb {R}^{3}$, and $(r_{i}, \delta ^{\theta }_{i})$ would be constant for a set of 180/N_p = 60 angles.

A lot of work has been done in various applications, such as scanning position error correction for image reconstruction in the fields of electron tomography [8, 9] and ptychography [10, 11], addressing the importance of accurate system modeling. In the field of X-ray tomography, scientists at Argonne National Laboratory have developed algorithms to calibrate the center of rotation errors [12] using numerical optimization, and drifts in scanning positions [13] using targeted calibration models. In the application where uncertain view angles need to be estimated for computed tomography in addition to image reconstruction, approaches such as uncertainty quantification have been proposed, and they seek to quantify scanning angles via a model-discrepancy formulation [14, 15]. Though very different from each other in nature, many of these methods share a similar framework called the block coordinate descent (BCD), which alternatively optimizes for the unknown parameters p and the image of interest x; see Algorithm 1. While the minimization step with respect to x (step 3 of Algorithm 1) is linear, the optimization with respect to p (step 4 of Algorithm 1) is non-linear, because A depends non-linearly on p. Note that sometimes Algorithm 1 is also referred to as alternating minimization.

Algorithm 1

Block coordinate descent.

We make the remark that Algorithm 1 should be regarded as a generic framework for solving (3). In the linear optimization step (step 3), the regularization parameter λ_k can be chosen of as a fixed parameter for the linear solver in iteration k of BCD, or as an adaptively selected sequence of λ_k,i, i = 0, 1, 2,⋯ for each iteration i in the linear solver. Methods for adaptively setting regularization parameters include, e.g., weighted generalized cross validation [16] and discrepancy principle [17, 18]. We also remark that because we do not have an analytical expression for A(p), we cannot provide any theoretical results on convergence of the non-linear least squares problem in step 4 of Algorithm 1. We can, however, note that the Jacobian is an M × 2N_p matrix, with M = N_τ ⋅ N_𝜃 ≫ 2N_p, and in all of our numerical experiments, we observed the Jacobian to always be full rank and well-conditioned. This situation improves further when exploiting separability, as discussed in Section 2.1.

The non-linear optimization step (step 4) in Algorithm 1 is usually very expensive, and depends heavily on the initial guess. Hence, if p₀ is far from the true p, the accuracy of results given by the non-linear step, and BCD as a whole may be sacrificed. In this paper, we present a hybrid machine learning and block coordinate descent method (ML-BCD), which incorporates a machine learning model $\widehat {\Phi }$ that maps b to p. When given an observation b, we first use the ML model to make a prediction for p, which is then fed into the BCD algorithm as an initial guess. Through this approach, we are able to improve the accuracy of both the calibrated geometry parameters and the reconstructed image when compared to using BCD or ML alone.

This paper is organized as follows. In Section 2, we go over the baseline block coordinate descent method (BCD) and discuss how to make it run more efficiently for our problem (3). We also present the baseline machine learning (ML) model for learning geometry parameters. In Section 3, we introduce the new, machine learning - block coordinate descent (ML-BCD) hybrid algorithm that combines ML with BCD, and describe the training of the ML model. Numerical experiments are presented in Section 4. We finish off with some conclusions and future work directions in Section 5.

2 Background

2.1 Block coordinate descent

Recall that block coordinate descent (BCD) is a numerical algorithm that alternatively optimizes with respect to different subsets of the unknown variable. Hence, it can be used to alternatively solve for x and p in Problem (3). The idea is simple: for the unknowns x and p, we can fix one and solve for the other, and repeat this process multiple times. The algorithm is summarized in Algorithm 1 in Section 1.

The linear steps 2 and 6 of Algorithm 1 can be solved with a linear inverse problem solver such as LSQR. But for the model update step (step 4), since A depends non-linearly on p, we need to use a non-linear solver such as Gauss-Newton based imfil [19], and this non-linear step can be expensive for large values of N_p. Note that for this step, we can actually reduce problem size by exploiting separability of A(p). That is, the minimization problem in step 4 of Algorithm 1 can be equivalently written as

$$ \min_{\boldsymbol p} \left\lVert \left[ \begin{array}{c} \boldsymbol A(p_{1}) \\ \boldsymbol A(p_{2})\\ {\vdots} \\ \boldsymbol A(p_{N_{p}}) \end{array} \right]\boldsymbol x - \left[ \begin{array}{c} \boldsymbol b_{1} \\ \boldsymbol b_{2} \\ {\vdots} \\ \boldsymbol b_{N_{p}} \end{array} \right] \right\rVert^{2} = {\sum}_{i=1}^{N_{p}} \min_{p_{i}}\|\boldsymbol A(p_{i})\boldsymbol x - \boldsymbol b_{i}\|^{2}. $$

(4)

By doing so, we divide the big non-linear problem into N_p small problems, which can be solved in parallel. The resulting algorithm is summarized in Algorithm 2.

Algorithm 2

Block coordinate descent—separable non-linear step.

The separability property works very well with our proposed BCD framework, but other approaches such as variable projection [20, 21] would not be able to utilize this nice property. On the other hand, the non-linear solver can depend heavily on the initial guess, and may converge to a local minimum rather than the global minimum, which affects all subsequent x_k’s and p_k’s. Hence, although we can conveniently define p₀ as the theoretical value for p, it might be worthwhile to look for other ways of defining p₀ that allows for better convergence of the overall BCD solver.

2.2 Machine learning

Since the non-linear optimization step is very costly and takes a long time to run, it would be even better if we can find a way to avoid running this step. Inspired by [22], which trains neural networks to learn regularization parameters for inverse problems, we are interested in building machine learning models to learn the unknown CT geometry parameters. In other words, by training a machine learning model $\widehat {\boldsymbol {\Phi }}:\boldsymbol b\to \boldsymbol p$ that maps sinogram b to geometry parameters p, we may be able to avoid running the alternating minimization scheme. And as a result, we only need to run one linear step to solve for x. This framework is summarized in Algorithm 3.

Algorithm 3

Learning geometry parameters.

To train the model $\widehat {\boldsymbol {\Phi }}:\boldsymbol b\to \boldsymbol p$, we need the following training data:

• $\widehat {\boldsymbol B}\in \mathbb {R}^{J\times M}$ is (feature) matrix with J rows. Each row is a vectorized sinogram b_j of length M, constructed using random r_j and $\boldsymbol \delta ^{\theta }_{j}$, with superimposed Gaussian noise, i.e., $\boldsymbol b_{j} = \boldsymbol A(\boldsymbol r_{j}, \boldsymbol \delta ^{\theta }_{j}){\boldsymbol x}^{\textrm {{ex}}}_{j}+\boldsymbol \eta _{j}$, with ${\boldsymbol x}^{\textrm {{ex}}}_{j}$ the true phantom and η_j the random noise vector.

• $\boldsymbol R,\boldsymbol D\in \mathbb {R}^{J\times N_{p}}$ are matrices of true geometry parameters, with rows r_j and $\boldsymbol \delta ^{\theta }_{j}$ corresponding to sinogram b_j.

One important consideration during the training phase is choosing the phantom images ${\boldsymbol x}^{\textrm {{ex}}}_{j}$. If we fix ${\boldsymbol x}^{\textrm {{ex}}}_{j}$ to be a constant phantom image for all j, then we would expect that the trained model only works well for the phantom that the model is trained on. In other words, the model would be best at predicting CT geometry parameters when the phantom being reconstructed is the same phantom that the training data is built upon, and may not generalize well to other phantoms. Since in a real-world CT reconstruction problem, we do not know what the phantom is, using a model that is trained upon a fixed phantom may not render good solutions.

However, if we use different phantoms ${\boldsymbol x}^{\textrm {{ex}}}_{j}$’s when generating the training data, the model may become confused due to the problem of non-uniqueness. It is possible that there exist (p₁,x₁), (p₂,x₂) with p₁≠p₂ and x₁≠x₂, such that A(p₁)x₁ = A(p₂)x₂ = b. This means that the mapping $\widehat {\boldsymbol {\Phi }}:\boldsymbol b\to \boldsymbol p$ may not be one-to-one. Therefore, the model may predict parameters p that are very far from the true value, thus rendering far-from-true solution x in Algorithm 3. Disturbance-based strategies have been used in applications like Power Systems [23, 24] to help with non-uniqueness. If we translate this strategy into our context, we may apply “disturbances,” i.e., different phantoms and different noise levels to generate many training samples that correspond to the same set of geometry parameters p. That is, for each p, we generate l training samples b_i = A(p)x_i + η_i for i = 1,⋯ ,l using l different phantoms and noise levels. We will see how the disturbance-based strategy performs in Section 4.

3 Method

In this section, we describe a hybrid method that combines machine learning with block coordinate descent for solving (3). We will also explain technical details for training the machine learning model.

We have mentioned previously that the machine learning problem of learning geometry parameters when the phantom ${\boldsymbol x}^{\textrm {{ex}}}_{j}$ is not fixed in the training data may suffer from non-uniqueness. Although in our experience, using Algorithm 3 with an ML model trained using non-fixed ${\boldsymbol x}^{\textrm {{ex}}}_{j}$’s does not deliver solutions that are too far from the true images, we do notice that relative errors in the predicted parameters on the testing set have increased compared to the case with a fixed ${\boldsymbol x}^{\textrm {{ex}}}_{j}$, but the relative errors are still very low compared to the theoretical values (more on this in Section 4).

One natural approach that comes to mind is using a hybrid method that combines a machine learning model and BCD. That is, we may first use the trained ML model to predict p, then feed the predicted p as a starting guess to the BCD algorithm to run a few iterations to refine the solution. This hybrid framework is described in Algorithm 4.

Algorithm 4

ML-BCD hybrid framework.

While there are many machine learning models to choose from, we consider one of the simplest models—a multi-output linear regression model, which can also be thought of as a one-layer neural network. This ML model assumes a linear relationship between input and output, and for simplicity, we take a zero bias term. To build this model, we learn weights $\boldsymbol W\in \mathbb {R}^{M\times 2N_{p}}$ by solving the least squares problem

$$ \min_{\boldsymbol W} \|\widehat{\boldsymbol B}\boldsymbol W - [\boldsymbol R\ \boldsymbol D] \|_{F}^{2}. $$

(5)

Then, given new data $\boldsymbol b_{j^{\prime }}\in \mathbb {R}^{M}$, we simply need to compute

$$ \boldsymbol p_{j^{\prime}}=[\boldsymbol r_{j^{\prime}}; \boldsymbol \delta^{\theta}_{j^{\prime}}] = \boldsymbol b_{j^{\prime}}^{T} \boldsymbol W $$

(6)

to obtain the predicted geometry parameters. To further explain why (6) makes sense, we consider a simplified case where there is only one unknown geometry parameter r. In this case, we look for weights w = [w₁;⋯ ;w_M] (here w is a vector instead of a matrix because there is only one unknown geometry parameter) to build a single-output linear regression model $\widehat {\Phi } (\boldsymbol b) = {\sum }_{m=1}^{M} b_{m} w_{m} = \boldsymbol b^{T}\boldsymbol w = r$. When generalizing to multiple unknown geometry parameters, we need to seek weight matrix $\boldsymbol W\in \mathbb {R}^{M\times 2N_{p}}$ in order to map b to $\boldsymbol p = [\boldsymbol r;\ \boldsymbol \delta ^{\theta }] \in \mathbb {R}^{2N_{p}}$, which can be done by taking the inner product of b and W. The predicted geometry parameters p can then be fed as initial guess p₀ into the BCD algorithm.

We have chosen the loss function to be $\|\cdot \|_{F}^{2}$, which makes the minimization problem separable (similar to the non-linear step of BCD). Since $\boldsymbol R = [\widehat {\boldsymbol r}_{1} {\cdots } \widehat {\boldsymbol r}_{N_{p}}]$ with column vectors $\widehat {\boldsymbol r}_{i}$, and $\boldsymbol D = \widehat {\boldsymbol d}_{1} {\cdots } \widehat {\boldsymbol d}_{N_{p}}]$ with column vectors $\widehat {\boldsymbol d}_{i}$, (5) is equivalent to

$$ {\sum}_{i=1}^{N_{p}} \min_{\widehat{\boldsymbol w}_{r,i}\in\mathbb{R}^{M}} \|\widehat{\boldsymbol B}\widehat{\boldsymbol w}_{r,i} - \widehat{\boldsymbol r}_{i}\|_{2}^{2} + {\sum}_{i=1}^{N_{p}} \min_{\widehat{\boldsymbol w}_{d,i}\in\mathbb{R}^{M}} \|\widehat{\boldsymbol B}\widehat{\boldsymbol w}_{d,i} - \widehat{\boldsymbol d}_{i}\|_{2}^{2}, $$

(7)

where $\widehat {\boldsymbol w}_{r,i}$ and $\widehat {\boldsymbol w}_{d,i}$ are column vectors of W_R and W_D such that $\boldsymbol W_{R} = [\widehat {\boldsymbol w}_{r,1} {\cdots } \widehat {\boldsymbol w}_{r,N_{p}}]$, $\boldsymbol W_{D} = [\widehat {\boldsymbol w}_{d,1} {\cdots } \widehat {\boldsymbol w}_{d,N_{p}}]$, and W = [W_R W_D]. The sub-problems $\min \limits _{\widehat {\boldsymbol w}_{r,i}} \|\widehat {\boldsymbol B}\widehat {\boldsymbol w}_{r,i} - \widehat {\boldsymbol r}_{i}\|_{2}^{2}$ and $\min \limits _{\widehat {\boldsymbol w}_{d,i}} \|\widehat {\boldsymbol B}\widehat {\boldsymbol w}_{d,i} - \widehat {\boldsymbol d}_{i}\|_{2}^{2}$ are large and non-square linear systems, and we need to use an iterative solver such as standard LSQR to solve each of them. Algorithm 5 contains more detailed description of the hybrid method.

Algorithm 5

ML-BCD hybrid algorithm.

4 Numerical experiments

In this section, we present several numerical experiments comparing performances of Algorithms 1, 3, and 5. We have used the PRtomo function of IR Tools [25] to generate all training data in this section. The linear solver used is IRhybrid_lsqr from IRTools and the non-linear solver is imfil [19]. We have used the default configurations of IRhybrid_lsqr whenever we run the linear solve, i.e., we take the Tikhonov regularization term $\mathcal {R}(\boldsymbol x) = \|\boldsymbol x\|_{2}^{2}$ and use weighted GCV to adaptively select regularization parameters. The stopping criterion is when the GCV function stabilizes or starts to increase (see [25] Sect. 2.5 for details). For the non-linear solver imfil, we have set the budget, i.e., the maximum number of function evaluations in Gauss-Newton, to be 50. We have also fixed the number of BCD iterations to be 10, and always report the reconstruction at the 10th BCD iteration unless otherwise stated.

Test 1: 64 by 64 fixed phantom problem with N _p = 3

We first consider a 64 × 64 fixed Shepp-Logan phantom (see Fig. 2) as ${\boldsymbol x}^{\textrm {{ex}}}_{j}\ \forall j$ when generating the training data. We use 180 scanning angles, i.e., 0:2:359 and N_p = 3, so there are 6 unknown geometry parameters in total: 3 r_i’s and 3 $\delta ^{\theta }_{i}$’s, with each pair of $(r_{i}, \delta ^{\theta }_{i})$ corresponding to 60 adjacent scanning angles. As a result, each $\boldsymbol b_{j}\in \mathbb {R}^{16380}$, so $\widehat {\boldsymbol B}\in \mathbb {R}^{J\times 16380}$, R and $\boldsymbol D\in \mathbb {R}^{16380\times 3}$. Random white noise with fixed noise level 0.01 is superimposed onto each b_j.

Fig. 2

64 by 64 exact phantom

We have generated training data $\widehat {\boldsymbol B}$, R and D with J = 20000 training samples, and an additional testing set $\widehat {\boldsymbol B}_{\text {\small test}}$, R_test, and D_test of 2000 samples. We train ML model weights using the method described in Section 3, i.e., computing weight matrix W = [W_R W_D] by solving every subproblem of (7). We train weights W using training sets of different sizes: 2000, 4000, 6000,⋯ , 20000, compute the predicted geometry parameters

$$\boldsymbol R_{\text{\small pred}} = \widehat{\boldsymbol B}_{\text{\small test}}\boldsymbol W_{R} \quad \text{and}\quad \boldsymbol D_{\text{\small pred}} = \widehat{\boldsymbol B}_{\text{\small test}}\boldsymbol W_{D},$$

and evaluate testing errors

$$\frac{\|\boldsymbol R_{\text{\small pred}}-\boldsymbol R_{\text{\small test}}\|_{F}}{\|\boldsymbol R_{\text{\small test}}\|_{F}} \quad\text{and}\quad \frac{\|\boldsymbol D_{\text{\small pred}}-\boldsymbol D_{\text{\small test}}\|_{F}}{\|\boldsymbol D_{\text{\small test}}\|_{F}}$$

on the testing set of 2000 samples. We plot testing errors against training set size in Fig. 3.

Fig. 3

Relative errors in R_pred (left) and D_pred (right) on testing set

We can observe that as the training set size increases, relative error in the predicted geometry parameters decreases. This is because as the training set becomes larger, it covers more variations in the different combinations of geometry parameters, which makes predictions more accurate. Also, the relative errors in R_pred and D_pred are very different in magnitude, meaning that it is much easier to predict r parameters more accurately.

Figure 4 shows solutions using theoretical parameters, true parameters, ML-predicted parameters (Algorithm 3), and BCD (Algorithm 1). The ML model weights are trained on a training set of size 20000. We can observe in Fig. 4 that if we leave the geometry parameters uncalibrated, the solution images will have very poor quality. If we use the BCD scheme (Algorithm 1), the reconstruction quality seems to have improved, but the solutions are still fuzzy and unclear. Using Algorithm 3 to predict geometry parameters using learned ML model weights, we obtain highly accurate solutions, resembling solutions computed using the true parameters (which represents the case of perfect calibration).

Fig. 4

Phantom reconstructions of 3 testing samples that share the same underlying phantom with training set (1 testing sample per row). 1st column: solutions using theoretical parameters (i.e., uncalibrated). 2nd column: solutions using true parameters (i.e., perfect calibration). 3rd column: solutions using ML-predicted parameters (Algorithm 3). 4th column: solutions using 10 BCD iterations (Algorithm 1)

The model weights trained in this test are based on training data generated with the same phantom. Therefore, if the solution image we are looking for is different from the phantom that the weights are trained on, then the ML model may not generalize well. As we observe in Fig. 5, the test samples have different underlying phantoms (different from what is in the training data). As a result, Algorithm 3 no longer yields accurate solutions, and no longer has an advantage over BCD.

Fig. 5

Phantom reconstructions of 2 testing samples that have different underlying phantom than training set (1 testing sample per row). Column order same as Fig. 4

Test 2: testing disturbances

While we want to train models that generalize well to different phantoms, the problem of non-uniqueness may affect the training of machine learning models. In this test, we explore the effect of disturbances by generating the training data using different phantoms ${\boldsymbol x}^{\textrm {{ex}}}_{j}$’s. Examples of such phantoms used are shown in Fig. 6. It can be seen that each phantom is created by altering the original phantom by randomly removing ellipses and slightly varying ellipse sizes and angles. Random noise of noise level chosen randomly in the range 0.1 to 2% is superimposed to each sample.

Fig. 6

Examples of different phantoms used

Two training sets are created. We apply the disturbance strategy in the first training set by generating 5 different phantoms and noise levels for each p_j, with 7000 p_j’s in total, i.e., there are 35000 samples in the dataset. As a frame of reference, we compare results given by another training set of the same size, but without disturbances. That is, 35000 samples each with a different p_j, phantom and noise level.

We use these two training sets and subsets of the data sets to train ML model weights. We compare the relative errors of the ML-predicted p for the testing set consisting of 1000 samples (generated with different samples in the same way as illustrated in Fig. 6). In Fig. 7, we show convergence of relative errors in the geometry parameters R_pred and D_pred predicted by ML models trained using 5000:5000:35000 samples of the two data sets. Note that, for example, with the training set size 15000, one training set consists of 3000 p_j’s each having 5 disturbances (i.e., phantoms and noise levels), the other training set has 15000 p_j’s (each having their own phantom and noise level). We also notice that when the model is trained on training data generated using different phantoms, the relative errors in the geometry parameters are around 10 times larger than the relative errors presented in Test 1 due to the variance of phantoms.

Fig. 7

Relative errors in R_pred and D_pred on testing set

We see in Fig. 7 that the relative errors decrease for both training sets as training set size increases. If we compare the relative errors vertically, we can see that the errors are not so different for the two training sets. The slight difference may be caused by randomness in generating the two sets. We believe it is only fair to compare results using training sets of the same size, since, for example, if we compare results given by one training set of 5000 samples with results given by another training set of 5000 samples each with 5 disturbances, the decrease in relative errors may be caused by the increased training set size, not disturbance. Therefore, given the results in this test, it is hard to conclude that disturbances help improve accuracy in the predicted geometry parameters.

Test 3: 128 by 238 varying phantom problem with N _p = 6

We have observed in Tests 1 and 2 that errors in the predicted geometry parameters would increase if the ML model is not trained and tested on the same phantom images. We have also seen that, in this case, although errors in δ^𝜃 are quite large, relative errors in r are still relatively low.

In this test, we focus on the case where phantoms vary across training and testing samples. We increase phantom size to n = 128 and number of geometry parameters to N_p = 6. Hence, with 180 scanning angles 0:2:358, each pair of $(r_{i}, \delta ^{\theta }_{i})$ will be constant for 30 adjacent angles. We compare solutions using the BCD (Algorithm 1), ML (Algorithm 3) and ML-BCD hybrid (Algorithm 5) methods. The ML weights are trained using the 40000 training samples. We evaluate the ML-BCD hybrid method and BCD method (each with 10 iterations) on a testing set of 100 samples, calculate the relative errors in x_k, r_k and $\boldsymbol \delta ^{\theta }_{i}$ for each BCD iteration k, and generate the histograms in Fig. 8.

Fig. 8

1st row: BCD iteration number with the minimum relative error. 2nd row: minimum relative error across all iterations. 3rd row: relative error at the 10th BCD iteration

In the first row of Fig. 8, frequencies of the iteration at which the minimum error occurs are plotted. Note that iteration 0 represents the initial guess, i.e., for BCD, this would be the uncalibrated solution; and for ML-BCD hybrid, this would be obtained directly from using ML-predicted parameters without further refining with BCD. We can draw the conclusion that the hybrid method has better convergence properties for x, where for nearly 40% of testing samples, BCD reaches the minimum relative error of x in the last iteration. While for BCD, in more than 50% of testing samples, the minimum relative error in x is either reached at the initial guess or the first iteration, which means that BCD is not very effective at improving solution accuracy. This is further confirmed in the distribution of relative errors in the second and third rows of Fig. 8, in which we notice that in general, the relative errors in both the solutions and the calibrated geometry parameters given by the ML-BCD hybrid method are very low compared to BCD.

In Fig. 9, we display solutions of 3 test samples using different methods: ML-only (Algorithm 3), ML-BCD hybrid (Algorithm 5), and BCD-only (Algorithm 1) (solutions at the last BCD iteration are shown). As a point of reference, we also present the solutions obtained using the true parameters to showcase the best solution possible. The 3 test samples are randomly picked from the 100 testing samples, and we see that for 2 out of 3, the BCD refinement step of the hybrid method has improved solution accuracy over using ML alone, and for these 2 samples, the hybrid solutions have significantly higher accuracy compared to the BCD solutions. For the first test sample, however, the BCD-refinement step of the hybrid method seems to not have improved solution accuracy. This is also expected because we have observed in the histograms of Fig. 8 that in some cases, the hybrid method may not work so well—but it is evident that ML-BCD hybrid is more advantageous over BCD on average in the tasks of parameter calibration and image reconstruction.

Fig. 9

Phantom reconstructions of 3 testing samples (1 test sample per row). 1st column: solutions using theoretical parameters (i.e., uncalibrated). 2nd column: solutions using true parameters (i.e., perfect calibration). 3rd column: solutions using ML-predicted parameters (Algorithm 3). 4th column: solutions using ML-BCD hybrid method with 10 BCD iterations (Algorithm 5). 5th column: solutions using 10 BCD iterations (Algorithm 1)

5 Conclusions

In the CT image acquisition process, geometry parameters in the forward model are prone to perturbation due to experimental errors. Hence, the forward model needs to be calibrated in order to obtain meaningful reconstructions of the imaged object. In this paper, we have proposed an enhanced, hybrid BCD framework that incorporates machine learning for solving the model calibration problem. By training a machine learning model (multi-output linear regression model) that maps the observation b to p and feeding the predicted parameters as initial guesses to BCD, we are able to improve the accuracy of both the calibrated geometry parameters and the reconstructed image.

Interesting future directions include the development of more complex machine learning models that allows for higher parameter calibration capability. For example, models that can predict N_p, i.e., the number of geometry parameters that need to be tuned, and calibrate the corresponding geometry parameters simultaneously. On the other hand, the expensive non-linear step for solving (3) calls for more efficient solvers, for which approximation methods may be developed and utilized.