On nested Picard iterative integrators for highly oscillatory second-order differential equations

Abstract

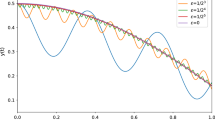
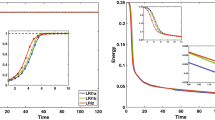
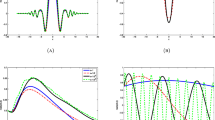
This paper is devoted to the construction and analysis of uniformly accurate (UA) nested Picard iterative integrators (NPI) for highly oscillatory second-order differential equations. The equations involve a dimensionless parameter ε ∈ (0,1], and their solutions are highly oscillatory in time with wavelength at $\boldsymbol {\mathcal {O}}(\varepsilon ^{2})$, which brings severe burdens in numerical computation when ε ≪ 1. In this work, we first propose two NPI schemes for solving a differential equation. The schemes are uniformly first- and second-order accurate for all ε ∈ (0,1]. Moreover, they are super convergent when the time-step size is smaller than ε². Then, the schemes are generalized to a system of differential equations with the same uniform accuracies. Error bounds are rigorously established and numerical results are reported to confirm the error estimates.

Appendices

Appendix 1

Define

$$ \begin{array}{@{}rcl@{}} {a_{1}^{n}} := \lvert y^{n}\rvert^{2} + \lvert \frac{\dot{y}^{n}}{\lambda}\rvert^{2}, \quad {b_{1}^{n}} := \lvert y^{n}\rvert^{2} - \lvert \frac{\dot{y}^{n}}{\lambda}\rvert^{2}, \quad {c_{1}^{n}} := \frac{\overline{y^{n}} \dot{y}^{n} + \overline{\dot{y}^{n}} y^{n}}{\lambda},\\ {A_{1}^{n}} := (2{a_{1}^{n}} + {b_{1}^{n}}) y^{n} + {c_{1}^{n}} \frac{\dot{y}^{n}}{\lambda},\qquad {B_{1}^{n}} := {b_{1}^{n}} y^{n} - {c_{1}^{n}} \frac{\dot{y}^{n}}{\lambda},\\ {C_{1}^{n}} := {c_{1}^{n}} y^{n} + (2{a_{1}^{n}} - {b_{1}^{n}}) \frac{\dot{y}^{n}}{\lambda},\qquad {D_{1}^{n}} := {c_{1}^{n}} y^{n} + {b_{1}^{n}} \frac{\dot{y}^{n}}{\lambda}. \end{array} $$

The functions used in the first-order NPI scheme (11) with (8) are:

$$ \begin{array}{@{}rcl@{}} f_{1}^{n, 1}(s) = - \frac{1}{32\varepsilon^{2}\lambda^{2}} \left( {B_{1}^{n}}-4\lambda s{C_{1}^{n}}\right), \qquad f_{3}^{n, 1}(s) = \frac{1}{32\varepsilon^{2}\lambda^{2}} {B_{1}^{n}},\\ g_{1}^{n, 1}(s) = - \frac{1}{32\varepsilon^{2}\lambda^{2}} \left( 4 \lambda s {A_{1}^{n}} + 4{C_{1}^{n}} + 3{D_{1}^{n}}\right),\qquad g_{3}^{n, 1}(s) = \frac{1}{32\varepsilon^{2}\lambda^{2}} {D_{1}^{n}}. \end{array} $$

For the second-order NPI scheme, we further define

$$ \begin{array}{@{}rcl@{}} &&{a_{2}^{n}} := (y^{n})^{2} + \left( \frac{\dot{y}^{n}}{\lambda}\right)^{2}, \quad {b_{2}^{n}} := (y^{n})^{2} - \left( \frac{\dot{y}^{n}}{\lambda}\right)^{2}, \quad {c_{2}^{n}} := \frac{2y^{n} \dot{y}^{n}}{\lambda},\\ &&{A_{2}^{n}} = \overline{{A_{1}^{n}}}, \qquad {B_{2}^{n}} = \overline{{B_{1}^{n}}}, \qquad {C_{2}^{n}} = \overline{{C_{1}^{n}}}, \qquad {D_{2}^{n}} = \overline{{D_{1}^{n}}}. \end{array} $$

The functions used in the second-order NPI scheme (12) with (10) are:

$$ \begin{array}{@{}rcl@{}} f_{k}^{n,2}(s) &=& \frac{1}{3072\varepsilon^{4}\lambda^{4}}\left( 2f_{k,1}^{n,2}(s) + f_{k, 2}^{n, 2}(s)\right),\\ g_{k}^{n,2}(s) &=& \frac{1}{3072\varepsilon^{4}\lambda^{4}}\left( 2g_{k,1}^{n,2}(s) + g_{k, 2}^{n, 2}(s)\right), \end{array} $$

for k = 1, 3, 5 with

$$ \begin{array}{@{}rcl@{}} f_{1, j}^{n, 2}(s) & =& 9 b_j^n A_j^n - 6a_j^n B_j^n + 2b_j^n B_j^n - 21 c_j^n C_j^n - 8c_j^n D_j^n \\ && \quad + 24(c_j^n A_j^n -c_j^n B_j^n - 6a_j^n C_j^n + b_j^n C_j^n - 3a_j^n D_j^n + 2b_j^n D_j^n) \lambda s\\ && \quad + 24(- 2 a_j^n A_j^n + b_j^n A_j^n + c_j^n C_j^n) \lambda^2 s^2, \\ f_{3, j}^{n, 2}(s) & =& -9b_j^n A_j^n + 6a_j^n B_j^n - 3b_j^n B_j^n + 21c_j^n C_j^n + 9c_j^n D_j^n\\ && \quad + 12(c_j^n A_j^n + b_j^n C_j^n)\lambda s,\\ f_{5, j}^{n, 2}(s) & =& b_j^n B_j^n - c_j^n D_j^n,\\ g_{1, j}^{n, 2}(s) & = &-9c_j^n A_j^n + 28c_j^n B_j^n + 144a_j^n C_j^n + 27b_j^n C_j^n +54a_j^n D_j^n - 26b_j^n D_j^n \\ && \quad + 24(2a_j^n A_j^n - b_j^n A_j^n + a_j^n B_j^n + c_j^n C_j^n + c_j^n D_j^n) \lambda s\\ && \quad + 24(c_j^n A_j^n -2a_j^n C_j^n - b_j^n C_j^n) \lambda^2 s^2, \\ g_{3, j}^{n, 2}(s) & =& -9c_j^n A_j^n - 3c_j^n B_j^n - 21b_j^n C_j^n + 6a_j^n D_j^n - 9b_j^n D_j^n\\ && \quad - 12(b_j^n A_j^n - c_j^n C_j^n)\lambda s,\\ g_{5, j}^{n, 2}(s) & = &c_j^n B_j^n + b_j^n D_j^n, \end{array} $$

for j = 1, 2.

Appendix 2

Define

$$ \begin{array}{@{}rcl@{}} a^{n} := \lvert \textbf{z}^{n}\rvert^{2} + \lvert {\Lambda}^{-1} \dot{\mathbf{z}}^{n}\rvert^{2}, \quad b^{n} := \lvert \textbf{z}^{n}\rvert^{2} - \lvert {\Lambda}^{-1} \dot{\mathbf{z}}^{n}\rvert^{2}, \\ c^{n} := (\textbf{z}^{n})^{*} {\Lambda}^{-1} \dot{\mathbf{z}}^{n} + (\dot{\mathbf{z}}^{n})^{*} {\Lambda}^{-1}\textbf{z}^{n},\\ \textbf{A}^{n} := (2a^{n} + b^{n}) \textbf{z}^{n} + c^{n} {\Lambda}^{-1} \dot{\mathbf{z}}^{n},\qquad \textbf{B}^{n} := b^{n} \textbf{z}^{n} - c^{n} {\Lambda}^{-1} \dot{\mathbf{z}}^{n},\\ \textbf{C}^{n} := c^{n} \textbf{z}^{n} + (2a^{n} - b^{n}) {\Lambda}^{-1} \dot{\mathbf{z}}^{n},\qquad \textbf{D}^{n} := c^{n} \textbf{z}^{n} + b^{n} {\Lambda}^{-1} \dot{\mathbf{z}}^{n}. \end{array} $$

The functions used in the modified first-order NPI scheme (19)–(21) are:

$$ \begin{array}{@{}rcl@{}} \textbf{f}_{1}^{n, 1}(s) = - \frac{{\Lambda}^{-1}}{32\varepsilon^{2}} \left( \varepsilon^{2}\textbf{B}^{n}-4s\textbf{C}^{n} \right), \qquad \textbf{f}_{3}^{n, 1}(s) = \frac{{\Lambda}^{-1}}{32} \textbf{B}^{n},\\ \textbf{g}_{1}^{n, 1}(s) = - \frac{{\Lambda}^{-1}}{32\varepsilon^{2}} \left( 4 s \textbf{A}^{n} + 4\varepsilon^{2}\textbf{C}^{n} + 3\varepsilon^{2}\textbf{D}^{n}\right),\qquad \textbf{g}_{3}^{n, 1}(s) = \frac{{\Lambda}^{-1}}{32} \textbf{D}^{n},\\ \dot{\textbf{f}}_{1}^{n, 1}(s) = - \frac{1}{32\varepsilon^{2}} \left( 4 s \textbf{A}^{n} + 3\varepsilon^{2}\textbf{D}^{n}\right), \qquad \dot{\textbf{f}}_{3}^{n, 1}(s) = \frac{3}{32} \textbf{D}^{n},\\ \dot{\textbf{g}}_{1}^{n, 1}(s) = - \frac{1}{32\varepsilon^{2}} \left( 4 \varepsilon^{2} \textbf{A}^{n} - \varepsilon^{2}\textbf{B}^{n} + 4s\textbf{C}^{n} \right),\qquad \dot{\textbf{g}}_{3}^{n, 1}(s) = -\frac{3}{32} \textbf{B}^{n}. \end{array} $$

When considering the nonlinearity f(z) = diag(zz^∗)z, we only need to change the above aⁿ,bⁿ,cⁿ to the following expressions:

$$ \begin{array}{@{}rcl@{}} a^{n} := \text{diag} (\textbf{z} \textbf{z}^{*}) + \text{diag}({\Lambda}^{-1}\dot{\textbf{z}}\dot{\textbf{z}}^{*} {\Lambda}^{-1}), \\ b^{n} := \text{diag} (\textbf{z} \textbf{z}^{*}) - \text{diag}({\Lambda}^{-1}\dot{\textbf{z}}\dot{\textbf{z}}^{*} {\Lambda}^{-1}), \\ c^{n} := \text{diag}(\textbf{z}^{n} (\dot{\textbf{z}}^{n})^{*} {\Lambda}^{-1}) + \text{diag}({\Lambda}^{-1} \dot{\textbf{z}}^{n} (\textbf{z}^{n})^{*}). \end{array} $$

Appendix 3

Proof Proof of Theorem 2

Noticing that $\lvert {\sin \limits } x\rvert \le \lvert x\rvert$, we could modify the estimates (34), (35), (41), and (42), respectively, as

$$ \begin{array}{@{}rcl@{}} && \lvert \tilde{I}^{n,1}(s)\rvert \le {{\int}_{0}^{s}} \lvert \sin(\lambda(s-w))f(\tilde{y}^{n,0}(w))\rvert dw \le C \frac{\tau^{2}}{\varepsilon^{2}}, \end{array} $$

(45)

$$ \begin{array}{@{}rcl@{}} && \lvert \tilde{f}^{n,1}(s) - f(\tilde{y}^{n,1}(s))\rvert \le C \lvert \tilde{I}^{n,1}(s)\rvert^{2} \le C\frac{\tau^{4}}{\varepsilon^{4}}, \end{array} $$

(46)

$$ \begin{array}{@{}rcl@{}} && \lvert \xi^{n, 0}(s)\rvert \le {{\int}_{0}^{s}} \lvert \sin(\lambda(s-w)) f(y(t_{n}+w))\rvert dw \le C \frac{\tau^{2}}{\varepsilon^{2}}, \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} && \lvert \xi^{n, 1}(s)\rvert \le {{\int}_{0}^{s}} \lvert \sin(\lambda(s-w)) \left( y^{n, 0}(w) - y(t_{n}+w)\right)\rvert dw \le C \frac{\tau^{4}}{\varepsilon^{4}}. \end{array} $$

(48)

Thus, the error estimate for the error energy becomes

$$ \begin{array}{@{}rcl@{}} && \mathcal{E}(e^{n+1}, \dot{e}^{n+1}) - \mathcal{E}(e^n, \dot{e}^n)\\ &\le & ~ \tau \mathcal{E}(e^n, \dot{e}^n) + C (\tau + 1) \left( \frac{\tau^9}{\varepsilon^8}+ {\int}_{0}^{\tau} \lvert f(y(t_n+s)) - f(\tilde{y}^{n, 1}(s))\rvert^2 ds\right),\\ &\le & C\left( \tau \mathcal{E}(e^n, \dot{e}^n) + \frac{\tau^9}{\varepsilon^8}\right), \end{array} $$

which leads to the error bound $\lvert y(t_{n}) - y^{n}\rvert + \varepsilon ^{2} \lvert \dot {y}(t_{n}) - \dot {y}^{n}\rvert \le C \frac {\tau ^{4}}{\varepsilon ^{4}}$. □

Appendix 4

Table 1 Numerical error e_τ(1) of EIs for (3)

Table 2 Numerical error e_τ(1) of MTIs for (3)

Table 3 Numerical error e_τ(1) of NPIs for (3)

Table 4 Numerical error e_τ(1) of mNPIs for (13)