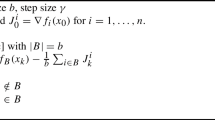1 Introduction

Variance-reduced stochastic gradient (VR-SG) methods is a family of iterative optimization algorithms that combine the low per-iteration computational cost of the ordinary stochastic gradient descent and the attractive convergence properties of gradient descent. Just as ordinary stochastic gradient descent, VR-SG methods solve smooth optimization problems on finite sum form,

$$ \begin{array}{@{}rcl@{}} &\underset{x\in\mathbb{R}^{N}}{\min} \frac{1}{n} {\sum}_{j=1}^{n} f_{i}(x) \end{array} $$
(1)

where, for all \(i\in \{1,\dots ,n\}\), \(f_{i}:\mathbb {R}^{N} \to \mathbb {R}\) is a convex function that is L-smooth, i.e., fi is differentiable with L-Lipschitz continuous gradient. These types of problems are common in model fitting, supervised learning, and empirical risk minimization which, together with the nice convergence properties of VR-SG methods, has lead to a great amount of research on VR-SG methods and the development of several different variants, e.g., [1, 15, 16, 21,22,23,24,25, 27, 30, 33, 40, 41, 43, 45].

Broadly speaking, VR-SG methods form a stochastic estimate of the objective gradient by combining one or a few newly evaluated terms of the gradient with all previously evaluated terms. Classic examples of this can be seen in the SAG [27, 40] and SAGA [15] algorithms. Given some initial iterates \(x^{0},{y_{1}^{0}},\dots ,{y_{n}^{0}}\in \mathbb {R}^{N}\) and step-size λ > 0, SAGA samples ik uniformly from \(\{1,\dots ,n\}\) and then updates the iterates as

$$ \begin{array}{@{}rcl@{}} &x^{k+1} = x^{k} - \lambda \Big(\nabla f_{i^{k}}(x^{k}) - y_{i^{k}}^{k} + \frac{1}{n}{\sum}_{j=1}^{n} {y_{j}^{k}}\Big), \\ &{}y_{i^{k}}^{k+1} = \nabla f_{i^{k}}(x^{k}), \\ &{\kern-6.4pc}y_{j}^{k+1} = {y_{j}^{k}} \quad\text{for all}\quad j \neq i^{k}, \end{array} $$

for \(k\in \{0,1,\dots \}\). The update of xk+ 1 is said to be unbiased since the expected value of xk+ 1 at iteration k is equal to an ordinary gradient descent update. This is in contrast to the biased SAG, which is identical to SAGA except that the update of xk+ 1 is

$$ \begin{array}{@{}rcl@{}} x^{k+1} &= x^{k} - \lambda \left( \frac{1}{n}\big(\nabla f_{i^{k}}(x^{k}) - y_{i^{k}}^{k} \big) + \frac{1}{n}{\sum}_{j=1}^{n} {y_{j}^{k}} \right) \end{array} $$

and the expected value of xk+ 1 now includes a term containing the old gradients \(\frac {1}{n}{\sum }_{i=1}^{n} {y_{i}^{k}}\). Although SAG shows that unbiasedness is not essential for the convergence of VR-SG methods, the effects of this bias are unclear. The majority of VR-SG methods are unbiased but existing works have not established any clear advantage of either the biased SAG or the unbiased SAGA. This paper will examine the effect of bias and its interplay with different problem assumptions for SAG/SAGA-like methods.

1.1 Problem and algorithm

Instead of solving (1) directly, we consider a closely related but more general root-finding problem. Throughout the paper, we consider the Euclidean space \(\mathbb {R}^{N}\) and the problem of finding \(x\in \mathbb {R}^{N}\) such that

$$ \begin{array}{@{}rcl@{}} 0 &= Rx := \frac{1}{n}{\sum}_{i = 1}^{n} R_{i}x \end{array} $$
(2)

where \(R_{i} : \mathbb {R}^{N} \to \mathbb {R}^{N}\) is \(\frac {1}{L}\)-cocoercive—see Section 2—for all \(i\in \{1,\dots ,n\}\). Since L-smoothness of a convex function is equivalent to \(\frac {1}{L}\)-cocoercivity of the gradient [2, Corollary 18.17], the smooth optimization problem in (1) can be recovered by setting Ri = ∇fi for all \(i\in \{1,\dots ,n\}\) in (2). Problem (2) is also interesting in its own right with it and the closely related fixed point problem of finding \(x\in \mathbb {R}^{N}\) such that x = (Id − αR)x where α ∈ (0,2L− 1) both having applications in for instance feasibility and non-linear signal recovery problems, see [8, 10, 13] and the references therein. To solve this problem, we present the Stochastic Variance Adjusted Gradient (SVAG) algorithm.

figure a

SVAG is heavily inspired by SAG and SAGA with both being special cases, 𝜃 = 1 and 𝜃 = n respectively. Just like SAG and SAGA, in each iteration, SVAG evaluates one operator \(R_{i^{k}}\) and stores the results in \(y_{i^{k}}^{k+1}\). An estimate of the full operator is then formed as

$$ \begin{array}{@{}rcl@{}} Rx^{k} \approx \widetilde{R}^{k} &= \frac{\theta}{n} (R_{i^{k}}x^{k} - y_{i^{k}}^{k}) + \frac{1}{n}{\sum}_{j=1}^{n} {y_{j}^{k}}. \end{array} $$
(3)

The scalar 𝜃 determine how much weight should be put on the new information gained from evaluating \(R_{i^{k}}x^{k}\). If the innovation, \(R_{i^{k}}x^{k} - y_{i^{k}}^{k}\), is highly correlated with the total innovation, \(Rx^{k} - \frac {1}{n}{\sum }_{j=1}^{n} {y_{j}^{k}}\), a large innovation weight 𝜃 can be chosen and vice versa. The innovation weight 𝜃 also determines the bias of SVAG. Taking the expected value \(\widetilde {R}^{k}\) given the information at iteration k gives

$$ \begin{array}{@{}rcl@{}} \mathbb{E}[\widetilde{R}^{k}|x^{k}, {y_{1}^{k}},\dots,{y_{n}^{k}}] &= \frac{\theta}{n} Rx^{k} + \left( 1-\frac{\theta}{n}\right)\frac{1}{n} {\sum}_{j=1}^{n} {y_{j}^{k}} \end{array} $$

which reveals that \(\widetilde {R}^{k}\) is an unbiased estimate of Rxk if 𝜃 = n, i.e., in the SAGA case. Any other choice, for instance SAG where 𝜃 = 1, yields a bias towards \(\frac {1}{n}{\sum }_{j=1}^{n} {y_{j}^{k}}\).

1.2 Contribution

The theory behind finding roots of monotone operators in general, and cocoercive operators in particular, has been put to good use when analyzing first-order optimization methods, examples include [2, 4, 14, 26, 38, 44]. For instance can both the proximal-gradient and ADMM methods be seen as instances of classic root-finding fixed point iterations and analyzed as such, namely forward-backward and Douglas–Rachford respectively. The resulting analyses can often be simple and intuitive and even though the root-finding formulation is more general—not all cocoercive operators are gradients of convex functions—the analyses are not necessarily more conservative. For example, analyzing proximal-gradient as forward-backward splitting yields the same rates and step-size conditions as analyzing it as a minimization method in the smooth/cocoercive setting, see for instance [32, Theorem 2.1.14] and [2, Example 5.18 and Proposition 4.39]. However, the main contribution of this paper is to show that the same is not true for VR-SG methods, in particular it is not true for SVAG when it is biased.

The results consist of two main convergence theorems for SVAG: one in the cocoercive operator case and one in the cocoercive gradient case, the later being equivalent to the minimization of a smooth and convex finite sum. Both of these theorems match or improve upon previously known results for the SAG and SAGA special cases. Comparing the two settings reveal that SVAG can use significantly larger step-sizes, with faster convergence as a result, in the cocoercive gradient case compared to the general cocoercive operator case. In the operator case, an upper bound on the step-size that scales as \(\mathcal {O}(n^{-1})\) is found where n is the number of terms in (2). However, the restrictions on the step-size loosen with reduced bias and the unfavorable \(\mathcal {O}(n^{-1})\) scaling disappears completely when SVAG is unbiased. In the gradient case, this bad scaling never occurs, regardless of bias. We provide examples in which SVAG diverges with step-sizes larger than the theoretical upper bounds in the operator case. Since the gradient case is proven to converge with much larger step-sizes, this verifies the difference between the convergence behavior of cocoercive operators and gradients.

These results indicate that it is inadvisable to only rely on the more general monotone operator theory and not explicitly use the gradient property when analyzing VR-SG methods meant for optimization. However, the large impact of bias in the cocoercive operator setting also raises the question regarding its importance in other non-gradient settings as well. One such setting of interest, where the operators are not gradients of convex functions, is the case of saddle-point problems. These problems are of importance in optimization due to their use in primal-dual methods but recently they have also gained a lot of attention due to their applications in the training of GANs in machine learning. Because of this, and due to the attractive properties of VR-SG methods in the convex optimization setting, efforts have gone into applying VR-SG methods to saddle-point problems as well [5, 7, 34, 42, 46]. Most of these efforts have been unbiased, something our analysis suggests is wise. With that said, it is important to note that our analysis is often not directly applicable due the fact that saddle-point problems rarely are cocoercive.

The main reason for the recent rise in popularity of variance-reduced stochastic methods is their use in the optimization setting, but, although bias plays a big role in the cocoercive operator case, our results are not as clear in this setting. For instance, the theoretical results for the SAG and SAGA special cases yield identical rates and step-size conditions with no clear advantage to either special case. Further experiments are therefore performed where several different choices of bias in SVAG are examined on a set of logistic regression and SVM optimization problems. However, the results of these experiments are in line with existing works with no significant advantage of any particular bias choice in SVAG. Although the performance difference is significant in some cases, no single choice of bias performs best for all problems and all bias choices eventually converge with the same rate in the majority of the cases. Furthermore, the theoretical maximal step-size can routinely be exceeded in these experiments, indicating that there is room for further theoretical improvements.

1.3 Related work

There is a large array of options for solving (2). For n ∈{1,2,3,4}, several operator splitting methods exist with varying assumptions on the operator properties, see for instance [4, 18, 19, 28, 29, 44] and the references therein. However, while these methods also can be applied for larger n by simply regrouping the terms, they do not utilize the finite sum structure of the problem. Algorithms have therefore been designed to utilize this structure for arbitrary large n with the hopes of reducing the total computational costs, e.g., [9,10,11, 36]. In particular the problem and method in [10] is closely related to the root-finding problem and algorithm considered in this paper.

Using the notation of [10], when T0 = Id, the fixed point problem of [10] can be mapped to (2) via Ri = ωi(Id − Ti) and vice verse. Footnote 1 Many applications considered in [10] can therefore, at least in part, be tackled with our algorithm as well. In particular, the problem of finding common fixed points of firmly nonexpansive operators can directly be solved by our algorithm. However, [10] is more general in that it allows for T0≠Id and works in general real Hilbert spaces. Looking at the algorithm of [10] we see that, just as our algorithm is a generalization of SAG/SAGA, it can be seen as a generalization of Finito [16], another classic VR-SG method. It generalize Finito in several way, for instance it allows for an additional proximal/backward step and it replaces the stochastic selection with a different selection criteria. However, in the optimization setting it still suffers from the same drawback as Finito when compared to SAG/SAGA-like algorithms. It still needs to store a full copy of the iterate for each term in objective. Since SAG, SAGA, and SVAG only need to store the gradient of each term, they can utilize any potential structure of the gradients to reduce the storage requirements [27]. Although the differences above are interesting in their own right, the notion of bias we examine in this paper is not applicable to Finito-like algorithms.

SAG and SAGA were compared in [15] but with no direct focus on the effects of bias. Other examples of research on SAG and SAGA include acceleration, sampling strategy selection, and ways to reduce the memory requirement [20, 22, 31, 35, 39, 47]. However, none of these works, including [31] that was written by the authors, analyze the biased case we consider in this paper. Even the works considering non-uniform sampling of gradients [20, 31, 35, 39] perform some sort of bias correction in order to remain unbiased. Furthermore, in order to keep the focus on the effects of the bias we have refrained from bringing in such generalizations into this work, making it distinct from the above research. To the authors’ knowledge, the only theoretical convergence result for biased VR-SG methods are the ones for SAG [27, 40]. But, since they only consider SAG, they fail to capture the breadth of SVAG and our proof is the first to simultaneously capture SAG, SAGA, and more.

Since the release of the first preprint of this paper, [17] has also provided a proof covering the gradient case of both SAG and SAGA, and some choices of bias in SVAG. All though [17] does not consider cocoercive operators, it is some sense more general with them considering a general biased stochastic estimator of the gradient. This generality comes at the cost of a more conservative analysis with their step-size scaling with \(\mathcal {O}(n^{-1})\) in all cases.

2 Preliminaries and notation

Let \(\mathbb {R}\) denote the real numbers and let the natural numbers be denoted \(\mathbb {N} = \{0,1,2,\dots \}\). Let 〈⋅,⋅〉 denote the standard Euclidean inner product and \(\|{\cdot }\| = \sqrt {\langle {\cdot },{\cdot }\rangle }\) the standard 2-norm. The scaled inner product and norm we denote as 〈⋅,⋅〉Σ = 〈Σ(⋅),⋅〉 and \(\|{\cdot }\|_{{\varSigma }} = \sqrt {\langle {\cdot },{\cdot }\rangle _{{\varSigma }}}\) where Σ is a positive definite matrix. If Σ is not positive definite, ∥⋅∥Σ is not a norm but we keep the notation for convenience.

Let n be the number of operators in (2). The vector 1 is the vector of all ones in \(\mathbb {R}^{n}\) and ei is the vector in \(\mathbb {R}^{n}\) of all zeros except the i:th element which contains a 1. The matrix I is an identity matrix with the size derived from context and \(E_{i} = e_{i}{e_{i}^{T}}\).

The symbol ⊗ denotes the Kronecker product of two matrices. The Kronecker product is linear in both arguments and the following properties hold

$$ (A\otimes B)^{T} = A^{T} \otimes B^{T}, \qquad (A\otimes B)(C\otimes D) = (AC)\otimes (BD). $$

In the last property it is assumed that the dimensions are such that the matrix multiplications are well defined. The eigenvalues of A ⊗ B are given by

$$ \begin{array}{@{}rcl@{}} \tau_{i}\mu_{j} \text{ for all } i \in \{1,{\dots} ,m\}, j \in \{ 1,{\dots} ,l \} \end{array} $$
(4)

where τi and μj are the eigenvalues of A and B respectively.

The Cartesian product of two sets C1 and C2 is defined as

$$ \begin{array}{@{}rcl@{}} C_{1}\times C_{2} = \{(c_{1},c_{2}) \mid c_{1}\in C_{1}, c_{2}\in C_{2}\}. \end{array} $$

From this definition we see that if C1 and C2 are closed and convex, so is C1 × C2.

Let X⋆ be the set of all solutions of (2),

$$ \begin{array}{@{}rcl@{}} X^{\star} = \{x | 0 = {\textstyle\frac{1}{n}{\sum}_{i=1}^{n}} R_{i}x \} \end{array} $$

and define Z⋆ as the set of primal-dual solutions

$$ \begin{array}{@{}rcl@{}} Z^{\star} = \{(x, R_{1}x,{\dots} , R_{n}x) | 0 = {\textstyle\frac{1}{n}{\sum}_{i=1}^{n}} R_{i}x \}. \end{array} $$

Assuming they exists, x⋆ denotes a solution to (2) and z⋆ denotes a primal-dual solution, i.e., x⋆ ∈ X⋆ and z⋆ ∈ Z⋆.

A single valued operator \(R: \mathbb {R}^{N} \to \mathbb {R}^{N}\) is \(\frac {1}{L}\)-cocoercive if

$$ \begin{aligned} &\langle{Rx - Ry}{x-y}\rangle \geq \frac{1}{L} \|{Rx - Ry}\|^{2} \end{aligned} $$
(5)

holds for all \(x,y \in \mathbb {R}^{N}\). An operator that is \(\frac {1}{L}\)-cocoercive is L-Lipschitz continuous. The set of zeros of a cocoercive operator R is closed and convex.

A differentiable convex function \(f: \mathbb {R}^{N} \to \mathbb {R}\) is called L-smooth if the gradient is \(\frac {1}{L}\)-cocoercive. Equivalently, a differentiable convex function is L-smooth if

$$ f(y) \leq f(x) + \langle{\nabla f(x)}{y-x}\rangle + \frac{L}{2}\|{y-x}\|^{2} $$
(6)

holds for all \(x,y \in \mathbb {R}^{N}\).

If \(f_{i}: \mathbb {R}^{N} \to \mathbb {R}\) is a differentiable convex function for each \(i\in \{1,\dots ,n\}\), the minimization of \({\sum }_{i=1}^{n} f_{i}(x)\) is equivalent to (2) with Ri = ∇fi.

For more details regarding monotone operators and convex functions see [2, 32].

To establish almost sure sequence convergence of the stochastic algorithm, the following propositions will be used. The first is from [37] and establishes convergence of non-negative almost super-martingales. The second is based on [12] and provides the tool to show almost sure sequence convergence.

Proposition 2.1

Let \(({{\varOmega }}, \mathcal {F}, P)\) be a probability space and \(\mathcal {F}_{0} \subset \mathcal {F}_{1} \subset \dots \) be a sequence of sub-σ-algebras of \(\mathcal {F}\). For all \(k \in \mathbb {N}\), let zk, βk, ξk and ζk be non-negative \(\mathcal {F}_{k}\)-measurable random variables. If \({\sum }_{i=0}^{\infty } \beta ^{i} < \infty \), \({\sum }_{i=0}^{\infty } \xi ^{i} < \infty \) and

$$ \begin{array}{@{}rcl@{}} \mathbb{E}[z^{k+1}|\mathcal{F}_{k}] \leq (1 + \beta^{k})z^{k} + \xi^{k} - \zeta^{k} \end{array} $$

hold almost surely for all \(k \in \mathbb {N}\), then zk converges a.s. to a finite valued random variable and \({\sum }_{i=0}^{\infty } \zeta ^{i} < \infty \) almost surely.

Proof 1

See [37, Theorem 1]. □

Proposition 2.2

Let Z be a non-empty closed subset of a finite dimensional Hilbert space H, let \(\phi : [0,\infty ) \to [0,\infty )\) be a strictly increasing function such that \(\phi (t) \to \infty \) as \(t \to \infty \), and let \((x^{k})_{k\in \mathbb {N}}\) be a sequence of H-valued random variables. If ϕ(∥xk − z∥) converges a.s. to a finite valued non-negative random variable for all z ∈ Z, then the following hold:

  1. 1.

    HCode \((x^{k})_{k\in \mathbb {N}}\) is bounded almost surely.

  2. 2.

    Suppose the cluster points of \((x^{k})_{k\in \mathbb {N}}\) are a.s. in Z, then \((x^{k})_{k\in \mathbb {N}}\) converge a.s. to a Z-valued random variable.

Proof 2

In finite dimensional Hilbert spaces, these two statements are the same as statements (ii) and (iv) of [12, Proposition 2.3]. Hence, consider the proof of [12, Proposition 2.3] restricted to finite dimensional Hilbert spaces. The proof of (ii) in [12, Proposition 2.3] only relies on the a.s. convergence of ϕ(∥xk − z∥) and hence is implied by the assumptions of this proposition. This proves our first statement. The proof of (iv) in [12, Proposition 2.3] only relies on (iii) of [12, Proposition 2.3] which in turn is implied by (ii) of [12, Proposition 2.3], i.e., our first statement. This proves our second statement. □

3 Convergence

Throughout the analysis we will use the following two assumptions on the operators in (2).

Assumption 3.1

For each \(i\in \{1,\dots ,n\}\), let Ri be \(\frac {1}{L}\)-cocoercive and X⋆≠∅, i.e., (2) has at least one solution.

Assumption 3.2

For each \(i\in \{1,\dots ,n\}\), let Ri = ∇fi for some differentiable function fi and define \(F = \frac {1}{n}{\sum }_{i=1}^{n} f_{i}\). Furthermore, let Assumption 3.1 hold, i.e., fi is L-smooth and convex and \(\arg \!{\min \limits } F(x)\) exists.

3.1 Reformulation

We begin by formalizing and reformulating Algorithm 1 into a more convenient form. Let \(({{\varOmega }}, \mathcal {F}, P)\) be the underlying probability space of Algorithm 1. The index selected at iteration k is then a uniformly distributed random variable \(i^{k}: {{\varOmega }} \to \{1,\dots ,n\}\). For each \(k\in \mathbb {N}\), define the random variable \(z^{k}:{{\varOmega }}\to \mathbb {R}^{N(n+1)}\) as \(z^{k} = (x^{k},{y_{1}^{k}},{\dots } ,{y_{n}^{k}})\) where xk and \({y_{i}^{k}}\) for \(i \in \{1,\dots ,n\}\) are the iterates of Algorithm 1. Let \(\mathcal {F}_{0} \subset \mathcal {F}_{1} \subset \dots \) be a sequence of sub-σ-algebras of \(\mathcal {F}\) such that zk are \(\mathcal {F}_{k}\)-measurable and ik is independent of \(\mathcal {F}_{k}\). With the operator \(\mathbf {B} : \mathbb {R}^{N(n+1)} \to \mathbb {R}^{2Nn}\) defined as \(\mathbf {B}(x,y_{1},\dots ,y_{n}) = (R_{1}x,{\dots } ,R_{n}x,y_{1},{\dots } ,y_{n})\), one iteration of Algorithm 1 can be written as

$$ \begin{array}{@{}rcl@{}} z^{k+1} = z^{k} - (U_{i^{k}}\otimes I)\mathbf{B}z^{k} \end{array} $$
(7)

where \(z^{0} \in \mathbb {R}^{N(n+1)}\) is given and

$$ \begin{array}{@{}rcl@{}} U_{i} = \begin{bmatrix} \frac{\lambda}{n}\theta {e_{i}^{T}} & -\frac{\lambda}{n}\theta {e_{i}^{T}}+\frac{\lambda}{n}\mathbf{1}^{T} \\ -E_{i} & E_{i} \end{bmatrix} \end{array} $$

for all \(i\in \{1,\dots ,n\}\). The vector ei and the matrix Ei are defined in Section 2.

The following lemma characterizes the zeros of (Ui ⊗ I)B and hence the fixed points of (7) and Algorithm 1.

Lemma 3.3

Let Assumption 3.1 hold, each z⋆ in Z⋆ is then a zero of (Ui ⊗ I)B for all \(i\in \{1,\dots ,n\}\), i.e.,

$$ \begin{array}{@{}rcl@{}} \forall z^{\star} \in Z^{\star}, \forall i \in \{1,{\dots} ,n\}: \quad 0 = (U_{i}\otimes I)\mathbf{B}z^{\star}. \end{array} $$

Furthermore, the set Z⋆ is closed and convex and \(R_{i}x^{\star } = R_{i}\bar {x}^{\star }\) for all \(x^{\star },\bar {x}^{\star } \in X^{\star }\) and for all \(i\in \{1,\dots ,n\}\).

Proof 3 (Proof of Lemma 3.3)

The zero statement, 0 = (Ui ⊗ I)Bz⋆, follows from definition of z⋆. For closedness and convexity of Z⋆, we first prove that Rix⋆ is unique for each \(i\in \{1,\dots ,n\}\). Taking x,y ∈ X⋆, which implies \({\textstyle {\sum }_{i=1}^{n}} R_{i}x = {\textstyle {\sum }_{i=1}^{n}}R_{i}y = 0\), and using cocoercivity (5) of each Ri gives

$$ \begin{array}{@{}rcl@{}} 0 = \langle{{\textstyle{\sum}_{i=1}^{n}} R_{i}x - {\textstyle{\sum}_{i=1}^{n}} R_{i}y},{x-y}\rangle &=& {\textstyle{\sum}_{i=1}^{n}} \langle{R_{i}x - R_{i}y}{x-y}\rangle \\ &\geq& {\textstyle{\sum}_{i=1}^{n}} \frac{1}{L}\|{R_{i}x - R_{i}y}\|^{2} \geq 0, \end{array} $$

hence must Rix = Riy for all \(i\in \{1,\dots ,n\}\). The set Z⋆ is a Cartesian product of X⋆ and the points ri = Rix⋆ for \(i\in \{1,\dots ,n\}\) for any x⋆ ∈ X⋆. A set consisting of only one point is closed and convex and X⋆ is closed and convex since \(\frac {1}{n}{\sum }_{i=1}^{n}R_{i}\) is cocoercive [2, Proposition 23.39], hence is Z⋆ closed and convex. □

The operator B in the reformulated algorithm can be used to enforce the following property on the sequence \((z^{k})_{k\in \mathbb {N}}\).

Lemma 3.4

Let \(({{\varOmega }}, \mathcal {F}, P)\) be a probability space and \((z^{k})_{k\in \mathbb {N}}\) be a sequence of random variables \(z^{k}: {{\varOmega }} \to \mathbb {R}^{N(n+1)}\). If Bzk →Bz⋆ a.s. where z⋆ ∈ Z⋆, then any cluster point of \((z^{k})_{k\in \mathbb {N}}\) will almost surely be in Z⋆.

Proof 4 (Proof of Lemma 3.4)

Let z be a cluster point of \((z^{k})_{k\in \mathbb {N}}\). Take an ω ∈Ω such that Bzk(ω) →Bz⋆. For this ω and for all \(k\in \mathbb {N}\), we define the realizations of z and zk as

$$ \begin{array}{@{}rcl@{}} z(\omega) = (\bar{x},\bar{y}_{1},\dots,\bar{y}_{n}) ,\quad z^{k}(\omega) = (\bar{x}^{k},\bar{y}_{1}^{k},\dots,\bar{y}_{n}^{k}) \end{array} $$

where \(\bar {x},\bar {y}_{1},\dots ,\bar {y}_{n}\in \mathbb {R}^{N}\) and \(\bar {x}^{k},\bar {y}_{1}^{k},\dots ,\bar {y}_{n}^{k}\in \mathbb {R}^{N}\) for all \(k\in \mathbb {N}\).

Since \(\mathbf {B}\bar {z}^{k} \to \mathbf {B}z^{\star }\) we directly have \(\bar {y}_{i}^{k} \to R_{i} x^{\star }\) for x⋆ ∈ X⋆ and hence must \(\bar {y}_{i} = R_{i}x^{\star }\) for all \(i\in \{1,\dots ,n\}\). Note, Rix⋆ is independent of which x⋆ ∈ X⋆ was chosen, see Lemma 3.3. Furthermore, \(\mathbf {B}\bar {z}^{k} \to \mathbf {B}\bar {z}^{\star }\) implies that \(R_{i}\bar {x}^{k} \to R_{i} x^{\star }\) for all \(i\in \{1,\dots ,n\}\). Let \((\bar {x}^{k(l)})_{l\in \mathbb {N}}\) be a subsequence converging to \(\bar {x}\), then

$$ \begin{array}{@{}rcl@{}} \|{{\textstyle\frac{1}{n}{\sum}_{i=1}^{n} R_{i}}\bar{x}}\| &\leq& \|{{\textstyle\frac{1}{n}{\sum}_{i=1}^{n}R_{i}}\bar{x}^{k(l)} - {\textstyle\frac{1}{n}{\sum}_{i=1}^{n}R_{i}}\bar{x}}\| + \|{{\textstyle\frac{1}{n}{\sum}_{i=1}^{n}R_{i}}\bar{x}^{k(l)}}\| \\ &\leq& L\|{\bar{x}^{k(l)} - \bar{x}}\| + \|{{\textstyle\frac{1}{n}{\sum}_{i=1}^{n}R_{i}}\bar{x}^{k(l)}}\| \to \|{{\textstyle\frac{1}{n}{\sum}_{i=1}^{n}R_{i}}x^{\star}}\| = 0 \end{array} $$

as \(l \to \infty \) where L-Lipschitz continuity of \(\frac {1}{n}{\sum }_{i=1}^{n}R_{i}\) was used. This concludes that \(\bar {x} \in X^{\star }\) and since \(\bar {y}_{i} = R_{i}x^{\star } = R_{i}\bar {x}\) for all \(i\in \{1,\dots ,n\}\) by Lemma 3.3, we have that z(ω) ∈ Z⋆. Since this hold for any ω such that Bzk(ω) →Bz⋆ and the set in \(\mathcal {F}\) of all such ω have probability one due to the almost sure convergence of Bzk →Bz⋆, we have z ∈ Z⋆ almost surely. □

The reformulation (7) further allows us to concisely formulate two Lyapunov inequalities.

Lemma 3.5

Let Assumption 3.1 hold, the update (7) then satisfies

$$ \begin{array}{@{}rcl@{}} &&\mathbb{E}[\|{z^{k+1} - z^{\star}}\|_{H\otimes I}^{2} | \mathcal{F}_{k}]\\ &&\quad\leq \|{z^{k} - z^{\star}}\|_{H\otimes I}^{2} - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{(2 M - \mathbb{E}[U_{i^{k}}^{T}HU_{i^{k}}] - \xi I) \otimes I }^{2} \\ &&\qquad- {\xi n L}\langle{Rx^{k}}{x^{k} - x^{\star}}\rangle \end{array} $$

for all \(k\in \mathbb {N}\) and \(\xi \in [0,\frac {2\lambda }{nL}]\), where the matrices H and M are given by

$$ \begin{array}{@{}rcl@{}} H = \begin{bmatrix} 1 & - \frac{\lambda}{n}(n-\theta) \mathbf{1}^{T} \\ -\frac{\lambda}{n}(n-\theta)\mathbf{1} & \frac{\lambda}{L} I + \frac{\lambda^{2}}{n^{2}}(n-\theta)^{2} \mathbf{11}^{T} \end{bmatrix} \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} M = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \otimes \frac{1}{2n} \frac{\lambda}{L} I - \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \otimes \frac{\lambda^{2}}{2 n^{2}}(n-\theta)\mathbf{11}^{T}. \end{array} $$

Lemma 3.6

Let Assumption 3.2 hold, the update (7) then satisfies

$$ \begin{array}{@{}rcl@{}} \mathbb{E}[F((K\otimes I) z^{k+1})|\mathcal{F}_{k}] \leq F((K\otimes I) z^{k}) - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}_{\frac{1}{2}S\otimes I} \end{array} $$

for all \(k\in \mathbb {N}\), where \(K = \begin {bmatrix} 1 & \frac {\lambda }{n}\mathbf {1}^{T} \end {bmatrix}\) and

$$ \begin{array}{@{}rcl@{}} S &=& \begin{bmatrix} 2 & -1 \\ -1 & 0 \end{bmatrix} \otimes (\theta - 1)\frac{\lambda}{n^{3}} \mathbf{11}^{T} - \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \otimes (\theta - 1)^{2}\frac{L\lambda^{2}}{n^{3}} I \\ &\quad+& \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \otimes \frac{\lambda}{n^{2}} \mathbf{11}^{T}. \end{array} $$

Proof 5 (Proof of Lemma 3.5)

Take \(k\in \mathbb {N}\), note that since \(U_{i^{k}}\) is independent of \(\mathcal {F}_{k}\) and zk is \(\mathcal {F}_{k}\)-measurable we have

$$ \begin{array}{@{}rcl@{}} &\mathbb{E}[\langle{(U_{i^{k}}\otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle_{H\otimes I} |\mathcal{F}_{k}] \\ &\quad = \langle{(H\mathbb{E} [U_{i^{k}}]\otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle. \end{array} $$

The matrix \(H\mathbb {E} [U_{i^{k}}]\) is given by

$$ \begin{array}{@{}rcl@{}} H\mathbb{E} [U_{i^{k}}] = \begin{bmatrix} \frac{\lambda}{n}\mathbf{1}^{T} & 0 \\ - \frac{\lambda^{2}}{n^{2}}(n-\theta)\mathbf{11}^{T} - \frac{\lambda}{nL}I & \frac{\lambda}{nL}I \end{bmatrix}, \end{array} $$

see the supplementary material for verification of this and other matrix identities. We also note that

$$ \begin{array}{@{}rcl@{}} \langle{Rx^{k} - Rx^{\star}}{x^{k} -x^{\star}}\rangle = \langle{(\begin{bmatrix} \frac{1}{n}\mathbf{1}^{T} & 0 \\ 0 & 0 \end{bmatrix} \otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle. \end{array} $$

Taking \(\xi \in [0,\frac {2\lambda }{nL}]\) and putting these two expression together yield

$$ \begin{array}{@{}rcl@{}} &&\mathbb{E}[\langle{(U_{i^{k}}\otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle_{H\otimes I} |\mathcal{F}_{k}] - \frac{\xi n L}{2}\langle{Rx^{k} - Rx^{\star}}{x^{k} -x^{\star}}\rangle\\ &&\quad=\langle{(\begin{bmatrix} (\frac{\lambda}{n} -\frac{\xi L}{2})\mathbf{1}^{T} & 0 \\ - \frac{\lambda^{2}}{n^{2}}(n-\theta)\mathbf{11}^{T} - \frac{\lambda}{nL}I & \frac{\lambda}{nL}I \end{bmatrix} \otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle. \end{array} $$

Using \(\frac {1}{L}\)-cocoercivity of Ri for each \(i\in \{1,\dots ,n\}\) gives

$$ \begin{array}{@{}rcl@{}} &&\mathbb{E}[\langle{(U_{i^{k}}\otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle_{H\otimes I} |\mathcal{F}_{k}] - \frac{\xi n L}{2}\langle{Rx^{k} - Rx^{\star}}{x^{k} -x^{\star}}\rangle\\ &&\quad\geq \langle{(\begin{bmatrix} (\frac{\lambda}{nL} -\frac{\xi}{2}) I & 0 \\ - \frac{\lambda^{2}}{n^{2}}(n-\theta)\mathbf{11}^{T} - \frac{\lambda}{nL}I & \frac{\lambda}{nL}I \end{bmatrix} \otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{\mathbf{B}z^{k}-\mathbf{B}z^{\star}}\rangle \end{array} $$

Setting

$$ \begin{array}{@{}rcl@{}} \bar{M} = \begin{bmatrix} \frac{\lambda}{nL} I & 0 \\ - \frac{\lambda^{2}}{n^{2}}(n-\theta)\mathbf{11}^{T} - \frac{\lambda}{nL}I & \frac{\lambda}{nL}I \end{bmatrix} \end{array} $$

gives

$$ \begin{array}{@{}rcl@{}} &&\mathbb{E}[\langle{(U_{i^{k}}\otimes I) (\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle_{H\otimes I} |\mathcal{F}_{k}] - \frac{\xi n L}{2}\langle{Rx^{k} - Rx^{\star}}{x^{k} -x^{\star}}\rangle\\ &&\quad\geq \langle{(\bar{M}\otimes I)(\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{\mathbf{B}z^{k}-\mathbf{B}z^{\star}}\rangle \\ &&\qquad- \langle{(\begin{bmatrix} \frac{\xi}{2} I & 0 \\ 0 & 0 \end{bmatrix} \otimes I)(\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{\mathbf{B}z^{k}-\mathbf{B}z^{\star}}\rangle\\ &&\quad\geq \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}_{\frac{1}{2}(\bar{M} + \bar{M}^{T}) \otimes I} - \frac{\xi}{2}\|{\mathbf{B}z^{k}-\mathbf{B}z^{\star}}\|^{2} \\ &&\quad= \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}_{(M - \frac{\xi}{2}I)\otimes I} \end{array} $$

where \(M = \frac {1}{2}(\bar {M} + \bar {M}^{T})\) is the matrix in the statement of the lemma. Finally, using this inequality and \(0 = (U_{i^{k}}\otimes I)\mathbf {B}z^{\star }\) from Lemma 3.3 gives

$$ \begin{array}{@{}rcl@{}} &&\mathbb{E}[\|{z^{k+1} - z^{\star}}\|_{H\otimes I}^{2}|\mathcal{F}_{k}] \\ &&\quad= \mathbb{E}[\|{\big(z^{k} - (U_{i^{k}}\otimes I)\mathbf{B}z^{k}\big) - \big(z^{\star} - (U_{i^{k}}\otimes I)\mathbf{B}z^{\star}\big) }\|_{H\otimes I}^{2} |\mathcal{F}_{k}]\\ &&\quad= \|{z^{k} - z^{\star}}\|_{H\otimes I}^{2} + \mathbb{E}[\|{(U_{i^{k}}\|\otimes I)(\mathbf{B}z^{k} - \mathbf{B}z^{\star})}_{H\otimes I}^{2}|\mathcal{F}_{k}] \\ &&\quad\quad- 2\mathbb{E}[\langle{(U_{i^{k}}\otimes I)(\mathbf{B}z^{k} - \mathbf{B}z^{\star})}{z^{k}-z^{\star}}\rangle_{H\otimes I} |\mathcal{F}_{k}]\\ &&\quad\leq \|{z^{k} - z^{\star}}\|_{H\otimes I}^{2} + \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{\mathbb{E}[U_{i^{k}}^{T}HU_{i^{k}} ] \otimes I}^{2} \\ &&\quad\quad - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}_{(2M - \xi I)\otimes I} - {\xi n L}\langle{Rx^{k} - Rx^{\star}}{x^{k} - x^{\star}}\rangle \\ &&\quad= \|{z^{k} - z^{\star}}\|_{H\otimes I}^{2} - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{(2 M - \mathbb{E}[U_{i^{k}}^{T}HU_{i^{k}}] - \xi I) \otimes I }^{2} \\ &&\qquad- {\xi n L}\langle{Rx^{k}}{x^{k} - x^{\star}}\rangle. \end{array} $$

□

Proof 6 (Proof of Lemma 3.6)

Take \(k\in \mathbb {N}\) and note that

$$ \begin{array}{@{}rcl@{}} (K\otimes I)z^{k+1} =(K\otimes I)(z^{k} - (U_{i^{k}}\otimes I)\mathbf{B}z^{k}) = x^{k} - (Q_{i^{k}} \otimes I)\mathbf{B}z^{k} \end{array} $$

where \(Q_{i^{k}} = \frac {\lambda }{n} \begin {bmatrix} (\theta - 1)e_{i^{k}}^{T} & -(\theta - 1)e_{i^{k}}^{T} \end {bmatrix}\). Furthermore, with \(G = \frac {1}{n}\begin {bmatrix} \mathbf {1}^{T} & 0 \end {bmatrix}\), we have ∇F(xk) = (G ⊗ I)Bzk. From the definition of z⋆ we have \(0 =(G\otimes I)\mathbf {B}z^{\star } = (Q_{i^{k}} \otimes I)\mathbf {B}z^{\star }\). Using L-smoothness, (6), of F yields

$$ \begin{array}{@{}rcl@{}} &&\mathbb{E}[F((K\otimes I)z^{k+1})|\mathcal{F}_{k}] \\ &&\quad= \mathbb{E}[F(x^{k} - (Q_{i^{k}} \otimes I)\mathbf{B}z^{k})|\mathcal{F}_{k}]\\ &&\quad\leq F(x^{k}) - \langle{\nabla F(x^{k})}{(\mathbb{E}[Q_{i^{k}}] \otimes I)\mathbf{B}z^{k}}\rangle + {\textstyle\frac{L}{2}}\mathbb{E}[\|{(Q_{i^{k}} \otimes I)\mathbf{B}z^{k}}\|^{2}|\mathcal{F}_{k}] \\ &&\quad= F(x^{k}) - \langle{(G\otimes I)\mathbf{B}z^{k}}{(\mathbb{E}[Q_{i^{k}}] \otimes I)\mathbf{B}z^{k}}\rangle + \|{\mathbf{B}z^{k}}\|_{\frac{L}{2}\mathbb{E}[Q_{i^{k}}^{T}Q_{i^{k}}] \otimes I}^{2} \\ &&\quad= F(x^{k}) - \|{\mathbf{B}z^{k}}\|_{\frac{1}{2}\mathbb{E}[Q_{i^{k}}^{T} G + G^{T} Q_{i^{k}}]\otimes I}^{2} + \|{\mathbf{B}z^{k}}\|_{\frac{L}{2}\mathbb{E}[Q_{i^{k}}^{T}Q_{i^{k}}] \otimes I}^{2} \\ &&\quad= F(x^{k}) - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{\frac{1}{2}S_{L} \otimes I}^{2} \end{array} $$

where \(S_{L} = \mathbb {E}[Q_{i^{k}}^{T} G + G^{T} Q_{i^{k}} - L Q_{i^{k}}^{T} Q_{i^{k}}]\).

With \(D = \begin {bmatrix} 0 & \mathbf {1}^{T} \end {bmatrix}\) we have \((K\otimes I)z^{k} = x^{k} + \frac {\lambda }{n}(D\otimes I)\mathbf {B}z^{k}\). Using the first-order convexity condition on F and 0 = (D ⊗ I)Bz⋆ = (G ⊗ I)Bz⋆ yields

$$ \begin{aligned} F((K\otimes I)z^{k}) &= F(x^{k} + \frac{\lambda}{n}(D \otimes I)\mathbf{B}z^{k}) \\ &\geq F(x^{k}) + \langle{\nabla F(x^{k})}{ \frac{\lambda}{n}(D \otimes I)\mathbf{B}z^{k}}\rangle \\ &= F(x^{k}) + \langle{(G\otimes I) \mathbf{B}z^{k}}{ \frac{\lambda}{n}(D \otimes I)\mathbf{B}z^{k}}\rangle \\ &= F(x^{k}) + \|{\mathbf{B}z^{k}}\|_{\frac{1}{2}\frac{\lambda}{n}(D^{T}G + G^{T}D)\otimes I}^{2} \\ &= F(x^{k}) + \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{\frac{1}{2}S_{C} \otimes I}^{2} \end{aligned} $$
(8)

where \(S_{C} = \frac {\lambda }{n}(D^{T}G + G^{T}D)\). Combining these two inequalities gives

$$ \begin{array}{@{}rcl@{}} \mathbb{E}[F((K\otimes I) z^{k+1})|\mathcal{F}_{k}] \leq F((K\otimes I) z^{k}) - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}_{\frac{1}{2}S\otimes I} \end{array} $$

where S = SL + SC. □

3.2 Convergence theorems

We are now ready to state the main convergence theorems for SVAG. They are stated with the notation from Algorithm 1 but are proved at the end of this section with the help of the reformulation in (7) and the lemmas above.

Theorem 3.7

For all \(i\in \{1,\dots ,n\}\), let \((x^{k})_{k\in \mathbb {N}}\) and \(({y_{i}^{k}})_{k\in \mathbb {N}}\) be the sequences generated by Algorithm 1. If Assumption 3.1 hold and the step-size, λ > 0, and innovation weight, \(\theta \in \mathbb {R}\), satisfy

$$ \begin{array}{@{}rcl@{}} \frac{1}{L(2 + |n - \theta|)} > \lambda, \end{array} $$

then \(x^{k} \rightarrow x^{\star }\) and \({y_{i}^{k}} \rightarrow R_{i} x^{\star }\) almost surely for all \(i\in \{1,\dots ,n\}\), where x⋆ is a solution to (2). For all \(i\in \{1,\dots ,n\}\), the residuals converge a.s. as

$$ \begin{array}{@{}rcl@{}} \min_{k \in \{0,\dots,t\}} \mathbb{E}[\|{R_{i}x^{k} - R_{i}x^{\star}}\|^{2}] &\leq& \frac{n}{\lambda(L^{-1} - \lambda c)} \frac{1}{t+1} C_{R}, \\ \min_{k \in \{0,\dots,t\}} \mathbb{E}[\|{{y_{i}^{k}} - R_{i}x^{\star}}\|^{2}] &\leq& \frac{n}{\lambda(L^{-1} - \lambda c)} \frac{1}{t+1} C_{R} \end{array} $$

where c = 2 + |n − 𝜃| and

$$ \begin{array}{@{}rcl@{}} C_{R} &=& \min_{x\in X^{\star}} \|{x^{0} - x}\|^{2} + \frac{\lambda}{L}{\textstyle{\sum}_{i=1}^{n}}\|{{y_{i}^{0}}\| - R_{i}x^{\star}}^{2} + \lambda^{2}(n-\theta)^{2}\|{\frac{1}{n}{\textstyle{\sum}_{i=1}^{n}}{y_{i}^{0}}}\|^{2} \\ &&\qquad\quad - 2\lambda(n-\theta)\langle{x^{0}-x}{\frac{1}{n}{\textstyle{\sum}_{i=1}^{n}}{y_{i}^{0}}\rangle } \end{array} $$

for any x⋆ ∈ X⋆.

Theorem 3.8

For all \(i\in \{1,\dots ,n\}\), let \((x^{k})_{k\in \mathbb {N}}\) and \(({y_{i}^{k}})_{k\in \mathbb {N}}\) be the sequences generated by Algorithm 1. If Assumption 3.2 hold and the step-size, λ > 0, and innovation weight, 𝜃 ∈ [0,n], satisfy

$$ \begin{array}{@{}rcl@{}} \frac{1}{L}\frac{1}{2 + (n-\theta)\frac{\theta-1}{n}\big(\frac{\theta - 1}{n} - 1 + \frac{\theta - 1}{|\theta - 1|} \sqrt{2}\big)} > \lambda, \end{array} $$

then \(x^{k} \rightarrow x^{\star }\) and \({y_{i}^{k}} \rightarrow \nabla f_{i}(x^{\star })\) almost surely, where x⋆ is a solution to (2). For all \(i\in \{1,\dots ,n\}\), the residuals converge a.s. as

$$ \begin{array}{@{}rcl@{}} \min_{k \in \{0,\dots,t\}} \mathbb{E}[\|{\nabla f_{i}(x^{k}) - \nabla f_{i}(x^{\star})}\|^{2}] &&\leq \frac{n}{\lambda(L^{-1} - \lambda c)} \frac{1}{t+1} (C_{R} + C_{F}), \\ \min_{k \in \{0,\dots,t\}} \mathbb{E}[\|{{y_{i}^{k}} - \nabla f_{i}(x^{\star})}\|^{2}] &&\leq \frac{n}{\lambda(L^{-1} - \lambda c)} \frac{1}{t+1} (C_{R} + C_{F}), \\ \min_{k \in \{0,\dots,t\}} \mathbb{E}[F(x^{k}) - F(x^{\star})] &&\leq \frac{1}{\lambda(1 - L\lambda c)} \frac{1}{t+1} (C_{R} + C_{F}) \end{array} $$

where

$$ \begin{array}{@{}rcl@{}} c &=& 2 + (n-\theta)\frac{\theta-1}{n}\big(\frac{\theta - 1}{n} - 1 + \frac{\theta-1}{|\theta-1|} \sqrt{2}\big), \\ C_{R} &=& \min_{x\in X^{\star}} \|{x^{0} - x}\|^{2} + \frac{\lambda}{L}{\textstyle{\sum}_{i=1}^{n}}\|{{y_{i}^{0}}\| - R_{i}x^{\star}}^{2} + \lambda^{2}(n-\theta)^{2}\|{\frac{1}{n}{\textstyle{\sum}_{i=1}^{n}}{y_{i}^{0}}}\|^{2} \\ & -& 2\lambda(n-\theta)\langle{x^{0}-x}{\frac{1}{n}{\textstyle{\sum}_{i=1}^{n}}{y_{i}^{0}}\rangle }, \\ C_{F} &=& 2\lambda(n-\theta)\big(F(x^{0} + \frac{\lambda}{n}{\textstyle{\sum}_{i=1}^{n}} {y_{i}^{0}}) - F(x^{\star}) \big) \end{array} $$

for any x⋆ ∈ X⋆.

Both Theorems 3.7 and 3.8 give the step-size condition \(\lambda \in (0,\frac {1}{2L})\) for the SAGA special case, i.e., 𝜃 = n. This is the same as the largest upper bound found in the literature [15] and appears to be tight [31]. Theorem 3.8 also give this step-size condition when 𝜃 = 1, i.e., SAG in the optimization case. This bound improves on upper bound of \(\frac {1}{16L} \leq \lambda \) presented in [40].

In the cocoercive operator setting with 𝜃≠n, Theorem 3.7 gives a step-size condition that scales with n− 1. This step-size scaling is significantly worse compared to the gradient case in Theorem 3.8 in which the step-size’s dependence on n is \(\mathcal {O}(1)\) for all 𝜃. This difference is indeed real and not an artifact of the analysis since we in Section 4 present a problem for which the cocoercivity result appears to be tight. A consequence of this unfavorable step-size scaling in the operator setting is slow convergence. There is therefore little reason to use anything else than 𝜃 = n in SVAG when Ri is not a gradient of a smooth function for all \(i\in \{1,\dots ,n\}\).

The rates of Theorem 3.7 and 3.8 are of \(\mathcal {O}(\frac {1}{t+1})\) type with two sets of multiplicative factors. One factor which only depend on the algorithm parameters, \(\frac {n}{\lambda (L^{-1} - \lambda c)}\), and one set which depend on how the algorithm initialization relates to the solution set, CR and CR + CF. The initialization dependent factors also depend on the algorithm parameters, but, since knowing the exact dependency requires knowing the solution set, we will not attempt to tune the parameters to decrease this factor. Only considering the first factor, the rate becomes better if c is decreased and, since c is independent of λ, the best choice of step-size is λ = (2Lc)− 1. This means that λ = (4L)− 1 and 𝜃 = n are the best parameter choices in the cocoercive operator setting. In the optimization case the best step-size is also λ = (4L)− 1 but the innovation weight can be selected as either 𝜃 = n or 𝜃 = 1.

However, in the optimization case we do not believe that these theoretical rates reflects real world performance and parameter choices based on them might therefore not perform particularly well. We base this belief on our experience with numerical experiments. For 𝜃≠n and 𝜃≠ 1, we have not found any optimization problem where the step-size condition in Theorem 3.8 appears to be tight. Also, using λ = (2Lc)− 1 as suggested by Theorem 3.8 can in some cases lead to impractically small step-sizes. For instance, if λ = (2Lc)− 1 was used in the experiments in Section 4, a couple of the experiments would have step-sizes over 1000 times smaller than the ones used now. One can of course not disprove a worst case analysis with experiments but we still feel they indicate a conservative analysis, even though the analysis improves on the previous best results.

Proof 7 (Proof of Theorem 3.7)

Apply Lemma 3.5 with ξ = 0, the iterates given by (7) then satisfy the following for all z⋆ ∈ Z⋆,

$$ \begin{aligned} &\mathbb{E}[\|{z^{k+1} - z^{\star}}\|_{H\otimes I}^{2} | \mathcal{F}_{k}] \\ &\qquad\leq \|{z^{k} - z^{\star}}\|_{H\otimes I}^{2} - \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{(2 M - \mathbb{E}[U_{i^{k}}^{T}HU_{i^{k}}]) \otimes I }^{2}. \end{aligned} $$
(9)

Assuming H ≻ 0 and \(2M - \mathbb {E} [U_{i^{k}}^{T} H U_{i^{k}}] \succ 0\), Proposition 2.1 can be applied. We will later prove that this assumption indeed does hold. Proposition 2.1 gives a.s. summability of \(\|{\mathbf {B}z^{k} - \mathbf {B}z^{\star }}\|_{(2 M - \mathbb {E} [U_{i^{k}}^{T}HU_{i^{k}}]) \otimes I }^{2}\) and hence will Bzk →Bz⋆ almost surely. Lemma 3.4 then gives that all cluster points of \((z^{k})_{k\in \mathbb {N}}\) are in Z⋆ almost surely. Finally, since Proposition 2.1 ensures the a.s. convergence of \(\|{z^{k} - z^{\star }}\|_{H\otimes I}^{2}\) and since \(\mathbb {R}^{N(n+1)}\) with the inner product 〈(H ⊗ I)⋅,⋅〉 is a finite dimensional Hilbert space, Proposition 2.2 gives the almost sure convergence of zk → z⋆ ∈ Z⋆.

There always exists a λ such that \(2M - \mathbb {E} [U_{i^{k}}^{T} H U_{i^{k}}]\) and H are positive definite. First we show that H ≻ 0 always holds for λ > 0. Taking the Schur complement of 1 in H gives

$$ \begin{array}{@{}rcl@{}} \frac{\lambda}{L}I + \frac{\lambda^{2}}{n^{2}}(n-\theta)^{2} \mathbf{11}^{T} - \frac{\lambda^{2}}{n^{2}}(n-\theta)^{2}\mathbf{11}^{T} = \frac{\lambda}{L}I \succ 0. \end{array} $$

Hence is H ≻ 0 since the Schur complement is positive definite.

We now show \(2M - \mathbb {E} [U_{i^{k}}^{T} H U_{i^{k}}] \succ 0\). Straightforward algebra, see the supplementary material, yields

$$ \begin{array}{@{}rcl@{}} 2M - \mathbb{E} [U_{i^{k}}^{T} H U_{i^{k}}] &=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \frac{\lambda}{nL} I - \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \frac{\lambda^{2}}{n} I + \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \otimes \frac{\lambda^{2}}{n}(I - \frac{1}{n}\mathbf{11}^{T}) \\ &\quad -& \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \otimes (n-\theta)\frac{\lambda^{2}}{n^{2}}\mathbf{11}^{T} + \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \otimes \frac{\lambda^{2}}{n^{2}}\mathbf{11}^{T}. \end{array} $$

Positive definiteness of this matrix is established by ensuring positivity of the smallest eigenvalue \(\sigma _{\min \limits }\). The smallest eigenvalue \(\sigma _{\min \limits }\) is greater than the sum of the smallest eigenvalue of each term. For the eigenvalues of the Kronecker products, see (4). This gives that

$$ \begin{array}{@{}rcl@{}} \sigma_{\min} \geq \frac{\lambda}{nL} - \frac{\lambda^{2}}{n} - \frac{\lambda^{2}}{n} - \frac{\lambda^{2}}{n}|n-\theta| + 0 = \frac{\lambda}{n}\big(L^{-1} - \lambda(2 + |n-\theta|)\big). \end{array} $$

Since λ > 0 by assumption, if

$$ \begin{array}{@{}rcl@{}} \frac{1}{L(2 + |n - \theta|)} > \lambda. \end{array} $$

we have \(\sigma _{\min \limits } > 0\) and \(2M - \mathbb {E}[U_{i^{k}}^{T} H U_{i^{k}}]\) is positive definite.

Rates are gotten by taking the total expectation of (9) and adding together the inequalities from k = 0 to k = t, yielding

$$ \begin{array}{@{}rcl@{}} \|{z^{0} - z^{\star}}\|_{H\otimes I}^{2} &= &\mathbb{E}[\|{z^{0} - z^{\star}}\|_{H\otimes I}^{2}] - \mathbb{E}[\|{z^{t+1} - z^{\star}}\|_{H\otimes I}^{2}] \\ &\geq& {\textstyle{\sum}_{k=0}^{t}} \mathbb{E}\big[ \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{(2 M - \mathbb{E}[U_{i^{k}}^{T}HU_{i^{k}}]) \otimes I }^{2} \big] \\ &\geq& {\textstyle{\sum}_{k=0}^{t}} \sigma_{\min} \mathbb{E}[\|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2} ] \\ &\geq& \sigma_{\min}(t+1) \min_{k\in\{0,\dots,t\}} \mathbb{E}[\|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}]. \end{array} $$

Putting in the lower bound on \(\sigma _{\min \limits }\) and rearranging yield

$$ \begin{array}{@{}rcl@{}} \min_{k\in\{0,\dots,t\}} \mathbb{E}[\|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}] \leq \frac{n}{\lambda(L^{-1} - \lambda(2 + |n-\theta|))(t+1)}\|{z^{0} - z^{\star}}\|_{H\otimes I}^{2}. \end{array} $$

From the definition of H in Lemma 3.5 we have

$$ \begin{array}{@{}rcl@{}} \|{z^{0} - z^{\star}}\|_{H\otimes I}^{2} &= \|{x^{0} - x^{\star}}\|^{2} + \frac{\lambda}{L}{\textstyle{\sum}_{i=1}^{n}}\|{{y_{i}^{0}} - R_{i}x^{\star}}\|^{2} + \lambda^{2}(n-\theta)^{2}\|{\frac{1}{n}{\textstyle{\sum}_{i=1}^{n}}{y_{i}^{0}}}\|^{2} \\ &\quad - 2\lambda(n-\theta)\langle{x^{0}-x^{\star}}{\frac{1}{n}{\textstyle{\sum}_{i=1}^{n}}{y_{i}^{0}}\rangle } \end{array} $$

where \(z^{\star } = (x^{\star },R_{1}x^{\star },\dots ,R_{n}x^{\star })\). Since this hold for any z⋆ ∈ Z⋆ and hence any x⋆ ∈ X⋆, the results of theorems follows by minimizing the RHS over x⋆ ∈ X⋆. Note, since Rix⋆ constant for all x⋆ ∈ X⋆, the objective is convex and, since X⋆ is closed and convex, the minimum is then attained. □

Proof 8 (Proof of Theorem 3.8)

Combining Lemma 3.5 and 3.6 yield

$$ \begin{array}{@{}rcl@{}} &\mathbb{E}&[\|{z^{k+1} - z^{\star}}\|_{H\otimes I}^{2} + 2\lambda (n-\theta)(F((K\otimes I)z^{k+1}) - F(x^{\star}))| \mathcal{F}_{k}] \\ &\quad\leq& \|{z^{k} - z^{\star}}\|_{H\otimes I}^{2} + 2\lambda (n-\theta)(F((K\otimes I)z^{k}) - F(x^{\star}))\\ &\quad\quad-& \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{(2 M - \mathbb{E} [U_{i^{k}}^{T}HU_{i^{k}}] + \lambda (n-\theta)S - \xi I) \otimes I }^{2} - {\xi n L}\langle{\nabla F(x^{k}) }{x^{k} - x^{\star}}\rangle \end{array} $$

which holds for all \(k\in \mathbb {N}\), \(\xi \in [0, \frac {2\lambda }{nL}]\), and z⋆ ∈ Z⋆. Since H ≻ 0 for λ > 0, see the proof of Theorem 3.7, the first term is non-negative while the second term is non-negative if 𝜃 ≤ n. From cocoercivity of ∇F, the last term is non-positive and we assume, for now, that there exists λ > 0 and \(\frac {2\lambda }{nL}\geq \xi > 0\) such that \(2 M - \mathbb {E} [U_{i^{k}}^{T}HU_{i^{k}}] + \lambda (n-\theta ) S - \xi I \succ 0\), making the third term non-positive.

Applying Proposition 2.1 gives the a.s. summability of

$$ \begin{array}{@{}rcl@{}} \|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|_{(2 M - \mathbb{E} [U_{i^{k}}^{T}HU_{i^{k}}] + \lambda (n-\theta)S - \xi I) \otimes I }^{2} + {\xi n L}\langle{\nabla F(x^{k}) - \nabla F(x^{\star})}{x^{k} - x^{\star}}\rangle. \end{array} $$

Since both term are positive, both terms are a.s. summable. From the first term we have the a.s. convergence of Bzk →Bz⋆ and Lemma 3.4 then gives that all cluster points of \((z^{k})_{k\in \mathbb {N}}\) are almost surely in Z⋆. For the second term we note that by convexity we have

$$ \begin{array}{@{}rcl@{}} \langle{\nabla F(x^{k}) - \nabla F(x^{\star})}{x^{k} - x^{\star}}\rangle \geq F(x^{k}) - F(x^{\star}) \geq 0 \end{array} $$

and F(xk) − F(x⋆) then is summable a.s. since ξnL > 0. Using smoothness of F, (6) and the notation from (8) gives

$$ \begin{array}{@{}rcl@{}} F(x^{\star}) &\leq& F((K\otimes I)z^{k}) \\ &=& F(x^{k} + \frac{\lambda}{n}(D\otimes I)\mathbf{B}z^{k}) \\ &\leq& F(x^{k}) + \langle{(G\otimes I) \mathbf{B}z^{k}}{\frac{\lambda}{n}(D\otimes I) \mathbf{B}z^{k}}\rangle + \frac{L}{2}\|{\frac{\lambda}{n}(D\otimes I)\mathbf{B}z^{k}}\|^{2} \\ &\leq& F(x^{k}) + \|{(G\otimes I) \mathbf{B}z^{k}}\|\|{\frac{\lambda}{n}(D\otimes I) \mathbf{B}z^{k}}\| + \frac{L}{2}\|{\frac{\lambda}{n}(D\otimes I)\mathbf{B}z^{k}}\|^{2} \\ &\to& F(x^{\star}) \text{ a.s.} \end{array} $$

since (G ⊗ I)Bzk → (G ⊗ I)Bz⋆ = 0 and (D ⊗ I)Bzk → (D ⊗ I)Bz⋆ = 0 almost surely. Therefore we have the a.s. convergence of F((K ⊗ I)zk) − F(x⋆) → 0.

From Proposition 2.1 we can also conclude that \(\|{z^{k} - z^{\star }}\|_{H\otimes I}^{2} + 2\lambda (n-\theta )(F((K\otimes I)z^{k}) - F(x^{\star }))\) a.s. converge to a non-negative random variable. Since F((K ⊗ I)zk) − F(x⋆) → 0 a.s. we have that \(\|{z^{k} - z^{\star }}\|_{H\otimes I}^{2}\) also must a.s. converge to a non-negative random variable. Proposition 2.2 then give the almost sure convergence of \((z^{k})_{k\in \mathbb {N}}\) to Z⋆.

We now show that there exists λ > 0 and ξ > 0 such that

$$ \begin{array}{@{}rcl@{}} &&2M - \mathbb{E} [U_{i^{k}}^{T} H U_{i^{k}}] + \lambda (n-\theta) S - \xi I \\ &&\quad= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \frac{\lambda}{nL} I - \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \frac{\lambda^{2}}{n} I + \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \otimes \frac{\lambda^{2}}{n}(I - \frac{1}{n}\mathbf{11}^{T}) + \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \otimes \frac{\lambda^{2}}{n^{2}}\mathbf{11}^{T} \\ &&\quad\quad + \begin{bmatrix} 2 & -1 \\ -1 & 0 \end{bmatrix} \otimes (n-\theta)(\theta - 1)\frac{\lambda^{2}}{n^{3}} \mathbf{11}^{T} - \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \otimes (n-\theta)(\theta - 1)^{2}\frac{L\lambda^{3}}{n^{3}} I \\ &&\quad\quad- \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \otimes \xi I \succ 0. \end{array} $$

We show positive definiteness by ensuring that the smallest eigenvalue is positive. The smallest eigenvalue \(\sigma _{\min \limits }\) is greater than the sum of the smallest eigenvalues of each term,

$$ \begin{array}{@{}rcl@{}} \sigma_{\min} &\geq &\frac{\lambda}{nL} - \frac{\lambda^{2}}{n} - \frac{\lambda^{2}}{n} + 0 + (1 - \frac{\theta-1}{|\theta-1|} \sqrt{2})(n-\theta)(\theta - 1)\frac{\lambda^{2}}{n^{2}} \\ &&- 2(n-\theta)(\theta - 1)^{2} \frac{L\lambda^{3}}{n^{3}} - \xi. \end{array} $$

Assuming \(\lambda \leq \frac {1}{2L}\) yields the following lower bound on the smallest eigenvalue

$$ \begin{array}{@{}rcl@{}} \sigma_{\min} &\geq& \frac{\lambda}{nL} - \frac{2\lambda^{2}}{n} + (1- \frac{\theta-1}{|\theta-1|} \sqrt{2})(n-\theta)(\theta-1)\frac{\lambda^{2}}{n^{2}} - (n-\theta)(\theta - 1)^{2} \frac{\lambda^{2}}{n^{3}} - \xi \\ &=& \frac{\lambda}{n}\big(L^{-1} - \lambda\big(2 + (n-\theta)\frac{\theta-1}{n}\big(\frac{\theta - 1}{n} - 1 + \frac{\theta-1}{|\theta-1|} \sqrt{2}\big)\big)\big) - \xi. \end{array} $$

Selecting

$$ \begin{array}{@{}rcl@{}} \xi = \frac{\lambda}{2n}\big(L^{-1} - \lambda\big(2 + (n-\theta)\frac{\theta-1}{n}\big(\frac{\theta - 1}{n} - 1 + \frac{\theta-1}{|\theta-1|} \sqrt{2}\big)\big)\big), \end{array} $$

which satisfy the assumption \(\frac {2\lambda }{nL}\geq \xi > 0\), yield \(\sigma _{\min \limits } \geq \xi \). Since λ > 0 by assumption, if

$$ \begin{array}{@{}rcl@{}} \frac{1}{L} \frac{1}{2 + (n-\theta)\frac{\theta-1}{n}(\frac{\theta - 1}{n} - 1 + \frac{\theta-1}{|\theta-1|} \sqrt{2})} > \lambda \end{array} $$

we have that \(\sigma _{\min \limits } \geq \xi > 0\) and hence that the examined matrix is positive definite. Furthermore, if λ satisfies the above inequality it also satisfies the assumption \(\lambda \leq \frac {1}{2L}\).

Rates are gotten in the same way as for Theorem 3.7, the total expectation is taken of the Lyapunov inequality at the beginning of the proof and the inequalities are summed from k = 0 to k = t.

$$ \begin{array}{@{}rcl@{}} &&\|{z^{0} - z^{\star}}\|_{H\otimes I}^{2} + 2\lambda (n-\theta)(F((K\otimes I)z^{0}) - F(x^{\star}))\\ &&\quad\geq {\textstyle{\sum}_{k=0}^{t}}\big(\sigma_{\min} \mathbb{E}[\|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}] + \mathbb{E}[\sigma_{\min} n L\langle{\nabla F(x^{k}) }{x^{k} - x^{\star}}\rangle]\big) \\ &&\quad\geq \sigma_{\min}(t+1) \min_{k\in\{1,\dots,t\}}\big(\mathbb{E}[\|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}] + \mathbb{E}[ n L\langle{\nabla F(x^{k}) }{x^{k} - x^{\star}}\rangle]\big) \\ &&\quad\geq \sigma_{\min}(t+1) \min_{k\in\{1,\dots,t\}}\big(\mathbb{E}[\|{\mathbf{B}z^{k} - \mathbf{B}z^{\star}}\|^{2}] + nL\mathbb{E}[F(x^{k}) - F(x^{\star})]\big). \end{array} $$

Inserting the lower bound on \(\sigma _{\min \limits }\), rearranging and minimizing over x⋆ ∈ X⋆ yield the results of the theorem. □

4 Numerical experiments

A number of experiments, outlined below, were performed to verify the tightness of the theory in the cocoercive operator case and examine the effect of bias in the cocoercive gradient case. The experiments were implemented in Julia [3] and, together with several other VR-SG methods, can be found at https://github.com/mvmorin/VarianceReducedSG.jl.

4.1 Cocoercive operators case

In order for the difference between cocoercive operators and cocoercive gradients to not be an artifact of our analysis, the results in the operator case can not be overly conservative. We therefore construct a cocoercive operator problem for which the results appear to be tight, thereby verifying the difference. Consider problem (2) where the operator \(R_{i} : \mathbb {R}^{2} \to \mathbb {R}^{2}\) is an averaged rotation

$$ \begin{array}{@{}rcl@{}} R_{i} = \frac{1}{2} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + \frac{1}{2} \begin{bmatrix} \cos\tau & -\sin\tau\\ \sin\tau & \cos\tau \end{bmatrix} \end{array} $$

for all \(i \in \{1,\dots ,n\}\) and some τ ∈ [0,2π). The operators are 1-cocoercive and the zero vector is the only solution to (2) if τ≠π. The step-size condition from Theorem 3.7 appears to be tight for 𝜃 ∈ [0,n] when the angle of rotation τ approaches π. We therefore let \(\tau = \frac {179}{180}\pi \) and solve the problem with different configurations of step-size λ and innovation weight 𝜃.

Figure 1 displays the relative distance to the solution after 100n iterations of SVAG together with the upper bound on the step-size. When 𝜃 ∈ [0,n] and λ exceeds the upper bound, the distance to the solution increases for both n = 100 and n = 10000, i.e., the method does not converge. Hence, for 𝜃 ∈ [0,n], the step-size bound in Theorem 3.7 appears to be tight. However, it is noteworthy that for this particular problem it seems beneficial to exceed the step-size bound when 𝜃 > n.

Fig. 1
figure 1

Root-finding of averaged rotations: Relative distance to the solution after 100n iterations of SVAG together the step-size upper bound, λL < (2 + |n − 𝜃|)− 1. Note how well the 0th level, i.e., the boundary between convergence and divergence, follow the upper bound on the step-size

Full size image

4.2 Cocoercive gradients case

Since, as we stated in Section 3.2, we do not believe that the theoretical rates are particularly tight in the optimization case, we examine the effects of the bias numerically. These experiments can of course not be exhaustive and we choose to focus on only the bias parameter 𝜃 and therefore perform all experiments with the same step-size. This also demonstrate why we believe the analysis to be conservative since the chosen step-size in some cases are a 1000 times larger than upper bound from Theorem 3.8. Convergence with this large of a step-size have also been seen elsewhere with both [40] and [17] disregarding their own the theoretical step-size conditions.

The experiments are done by performing a rough parameter sweep over the innovation weight 𝜃 on two different binary classification problems and we will look for patterns in how the convergence is affected. ’ The first problem is logistic regression,

$$ \begin{array}{@{}rcl@{}} &\underset{x\in\mathbb{R}^{N}}{\min} \frac{1}{n}{\sum}_{i=1}^{n} \log(1 + e^{-y_{i} {a_{i}^{T}} x}). \end{array} $$

The second is SVM with a square hinge loss,

$$ \begin{array}{@{}rcl@{}} &\underset{x\in\mathbb{R}^{N}}{\min} \frac{1}{n}{\sum}_{i=1}^{n}\big(\max(0,1-y_{i} {a_{i}^{T}} x)^{2} + \frac{\gamma}{2}\|{x}\|^{2}\big) \end{array} $$

where γ > 0 is a regularization parameter. In both problems are yi ∈{− 1,1} the label and \(a_{i} \in \mathbb {R}^{N}\) the features of the i th training data point. Note, although not initially obvious, \(\max \limits (0,\cdot )^{2}\) is convex and differentiable with Lipschitz continuous derivative and the second problem is therefore indeed smooth. The logistic regression problem does not necessarily have a unique solution and the distance to the solution set is therefore hard to estimate. For this reason, we examine the convergence of ∥∇F(xk)∥→ 0 instead of the distance to the solution set.

The datasets for both these classification problems are taken from the LibSVM [6] collection of datasets. The number of examples in the datasets varies between n = 683 and n = 60,000 while the number of features is between N = 10 and N = 5,000. Two of the datasets, mnist.scale and protein, consist of more than 2 classes. These are converted to binary classification problems by grouping the different classes into two groups. For the digit classification dataset mnist.scale, the digits are divided into the groups 0–4 and 5–9. For the protein data set, the classes are grouped as 0 and 1–2. The results of solving the classification problems above can be found in Figs. 2 and 3.

Fig. 2
figure 2

Logistic regression: Expected gradient norm for each iteration. The expected value is estimated with the sample average of 100 runs. A step-size of \(\lambda = \frac {1}{2L}\) was used in all cases

Full size image
Fig. 3
figure 3

Square hinge loss SVM: Expected gradient norm for each iteration. The expected value is estimated with the sample average of 100 runs. A step-size of \(\lambda = \frac {1}{2L}\) was used in all cases

Full size image

From Figs. 2 and 3 it appears like the biggest difference between the innovation weights are in the early stages of the convergence. Most innovation weight choices appear to eventually converge with the same rate. In the cases where this does not happen, the fastest converging choice of innovation weight actually reaches machine precision. It is therefore not possible to say whether these cases would eventually reach the same rate as well. Since none of the choices of 𝜃 appears to consistently be at a significant disadvantage, even though the step-size used exceeds the upper bound in Theorem 3.8 when 𝜃 = 0.1n and 𝜃 = 0.01n, we conjecture that the asymptotic rates for a given step-size is independent of 𝜃.

The initial phase can clearly have a large impact on the convergence and it can therefore still be beneficial to tuning the bias. However, comparing the different choices of innovation weight yields no clear conclusion since no single choice of innovation weight consistently outperforms another. In most cases do the lower bias choices—𝜃 = n (SAGA) or 𝜃 = 0.1n—seem perform best but, when they do not, the high bias choices—𝜃 = 1 (SAG) and 𝜃 = 0.01n—perform significantly better. Another observation is that lowering 𝜃 increases any oscillations. We speculate that it is due to the increased inertia and we also believe that this inertia is what allows the lower innovation weights to sometimes perform better.

5 Conclusion

We presented SVAG, a variance-reduced stochastic gradient method with adjustable bias and with SAG and SAGA as special cases. It was analyzed in two scenarios, one being the minimization of a finite sum of functions with cocoercive gradients and the other being finding a root of a finite sum of cocoercive operators. The analysis improves on the previously best known analyses in both settings and, more significantly, the two different scenarios gave different convergence conditions for the step-size. In the cocoercive operator setting a much more restrictive condition was found and it was verified numerically. This difference is not present in ordinary gradient descent and can therefore easily be overlooked, however, these results suggest that is inadvisable in the variance-reduced stochastic gradient setting.

The theoretical results in the minimization case was further examined with numerical experiments. Several choices of bias were examined but we did not find the same dependence on the bias that the theory suggests. In fact, the asymptotic convergence behavior was similar for the different choices of bias, indicating that further improvements of the theory is still needed. The bias mainly impacted the early stages of the convergence and in a couple of cases this impact was significant. There might therefore still be benefits to tuning the bias to the particular problem but further work is needed to efficiently do so.