Abstract
Two-level Schwarz domain decomposition methods are very powerful techniques for the efficient numerical solution of partial differential equations (PDEs). A two-level domain decomposition method requires two main components: a one-level preconditioner (or its corresponding smoothing iterative method), which is based on domain decomposition techniques, and a coarse correction step, which relies on a coarse space. The coarse space must properly represent the error components that the chosen one-level method is not capable to deal with. In the literature, most of the works introduced efficient coarse spaces obtained as the span of functions defined on the entire space domain of the considered PDE. Therefore, the corresponding two-level preconditioners and iterative methods are defined in volume. In this paper, we use the excellent smoothing properties of Schwarz domain decomposition methods to define, for general elliptic problems, a new class of substructured two-level methods, for which both Schwarz smoothers and coarse correction steps are defined on the interfaces (except for the application of the smoother that requires volumetric subdomain solves). This approach has several advantages. On the one hand, the required computational effort is cheaper than the one required by classical volumetric two-level methods. On the other hand, our approach does not require, like classical multi-grid methods, the explicit construction of coarse spaces, and it permits a multilevel extension, which is desirable when the high dimension of the problem or the scarce quality of the coarse space prevents the efficient numerical solution. Numerical experiments demonstrate the effectiveness of the proposed new numerical framework.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Domain decomposition (DD) methods are powerful divide-and-conquer strategies that permit the solution of linear systems of equations, generally discrete partial differential equation (PDE) problems, by efficient parallelization processes [20, 48, 52]. Over the course of the time, several different parallel DD strategies have been developed; see [28] for an elegant review with a historical flavor. The first idea of parallelizing a Schwarz method goes back to P.L. Lions, who introduced the classical parallel Schwarz method [47]. This method is based on Dirichlet transmission conditions and its discrete version is proved to be equivalent to the famous Restricted Additive Schwarz (RAS) method [28], which was discovered much later in [6]. Similar to RAS is the famous Additive Schwarz (AS) method introduced in [54]. Even though both RAS and AS are based on Dirichlet transmission conditions, they are not equivalent methods; see, e.g., [24] for a detailed comparison analysis. If different transmission conditions are used, one obtains different DD methods, like the optimized Schwarz method [27, 36], the Neumann-Neumann (or FETI) method [9, 52], the Dirichlet-Neumann method [7, 48], etc. The main drawback of these classical one-level DD methods is that they are not (weakly) scalable, since their convergence generally deteriorates when the number of subdomains increases; see, e.g., [7, 20, 52]. Only in few cases a particular scalability behavior has been proved and investigated [7, 10,11,12, 16, 17]. To overcome this scalability issue, a coarse correction step is usually used. This leads to “two-level DD methods”. In the literature, with “two-level DD method” one refers to either a two-level preconditioner [1,2,3,4, 19, 21, 23, 25, 26, 33, 39, 44, 45, 49, 50, 55], or to a two-level stationary method [8, 9, 14, 22, 30,31,32, 34, 35, 37]. While in the first class one seeks for a coarse space matrix to add to the one-level DD preconditioner, in the second class the goal is to design a correction step, where the residual equation is solved on a coarse space. This second class follows an idea similar to the one of multi-grid methods [42].
For any given one-level DD method (stationary or preconditioning), the choice of the coarse space influences very strongly the convergence behavior of the corresponding two-level method. For this reason, the main focus of all the references mentioned above is the definition of different coarse spaces and new strategies to build coarse space functions, leading to efficient two-level DD stationary and preconditioning methods. Despite that the mentioned references consider several one-level DD methods and different partial differential equation (PDE) problems, it is still possible to classify them in two main groups. These depend on the idea governing the definition of the coarse space. To explain it, let us consider a DD iterative method (e.g., RAS) applied to a well-posed PDE problem. Errors and residuals of the DD iterative procedure have generally very special forms. The errors are predominant in the overlaps and are harmonic, in the sense of the underlying PDE operator, in the interior of the subdomains (excluding the interfaces). The residuals are predominant on the interfaces and zero outside the overlap. For examples and more details, see, e.g., [14, 15, 32]. This difference motivated, sometimes implicitly, the construction of different coarse spaces. On the one hand, many references use different techniques to define coarse functions in the overlap (where the error is predominant), and then extend them on the remaining part of the neighboring subdomains; see, e.g., [19, 21, 23, 25, 26, 44, 45, 49, 50]. On the other hand, in other works the coarse space is created by first defining basis functions on the interfaces (where the residual is nonzero), and then extending them (in different ways) on the portions of the neighboring subdomains; see, e.g., [1, 2, 8, 9, 14, 30, 32,33,34,35, 37, 44]. For a good, compact and complete overview of several of the different coarse spaces, we refer to [44, Section 5]. For Helmholtz and time-harmonic equations, we refer to [3, 4, 39], where the coarse space is based on a (volumetric) coarse mesh. For other different techniques and other related discussions, see, e.g., [20, 22, 30, 31, 40, 55].
The starting point of this work is related to an important property of Schwarz methods: one-level Schwarz iterative methods are generally very efficient smoothers; see, e.g., [10, 13, 27, 37] and references therein. This property was already discussed in [42, Chapter 15], where Schwarz methods are used as classical smoothers in the context of multi-grid methods or to define local defect corrections; see, e.g., [37, 41]. In these frameworks, Schwarz methods are used to smooth and correct the approximation in some subdomains of the entire computational domain. However, as we already mentioned, after one Schwarz smoothing iteration, the residuals are generally predominant on the interfaces and in some cases even zero outside the interfaces. This remark is the key starting point of our work. We introduce for the first time so-called two-level and multilevel DD substructured methods. We call these methods Geometric 2-level Substructured (G2S) method and Geometric Multilevel Substructured (GMS) method. The term “substructured” indicates that iterations and coarse correction steps are defined on the interfaces (or more precisely on the substructuresFootnote 1) of the domain decomposition (note that volumetric subdomains solves are still required to apply the smoother). With this respect, our methods are defined in the same spirit as two-level methods whose coarse spaces are extensions in volume of interfaces basis functions: they attempt to correct the residual only where it is truly necessary. The G2S method is essentially a two-grid parallel Schwarz method defined on the substructures, for which the coarse correction is performed on coarser interface grids. The GMS is the extension of the G2S to a multilevel framework. In other words, by the G2S and GMS methods, we propose a new methodology that attempts the best use of Schwarz smoothers in the context of two-grid and multi-grid methods. Direct numerical experiments show that these methods converge in less iterations than classical two-grid methods defined in volume and using a Schwarz smoother. In many cases, this improvement in terms of iteration number is significantly high. Moreover, our new methods have, in addition, other advantages. On the one hand, like classical multi-grid methods, the G2S method does not require the explicit construction of coarse spaces, and it permits a multilevel extension, which is desirable when the dimension of the coarse space becomes too large. On the other hand, since the entire solution process is defined on the substructures, less memory storage is required and it is not necessary to store the entire approximation array on each point of the (discrete) domain. For a three-dimensional problem with mesh size h, a discrete substructure array is of size O(1/h2). This is much smaller than O(1/h3), which is the size of an array corresponding to an approximation in volume. For this reason, the resulting interface restriction and prolongation operations are generally much cheaper and the dimension of the coarse space is much smaller.
This paper is organized as follows. In Section 2, we formulate the classical parallel Schwarz method in a substructured form. This is done at the continuous level and represents the starting point for the G2S method introduced in Section 3, where also a convergence analysis is presented for two subdomains in 2d. In Section 4, we discuss implementation details and multilevel extensions of the G2S method. Extensive numerical experiments are presented in Section 5, where the robustness of the proposed methods with respect to mesh refinement and physical parameters is studied. Finally, we present our conclusions in Section 6.
2 Substructured Schwarz domain decomposition methods
Consider a bounded Lipschitz domain \({\varOmega } \subset \mathbb {R}^{d}\) for d ∈{2,3}, a general second-order linear elliptic operator \({\mathscr{L}}\) and a function f ∈ L2(Ω). Our goal is to introduce new domain decomposition-based methods for the efficient numerical solution of the general linear elliptic problem
which we assume to be uniquely solved by a \(u \in {H_{0}^{1}}({\varOmega })\).
To formulate our methods, we need to fix some notation. Given a bounded set Γ with boundary ∂Γ, we denote by ρΓ(x) the distance of x ∈Γ from ∂Γ. The space \(H_{00}^{1/2}({\varGamma })\) is then defined as
and it is also known as the Lions-Magenes space; see, e.g., [46, 48, 51]. Equivalently, \(H_{00}^{1/2}({\varGamma })\) can be defined as the space of functions in H1/2(Γ) such that their extensions by zero to a superset \(\widetilde {{\varGamma }}\) of Γ are in \(H^{1/2}(\widetilde {{\varGamma }})\); see, e.g., [51].
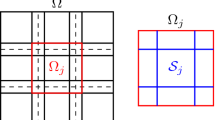
Next, consider a decomposition of Ω into N overlapping Lipschitz subdomains Ωj, that is \({\varOmega } = \cup _{j \in \mathcal {I}} {\varOmega }_{j}\) with \(\mathcal {I}:=\{1,2,\dots ,N\}\). For any \(j \in \mathcal {I}\), we define the set of neighboring indexes \(\mathcal {N}_{j} :=\{ \ell \in \mathcal {I} : {\varOmega }_{j} \cap \partial {\varOmega }_{\ell } \neq \emptyset \}\). Notice that \(j\notin \mathcal {N}_{j}\), and \(\cup _{j\in \mathcal {I}} \mathcal {N}_{j} = \mathcal {I}\). Given a \(j \in \mathcal {I}\), we introduce the substructure of Ωj defined as \(\mathcal {S}_{j} := \cup _{\ell \in \mathcal {N}_{j}} \bigl (\partial {\varOmega }_{\ell } \cap {\varOmega }_{j}\bigr )\), that is the union of all portions of ∂Ωℓ intersecting with Ωj with \(\ell \in \mathcal {N}_{j}\).Footnote 2 The sets \(\mathcal {S}_{j}\) are open and their closures are \(\overline {\mathcal {S}_{j}} = \mathcal {S}_{j} \cup \partial \mathcal {S}_{j}\), with \(\partial \mathcal {S}_{j} := \cup _{\ell \in \mathcal {N}_{j}} \bigl (\partial {\varOmega }_{j} \cap \partial {\varOmega }_{\ell } \bigr )\). The substructure of Ω is defined as \(\mathcal {S}:=\cup _{j \in \mathcal {I}}\overline {\mathcal {S}_{j}}\). Figure 1 provides an illustration of substructures corresponding to a commonly used decomposition of a rectangular domain. We denote by \(\mathcal {E}_{j}^{0} : L^{2}(\mathcal {S}_{j}) \rightarrow L^{2}(\mathcal {S})\) the extension by zero operator. Now, we consider a set of continuous functions \(\chi _{j} : \overline {\mathcal {S}_{j}} \rightarrow [0, 1]\), \(j=1,\dots ,N\), such that
and \({\sum }_{j\in \mathcal {I}} \mathcal {E}_{j}^{0} \chi _{j} \equiv 1\), which means that the functions χj form a partition of unity. Further, we assume that the functions χj, \(j \in \mathcal {I}\), satisfy the condition \(\chi _{j} / \rho _{\mathcal {S}_{j}}^{1/2}~\in ~L^{\infty }(\mathcal {S}_{j})\). This is satisfied, for example, in the case of Fig. 1 with piecewise linear partition of unity function χj.
For any \(j \in \mathcal {I}\), we define \({\varGamma }_{j}^{\text {int}} := \partial {\varOmega }_{j} \cap \bigl (\cup _{\ell \in \mathcal {N}_{j}} {\varOmega }_{\ell } \bigr )\) and introduce the following trace and restriction operators
It is well known that (1) is equivalent to the domain decomposition system (see, e.g., [48])
where \(f_{j} \in L^{2}({\varOmega }_{j})\) is the restriction of f on Ωj. Notice that χℓτℓuℓ lies in \(H_{00}^{1/2}(\mathcal {S}_{\ell })\), \(\mathcal {E}_{\ell }^{0}(\chi _{\ell } \tau _{\ell } u_{\ell }) \in H^{1/2}(\mathcal {S})\). Moreover, for \(\ell \in \mathcal {N}_{j}\), it holds that \(\tau _{j}^{\text {int}} \mathcal {E}_{\ell }^{0}(\chi _{\ell } \tau _{\ell } u_{\ell }) \in H_{00}^{1/2}({\varGamma }_{j}^{\text {int}})\) if \({\varGamma }_{j}^{\text {int}} \subsetneq \partial {\varOmega }_{j}\), and \(\tau _{j}^{\text {int}} \mathcal {E}_{\ell }^{0}(\chi _{\ell } \tau _{\ell } u_{\ell }) \in H^{1/2}({\varGamma }_{j}^{\text {int}})\) if \({\varGamma }_{j}^{\text {int}} = \partial {\varOmega }_{j}\).
Given a \(j \in \mathcal {I}\) such that \(\partial {\varOmega }_{j}\setminus {\varGamma }_{j}^{\text {int}}\neq \emptyset \), we define the extension operator \(\mathcal {E}_{j} : H^{1/2}_{00}({\varGamma }_{j}^{\text {int}}) \times L^{2}({\varOmega }_{j}) \rightarrow H^{1}({\varOmega }_{j})\) as \(w=\mathcal {E}_{j}(v,f_{j})\), where w solves the problem
for a \(v \in H_{00}^{1/2}({\varGamma }_{j}^{\text {int}})\). Otherwise, if \({\varGamma }_{j}^{\text {int}}\equiv \partial {\varOmega }_{j}\), we define \(\mathcal {E}_{j}:H^{1/2}({\varGamma }_{j}^{\text {int}})\times L^{2}({\varOmega }_{j})\rightarrow H^{1}({\varOmega }_{j})\) as \(w=\mathcal {E}_{j}(v,f_{j})\), where w solves the problem
for a \(v\in H^{1/2}({\varGamma }_{j}^{\text {int}})\).
The domain decomposition system (3) can be then written as
If we define vj := χjτjuj, \(j\in \mathcal {I}\), then system (6) becomes
where \(g_{j} := \chi _{j} \tau _{j}\mathcal {E}(0,f_{j})\) and the operators \(G_{j,\ell } : H_{00}^{1/2}(\mathcal {S}_{\ell }) \rightarrow H_{00}^{1/2}(\mathcal {S}_{j})\) are defined as
System (7) is the substructured form of (3). The equivalence between (3) and (7) is explained by the following theorem.
Theorem 1 (Relation between (3) and (7))
Let \(u_{j} \in H^{1}({\varOmega }_{j})\), \(j\in \mathcal {I}\), solve (3), then vj := χjτjuj, \(j\in \mathcal {I}\), solve (7). Let \(v_{j} \in H^{1/2}_{00}(\mathcal {S}_{j})\), \(j\in \mathcal {I}\), solve (7), then \(u_{j} := \mathcal {E}_{j}(\tau _{j}^{\text {int}}{\sum }_{\ell \in \mathcal {N}_{j}} \mathcal {E}_{\ell }^{0} (v_{\ell }),f_{j})\), \(j\in \mathcal {I}\), solve (3).
Proof
The first statement is proved before Theorem 1, where the substructured system (7) is derived. To obtain the second statement, we use (7) and the definition of uj to write \(v_{j} = \chi _{j} \tau _{j} \mathcal {E}_{j}(\tau _{j}^{\text {int}} {\sum }_{\ell \in \mathcal {N}_{j} } \mathcal {E}_{\ell }^{0} (v_{\ell }),f_{j}) = \chi _{j} \tau _{j} u_{j}\). The claim follows by using this equality together with the definitions of uj and \(\mathcal {E}_{j}\). □
Take any function \(w \in {H^{1}_{0}}({\varOmega })\) and consider the initialization \({u_{j}^{0}}:=w|_{{\varOmega }_{j}}\), \(j \in \mathcal {I}\). The parallel Schwarz method (PSM) is then given by
for \(n \in \mathbb {N}^{+}\), and has the substructured form
initialized by \({v_{j}^{0}} := \chi _{j} \tau _{j} {u_{j}^{0}} \in H^{1/2}_{00}(\mathcal {S}_{j})\). Notice that the iteration (10) is well posed in the sense that \({v_{j}^{n}} \in H^{1/2}_{00}(\mathcal {S}_{j})\) for \(j \in \mathcal {I}\) and \(n \in \mathbb {N}\). Equations (10) and (7) allow us to obtain the substructured PSM in error form, that is
for \(n \in \mathbb {N}^{+}\), where \({e_{j}^{n}}:=v_{j}-{v_{j}^{n}}\), for \(j \in \mathcal {I}\) and \(n\in \mathbb {N}\). Equation (7) can be written in the matrix form Av = b, where \(\textbf {v}=[v_{1},\dots ,v_{N}]^{\top }\), \(\textbf {b}=[g_{1},\dots ,g_{N}]^{\top }\) and the entries of A are
where Id, j are the identities on \(L^{2}(\mathcal {S}_{j})\), \(j \in \mathcal {I}\). Similarly, we define the operator G as
which allows us to write (10) and (11) as vn = Gvn− 1 + b and en = Gen− 1, respectively, where \(\textbf {v}^{n} :=[{v_{1}^{n}},\dots ,{v_{N}^{n}}]^{\top }\) and \(\textbf {e}^{n} :=[{e_{1}^{n}},\dots ,{e_{N}^{n}}]^{\top }\). Notice that \(G=\mathbb {I}-A\), where \(\mathbb {I}:=\text {diag}_{j=1,\dots ,N}(I_{d,j})\). Moreover, we wish to remark that neither the operator A nor G is necessarily symmetric.
If the iteration vn = Gvn− 1 + b converges, then the limit is the solution to the problem Av = b. From a numerical point of view, this is not necessarily true if the (discretized) subproblems (9) are not solved exactly. For this reason, we assume in what follows that the subproblems (9) are always solved exactly.
3 G2S: geometric two-level substructured DD method
In this section, we introduce our G2S method. The main drawback of many two-level DD methods (including our two-level G2S method) is that the dimension of the coarse space can grow for increasing number of subdomains. This situation becomes even worse if the basis functions are not “good enough”, a fact that would require an even larger dimension of the coarse space. In this case, the extension from two-level to multilevel framework would be suitable. These comments lead to the following questions. Is it possible to avoid the explicit construction of a coarse space? Is there any practical way to implicitly define a coarse space? Can one define a framework in which an extension of the two-level method to a multilevel framework is possible and easy?
In this section, we answer the above questions by introducing the so-called Geometric 2-level Substructured (G2S) method, which is a two-grid-type method (allowing a multi-grid generalization). This is detailed in Section 3.1. The corresponding convergence analysis for a two-subdomain case is presented in Section 3.2.2.
3.1 Description of the G2S method
Let us consider a discretization of the substructures such that \(\mathcal {S}_{j}\) is approximated by a mesh of Nj points, \(j\in \mathcal {I}\). The discrete substructures are denoted by \(\mathcal {S}_{j}^{N_{j}}\), \(j \in \mathcal {I}\). An example is given in Fig. 2 (left).
Left: The subdomain Ωj as in Fig. 1, its substructure \(\mathcal {S}_{j}\) (blue lines) and the corresponding discrete substructure \(\mathcal {S}^{N_{j}}_{j}\)(black circles). Right: The coarse discrete substructure \(\mathcal {S}^{M_{j}}_{j}\) is marked by red crosses
Moreover, we set \(N^{s} := {\sum }_{j \in \mathcal {I}} N_{j}\). The corresponding finite-dimensional discretization of the operators Gj, ℓ in (8) are denoted by \(G_{h,j,\ell } \in \mathbb {R}^{N_{j} \times N_{\ell }}\). Similarly as in (12), we define the block operators \(A_{h} \in \mathbb {R}^{N^{s} \times N^{s}}\) and \(G_{h} \in \mathbb {R}^{N^{s} \times N^{s}}\) as
where \(I_{h,j} \in \mathbb {R}^{N_{j} \times N_{j}}\) are identity matrices. Notice that \(A_{h} = \mathbb {I}_{h} - G_{h}\), where \(\mathbb {I}_{h}=\text {diag}(I_{h, 1},\dots ,I_{h,N})\). Therefore, the substructured problem Av = b becomes
where \(\textbf {b}_{h} = [\textbf {b}_{h, 1},\dots ,\textbf {b}_{h,N}]\), and the PSM is then
The matrices Gh and \(A_{h}=\mathbb {I}_{h} - G_{h}\) are not necessarily symmetric and never assembled explicitly. Instead their action of given vectors is computed directly. Notice that the computation of the action of Gh, j, ℓ on a given vector requires a subdomain solve. We insist on the fact that this subdomain solve is performed exactly. Furthermore, if the discrete PSM (14) converges, then ρ(Gh) < 1 and the matrix Ah is invertible.
Next, we introduce coarser discretizations \(\mathcal {S}_{j}^{M_{j}}\), \(j \in \mathcal {I}\), where the j th substructure is discretized with Mj < Nj points. An example is given in Fig. 2 (right). The total number of discrete coarse points is \(M^{s}:= {\sum }_{j \in \mathcal {I}} M_{j}\). For each \(j \in \mathcal {I}\) we introduce restriction and prolongation matrices \(R_{j} \in \mathbb {R}^{M_{j}\times N_{j}}\) and \(P_{j} \in \mathbb {R}^{N_{j}\times M_{j}}\). These could be classical interpolation operators used, e.g., in multi-grid methods. If for example \(\mathcal {S}_{j}\) is a one-dimensional interval, then the prolongation matrix can be chosen as
and the corresponding restriction matrix would be the full weighting restriction operator \(R_{j}:=\frac {1}{2} P_{j}^{\top }\). The global restriction and prolongation matrices are defined as \(R:=\text {diag}(R_{1},\dots ,R_{N}) \in \mathbb {R}^{M^{s}\times N^{s}}\) and \(P:=\text {diag}(P_{1},\dots ,P_{N}) \in \mathbb {R}^{N^{s}\times M^{s}}\). The restriction of Ah on the coarse level is then defined as A2h := RAhP. Notice that this matrix can be either precomputed exactly or assembled in an approximate way. For more details see Section 4.1.
Remark 1
Notice that, for the definition of the G2S method, fine and coarse meshes need not to be nested and the sets \(\mathcal {S}_{j}^{M_{j}}\) need not to coincide on overlapping areas. In this manuscript, we work with nested meshes. The case of non-nested meshes is beyond the scope of this paper and will be the subject of future work. Moreover, it is natural to include cross points in both fine and coarse discrete substructures, since these are generally the corners of the (overlapping) subdomains (see, e.g., Figs. 2 and 7).
The G2S procedure is defined by the following Algorithm 1, where n1 and n2 are the numbers of the pre- and post-smoothing steps.

This is a classical two-grid type iteration, but instead of having the classical grids in volume, we consider two discrete levels on the substructures. This has the advantage of performing all restriction and interpolation operations of smaller coarse problems. More details are given in Section 4.1. We insist on the fact that the G2S method does not require the explicit construction of a coarse space Vc, but it exploits directly a discretization of the interfaces. Moreover, it is clear that a simple recursion allows us to embed the G2S method into a multi-grid framework. Further implementation details are discussed in Section 4.
Formally, one iteration of our G2S method can be represented as
where \(\widetilde {M}\) is a matrix which acts on the right-hand side vector bh and which can be regarded as the preconditioner corresponding to our two-level method. In error form, the iteration (16) becomes
where enew := v −vnew and eold := v −vold.
3.2 Analysis of the G2S method
In this section, we analyze the convergence of the G2S method. To do so, we recall our model problem (1) and assume a two-subdomain decomposition Ω = Ω1 ∪Ω2 such that the two substructures \(\mathcal {S}_{1}\) and \(\mathcal {S}_{2}\) are two segments of the same length \(\widetilde {L}\). Notice that in this case the substructures coincide with the interfaces. An example for Ω equal to a rectangle is given in Fig. 3.
For a given \(\ell \in \mathbb {N}^{+}\), ℓ ≥ 2, we discretize (1) using a uniform grid of Nh = 2ℓ − 1 points on each substructure (without counting the two points on ∂Ω) so that the grid size is \(h=\frac {\widetilde {L}}{N_{h}+1}\). Notice that Nh = N1 = N2, where Nj are used in Section 3.1 to denote the number of discretization points of the substructures. We also introduce a coarser mesh of Nc = 2ℓ− 1 − 1 points on each substructure and mesh size \(h_{c}=\frac {\widetilde {L}}{N_{c}+1}\). We define the geometric prolongation operator \(P\in \mathbb {R}^{2N_{h} \times 2N_{c}}\) as \(P :=\text {diag}(\widetilde {P},\widetilde {P})\), where \(\widetilde {P}=P_{1}=P_{2}\) is the matrix given in (15). The operator \(R\in \mathbb {R}^{2N_{c} \times 2N_{h}}\) is defined as \(R :=\text {diag}(\widetilde {R},\widetilde {R})\), where \(\widetilde {R}\) is the full weighting restriction matrix \(\widetilde {R}:=\frac {1}{2} \widetilde {P}^{\top }\). Due to the special decomposition into two subdomains, let us simplify the notation defining Gh, 1 := Gh, 1,2 and Gh,2 := Gh,2, 1, that is the action of Gh, j represents a subdomain solution in the j th subdomain. We suppose that the operators Gh, 1 and Gh,2 have eigenvectors ψk with eigenvalues ρj(k), \(k=1,\dots ,N_{h}\), j = 1, 2. Here, ψk are discrete Fourier modes given by \((\boldsymbol {\psi }_{k})_{j}=\sin \limits (k\pi h j)\), for \(j,k=1,\dots ,N_{h}\). Notice that \(\boldsymbol {\psi }_{\ell }^{\top } \boldsymbol {\psi }_{k} = \delta _{\ell ,k}\frac {N_{c}+1}{2}\), with δℓ, k the Kronecker delta.
It is well known that the actions of \(\widetilde {R}\) and \(\widetilde {P}\) on the combination of a low-frequency mode ψk with its high-frequency companion \(\boldsymbol {\psi }_{\widetilde {k}}\), with \(\widetilde {k}=N_{h}-k+1\), are
where \(c_{k}=\cos \limits (k\pi \frac {h}{2})\), \(s_{k}=\sin \limits (k\pi \frac {h}{2})\) for \(k=1,\dots ,N_{c}\) and \((\boldsymbol {\phi }_{k})_{j}=\sin \limits (k\pi 2hj)\), for \(k=1,\dots ,\frac {N_{h}+1}{2}-1\) and \(j=1,\dots ,\frac {N_{h}+1}{2}-1=N_{c}\) (notice that the two points on ∂Ω are excluded); see, e.g., [13, 42]. The vectors ϕk are Fourier modes on the coarse grid. As before, the coarse matrix is A2h = RAhP, and the G2S iteration operator is \(T_{h}=G_{h}^{n_{2}}(I-P A_{2h}^{-1}R A_{h})G_{h}^{n_{1}}\).
In the following subsections, we prove that G2S method is well posed and convergent. Well-posedness follows by the invertibility of the coarse matrix A2h, which is proved in Section 3.2.1 along with an interpretation of the G2S method. A detailed convergence analysis is presented in Section 3.2.2, where sharp estimates of the spectral radius of Th are derived under certain assumptions. Finally, in Section 3.2.3 we discuss the relations between our G2S method and a classical two-grid method in volume using the PSM as a smoother.
3.2.1 Interpretation of G2S as a general two-level method
Let us begin by considering any invertible matrix \(U \in \mathbb {R}^{2 N_{c} \times 2 N_{c}}\) and compute
where \(\widehat {P}:=P U\), \(\widehat {R} = U^{-1} R\) and \(\widehat {A}_{2h}:=\widehat {R} A_{h} \widehat {P}\).
Let us define the orthogonal matrices \({\varPhi }=\frac {2}{N_{c}+1}[\boldsymbol {\phi }_{1},\dots ,\boldsymbol {\phi }_{N_{c}}]\) and U := diag(Φ, Φ), and the operators \(\widehat {P}:=P U\), \(\widehat {R} = U^{\top } R\)Footnote 3 and \({\widehat {A}_{2h}}:=\widehat {R} A_{h} \widehat {P}\). Notice that the columns of \(\widehat {P}:=P U\) are the vectors spanning the space
where the relation (17) is used. This means that the G2S method can be written as a two-level method characterized by an iteration operator \(\widehat {T}_{h}\) defined via the prolongation and restriction operators \(\widehat {P}\) and \(\widehat {R}\). Moreover, in this case the actions of \(\widehat {P}\) and \(\widehat {R}\) on two vectors can be expressed by
for any \(\textbf {v},\textbf {w} \in \mathbb {R}^{N_{c}}\) and any \(\textbf {f},\textbf {g} \in \mathbb {R}^{N_{h}}\), where 〈⋅,⋅〉 denotes the usual Euclidean scalar product.
Now, we turn our attention to the matrix A2h, whose invertibility is proved in the following lemmas.
Lemma 1 (Invertibility of a coarse operator A c)
Let \((\mathcal {X}_{j},\langle \cdot ,\cdot \rangle _{j})\), j = 1,2 be two inner-product spaces. Define the space \(\mathcal {X}:=\mathcal {X}_{2} \times \mathcal {X}_{1}\) endowed with the inner product 〈(a, b),(c, d)〉 := 〈a, c〉2 + 〈b, d〉1 for all \((a,b),(c,d) \in \mathcal {X}\). Consider some bases \(\{\psi _{\ell }^{j}\}_{\ell \in \mathbb {N}} \subset \mathcal {X}_{j}\), j = 1,2. Let Vc be a finite-dimensional subspace of \(\mathcal {X}\) given by the span of the basis vectors \(({\psi _{1}^{2}},0),\dots ,({\psi _{m}^{2}},0)\) and \((0,{\psi _{1}^{1}}),\dots ,(0,{\psi _{m}^{1}})\), for a finite integer m > 0. Let \(\mathbb {P}_{V_{c}}\) be the orthogonal projection operator onto Vc. Consider an invertible operator \(A : \mathcal {X} \rightarrow \mathcal {X}\) and the matrix \(A_{c} = {\mathcal {R}} A {\mathcal {P}} \in \mathbb {R}^{2m \times 2m}\), where \({\mathcal {P}}\) and \(\mathcal {R}\) are defined as
Then Ac has full rank if and only if \(\mathbb {P}_{V_{c}}(A \textbf {v} ) \neq 0 \forall \textbf {v} \in V_{c}\setminus \{0\}\).
Proof
We first show that if \(\mathbb {P}_{V_{c}}(A\textbf {v} ) \neq 0\) for any v ∈ Vc ∖{0}, then \(A_{c} = {\mathcal {R}} A {\mathcal {P}}\) has full rank. This result follows from the rank-nullity theorem, if we show that the only element in the kernel of Ac is the zero vector. To do so, we recall the definitions of \({\mathcal {P}}\) and \({\mathcal {R}}\) given in (21). Clearly, \({\mathcal {P}} \textbf {z}=0\) if and only if z = 0. For any \(\textbf {z} \in \mathbb {R}^{2m}\) the vector \({\mathcal {P}} \textbf {z}\) is in Vc. Since A is invertible, then \(A{\mathcal {P}}\textbf {z}=0\) if and only if z = 0. Moreover, by our assumption it holds that \(\mathbb {P}_{V_{c}}(A {\mathcal {P}}\textbf {z}) \neq 0\). Now, we notice that \({\mathcal {R}}\textbf {w} \neq 0\) for all w ∈ Vc ∖{0}, and \({\mathcal {R}}\textbf {w} = 0\) for all \(\textbf {w} \in V_{c}^{\perp }\), where \(V_{c}^{\perp }\) denotes the orthogonal complement of Vc in \(\mathcal {X}\) with respect to 〈⋅,⋅〉. Since \((\mathcal {X},\langle \cdot , \cdot \rangle )\) is an inner-product space, we have \(A{\mathcal {P}}\textbf {z} = \mathbb {P}_{V_{c}}(A{\mathcal {P}}\textbf {z}) + (I-\mathbb {P}_{V_{c}})(A{\mathcal {P}}\textbf {z})\) with \((I-\mathbb {P}_{V_{c}})(A{\mathcal {P}}\textbf {z}) \in V_{c}^{\perp }\). Hence, \({\mathcal {R}} A {\mathcal {P}}\textbf {z} = {\mathcal {R}}\mathbb {P}_{V_{c}}(A {\mathcal {P}}\textbf {z}) \neq 0\) for any nonzero \(\textbf {z} \in \mathbb {R}^{2m}\).
Now we show that, if \(A_{c} = {\mathcal {R}} A {\mathcal {P}}\) has full rank, then \(\mathbb {P}_{V_{c}}(A\textbf {v} ) \neq 0\) for any v ∈ Vc ∖{0}. We proceed by contraposition and prove that if there exists a v ∈ Vc ∖{0} such that \(A\textbf {v} \in V_{c}^{\perp }\), then \(A_{c} = {\mathcal {R}} A {\mathcal {P}}\) has not full rank. Assume that there is a v ∈ Vc ∖{0} such that \(A\textbf {v} \in V_{c}^{\perp }\). Since v is in Vc, there exists a nonzero vector \(\textbf {z} \in \mathbb {R}^{2m}\) such that \(\textbf {v}=\mathcal {P}\textbf {z}\). Hence \(A {\mathcal {P}}\textbf {z} \in V_{c}^{\perp }\). We can now write that \(A_{c} \textbf {z}= {\mathcal {R}} (A {\mathcal {P}}\textbf {z})=0\), which implies that Ac has not full rank. □
Lemma 2 (Invertibility of A 2h)
Assume that ρ1(k), ρ2(k) ∈ [0, 1) for all k and that \(\rho _{1}(k)\geq \rho _{1}(\widetilde {k})\) and \(\rho _{2}(k)\geq \rho _{2}(\widetilde {k})\) for any \(k=1,\dots ,N_{c}\) and \(\widetilde {k}=N_{h}-k+1\). The matrix \(A_{2h}:={R} A_{h} {P} \in \mathbb {R}^{2N_{c} \times 2N_{c}}\) has full rank.
Proof
Since \(A_{2h} = U \widehat {A}_{2h} U^{\top }\), it is enough to show that \(\widehat {A}_{2h}\) is invertible. To do so, we recall that \(\widehat {A}_{2h}={\widehat {R}} A_{h} {\widehat {P}}\) and we wish to prove that for any z ∈ Vc ∖{0} (with Vc defined in (19)) it holds \(\mathbb {P}_{V_{c}}(A_{h}\textbf {z}) \neq 0\) and then invoke Lemma 1. Here the orthogonality is understood with respect to the classical scalar product of \(\mathbb {R}^{2N_{h}}\). First, it is possible to show that the orthogonal complement of Vc is
Notice that \({\dim (V_{c}) = 2N_{c}}\), \({\dim (V_{c}^{\perp }) = 2(N_{c}+1)}\), and \({\dim (V_{c})} + {\dim (V_{c}^{\perp }) = 2N_{h}}\), since Nh = 2Nc + 1.
Since the vectors spanning Vc in (19) are orthogonal, we have \(\mathbb {P}_{V_{c}}(\textbf {w}) = {\widehat {P}\widehat {P}^{\top }} \textbf {w}\) for any \(\textbf {w} \in \mathbb {R}^{2N_{h}}\), Since \({\widehat {P}}\) has full rank, to prove that \(\mathbb {P}_{V_{c}}(A_{h}\textbf {z}) \neq 0\) for any z ∈ Vc ∖{0} it is sufficient to show that \({\widehat {P}^{\top }} A_{h} \textbf {v} \neq 0\) holds for any column v of \({\widehat {P}}\), that is any element of the form \([(\widetilde {P}\boldsymbol {\phi }_{k})^{\top } , (\widetilde {P}\boldsymbol {\phi }_{\ell })^{\top } ]^{\top }\). Therefore, we use (17) and compute
for any \(k,\ell =1,\dots ,N_{c}\), where \(\widetilde {k}=N_{h}-k+1\) and \(\widetilde {\ell }=N_{h}-\ell +1\), for \(k,\ell =1,\dots ,N_{c}\). Now, a direct calculation shows that
for any \(k=1,\dots ,N_{c}\). Inserting this equality into (22), multiplying to the left with \([(\widetilde {P}\boldsymbol {\phi }_{k})^{\top } , (\widetilde {P}\boldsymbol {\phi }_{\ell })^{\top } ]\) and using (17) together with the orthogonality relation \(\boldsymbol {\psi }_{\ell }^{\top } \boldsymbol {\psi }_{k} = \delta _{\ell ,k}\frac {N_{c}+1}{2}\), we obtain for k≠ℓ that
Similarly, for k = ℓ we obtain that
A direct calculation using the assumptions on ρj(k) shows that this is nonzero. □
3.2.2 Convergence of the G2S method
The previous section focused on the well-posedness of the method. In particular, we proved Lemma 2 that guarantees that A2h is invertible and that the G2S method is well posed. In this section, our attention is turned to the analysis of the G2S convergence behavior. This is performed by studying the spectral properties of the G2S iteration operator. Our first key result is the following technical lemma.
Lemma 3
Consider the G2S matrix \(T_{h}:=G_{h}^{n_{2}}(I-{P}A_{2h}^{-1}{R}A_{h})G_{h}^{n_{1}}\). The action of Th on \(\left [\begin {array}{llll} \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} & 0 & 0\\ 0 & 0 & \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} \end {array}\right ]\) is given by
where \(\widetilde {G}_{k}:=D_{n_{2}}(k)(D_{n_{1}}(k)-V(k){\varLambda }_{2}^{-1}(k){\varLambda }_{1}(k))\) with
and Dn(k) is given by
for n even and for n odd, respectively, whose entries are π(k) := (ρ1(k)ρ2(k))1/2, \(\pi _{12}(k,n):=\rho _{1}(k)^{\frac {n-1}{2}}\rho _{2}(k)^{\frac {n+1}{2}}\), and \(\pi _{21}(k,n):=\rho _{1}(k)^{\frac {n+1}{2}}\rho _{2}(k)^{\frac {n-1}{2}}\).
Proof
We consider the case in which both n1 and n2 are even. The other cases can be obtained by similar arguments. Since n1 is even, we have that
Because of the relation \((G_{h, 1}G_{h,2})^{n_{1}/2} \boldsymbol {\psi }_{k} = (G_{h,2}G_{h, 1})^{n_{1}/2} \boldsymbol {\psi }_{k} = \pi (k)^{n_{1}} \boldsymbol {\psi }_{k}\), where π(k) := (ρ1(k)ρ2(k))1/2, we get
Similarly, we obtain that \(G_{h}^{n_{2}} \left [\begin {array}{cccc} \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} & 0 & 0\\ 0 & 0 & \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} \end {array}\right ] = \left [\begin {array}{cccc} \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} & 0 & 0\\ 0 & 0 & \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} \end {array}\right ] D_{n_{2}}(k)\). Moreover, direct calculations reveal that
and
where we used (17). It follows that \(\setlength \arraycolsep {0.9pt} {R}A_{h} {G_{h}^{n_{1}}} \left [\begin {array}{cccc} \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} & 0 & 0\\ 0 & 0 & \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} \end {array}\right ] = \left [\begin {array}{cccc} \boldsymbol {\phi }_{k} & 0\\ 0 & \boldsymbol {\phi }_{k} \end {array}\right ] {\varLambda }_{1}(k). \) Let us now study the action of the coarse matrix A2h on \(\left [\begin {array}{cc} \boldsymbol {\phi }_{k} & 0\\ 0 & \boldsymbol {\phi }_{k} \end {array}\right ]\). We use (17), (24) and (25) to write
Thus, we have \(A_{2h} \left [\begin {array}{cc} \boldsymbol {\phi }_{k} & 0\\ 0 & \boldsymbol {\phi }_{k} \end {array}\right ] = \left [\begin {array}{cc} \boldsymbol {\phi }_{k} & 0\\ 0 & \boldsymbol {\phi }_{k} \end {array}\right ] {\varLambda }_{2}(k)\), and since A2h is invertible by Lemma 2, we get
A direct calculation reveals that the eigenvalues of Λ2(k) are \(\lambda _{1,2}={c_{k}^{4}}+{s_{k}^{4}}\pm \sqrt {({c_{k}^{4}}\rho _{1}(k)+{s_{k}^{4}}\rho _{1}(\widetilde {k}))({c_{k}^{4}}\rho _{2}(k)+{s_{k}^{4}}\rho _{2}(\widetilde {k}))}\) and they are nonzero for \(k=1,\dots ,N_{c}\). Hence, Λ2(k) is invertible and, using (26), we get
Summarizing our results and using the definition of Th, we conclude that
and our claim follows. □
Using Lemma 3, it is possible to factorize the iteration matrix Th. This factorization is obtained in the following theorem.
Theorem 2 (Factorization of the iteration matrix T h)
There exists an invertible matrix Q such that \(T_{h}=Q \widetilde {G} Q^{-1}\), where the G2S iteration matrix Th is defined in Lemma 3 and
where the matrices \(\widetilde {G}_{k}\in \mathbb {R}^{4\times 4}\) are defined in Lemma 3 and \(\gamma _{j}(\frac {N_{h}+1}{2})\) depend on n1, n2 and the eigenvalues \(\rho _{j}(\frac {N_{h}+1}{2})\) of Gh, j, for j = 1,2.
Proof
We define the invertible matrix
Equation (23) says that \(T_{h} \left [\begin {array}{cccc} \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} & 0 & 0 \\ 0 & 0 & \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} \end {array}\right ] = \left [\begin {array}{cccc} \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} & 0 & 0 \\ 0 & 0 & \boldsymbol {\psi }_{k} & \boldsymbol {\psi }_{\widetilde {k}} \end {array}\right ] \widetilde {G}_{k}\), for every \(k=1,{\dots } , N_{c}=\frac {N_{h}+1}{2}-1\) and \(\widetilde {k}=N_{h}-k+1\). Moreover, the frequency \(\boldsymbol {\psi }_{\frac {N_{h}+1}{2}}\) is mapped to zero by the restriction operator, \({R} \left [\begin {array}{cc} \boldsymbol {\psi }_{\frac {N_{h}+1}{2}} & 0\\ 0 & \boldsymbol {\psi }_{\frac {N_{h}+1}{2}} \end {array}\right ] =0\), and we get
where the expressions of \(\gamma _{1}(\frac {N_{h}+1}{2})\) and \(\gamma _{2}(\frac {N_{h}+1}{2})\) depend on n1 and n2. For instance, if n1 + n2 is an even number, then \(\gamma _{1}(\frac {N_{h}+1}{2})=\gamma _{2}(\frac {N_{h}+1}{2}):=(\rho _{1}(\frac {N_{h}+1}{2})\rho _{2}(\frac {N_{h}+1}{2}))^{\frac {n_{1}+n_{2}}{2}}\). Hence, we conclude that \(T_{h}Q=Q\widetilde {G}\) and our claim follows. □
The factorization of Th proved in Theorem 2 allows one to obtain accurate convergence results of a G2S method. Clearly, an optimal result would be a direct calculation of the spectral radii of the matrices \(\widetilde {G}_{k}\). However, this is in general a difficult task that requires cumbersome calculations. Nevertheless, in Theorem 3 we obtain an explicit expression for the spectral radii of \(\widetilde {G}_{k}\) under some reasonable assumptions that are in general satisfied in case of Schwarz methods and symmetric decompositions; see, e.g., [29, Section 3]. Notice also that Theorem 3 guarantees that only one (pre- or post-) smoothing step is necessary for the G2S method to converge.
Theorem 3
Assume that 1 > ρ1(k) = ρ2(k) = ρ(k) ≥ 0 for any k and that ρ(k) is a decreasing function of k. The convergence factor of the G2S method is
Proof
The convergence factor of the G2S is given by the spectral radius of the iteration matrix Th. Theorem 2 implies that
Regardless of the values of n1 and n2, direct calculations show that the matrices \(\widetilde {G}_{k}\) have four eigenvalues:
Moreover, we observe that
where we used the monotonicity of ρ(k). On the other hand, since ρ1(k) = ρ2(k) = ρ(k), we have \(\gamma _{1}(\frac {N_{h}+1}{2})=\gamma _{2}(\frac {N_{h}+1}{2})=\rho (\frac {N_{h}+1}{2})^{n_{1}+n_{2}}\). Therefore, we have that
and the result follows by observing that \(\lambda _{3}\left (\frac {N_{h}+1}{2}\right )=\rho \left (\frac {N_{h}+1}{2}\right )^{n_{1}+n_{2}}\), since \(\rho (\widetilde {k})=\rho (k)\) for \(k=\frac {N_{h}+1}{2}\). □
3.2.3 Two-level substructured and volumetric methods
At this stage, it is fair to pose the following questions: What is the difference between our G2S and other two-level DD methods? Is our G2S different from a classical two-grid method that uses a PSM as smoother? Is there any relation between these two apparently similar approaches? The answers are given in this section.
Let Avu = f be a discretization of our problem (1). In particular, \(A_{v} \in \mathbb {R}^{N^{v}\times N^{v}}\) is the discretization of the elliptic operator \({\mathscr{L}}\), while \(\textbf {u} \in \mathbb {R}^{N^{v}}\) and \(\textbf {f} \in \mathbb {R}^{N^{v}}\) are the discrete counterparts of the solution u and the right-hand side function f. Consider the following splittings of the matrix Av:
where \(A_{j} \in \mathbb {R}^{{N^{a}_{j}} \times {N^{a}_{j}}}\) for j = 1,2. Notice that these correspond to a two-subdomain decomposition. We assume that Av, A1 and A2 are invertible. The matrices \(\widehat {R}_{1} \in \mathbb {R}^{N_{1} \times (N^{v}-{N^{a}_{1}})}\) and \(\widehat {R}_{2} \in \mathbb {R}^{N_{2} \times (N^{v}-{N^{a}_{2}})}\) are restriction operators that take as input vectors of sizes \(N^{v}-{N^{a}_{1}}\) and \(N^{v}-{N^{a}_{2}}\) and returns as output substructure vectors of sizes N1 (substructure \(\mathcal {S}_{1}\)) and N2 (substructure \(\mathcal {S}_{2}\)). The two matrices \(E_{1} \in \mathbb {R}^{{N^{a}_{1}} \times N_{1}}\) and \(E_{2} \in \mathbb {R}^{{N^{a}_{2}} \times N_{2}}\) are extension by zero operators. In order to obtain a discrete substructured problem, we introduce the augmented system
where \(A_{a} = \left [\begin {array}{cc} A_{1} & E_{1} R_{1} \\ E_{2} R_{2} & A_{2} \end {array}\right ]\), \(\textbf {u}_{a} = \left [\begin {array}{cc} \textbf {u}_{1} \\ \textbf {u}_{2} \end {array}\right ]\), and \( \textbf {f}_{a} = \left [\begin {array}{cc} \textbf {f}_{1} \\ \textbf {f}_{2} \end {array}\right ]\), with \(A_{j} \in \mathbb {R}^{{N^{a}_{j}} \times {N^{a}_{j}}}\) and \(\textbf {u}_{j} , \textbf {f}_{j}\in \mathbb {R}^{{N^{a}_{j}}}\), for j = 1,2. The matrices \(R_{1} \in \mathbb {R}^{N_{1} \times {N^{a}_{2}}}\) and \(R_{2} \in \mathbb {R}^{N_{2} \times {N^{a}_{1}}}\) are restriction operators that map volume vectors, of sizes \({N^{a}_{2}}\) (second subdomain) and \({N^{a}_{1}}\) (first subdomain), respectively, to substructure vectors, of sizes N1 (substructure \(\mathcal {S}_{1}\)) and N2 (substructure \(\mathcal {S}_{2}\)), respectively. Notice that \(R_{j} R_{j}^{\top } = I_{N_{j}}\), with \(I_{N_{j}}\) the identity of size Nj, for j = 1,2. Moreover, we define Ns := N1 + N2 and \(N^{a} := {N^{a}_{1}}+{N^{a}_{2}}\).
The substructure vectors v21 := R1u2 and v12 := R2u1 solve the discrete substructured system
where \(A_{h} =\left [\begin {array}{cc} I_{N_{2}} & R_{2} A_{1}^{-1} E_{1} \\ R_{1} A_{2}^{-1} E_{2} & I_{N_{1}} \end {array}\right ]\). The vectors v12 and v21 are restrictions on the substructures \(\mathcal {S}_{2}\) and \(\mathcal {S}_{1}\) of the solution vectors u1 and u2, and (28) is the substructured form of (27). Notice that (28) is the discrete counterpart of the substructured problem (10).
The block-Jacobi method applied to (27) and (28) leads to the iteration matrices
where Gh is the discretization of G, as denoted in Sections 3.1 and 3.2.
Let us now introduce the matrices
It is easy to verify the relations
In particular, the relation \(\widetilde {T}\widetilde {T}^{\top } = I_{N^{s}}\) is trivial, and \(A_{h} \widetilde {T} = \widetilde {T} D A_{a}\) can be obtained by calculating
A similar calculation allows us to obtain that \(G_{h} \widetilde {T} = \widetilde {T} G_{a}\).
Since the matrices Gh and Ga are two different representations of the PSM, one expects that their spectra coincide. This is shown in the next lemma.
Lemma 4
The matrices \(G_{h} \in \mathbb {R}^{N^{s}\times N^{s}}\) and \(G_{a} \in \mathbb {R}^{N^{a}\times N^{a}}\) have the same nonzero eigenvalues, that is σ(Gh) = σ(Ga) ∖{0}.
Proof
Recalling the structure of Ga, one can clearly see that rank(Ga) = Ns, because the matrices EjRj have rank Nj for j = 1,2. Hence, Ga has Ns nonzero eigenvalues. Take any eigenvector \(\textbf {v} \in \mathbb {R}^{N^{a}}\) of Ga with eigenvalue λ≠ 0. We note that \(\widetilde {T} \textbf {v}\neq 0\), otherwise we would have \(G_{a}\textbf {v}=-D\widetilde {E}\widetilde {T}\textbf {v}=0\), which contradicts the hypothesis λ ≠ 0. Using the last relation in (29), we write \(G_{h} \widetilde {T}\textbf {v} = \widetilde {T} G_{a} \textbf {v} = \lambda \widetilde {T} \textbf {v}\). Hence \((\widetilde {T} \textbf {v},\lambda )\) is an eigenpair of Gh. Since this holds for any eigenpair (v, λ) of Ga, the result follows. □
Let us now consider arbitrary restriction and prolongation operators Rs and Ps (with \(R_{s} = P_{s}^{\top }\)). The corresponding discrete substructured two-level iteration matrix is then given by
Our goal is to find a volumetric two-level iteration operator \(G_{a}^{2L}\) that has the same spectrum of \(G_{h}^{2L}\). Such a volumetric operator must be formulated for the augmented system (27) and based on the iteration matrix Ga. Let us recall (29) and compute
where \(P_{a}:=\widetilde {T}^{\top } P_{s}\), \(R_{a}:= R_{s} \widetilde {T} = P_{a}^{\top }\) and
We obtained that \(G_{h}^{2L} \widetilde {T} = \widetilde {T} G_{a}^{2L}\). Similarly as in the proof of Lemma 4, one can show that \(\sigma (G_{h}^{2L}) = \sigma (G_{a}^{2L}) \setminus \{0\}\). This means that we have found a two-level volumetric iteration operator that is spectrally equivalent to our substructured two-level operator. Moreover, for any invertible matrix \(U \in \mathbb {R}^{N^{a} \times N^{a}}\) we can repeat the calculations done in (18), to obtain
where \(\widetilde {P}_{a} = P_{a} U\) and \(\widetilde {R}_{a} = U^{-1} R_{a}\) (with \(\widetilde {R}_{a} = \widetilde {P}_{a}^{\top }\) if U is orthogonal). This means that there exist many two-level DD methods in volume that are equivalent to our substructured two-level methods. We can summarize the obtained result in the following theorem.
Theorem 4 (Volumetric formulation of substructured methods)
Consider the substructured two-level iteration operator \(G_{h}^{2L}\) given in (30) and denote its spectrum by \(\sigma (G_{h}^{2L})\). For any invertible matrix \(U \in \mathbb {R}^{N^{a} \times N^{a}}\), the spectrum of the matrix \(G_{a}^{2L}\) given in (32) satisfies the relation \(\sigma (G_{h}^{2L}) = \sigma (G_{a}^{2L}) \setminus \{0\}\).
The matrix \(G_{a}^{2L}\) has a special structure. Since D is the block-Jacobi preconditioner for the augmented system (27), one can say that \(G_{a}^{2L}\) corresponds to a two-level method applied to the preconditioned system DAaua = Dfa, in a similar spirit of the smoothed aggregation method defined in [5, Section 2].
Let us now focus on the question: what is the relation between our G2S method and a two-grid (volumetric) method that uses the same smoother (PSM)? A two-grid method in volume applied to the augmented system (27) would correspond to an iteration operator \(\widehat {G}_{a}^{2L}\) of the form
Natural choices for \(\widehat {P}_{a}\) and \(\widehat {R}_{a}\) are the usual (volumetric) restriction and prolongation operators. For example, for a one-dimensional problem a natural choice is the prolongation matrix \(\widehat {P}_{a}\) given in (15) and \(\widehat {R}_{a} = \frac {1}{2} P_{a}^{\top }\). On the other hand, our prolongation operator \(P_{a}:=\widetilde {T}^{\top } P_{s}\) is an extension by zero of a coarse substructure vector to a fine volumetric vector. Moreover, \(R_{a}:= R_{s} \widetilde {T}\) restricts a fine volumetric vector v to a coarse substructure vector by only interpolating the components of v belonging to the (fine) substructures. Another crucial difference is that \(G_{a}^{2L}\) is constructed on DAa, while \(\widehat {G}_{a}^{2L}\) is obtained using the matrix Aa. Therefore, \(\widehat {G}_{a}^{2L}\) is constructed on the original augmented system Aaua = fa, while \(G_{a}^{2L}\) is defined over the preconditioned system DAaua = Dfa.
These facts indicate clearly that our method is by far distant from a classical volumetric two-grid method that uses the PSM as smoother. This is also confirmed by the numerical results shown in Fig. 4, where the spectral radii of three different two-level iteration matrices are depicted.
In particular, we consider the Laplace problem defined on a unit square Ω (of side \(\widetilde {L}=1\)). This domain is decomposed into two overlapping rectangles of width \(L=\frac {1}{2}+\delta \). Hence, the length of the overlap is 2δ. This problem is discretized using a classical second-order finite difference scheme with a uniform grid of size \(h = \frac {1}{N_{h}+1}\), where Nh = 2ℓ − 1. The length of the overlap is δ = (Nov + 1)h, for some positive odd integer Nov. We consider three different two-level iterations matrices \(G_{h}^{2L}\), \(\widehat {G}_{a}^{2L}\) and \(G_{RAS}^{2L}\). The first one \(G_{h}^{2L}\) is the iteration matrix corresponding to our G2S method. The second one \(\widehat {G}_{a}^{2L}\) is the iteration matrix of a two-level method applied on the augmented volumetric system (27). In both cases, the same classical Schwarz method is used as smoother. The third matrix \(G_{RAS}^{2L}\) is the iteration operator of a classical two-grid method applied to the volumetric system Avu = f and using as smoother the RAS method. In all cases, restriction and prolongation operators correspond to linear interpolation matrices (as in (15)) and to the full weighting restriction matrices, respectively. Indeed, for our G2S method these are one-dimensional operators, while for the other two methods they are two-dimensional operators. In particular, for the augmented system these interpolation and restriction operators take into account the nonzero values of the discrete functions on the substructures. For the two-level RAS method, they are obtained by a two-dimensional extension of (15).
In Fig. 4, we show the spectral radii of \(G_{h}^{2L}\), \(\widehat {G}_{a}^{2L}\) and \(G_{RAS}^{2L}\), obtained by a direct numerical computation, as a function of Nov, hence the size of the overlap. The two figures correspond to two different discretizations. It is clear that our G2S method outperforms the other two methods, which have also very small contraction factors. Moreover, by comparing the two plots, we observe that the coarse correction makes all the methods very robust with respect to the number of discretization points.
4 Implementation details and multilevel algorithm
In Section 4.1, after having explained pro and cons of substructured and volume two-level methods, we reformulate Algorithm 1 in equivalent forms, which are essential to make our method computationally efficient. In Section 4.2, we explain how to extend our G2S method to a multi-grid strategy.
4.1 A practical form of two-level substructured methods
One of the advantages of our new substructured framework is that a large part of the computations are performed with objects (vectors, matrices, arrays, etc.) that are defined on the substructures and hence have very small sizes if compared to their volumetric counterparts. This is clear if one carefully studies Algorithm 1, where for example the products Rr and Pvc are performed on substructure vectors. In volumetric two-level methods, the same prolongation and restriction operators involve volume entities, thus their application is more costly and they might be generally more difficult to implement due to the higher dimensions.
We now compare the computational costs of one iteration of the G2S and of a 2-grid method in volume that uses the same smoother. Let Nv be the size of the volume problem and Ns the size of the substructured problem (Ns ≪ Nv). The size of each subdomain volume problem is Nsub. The coarse spaces are of dimension Ms for the G2S method and Mv for the volume method. The restriction and prolongation operators in volume are denoted by Rv and Pv. For simplicity we assume n1 = 1, n2 = 0.
The computational costs of one iteration are reported in Table 1.
The first row of this table corresponds to the smoothing step performed by G2S and a DD method in volume. Since we assumed that both strategies use the same DD smoother, their computational costs coincide and are equal to O(γc(Nsub)), where γc depends on the choice of the linear solver. For example, for a Poisson problem, one has \({\gamma _{c}}(N_{\text {sub}})=N_{\text {sub}}\log (N_{\text {sub}})\) if a fast Poisson solver is used, or γc(Nsub) = bNsub for sparse banded matrices with bandwidth b; see, e.g., [38]. For a general problem, the complexity of sparse direct solvers is a power of Nsub, which depends on the dimension. Moreover, one could consider the precomputation of the factorization of the subdomain matrices and just using forward and backward substitutions along the iterations.
For simplicity, we assume that restriction and prolongation operations are classical nodal operations whose computational costs are supposed to grow linearly with the dimension of the problem. Notice that since Ns ≪ Nv, assuming that the same interpolation method is used, the cost in the substructured case is much lower than the corresponding cost in volume; see last row in Table 1.
Let us now discuss the third row of Table 1, which corresponds to the solution of the coarse problems. Since the dimension of the substructured coarse space is smaller, the G2S could require much less computational effort in the solution of the coarse problem. We remark that on the one hand, the coarse matrix A2h is typically block sparse, where the block structure is related to the connectivity among the subdomains (namely the j th block-row of Gh has a sparsity pattern governed by the set \(\mathcal {N}_{j}\)). Furthermore, for a large class of PDE problems, these blocks admit very accurate low-rank approximations that can make the solution process more efficient; see, e.g., [43] and references therein. On the other hand, Avc is typically a sparse matrix, whose sparsity pattern depends on the discretization method used (e.g., finite differences, finite elements, etc). In both cases there exist sophisticated algorithms for the solution of the corresponding linear systems; see, e.g., [18, 38, 43] and references therein. For this reason, we use the two functions γs and γv to indicate the computational cost of the coarse solvers. A general direct comparison in this sense is problem dependent, it could be very complicated, and it is beyond the scope of this paper. Nevertheless, we provide in Section 5.1 a detailed analysis for a specific test case.
Let us now turn our attention to the second row of Table 1, which corresponds to the computation of the residual. Here, a volumetric method requires \(O((N^{v})^{\gamma _{m}})\) operations, where γm depends on the sparsity structure of Av. For example, if Av is a second-order finite difference matrix, then γm = 1. In contrast to this favorable situation, the computation of the residual for a G2S method requires the action of Ah on a vector \({\textbf {v}}^{n+\frac {1}{2}}\), which in turn requires a subdomain solve that is assumed to cost O(γc(Nsub)) (as discussed above). Hence, two smoothing steps are needed by the G2S method. If we could avoid this extra cost, then all the other steps of the G2S methods are cheaper since they are performed on arrays of much smaller sizes. Moreover, we wish to remark that, as we are going to see in Section 5, the G2S method requires in general less iterations than the corresponding method in volume. Hence, if we could avoid one of the two smoothing applications in each iteration, we would get a method which is faster in terms of iterations and computational cost per iteration. To avoid one of the two applications of the smoother in the G2S method, we exploit the special form of the matrix \(A_{h}=\mathbb {I}_{h}-G_{h}\) and propose two new versions of Algorithm 1. These are called G2S-B1 and G2S-B2 and given by Algorithms 2 and 3.


These substructured algorithms require only one smoothing step per iteration. Hence, they are potentially cheaper than a two-grid method using the same smoother. Moreover, it turns out that G2S and G2S-B1 are equivalent and they have the same spectral properties of G2S-B2. These relations are proved in the following theorem.
Theorem 5 (Equivalence between G2S, G2S-B2 and G2S-B1)
-
(a) Algorithm 2 generates the same iterates of Algorithm 1.
-
(b) Algorithm 3 corresponds to the stationary iterative method
$$ \textbf{v}^{n}=G_{h}(\mathbb{I}_{h}-PA_{2h}^{-1}RA_{h})\textbf{v}^{n-1} + \widetilde{M}\textbf{b}_{h}, $$where \(G_{h}(\mathbb {I}_{h}-PA_{2h}^{-1}RA_{h})\) is the iteration matrix and \(\widetilde {M}\) the relative preconditioner. Moreover, Algorithm 3 and Algorithm 2 have the same convergence behavior.
Proof
For simplicity, we suppose to work with the error equation and thus bh = 0. We call \(\widetilde {\textbf {v}}^{0}\) the output of the first five steps of Algorithm 2 and \(\widehat {\textbf {v}}^{0}\) the output of Algorithm 1. Then given an initial guess v0, we have
To verify that steps 6-10 of G2S-B1 are equivalent to an iteration of Algorithm 1, let \(\textbf {v}^{0,k-1}:=\textbf {v}^{1,k-1}+P\textbf {v}_{c}\) be the output on line 10 of the (k − 1)-th iteration of the G2S-B1 algorithm. Then the smoothing step on line 6 of the k-iteration reads
where we use the definition of \(\widetilde {P}\) and the quantity wk− 1 computed at the previous iteration. Steps 7–8 are just the residual computation using the identity Ah = I − Gh and the remaining steps are standard. For the second part of the Theorem, we write one iteration of Algorithm 3 as
Hence, Algorithm 3 performs a post-smoothing step instead of a pre-smoothing step as Algorithm 2 does. The method still has the same convergence behavior since the matrices \(G_{h}(\mathbb {I}_{h}-PA_{2h}^{-1}RA_{h})\) and \((\mathbb {I}_{h}-PA_{2h}^{-1}RA_{h})G_{h}\) have the same eigenvaluesFootnote 4. □
Notice that Algorithm 2 requires for the first iteration two applications of the smoothing operator Gh. The next iterations, given by Steps 6-10, need only one application of the smoothing operator Gh. Theorem 5 (a) shows that Algorithm 2 is equivalent to Algorithm 1. This means that each iteration of Algorithm 2 after the first one is computationally less expensive than one iteration of a volume two-level DD method. Since two-level DD methods perform generally few iterations, it could be important to get rid of the expensive first iteration. For this reason, we introduce Algorithm 3, which overcomes the problem of the first iteration. Theorem 5 (b) guarantees that Algorithm 3 is exactly a G2S method with no pre-smoothing and one post-smoothing step. Moreover, it has the same convergence behavior of Algorithm 2.
We wish to remark that, the reformulations G2S-B1 and G2S-B2 require to store the (substructured) matrix \(\widetilde {P}:= G_{h} P\). This matrix is anyway computed in a precomputation phase to assemble the coarse matrix \(A_{2h}=RA_{h}P = RP - RG_{h} P =RP - R\widetilde {P}\). Hence, no extra cost is required. These implementation tricks can be readily generalized to a general number of pre- and post-smoothing steps.
Concerning the specific implementation details for the G2S, we remark that one can lighten the off-line assembly of the matrix A2h = RAhP, using instead the matrix
which corresponds to a direct discretization of A on the coarse level. Moreover, since our two-level method works directly on the interfaces, we have more freedom in the discretization of the smoothing operators on each level. For instance, one could keep the corresponding volume mesh close to the substructures, while having a coarser grid away from them. This strategy would follow a similar idea of the methods discussed in, e.g., [15] and references therein.
4.2 GMS: extension to multilevel framework
The solution of large problems can be challenging using classical two-level methods in volume. This is mainly due to the dimension of the coarse space, which can still be too large in volume to be solved exactly. In our substructured framework, the size of the substructured coarse matrix corresponds to the number of degrees of freedom on the coarse substructures, and thus it is already much smaller if compared to the volume case (see Section 5.1 for a comparison of their sizes in a concrete model problem). However, there might be problems for which the direct solution of the coarse problem is inconvenient also in our substructured framework. For instance, if we considered multiple subdomains, then we would have several substructures and therefore the size of the substructured coarse matrix increases.
The G2S is suitable to a multilevel generalization following a classical multigrid strategy [42]. Given a sequence of grids on the substructures labeled from the coarsest to the finest by \(\{ \ell _{\min \limits },\ell _{\min \limits }+1,\dots ,\ell _{\max \limits }\}\), we denote by \(P^{\ell }_{\ell -1}\) and \(R^{\ell }_{\ell -1}\) the interpolation and restriction operators between grids ℓ and ℓ − 1. To build the substructured matrices on the different grids we have two possible choices. The first one corresponds to the standard Galerkin projection. Being \(A_{\ell _{\max \limits }}\) the substructured matrix on the finest grid, we can define the coarse matrices \(A_{\ell }:=R^{\ell +1}_{\ell }A_{\ell +1}P^{\ell +1}_{\ell }\), for \(\ell \in \{ \ell _{\min \limits },\ell _{\min \limits }+1,\dots ,\ell _{\max \limits }-1 \}\). The second choice consists in defining Aℓ directly as the discretization of (12) on the grid labeled by ℓ, and corresponds exactly to (33) for the two-grid case. The two choices are not equivalent. On the one hand, the Galerkin approach leads to a faster method in terms of iterations. However, the Galerkin matrices Aℓ do not have the block structure as in (12). For instance, \(A_{\ell _{\max \limits }-1}=R^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}A_{\ell _{\max \limits }}P^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}=R^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}P^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}-R^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}G_{\ell _{\max \limits }}P^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}\). Thus, the identity matrix is replaced by the sparse matrix \(R^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}P^{\ell _{\max \limits }}_{\ell _{\max \limits }-1}\). On the other hand, defining Aℓ directly on the current grid ℓ as in (33) leads to a minimum increase of the iteration number, but it permits to preserve the original block-diagonal structure (which is important if one wants to use G2S-B1 and G2S-B2). The difference between the two approaches is also studied by numerical experiments in Section 5.
In spite of the choice for Aℓ, we define the geometric multilevel substructured DD method (GMS) in Algorithm 4, which is a substructured multi-grid V-cycle.

5 Numerical experiments
In this section, we demonstrate the effectiveness of our new computational framework by extensive numerical experiments. These experiments have two main purposes. On the one hand, we wish to validate the theoretical results of Section 3.1, while discussing the implementation details of Section 4.1 and comparing our new method with other classical existing methods, like a two-grid method in volume using RAS as smoother. This is the focus of Section 5.1, where a Poisson problem on two-dimensional and three-dimensional boxes is considered. Both convergence rates and computational times are studied.
On the other hand, we wish to show the effectiveness of our new methods in case of multiple-subdomain decompositions and for classical test problems. In particular, in Section 5.2 we consider a multiple-subdomain decomposition for a classical Poisson problem, while in Section 5.3 a diffusion problem with highly jumping diffusion coefficients is solved. For the efficient solution of these two problems different discretization methods are required. These are the finite difference method, for the classical Poisson problem, and the finite-volume method, in case of jumping diffusion coefficients. These two methods require different definitions of restriction and prolongation operators. We thus sketch some implementation details of our algorithms for a regular decomposition. In both cases, the robustness of our methods for increasing number of subdomains is studied and compared to classical two-grid and multi-grid methods defined in volume and using RAS as smoother. The obtained numerical results show clearly, and particularly for the jumping diffusion coefficient case, that our methods converge in less iterations than the classical two-level RAS method. In Sections 5.1 and 5.2, all the methods are used as iterative solvers, without any Krylov acceleration, while in Section 5.3 we test their efficiency as preconditioners for GMRES.
5.1 Laplace equation on 2D and 3D boxes
We first consider the Poisson equation −Δu = f with homogeneous Dirichlet boundary condition. The geometry of the domain and its decomposition are shown in Fig. 3, where Ω is decomposed into two overlapping rectangles Ω1 = (− 1, δ) × (0, 1) and Ω2 = (−δ, 1) × (0, 1). The length of the overlap is 2δ. On each subdomain, we use a standard second-order finite difference scheme based on a uniform grid of Ny = 2ℓ − 1 interior points in direction y and Nx = Ny interior points in direction x. Here, ℓ is a positive integer. The grid size is denoted by h. The overlap is assumed to be δ = hNov, where Nov represents the number of interior points in the overlap in direction x.
The results of our numerical experiments are shown in Fig. 5. All figures show the decay of the relative errors with respect to the number of iterations. To study the asymptotic convergence behavior of the G2S and compare it with the theoretical results of Section 3.2, all methods are stopped if the relative error is smaller than the very low tolerance 10− 12.
The problem is solved by the classical parallel Schwarz method, a classical two-grid and a three-grid method using RAS as smoother (“2L-RAS” and “3L-RAS” in the figures), the G2S method, and its extension to three-grid denoted by G3S. For the G2S method, we further distinguish two cases: “G2S” indicates the G2S method using the coarse matrix A2h := RAhP, while “\(\widetilde {\text {G2S}}\)” refers to the G2S method using the coarse matrix obtained by a direct discretization of A on the coarse grid (instead of A2h := RAhP), see (33) and the discussion in Section (4.2). For the G2S and \(\widetilde {\text {G2S}}\) methods, we use the one-dimensional linear interpolation operator P = diag(P1, P2), where the expression of Pj, j = 1,2 is given in (15), and \(R=\frac {1}{2}(P)^{\top }\) (as explained in Section 3.1 and Fig. 3). For 2L-RAS, we use the classical full weighting restriction and interpolation operators, PV = kron(Px, Py), \(R_{V}=\frac {1}{4}P_{V}^{\top }\), where Px, Py are one-dimensional interpolation operators of the same form of (15).
The left panels of Fig. 5 validate the theoretical convergence factor obtained in Theorem 3. The center panels compare the classical one-level PSM, the G2S and \(\widetilde {\text {G2S}}\) method and the 2L-RAS method. The slower performance of 2L-RAS with respect to G2S can be traced back to the interpolation step. This operation breaks the harmonicity of the obtained correction, which therefore does not lie any more in the space of the error; see, e.g., [34]. One could use interpolators which extend harmonically the correction inside the overlapping subdomains although this would increase significantly the computational cost of each iteration. We refer also to [37] for a similar observation. Further notice that, while the G2S coarse space has dimension about Ny, the one corresponding to the 2L-RAS method has dimension about \(N_{x} N_{y} /4 \approx {N_{y}^{2}}/2 \gg N_{y}\). In the setting of Fig. 5, the dimensions of the coarse spaces of G2S and 2L-RAS are about 60 and 1900, respectively. Notice that the convergence of \(\widetilde {\text {G2S}}\) is comparable to 2L-RAS, hence a little slower than G2S, but the assembly of the coarse matrix is cheaper.
The right panels compare the convergence behavior of the two-grid methods, G2S and 2L-RAS, with their three-level variants. We remark that the addition of a third level does not result in a noticeable convergence deterioration.
Next, we are interested in computational times and in numerically validating the computational cost presented in Table 1. To do so, we consider a three-dimensional box Ω = (− 1, 1) × (0, 1) × (0, 1) decomposed into two overlapping subdomains Ω1 = (− 1, δ) × (0, 1) × (0, 1) and Ω2 = (−δ, 1) × (0, 1) × (0, 1). We solve the problem (up to a tolerance of 10− 6 on the relative error) using the G2S method, its equivalent forms G2S-B1 and G2S-B2, introduced in Section 4.1, and 2L-RAS. The length of the overlap is δ = hNov, where h is the grid size and Nov is fixed to 4. Hence the overlap is proportional to the grid size. The experiments have been performed on a workstation with a processor Intel Core i9-10900X CPU 3.7GHz and with 32GB of RAM. The subdomain problems are solved sequentially using the Matlab backslash command, which calls a direct solver for sparse banded matrices (with small band density threshold) with almost linear complexity. The smoothing steps have the same cost for both 2L-RAS and G2S implementations, and it permits to better remark the advantages of the substructured methods in the coarse step and the prolongation/restriction steps. The results are shown in Tables 2 and 3.
The G2S method outperforms 2L-RAS in terms of iteration numbers and computational times. To better understand why the G2S method is faster and to validate the computational cost analysis presented in Table 1, Fig. 6 shows the computational time spent by the G2S and 2L-RAS methods in the different steps of a two-level method. As expected, the smoothing step requires the same effort in both methods. This is shown in Fig. 6 (left). In Fig. 6 (right) we compare the computational times required by one coarse correction step performed by the two methods. The two curves correspond to the same volumetric dimensions of the problem (as in Table 3), but the coarse space dimensions corresponding to G2S and 2L-RAS are different. This means that, the k th point (circle) from the left of the G2S curve has to be compared with the k th point (cross) from the left of the 2L-RAS curve. It must also be said that for both cases we use the Matlab backslash command. This is clearly a choice more favorable for the 2L-RAS coarse problem (which is sparse and banded). A different and more appropriate solver for the G2S coarse matrix exploiting the block-sparse structure (see, e.g., [38]) could lead to further improvement of these computational times.
5.2 Decompositions into many subdomains
In this section, we consider a square domain Ω decomposed into M × M non-overlapping square subdomains \(\widetilde {{\varOmega }}_{j}\), \(j=1,\dots ,M^{2}=N\). Each subdomain \(\widetilde {{\varOmega }}_{j}\) contains Nsub = (2ℓ − 1)2 interior degrees of freedom. Extending the subdomains \(\widetilde {{\varOmega }}_{j}\) by Nov points, we obtain the overlapping subdomains Ωj with overlap δ = 2Novh. On each subdomain Ωj, we locate the discrete substructure \(\mathcal {S}^{N_{j}}_{j}\), marked with blue lines in Fig. 7, which is made by four (one-dimensional) segments.
An interior non-overlapping subdomain \(\widetilde {{\varOmega }}_{j}\) is enlarged by Nov = 2 points in each direction. The discrete substructure \(\mathcal {S}^{N_{j}}_{j}\) is denoted by a blue line. On the right panel, the coarse discrete substructure \(\mathcal {S}^{M_{j}}_{j}\) is marked by red crosses
For each discrete substructure \(\mathcal {S}^{N_{j}}_{j}\), the interpolation operator Pj acts block-wise on each one-dimensional interval, i.e., \(P_{j}=\text {diag}\{\widetilde {P}_{1},\widetilde {P}_{2},\widetilde {P}_{3},\widetilde {P}_{4}\}\), where each \(\widetilde {P}_{k}\), \(k=1,\dots ,4\), corresponds to the prolongation matrix (15). We remark that using \(\widetilde {P}_{k}\) implies assuming that on the boundary of \(\mathcal {S}_{j}\) the function attains zero. This holds since on each substructure \(v_{j} \in H^{\frac {1}{2}}_{00}(\mathcal {S}_{j})\), due to the partition of unity.
The results of our numerical experiments are reported in Fig. 8. The left panel shows the dependence of the spectral radius on the size of the overlap for the different methods and N = 16, ℓ = 5. We then study the robustness of the method with respect to an increasing number of subdomains. We first keep the size of each subdomain fixed, Nsub = (25 − 1)2, and thus we consider larger global problems as N grows. Then, we fix a global domain Ω with approximately 17 ⋅ 103 interior degrees of freedom, and we get smaller subdomains as N grows. In both cases, we observe that the spectral radius of both 2L-RAS and G2S does not deteriorate as the number of subdomains increases.
We further compare G2S, 2L-RAS and Geometric MultiGrid (GMG) for the solution of the Poisson equation −Δu = 1. We decompose Ω into N = 9 and N = 16 subdomains and set Nov = 2. Table 4 reports the number of iterations and computational times to reach a relative tolerance of 10− 6. For the G2S method, we preassembled the coarse matrix.
Concerning GMG, we implemented a V-cycle with two pre- and post-smoothing steps using a damped Jacobi smoother with optimal damping parameter ω = 4/5 [53]. The coarsest level of GMG corresponds to ℓ = 3 and the size of the coarse matrix is 961. Concerning the implementation of the DD methods, the subdomain problems are solved in parallel, using the Matlab parallel Toolbox. The G2S method is implemented according to Algorithm 3. The sizes of the G2S coarse matrices are 3096, 6168, 12312 for ℓ = 7,8,9, respectively. For both G2S and GMG, we compute once for all the LU decompositions of the corresponding coarse matrices as their size is small. The cost of the LU decompositions is included in the computational times reported. Table 4 shows the G2S is competitive with GMG.
5.3 Diffusion problem with jumping diffusion coefficients
In this section, we test our method for the solution of a diffusion equation −div(α∇u) = f in a square domain Ω := (0, 1)2 with \(f:=\sin \limits (4\pi x)\sin \limits (2\pi y)\) \(\sin \limits (2\pi xy)\). The domain Ω is decomposed into 16 non-overlapping subdomains.
We suppose α = 1 everywhere except in some channels where α takes the values 102, 104 and 106. We consider two configurations represented in Fig. 9.
Decomposition of Ω into 16 subdomains with two different patterns of channels (left and center). The yellow regions correspond to large values of the diffusion coefficient. The blue-green area shows the non-overlapping decomposition. The right panel shows the solution of the equation with the central pattern
We use a finite-volume discretization, where each non-overlapping subdomain is discretized with Nsub = 22ℓ cells and it is enlarged by Nov cells to create an overlapping decomposition with overlap δ = 2Novh. We further assume that the discontinuities of the diffusion coefficient are aligned with the edges of the cells and they do not cross any cell. The mapping between the fine and coarse mesh is illustrated in Fig. 10.
At the volume level, the restriction operator maps four fine cells to a single coarse cell by averaging the four cell values and the interpolation operator is its transpose. At the substructured level, the restriction operator maps two fine cells to a single coarser cell by averaging. The interpolation operator splits one coarse cell to two fine cells assigning the same coarse value to each new cell. It still holds that the interpolation operator is the transpose of the restriction operator.
In this setting, we study the robustness of the G2S method with respect to the mesh size and the amplitudes of the jumps of α and we compare it to the 2L-RAS method. In Table 5 we report the number of iterations to reach a relative error of Tol = 10− 6.
Both methods are used as iterative solvers. The iterations performed by the G2S method are the numbers on the left in each cell of the table, while the iterations of the 2L-RAS are the numbers in brackets on the right. We can observe that the G2S outperforms 2L-RAS. Figure 11 show the convergence curves for a fixed mesh size and three different values of α.
These results show that the G2S method is robust both with respect to the jumps of the diffusion coefficient and the mesh size, and that it outperforms the 2L-RAS method.
Now, we study the performance of G2S and 2L-RAS as preconditioners for GMRES. Table 6 reports the number of iterations when both methods are used to accelerate GMRES. We further specify the final size of the Krylov subspaces. GMRES preconditioned by the G2S method builds a much smaller Krylov subspace as the system and preconditioner have dimensions equal to the size of the substructured space.
6 Conclusions
In this work we introduced a new framework of two-level and multilevel substructured DD methods, namely the G2S method and its extension called GMS method. These are formulated on the substructures of the considered overlapping domain decomposition. Under certain reasonable hypotheses, for 2 subdomains in 2d, we proved that the G2S method is well posed and convergent, and we also estimated the corresponding convergence factor. The effectiveness of our new methods is confirmed by extensive numerical experiments, where elliptic PDE problems with possibly highly jumping diffusion coefficients are efficiently solved.
Change history
18 July 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
Notice that the term “substructured” refers very often to DD methods that are defined on non-overlapping subdomains; see, e.g., [48, 52]. However, in this work it indicates methods that are purely defined on the interfaces, independently of the type of (overlapping or non-overlapping) decomposition of the domain; see, e.g., [27, Section 5]. Here, we consider an overlapping domain decomposition.
Notice that the substructure of a subdomain is sometimes called “skeleton”; see, e.g., [17].
Notice that \((\widehat {P})^{\top } = U^{\top } P^{\top } = 2 U^{\top } R = 2 \widehat {R}\), since \(\widetilde {R}=\frac {1}{2} \widetilde {P}^{\top }\).
Given two matrices A and B, AB and BA share the same nonzero eigenvalues.
References
Aarnes, J., Hou, T.Y.: Multiscale domain decomposition methods for elliptic problems with high aspect ratios. Acta Math. Appl. Sin. 18(1), 63–76 (2002)
Bjorstad, P., Gander, M.J., Loneland, A., Rahman, T.: Does SHEM for Additive Schwarz work better than predicted by its condition number estimate? Domain Decomposition Methods in Science and Engineering XXIV, LNCSE, Springer –(–), 129–138 (2018)
Bonazzoli, M., Dolean, V., Graham, I., Spence, E., Tournier, P.H.: Domain decomposition preconditioning for the high-frequency time-harmonic maxwell equations with absorption. Math. Comput. 88(320), 2559–2604 (2019)
Bonazzoli, M., Dolean, V., Graham, I.G., Spence, E.A., Tournier, P.H.: Two-Level Preconditioners for the Helmholtz Equation. In: Domain Decomposition Methods in Science and Engineering XXIV. Springer International Publishing (2018)
Brezina, M., Manteuffel, T., McCormick, S., Ruge, J., Sanders, G.: Towards adaptive smoothed aggregation (α SA) for nonsymmetric problems. SIAM J. Sci. Comput. 32(1), 14–39 (2010)
Cai, X.C., Sarkis, M.: A restricted additive Schwarz preconditioner for general sparse linear systems. SIAM J. Sci. Comp. 21(2), 792–797 (1999)
Chaouqui, F., Ciaramella, G., Gander, M.J., Vanzan, T.: On the scalability of classical one-level domain-decomposition methods. Vietnam J. Math. 46(4), 1053–1088 (2018)
Chaouqui, F., Gander, M.J., Santugini-Repiquet, K.: A Coarse Space to Remove the Logarithmic Dependency in Neumann–Neumann Methods. In: Domain decomposition methods in science and engineering XXIV, pp 159–167. Springer International Publishing, Cham (2018)
Chaouqui, F., Gander, M.J., Santugini-Repiquet, K.: A local coarse space correction leading to a well-posed continuous Neumann-Neumann method in the presence of cross points. In: Domain decomposition methods in science and engineering XXV, pp 83–91. Springer International Publishing, Cham (2020)
Ciaramella, G., Gander, M.J.: Analysis of the parallel Schwarz method for growing chains of fixed-sized subdomains: Part I. SIAM J. Numer. Anal. 55(3), 1330–1356 (2017)
Ciaramella, G., Gander, M.J.: Analysis of the parallel Schwarz method for growing chains of fixed-sized subdomains: Part II. SIAM J. Numer. Anal. 56(3), 1498–1524 (2018)
Ciaramella, G., Gander, M.J.: Analysis of the parallel Schwarz method for growing chains of fixed-sized subdomains: Part III. Electron. Trans. Numer. Anal. 49, 201–243 (2018)
Ciaramella, G., Gander, M.J.: Iterative Methods and Preconditioners for Systems of Linear Equations. Fundamentals of Algoriths. SIAM (2022)
Ciaramella, G., Gander, M.J., Halpern, L., Salomon, J.: Methods of reflections: relations with Schwarz methods and classical stationary iterations, scalability and preconditioning. The SMAI J. Comput. Math. 5, 161–193 (2019)
Ciaramella, G., Gander, M.J., Mamooler, P.: The Domain Decomposition Method of Bank and Jimack as an Optimized Schwarz Method. In: Domain Decomposition Methods in Science and Engineering XXV, pp 285–293. Springer International Publishing, Cham (2020)
Ciaramella, G., Hassan, M., Stamm, B.: On the Scalability of the Parallel Schwarz Method in One-Dimension. In: Domain Decomposition Methods in Science and Engineering XXV, pp 151–158. Springer International Publishing, Cham (2020)
Ciaramella, G., Hassan, M., Stamm, B.: On the scalability of the Schwarz method. The SMAI J. Comput. Math. 6, 33–68 (2020)
Davis, T.A.: Direct Methods for Sparse Linear Systems (Fundamentals of Algorithms 2). Society for Industrial and Applied Mathematics, USA (2006)
Dohrmann, C.R., Klawonn, A., Widlund, O.B.: A family of energy minimizing coarse spaces for overlapping Schwarz preconditioners. In: Domain Decomposition Methods in Science and Engineering XVII, pp 247–254 (2008)
Dolean, V., Jolivet, P., Nataf, F.: An introduction to domain decomposition methods. SIAM, Philadelphia PA (2015)
Dolean, V., Nataf, F., Scheichl, R., Spillane, N.: Analysis of a two-level Schwarz method with coarse spaces based on local dirichlet-to-Neumann maps. Comput. Meth. in Appl. Math. 12(4), 391–414 (2012)
Dubois, O., Gander, M.J., Loisel, S., St-Cyr, A., Szyld, D.B.: The optimized Schwarz method with a coarse grid correction. SIAM J. Sci. Comput. 34(1), 421–458 (2012)
Efendiev, Y., Galvis, J., Lazarov, R., Willems, J.: Robust domain decomposition preconditioners for abstract symmetric positive definite bilinear forms. ESAIM Math. Model. Numer. Anal. 46(5), 1175–1199 (2012)
Efstathiou, E., Gander, M.J.: Why restricted additive Schwarz converges faster than additive Schwarz. BIT Numer. Math. 43(5), 945–959 (2003)
Galvis, J., Efendiev, Y.: Domain decomposition preconditioners for multiscale flows in high-contrast media. Multiscale Model. Sim. 8(4), 1461–1483 (2010)
Galvis, J., Efendiev, Y.: Domain decomposition preconditioners for multiscale flows in high contrast media: reduced dimension coarse spaces. Multiscale Model Sim. 8(5), 1621–1644 (2010)
Gander, M.J.: Optimized Schwarz methods. SIAM J. Numer. Anal. 44(2), 699–731 (2006)
Gander, M.J.: Schwarz methods over the course of time. Electron. Trans. Numer. Anal. 31, 228–255 (2008)
Gander, M.J.: On the influence of geometry on optimized schwarz methods. SeMA Journal 53(1), 71–78 (2011)
Gander, M.J., Halpern, L., Repiquet, K.: A new coarse grid correction for RAS/AS. In: Domain Decomposition Methods in Science and Engineering XXI, pp 275–283. Springer (2014)
Gander, M.J., Halpern, L., Santugini-Repiquet, K.: On optimal coarse spaces for domain decomposition and their approximation. In: Domain Decomposition Methods in Science and Engineering XXIV, pp 271–280. Springer International Publishing, Cham (2018)
Gander, M.J., Loneland, A.: SHEM: an optimal coarse space for RAS and its multiscale approximation. In: Domain Decomposition Methods in Science and Engineering XXIII, pp 313–321. Springer (2017)
Gander, M.J., Loneland, A., Rahman, T.: Analysis of a new harmonically enriched multiscale coarse space for domain decomposition methods. arXiv:1512.05285 (2015)
Gander, M.J., Song, B.: Complete, optimal and optimized coarse spaces for additive Schwarz. In: Domain Decomposition Methods in Science and Engineering XXIV. Springer (2018)
Gander, M.J., Van Criekingen, S.: New coarse corrections for optimized restricted additive Schwarz using PETSc. In: Domain Decomposition Methods in Science and Engineering XXV, pp 483–490. Springer International Publishing, Cham (2020)
Gander, M.J., Vanzan, T.: Heterogeneous optimized Schwarz methods for second order elliptic PDEs. SIAM J. Sci. Comput. 41(4), A2329–A2354 (2019)
Gander, M.J., Vanzan, T.: Multilevel optimized Schwarz methods. SIAM J. Sci. Comput. 42(5), A3180–A3209 (2020)
Golub, G.H., Van Loan, C.F.: Johns Hopkins Studies in the Mathematical Sciences, Fourth Edition. Johns Hopkins University Press, Baltimore, MD (2013)
Graham, I., Spence, E., Vainikko, E.: Domain decomposition preconditioning for high-frequency helmholtz problems with absorption. Math. Comput. 86(307), 2089–2127 (2017)
Graham, I.G., Lechner, P.O., Scheichl, R.: Domain decomposition for multiscale PDEs. Numer. Math. 106(4), 589–626 (2007)
Hackbusch, W.: Local Defect Correction Method and Domain Decomposition Techniques, pp. 89–113. Vienna (1984)
Hackbusch, W.: Multi-Grid Methods and Applications. Series in Computational Mathematics. Springer, Berlin (2013)
Hackbusch, W.: Hierarchical Matrices: Algorithms and Analysis, 1st Edn. Springer Publishing Company, Incorporated (2015)
Heinlein, A., Klawonn, A., Knepper, J., Rheinbach, O.: Multiscale coarse spaces for overlapping Schwarz methods based on the ACMS space in 2D. Electron. Trans. Numer. Anal. 48, 156–182 (2018)
Klawonn, A., Radtke, P., Rheinbach, O.: FETI-DP Methods with an adaptive coarse space. SIAM J. Numer. Anal. 53(1), 297–320 (2015)
Lions, J., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications (Vol I). Die Grundlehren der mathematischen Wissenschaften. Springer, Berlin (1972)
Lions, P.L.: On the Schwarz alternating method. I. First international symposium on domain decomposition methods for partial differential equations, pp. 1–42 (1988)
Quarteroni, A., Valli, A.: Domain decomposition methods for partial differential equations. Numerical mathematics and scientific computation oxford science publications (1999)
Spillane, N., Dolean, V., Hauret, P., Nataf, F., Pechstein, C., Scheichl, R.: A robust two-level domain decomposition preconditioner for systems of PDEs. C. R. Math. 349(23), 1255–1259 (2011)
Spillane, N., Dolean, V., Hauret, P., Nataf, F., Pechstein, C., Scheichl, R.: Abstract robust coarse spaces for systems of PDEs via generalized eigenproblems in the overlaps. Numer. Math. 126(4), 741–770 (2014)
Tartar, L.: An Introduction to Sobolev Spaces and Interpolation Spaces. Lecture Notes of the Unione Matematica Italiana. Springer, Berlin (2007)
Toselli, A., Widlund, O.: Domain Decomposition Methods: Algorithms and Theory Series in Computational Mathematics, vol. 34. Springer, New York (2005)
Trottenberg, U., Ulrich Trottenberg, C., Oosterlee, C., Schuller, A., Brandt, A., Oswald, P., Stüben, K.: Multigrid elsevier science (2001)
Widlund, O., Dryja, M.: An additive variant of the Schwarz alternating method for the case of many subregions. Tech. rep., Department of Computer Science Courant Institute (1987)
Zampini, S., Tu, X.: Multilevel balancing domain decomposition by constraints deluxe algorithms with adaptive coarse spaces for flow in porous media. SIAM J. Sci. Comput. 39(4), A1389–A1415 (2017)
Acknowledgements
Gabriele Ciaramella and Tommaso Vanzan are members of GNCS (Gruppo Nazionale per il Calcolo Scientifico) of INdAM.
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Data availability
No datasets were generated or analyzed during the current study.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ciaramella, G., Vanzan, T. Substructured two-grid and multi-grid domain decomposition methods. Numer Algor 91, 413–448 (2022). https://doi.org/10.1007/s11075-022-01268-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-022-01268-0