Sinusoidal oscillator parametrically forced to robust hyperchaotic states: the lumpkin case

Abstract

The objective of this paper is to showcase the capability of the conventional circuit structure known as the Lumpkin oscillator, widely employed in practical applications, to operate in robust chaotic or hyperchaotic steady states. Through numerical analysis, we demonstrate that the generated signals exhibit a significant level of unpredictability and randomness, as evidenced by positive Lyapunov exponents, approximate entropy, recurrence plots, and other indicators of complex dynamics. We establish the structural stability of strange attractors through design and practical construction of a flow-equivalent fourth-order chaotic oscillator, followed by experimental measurements. The oscilloscope screenshots captured align well with the plane projections of the approximate solutions derived from the underlying mathematical models.

1 Introduction

Chaos and hyperchaos are terms initially adopted to describe the complex, seemingly random behavior observed in natural systems where internal order is not readily apparent. When it comes to lumped electronic circuits, chaos (or hyperchaos) denotes irregular, noise-like behavior stemming from nonlinear deterministic dynamical systems with at least three (or four) degrees of freedom, typically represented by state variables. Both types of dynamic motion can be viewed as steady states and possess distinct characteristics: sensitivity to minor differences in initial conditions, lack of an analytical closed-form solution, dense state attractors confined within a finite volume of phase space, mixing, and a continuous and wide-band frequency spectrum. Due to these properties, the analysis of such systems relies heavily on numerical algorithms, often involving problem discretization and integration processes. Despite providing only approximate solutions depending on the chosen method and integration step size, the existence of structurally stable chaotic and hyperchaotic solutions is typically demonstrated through the construction of analog chaotic oscillators followed by laboratory measurements [1]. This methodology serves as a means to establish the long-term structural stability of any prescribed state attractor, a task that is challenging to replicate using artificial intelligence-powered text generation programs [2].

Both chaotic and hyperchaotic behaviors, as described earlier, have been observed in various analog electronic circuits, even those designed to generate regular and predictable signals. Sinusoidal oscillators, which inherently produce fundamental frequency components, belong to a broad class of circuit structures that may exhibit chaotic behavior. For instance, the evolution of chaos in the well-known Colpitts oscillator has been extensively studied [3, 4]. This oscillator, a simple single-stage transistor-based circuit comprising two capacitors and one inductor, has been shown to exhibit chaotic self-oscillations [5]. Similarly, the Hartley oscillator, obtained by interchanging capacitors and inductors in the Colpitts configuration, has also been demonstrated to produce chaotic behavior [6, 7]. When the feedback inductor in a Colpitts oscillator is replaced by a series resonant circuit, the resulting circuit, commonly known as a Clapp oscillator, can exhibit either chaotic or hyperchaotic behavior [8]. Low-frequency oscillators designed for modest applications typically consist of a wideband amplifier (either non-inverting or inverting) and a fully passive frequency-dependent feedback two-port composed of resistors and capacitors. The Wien-bridge oscillator, a member of this group, employs a non-inverting amplifier and a feedback network acting as a second-order band-pass filter. Research has shown that slight modifications to such network structures can induce robust chaotic behavior [9,10,11]. Passive ladder feedback networks are constructed as cascaded basic RC low-pass or CR high-pass filters, This class of systems, known as phase shift oscillators, can generate chaotic waveforms under certain conditions [12].

Chaos can easily emerge from a third-order sinusoidal oscillator, hence from autonomous deterministic circuit having three accumulation elements. However, chaos is still possible in second-order circuits when an additional degree of freedom is introduced by an input signal with periodic, but not necessarily harmonic, behavior. This observation led to the discovery of robust chaos in biquadratic frequency filtering structures. For instance, in [13], chaos generation was investigated in a state variable filter employing saturation-type lossless integrators. Additionally, simple chaotic systems proposed in [14] were found to be closely related to state variable filters commonly used in practical applications. The closed-loop configuration of a phase detector, low-pass filter, and voltage-controlled oscillator forms the fundamental structure of a phase-locked loop (PLL) circuit. These functional blocks are inherently higher-dimensional, and the total number of degrees of freedom depends on the order of the low-pass filter. PLLs can operate in various regimes, including clock signal synchronization, signal demodulation, programmable oscillators, and frequency synthesizing. The existence of chaos in these analog building blocks has been explored in papers such as [15, 16]. In contrast to the networks mentioned earlier, amplifiers are typically regarded as ideally linear two-ports, amplifying input signals without introducing additional harmonic components and providing zero total harmonic distortion (THD). However, real-world practice often diverges from ideal behavior. While THD remains low for small input signals, it increases rapidly in power amplifiers as output power rises. In [17], it was demonstrated both numerically and experimentally that the large-signal model of a bipolar transistor can induce chaotic self-oscillations even in a significantly simplified mathematical model of a class C amplifier.

Power electronic circuits, owing to the nonlinear characteristics of their active components and needful presence of nonlinear semiconductor elements, are also capable of generating chaotic waveforms. For instance, general insights into chaos phenomena in DC–DC converters can be found in [18, 19]. A more in-depth investigation into the complex dynamics of DC–DC buck converters is provided in [20], while the chaotic behavior of DC–DC boost converters is addressed in [21, 22]. The chaotic behavior of current-programmed Cuk converters is discussed in [23], and the evolution of chaos in DC–DC switching converters is reviewed in [24]. Moreover, complex behavior has been observed in multi-state static memory cells composed of pairs of resonant tunneling diodes. For instance, [25] focuses on the analysis of such memories, where the ampere-voltage characteristics of both diodes are approximated by piece-wise linear functions. Similarly, [26] analyzes the same circuit topology, where both diodes are approximated by third-order odd-symmetrical zero-offset polynomial functions. In addition to case studies, there are numerous comprehensive review papers and books on chaotic circuits, such as [27,28,29,30]. These resources offer valuable insights into chaotic circuits from both theoretical and practical perspectives.

As noted, there is a plenty of analog functional blocks where chaos or hyperchaos has been observed, either intentionally or accidentally. The list of originally regular circuits where chaotic behavior has been detected is continuously expanding due to the intensive research in this area. New analog signal processing blocks with associated chaotic and/or hyperchaotic behavior are emerging regularly. Indeed, the content of this paper can be viewed as direct contribution to this growing list, presenting yet another example of naturally sinusoidal, quasilinear circuit: the fourth-order Lumpkin oscillator.

This paper is structured as follows. Section 2 delves into constructing the mathematical model hidden behind principal structure of the Lumpkin oscillator, preparing it for subsequent numerical analysis. Following the derivation of the mathematical model, the paper proceeds to employ numerical algorithms to explore the complex motion of the dynamical system with different sets of internal parameters, aiming to uncover fingerprints of chaos and/or hyperchaos in global dynamics. Section 3 is dedicated to a comprehensive numerical analysis of the “chaotic cases” discovered during the search routine. In Sect. 4, the lumped circuit design of the flow-equivalent circuit for the Lumpkin oscillator is presented. Additionally, it focuses on the experimental confirmation of chaos/hyperchaos working regimes. Measured strange attractors are captured as plane projections using an oscilloscope and compared to expected, numerically integrated results. Finally, Sect. 5 concludes the paper with summarizing remarks and outlines potential directions for future research in this area.

2 Dynamical mathematical models

The analysis of any dynamical system in electrical engineering practice typically begins with the development of a mathematical model. This model should strike a balance between simplicity, with a finite number of state variables and system parameters, and precision, accurately representing the expected operational regime. In the upcoming subsections of this paper, the focus shifts to the mathematical model derived directly from the well-known fundamental circuit structure of the fourth-order sinusoidal oscillator: the Lumpkin topology. This dynamical system will be inherently nonlinear, characterized by a single smooth polynomial scalar function originating from the internal structure of the active device. While conventional linear analysis may fall short in providing a comprehensive overview of global dynamics, system linearization near the origin of the state space and subsequent linear analysis will play a role in the search-for-chaos optimization routine.

The Lumpkin sinusoidal oscillator belongs to a large class of LC oscillators and is capable of operating within frequency bands ranging from tens of kHz up to several MHz. The principal schematic is depicted in Fig. 1. We start with circuit ready for AC analysis, where coupling capacitors have been already shorted and resistors dedicated to setup bias point of bipolar transistor were removed. DC supply voltage source was grounded, turning reduced network into closed loop composed of single-stage common-collector two-port and passive fourth-order feedback. In the upcoming analysis, both linear and nonlinear, hypothetical bias point of a generalized bipolar transistor will be assumed, and this two-port active device will be modeled by a set of four frequency-independent impedance parameters. The rest of the circuit consists of three independent inductors, with individual windings not coupled via magnetic flux. An example of the Lumpkin oscillator with an ideal transistor working on the edge of stability is provided in Fig. 1. The initial condition for generation of stable sinusoidal signal is set via internal parameter of the capacitor (voltage across the capacitor at zero time is set to 1 V, IC = 1). The output resistance of the bipolar transistor is negligible; however, its presence is necessary to break the loop with the inductor and voltage source.

The characteristic equation (CHE) is an essential polynomial formula that describes, through its generally complex roots, the transient behavior of the investigated circuit. The CHE can be intuitively derived from a looped cascade of a trans-admittance ladder filter folded gradually by elements $z_{22}$, $L_{3}$, $L_{1}$, C, $L_{2}$, $z_{11}$ and a voltage source controlled by current. The mentioned voltage between the collector and emitter of the transistor forms the input of the feedback filter while the transistor’s base current flowing through $z_{11}$ is the output variable of the filter. Then, the CHE can be expressed as $z_{21} N(s) - D(s) = 0$, where s is the complex frequency, N(s) and D(s) are numerator and denominator polynomials of feedback transfer function respectively, as shown in Fig. 2.

For the generalized bipolar transistor described by the full set of impedance parameters $z_{11}, z_{12}, z_{21}, z_{22}$, the matrix method of loop currents offers an elegant alternative convenient for symbolic evaluation of the CHE. The directions of loop currents (for the schematic illustrated in Fig. 2) are selected as follows. Loop $I_{S1}$ encompasses the series resonant combination of $L_{1}$ and $C$, along with inductor $L_{2}$ and $L_{3}$. Loop $I_{S2}$ traverses the input part of the transistor (base-emitter) and inductor $L_{2}$. Finally, loop $I_{S3}$ consists of the output section of the transistor (collector-emitter) and inductor $L_{3}$. Hence, the CHE can be expressed in matrix form as follows:

$$\begin{aligned}{} & {} det\left[ \begin{pmatrix} \frac{1}{sC} + s(L_{1}+L_{2}+L_{3}) &{} -sL_{2} &{} sL_{3} \\ -sL_{2} &{} sL_{2} &{} 0 \\ {s}L_{3} &{} 0 &{} sL_{3} \end{pmatrix} \right. \nonumber \\{} & {} \left. \quad + \begin{pmatrix} 0 &{} 0 &{} 0 \\ 0 &{} z_{11} &{} z_{12} \\ 0 &{} z_{21} &{} z_{22} \end{pmatrix} \right] = 0 \end{aligned}$$

(1)

where $s$ is a complex frequency, leading to a more detailed form of the equation:

Fig. 1

The Lumpkin oscillator: a the simplified circuit ready for AC analysis, b Orcad Pspice realization with an ideal bipolar transistor and considering normalized values of passive components, c the generated sinusoidal waveform with period $2 \pi$ s, d) the plane projections of limit cycles, the amplitudes of current signals are $i_{L1}=1 A$ and $i_{L2}=i_{L3}=700 mA$. The yellow area specify the ideal transistor in a two-port configuration with a current-controlled voltage-source. (Color figure online)

Fig. 2

The Lumpkin oscillator: the circuit ready for symbolic analysis: a the approach suitable for derivation of the so-called Berkhausen conditions for stable oscillations, b the matrix method of loop currents with the chosen orientation of loops

Fig. 3

The Lumpkin oscillator: the equivalent circuit with an active nonlinear two-port described by impedance parameters, network structure dedicated for chaos/hyperchaos detection and numerical investigation

$$\begin{aligned}&s^{4} + \left[ \frac{1}{L_{1}}(z_{11}+z_{22}-z_{12}-z_{21}) + \frac{z_{11}}{L_{2}}+\frac{z_{22}}{L_{3}} \right] s^{3} \nonumber \\&\quad + \left[ det\,{\textbf {Z}}(\frac{1}{L_{1}L_{2}}+\frac{1}{L_{1}L_{3}}+\frac{1}{L_{2}L_{3}}) + \frac{1}{L_{1}C}\right] s^{2} \nonumber \\&\quad + \frac{1}{L_{1}C}(\frac{z_{11}}{L_{2}}+\frac{z_{22}}{L_{3}})s + \frac{det\,{\textbf {Z}}}{L_{1}L_{2}L_{3}C} = 0 \end{aligned}$$

(2)

If generalized bipolar transistor is involved, frequency of stable oscillations will be given by following relation:

$$\begin{aligned}&f_{osc} = \frac{1}{2\pi } \nonumber \\&\ \sqrt{\frac{L_{3}z_{11}+L_{2}z_{22}}{L_{2}L_{3}C(z_{11}+z_{22}-{z_{12}}-z_{21})+L_{1}C(L_{3}z_{11}+L_{2}z_{22})}}\nonumber \\ \end{aligned}$$

(3)

An ideal transistor in an active operational regime can be characterized by a zero backward trans-resistance ($z_{12} = 0\, \Omega$), with an ideal current controlled voltage source connected between the collector and emitter, without resistance connected in series with this voltage source ($z_{22} = 0\, \Omega$). By considering this simplification and by setting $z_{11} = z_{21}$, the oscillation frequency reduces into Thomson’s formula:

$$\begin{aligned} f_{osc} = \frac{1}{2\pi \sqrt{L_{1}C}} \end{aligned}$$

(4)

Other non-ideal features of conventional discrete bipolar transistor, such as the Early effect, lead resistances, or parasitic capacitances between terminals, are neglected at this moment. This type of analysis is limited to single-tone harmonic steady-state conditions. Different selections of loop currents will yield the identical CHE form. However, not every choice is suitable for manual calculations.

Regarding the impedance parameters, both the input and output impedance $z_{11}$ and $z_{22}$ will exhibit linearity. The backward trans-resistance is assumed to be relatively small and linear, while the forward trans-resistance $z_{21}$ conforms to an odd-symmetrical cubic polynomial function $z_{21} (i_{b}) = \alpha i_{b}^{3} + \beta i_{b}$. Saturation shape of this function is preserved by strict conditions $\alpha < 0$ and $\beta > 0$ that will be retained in upcoming numerical investigations. Adhering to these specifications, the analyzed system is illustrated in Fig. 3, and its behavior is uniquely defined by the following set of ordinary differential equations (ODEs):

$$\begin{aligned}&\frac{d}{dt}v_{c} = \frac{1}{C}i_{1} \nonumber \\&\frac{d}{dt}i_{1} = \frac{1}{L_{1}}\left[ -v_{c} \right. \nonumber \\&+ \left( z_{12}-z_{11}-z_{22} \right) i_{1} + z_{11}i_{2} + \left( z_{12}-z_{22} \right) i_{3} - z_{21}\nonumber \\&\left. \left( i_{2}-i_{1} \right) \right] \nonumber \\&\frac{d}{dt}i_{2} = \frac{1}{L_{2}} \left[ \left( z_{11}-z_{12} \right) i_{1} - z_{11}i_{2} - z_{12}i_{3} \right] \nonumber \\&\frac{d}{dt}i_{3} = \frac{1}{L_{3}} \left[ -z_{22}i_{1} -z_{22}i_{3} - z_{21}\left( i_{2}-i_{1} \right) \right] , \end{aligned}$$

(5)

where the state vector is ${\textbf {x}} = (v_{c}, i_{1}, i_{2}, i_{3})$. Obviously, either $z_{11}$ or $z_{12}$ needs to be different from zero. Otherwise, the base-emitter voltage of the bipolar transistor becomes shorted, removing the second inductor from our analysis completely.

To maintain the tractability of the forthcoming search-for-chaos problem, the total dimension of the investigated hyperspace of system parameters needs to be reduced. To achieve this, all working accumulation elements will be normalized to unity. This implies that the set of normalized values for the Lumpkin oscillator is $L_{1}=L_{2}=L_{3} = 1\,H$ and $C = 1\,F$. Before commencing the optimization routine, it’s essential to identify the basic properties of the dynamical system (Eq. 5). Henceforth, positive real values of impedance parameters are assumed. Straightforward analysis leads to the determination of fixed points. Apart from the equilibrium point located at zero, there are additional two fixed points at the positions:

$$\begin{aligned} {\textbf {x}}_{0}&= \begin{pmatrix} \left[ z_{11} - \frac{z_{11}}{z_{12}}(z_{11}-z_{22})-\beta \right] i^{0}_{2}-\alpha (i^{0}_{2})^{3} \\ 0 \\ i^{0}_{2} \\ -\frac{z_{11}}{z_{12}}i^{0}_{2} \\ \end{pmatrix}, \,\, \nonumber \\ i^{0}_{2}&= \pm \sqrt{\frac{z_{11}z_{22}-\beta z_{12}}{\alpha z_{12}}} \end{aligned}$$

(6)

To find chaotic regimes of the Lumpkin oscillator, lets focus on self-excited attractors caused by unstable equilibrium located at origin of state space. For unity values of all accumulation elements, the most general symbolic expression of linearization matrix is:

$$\begin{aligned}&{{\textbf {J}}}_{i,k} ({x}) = \frac{\partial {{\textbf {F}}}_{i}}{\partial {{\textbf {x}}}_{k}} = \begin{pmatrix} 0 &{} {1} &{} 0 &{} 0 \\ -1 &{} \beta - z_{11} + z_{12}-z_{22} + 3\alpha (i_{1}-i_{2})^{2} &{} z_{11}-\beta - 3\alpha (i_{1}-i_{2})^{2} &{} z_{12}-z_{22} \\ 0 &{} z_{11}-z_{12} &{} -z_{11} &{} -z_{12} \\ 0 &{} \beta -z_{22} + 3\alpha (i_{1}-i_{2})^{2} &{} -\beta -3\alpha (i_{1}-i_{2})^{2} &{} -z_{22} \end{pmatrix} \end{aligned}$$

(7)

Considering the position of the fixed point at the origin of the state space, the corresponding CHE can be expressed as:

$$\begin{aligned}&det \left[ \lambda {{\textbf {E}}} - {{\textbf {J}}}({{\textbf {x}}}) \right] = \lambda ^{4} + (2z_{11}- \beta - z_{12}+2z_{22})\lambda ^{3} \nonumber \\&\quad +(3z_{11}z_{22}-3\beta z_{12}+1)\lambda ^{2} +(z_{11}+z_{22})\lambda \nonumber \\&\quad + z_{11}z_{22}-\beta z_{12} = 0 \end{aligned}$$

(8)

where E stands for unity matrix and $\lambda$ is symbol adopted for eigenvalues. Note that the absolute term of this polynomial represents the determinant of the transistor’s impedance matrix after local linearization. The divergence of the vector field can be established using the global Jacobi matrix as:

$$\begin{aligned} \nabla {{\textbf {F}}} = \sum _{k=1}^{4}\frac{\partial {{\textbf {F}}}_{k}}{\partial {{\textbf {x}}}_{k}} = \beta - 2z_{11}+z_{12}-2z_{22}+3\alpha (i_{1}-i_{2})^{2} \end{aligned}$$

(9)

The quadratic function of the transistor’s base current determines the divergence of the vector field. A negative value (at least on average along the state trajectory) of the vector field divergence is an important quantity because it predicts the existence of attractors.

3 Numerical analysis

In accordance with the fundamental definition of chaos, obtaining a time-domain solution in closed form is not possible. Therefore, the analysis of chaotic systems is restricted to numerical algorithms, often based on integration processes. In the upcoming subsections of this paper, the fourth-order Runge–Kutta method with a fixed time step has been utilized. Due to local abrupt changes in system dynamics, the maximum time step needs to be chosen carefully, considering the maximal local divergence of two neighboring state space orbits [31]. This rule should be respected both

in the search-for-chaos optimization routine and the subsequent investigation of individual discoveries. The described metaheuristic algorithms are commonly used in tasks such as finding chaotic parameter subspaces of existing network structures or even discovering new circuit topologies that generate robust chaotic waveforms [32]. To observe a two-dimensional routing-to-chaos scenario, the swept parameters can be reduced to the forward (linear term) and backward trans-resistance of the bipolar transistor.

Through the application of a brute-force numerical search-for-chaos algorithm, the following set of internal system parameters that leads to robust weakly hyperchaotic behavior has been discovered:

$$\begin{aligned} z_{11}&= z_{22} = 0\,\Omega , \, z_{12} = 400\,m\Omega , \,\nonumber \\ \alpha&= -1\,V^{3}A^{-1},\, \beta = 1.9\,\Omega \end{aligned}$$

(10)

Note that these values can be easily physically justified. Parameters $z_{11}$ and $z_{22}$ represent the bias point of the active two-port, where both input and output impedance are close to zero. A significant level of backward trans-resistance (comparable to the working resistance) indicates that the generalized bipolar transistor operates far from the unilateral regime. By calculating the roots of the polynomial (Eq. 8) with the values (Eq. 8), we learn that the state space origin is a repelling fixed point and the local vector field geometry is characterized by eigenvalues:

$$\begin{aligned} \lambda _{1} = 0.153\pm \, j0.564,\,\lambda _{3} = 2.793,\,\lambda _{4} = -0.798 \end{aligned}$$

(11)

This implies that the trajectory evolution in the close neighborhood of the origin is composed of three components: an unstable spiral, and movement along the unstable and stable eigenvectors.

Let’s consider another group of normalized “chaotic” parameters:

$$\begin{aligned} z_{11} = z_{22} = 0\,\Omega , \, z_{12} = 1\,\Omega , \, \alpha = -1\,V^{3}A^{-1},\, \beta = 0\,\Omega \end{aligned}$$

(12)

This set of system parameters leads to the following set of eigenvalues associated with the fixed point at the origin:

$$\begin{aligned} \lambda _{1} = 0.5\pm \, j0.866,\,\lambda _{3} = \lambda _{4} = 0 \end{aligned}$$

(13)

Obviously, this case deviates significantly from the conventional understanding of transistor behavior. The forward trans-resistance exhibits insensitivity to small (zero offset) signals, while the backward trans-resistance becomes even more significant. However, it is still worth mentioning this solution of the Lumpkin oscillator for two reasons. Firstly, the vector field is different from the previous case with only a single fixed point located at the origin. Secondly, the dynamical system exhibits hyperchaotic behavior with a pair of two positive Lyapunov Exponents (LE) $\bigl \{0.045, 0.013\bigr \}$ and a Kaplan–Yorke dimension (KYD) of about 3.074. Another interesting adjustment of the impedance parameters is worth mentioning. For an increased value $\beta = 0.2\,\Omega$, the Lumpkin oscillator possesses three fixed points again, placed symmetrically with respect to the state space origin $\bigl \{-i_{2}^0, 0, i_{2}^0\bigr \}$. In this case, the value of KYD increases to 3.189. This is the highest value of KYD among all parameter configurations investigated in the study of the simplified Lumpkin oscillator.

Figure 4 illustrates a typical strange attractor generated by the Lumpkin oscillator with the parameter set given in (Eq 9). For numerical integration, the fourth-order Runge-Kutta method with a final time of 1000 s, a time step of 1 ms, and initial conditions ${\textbf {x}}_{0} = (0,2,1,-3)^T$ were employed. This attractor evolves within a limited state space volume, specifically $v_{c} \in (-4,4)\,V$, $i_{1} \in (-4,4)\,A$, $i_{2} \in (-4,4)\,A$ and $i_{3} \in (-4,4)\,A$. The state attractor is bounded, dense, and chaotic, characterized by KYD about 2.04. Furthermore, Fig. 4 demonstrates that the Lumpkin oscillator with the discovered “chaotic” set of parameters is extremely sensitive to small changes in initial conditions. To illustrate this, a group of $10^4$ initial conditions were randomly distributed with a uniform distribution around the origin of the state space, resulting in a hypercube with an edge length of 0.01. Subsequently, the final states after 1 s of time evolution (orange dots), 10 s of evolution (red dots), and 100 s of elapsed time (blue dots) are visualized. It is evident that a time span of 100 s is sufficient to settle and display the entire shape of the strange attractor for all cases.

Fig. 4

Full gallery of 3D projections of typical strange attractor associated with chaotic Lumpkin oscillator: a $v_{c}-i_{1}-i_{2}$, b $v_{c}-i_{1}-i_{3}$, c $v_{c}-i_{2}-i_{3}$, and d $i_{1}-i_{2}-i_{3}$. Sensitivity dependance on initial conditions of chaotic system: e $i_{1}-i_{2}$, f plane $v_{c}-i_{3}$, g plane $v_{c}-i_{2}$, and h plane $v_{c}-i_{1}$. Monge projections of hyperchaotic attractor: i $v_{c}-i_{1}-i_{2}$, j $v_{c}-i_{1}-i_{3}$, k $v_{c}-i_{2}-i_{3}$, and m $i_{1}-i_{2}-i_{3}$. Demonstration of system sensitivity: n $i_{1}-i_{2}$, o plane $v_{c}-i_{3}$, p plane $v_{c}-i_{2}$, and q plane $v_{c}-i_{1}$. Plane projections for hyperchaotic system with three fixed points: r $i_{1}-i_{2}$, s plane $v_{c}-i_{3}$, t) plane $v_{c}-i_{2}$, and u plane $v_{c}-i_{1}$ and corresponding sensitivities: v zoomed area of initial conditions and short-time evolution, w $v_{c}-i_{1}-i_{2}$, x $v_{c}-i_{1}-i_{3}$, y $v_{c}-i_{2}-i_{3}$, and z $i_{1}-i_{2}-i_{3}$

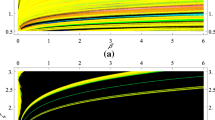
Figure 5 provides an illustrative example of the chaotic fingerprints derived from the time responses generated by the mathematical model of the Lumpkin oscillator. Firstly, the quantity known as approximate entropy [33, 34] is plotted with respect to the natural bifurcation parameters $z_{12}$ and $\beta$. Using an embedding dimension of 4, a tolerance value of 0.1, and a time evolution of the state variable $v_{c}$ over 500 s, a maximal value of 0.26 has been reached. Recurrence plots suggest complex patterns presented in all waveforms generated by the chaotic Lumpkin dynamical system. In this simulation, the voltage across the capacitor is analyzed, with a time evolution of 1000 s and a time step of 10 ms. A circle with a radius of $\epsilon _{r} = 0.05$ is adopted as an essential input parameter of the used routine, defining the pattern resolution of the final plot. Finally, one-dimensional bifurcation diagrams are plotted for two state variables and uniform parameter steps $1\,m\Omega$.

Fig. 5

Rainbow-scaled 5-contour plot of approximate entropy associated with the chaotic Lumpkin oscillator, waveform $v_{c}(t)$: a $z_{12} \in (0.9,1)\,\Omega$ and $\beta \in (1.8,1.9)\,\Omega$, b $z_{12} \in (1,1.1)\,\Omega$ and $\beta \in (1.8,1.9)\,\Omega$, c $z_{12} \in (1.1,1.2)\,\Omega$ and $\beta \in (1.8,1.9)\,\Omega$, d $z_{12} \in (0.9,1)\,\Omega$ and $\beta \in (1.7,1.8)\,\Omega$, e $z_{12} \in (1,1.1)\,\Omega$ and $\beta \in (1.7,1.8)\,\Omega$, and f $z_{12} \in (1.1,1.2)\,\Omega$ and $\beta \in (1.7,1.8)\,\Omega$. Recurrence plots visualized for all state variables: g voltage $v_{c}$, h current $i_{1}$, i current $i_{2}$, and j current $i_{3}$. Illustrative bifurcation diagrams plotted with Poincaré plane $v_{c} = 0\,V$ and for: k $z_{12} \in (320,750)\,m\Omega$, and m $z_{12} \in (1.70,2.13)\,\Omega$

Fig. 6

Rainbow-scaled 5-contour plot of approximate entropy associated with the chaotic Lumpkin oscillator, waveform $v_{c}(t)$: a $z_{12} \in (0.9,1)\,\Omega$ and $\beta \in (100,200)\,m\Omega$, b $z_{12} \in (1,1.1)\,\Omega$ and $\beta \in (100,200)\,m\Omega$, c $z_{12} \in (1.1,1.2)\,\Omega$ and $\beta \in (100,200)\,m\Omega$, d $z_{12} \in (0.9,1)\,\Omega$ and $\beta \in (0,100)\,m\Omega$, e $z_{12} \in (1,1.1)\,\Omega$ and $\beta \in (0,100)\,m\Omega$, and f $z_{12} \in (1.1,1.2)\,\Omega$ and $\beta \in (0,100)\,m\Omega$. Recurrence plots visualized for all state variables: g voltage $v_{c}$, h current $i_{1}$, i current $i_{2}$, and j current $i_{3}$. Attractor volume rescaling for $\beta = 0\,\Omega$ and $z_{12} = 900\,m\Omega$ plotted in different views: k $i_{2}$ versus $i_{1}$, m $v_{c}$ versus $i_{1}$, and n $v_{c}$ versus $i_{2}$

Figure 6 illustrates the same types of analysis for the Lumpkin oscillator but covering the parameter set (Eq. 11). The calculation results reveal that the parameter areas where behavior is complex are bounded, surrounded by many more “trivial” solutions (having minimal self-similarity of time domain segments). For each calculation based on the time domain response, transient behavior was omitted by considering initial conditions after 500 s of the system’s preliminary evolution. The last set of three state trajectories (cases k), m), and n)) are bounded to the mathematical description of the dynamical system. It is demonstrated that the state space volume occupied by the chaotic attractor can be systematically increased or decreased by changing a single parameter $\alpha$ up to some degree. The individual plotted cases were $\alpha = -1\,V^{3}A^{-1}$ (original orbit), $\alpha = -2\,V^{3}A^{-1}$ (blue orbit), and $\alpha = -5\,V^{3}A^{-1}$ (black trajectory).

Fig. 7

Surface-contour plot showing regions of chaotic and hyperchaotic (red dots) behavior associated with Lumpkin oscillator, fragments of $z_{12}$ versus $\beta$ plane. (Color figure online)

Fig. 8

Surface-contour plot showing regions of chaotic and hyperchaotic (red dots) behavior associated with Lumpkin oscillator, fragments of $z_{12}$ versus $\beta$ plane. (Color figure online)

Fig. 9

Surface-contour plot showing regions of chaotic and hyperchaotic (red dots) behavior associated with Lumpkin oscillator, fragments of $z_{12}$ versus $\beta$ plane. (Color figure online)

Figures 7, 8 and 9 depict rainbow-scaled surface-contour plots of the largest Lyapunov exponent as a two-dimensional function of the natural bifurcation parameters $\bigl \{z_{12}, \beta \bigr \}$. The red dots represent parameter configurations where two positive Lyapunov exponents suddenly appear. It is noteworthy that, in accordance with simulation results, individual red dots are not connected, indicating that hyperchaos is quite rare and alternates with “simple” chaotic motion.

4 Circuit models and measurement

The numerical methods employed for investigating dynamical motion are still only approximations of reality, subject to conventional disadvantages such as rounding errors and problem discretization. In contrast, analog circuits work in real time and offer smooth integration processes. Using large final times relative to small time constants of the constructed circuit results in captured oscilloscope screenshots that correspond to steady states, without the need for waiting or wasting electrical energy. However, parasitic and non-ideal properties of active elements can introduce both linear and nonlinear terms to the original set of ordinary differential equations. If so, system dynamics can be affected, potentially causing the desired strange attractor to be altered, deformed, or to disappear altogether.

Nonlinear circuit synthesis based on a predefined set of ordinary differential equations is a task with multiple correct solutions. Numerous research papers have been dedicated to this problem, as exemplified by the comprehensive review work by Itoh [35]. An interesting approach suitable for design of arbitrary chaotic system is based on its integrator block schematic [36]. This method originates in analog computers (AC), ancient universal analog machines capable to solve simple ordinary differential equations. Obvious drawback of chaotic oscillators constructed as AC is the necessity to use many active elements, which can be reduced by utilizing a field programmable analog array (FPAA) [37]. Although the graphical user interface of commercially available FPAA platforms greatly simplifies the design process, the size of the working area dedicated to inserting electronic components is limited. Some authors use field programmable gate arrays (FPGAs) as a tool for verifying the chaotic nature of system [38]. However, it is more likely a bridge between numerical analysis of differential equations and experimental verification. On the other hand, the generated chaotic signal can be directly used for FPGA-based post-processing, such as image encryption, chaos-based modulation, secure communication purposes, and many other applications. A considerable number of papers focus on the circuit implementation of specific dynamical systems, such as fractional-order memristor-based chaotic oscillators [39].

Certainly, a chaotic Lumpkin oscillator can be constructed using various synthesis concepts, including AC mentioned above. Before practical construction, Orcad Pspice circuit simulations can indicate the correctness of the selected solution. In Fig. 10, we illustrate the initial step toward the chaotic oscillatory system, where the yellow rectangle denotes the two-port described by impedance parameters. Both trans-resistances and polynomial nonlinearity are realized using ideal controlled sources and ideal multipliers (MULT blocks). For the chosen time constants, setting a final time of 100 ms is sufficient for the chaotic attractor to fully evolve.

Fig. 10

Chaotic Lumpkin-like oscillator: a simplified construction using ideal multipliers and controlled sources, b Orcad Pspice circuit simulation in time domain, 2D visualization of all currents versus voltage across grounded capacitor

To avoid the realization of three precise inductors, the duality principle can be applied. According to this general rule, a set of ordinary differential equations remains formally the same, but the state variables change into their duals (inductor currents into voltages across capacitors and vice versa). Figure 11 can be understood as a dual Lumpkin oscillator, again with ideal active circuit components. A working example of a Lumpkin-based chaotic system (5) with parameter set (12) is provided in Fig. 12, including numerical values of all network elements. After substituting normalized parameters into the differential equations, all parameters of the dynamical system become unity, simplifying the system significantly. Thus, the final chaotic oscillator is simple as well. Integrated circuits AD844 serve as positive second-generation current conveyors, and the outputs of U1, U2, and U3 can be directly used for oscilloscope probes. The set of describing ordinary differential equations is as follows:

$$\begin{aligned}&{\frac{d}{dt}i_{L} = \frac{1}{L}v_{y},}\, \nonumber \\&\quad {\frac{d}{dt}v_{y} = \frac{1}{C_{1}}\left[ -i_{L} + \frac{1}{R_{1}}(v_{z}-v_{y})^{3} - \frac{1}{R_{2}}(v_{w}-v_{y}) \right] ,} \nonumber \\&\quad {\frac{d}{dt}v_{z} = \frac{1}{C_{2}R_{2}}(v_{w}-v_{y}),}\, \nonumber \\&\quad {\frac{d}{dt}v_{w} = -\frac{1}{C_{3}R_{3}}(v_{w}-v_{y})^{3}.} \end{aligned}$$

(14)

The new vector of state variables is ${\textbf {x}} = (v_{c}\, i_{1}\, i_{2}\, i_{3}) \rightarrow (i_{L1}\, v_{y}\, v_{z}\, -v_{w})$, indicating a basic linear change of coordinates. The resistors $R_{4}$, $R_{5}$, $R_{6}$, and $R_{7}$ do not appear in Eq. (14) since they only compensate for the internally trimmed transfer constant of the four-quadrant analog multipliers $K = 0.1$. Figure 12 also provides circuit simulation results, namely plane projections of typical chaotic attractor and frequency spectras of two generated voltage waveforms. A form of period doubling route to chaos scenario was observed, although limit cycles are not depicted. The frequency spectrum of the chaotic signal is broad-band and resembles noise in many aspects. Figure 13 provides a graphical demonstration illustrating the close correspondence between individual circuit measurement results and numerical analysis. By visually comparing the related attractors, any discrepancies can be easily judged.

Fig. 11

Chaotic oscillator dual to classical Lumpkin oscillator: a simplified construction using ideal multipliers and controlled sources, b Orcad Pspice circuit simulation in time domain, 2D visualization of all voltages versus inductor current. Yellow area specifies polynomial voltage transfer function. (Color figure online)

Searching for the optimal circuitry realization from the viewpoint of practical experimentation could lead to a design method based on inverting integrators. An example of this is provided in Fig. 14, and this schematic is ready for simulation as well as practical measurement. Figure 15 shows the comparison between numerically integrated strange attractors and those experimentally verified using the same horizontal and vertical scales. Note that only four integrated circuits are needed, as the integrated circuit TL084 contains four operational amplifiers. The describing set of differential equations is as follows:

$$\begin{aligned}&\frac{d}{dt}v_{x} = -\frac{1}{C_{1}R_{1}}v_{y}, \nonumber \\&\frac{d}{dt}v_{y} = \frac{1}{C_{2}} \nonumber \\&\quad \left[ \frac{1}{R_{3}}\left( \frac{R_{14}}{R_{13}}v_{w} + \frac{R_{14}}{R_{12}}v_{y} \right) + \frac{1}{R_{2}} \frac{R_{5}}{R_{4}}v_{x}\right] + \nonumber \\&\quad \frac{1}{C_{2}} \left[ \frac{1}{R_{6}} \left( \frac{R_{10}}{R_{11}}v_{y} + \frac{R_{10}}{R_{16}}v_{z} \right) - \frac{K}{R_{7}} \left( \frac{R_{10}}{R_{11}}v_{y} + \frac{R_{10}}{R_{16}}v_{z} \right) ^{3} \right] , \nonumber \\&\frac{d}{dt}v_{z} = \frac{1}{C_{3}R_{15}}\left( \frac{R_{14}}{R_{12}}v_{y} + \frac{R_{14}}{R_{13}}v_{w} \right) ,\, \nonumber \\&\frac{d}{dt}v_{w} = \frac{1}{C_{4}}\nonumber \\&\quad \left[ \frac{1}{R_{9}} \left( \frac{R_{10}}{R_{11}}v_{y} + \frac{R_{10}}{R_{16}}v_{z} \right) - \frac{K}{R_{8}} \left( \frac{R_{10}}{R_{11}}v_{y} + \frac{R_{10}}{R_{16}}v_{z} \right) ^{3} \right] \end{aligned}$$

(15)

and individual terms can be compared with the coefficients of the mathematical model (5). Note that a state vector transformation ${\textbf {x}} = (v_{c}\, i_{1}\, i_{2}\, i_{3}) \rightarrow (-v_{x}\, v_{y}\, -v_{z}\, v_{w})$ has been applied to simplify the final circuit realization. Resistors $R_{17}$ and $R_{18}$ do not appear in Eq. (15) since they only compensate for the transfer constant of the first analog multiplier in the cascade. Circuit simulation can be found in Fig. 14, where two plane projections of typical strange attractor are visualized. Figure 15 confirms that there is a very good correspondence between theoretical expectations and practical observations.

Both experimental measurements mentioned above revealed the following facts: (a) The amplitudes of the generated signals corresponds to the amplitudes of numerically integrated trajectories, and, simultaneously, fall within the dynamical ranges of linear operation of active elements. (b) The generated signals have limited amplitudes only for system parameters for which the mathematical model exhibits an unbounded solution. For bounded solution associated with the math model, all outputs of active elements remain unsaturated. (c) During the real measurement of the circuit given in Fig. 12, the total power dissipation did not exceed $1\,W$ per supply voltage branch (either positive or negative). For the AC design provided in Fig. 14, the total power dissipation decreases to a maximum of $800\,mW$ per supply branch. Low power consumption prevents overheating of discrete circuit components.

The time constants of the circuit were adjusted such that non-ideal and parasitic effects of active devices can be neglected. Otherwise, the intrinsic low-pass filtering effect common to all active elements can remove high frequency component of chaotic signal, turning the generated waveform into quasi-periodic. For more details about this topic, please refer to the paper by Munoz-Pacheco et al. [40] and references cited therein.

Fig. 12

Circuitry realization of dual Lumpkin oscillator, Orcad Pspice circuit simulation (selected plane projections and frequency spectra), and screenshot of the measured plane projection of strange attractor, where the inductor current was converted into voltage (horizontal axis) via sensing resistor

Fig. 13

Visual comparison between experimentally measured (first and third row) and numerically integrated counterparts, dual Lumpkin oscillator realization. The parameters for given pairs of images are following: a $z_{12} = 2\ \Omega$ and $\beta = 0.3\ \Omega$ resulting to $R_{1} = R_{3} = 3.3 \ k\Omega$ and $R_{2} = 470 \ \Omega$, b $z_{12} = 1.8\ \Omega$ and $\beta = 0.6\ \Omega$ represented by values $R_{1} = R_{3} = 1.6 \ k\Omega$ and $R_{2} = 1.8 \ k\Omega$, c $z_{12} = 1\ \Omega$ and $\beta = 0.25\ \Omega$ leading to $R_{1} = R_{3} = 4 \ k\Omega$ and $R_{2} = 1 \ k\Omega$, d $z_{12} = 1.8\ \Omega$ and $\beta = 0.3\ \Omega$ leading to $R_{1} = R_{3} = 3.3 \ k\Omega$ and $R_{2} = 560 \ \Omega$, e $z_{12} = 0.7\ \Omega$ and $\beta = 1.8\ \Omega$ which correspond to $R_{1} = R_{3} = 560 \ \Omega$ and $R_{2} = 1.4 \ k\Omega$, f $z_{12} = 1\ \Omega$ and $\beta = 0.05\ \Omega$ leading to $R_{1} = R_{3} = 10 \ k\Omega$ and $R_{2} = 1 \ k\Omega$, g $z_{12} = 2.3\ \Omega$ and $\beta = 0.8\ \Omega$ resulting to $R_{1} = R_{3} = 1.2 \ k\Omega$ and $R_{2} = 470 \ \Omega$, h $z_{12} = 1.8\ \Omega$ and $\beta = 0.3\ \Omega$ which corresponds to values of resistors $R_{1} = R_{3} = 3.3 \ k\Omega$ and $R_{2} = 560 \ \Omega$

Fig. 14

Circuitry realization of flow-equivalent Lumpkin oscillator, Orcad Pspice simulation and two plane projections of typical chaotic attractor, shapes of typical strange attractor in two available plane projections visualized using Orcad Pspice circuit simulator

Fig. 15

Direct comparison of oscilloscope screenshots captured as oscilloscope photos and numerically integrated counterparts, AC based design. Parameters for provided paired images are following: a, b $z_{12} = 0.42\,\Omega$ and $\beta = 0.86\,\Omega$ leading to $R_{6} = R_{8} = 11.4\,k\Omega$ and $R_{14} = 4.2\,k\Omega$, c, e $z_{12} = 0.42\, \Omega$ and $\beta = 1.3\,\Omega$ leading to $R_{6} = R_{8} = 7.7\,k\Omega$ and $R_{14} = 4.2\,k\Omega$, d $z_{12} = 0.84\,\Omega$ and $\beta = 2\,\Omega$ leading to $R_{6} = R_{8} = 5\,k\Omega$ and $R_{14} = 8.4\,k\Omega$, f $z_{12} = 0.9\,\Omega$ and $\beta = 1.9\,\Omega$ leading to $R_{6} = R_{8} = 5.3\,k\Omega$ and $R_{14} = 9\,k\Omega$, g $z_{12} = 0.7\,\Omega$ and $\beta = 1.7\,\Omega$ resulting in $R_{6} = R_{8} = 5.9\,k\Omega$ and $R_{14} = 7\,k\Omega$, h $z_{12} = 0.9\,\Omega$ and $\beta = 2.7\,\Omega$ resulting in values of resistors $R_{6} = R_{8} = 3.7\,k\Omega$ and $R_{14} = 9\,k\Omega$

5 Conclusion

This paper presents a brute-force heuristic numerical approach to uncover chaos in the fundamental topology of a fourth-order Lumpkin-type sinusoidal oscillator. The circuit comprises a single generalized bipolar transistor with hypothetical biasing but realistic parameters. Chaos is demonstrated through both numerical analysis and experimental verification, employing various various commonly used numerical algorithms to confirm the observed dynamical motion’s authenticity. The chaotic or hyperchaotic motion observed is robust, structurally stable, and not a numerical artifact or systematic error.

The Lumpkin oscillator case is intriguing for several reasons:

• (A) It offers a straightforward practical construction of isolated electronic system operating in a hyperchaotic regime.

• (B) Chaos is confirmed for different local formations of the vector field near the fixed point at the origin.

• (C) The analyzed Lumpkin case, a hybrid Clapp-Hartley topology in essence, provides insight into intermittent hyperchaos in fourth-order autonomous deterministic dynamical systems.

• (D) The strange attractor can be effectively rescaled by a single system parameter.

Several avenues for future research are suggested, including investigating hidden chaotic attractors, exploring multistability, studying chameleon dynamics, and exploring the fractional-order nature of the Lumpkin system. The paper leaves potential practical applications of the proposed novel chaotic and/or hyperchaotic system to curious readers.