1 Introduction

Nonlinear Evolution Equations (NLEEs) are essential in studying various dynamic processes, including nonlinear optics, solid-state physics, geology, image processing, oceanography, thermodynamics, fluid mechanics, quantum field theory, and chemical reactions [1, 8]. In recent years, numerous analytical and numerical methods have been proposed and applied to address NLEEs. Some of these methods are: Hirota bilinear method [9], tanh-coth expansion method [10,11,12,13], IBSEF method [14], solitary wave ansatz method [15], first integral method, [16] a new version of trial equation method [17], spectral Tau method [18], exp(-\(\phi \)(\(\eta \)))-expansion method [19], generalized He’s Exp-function method [20], rational sine-cosine method [21, 22], Aboodh transform decomposition method [23], Riccati equation method [24], and bilinear neural network method [29,30,31,32]. These methods transform the NLEEs into solvable differential equations, allowing efficient solutions for nonlinear differential equations.

The Kadomtsev-Petviashvili (KP) equation is essential for studying the stability of the one-soliton solution of the Korteweg-de Vries (KdV) equation under transverse perturbations. In the 1970 s, the \((2+1)\)-dimensional KP equation that now bears the names of the two physicists was derived as a model for investigating the evolution of small amplitude long ion-acoustic waves propagating in plasmas and defined as [33]:

$$\begin{aligned} (G_t +6 G G_x +G_{xxx})_x +3\gamma ^2 G_{yy}=0, \end{aligned}$$
(1.1)

where \(G=G(x,y,t)\), the longitudinal and transverse spatial coordinates are denoted by x and y, respectively. This equation contains weak transversal perturbations, weakly dispersive waves with weak dispersion \(G_{xxx}\), and quadratic nonlinearity \( G G_x\).

  • If \(\gamma =\sqrt{-1}\), the Eq. (1.1) describes the KP-I equation, which is used to model waves in thin films with high surface tension.

  • If \(\gamma =1\), the Eq. (1.1) converts to KP-II equation which describes low surface tension water waves.

Physicists differentiate between KP- I and II in the classical KP equation based on the \(\textit{sign}\) of the dispersive term, indicating positive or negative dispersion in media.

Considering the KP model’s many applications, researchers have become more interested in studying its exact traveling wave solutions in recent years. Yue et al. [34] investigated \((3 + 1)\)-dimensional KP equation by modified Khater and Jacobi elliptical function methods. Khan and Akbar applied the exp\((-\Phi (\xi ))\)-expansion method to \((2 + 1)\)-dimensional KP equation in [35]. Raza et al. implemented a linear superposition technique to \(n+1\)- dimensional integrable extension of KP equation [36], and references therein [37, 39].

In this work, we will focus on a more general form of extended \((2 + 1)\)-dimensional KP equation [40]

$$\begin{aligned} ( G_t -6 GG_x +G_{xxx})_x+\chi _1 G_{yy}+\chi _2 G_{tt}+\chi _3 G_{ty}=0, \end{aligned}$$
(1.2)

where \(\chi _1, \chi _2, \chi _3\) are real constants. The terms \(\chi _1\), \(\chi _2\), and \(\chi _3\) symbolize the terms related to dispersion effects. Specifically, \(\chi _1 G_{yy}\) represents spatial dispersion, \(\chi _2 G_{tt}\) represents temporal dispersion, and \(\chi _3 G_{ty}\) represents the cross-dispersion effect. These terms contribute to the characterization of dispersion phenomena within the equation.

This work aims to obtain various families of exact solutions for the given Eq. (1.2) and analyze their physical states in detail. Obtaining analytical solutions to the Kadomtsev-Petviashvili (KP) equation provides insights into the system’s behavior described by the equation. They can reveal fundamental properties, such as the existence of certain types of waves, solitons, or other coherent structures, shedding light on the underlying dynamics. Besides, analytical solutions allow for the prediction of specific behaviors under different conditions without extensive computational simulations. This predictive capability is invaluable in various fields, including fluid dynamics, plasma physics, and nonlinear optics.

The rest of the article is structured as follows. Section 2 and 3 explain the modified extended tanh-function and generalized Kudryashov methods. In Sect. 4, new exact solutions for the generalized extended Kadomtsev-Petviashvili equation are presented. Section 5 presents the dynamical strategy sensitivity, while Sect. 6 provides a brief analysis of the stability. Benefits, limitations of this proposed scheme, and graphical behaviors are discussed in Sect. 7. Finally, a brief conclusion is presented in the last section.

2 Modified extended tanh-function method

To demonstrate the main idea of the modified extended tanh-function method, we examine the partial differential equation as [41, 42].

$$\begin{aligned} \Psi (G_x, G_t, G_{xx},G_{tt},G_{xt},...)=0, \end{aligned}$$
(2.1)

where \(\Psi \) is a polynomial in G(x, t) with nonlinear components in its partial derivatives.

The traveling wave transformation is defined as:

$$\begin{aligned} G (x, t) = g( \zeta ), \quad \zeta = k(x-ct). \end{aligned}$$
(2.2)

Eq. (2.1) is transformed into an ordinary differential equation (ODE) using the transformation described in Eq. (2.2), which is then given in the following form:

$$\begin{aligned} {N}(g( \zeta ),g^{\prime }( \zeta ),g^{\prime \prime }( \zeta ),\ldots ) =0. \end{aligned}$$
(2.3)

Assume that the solution to Eq. (2.3) takes on the following form,

$$\begin{aligned} g( \zeta )=a_0+\sum _{j=1}^{M}\left( a_j H^j( \zeta )+b_j H^{-j}( \zeta )\right) . \end{aligned}$$
(2.4)

To verify that \(H( \zeta )\) satisfies the Riccati equation and to satisfy the requirements \(a_{M}\ne 0\), \(b_{M}\ne 0\), the constants \(a_j\) and \(b_j\) must be established,

$$\begin{aligned} H'( \zeta )-{H( \zeta )}^2-\lambda =0, \end{aligned}$$
(2.5)

where \(\lambda \) is a constant that will be determined later. Several different solutions can be obtained for Eq. (2.5), as illustrated below,

  • When \(\lambda <0\)

    $$\begin{aligned} H( \zeta )= & {} -\sqrt{-\lambda }tanh(\sqrt{-\lambda } \zeta )\ \ or\\ H( \zeta )= & {} -\sqrt{-\lambda }coth(\sqrt{-\lambda } \zeta ). \end{aligned}$$

  • When \(\lambda >0\)

    $$\begin{aligned} H( \zeta )=\sqrt{\lambda }tan(\sqrt{\lambda } \zeta )\ \ or\ \ H( \zeta )=-\sqrt{\lambda }cot(\sqrt{\lambda } \zeta ). \end{aligned}$$

  • When \(\lambda =0\)

    $$\begin{aligned} H( \zeta )=-\frac{1}{ \zeta }. \end{aligned}$$

Determining the positive integer M in Eq. (2.4) requires balancing the nonlinear variables and highest-order derivatives. The values of \(a_j\) and \(b_j\) may be obtained using symbolic calculations by substituting Eq. (2.4), together with its derivative, and Eq. (2.5), in Eq. (2.3). After that, exact solutions for Eq. (2.1) may be calculated by collecting terms with the same power \(H^{j}\), where \((j=0,1,2,\cdots ,M)\), and setting them to zero. By substituting the determined values into the Eq. (2.4), together with the responses to the Eq. (2.5), the exact solutions to Eq. (2.1) are obtained.

3 The modified generalized Kudryashov method

This section presents the generalized modified Kudryas hov approach [7]. The subsequent phases should be implemented analogously to executing the initial two steps in the preceding methodology.

Exact solutions can be constructed as a finite series as

$$\begin{aligned} u(\zeta ) = \sum _ {r = 0}^M \frac{b_r}{(1+H(\zeta ))^r}, \end{aligned}$$
(3.1)

where, the constant \(b_r\), (\( r = 0, 1,\ldots , M\)) is undetermined. Furthermore, the following Riccati equation will be satisfied by \(Q(\zeta )\),

$$\begin{aligned} H'(\zeta )=\sigma +\delta H(\zeta )+\tau H(\zeta )^2, \end{aligned}$$
(3.2)

where \(\sigma ,\delta \) and \(\tau \) denote real constants. Following is a summary of the solutions to Eq. (3.2) for various cases of these coefficients:

  • When \(\tau \ne 0\) and \(\sigma ,\delta \) are arbitrary constants, then \(H(\zeta )\) can be written as

    $$\begin{aligned} H(\zeta )=\frac{\sqrt{4 \tau \sigma -\delta ^2} \tan \left( \frac{1}{2} (d+\zeta ) \sqrt{4 \tau \sigma -\delta ^2}\right) -\delta }{2 \tau }. \end{aligned}$$
    (3.3)

  • When \(\tau \) is an arbitrary constant, \(\delta \ne 0\), and \(\sigma = 0\), \(H(\zeta )\) can be expressed as

    $$\begin{aligned} H(\zeta )=-\frac{\delta \textrm{e}^{\delta (d+\zeta )}}{\tau \textrm{e}^{\delta (d+\zeta )}-1}. \end{aligned}$$
    (3.4)

  • When \(\sigma \) is an arbitrary constant, \(\delta \ne 0\) and \(\tau = 0\), the expression for \(H(\zeta )\) is given by,

    $$\begin{aligned} H(\zeta )=\frac{\textrm{e}^{\delta (d+\zeta )}}{\delta }-\frac{\sigma }{\delta }. \end{aligned}$$
    (3.5)

To find the solutions to the equation, the last phase of the previous method is also applied.

4 Application of the techniques

This section shows the effectiveness of the modified generalized Kudryashov and the modified extended tanh-function methods in obtaining the solitary wave solutions of the model (2.1), which are the generalized extended KP equation using \(G(x,y,t)=g(\zeta )\), \(\zeta =x+my+ct\), we get

$$\begin{aligned} \left( c \left( c \chi _2+m \chi _3+1\right) +m^2 \chi _1\right) g+g''-3 g^2=0.\nonumber \\ \end{aligned}$$
(4.1)

Balancing, \(g^{2}=2M, g''=M+2\) results in \(M=2\), the following exact solutions are derived.

4.1 Analytical solutions by modified extended tanh-function method

By taking \(M=2\), the series of sums (2.4) is as follows:

$$\begin{aligned} g =a_0 +a_1 H(\zeta ) + a_2 H(\zeta )^2+\frac{b_1}{H(\zeta )}+\frac{b_2}{H(\zeta )^2}. \end{aligned}$$
(4.2)

When combined with Eq. (4.1), the algebraic system that follows is created.

$$\begin{aligned} 0= & {} 6 a_2-3 a_2^2, \\ 0= & {} 2 a_1-6 a_1 a_2, \\ 0= & {} 6 \lambda ^2 b_2-3 b_2^2, \\ 0= & {} 2 \lambda ^2 b_1-6 b_1 b_2, \\ 0= & {} -6 a_0 b_2+ c^2 \chi _2 b_2 + c m \chi _3 b_2 +c b_2 \\{} & {} +8\lambda b_2 + m^2 \chi _1 b_2 -3 b_1^2, \\ 0= & {} -6 a_0 b_1-6 a_1 b_2+ c^2 \chi _2b_1+ c m \chi _3 b_1 \\{} & {} + c b_1 +2 b_1 \lambda + \chi _1 m^2 b_1, \\ 0= & {} c^2 \chi _2 a_2 + c m \chi _3 a_2 +a_2 c+8 a_2 \lambda \\{} & {} + m^2 \chi _1 a_2 -3 a_1^2-6 a_0 a_2, \\ 0= & {} -6 a_2 b_1+a_1 c^2 \chi _2+a_1 c m \chi _3+a_1 c+2 a_1 \lambda \\{} & {} + m^2 \chi _1a_1 -6 a_0 a_1, \\ 0= & {} -6 a_1 b_1-6 a_2 b_2+a_0 c^2 \chi _2+a_0 c m \chi _3+a_0 c\\{} & {} +2 a_2 \lambda ^2+a_0 m^2 \chi _1-3 a_0^2+2 b_2. \end{aligned}$$

Six cases of solutions for the coefficients \(a_0\), \(a_1\), \(a_2\),\(b_1\), and c are obtained.

case 1

$$\begin{aligned} a_0= & {} 2 \lambda ;a_1=0;a_2=0;b_1=0;b_2=2 \lambda ^2; \nonumber \\ c= & {} \pm \frac{\mp m \chi _3\mp 1+\sqrt{4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( -m \chi _3-1\right) ^2}}{2 \chi _2}. \nonumber \\ \end{aligned}$$
(4.3)

\(\bullet \) For \(\lambda <0, \ \chi _2 \ne 0\)

$$\begin{aligned} g_{1.1}(x,y,t)&= 2 \lambda -2 \lambda \coth ^2\left( \sqrt{-\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) }{2 \chi _2}t\right) \right) , \nonumber \\ g_{1.2}(x,y,t)&=2 \lambda -2 \lambda \tanh ^2\left( \sqrt{-\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _2}\mp m \chi _3\mp 1\right) }{2 \chi _2}t\right) \right) , \nonumber \\ \end{aligned}$$
(4.4)

where \(\Delta _1= 4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( - m \chi _3-1\right) {}^2 \ge 0\), and \(\Delta _2= 4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( m \chi _3-1\right) ^2 \ge 0. \)

\(\bullet \) For \(\lambda >0, \ \chi _2\ne 0\)

$$\begin{aligned} g_{1.3}(x,y,t)&=2 \lambda \csc ^2 \left( \sqrt{\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) }{2 \chi _2}t\right) \right) ,\nonumber \\ g_{1.4}(x,y,t)&=2 \lambda \sec ^2\left( \sqrt{\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) }{2 \chi _2}t\right) \right) , \end{aligned}$$
(4.5)

where \(\Delta _1 = 4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( m \chi _3+1\right) {}^2\ge 0\).

\(\bullet \) For \(\lambda =0\)

$$\begin{aligned} g_{1.5}(x,y,t)=0. \end{aligned}$$
(4.6)

case 2

$$\begin{aligned} a_0= & {} 2 \lambda ; a_1=0; a_2=2; b_1=0; b_2=0; \nonumber \\ c= & {} \pm \frac{ \sqrt{4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( -m \chi _3-1\right) {}^2} \mp m \chi _3\mp 1}{2 \chi _2} \nonumber \\ \end{aligned}$$
(4.7)

\(\bullet \) For \(\lambda <0, \chi _2\ne 0\)

$$\begin{aligned} g_{2.1}(x,y,t)&=2 \lambda -2 \lambda \tanh ^2\left( \sqrt{-\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) \right) , \nonumber \\ g_{2.2}(x,y,t)&=2 \lambda -2 \lambda \coth ^2\left( \sqrt{-\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) \right) , \nonumber \\ \end{aligned}$$
(4.8)

where \(\Delta _1= 4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( -m \chi _3-1\right) {}^2 \ge 0. \)

\(\bullet \) For \(\lambda >0, \ \chi _2\ne 0\)

$$\begin{aligned} g_{2.3}(x,y,t&=2 \lambda \sec ^2\left( \sqrt{\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) \right) , \nonumber \\ g_{2.4}(x,y,t)&=2 \lambda \csc ^2\left( \sqrt{\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _1}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) \right) , \nonumber \\ \end{aligned}$$
(4.9)

where \(\Delta _1 = 4 \chi _2 \left( 4 \lambda -m^2 \chi _1\right) +\left( m \chi _3+1\right) {}^2\ge 0\).

\(\bullet \) For \(\lambda =0, \ \chi _2\ne 0\)

$$\begin{aligned} g_{2.5}(x,y,t)= \frac{2}{\left( x+m y\pm \frac{ \left( \sqrt{\Delta _3}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) {}^2}, \end{aligned}$$
(4.10)

where \(\Delta _3=\left( -m \chi _3-1\right) {}^2-4 m^2 \chi _1 \chi _2\ge 0.\)

case 3

$$\begin{aligned} a_0= & {} 4 \lambda ; a_1= 0; a_2= 2; b_1= 0; b_2= 2 \lambda ^2; \nonumber \\ c= & {} \pm \frac{\sqrt{4 \chi _2 \left( 16 \lambda -m^2 \chi _1\right) +\left( -m \chi _3-1\right) {}^2}\mp m \chi _3\mp 1}{2 \chi _2}. \nonumber \\ \end{aligned}$$
(4.11)

\(\bullet \) For \(\lambda <0, \ \chi _2\ne 0\)

$$\begin{aligned}&g_{3.1}(x,y,t)= 4 \lambda -2 \lambda \tanh ^2\left( \sqrt{-\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _4}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) \right) \nonumber \\&\quad -2 \lambda \coth ^2\left( \sqrt{-\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y\pm \frac{ \left( \sqrt{\Delta _4}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) \right) , \end{aligned}$$
(4.12)

where \(\Delta _4 = 4 \chi _2 \left( 16 \lambda -m^2 \chi _1\right) +\left( m \chi _3- 1\right) ^2 \ge 0.\)

\(\bullet \) For \(\lambda >0, \ \chi _2\ne 0\)

$$\begin{aligned}{} & {} \!\!\!\!\! g_{3.2}(x,y,t) \nonumber \\{} & {} =8 \lambda \csc ^2\left( \frac{ 2 \chi _2 (x+m y)\pm \sqrt{\lambda } \left( \left( \sqrt{\Delta _5}\mp m \chi _3\mp 1\right) \right) t}{\chi _2}\right) , \nonumber \\ \end{aligned}$$
(4.13)

where \(\Delta _5= \chi _2 \left( 64 \lambda -4 m^2 \chi _1\right) +\left( m \chi _3+1\right) ^2\ge 0. \)

\(\bullet \) For \(\lambda =0, \ \chi _2\ne 0.\)

$$\begin{aligned} g_{3.3}(x,y,t)= \frac{2}{\left( x+m y\pm \frac{ \left( \sqrt{\Delta _3}\mp m \chi _3\mp 1\right) t}{2 \chi _2}\right) {}^2}, \end{aligned}$$
(4.14)

where \(\Delta _3=\left( -m \chi _3-1\right) {}^2-4 m^2 \chi _1 \chi _2\ge 0.\)

case 4

$$\begin{aligned} a_0= & {} \frac{2 \lambda }{3};a_1=0;a_2=0;b_1=0;b_2=2 \lambda ^2; \nonumber \\ c= & {} \frac{\mp \sqrt{\left( m \chi _3+1\right) ^2-4 \chi _2 \left( 4 \lambda +m^2 \chi _1\right) }-m \chi _3-1}{2 \chi _2}. \nonumber \\ \end{aligned}$$
(4.15)

\(\bullet \) For \(\lambda <0, \chi _2 \ne 0\)

$$\begin{aligned} g_{4.1}(x,y,t)= & {} \frac{2 \lambda }{3}-2 \lambda \coth ^2\left( \sqrt{-\lambda } \left( x \right. \right. \nonumber \\{} & {} \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _6}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) , \nonumber \\ g_{4.2}(x,y,t)= & {} \frac{2 \lambda }{3}-2 \lambda \tanh ^2\left( \sqrt{-\lambda } \left( x \right. \right. \nonumber \\{} & {} \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _6}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) .\nonumber \\ \end{aligned}$$
(4.16)

\(\bullet \) For \(\lambda >0, \chi _2\ne 0\)

$$\begin{aligned}{} & {} g_{4.3}(x,y,t)= \frac{2}{3} \lambda \left( 1+3 \cot ^2\left( \sqrt{\lambda } \left( x \right. \right. \right. \nonumber \\{} & {} \quad \left. \left. \left. +m y\mp \frac{ \left( \sqrt{\Delta _6}\pm m \chi _3\pm 1\right) t}{2 \chi _2}\right) \right) \right) ,\nonumber \\ g_{4.4}(x,y,t)= & {} \frac{2}{3} \lambda \left( 1+3 \tan ^2\left( \sqrt{\lambda } \left( x \right. \right. \right. \nonumber \\{} & {} \quad \left. \left. \left. +m y\mp \frac{ \left( \sqrt{\Delta _6}\pm m \chi _3\pm 1\right) t}{2 \chi _2}\right) \right) \right) ,\nonumber \\ \end{aligned}$$
(4.17)

where \(\Delta _6= \left( m \chi _3+1\right) {}^2-4 \chi _2 \left( 4 \lambda +m^2 \chi _1\right) \ge 0.\)

\(\bullet \) For \(\lambda =0\)

$$\begin{aligned} g_{4.5}(x,y,t)=0. \end{aligned}$$
(4.18)

case 5

$$\begin{aligned} a_0= & {} \frac{2 \lambda }{3};a_1=0;a_2=2;b_1=0;b_2=0; \nonumber \\ c= & {} \frac{\mp \sqrt{\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( 4 \lambda +m^2 \chi _1\right) }-m \chi _3-1}{2 \chi _2}. \nonumber \\ \end{aligned}$$
(4.19)

\(\bullet \) For \(\lambda <0, \chi _2 \ne 0\)

$$\begin{aligned} g_{5.1}(x,y,t)= & {} \frac{2 \lambda }{3}-2 \lambda \tanh ^2\left( \sqrt{-\lambda } \left( x\right. \right. \nonumber \\{} & {} \left. \left. +my +\frac{ \left( \mp \sqrt{\Delta _6}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) ,\nonumber \\ g_{5.2}(x,y,t)= & {} \frac{2 \lambda }{3}-2 \lambda \coth ^2\left( \sqrt{-\lambda } \left( x\right. \right. \nonumber \\{} & {} \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _6}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) .\nonumber \\ \end{aligned}$$
(4.20)

\(\bullet \) For \(\lambda >0, \chi _2 \ne 0\)

$$\begin{aligned} g_{5.3}(x,y,t)= & {} \frac{2}{3} \lambda \left( 1+3 \tan ^2\left( \sqrt{\lambda } \left( x \right. \right. \right. \nonumber \\{} & {} \left. \left. \left. +m y\mp \frac{ \left( \sqrt{\Delta _6}+m \chi _3+1\right) t}{2 \chi _2}\right) \right) \right) , \nonumber \\ g_{5.4}(x,y,t)= & {} \frac{2}{3} \lambda \left( 1+3 \cot ^2\left( \sqrt{\lambda } \left( x \right. \right. \right. \nonumber \\{} & {} \left. \left. \left. +my \mp \frac{ \left( \sqrt{\Delta _6}+m \chi _3+1\right) t}{2 \chi _2}\right) \right) \right) . \nonumber \\ \end{aligned}$$
(4.21)

\(\bullet \) For \(\lambda =0, \chi _2 \ne 0\)

$$\begin{aligned} g_{5.5}(x,y,t)= \frac{2}{\left( x+m y+\frac{ \left( \mp \sqrt{\Delta _3}-m \chi _3-1\right) t}{2 \chi _2}\right) {}^2}. \end{aligned}$$
(4.22)

case 6

$$\begin{aligned} a_0= & {} -\frac{4 \lambda }{3}; \ a_1=0;\ a_2=2;\ b_1=0;\ B_2=2 \lambda ^2; \nonumber \\ c= & {} \frac{\mp \sqrt{\left( m \chi _3+1\right) ^2-4 \chi _2 \left( 16 \lambda +m^2 \chi _1\right) }-m \chi _3-1}{2 \chi _2} \nonumber \\ \end{aligned}$$
(4.23)

\(\bullet \) For \(\lambda <0, \chi _2 \ne 0\)

$$\begin{aligned}&g_{6.1}(x,y,t)=-\frac{4 \lambda }{3}-2 \lambda \tanh ^2\left( \sqrt{-\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _{7}}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) \nonumber \\&\quad -2 \lambda \coth ^2\left( \sqrt{-\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _{7}}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) . \end{aligned}$$
(4.24)

\(\bullet \) For \(\lambda >0,\ \chi _2 \ne 0\)

$$\begin{aligned}&g_{6.2}(x,y,t)=-\frac{4 \lambda }{3}+2 \lambda \tan ^2\left( \sqrt{\lambda } \left( x \right. \right. \nonumber \\&\quad \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _{7}}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) \nonumber \\&\quad +2 \lambda \cot ^2\left( \sqrt{\lambda } \left( x\right. \right. \nonumber \\&\quad \left. \left. +m y+\frac{ \left( \mp \sqrt{\Delta _{7}}-m \chi _3-1\right) t}{2 \chi _2}\right) \right) , \end{aligned}$$
(4.25)

where \(\Delta _{7}=\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( 16 \lambda +m^2 \chi _1\right) \ge 0. \)

\(\bullet \) For \(\lambda =0,\ \chi _2 \ne 0\)

$$\begin{aligned} g_{6.3}(x,y,t)= \frac{2}{\left( x+m y+\frac{ \left( \mp \sqrt{\Delta _3}-m \chi _3-1\right) t}{2 \chi _2}\right) {}^2}, \nonumber \\ \end{aligned}$$
(4.26)

where \(\Delta _3=\left( m \chi _3+1\right) {}^2-4 m^2 \chi _1 \chi _2\ge 0. \)

4.2 The modified generalized Kudryashov method solutions

By taking \(M=2\), Eq. (3.1) becomes,

$$\begin{aligned} g=s_0+\frac{s_1}{1+H(\zeta )}+\frac{s_2}{(1+H(\zeta ))^2}, \end{aligned}$$
(4.27)

and when considered together with the Eq. (3.2) here, the following algebraic system of equations is obtained,

$$\begin{aligned} 0= & {} 2 c^2 s_0 \chi _2+2 c^2 s_1 \chi _2+2 c^2 s_2 \chi _2+2 c m s_0 \chi _3\\{} & {} +2 c m s_1 \chi _3+2 c m s_2 \chi _3+2 c s_0+2 c s_1+2 c s_2\\{} & {} +2 m^2 s_0 \chi _1+2 m^2 s_1 \chi _1 +2 m^2 s_2 \chi _1\\{} & {} -2 \delta \sigma s_1-4 \delta \sigma s_2+4 \sigma ^2 s_1\\{} & {} +12 \sigma ^2 s_2-6 s_0^2-6 s_1^2-6 s_2^2\\{} & {} -12 s_0 s_1-12 s_0 s_2-12 s_1 s_2, \\ 0= & {} 8 c^2 s_0 \chi _2+6 c^2 s_1 \chi _2+4 c^2 s_2 \chi _2+8 c m s_0 \chi _3\\{} & {} +6 c m s_1 \chi _3+4 c m s_2 \chi _3+8 c s_0+6 c s_1\\{} & {} +4 c s_2+8 m^2 s_0 \chi _1+6 m^2 s_1 \chi _1\\{} & {} +4 m^2 s_2 \chi _1-2 \delta ^2 s_1-4 \delta ^2 s_2+4 \delta \sigma s_1+20 \delta \sigma s_2\\{} & {} +4 \sigma ^2 s_1-4 \sigma s_1 \tau -8 \sigma s_2 \tau -24 s_0^2-12 s_1^2\\{} & {} -36 s_0 s_1-24 s_0 s_2-12 s_1 s_2, \\ 0= & {} 12 c^2 s_0 \chi _2+6 c^2 s_1 \chi _2+2 c^2 s_2 \chi _2\\{} & {} +12 c m s_0 \chi _3+6 c m s_1 \chi _3\\{} & {} +2 c m s_2 \chi _3+12 c s_0+6 c s_1+2 c s_2\\{} & {} +12 m^2 s_0 \chi _1+6 m^2 s_1 \chi _1\\{} & {} +2 m^2 s_2 \chi _1+8 \delta ^2 s_2+6 \delta \sigma s_1-6 \delta s_1 \tau -12 \delta s_2 \tau \\{} & {} +16 \sigma s_2 \tau -36 s_0^2-6 s_1^2-36 s_0 s_1-12 s_0 s_2, \\ 0= & {} 8 c^2 s_0 \chi _2+2 c^2 s_1 \chi _2+8 c m s_0 \chi _3+2 c m s_1 \chi _3+8 c s_0\\{} & {} +2 c s_1+8 m^2 s_0 \chi _1+2 m^2 s_1 \chi _1+2 \delta ^2 s_1-4 \delta s_1 \tau \\{} & {} +12 \delta s_2 \tau +4 \sigma s_1 \tau -4 s_1 \tau ^2\\{} & {} -8 s_2 \tau ^2-24 s_0^2-12 s_0 s_1, \\ 0= & {} 2 c^2 s_0 \chi _2+2 c m s_0 \chi _3+2 c s_0+2 m^2 s_0 \chi _1+2 \delta s_1 \tau \\{} & {} -4 s_1 \tau ^2+4 s_2 \tau ^2-6 s_0^2. \end{aligned}$$

Two cases of solutions for the coefficients \(s_0\), \(s_1\), \(s_2\), \(b_1\), and c are obtained.

case 7

$$\begin{aligned}{} & {} s_0=\frac{1}{3} \left( \delta ^2-6 \delta \tau +2 \sigma \tau +6 \tau ^2\right) ,\nonumber \\{} & {} s_1=-2 (\delta -2 \tau ) (\delta -\sigma -\tau ),\ s_2=2 (\delta -\sigma -\tau )^2,\nonumber \\{} & {} c=\pm \frac{\sqrt{4 \chi _2 \left( \delta ^2-m^2 \chi _1-4 \sigma \tau \right) +\left( -m \chi _3-1\right) {}^2}\pm m \chi _3\pm 1}{2 \chi _2}. \end{aligned}$$
(4.28)

\(\bullet \) The following is the result of solving Eq. (3.3) with expression (4.28) inserted:

$$\begin{aligned}{} & {} g_{7.1}(x,y,t)=\frac{1}{3} \left( \delta ^2-6 \delta \tau +2 \sigma \tau +6 \tau ^2\right. \nonumber \\{} & {} \left. +\frac{24 \tau ^2 (-\delta +\sigma +\tau )^2}{\left( -\sqrt{4 \sigma \tau -\delta ^2} \tan \left( \frac{1}{2} \sqrt{4 \sigma \tau -\delta ^2} \left( d\pm \frac{t \left( \sqrt{\Delta _{11}}\pm m \chi _3\pm 1\right) }{2 \chi _2}+m y+x\right) \right) +\delta -2 \tau \right) {}^2}\right) \nonumber \\{} & {} +\frac{1}{3} \left( \frac{12 \tau (\delta -2 \tau ) (\delta -\sigma -\tau )}{-\sqrt{4 \sigma \tau -\delta ^2} \tan \left( \frac{1}{2} \sqrt{4 \sigma \tau -\delta ^2} \left( d\pm \frac{t \left( \sqrt{\Delta _{11}}\pm m \chi _3\pm 1\right) }{2 \chi _2}+m y+x\right) \right) +\delta -2 \tau }\right) , \end{aligned}$$
(4.29)

where \(\Delta _{11}=4 \chi _2 \left( \delta ^2-m^2 \chi _1-4 \sigma \tau \right) +\left( m \chi _3 \right. \) \( \left. +1\right) {}^2,\ \chi _2 \ne 0\).

\(\bullet \) The following is the result of solving Eq. (3.4) with expression (4.28) inserted:

$$\begin{aligned}{} & {} \hspace{-20pc}g_{7.2}(x,y,t) =\frac{\delta ^2 \left( (\delta -\tau )^2 \textrm{e}^{\frac{\delta \left( 2 \chi _2 (d+m y+x)+t \left( \sqrt{\Delta _{12}}-m \chi _3-1\right) \right) }{\chi _2}}-4 (\delta -\tau ) \textrm{e}^{\frac{\delta \left( 2 \chi _2 (d+m y+x)+t \left( \sqrt{\Delta _{12}}-m \chi _3-1\right) \right) }{2 \chi _2}}+1\right) }{3 \left( (\delta -\tau ) \textrm{e}^{\frac{\delta \left( 2 \chi _2 (d+m y+x)+t \left( \sqrt{\Delta _{12}}-m \chi _3-1\right) \right) }{2 \chi _2}}+1\right) {}^2},\nonumber \\{} & {} \hspace{-20pc}g_{7.3}(x,y,t)=\frac{1}{3} \delta ^2 \left( 1-\frac{6 (\delta -\tau ) \textrm{e}^{\frac{\delta \left( -2 \chi _2 (d+m y+x)+t \sqrt{\Delta _{12}}+m t \chi _3+t\right) }{2 \chi _2}}}{\left( \textrm{e}^{\frac{\delta \left( -2 \chi _2 (d+m y+x)+t \sqrt{\Delta _{12}}+m t \chi _3+t\right) }{2 \chi _2}}+\delta -\tau \right) {}^2}\right) , \end{aligned}$$
(4.30)

where \(\Delta _{12}=4 \chi _2 \left( \delta ^2-m^2 \chi _1\right) +\left( m \chi _3+1\right) {}^2,\ \chi _2 \ne 0\).

\(\bullet \) The following is the result of solving Eq. (3.5) with expression (4.28) inserted:

$$\begin{aligned} g_{7.4}(x,y,t)= \frac{\delta ^2}{3}+\frac{2 \delta ^2 (\sigma -\delta )}{\textrm{e}^{\pm \frac{\delta \left( \pm 2 \chi _2 (d+m y+x)+t \left( \sqrt{\Delta _{12}}\pm m \chi _3\pm 1\right) \right) }{2 \chi _2}}+\delta -\sigma }+\frac{2 \delta ^2 (\delta -\sigma )^2}{\left( \textrm{e}^{\pm \frac{\delta \left( \pm 2 \chi _2 (d+m y+x)+t \left( \sqrt{\Delta _{12}}\pm m \chi _3\pm 1\right) \right) }{2 \chi _2}}+\delta -\sigma \right) {}^2},\nonumber \\ \end{aligned}$$
(4.31)

where \(\Delta _{12}=4 \chi _2 \left( \delta ^2-m^2 \chi _1\right) +\left( m \chi _3+1\right) {}^2,\ \chi _2 \ne 0\).

case 8

$$\begin{aligned}{} & {} s_0=-2 \left( \delta \tau -\sigma \tau -\tau ^2\right) ,\ s_1=-2 (\delta -2 \tau ) (\delta -\sigma -\tau ),\ s_2=2 (\delta -\sigma -\tau )^2,\nonumber \\{} & {} c= \frac{\pm \sqrt{-4 \chi _2 \left( \delta ^2+m^2 \chi _1-4 \sigma \tau \right) +\left( -m \chi _3-1\right) {}^2}- m \chi _3- 1}{2 \chi _2}. \end{aligned}$$
(4.32)

\(\bullet \) The following is the result of solving Eq. (3.3) with expression (4.32) inserted:

$$\begin{aligned}{} & {} g_{8.1}(x,y,t)=-2 \left( \delta \tau -\sigma \tau -\tau ^2\right) +\frac{2 (\delta -\sigma -\tau )^2}{\left( \frac{\sqrt{4 \sigma \tau -\delta ^2} \tan \left( \frac{1}{2} \sqrt{4 \sigma \tau -\delta ^2} \left( d+\frac{t \left( \pm \sqrt{\Delta _{13}}-m \chi _3-1\right) }{2 \chi _2}+m y+x\right) \right) -\delta }{2 \tau }+1\right) {}^2}\nonumber \\{} & {} \quad -\frac{2 (\delta -2 \tau ) (\delta -\sigma -\tau )}{\frac{\sqrt{4 \sigma \tau -\delta ^2} \tan \left( \frac{1}{2} \sqrt{4 \sigma \tau -\delta ^2} \left( d+\frac{t \left( \pm \sqrt{\Delta _{13}}-m \chi _3-1\right) }{2 \chi _2}+m y+x\right) \right) -\delta }{2 \tau }+1}, \end{aligned}$$
(4.33)

where \(\Delta _{13}=\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( \delta ^2+m^2 \chi _1-4 \sigma \right. \left. \tau \right) ,\ \chi _2 \ne 0\).

\(\bullet \) The following is the result of solving Eq. (3.4) with expression (4.32) inserted:

$$\begin{aligned} \hspace{-20pc}{} & {} g_{8.2}(x,y,t)=-\frac{2 \delta ^2 (\delta -\tau ) \textrm{e}^{\delta \left( d+m y\pm \frac{t \left( \sqrt{\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( \delta ^2+m^2 \chi _1\right) }+\left( \pm 1\pm m \chi _3\right) \right) }{2 \chi _2}+x\right) }}{\left( (\delta -\tau ) \textrm{e}^{\delta \left( d+m y\pm \frac{t \left( \sqrt{\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( \delta ^2+m^2 \chi _1\right) }+\left( \pm 1\pm m \chi _3\right) \right) }{2 \chi _2}+x\right) }+1\right) {}^2}, \end{aligned}$$
(4.34)

where \(\chi _2 \ne 0\).

\(\bullet \) The following is the result of solving Eq. (3.5) with expression (4.32) inserted:

Fig. 1
figure 1

Graphical representation of sensitivity analysis under parametric values are \(c=0.1,~m=0.8,~\chi _1=0.2,~\chi _2=1~\text {and}~\chi _3=0.7\)

Full size image
$$\begin{aligned} g_{8.3}(x,y,t)=-\frac{2 \delta ^2 (\delta -\sigma ) \textrm{e}^{\delta \left( d+m y\pm \frac{t \left( \sqrt{\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( \delta ^2+m^2 \chi _1\right) }+\left( \pm 1\pm m \chi _3\right) \right) }{2 \chi _2}+x\right) }}{\left( \textrm{e}^{\delta \left( d+m y\pm \frac{t \left( \sqrt{\left( m \chi _3+1\right) {}^2-4 \chi _2 \left( \delta ^2+m^2 \chi _1\right) }+\left( \pm 1\pm m \chi _3\right) \right) }{2 \chi _2}+x\right) }+\delta -\sigma \right) {}^2}, \end{aligned}$$
(4.35)

where \(\chi _2 \ne 0\).

5 Sensitivity analysis

In this section, we examine the dynamical strategy sensitivity as suggested by Eq. (4.1). In considering this, let’s examine the dynamical system that follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dg}{dt}=Z_1, \\ \frac{dZ_1}{dt}{=}{-}\left( c \left( c \chi _2{+}m \chi _3{+}1\right) {+}m^2 \chi _1\right) g+3 g^2{=}0. \end{array}\right. } \end{aligned}$$
(5.1)

The following parameters are taken into account: \(c=0.1,~m=0.8,~\chi _1=0.2,~\chi _2=1~\text {and}~\chi _3=0.7\). The starting values are utilized since the system’s behavior is represented by the yellow waves with \((Z_1(0), Z_2(0))=(0.1,0)\). Similar to this, the proposed system’s green oscillatory dynamics are expected to have to start values of \((Z_1(0), Z_2(0))=(0.3,0)\), whereas the beginning values for the red oscillations are \((Z_1(0), Z_2(0))=(0.6,0)\).

The resulting outcomes are illustrated in Fig. 1. Figure observations show that even minor modifications to the starting values significantly impact the dynamics of the suggested system.

6 Stability analysis

To check the validity of solutions use the stability analysis

$$\begin{aligned} H=1/2\int _{-r}^{r}v^2(x) dx \end{aligned}$$
(6.1)

The following conditions are used for stability analysis

$$\begin{aligned} \frac{\partial H}{\partial c}>0. \end{aligned}$$
(6.2)

Let check, the stability using Eq. (4.29), we get:

$$\begin{aligned} \begin{aligned}&\frac{1}{3} \left( \delta ^2-6 \delta \tau +2 \sigma \tau +6 \tau ^2\right. \\&\left. +\frac{24 \tau ^2 (-\delta +\sigma +\tau )^2}{\left( -\sqrt{4 \sigma \tau -\delta ^2} \tan \left( \frac{1}{2} \sqrt{4 \sigma \tau -\delta ^2} \left( d\pm \frac{t \left( \sqrt{\Delta _{11}}\pm m \chi _3\pm 1\right) }{2 \chi _2}+m y+x\right) \right) +\delta -2 \tau \right) {}^2}\right) \\&+\frac{1}{3} \left( \frac{12 \tau (\delta -2 \tau ) (\delta -\sigma -\tau )}{-\sqrt{4 \sigma \tau -\delta ^2} \tan \left( \frac{1}{2} \sqrt{4 \sigma \tau -\delta ^2} \left( d\pm \frac{t \left( \sqrt{\Delta _{11}}\pm m \chi _3\pm 1\right) }{2 \chi _2}+m y+x\right) \right) +\delta -2 \tau }\right) >0. \end{aligned} \end{aligned}$$
(6.3)

Hence, the solution is stable on the interval \(x \in [-10, 10]\). Similarly, the stability of other solutions could be checked using the above process.

7 Graphs and discussion

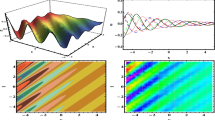
This section provides the results using graphical representations and specifies explanations for the obtained solutions. In Figs. 3 through 5, we employ the modified extended tanh-function method, while in Figs. 6 through 8, we utilize the modified generalized Kudryashov method.

Fig. 2
figure 2

Graphical illustration for stability analysis using different values of r

Full size image
Fig. 3
figure 3

3-D, 2-D and contour plots of mixed singular-dark soliton solution of Eq. (4.8) for \( \chi _1=-0.5, \, \chi _2=-0.71, \chi _3=0.31, \, \lambda =-1, \, y=1, \, m=0.19.\)

Full size image
Fig. 4
figure 4

3-D, 2-D and contour plots of periodic function solution of Eq. (4.9) for \(\chi _1=-0.5, \chi _2=0.71, \chi _3=0.31, \, \lambda =1, \, y=1, \, m=0.19.\)

Full size image
Fig. 5
figure 5

3-D, 2-D and contour plots of rational function solution of Eq. (4.10) for \(\chi _1=-0.5, \chi _2=0.71,\, \chi _3=0.31, \, \lambda =0, \, y=1, m=0.19\)

Full size image
Fig. 6
figure 6

3-D, 2-D and contour plots of periodic function solution of Eq. (4.29) for \(\chi _1=-0.27, \, \chi _2=-0.66, \, \chi _3=0.99, \, \lambda =-1, \, y=2, \, m=0.19, \, \delta =0.83, \, \tau =0.75, \, \sigma =0.68, \, d=0.56\)

Full size image
Fig. 7
figure 7

3-D, 2-D and contour plots of exponential function solution of Eq. (4.30) for \(\chi _1=-0.27, \, \chi _2=0.51, \, \chi _3=0.33, \, \lambda =-1, \, y=1, \, m=0.19, \, \delta =0.85, \, \tau =0.59, \, \sigma =0.68, \, d=0.8\)

Full size image
Fig. 8
figure 8

3-D, 2-D and contour plots of exponential function solution of Eq. (4.35) for \(\chi _1=0.27, \, \chi _2=-0.51, \, \chi _3=0.33, \, \lambda =1, \, y=1, \, m=0.19, \, \delta =-0.85, \, \tau =0.59, \, \sigma =0.68, \, d=0.8\)

Full size image

Remark 7.1

For \(M=2\), we choose the parameters in Fig. 3 as:

\( \chi _1\text {=}-0.5, \, \chi _2\text {=}-0.71, \, \chi _3\text {=}0.31, \, \lambda \text {=}-1, \, y=1, \, m=0.19.\)

For \(M=2\), we choose the parameters in Fig. 4 as:

\(\chi _1\text {=}-0.5, \, \chi _2\text {=}0.71, \, \chi _3\text {=}0.31, \, \lambda \text {=}1, \, y=1, \, m=0.19.\)

For \(M=2\), we choose the parameters in Fig. 5 as:

\(\chi _1=-0.27, \, \chi _2=-0.66, \, \chi _3=0.99, \, \lambda =-1, \, y=2, \, m=0.19, \, \delta =0.83, \, \tau =0.75, \, \sigma =0.68, \, d=0.56\)

For \(M=2\), we choose the parameters in Fig. 6 as:

\(\chi _1=-0.27, \, \chi _2=-0.66, \, \chi _3=0.99, \, \lambda =-1, \, y=2, \, m=0.19, \, \delta =0.83, \, \tau =0.75, \, \sigma =0.68, \, d=0.56\)

For \(M=2\), we choose the parameters in Fig. 7 as:

\(\chi _1=-0.27, \, \chi _2=0.51, \, \chi _3=0.33, \, \lambda =-1, \, y=1, \, m=0.19, \, \delta =0.85, \, \tau =0.59, \, \sigma =0.68, \, d=0.8\)

For \(M=2\), we choose the parameters in Fig. 8 as:

\(\chi _1=0.27, \, \chi _2=-0.51, \, \chi _3=0.33, \, \lambda =1, \, y=1, \, m=0.19, \, \delta =-0.85, \, \tau =0.59, \, \sigma =0.68, \, d=0.8\)

Remark 7.2

Within themselves, solutions (4.4), (4.8) and (4.12), solutions (4.5) and (4.9), solutions (4.10) and (4.14), solutions (4.16) and (4.20), solutions (4.17) and (4.21), solutions (4.22) and (4.26), solutions (4.24) and (4.25) exhibit analogous wave behaviors.

Remark 7.3

Based on the definitions and properties of hyperbolic and trigonometric functions, it follows that

$$\begin{aligned}&\tanh ^2 {\sqrt{-\lambda }}=- \tan ^2{\sqrt{\lambda }}.\end{aligned}$$

Therefore, solutions (4.16) and (4.17), as well as solutions (4.20) and (4.21), and solutions (4.24) and (4.25), exhibit the same behavior within themselves.

8 Conclusion

This study explores the new exact solutions of a recently formulated generalized extended (2+1)-dimensional Kadomtsev-Petviashvili equation employing two distinct methodologies. Initially, we employ the modified extended tanh-function method to derive solutions encompassing hyperbolic, trigonometric, and rational forms. Subsequently, we utilize the Kudryashov method to ascertain exact solutions, encompassing exponential, hyperbolic, trigonometric, and rational functions. Furthermore, we conduct a comprehensive analysis of the dynamic behaviors of these solutions through the utilization of three-dimensional, two-dimensional, and contour plots. Finally, we undertake sensitivity and stability analyses of selected analytical solutions. The solutions derived hold significant applicability in mathematical physics and allied domains, offering direct and robust solution expressions. As a future work, this new model can be solved analytically by other robust and reliable methods, such as the bilinear neural network method.