Abstract
In this paper we study a two infection SIR-SIR compartmental model, considering biological features described in dengue fever epidemiology. Due to a progressive loss of protective antibodies there is waning immunity in the first infection stage and disease enhancement or protection effects by the second infection stage. Bifurcation analysis reveals two codim-2 bifurcations as organizing centers. The unfolding of a cusp bifurcation describes the transition of the disease-free equilibrium into an endemic equilibrium by varying a parameter. These equilibria allow an analytical solution with explicit expressions which allow for a full geometrical interpretation of the occurring bifurcations related to stationary dynamics. A Bogdanov-Takens point is the starting point in the parameter space where oscillatory endemic dynamics occurs including a homoclinic connection. These findings bring additional insights on biological mechanisms able to generate rich and complicated dynamical behavior in simple epidemic models that are, so far, largely unexplored.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
With relevant biological applications, mathematical models applied to infectious disease transmission are dynamical systems of interest, often providing a framework to help to understand the behaviour of disease spreading and control.
The simplest mathematical models for infectious disease dynamics are based on the principle of the mass action contact model between infected and susceptible individuals and recovery of the infected. However, the incorporation of several aspects of the disease can imply rich dynamical behaviour. Study of existence, boundedness, phase-plane, stability and bifurcation analysis are useful tools to investigate qualitatively and quantitatively the behavior of such complex dynamical systems.
In epidemiology, the SIR (Susceptible-Infected-Recovered) modeling framework is often used to describe the dynamics of infectious disease transmitted from person to person. This translates into a compartmental model described by the following system of ordinary differential equations (ODEs)
for the temporal evolution of the number of individuals in each of the three compartments, where N represents the population size.
In a system of ODEs, a bifurcation occurs when the parameter value varies causing an immediate qualitative change in its dynamic behaviour [15, 22]. The basic SIR model has only two coexisting equilibrium as possible stationary solutions. By plotting the solutions of the system as function of a parameter, considering, for example, the prevalence of the population I with respect to the infection rate \(\beta \), a one-parameter bifurcation diagram is obtained. A bifurcation occurs at the specific threshold value \(\beta =\gamma \) (in epidemiology known as forward bifurcation) [11, 27], where by increasing the infection rate \(\beta \) one system eigenvalue passes through zero and thereby exchanging the stability of the Disease Free Equilibrium (DFE) and the Disease Endemic Equilibrium (DEE). One is necessarily unstable when the other is stable. This explains the importance of the threshold value of a parameter (often \(\beta \)) where the super-critical transcritical bifurcation occurs.
Dengue fever is the most important viral mosquito-borne disease worldwide, with approximately 3.9 billion people at risk of infection. Caused by any of the antigenically related but distinct viruses, DENV-1 to DENV-4, it is estimated that around 400 million dengue infections occur every year [6, 38]. Primary natural dengue infections often go unnoticed as they are asymptomatic, but the main risk factor for developing a severe form of the disease is a secondary dengue infection with a different serotype [17, 30, 32, 34]. Infection with one serotype results in lifelong protective immunity, while the high antibody titters attained after primary infection appear to generate a degree of cross-protection to all serotypes for a while, the so called temporary cross-immunity (TCI) period [37]. When the temporary cross-protection fades, patients who experience a secondary heterologous dengue virus infection face an increased risk of severe disease, primarily due to the Antibody-Dependent Enhancement process (ADE) [9, 16, 19, 29].
Dengue fever epidemiological dynamics shows large fluctuations in disease incidence, and several mathematical models describing the transmission of dengue viruses have been proposed to explain the irregular behavior of dengue epidemics [1, 2]. The combination of two realistic immunological aspects of dengue in a minimalistic host-to-host 2-serotype model lead to rich dynamical behavior, including to a new chaotic window in an unexpected and much wider biological parameter region [3], able to qualitatively describe well the available empirical incidence data in Thailand [5].
Motivated by the well-known complex dynamics observed in dengue fever epidemiological models, in this paper, we analyse a two infection SIR-SIR compartmental model. The proposed model describes differences between primary and secondary infections. Without strain structure of pathogens, we consider temporary immunity after a primary infection (analogous to the TCI period) and disease enhancement in a subsequent infection (analogous to the ADE effect).
In this paper, our primary focus is on the mathematical analysis of the system, specifically exploring the theoretical aspects of the nonlinear dynamical system and bifurcation theory. Our research builds upon a recent study ([35]) that investigates complex dynamics resulting from the widely recognized biological features of dengue epidemiology, namely TCI and ADE. The model counts six epidemiological compartments, and because the population size is constant, the dimension of the model is reduced to five.
The analysis of our model reveals two codim-2 bifurcations: the cusp CP-bifurcation and Bogdanov-Takens BT-bifurcation. These bifurcation structures act as organising centers from which a number of codim-1 bifurcation curves originate. A T-bifurcation emerges from the CP-bifurcation point lying on a transcritical TC-bifurcation curve. From the BT-bifurcation point a tangent T-bifurcation, a Hopf H-bifurcation and a global homoclinic G-bifurcation originate. Important is that the unfolding of the two codim-2 bifurcations is different from those found the literature dealing with epidemiological models.
Flow chart of the two-infection SIR-SIR multi-group compartmental model. The coupling between the primary and secondary SIRs is due to a waning immunity of the primary infected individuals where they become susceptible again with rate \(\alpha \) and became infected by disease enhancement/protection via a frequency-dependent force of infection for both primary and secondary susceptibles given by \(\beta (I_P+\phi I_S)/N\)
In the literature [23, 25, 28, 31] other types of extensions of the simple epidemiological models are discussed where besides introduction of additional compartments (such as Exposed and Treated) reformulation of epidemiological mechanisms by more complex are included. For instance, the linear incidence rate in the SIS or SIR model replaced by the saturating incidence rate, or the proportional susceptible recruitment rate by the logistic growth, and further, the saturated instead of proportional treatment rate, and finally, the number of hospital beds. These models are, sometimes after reduction, 2-dimensional and this makes a rigorous analysis of these model possible. Often the TC-bifurcation is not analysed in detail, but use is made of the next generation matrix approach to find the expression for \(\mathcal{{R}}_{0}\). In these models bifurcations with the same names used in this paper are analysed, but their unfolding into the underlying phase-plane dynamics is different. Generally the T-bifurcation, often part of a backward bifurcation and called a saddle-node bifurcation, occurs when one system eigenvalue is zero while all other have negative real parts. However, in the SIR-SIR model case also at the T-bifurcation one system eigenvalue is zero, but there is in addition one eigenvalue positive and therefore the T-point cannot be considered as saddle-node bifurcation: saddle-saddle bifurcation would be more appropriate.
The paper is organized as follows. Section 2 presents the SIR-SIR model including temporary immunity after a primary infection and disease enhancement or protection in a subsequent infection. Based on explicit expressions for the equilibrium solutions, Sect. 3 starts with a detailed analysis of the unfolding of the CP-bifurcation. After the description of the equilibria, their stability is studied in the second part of Sect. 3. In Sect. 4 a detailed numerical bifurcation analysis is performed whereby the baseline parameter values are taken from dengue epidemiology studies by Aguiar and co-workers. [3,4,5, 21]. The effects of temporary immunity and enhancement or protection of the secondary infection is discussed in Sect. 5. Section 6 concludes this work with a discussion on modeling approaches and results.
2 Description of the SIR-SIR model
As an extended version of the Kermack and McKendrick SIR model [11, 20], we study a 5-dimensional two infection epidemiological SIR-SIR model including a temporary immunity after a primary infection, and disease enhancement/protection in secondary infections. These additional mechanisms are likely to be present in various infectious diseases acting as a paradigmatic study system of much wider interest.
In Fig. 1 the disease epidemiological transmission processes occur with the infection rate \(\beta \), the recovery rate \(\gamma \) and the waning immunity \(\alpha \). The demographic transition processes by the birth and death rate is parameterized by \(\mu \).
While a first infection confers a period of immunity, parameterised by \(\alpha \), referring to the progressive loss of protective antibodies (analogous to the so called temporary cross-immunity period in dengue fever epidemiology), recurrent infection can evolve to a severe disease manifestation via disease enhancement/protection, parameterized by \(\phi \).
The parameter \(\phi \) is the ratio of secondary infection contribution to the overall frequency-dependent force of infection, \(\beta (I_P+\phi I_S)/N\), where \(\phi < 1\) acts decreasing the infectivity of secondary infection, due to the immunity level created by the previous infection. However, when \(\phi > 1\), infectivity of secondary infection is larger than in the primary infection. If \(\phi =1\), there is no protection nor enhancement, thus the secondary infected individuals transmit the disease as much as individuals experiencing a first infection.
The system of ordinary differential equations for the two-infection model is 6-dimensional, given by
under the initial conditions
The set of ordinary differential equations describing the temporary evolution of the number of individuals in each of the model compartments reads
The total population size \(N=S+I_P+R_P+S_P+I_S+R\) is constant, with the demographic birth rate of new susceptible individuals been equal to the death rate that is assumed to be equal for individuals in all compartments.
This model is a simplified version of the minimalistic multi-strain dengue model capturing differences between primary and secondary infection proposed in [5], and can be reduced by one dimension by replacing the Eq. (3f) to the constraint \(R=N-S-I_P-R_P-S_P-I_S\). Dimension reduction of the system to a four equations system is not possible only when \(\alpha =0\).
Note that the compartmental state variables are scaled with N, and for the sake of simplicity, we assume \(N=100\), with the results interpreted as percentages of the total population size. In this study, the parameters \(\beta \) and \(\gamma \) are named the primary parameters, while the two parameters, \(\alpha \) and \(\phi \) the secondary parameters.
3 Analysis of the epidemiological model
The model (2) defined by Eq. (3) is positive invariant, with the solutions lying in the non-negative first quadrant because for each zero state variable the time derivative is positive. The total non-negative sizes of the model compartments equals the total population size N, with all state variables in the interval [0, N] and therefore, the system is bounded.
3.1 Equilibria of the dynamical system
The equilibrium equations for the reduced system, given by Eq. (3), are
After some algebraic manipulations the following expressions for \(I^*_P\), \(R^*_P\), \(S_P^*\) and \(I^*_S\) depending on the single variable \(S^*\), can be derived:
Substituting these expressions, Eq. (4a) yields a third order polynomial in \(S^*\). This expression can be factorised in a linear factor \(N-S^*\) and a quadratic factor (second-order polynomial in \(S^*\)). The linear factor is the trivial DFE solution \(E_0=(N,0,0,0,0)^T\). Solving the quadratic factor gives the two solutions for \(S^*\):
and with Eq. (5) the explicit values for possibly coexisting DEE, \(E_1=(S^*,I_P^*,R_P^*,S_P^*,I_S^*)^T\). Two DEE exist when the discriminant (the expression under square-root) is non-negative and one DEE exists when the discriminant is zero.
The equilibrium curve in the equilibrium diagram for parameter \(\beta \) is a 90 degrees clock-wise rotated parabola. One of its branches intersect the horizontal axis where \(\beta =\gamma +\mu \). From Eq. (6) and with \(S^*=N\) we derive that the DFE and DEE curves intersect at a point where \(\beta =\gamma +\mu \).
Both (DEE) branches coincide when the discriminant of the quadratic factor in Eq. (6) is zero:
This occurs at the minimum \(\beta _T\) value of the tangent T-bifurcation point. A bifurcation point fixed as a minimum parameter point is also mentioned in [22, page 527].
In order to derive a criterion that all three equilibria coincide with \(S^*=N\) we take \(\gamma \) as an addition free parameter. The \((\beta , \gamma )\) combination where this occurs is fixed by the condition:
This gives the critical value for \(\gamma \):
Figure 2 shows for three \(\gamma \) values the equilibrium curves for the primary infected \(I_P\). When Eq. (9) is satisfied the equilibrium curve is symmetric with respect to the horizontal axis and the three solutions are all zero at \(\beta =\gamma _{CCP}+\mu \). Using the epidemiological literature terminology we conclude: when \(\gamma <\gamma _{CCP}\) the bifurcation is called a forward and when \(\gamma >\gamma _{CCP}\) a backward bifurcation.
Equilibrium curves for \(I_p\) as function of the parameter \(\beta \) for three values of parameter \(\gamma \). The equilibrium curves intersect the horizontal axis at \(\beta =\gamma +\mu \). For \(\gamma =\gamma _{CCP}=0.00962\) Eq. (9) is satisfied and the parabola is symmetric with respect to the horizontal axis. When \(\gamma <\gamma _{CCP}\) we have a forward and when \(\gamma >\gamma _{CCP}\) a backward bifurcation
These results ware obtained solely based on geometrical aspects, no stability criteria.
3.2 Stability of the equilibria and the TC-bifurcation when \(\beta \) is varied
The Jacobian matrix evaluated at a given point \(E=(S, I_P,R_P,S_P,I_P)\) reads
and, evaluated at the DFE \(E_0=(N,0,0,0,0)\), reads
giving the following eigenvalues:
Four eigenvalues are negative and only one is zero when \(\beta = \gamma +\mu \), where the equilibrium \(E_0\) changes stability. Therefore, a TC-bifurcation where it exchanges stability with \(E_1\) or a T-bifurcation can occur, see [15, Theorem 3.4.1]. Note that the \(\beta \)-value at the bifurcation point depends exclusively on the other primary parameter \(\gamma \), and is not directly dependent of the secondary parameters: the temporary immunity period \(\alpha \) and the disease enhancement/protection factor \(\phi \).
In order to identify these bifurcations transversality conditions have to be satisfied. They depend on the right-eigenvector \(V_0\) and left-eigenvector \(W_0\) of the Jacobian matrix \(J_0\) corresponding to the simple zero eigenvalue (where all other eigenvalues have negative real parts) given by
As described in [15, p 148], the transversality conditions for the TC-bifurcation occurs at \(\beta _{TC}=\gamma + \mu \) read:
and the transversality conditions for the T-bifurcation at \(\beta _{T}=\gamma + \mu \) are:
The expressions on the left hand side of the system Eq. (3) are evaluated at the TC-bifurcation point occurring at \(\beta =\gamma +\mu \), and are
While the first condition, Eq. (14a), and the second condition, Eq. (14b), are satisfied for the TC-bifurcation, the first condition for non-degeneracy for the T-bifurcation in Eq. (15a) is not satisfied along the \(\beta =\gamma + \mu \) curve. Hence, the third condition for the TC-bifurcation, Eq. (14c), determines whether the TC-bifurcation is not degenerated. The right hand side of Eq. (16c), denoted by CCP, is the critical point of the TC-bifurcation curve where a cusp point CP is located, i.e. the TC is degenerated when \({CCP}=0\). The evaluation of this criteria for the primary parameter \(\gamma \) gives
This expression is equals to Eq. (9) where it was derived based on geometrically stationary shape of the equilibrium curve.
3.3 Cusp bifurcation in the three-parameter space
In a similar way, as for the parameter \(\gamma \), we can derive the conditions for the CP-bifurcation where the secondary parameters \(\alpha \) and \(\phi \) are varied. For the immunity period parameter, \(\alpha \), we have:
depending on \(\phi \). At this critical point (where \(\beta =\gamma +\mu \)) the TC-bifurcation changes criticality, from super-critical to sub-critical. The TC-bifurcation is called supercritical when CCP is negative and subcritical when it is positive. Similarly, as described above, the critical point for the disease enhancement/protection parameter \(\phi \) is obtained:
Figure 3 shows the curve for \(\beta =\gamma +\mu \) and \(\alpha _{CCP}=0\) in the 3-dimensional parameter space (\(\beta ,\gamma ,\alpha \)). This curve is in the vertical TC-bifurcation sheet where above the \(\alpha _{CCP}\)-curve, the TC-bifurcation is subcritical and below supercritical.
The results discussed in this section are summarised in the following remarks. Remarks:
-
1.
System Eq. (3) has always a trivial equilibrium \(E_0= (N, 0,0,0,0)\), with at most two endemic equilibria in the positive invariant (biological) region \(\Omega = \{ (S, I_P, R_P, S_P, I_S, R) \in \textbf{R}^6 : S > 0, I_P \ge 0, R_P \ge 0, S_P \ge 0, I_S\ge 0 , S+ I_P+ R_P+ S_p+ I_S+ R=N \}\).
-
2.
The trivial equilibrium \(E_0= (N, 0,0,0,0)\) of the system Eq. (3) is locally asymptotically stable if \(\beta < \gamma + \mu \), and unstable otherwise.
-
3.
The TC-bifurcation occurs at \(\beta = \gamma + \mu \). The TC is supercritical, for \( \phi < \phi _{CCP}\), given by Eq. (19), \(\phi _{CCP}= \frac{(\gamma +\mu )(\alpha +\mu )}{\gamma \alpha }\). On the other hand, if \(\phi > \phi _{CCP}\), the TC is subcritical.
-
4.
At \(\beta = \gamma + \mu \), the transcritical TC is supercritical for \( \alpha < \alpha _{CCP}\), given by Eq. (18), \(\alpha _{CCP} = \frac{\mu (\gamma +\mu )}{(\gamma \phi -(\gamma +\mu ))}\). On the other hand, if \( \alpha > \alpha _{CCP} \), the TC is subcritical.
-
5.
If a supercritical TC occurs, System Eq. (3) has only one trivial equilibrium when \(\beta < \gamma + \mu \). If subcritical TC occurs, System Eq. (3) has two DEE for \(\beta < \gamma + \mu \).
Using computer packages such as Maple [26] it is often not possible to obtain explicit expressions where the TC-bifurcation (of DFE) and/or T-bifurcation (of DEE) occur or the expressions can be unmanageable. In those cases a (numerical) bifurcation analysis can be performed which yielding results for bifurcations of equilibria and limit cycles, and further local and global bifurcations.
4 Numerical bifurcation analysis
The numerical bifurcation analysis is performed using AUTO [14] and Matcont [10] software. A combination of one-, two- and three-parameter diagrams are discussed. The analysis of the one-parameter diagrams is extended with the analyses of state space dynamics. The baseline parameter values are given in Table 1.
The list of bifurcation structures, and its definitions, can be found in Table 2.
The bifurcation structures are studied by continuation and the numerical results are presented as follows. We start varying the two primary parameters \(\beta \) and \(\gamma \) separately and then simultaneously, with results shown for all possible combinations, \((\beta ,\gamma )\), \((\beta ,\alpha )\) and \((\alpha ,\gamma )\) where \((\alpha ,\phi )\) are fixed. In the next sections secondary parameters \((\alpha ,\phi )\) are fixed.
4.1 Cases where the two secondary parameters are zero.
With \(\alpha =0\) the SIR-SIR model Eq. (3) reduces to the SIR model Eq. (20) with three compartments, \(S,I_P,R_P\) and the plane \(S+I_P+R_P\) is attracting and invariant. The ordinary differential equations of the 3-dimensional system are
The bifurcation diagram with \(I_P\) as a function of the parameter \(\beta \) is shown in Fig. 4a. Here, the transcritical TC-bifurcation is supercritical since for \(\alpha =0\) it is smaller than \(\alpha _{CCP}=0.00962\).
With positive \(\beta \), either the stable trivial boundary equilibrium DFE, where all individuals are susceptible \(S=N\), or the stable endemic equilibrium DEE, where the state variables \(I_P, R_P\) are positive, exist. At the TC at \(\beta _{TC}=\gamma +\mu \) one eigenvalue of the Jacobian matrix is zero and the two equilibria, DFE and DEE, interchange stability.
(a) One-parameter diagram for primary infected \(I_P\) model compartment and bifurcation parameter \(\beta \) for life long immunity period (\(\alpha =0\)) and no disease protection (\(\phi =0\)). The other parameter values are given in Table 1. Stable equilibria are shown in green and unstable in magenta. One supercritical TC-bifurcation occurs at \(\beta _{TC}=\gamma +\mu \). (b) One-parameter diagram for primary infected \(I_P\) and secondary \(I_S\) compartments and bifurcation parameter \(\beta \) for the baseline immunity period value, \(\alpha =52\), and no disease protection, \(\phi =0\). The other parameter values are given in Table 1. For the primary infected \(I_P\), stable equilibria are shown in green. For the secondary infected \(I_S\), stable equilibria are shown in red. There is one TC-bifurcation at \(\beta _{TC}=\gamma +\mu \) which is supercritical
On the other hand, Fig. 4b shows the case when the temporary immunity period is equal to the baseline value \(\alpha =52\), and with no disease enhancement (\(\phi =0\)), i.e., no contribution of the secondary infections to the force of infection. In addition to the variable \(I_P\), the variable \(I_S\) is also shown as a function of the parameter \(\beta \). The TC occurs as in the SIR model at \(\beta _{TC}=\gamma +\mu \), where the equilibria DFE and DEE interchange stability. With \(\phi =0\), the SIR-SIR model reduces to the SIR model, and \(\phi =0<\phi _{CCP}=1.0006\). This shows that for the SIR-SIR model with \(\phi =0\) the TC-bifurcation is supercritical.
4.2 Effects of the two primary parameters \(\beta \) and \(\gamma \) varied simultaneously
The two-parameter bifurcation diagram with the two primary parameters \(\beta \) and \(\gamma \) as free parameters is shown in Fig. 5. The two secondary parameters \(\alpha \) and \(\phi \) are fixed as shown in Table 1. Note in Fig. 5 the TC bifurcation curve \(\beta =\gamma +\mu \) in red, and the T-bifurcation curve in blue. The T-bifurcation occurs when two equilibria collide in one endemic equilibrium. The DEE become unstable at a H-bifurcation. For a detailed list of the bifurcation structures identified in this study we refer to Table 2.
Left figure (a): The two-parameter \(\beta ,\gamma \) diagram of the model Eq. (3). There are three bifurcation curves, TC-bifurcation, T-bifurcation and Hopf H-bifurcation curves. A global homoclinic G-bifurcation curve approaches the TC-curve starting for the BT-bifurcation point. Right figure (b) Zooming of the right figure (a) for small \(\gamma \) and \(\beta \) parameter values. Two points are identified, the Bogdanov-Takens point BT and the CP-bifurcation point. A global homoclinic G-bifurcation curve represented by the green line, is originated at BT-bifurcation and converges to the TC-bifurcation curve for larger \(\beta \) values. The DFE (\(E_0\)) exists for lower \(\beta \) and higher \(\gamma \). The stable DEE (\(E_1\)), exists for higher \(\beta \) and also lower \(\gamma \), and an endemic stable limit cycle (DEL), \(L_1\), exists for higher \(\beta \) and high \(\gamma \) values
Figure 5b shows part of the diagram depicted in Fig. 5a, for smaller parameter values, highlighting the results for the region of \(0<\beta <0.8\) and \(0<\gamma <0.5\). In this region of the diagram, two codim-2 bifurcation points are identified as the organising centers of bifucartions, the CP and the BT points, from which the codim-1 bifurcation curves originate.
At the BT-bifurcation point, two eigenvalues of the Jacobian in the DEE (\(E_1\)), are zero. From this point, three bifurcation curves emerge, the T-bifurcation curve, H-bifurcation curve, and also a global homoclinic G-bifurcation curve (see [15, 22]).
In Fig. 5b it is possible to identified the bifurcation structures around the cusp CP point. From this point on, of the TC-curve of the DFE, the T-bifurcation curve of the DEE emerges. It marks also where the TC changes from supercritical to subcritical.
By increasing \(\beta \), the transition steps in Fig. 5b are observed as follows. The TC-bifurcation of the DFE that is supercritical below the CP-point, becomes subcritical, between CP and BT points, and emerges a T-bifurcation of the DEE. In order to get more insight in this process, we count the number of positive, \(n_{+}\), zero, \(n_{0}\) and negative real parts \(n_{-}\) of the total 5 eigenvalues, identified by \(n=(n_{+},n_{0},n_{-})\).
At point CP and also between the CP and BT points we have \(n=(1,0,4)\). At the BT point we have \(n=(0,2,3)\) and and above the BT on the T-bifurcation curve \(n=(1,1,2)\) and this does not change until \(\gamma =52\) (see also Fig. 5). From the BT-point at the H-bifurcation curve we have \(n=(0,2,3)\).
4.2.1 One-parameter diagrams for the infection rate parameter \(\beta \)
The one-parameter diagram where \(\beta \) is varied for the baseline parameter set given in Table 1, hence fixed \(\gamma \)-value 52, is shown in Fig. 6. The asymptotic solutions of the model for variables \(I_P\) and \(I_S\) are plotted as \(\beta \) changes in the interval [0, 104]. Below the TC-point there is only the stable DFE. The TC-point is subcritical. This means that for lower \(\beta \)-values DEEs exist. However, these DEEs are unstable in the \(\beta \) interval above the T-bifurcation. Starting from the TC-point where, the system eigenvalues count is \(n=(0,1,4)\) following the lower branch of the DEE we have \(n=(1,0,4)\), that is one eigenvalue is positive, and at the T point, \(n=(1,1,3)\). For the upper branch of the DEE, \(n=(2,0,3)\), with two eigenvalues positive in the whole interval, till \(\beta =104\).
The equilibrium values for the single unstable DEE read:
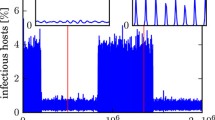
with the eigenvalues count \(n=(2,0,3)\). Starting simulations close to this saddle-focus point the solution spirals to a stable limit cycle with a large period shown in the phase-plane in Fig. 7 and its one period time dependency for the two infected populations \(I_P\) and \(I_S\), in Fig. 8. There is convergence to a homoclinic connection of the DFE (\(E_0\)) point at a homoclinic global G-bifurcation. Because there are time intervals where the state variables \(I_P\), \(R_P\)and \(I_S\) are small we call the dynamics pulsed.
One-parameter \(\beta \) diagram for the baseline parameter values in Table 1. There are three bifurcation points: transcritical TC, tangent T-bifurcation. There is also the global homoclinic G-bifurcation point that coincides with the TC point. The DEE, \(E_1\) is always an unstable equilibrium and the DEL \(L_1\) is a stable limit cycle
Projections of the stable cycle close to the G-bifurcation point for the susceptible sub-population, primary and secondary infections and recovered compartments S vs \(S_P\) (red), \(I_P\) vs \(I_S\) (green) and \(R_P\) vs R (blue), respectively. Parameter values: \(\beta =52.0154\). The open circles mark the endemic states of the unstable DEE (two conjugated eigenvalues have positive real part) where \(\beta =\gamma +\mu =52.0154\). The open squares mark the states of the DFE with \(S^*=N=100\) and all other state variables are zero
To get more insight in this dynamics we take the state variables \(I_P,I_S,R_P\) in the model equations of order \(\mathcal {O}(\epsilon )\) with \(\epsilon \) small. The system becomes:
Hence, during one cycle when the solutions for \(I_P,I_S,R_P\) are small also their rates \(\dot{I}_P,\dot{I}_S,\dot{R}_P\) are small and this explains the pulsed dynamics shown in Fig. 8.
In the two-parameter diagram \((\beta ,\gamma )\) Fig. 5a the G-bifurcation originates from the BT point which is not a DFE. Therefore we study the dynamics for \(\gamma =0.35\) instead of \(\gamma 52\). The one-parameter diagram is shown in Fig. 9
The projections of the cycles and the one-cycle time simulations for the infected stages are studied in the phase-plane in Fig. 10, and its time dependency in Fig. 11.
Projections of the stable cycle where \(\beta =0.3535\) and \(\gamma =0.35\) at the G bifurcation (see Fig. 9) for the susceptible sup-population, primary and secondary infected and recovered compartments, S vs \(S_p\) (red), \(I_P\) vs \(I_S\) (green) and \(R_P\) vs R (blue), respectively. The open circles mark the endemic states of the unstable DEE (two conjugated eigenvalues have positive real part)
One period time dependency of cycle close to homoclinic cycle at the G-bifurcation point for the primary and secondary infected compartments \(I_P\) (green) and \(I_S\) (red) for parameter values in Table 1
From the results in Fig. 10 it is clear that the homoclinic orbit DEL does not approach the DFE, instead it approaches the unstable lower branch of the DEE shown in Fig. 9.
The complicated dynamics as a result of the pulsed limit cycles gave numerical difficulties using continuation software. When parameters \(\beta \) and \(\gamma \) are smaller than 1, in the one-parameter diagrams in Fig.9, with \(\gamma =0.35\), the software AUTO was used. But for the one-parameter diagrams in Fig. 6, with \(\gamma =52\), we used the software Matlab, solver “ode45” adding in the “odeset” function the option “NonNegative”. This is necessary, to avoid negative numbers of the state variables knowing that the model solutions are in the non-negative quadrant of the 5-dimensional state space.
4.2.2 One parameter bifurcation diagram for the recovery rate \(\gamma \)
The equilibria for the two infected compartments as a function of the parameter \(\gamma \) are depicted in Fig. 12. Below the supercritical H-bifurcation the DEEs are stable. Observe that, for very low recovery rate \(\gamma \) values, \(I_P\) converges to a point where the population is almost completely infected, that is where:
One-parameter diagram of model for the recovery rate \(\gamma \). (a) There is a H-bifurcation point at \(\gamma = 9.58836\). Below H, the DEE is stable. Above H, stable endemic limit cycles (DEL) of which the maximum and minimum values are shown. (b) For small \(\gamma \) values the DEE is stable. Note that as \(\gamma \) goes to zero, almost all individuals are primary infected
5 The role of temporary immunity
In this section we analyze the two-parameter diagrams (\(\beta ,\alpha \)) and (\(\gamma ,\alpha \)) and continue with a one parameter bifurcation diagram varying the temporary immunity parameter \(\alpha \).
5.1 Two-parameter \((\beta ,\alpha )\) and \((\gamma ,\alpha )\) diagrams
Figure 13 show the two-parameter diagram where \(\beta \) and \(\alpha \) are varied simultaneously. The bifurcations curves and points detailed in the diagrams for the parameters \(\beta \) and \(\gamma \) in Fig. 5 are also seen in this figure. However, in this case, a subcritical H-bifurcation is occurring very close to the \(T_c\)-bifurcation of the emerging limit cycle.
In Fig. 14a the unfolding of the CP- and BT-points are shown. The \(T_c\)-bifurcation curve terminates at the G-bifurcation curve that is, as depicted, very close to the TC birfurcation curve.
Now, analysing the two-parameters \((\gamma ,\alpha )\) diagram, there is a H-bifurcation curve having \(n=(0,2,3)\) as showed in Fig. 14. Below the H-bifurcation curve a stable DEE \((E_1)\) having \(n=(0,0,5)\), and above the curve an unstable DEE having \(n=(2,0,3)\). In addition, a stable DEL, \((L_1)\) appears (see Fig. 14b). A \(T_c\)-bifurcation curve very close to the H-bifurcation is studied in more detail in the next section with the description of the one-parameter diagram for parameter \(\alpha \).
5.2 One-parameter diagrams of the secondary parameter \(\alpha \)
Figure 15 gives the diagram where \(\alpha \) is varied in a region around the H-bifurcation, for the values of the parameters fixed in the Table 1. This point occurs for the \(\alpha \) value depicted in Fig. 13, for \(\beta =104\) and for \(\gamma =52\).
Between the supercritical H-bifurcation and the \(T_c\)-bifurcation of the emerging stable, there is a coexistence of the stable DEE (\(E_1\)) and two stable DELs (\(L_1\)) of which the maximum and minimum values are shown. At the \(T_c\)-bifurcation one Floquet multiplier is equal to 1 and the other are inside the complex unit circle, that is, \(n=(0,1,3)\) (the one multiplier equal to 1, because it is a limit cycle, is not counted). The stable DEE and the two DELs for the infected stages \(I_P\) and \(I_S\), are show in the phase-plane in Fig. 16. In addition, below the \(T_c\)-bifurcation point the DEE is stable and above H point the DEL is stable.
5.3 Three parameter \((\beta ,\gamma ,\alpha )\) diagram
Unfortunately, the free available computer packages in AUTO [14] and MatCont [10] do not support continuation of the codim-2 bifurcations in three parameters. Therefore, to study the two codim-2 CP- and BT-bifurcation, we conciliate these curves in the three parameter diagram space for the parameters \((\beta ,\gamma ,\alpha )\) in Fig. 17, by continuation of the T-bifurcation and detection of the BT- and CP-points.
We start at a point on the T-bifurcation curve for a specific value of parameter \(\alpha \). By continuation, in the two (\(\beta ,\gamma \)) plane, both the BT and CP points were found. The procedure is repeated for a different initial \(\alpha \)-value. Finally, connecting those critical bifurcations points found, for the different \(\alpha \)-values, it will give the curves. Observe that the CP curve is the same as the degenerated TC curve in Fig. 3, that is, curve \(\alpha _{CCP}(\beta ,\gamma )\).
On the positive cube faces (see Fig. 17) the two-parameter diagram resulted are depicted as follows: \((\beta ,\gamma )\) from Fig. 5, \((\gamma ,\alpha )\) from Fig. 14 and \((\beta ,\alpha )\) from Fig. 13. In this way, the codim-1 bifurcation curves form connected curves in the 3 faces.
Projections of \(I_P(t)\) vs \(I_S(t)\) in phase space for \(\alpha =19\) (see Fig. 15) where the maximum and minimum values are shown. The open circle shows the stable DEE, \(E_1\), and further, the two stable (in red and blue) DEL, \(L_1\). There are three coexisting attractors
Three-parameter diagram of model for \(\beta ,\gamma ,\alpha \). Two codim-2 bifurcations curves exist the CP- (red) and BT-bifurcations (thick magenta). On the top-face, the two parameters \((\beta ,\gamma )\) diagram is shown (see also Fig. 5). On the right-face, the \((\gamma , \alpha )\) diagram (see also Fig. 14b). And on the back-face, \((\beta ,\alpha )\) diagram (see also Figs. 13 and 14a)
To finalize this analysis, Fig. 18 shows the codim-2 curves for a range closer to the origin and also highlighting part of the cube space in Fig. 17. In Fig. 18a the TC curve for \(\alpha =0\) in the bottom-face is shown. In that region of the parameter space the cusp is just above this curve in the vertical plane where \(\beta =\gamma +\mu \), except for the region close to the origin. There the CP curve bends sharply upwards. Figure 18b shows that the two codim-2 curves leave the cube very close to the bottom-face.
Zooming of Fig. 17, the three-parameter diagram for \(\beta ,\gamma ,\alpha \) showing two cusp CP-bifurcation (thick red) and BT-bifurcation (thick magenta) curves. (a) The curves pass the origin close and change direction sharply from a rather straight curve just above the bottom plane into a vertical line in a close vicinity to the vertical axis. (b) The curves close to the top \(\gamma =52\) back-face
6 The role of disease enhancement/protection
We follow the same analysis sequence as in the previous section to study the effects of the secondary infection contribution to the force of infection by taking \(\phi \) as bifurcation parameter together with \(\beta \) and \(\gamma \).
6.1 Two parameter \((\beta ,\phi )\) and \((\gamma ,\phi )\) diagrams
The two-parameter \((\beta ,\phi )\) diagram in Fig. 19 shows the same codim-1 and codim-2 bifurcation curves and points as found for the parameter \(\alpha \) in the previous section. However, in this diagram, the occurrence of a codim-2 Bautin B-bifurcation point for the H-bifurcation, where it changes criticality from supercritical \(H^+\) to subcritical \(H^-\) is showed. The parameter value where this point precisely occur is very hard to obtain, as well as, the \(T_c\)-bifurcation of emerging limit cycles are also not displayed. Moreover, the BT-bifurcation is the terminal point of the H-bifurcation curve, and the CP-bifurcation is the terminal point of the T-bifurcation curve.
On the left side of the TC-bifurcation curve the DFE is stable and the solutions of the system will converge to the stable DFE. In the right half plane and below the H-bifurcation curve the DEE is stable and above of the curve there is a stable (possibly pulsed with long episodes of infection states close to zero) DELs.
Two-parameter \((\beta ,\phi )\) diagram with the CP- (open circle) and BT- (closed circle) and B bifurcation points (square). The codim-1 bifurcations are also the same as in Fig. 13
The two-parameter diagram in Fig. 20a shows the B-bifurcation point of the H-bifurcation, where it changes criticality from subcritical to supercritical and visa-versa, where DELs emerges (not shown). Moreover, the BT-bifurcation as the terminal point of the H-bifurcation, and the CP-bifurcation as terminal point of the T-bifurcation are shown.
In the two parameter (\(\gamma ,\phi \)) diagram (see Fig. 20b), the H-bifurcation divided the parameter space into two regions. Below the H-bifurcation curve, the DEE are stable and above, a stable DEL exists.
6.2 One-parameter \(\phi \) diagram
Figure 21 gives the diagram where parameter \(\phi \) is varied in a region around the H-bifurcation point, at \(\phi = 1.75\). This H-bifurcation point occurs for the baseline parameters, that is, \(\alpha =52\), \(\gamma = 52\) and \(\beta =104\), as depicted, respectively, in the Figs. 19 and Fig. 20. The size of the two infected states \(I_P\) and \(I_S\) of the stable DEE, below the H-bifurcation point is remarkably small. Furthermore, the amplitude of the stable DEL just above the H-bifurcation increases very fast and the minimum values of the infected states DEL become very small.
6.3 Three parameter \((\beta ,\gamma ,\phi )\) diagram
The three-parameter bifurcation diagram for the parameters \((\beta , \gamma ,\phi )\) is showed in Fig. 22 and combines the three two-parameter diagrams \((\beta ,\gamma )\) (see Fig. 5a), \((\phi ,\beta )\) (see Fig. 19), and \((\gamma ,\phi )\) (see Fig. 20b). The codim-1 bifurcation curves form connected curves in the 3 planes (top, back and right, respectively). The 2-dimensional sheets of the codim-1 bifurcations within the cube are not shown. For instance, below and before this sheet of the H-bifurcation a stable endemic region exists in the 3-dimensional parameter space.
In this figure the CP- and BT-bifurcations are shown. It is striking that below the plane \(\phi =1\) we have only the vertical plane above the TC-curve in the bottom-face where \(\beta =\gamma +\mu \).
Three-parameter diagram of model for \(\beta ,\gamma ,\phi \). The top-face of the cube for \(\beta =104\), \(\gamma =52\), \(\phi =2.6\) is the case for the baseline parameter values with the CP (red) and BT-bifurcations (thick magenta) curves. On the top-plane the two parameters \((\beta ,\gamma )\) diagram (see Fig. 5), on the right-plane the \((\gamma ,\phi )\) diagram (see Fig. 20b ) and on the back-plane \((\beta ,\phi )\) diagram (see Figs. 19 and 20a)
7 Discussion and conclusions
Modeling insights for epidemiological scenarios characterized by complex dynamics have been largely unexplored. The development of mathematical guiding tools taking into account intrinsic dynamical behaviour of each modeling framework and its limitations for different epidemiological scenarios is of major importance.
In the epidemiological literature the basic reproduction number \(\mathcal{{R}}_{0}\) is considered as the most important quantity. In [12] it was introduced as the spectral radius of the next generation matrix. With applications in compartmental models this matrix is related to the Jacobian matrix evaluated for the DFE [11, 13, 36]. Is important to observe that the expressions for the elements of the decomposition of the Jacobian matrix are derived strictly by the epidemiological status of each compartment, for instance, the transmission is separated from transition, such as, the removal rate by death rate of individuals.
In this paper we do not use the method of the next generation matrix and calculation of the basic reproduction number \(\mathcal{{R}}_{0}\). The explicitly calculation of \(\mathcal{{R}}_{0}\) using this method can be found in [35]. Instead we use the nonlinear dynamical system theory approach for the continuous time ODE compartmental model. In this context the threshold condition \(\mathcal{{R}}_{0}=1\) is fixed by parameter values where the ODE system possesses a TC-bifurcation, or stated otherwise, where one eigenvalue of the Jacobian matrix is equals to zero. This is related to a zero natural rate of increase (Malthusian parameter) a fact not explicitly used here. The TC bifurcation can be either supercritical (forward) or subcritical (backward).
If a subcritical TC bifurcation occurs, in the SIR-SIR model the equilibrium curve is a 90 degrees clockwise rotated parabola of which the lower branch intersects the horizontal axis at the TC-bifurcation point and also a T-bifurcation occurs at the minimum \(\beta \) value of that equilibrium curve.
The exchange from forward to backward bifurcation, occurs when the equilibrium curve leaves the TC point on the horizontal axis perpendicularly where now the three equilibria coincide. This gives the conditions for the occurrence of the change of criticality of the TC-bifurcation. This simple procedure does not yield the results related to stability and unfolding of the involved codim-1 bifurcations and the CP-bifurcation itself. This criticality depends on transversality conditions [15, 33, 36] formulated at the TC point. The application of bifurcation theory gives a mathematically solid derivation of the system in the neighborhood of the cusp bifurcation.
In the SIR-SIR model we found the CP-bifurcation as one of the most important bifurcation. It fixes the point in the parameter space where the TC changes its criticality and the emergence of a T-bifurcation. Generally at a CP-bifurcation, two T-bifurcations emerge, but here a T-bifurcation of the DEE emerges at the CP point from a point on the TC-bifurcation curve. Hence, the complex dynamics is due to the larger dimension of the system (higher than two dimensional as in the case of the SIR model).
In order to illustrate that the CP-bifurcation is the point where the TC-bifurcation changes its criticality, we mention the numerical results discussed in [28] where a SIR model with logistic growth, nonlinear incidence rate and saturated treatment was analysed. The dynamics of that system shows some similarities with that of the model considered in this paper. In [28, Fig. 7] two cusp bifurcation points were calculated by continuation, but the fact that at these points the criticality of the TC-bifurcation changes is not mentioned.
The BT-bifurcation marks the emergence of a H-bifurcation and a G-bifurcation. This make more complex dynamics possible for instance Fig. 16 shows a near a subcritical H-bifurcation where one stable DEE coexists with two stable DELs.
In Fig. 23 the function \(\beta _{CPP}(\alpha ,\phi )\) derived from Eq. (19) whereby \(\beta =\gamma +\mu \), so that \(\beta _{CPP}\) is given by
For this we conclude that with moderately infection rates \(\beta \) the CP- and also the BT-bifurcations occur as organizing centers leading to complicated dynamics for \(\alpha >0\) and \(\phi >1\).
The role of secondary infection contribution to the force of infection can be rephrased observing that the feedback from the effects of the secondary infection is negative when \(\phi <1\) and positive when \(\phi >1\), (see also diagram Fig. 1). Complex dynamics is possible in a large region of the parameter space when the feedback of the secondary infection is positive.
The CP and BT-bifurcations were also found earlier in the epidemiological literature dealing with various other extensions of the classical SIS or SIR model [7, 8, 18, 23,24,25, 31, 33]). These models are described by 2-dimensional ODE systems allowing a more general analysis of the unfolding. Bifurcations of higher dimensional system as discussed in this work where also these bifurcations occur, may differ from those for 2-dimensional systems. As an example, the T-bifurcations for equilibria and \(T_c\)-bifurcations for the limit cycles found in this work are of a different type than the classical once. Of the unfolding bifurcations the number of the positive/zero/negative system eigenvalues differ. As a result, even with the existence of a “backward” bifurcation there is no hysteresis phenomenon and the system can be unconditional disease-free in the parameter range below the TC-bifurcation point.
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
Aguiar, M., et al.: Mathematical models for dengue fever epidemiology: a 10-year systematic review. Phys. Life Rev. 40, 65–92 (2022). https://doi.org/10.1016/j.plrev.2022.02.001
Aguiar, M., et al.: Prescriptive, descriptive or predictive models: What approach should be taken when empirical data is limited? Reply to comments on “Mathematical models for Dengue fever epidemiology: A 10-year systematic review. Phys. Life Rev. 46, 56–64 (2023). https://doi.org/10.1016/j.plrev.2023.05.003
Aguiar, M., Kooi, B.W., Stollenwerk, N.: Epidemiology of Dengue Fever: A model with temporary cross immunity and possibly secondary infection shows bifurcations and chaotic behaviors in wide parameter region. Math. Model. Nat. Phenom. 3(4), 48–70 (2008). https://doi.org/10.1051/mmnp:2008070
Aguiar, M., Stollenwerk, N., Kooi, B.W.: Torus bifurcations, isolas and chaotic attractors in a simple dengue model with ADE and temporary cross immunity. Int. J. Comput. Math. 86, 1867–1877 (2009). https://doi.org/10.1080/00207160902783532
Aguiar, M., Ballesteros, S., Kooi, B.W., Stollenwerk, N.: The role of seasonality and import in a minimalistic multi-strain dengue model capturing differences between primary and secondary infections: complex dynamics and its implications for data analysis. J. Theor. Biol. 289, 181–196 (2011). https://doi.org/10.1016/j.jtbi.2011.08.043
Bhatt, S., Gething, P.W., Brady, O.J., et al.: The global distribution and burden of dengue. Nature 496(7446), 504–507 (2013)
Capass, oV., Serio, G.: A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 42, 43–61 (1978)
Castillo-Chavez, C., Song, B.: Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 1(2), 361–404 (2004)
Dejnirattisai, W., Jumnainsong, A., Onsirisakul, N., Fitton, P., Vasanawathana, S., Limpitikul, W., Puttikhunt, C., Edwards, C., Duangchinda, T., Supasa, S., Chawansuntati, K., Malasit, P., Mongkolsapaya, J., Screaton, G.: Cross-reacting antibodies enhance dengue virus infection in humans. Science 328(5979), 745–748 (2010). https://doi.org/10.1126/science.1185181
Dhooge, A., Govaerts, W., Kuznetsov, Yu.A.: MatCont: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Transa. Math. Softw. 29, 141–164 (2003)
Diekmann, O., Heesterbeek, J.A.P.: Mathematical epidemiology of infectious diseases. Wiley series in mathematical and computational biology. Wiley, Chichester (2000)
Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.J.: On the definition and computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990). https://doi.org/10.1007/BF00178324
Diekmann, O., Heesterbeek, J.A.P., Roberts, M.G.: The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7(47), 873–885 (2010)
Doedel, E.J., Oldeman, B.: Auto 07p: Continuation and bifurcation software for ordinary differential equations. Concordia University, Montreal, Canada, Tech. rep. (2009)
Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Applied Mathematical Sciences. 42, Springer-Verlag, New York (1985)
Guzman, M.G., et al.: Dengue: a continuing global threat. Nat. Rev. Microbiol. 8(S12), S7–S16 (2010)
Guzman, M.G., Kouri, G.: Dengue: an update. The Lancet Infect. Dis. 1(2), 33–42 (2002)
Hadeler, P., Castillo-Chavez, C.: A core group model for disease transmission. Math. Biosci. 128, 41–55 (1995)
Halstead, B.S.: Neutralization and antibody-dependent enhancement of dengue viruses. Adv. Virus Res. 60, 421–467 (2003). https://doi.org/10.1016/S0065-3527(03)60011-4
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics. Proc. Roy. Soc. Lond. A. 115, 700–721 (1927)
Kooi, B.W., Aguiar, M., Stollenwerk, N.: Analysis of an asymmetric two-strain dengue model. Math. Biosci. 248, 128–139 (2014). https://doi.org/10.1016/j.mbs.2013.12.009
Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory. vol 112 of Applied Mathematical Sciences, 3rd edn. Springer-Verlag, New York (2004)
Lu, M., Huang, J., Ruan, S., Yu, P.: Bifurcation analysis of an SIRS epidemic model with a generalized nonmonotone and saturated incidence rate. J. Diff. Equs. 267(3), 1859–1898 (2019). https://doi.org/10.1016/j.jde.2019.03.005
Lu, M., Xiang, C., Huang, J.: Bogdanov-Takens bifurcation in a SIRS epidemic model with a generalized nonmonotone incidence rate. Discr. Cont. Dyn. Syst.-S. 13(11), 3125–3138 (2020). https://doi.org/10.3934/dcdss.2020115
Lu, M., Huang, J., Ruan, S., Yu, P.: Global dynamics of a Susceptible-Infectious-Recovered epidemic model with a generalized nonmonotone incidence rate. J. Dyn. Diff. Equat. 33, 1625–1661 (2021)
Maple, Maple Software: Maplesoft. Waterloo, Ontario, Canada (2016)
Martcheva, M.: An introduction to mathematical epidemiology. Springer, New York (2015)
Pérez, A.G.C., Avila-Vales, E., García-Almeida, G.E.: Bifurcation analysis of an sir model with logistic growth, nonlinear incidence, and saturated treatment. Complexity. 2019, 1–21 (2019). https://doi.org/10.1155/2019/9876013
Rothman, A. L.: Dengue Virus. Cellular Immunology of Sequential Dengue Virus Infection and its Role in Disease Pathogenesis. Springer Berlin Heidelberg, 83–98 (2009). https://doi.org/10.1007/978-3-642-02215-9_7
Sangkawibha, N., Rojanasuphot, S., Ahandrik, S., Viriyapongse, S., Jatanasen, S., Salitul, V., Phanthumachinda, B., Halstead, S.B.: Risk factors in dengue shock syndrome: A prospective epidemiologic study in Rayong, Thailand. Am. J. Epidemiol. 5(120), 653–669 (1984)
Shan, C., Zhu, H.: Bifurcations and complex dynamics of an SIR model with the impact of the number of hospital beds. J. Differ. Equs. 257, 1662–1688 (2014). https://doi.org/10.1016/j.jde.2014.05.030
Sierra, B., Perez, A.B., Vogt, K., Garcia, G., Schmolke, K., Aguirre, E., Alvarez, M., Kern, F., Kourí, G., Volk, H., Guzman, M.G.: Secondary heterologous dengue infection risk: Disequilibrium between immune regulation and inflammation? Cellul. Immunol. 2(262), 134–140 (2010)
Song, B., Du, W., Lou, J.: Different types of backward bifurcations due to density-dependent treatments. Math. Biosci. Eng. 10(5–6), 1651–1668 (2013). https://doi.org/10.3934/mbe.2013.10.1651
St John, A.L., Rathore, A.P.S.: Adaptive immune responses to primary and secondary dengue virus infections. Nat. Rev Immunol. 4(19), 218–230 (2019)
Steindorf, V., Srivastav, A.K., Stollenwerk, N., Kooi, B.W., Aguiar, M.: Modeling secondary infections with temporary immunity and disease enhancement factor: mechanisms for complex dynamics in simple epidemiological models. Chaos Solit. Fract. (2022). https://doi.org/10.1016/j.chaos.2022.112709
van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)
Weiskopf, D., Sette, A.: T-cell immunity to infection with dengue virus in humans. Front. Immunol. 5 (2014). https://www.frontiersin.org/articles/10.3389/fimmu.2014.00093/full
World Health Organization WHO: Dengue and severe dengue - Key facts. Retrieved from https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue
Acknowledgements
This research is supported by the Basque Government
Funding
M.A. acknowledges the financial support by the Ministerio de Ciencia e Innovacion (MICINN) of the Spanish Government through the Ramon y Cajal Grant RYC2021-031380-I funded by MICIU/AEI/10.13039/501100011033 and by the European Union extGenerationEU/ PRTR. A.K.S. acknowledged the financial support by the ministerio de ciencia e innovación (MICINN) of the Spanish Government through the juan de la cierva grant FJC-2021-046826-I /MICIU/AEI /10.13039/501100011033 y por la Unión Europea NextGenerationEU/ PRTR. This research is supported by the Basque Government through the “Mathematical Modeling Applied to Health” Project, BERC 2022- 2025 program and by the Spanish Ministry of Sciences, Innovation and Universities: BCAM Severo Ochoa accreditation CEX2021-001142-/MICIN/AEI/10.13039/501100011033.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aguiar, M., Steindorf, V., Srivastav, A.K. et al. Bifurcation analysis of a two infection SIR-SIR epidemic model with temporary immunity and disease enhancement. Nonlinear Dyn 112, 13621–13639 (2024). https://doi.org/10.1007/s11071-024-09710-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-024-09710-9