Effect of ratio threshold control on epidemic dynamics: analysis of an SIR model with non-monotonic incidence

Abstract

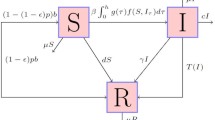
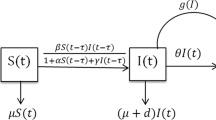
To describe non-continuous control strategy triggered by a predefined ratio of the concerned population in disease progression, an SIR epidemic model with non-monotone incidence is established, dealing with the integrated interventions of vaccination and isolation as ratio-dependent impulsive control. Based on the analysis of multiple equilibria and stability for the continuous subsystem, complex property of the impulsive controlled system is conducted theoretically and numerically. It is found that the ratio magnitude as well as the initial value plays an important role in the threshold dynamics, determining the trajectory convergence to the order-k(k$<3$) periodic solution, the endemic equilibria or the disease free equilibrium under certain conditions. Moreover, numerical examples are provided to demonstrate the theoretical results, and in particular, the case of converging to an order-2 periodic solution is presented in simulation, revealing the influence of the ratio threshold control on disease transmission.

Appendices

Appendix A

A1. Proof of Lemma 3.

Proof

Construct a Lyapunov function as

$$\begin{aligned} {{L}_{0}}(S,I)=S-{{S}_{0}}-{{S}_{0}}\ln \left( \frac{S}{{{S}_{0}}} \right) +I. \end{aligned}$$

Differentiating ${{L}_{0}}\left( t \right)$ along the solutions of model (1) yields

$$\begin{aligned}{} & {} \dfrac{d{{L}_{0}}\left( t \right) }{dt} =\frac{S-{{S}_{0}}}{S}\left( \theta {{S}_{0}}-\frac{\alpha SI}{1+\gamma I+\beta {{I}^{2}}}-\theta S \right) \\{} & {} \qquad +\frac{\alpha SI}{1+\gamma I+\beta {{I}^{2}}}-\left( \theta +r+\varepsilon \right) I \\{} & {} \quad =\frac{-\theta {{\left( S-{{S}_{0}} \right) }^{2}}}{S}+\frac{\alpha {{S}_{0}}I}{1+\gamma I+\beta {{I}^{2}}}-\left( \theta +r+\varepsilon \right) I \\{} & {} \quad =\frac{-\theta {{\left( S-{{S}_{0}} \right) }^{2}}}{S}+\left( \theta +r+\varepsilon \right) I\left( \frac{{{{\mathcal {R}}}_{0}}}{1+\gamma I+\beta {{I}^{2}}}-1 \right) . \end{aligned}$$

If $\gamma \ge 0$, it is obvious that $\frac{d{{L}_{0}}}{dt}\le 0$. If $-2\sqrt{\beta }<\gamma <0$, denoting ${{H}_{1}}\left( I \right) =1+\gamma I+\beta {{I}^{2}}$, then for any $I \ge 0$, we have

$$\begin{aligned} \min \{H_1(I)\}:={{H}_{1}}{{\left( I \right) }_{\min }}={{H}_{1}}\left( -\frac{\gamma }{2\beta } \right) =1-\frac{{{\gamma }^{2}}}{4\beta }. \end{aligned}$$

If $\gamma \ge -2\sqrt{\beta \left( 1-{{{\mathcal {R}}}_{0}} \right) }$, then ${{{\mathcal {R}}}_{0}}\le {{H}_{1}}{{\left( I \right) }_{\min }}$, thus $\frac{d{{L}_{0}}}{dt}\le 0$. Moreover, if ${{\mathcal {R}}}_0<{\mathcal {R}}_{*}$ and $\gamma \ge -2\sqrt{\beta \left( 1-{{{\mathcal {R}}}_{0}} \right) }$, it is valid that the set of $\left\{ \left( S,I \right) \in R_+^2:\frac{dL_{0}}{dt}=0 \right\}$ does not contain any other trajectory of system (1) except the disease-free equilibrium $E_{0}$. By LaSalle invariance principle [41], $E_{0}$ is globally asymptotically stable. $\square$

A2. Proof of Lemma 4.

Proof

Take $\alpha$ as the bifurcation parameter. If ${{\mathcal {R}}}_0 = 1$, then $\alpha ={{\alpha }^{*}}:=\frac{\theta (\theta +r+\varepsilon )}{\Lambda }$ and $E_{0}$ is a non-hyperbolic equilibrium. Redefine $S = x_{1}$ and $I = x_{2}$, then model (1) can be rewritten as

$$\begin{aligned} \begin{array}{lr} \frac{d{{x}_{1}}}{dt}=\Lambda -\frac{\alpha {{x}_{1}}{{x}_{2}}}{1+\gamma {{x}_{2}}+\beta x_{2}^{2}}-\theta {{x}_{1}}\doteq {{g}_{1}}, \\ \frac{d{{x}_{2}}}{dt}=\frac{\alpha {{x}_{1}}{{x}_{2}}}{1+\gamma {{x}_{2}}+\beta x_{2}^{2}}-\left( \theta +r+\varepsilon \right) {{x}_{2}}\doteq {{g}_{2}}. \\ \end{array} \end{aligned}$$

(6)

At ${R}_0 = 1$ and $\alpha ={{\alpha }^{*}}$, the Jacobi matrix of model (6) is $J({{E}_{0}},{{\alpha }^{*}})=\left( \begin{matrix} -\theta &{} -\frac{\Lambda {{\alpha }^{*}}}{\theta } \\ 0 &{} 0 \\ \end{matrix} \right) ,$ thus the left eigenvector of $J({{E}_{0}},{{\alpha }^{*}})$ is given by $y = [y_{1},y_{2}] = [0,1]$, and the right eigenvector is $z={{\left[ {{z}_{1}},{{z}_{2}} \right] }^{T}}={{\left[ -\frac{\Lambda {{\alpha }^{*}}}{{{\theta }^{2}}},1 \right] }^{T}}$. Calculating the correlation partial derivative of model (6) leads to

$$\begin{aligned}{} & {} {{\left( \frac{{{\partial }^{2}}{{g}_{2}}}{\partial {{x}_{1}}\partial {{x}_{2}}} \right) }_{{{E}_{0}}}}={{\alpha }^{*}},{{\left( \frac{{{\partial }^{2}}{{g}_{2}}}{\partial {{x}_{2}}\partial {{x}_{1}}} \right) }_{{{E}_{0}}}}={{\alpha }^{*}},\\{} & {} {{\left( \frac{{{\partial }^{2}}{{g}_{2}}}{\partial x_{2}^{2}} \right) }_{{{E}_{0}}}}=-\frac{2\Lambda {{\alpha }^{*}}}{\theta },{{\left( \frac{{{\partial }^{2}}{{g}_{2}}}{\partial {{x}_{2}}\partial {{\alpha }^{*}}} \right) }_{{{E}_{0}}}}=\frac{\Lambda }{\theta }. \end{aligned}$$

Then the bifurcation constants $a_{1}$ and $b_{1}$ are

$$\begin{aligned} {{a}_{1}}=-\dfrac{2\Lambda {{\left( {{\alpha }^{*}} \right) }^{2}}}{{{\theta }^{2}}}-\frac{2\Lambda {{\alpha }^{*}}\gamma }{\theta }, ~~~~{{b}_{1}}=\dfrac{\Lambda }{\theta }>0, \end{aligned}$$

respectively. By theorem 4.1 in [42], it gives that if $\gamma >\max \left\{ -\frac{\theta +r+\varepsilon }{\Lambda },-2\sqrt{\beta } \right\}$, i.e., $a_{1} < 0$, a forward bifurcation occurs at $E_{0}$. If $-2\sqrt{\beta }<\gamma <-\frac{\theta +r+\varepsilon }{\Lambda }$, i.e., $a_{1} > 0$, model (1) exhibits a backward bifurcation. $\square$

A3. Proof of Lemma 6.

Proof

Construct the following Lyapunov function

$$\begin{aligned} {{L}_{e}}\left( S,I \right) \!=\!\frac{1}{2}{{\left( S-{{S}_{e}}\!+\!I\!-\!{{I}_{e}} \right) }^{2}}\!+\!c\left( I-{{I}_{e}}\!-\!{{I}_{e}}\ln \frac{I}{{{I}_{e}}} \right) , \end{aligned}$$

here $c=\frac{\left( \theta +\theta +r+\varepsilon \right) \left( 1+\gamma {{I}_{e}}+\beta I_{e}^{2} \right) }{\alpha }$. Noting that $\Lambda =\theta {{S}_{e}}+(\theta +r+\varepsilon ){{I}_{e}}$, $\theta +r+\varepsilon =\frac{\alpha {{S}_{e}}}{1+\gamma {{I}_{e}}+\beta I_{e}^{2}}$, then derivation of ${{L}_{e}}\left( S,I \right)$ along the solution trajectory of model (1) yields

$$\begin{aligned}{} & {} \dfrac{d{{L}_{e}}}{dt} =\left( S-{{S}_{e}}+I-{{I}_{e}} \right) \left( \Lambda -\theta S-\left( \theta +r+\varepsilon \right) I \right) \\{} & {} \qquad +c\left( 1-\frac{{{I}_{e}}}{I} \right) \left( \frac{\alpha SI}{1+\gamma I+\beta {{I}^{2}}}-\left( \theta +r+\varepsilon \right) I \right) \\{} & {} \quad =-\theta {{\left( S-{{S}_{e}} \right) }^{2}}-\left( \theta +r+\varepsilon \right) {{\left( I-{{I}_{e}} \right) }^{2}}\\{} & {} \qquad -\left( \theta +\theta +r+\varepsilon \right) \left( S-{{S}_{e}} \right) \left( I-{{I}_{e}} \right) \\{} & {} \qquad +\frac{c\alpha }{1+\gamma {{I}_{e}}+\beta I_{e}^{2}}\left( S-{{S}_{e}} \right) \left( I-{{I}_{e}} \right) \\{} & {} \qquad -c\alpha \left( I-{{I}_{e}} \right) S\left( \frac{1}{1+\gamma {{I}_{e}}+\beta I_{e}^{2}}-\frac{1}{1+\gamma I+\beta {{I}^{2}}} \right) \\{} & {} \quad =-\theta {{\left( S-{{S}_{e}} \right) }^{2}}\\{} & {} \qquad -\left( \left( \theta +r+\varepsilon \right) +\frac{S\left( \theta +\theta +r+\varepsilon \right) }{1+\gamma I+\beta {{I}^{2}}}\left( \beta I+\beta {{I}_{e}}+\gamma \right) \right) \\{} & {} \quad {{\left( I-{{I}_{e}} \right) }^{2}}. \end{aligned}$$

Obviously, if $\gamma \ge 0$, there is $\frac{d{{L}_{e}}}{dt}\le 0$. By LaSalle invariance principle, $E_{e}$ is globally asymptotically stable. For the case of $-2\sqrt{\beta }<\gamma <0$, let

$$\begin{aligned} \Xi =\left( \theta +r+\varepsilon \right) +\frac{S\left( \theta +\theta +r+\varepsilon \right) }{1+\gamma I+\beta {{I}^{2}}}\left( \beta I+\beta {{I}_{e}}+\gamma \right) . \end{aligned}$$

If $\Xi \ge 0$, i.e.,

$\gamma \ge -\frac{\left( \theta +r+\varepsilon \right) \left( 1+\beta {{I}^{2}} \right) +S\left( \theta +\theta +r+\varepsilon \right) \left( \beta I+\beta {{I}_{e}} \right) }{\left( \theta +r+\varepsilon \right) I+S\left( \theta +\theta +r+\varepsilon \right) }:=-\Upsilon$,

it is valid that $\frac{d{{L}_{e}}}{dt}\le 0$. Furthermore,

$$\begin{aligned} \begin{array}{ll} \Upsilon \ge \frac{\left( \theta +r+\varepsilon \right) \left( 1+\beta {{I}^{2}} \right) +S\left( \theta +\theta +r+\varepsilon \right) \left( \beta I+\beta {{I}_{e}} \right) }{\left( \theta +\theta +r+\varepsilon \right) \left( S+I \right) }\\ ~~~ \ge \frac{\left( \theta +r+\varepsilon \right) \beta I\left( S+I \right) }{\left( \theta +\theta +r+\varepsilon \right) \left( S+I \right) }+\frac{\theta +r+\varepsilon }{\left( \theta +\theta +r+\varepsilon \right) \left( S+I \right) }+\frac{\beta {{I}_{e}}S}{S+I} \\ ~~~ \ge \frac{\theta }{\Lambda }\frac{\theta +r+\varepsilon }{\theta +\theta +r+\varepsilon }+\beta {{I}_{e}}\left( \frac{1}{1+q} \right) . \end{array} \end{aligned}$$

Thus, when $\gamma >\max \left\{ -\frac{\theta }{\Lambda }\frac{\theta +r+\varepsilon }{\theta +\theta +r+\varepsilon }-\beta {{I}_{e}}\left( \frac{1}{1+q} \right) ,\right. \left. -2\sqrt{\beta } \right\}$, there is $\Xi \ge 0$, and there exists no other trajectory of the system in the set $\left\{ \left( S,I \right) \in R_{+}^{2}:\frac{\text {d}{{L}_{e}}}{\text {d}t}=0 \right\}$ except for the endemic equilibrium $E_{e}$. By LaSalle invariance principle [41], we obtain the global stability of $E_{e}$. $\square$

Appendix B

B1. Proof of Lemma 7.

Proof

Combining $\frac{I}{S}=\kappa$ and $\frac{dS}{dt}=0$ gives

$h\left( I \right) :=\theta \beta {{I}^{3}}+\left( \theta \gamma +\alpha -\Lambda \beta \kappa \right) {{I}^{2}}+\left( \theta -\Lambda \gamma \kappa \right) I-\Lambda \kappa =0.$

The fact $h\left( 0 \right) =-\Lambda \kappa <0$ and $\underset{I\rightarrow \infty }{\mathop {\lim }}\,h\left( I \right) =\infty$ suggests that $h\left( I \right) =0$ has at least one positive root. In addition, ${h}'\left( I \right) =3\theta \beta {{I}^{2}}+2WI+U$, from which it is clear that if ${{W}^{2}}-3\theta \beta U\le 0$, then ${h}'\left( I \right) \ge 0$, and thus, $h\left( I \right)$ is monotonically increasing, implying that $h\left( I \right) =0$ has only one positive root. Otherwise, if ${{W}^{2}}-3\theta \beta U>0$, ${h}'\left( I \right) =0$ has two roots. Meanwhile, by calculating we have

$h\left( I \right) =\left( \frac{1}{3}I+\frac{1}{9}\frac{W}{\theta \beta } \right) {h}'\left( I \right) +\left( \frac{2}{3}U-\frac{2}{9}\frac{{{W}^{2}}}{\theta \beta } \right) I-\Lambda \kappa -\frac{1}{9}\frac{UW}{\theta \beta }$.

Therefore, (i) if ${h}'\left( I \right) =0$ has negative root, then $h\left( I \right) =0$ has only one positive root; (ii) if ${h}'\left( I \right) =0$ has two positive roots, denoted by $I_{1}$ and $I_{2}$, then $U>0$, $W<0$ and $h\left( {{I}_{1}} \right) h\left( {{I}_{2}} \right) =\tilde{G}\left( U,W \right) .$ As a result, it follows that

If $\tilde{G}\left( U,W \right) >0$, $h\left( I \right) =0$ has only one positive root.

If $\tilde{G}\left( U,W \right) =0$, $h\left( I \right) =0$ has two positive roots (excluding double roots).

If $\tilde{G}\left( U,W \right) <0$, $h\left( I \right) =0$ has three positive roots (excluding double roots). $\square$

B2. Proof of Lemma 8.

Proof

Combining $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ gives

$\beta \kappa \left( \theta +r+\varepsilon \right) {{I}^{2}}+\left( \gamma \kappa \left( \theta +r+\varepsilon \right) -\alpha \right) I+\kappa \left( \theta +r+\varepsilon \right) =0$,

with its discriminant being $\Delta _{1}^{(\kappa )}={{\left( \theta +r+\varepsilon \right) }^{2}}\left( {{\gamma }^{2}}-4\beta \right) {{\kappa }^{2}}-2\alpha \gamma \left( \theta +r+\varepsilon \right) \kappa +{{\alpha }^{2}}$. For the case of $\gamma \in \left( -2\sqrt{\beta },0 \right]$, it is obvious that $\gamma \kappa \left( \theta +r+\varepsilon \right) -\alpha <0$ and $\Delta _{_{1}}^{(\kappa )}=0$ has a positive root $\kappa =\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) }$. Consequently,

• (i) if $\kappa =\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) }$, i.e., $\Delta _{_{1}}^{(\kappa )}=0$, then $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ have a positive intersection;

• (ii) if $\kappa \in \left( 0,\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) } \right)$, i.e., $\Delta _{_{1}}^{(\kappa )}>0$, they have two positive intersections;

• (iii) if $\kappa \in \left( \frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) },+\infty \right)$, i.e., $\Delta _{_{1}}^{(\kappa )}<0$, they have no positive intersection.

On the other hand, for the case of $\gamma \in \left( 0,+\infty \right)$, if $\gamma \kappa \left( \theta +r+\varepsilon \right) -\alpha \ge 0$, i.e., $\kappa \ge \frac{\alpha }{\gamma \left( \theta +r+\varepsilon \right) }$, then $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ have no positive intersection. If $\gamma \kappa \left( \theta +r+\varepsilon \right) -\alpha < 0$, i.e., $\kappa < \frac{\alpha }{\gamma \left( \theta +r+\varepsilon \right) }$, then the intersection can be detailed for $\gamma \in \left( 0,2\sqrt{\beta } \right]$ and $\gamma \in \left( 2\sqrt{\beta },+\infty \right)$ respectively, in the similar way as for $\gamma \in \left( -2\sqrt{\beta },0 \right]$.

Actually, if $\gamma \in \left( 0,2\sqrt{\beta } \right]$, there exists a positive intersection when $\kappa =\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) }$. Otherwise, there exist two positive intersections when $\kappa \in \left( 0,\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) } \right)$, and there exists no positive intersection when $\kappa \in \left( \frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) },\frac{\alpha }{\gamma \left( \theta +r+\varepsilon \right) } \right)$. Moreover, if $\gamma \in \left( 2\sqrt{\beta },+\infty \right)$, then $\Delta _{_{1}}^{(\kappa )}=0$ has two positive roots $\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma +2\sqrt{\beta } \right) }$ and $\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma -2\sqrt{\beta } \right) }$. Noting that $\frac{\alpha }{\left( \theta +r+\varepsilon \right) \left( \gamma -2\sqrt{\beta } \right) }>\frac{\alpha }{\gamma \left( \theta +r+\varepsilon \right) }$, we have the same intersections for this case as $\gamma \in \left( 0,2\sqrt{\beta } \right]$. $\square$

Appendix C

C1. Analysis of five cases in proof of Theory 1.

Case 1: $\kappa <{{\kappa }_{1}}$. There are three types of intersecting of $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ (see Fig. 14):

Fig. 14

When $\kappa <{{\kappa }_{1}}$, the regional division for model (2). a $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ intersect at two points. b $\frac{I}{S}=\kappa$ is tangent to $\frac{dI}{dt}=0$. c $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ do not intersect

(1) When $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ intersect at two points (as shown in Fig. 14a), the region ${{\Gamma }_{12}}$ is divided into ${{\Gamma }_{121}}$ and ${{\Gamma }_{122}}$, and the region ${{\Gamma }_{13}}$ is adjacent to $\frac{I}{S}=\kappa$. The trajectory through the boundary of ${{\Gamma }_{122}}$ and ${{\Gamma }_{13}}$, due to $\frac{dI}{dt}=0$ and $\frac{dS}{dt}<0$, will go horizontally from right to left into ${{\Gamma }_{122}}$, and the trajectory through the boundary of ${{\Gamma }_{121}}$ and ${{\Gamma }_{13}}$ will go from right to left into ${{\Gamma }_{121}}$. The trajectory through the boundary of ${{\Gamma }_{121}}$ and ${{\Gamma }_{11}}$, due to $\frac{dI}{dt}<0$ and $\frac{dS}{dt}=0$, will go vertically from top to bottom into ${{\Gamma }_{11}}$. Next, it is shown that the trajectory from any $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{1i}}\left( i=1,2,3 \right)$ will eventually converge to $E_0$.

• (i)  If $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{122}}$, then both $S\left( t \right)$ and $I\left( t \right)$ will decrease in this region. The trajectory may enter the region ${{\Gamma }_{11}}$, ${{\Gamma }_{121}}$, ${{\Gamma }_{13}}$ or stay in ${{\Gamma }_{122}}$ constrained by the impulse, and the trajectory that stays in ${{\Gamma }_{122}}$ will eventually enter ${{\Gamma }_{11}}$, ${{\Gamma }_{121}}$ or ${{\Gamma }_{13}}$ after finite times impulse control due to the monotonicity of $S\left( t \right)$.

• (ii)  If $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{13}}$, then $S\left( t \right)$ will decrease and $I\left( t \right)$ will increase. The trajectory either enters ${{\Gamma }_{121}}$ or ${{\Gamma }_{122}}$, or reaches $\frac{I}{S}=\kappa$ and then the pulsed trajectory may reach ${{\Gamma }_{11}}$, ${{\Gamma }_{121}}$ or stay in ${{\Gamma }_{13}}$. After the pulse, the trajectory that stays in ${{\Gamma }_{13}}$ will eventually enter ${{\Gamma }_{11}}$ or ${{\Gamma }_{121}}$ after finite times impulse control. Combined with (i), it follows that the trajectory in region ${{\Gamma }_{13}}$ will end up in either ${{\Gamma }_{11}}$ or ${{\Gamma }_{121}}$.

• (iii)  If $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{121}}$, then both $S\left( t \right)$ and $I\left( t \right)$ will decrease in this region. If the trajectory cannot reach $\frac{I}{S}=\kappa$, it may converge to $E_0$ directly, or pass though the line $\frac{dS}{dt}=0$ and enter ${{\Gamma }_{11}}$ because of the global stability of $E_0$. Otherwise, if the trajectory can reach $\frac{I}{S}=\kappa$, then it may be in ${{\Gamma }_{11}}$ or ${{\Gamma }_{13}}$, or still in ${{\Gamma }_{121}}$ after being pulsed. The trajectory that stays in ${{\Gamma }_{121}}$, after finite number of pulses, either converges to $E_{0}$ or enters ${{\Gamma }_{11}}$. Combined with (ii), it follows that the trajectory in ${{\Gamma }_{121}}$ either converges to $E_{0}$, or eventually enters in ${{\Gamma }_{11}}$.

• (iv)  If $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{11}}$, then $S\left( t \right)$ will increase and $I\left( t \right)$ will decrease in this region. As a result, the trajectory in ${{\Gamma }_{11}}$ will eventually converge to $E_0$.

(2) When $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ intersect at one point (as shown in Fig. 14b), the region ${{\Gamma }_{13}}$ is not adjacent to $\frac{I}{S}=\kappa$, thus the trajectory in ${{\Gamma }_{13}}$ can not being pulsed. As a result, all the trajectories will pass through $\frac{dI}{dt}=0$ and enter ${{\Gamma }_{121}}$ or ${{\Gamma }_{122}}$. From (1), the trajectory eventually converges to $E_0$.

(3) When $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ do not intersect (as shown in Fig. 14c), from (1) and (2), we know that the trajectory in ${{\Gamma }_{13}}$ will pass through $\frac{dI}{dt}=0$ and enter ${{\Gamma }_{12}}$. The trajectory in ${{\Gamma }_{12}}$ is similar to that in ${{\Gamma }_{121}}$ (Fig. 14a), which either converges to $E_0$ or eventually enters ${{\Gamma }_{11}}$ and then converges to $E_0$.

Case 2: $\kappa ={{\kappa }_{1}}$.

The trajectory in this case is exactly the same as that in Case 1, and any trajectory will eventually converge to $E_0$ (see Fig. 15).

Fig. 15

When $\kappa ={{\kappa }_{1}}$, the regional division for model (2). a $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ intersect at two points. b $\frac{I}{S}=\kappa$ is tangent to $\frac{dI}{dt}=0$. c $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ do not intersect

Case 3: ${{\kappa }_{1}}< \kappa <{{\kappa }_{2}}$.

The region ${{\Gamma }_{11}}$ is divided into two parts, i.e., ${{\Gamma }_{111}}$ and ${{\Gamma }_{112}}$. There are also three scenarios of intersecting (as shown in Fig. 16), which are similar to those in Case 1. As $S\left( t \right)$ increases and $I\left( t \right)$ decreases in ${{\Gamma }_{112}}$, the trajectory can not reach $\frac{I}{S}=\kappa$ and directly enter ${{\Gamma }_{122}}$ (Fig. 16a, b) or ${{\Gamma }_{12}}$ (Fig. 16c). The trajectory in the remaining regions is exactly the same as that in Case 1. Therefore, the trajectory eventually converges to $E_0$.

Fig. 16

When ${{\kappa }_{1}}< \kappa <{{\kappa }_{2}}$, the regional division for model (2). a $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ intersect at two points. b $\frac{I}{S}=\kappa$ is tangent to $\frac{dI}{dt}=0$. c $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ do not intersect

Case 4: $\kappa ={{\kappa }_{2}}$.

In this case, $\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ do not intersect (see Fig. 17a). The region ${{\Gamma }_{11}}$ is divided into ${{\Gamma }_{111}}$ and ${{\Gamma }_{112}}$, similar to Case 3. From the above analysis, it can be seen that the trajectory in ${{\Gamma }_{13}}$ will eventually pass through $\frac{dI}{dt}=0$ and enter ${{\Gamma }_{12}}$. The trajectory in ${{\Gamma }_{112}}$ will cross $\frac{dS}{dt}=0$ into ${{\Gamma }_{12}}$, and that in ${{\Gamma }_{12}}$ either converges to $E_0$ or enters ${{\Gamma }_{111}}$ after finite times impulse control. Finally, the trajectory in ${{\Gamma }_{111}}$ will converge to $E_0$ as $S\left( t \right)$ increases and $I\left( t \right)$ decreases.

Fig. 17

The regional division for model (2). a $\kappa ={{\kappa }_{2}}$. b $\kappa >{{\kappa }_{2}}$

Case 5: $\kappa >{{\kappa }_{2}}$.

$\frac{I}{S}=\kappa$ and $\frac{dI}{dt}=0$ do not intersect (see Fig. 17b). Clearly, all the trajectories in ${{\Gamma }_{13}}$ will enter ${{\Gamma }_{12}}$ and then they either converge to $E_0$ or enter ${{\Gamma }_{11}}$ after finite times impulse control. The trajectories in ${{\Gamma }_{11}}$ above $I=\frac{1}{\sqrt{\beta }}$ will pass though $\frac{dS}{dt}=0$ into ${{\Gamma }_{12}}$, and the remaining ones will converge directly to $E_0$. The trajectories in ${{\Gamma }_{11}}$ and ${{\Gamma }_{12}}$ can not be periodic ones due to the monotonicity of I(t) ($\frac{dI}{dt}<0$). Therefore, the trajectory will eventually converge to $E_0$.

C2. Analysis of two scenarios in Case 1 in proof of Theory 5.

• (i) If ${{S}_{23}}<\frac{\Lambda }{\theta \left( 1+\kappa \right) }$, the region ${{\Gamma }_{31}}$ is divided into ${{\Gamma }_{311}}$ and ${{\Gamma }_{312}}$, and the region ${{\Gamma }_{34}}$ is divided into ${{\Gamma }_{341}}$ and ${{\Gamma }_{342}}$. The trajectory across the boundary of ${{\Gamma }_{311}}$ and ${{\Gamma }_{32}}$, due to $\frac{dI}{dt}=0$ and $\frac{dS}{dt}>0$, enters ${{\Gamma }_{32}}$ horizontally from left to right. However, the trajectory across the boundary of ${{\Gamma }_{311}}$ and ${{\Gamma }_{341}}$, due to $\frac{dI}{dt}<0$ and $\frac{dS}{dt}=0$, enters ${{\Gamma }_{311}}$ vertically from top to bottom, and the trajectory across the boundary of ${{\Gamma }_{32}}$ and ${{\Gamma }_{33}}$, due to $\frac{dI}{dt}>0$ and $\frac{dS}{dt}=0$, will enter ${{\Gamma }_{33}}$ vertically from bottom to top. As $\frac{dI}{dt}=0$ and $\frac{dS}{dt}<0$, the trajectory, passing through the boundary of ${{\Gamma }_{341}}$ and ${{\Gamma }_{33}}$ and the boundary of ${{\Gamma }_{33}}$ and ${{\Gamma }_{342}}$, will enter ${{\Gamma }_{341}}$ and ${{\Gamma }_{342}}$ horizontally from right to left. The trajectory across the boundary of ${{\Gamma }_{312}}$ and ${{\Gamma }_{342}}$, due to $\frac{dI}{dt}<0$ and $\frac{dS}{dt}=0$, will enter ${{\Gamma }_{342}}$ vertically from top to bottom. As a result, for $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{312}}$, the trajectory eventually crosses $\frac{dS}{dt}=0$ and enters ${{\Gamma }_{342}}$.

For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{311}}$, since S(t) increases and I(t) decreases, the trajectory either converges directly to $E_{e}$ because of the global asymptotic stability of $E_{e}$, or crosses $\frac{dI}{dt}=0$ into ${{\Gamma }_{32}}$. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{32}}$, by the vector field analysis, the trajectory either converges directly to $E_{e}$, or crosses $\frac{dS}{dt}=0$ and enters ${{\Gamma }_{33}}$, noticing that both S(t) and I(t) increase. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{33}}$, given that S(t) decreases and I(t) increases, the trajectory either converges directly to $E_{e}$, or crosses $\frac{dI}{dt}=0$ into ${{\Gamma }_{341}}$ or ${{\Gamma }_{342}}$, or reaches ${{A}_{2}}{{A}_{3}}$, experiences pulses and eventually enters any region of ${{\Gamma }_{311}}$, ${{\Gamma }_{32}}$, ${{\Gamma }_{341}}$ and ${{\Gamma }_{33}}$. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{34}}$, in view of S(t) as well as I(t) decreasing, in ${{\Gamma }_{341}}$, if the trajectory does not reach $\frac{I}{S}=\kappa$, then it either converges directly to $E_{e}$, or crosses $\frac{dS}{dt}=0$ into ${{\Gamma }_{311}}$. Otherwise, if the trajectory reaches $\frac{I}{S}=\kappa$, it may pulse into any region except ${{\Gamma }_{312}}$ or ${{\Gamma }_{342}}$. In ${{\Gamma }_{342}}$, the trajectory either reaches ${{A}_{3}}{{G}_{2}}$ or ${{G}_{3}}{{A}_{5}}$, which necessarily causes pulse, and then it is capable of reaching any region.

From the above analysis, it follows that the trajectory in ${{\Gamma }_{3i}}\left( i=1,2,3,4 \right)$, either converges directly to $E_{e}$, or arrives at ${{G}_{1}}{{G}_{2}}$ or ${{G}_{3}}{{A}_{5}}$ where the pulse occurs (both ${{G}_{1}}{{G}_{2}}$ and ${{G}_{3}}{{A}_{5}}$ are in the region $\frac{dS}{dt}<0$). After the pulse, the trajectory may reach the area of $\frac{dS}{dt}>0$ (${{\Gamma }_{311}},{{\Gamma }_{32}}$) or $\frac{dS}{dt}<0$ (${{\Gamma }_{33}},{{\Gamma }_{341}},{{\Gamma }_{312}},{{\Gamma }_{342}}$). (a) If the trajectory satisfies $\frac{dS}{dt}>0$, then with the increase of S(t), there exist two facts, i.e., $\textcircled {1}$ the trajectory may converge directly to $E_{e}$ in the region of ${{\Gamma }_{311}}$ and ${{\Gamma }_{32}}$, and $\textcircled {2}$ the trajectory may cross $\frac{dS}{dt}=0$ into ${{\Gamma }_{33}}$, converging to $E_{e}$ or reaching the pulse line again to generate a periodic solution. (b) If the trajectory satisfies $\frac{dS}{dt}<0$, there are also two facts, i.e., $\textcircled {1}$ when the trajectory does not intersect with $\frac{I}{S}=\kappa$ again, it either converges to $E_{e}$ or crosses $\frac{dS}{dt}=0$ into ${{\Gamma }_{311}}$, leading to its convergence to $E_{e}$ or to a periodic solution by (a), and $\textcircled {2}$ when the trajectory can intersect with $\frac{I}{S}=\kappa$ again, due to the monotonic decrease of S(t), the next intersection must be located to the left of the previous one, implying that the trajectory eventually either converges to $E_{e}$ or pulses into the area of $\frac{dS}{dt}>0$ after finite times of pulses, thus it converges to $E_{e}$ or to a periodic solution.

• (ii) If $\frac{\Lambda }{\theta \left( 1+\kappa \right) }$ is among the sequence ${{S}_{21}}<{{S}_{12}}<{{S}_{13}}<{{S}_{22}}<{{S}_{23}}$, the trajectory, either converging to $E_{e}$ or to a periodic solution, depends on the initial value, which can be detailed by the similar analysis as in (i).

C3. Analysis of two scenarios in Case 3 in proof of Theory 5.

• (i) ${{S}_{22}}<\frac{\Lambda }{\theta \left( 1+\kappa \right) }$. The region ${{\Gamma }_{31}}$ is divided into ${{\Gamma }_{311}}$, ${{\Gamma }_{312}}$ and ${{\Gamma }_{313}}$. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{31}}$, due to the fact that S(t) increases and I(t) decreases, all trajectories in ${{\Gamma }_{311}}$ cross $\frac{dI}{dt}=0$ into ${{\Gamma }_{32}}$. The trajectory in ${{\Gamma }_{312}}$ either converges directly to $E_{e}$ or crosses $\frac{dI}{dt}=0$ into ${{\Gamma }_{32}}$. All trajectories in ${{\Gamma }_{313}}$ cross $\frac{dS}{dt}=0$ into ${{\Gamma }_{34}}$. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{32}}$, with S(t) as well as I(t) increasing, the trajectory either converges directly to $E_{e}$, or crosses $\frac{dS}{dt}=0$ and enters ${{\Gamma }_{33}}$, or it reaches ${{A}_{2}}{{A}_{3}}$ and then the pulse occurs, which makes it reach ${{\Gamma }_{311}}$ or ${{\Gamma }_{32}}$. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{33}}$, as S(t) decreases and I(t) increases, the trajectory either converges directly to $E_{e}$ or crosses $\frac{dI}{dt}=0$ into ${{\Gamma }_{34}}$. For $\left( {{S}^{0}},{{I}^{0}} \right) \in {{\Gamma }_{34}}$, noting that both S(t) and I(t) decrease, the trajectory either converges directly to $E_{e}$, or arrives at ${{G}_{2}}{{A}_{5}}$ and then reaches any one of the regions after experiencing the pulse. As a result, if a pulse occurs, the trajectory in ${{\Gamma }_{3i}}\left( i=1,2,3,4 \right)$ will necessarily reach ${{A}_{2}}{{A}_{3}}$ or ${{G}_{2}}{{A}_{5}}$. The trajectory that reaches ${{G}_{2}}{{A}_{5}}$ and undergoes pulses can reach any region. If the trajectory reaches ${{\Gamma }_{33}}$ or stays in ${{\Gamma }_{34}}$, then periodic solution can not exist due to the decreasing of S(t). If the trajectory reaches ${{\Gamma }_{313}}$, then it will enter into ${{\Gamma }_{34}}$ again and no periodic solution is generated due to the decrease of I(t). If the trajectory arrives at ${{\Gamma }_{311}}$, ${{\Gamma }_{312}}$ or ${{\Gamma }_{32}}$, then it either converges to $E_{e}$, or passes through ${{\Gamma }_{32}}$ to ${{\Gamma }_{33}}$ and reaches ${{G}_{2}}{{A}_{5}}$ again, which may result in an orbitally asymptotically stable periodic solution. The trajectory that reaches ${{A}_{2}}{{A}_{3}}$ and undergoes pulses may go into ${{\Gamma }_{311}}$ or ${{\Gamma }_{32}}$. Furthermore, the ones arriving at ${{\Gamma }_{311}}$ will enter into ${{\Gamma }_{32}}$ again and eventually converge to $E_{e}$ or to the period solution, with the increase of S(t) and I(t). In addition, the trajectories that stay in ${{\Gamma }_{32}}$ after the pulses, will also either converge to $E_{e}$ or to the periodic solution.

• (ii) ${{S}_{21}}<\frac{\Lambda }{\theta \left( 1+\kappa \right) }\le {{S}_{22}}$ or ${{S}_{13}}<\frac{\Lambda }{\theta \left( 1+\kappa \right) }\le {{S}_{21}}$. It can be similarly analyzed that the trajectory either converges to $E_{e}$, or reaches ${{A}_{3}}{{G}_{1}}$ and experiences pulses, after which it is characterized by $\frac{dS}{dt}>0$. As a result, the trajectory either converges to $E_{e}$ or generates periodic solution.