Dynamics and energy harvesting from parametrically coupled self-excited electromechanical oscillator

Abstract

The investigated parametrically coupled electromechanical structure is composed of a mechanical Duffing oscillator whose mass sits on a moving belt surface. The driving electrical network is a van der Pol oscillator whose aim is to actuate the attached DC motor to provide some rotatry unbalances and parametric coupling in the vibrating structure. The coupled oscillator is applied to energy harvesting and overcomes the limitation of low energy generation associated with a single oscillator of this kind. The system was solved analytically and validated by numerical methods. The global dynamics of the structure were investigated, and nonlinear phenomena such as Neimark–Sacker bifurcation, discontinuity-induced bifurcation, grazing–sliding, and bifurcation to multiple tori were identified. These nonlinear behaviors affect the harvested energy at bifurcation points, resulting in jumps from one energy level to another. In addition to harnessing the highest energy under hard parametric coupling, the coupling ensures that higher and more useful energy is harvested over a wider range of belt speeds. Finally, the qualitative validation of the numerical concept by experimental setup verifies the workings of the model.

1 Introduction

Electromechanical oscillations have been found in modern systems such as speakers, specialized sensors, and power grids [1,2,3]. In power systems, such oscillations pose severe threats to the stable workings of interconnected grids and angular instability [3, 4]. The oscillations stem from associated nonlinearities of power converters and are undesirable, requiring dynamical analysis, damping measurements, and control. Kenmogne et al. [5], however, converted such unwanted oscillations of an electromechanical system with irrational nonlinearities to a novel sand sieve application by analyzing the damping effects on the system’s dynamics. The system consists of an electrically forced van der Pol oscillator magnetically coupled to a network of elastically coupled mechanical subsystems. Other coupled electromechanical systems are the unforced van der Pol and Duffing oscillators with elastic couplings [6], dissipative couplings [7], forced and combined couplings [8], parametric couplings [9]; and have found applications in neuron models, information coding, sensors and actuators such as the skin impedance measurement unit [10]. Despite the notable presence of these coupled oscillators and their dynamical analyses, the configuration with friction-induced excitation is lacking in the literature. Balaram et al. [11] investigated friction-induced stick-slip vibrations in a three degree of freedom (3 DoF) discontinuous model of a disc brake system with the aim of suppressing the unwanted vibration. The undesired oscillations were suppressed using normal harmonic forcing for frequency entrainment of the nonsmooth limit cycles. Similar structures with friction-induced vibration have been carried out by researchers in [12,13,14,15], in which a mass on the moving belt forms the central substructure, and the speed of the belt creates the induced self-excitation. Insights into the instability of multi-degree of freedom of such models were investigated by Li et al. [16]. Other structures with friction-induced mechanisms, including constraints and discontinuities are studied in the works [17,18,19,20,21]. Though the dynamics of the highlighted systems were highly investigated, their applications towards energy harvesting were not extended.

Vibration energy harvesting (VEH) utilizing nonlinear and nonideal sources has proven to be vital technology in meeting ever-increasing energy demands [22, 23]. Besides being environmentally friendly, it supplies small electronic devices such as wireless sensor networks, communications device packs, Internet of Things (IoT), wearable medical applications, and transportation systems [24,25,26]. Wang et al. [27] numerically investigate the conversion of friction-induced vibration (FIV) of mechanical structures composed of mass on a moving belt under normal loads into harvested energy. The study showed that both the normal load and the belt’s speed significantly influence generated power, and the energy is greater in the unstable region. A similar investigation was carried out by Han and Zhang [28] for a disc brake system, modeled as a V-shape structure of springs-connected mass on a moving belt. The self-excited system had additional surface nonlinearity of quasi-zero stiffness. The study showed multiple stability of single, double, and triple potential wells and stick-slip motion. An electromagnetic harvester was used to convert the FIV into electrical energy. In another development, Xiang et al. [29] performed a study on a simultaneous FIV reduction and energy harvesting from the braking system of a high-speed train. The harvester serves as a damper for reducing vibrations and, at the same time, converting the FIV into energy. The dynamic contact surface behavior, modeled as an exponential function of the relative speed between the mass and the belt, significantly influenced the harvested energy. Xiao et al. [30] expanded on similar effects of Stribeck friction surface behaviors (model parameters) of a designed energy generator from FIV in a 1 DoF friction system. The results show that the coefficient of static and dynamic friction, and the exponential decay constant notably affect the energy generation. The FIV systems considered so far are those of rigid mass on belt structures. Chen et al. [31] considered a mass frame that encloses a cantilever with a tip magnet, and a fixed magnet separated by an air gap. The frame rests on the moving belt and converts the FIV into helpful electricity. The stick-slip system is bistable, with poor output power generation in the chaotic region. A more recent study by Sani et al. [32] used a body frame (mass) on the belt, which houses a rotary unbalanced mass that provides parametric excitation as an additional nonideal energy source. The frame was placed on the moving belt so that both the self–excitation from the FIV and the parametric excitation were present. It was demonstrated that while useful energy was harvested due to the surface–excitation alone, the parametric excitation helped to increase the speed bandwidth over which the energy was harvested. The considered literature, in some cases, pointed out the limitation of 1 DoF system, characterized by low energy generation. Where friction-induced vibration of the mass–belt relation was used, energy harvesting was also limited to a small range of belt speeds.

The goal of this study is to overcome these limitations by introducing an electrical subcircuit of the van der Pol oscillator and parametrically coupling it with the mechanical substructure. The advantages are

• (i) The mass on the belt structure allows for the attachment of MFC (piezoelectric) filaments, which are reliable and practical for energy harvesting applications.

• (ii) The parametric coupling of van der Pol subcircuit provides two non-ideal energy sources: the parametric excitation (from the coupling) and the self-excitation from negative damping, of which both inject energy into the system for self-sustained oscillations.

• (iii) Simple enough for energy harvesting applications since only the mechanical subsystem requires physical construction, thus saving costs.

The proposed design overcomes the limitation of low energy harvesting associated with the FIV of 1 DoF substructures and inherent energy harvesting that is only possible over a small range of belt speeds. The system was solved analytically by multiple scales method, and validated by numerical comparisons of the results. Further contributions include the numerical treatment of the system, which identified the underlying nonlinear dynamic behaviors and their effects on harvested energy. At bifurcation points, there are jumps in the values of harvested energy, while maximum power was generated in the region of hard parametric coupling. Finally, experimental verification of the established model was carried out to validate some known numerical results qualitatively. The rest of the paper is organized as follows. Section 2 deals with system modeling, the governing equations, and the state-space by Filippov method. In section 3, the analytical solution by multiple scale method of the non-resonant scenario, identifying the various resonance conditions in the system, was established. Numerical treatment of the system for bifurcation analysis and effects of the behavioral dynamics on energy were carried out in Sect. 4, while experimental work was performed in Sect. 5. Finally, the concluding remark was given in Sect. 6.

2 System modeling

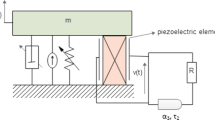
The conceptual model of the electromechanical system is given in Fig. 1. Let the initial voltage $V_c$ of the capacitor with capacitance C be substantially greater than zero. The current I will flow through the nonlinear resistor R, and the inductor (of inductance, L) feeds the coupling network of drivers M(t) to the stepper motor, which in turn provides some unbalanced rotations on the body mass.

Fig. 1

Conceptual model of the electromechanical system

The lumped mass $M_0$ of the frame with the attached stepper motor is displaced by q. At the same time, the nonlinear stiffness $k(q)=k_1+k_2 q^2$, and the viscous damper d create the restoring forces and cause the mechanical subsystem to act back on the electrical subcircuit via the parametric coupling. Additionally, the mass $M_0$ is connected with a macro-fiber composite (MFC) piezoelectric crystal for energy harvesting applications. The MFC subcircuit is indicated as having the resistance, capacitance, and equivalent electromechanical coupling coefficient denoted as $R_p$, $C_p$, and $\chi$, respectively. When the belt moves at constant speed $v_0$, dry frictional force $f_r$ exists between the belt and the mass $M_0$ and serves as a source of self-excitation to the mechanical subsystem.

Fig. 2

Stepper Motor cross-section (a) and subcircuit (b)

It is interesting to show a simple cross-section of the stepper motor and its subcircuit in Fig. 2 where the rotor speed is a function of the number of pole pairs p and rotation angle $\theta$. The direction and speed also depend on the excitation phase and frequency. From the subcircuit of Fig. 2b, $R_a$ and $L_a(\theta )$, represent the resistance and the inductance of phase A winding, respectively. However, the inductance is also a function of the rotor position such that

$$\begin{aligned} L_a(\theta ) = L_0 + L_1 cos(N_r\theta ), \end{aligned}$$

(1)

where $L_0$ is the average inductance, $L_1$ is the maximum inductance variation, and $N_r$ is the rotor teeth number. But if the magnets introduced non–negligible amount of air gap, the winding inductance of the stepper motor is considered to be independent of the rotor position. Then, the back electromotive force (EMF), given by $e_a(\theta )$ becomes a function of the rotor position

$$\begin{aligned} e_a(\theta ) = -p\psi _m sin(p\theta ) \omega , \end{aligned}$$

(2)

where $\psi _m$ is the motor maximum magnetic flux, and $\omega =\dot{\theta }$. It implies that $\omega \Delta t = \Delta \theta$ for small changes $\Delta$ in $\theta$ per unit time t, at which point, two pole pairs are energized ($p=2$). Thus, the parametric coupling M(t) is modeled as

$$\begin{aligned} M(t)=k_l + k_n cos(2 \omega t), \end{aligned}$$

(3)

where $k_l$ and $k_n$ are the mutual coupling coefficients due to the interactions between the winding inductances and the magnetic flux of the back EMF. The electromagnetic torque $T_e$ generated [33] is given as

$$\begin{aligned} T_e=J \frac{d \omega }{dt} + B \omega + T_L, \end{aligned}$$

(4)

where J is the total inertia, B is the total friction coefficient, and $T_L$ is the load torque. Hence, the system’s governing equations can now be established.

2.1 The governing equations

Considering the model in Fig. 1, let Q be the unit charge on the inductive element. The current $I=\frac{d Q}{dt}$ flows in the electrical subcircuit when energized by the capacitive voltage $V_c$. The nonlinear resistor R offers a dissipative characteristic force that must be normalized. Thus, $Q_0$ and $R_0$ are the normalization charge and resistance such that the normalization current is $I_0 = \frac{d Q_0}{dt}$. In our previous studies [9], the governing equations without the moving belt were established using the Euler–Lagrange technique for a system with similar coupling terms. Adopting this approach and including the moving belt mechanism and energy harvesting components, the following governing equations are arrived at:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}L\frac{d^2I}{dt^2}-R_0\left[ 1-\left( \frac{I}{I_0}\right) ^2\right] \frac{dI}{dt}+\frac{I}{C} \\ &{}\quad - (k_l+k_n \ cos(2\omega t))(q-I) = 0,\\ &{}M_0\frac{d^2q}{dt^2}+d\frac{dq}{dt}+k_1q+k_2q^3 + \chi \vartheta - f_r \\ &{}\quad - (k_l+k_n \ cos(2\omega t))(I-q) = 0,\\ &{}C_p \frac{d \vartheta }{dt} + \frac{\vartheta }{R_p}-\chi \frac{d q}{dt} = 0, \end{array}\right. } \end{aligned}$$

(5)

where $\vartheta$ is the generated voltage from the MFC piezoelectric crystal of mass $m_p$, $f_r = M_0 g \mu (v_r)$, and g is the acceleration due to gravity. The relative velocity is $v_r=v_0 -\dot{q}$ and the dry friction coefficient $\mu (v_r)$ is defined as,

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\mu (v_r) = \mu _s sgn(v_r)-\mu _1 v_r + \mu _3 v_r^3, \ \forall \ v_0 \ne \dot{q},\\ &{}\mu (v_r) = 0, \ \ \forall \ v_0 = \dot{q} \end{array}\right. }\nonumber \\ \end{aligned}$$

(6)

where the over–dot ($^.$) represents a time derivative $\frac{d}{dt}$; $\mu _s$, $\mu _1$, and $\mu _3$ are the coefficients of Stribeck friction model. The first part of Eq. (5) represents the equation of the van der Pol electrical subcircuit, while the second part is that of a mechanical Duffing oscillator on friction-induced surface. The nondimensional form of the system (5)–(6) can now be presented.

2.2 Dimensionless form of the governing equations

Assuming that the natural frequency of the mechanical substructure occurs at the pulsation of the electrical subcircuit,

$$\begin{aligned} \Omega _e=\frac{1}{\sqrt{LC}}=\sqrt{\frac{k_1}{M_0}}. \end{aligned}$$

(7)

It follows that Eq. (7) presents the synchronized frequency of the coupled system. Then, the static deflection of the structure is anchored to the normalization current, $I_0$ such that,

$$\begin{aligned} y_{st}=\frac{M_0g}{k_1} |_{I_0 = \dot{Q}_0} \end{aligned}$$

(8)

Using the dimensionless variables $\tau =\Omega _e t$, $x=\frac{I}{I_0}$, $y=\frac{q}{y_{st}}$, the initial voltage of the MFC crystal is $\vartheta _0=\frac{m_pg}{\Omega _e R_p C_p}$ so that $\phi =\frac{\vartheta }{\vartheta _0}$. Then, $\frac{d}{dt}=\ \Omega _e\frac{d}{d\tau }$, $\frac{d^2}{dt^2}=\ \Omega _e^2\frac{d^2}{d\tau ^2}$, Eqs. (5) and (6) become

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\ddot{x}-\alpha \left( 1-x^2\right) {\dot{x}}+x-\lambda N_1 (1+ \mu _p \ cos(2\Omega \tau ))\\ &{}\quad \times \left( y-x\right) =0, \\ &{}\ddot{y}+\beta {\dot{y}}+y+\gamma y^3 + \chi \phi - \rho \mu ({\bar{v}}_r) \\ &{}\quad -\lambda \ (1+ \mu _p \ cos(2\Omega \tau ))\left( x-y\right) =0,\\ &{}{\dot{\phi }} + \Theta \phi -\chi \Lambda \dot{y} = 0, \end{array}\right. } \end{aligned}$$

(9)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu ({\bar{v}}_r) &{}= \mu _s sgn({\bar{v}}_r)\\ &{}\quad -{\bar{\mu }}_1 {\bar{v}}_r + {\bar{\mu }}_3 {\bar{v}}_r^3, \ \forall \ v_b \ne \dot{y},\\ \mu ({\bar{v}}_r) &{}= 0, \ \ \forall \ v_b = \dot{y}, \end{array}\right. } \end{aligned}$$

(10)

where ${\bar{v}}_r=v_b -\dot{y}$ $\alpha =R_0C \Omega _e$, $\beta =d\ \sqrt{\frac{1}{k_1M_0}}$, $\gamma =\frac{k_2y_{st}^2}{k_1}$, $\Omega =\frac{\omega }{\Omega _e}$, $\lambda = \frac{k_l}{k_1}$ , $\mu _p=\frac{k_n}{k_l}$, $\rho =\frac{g}{\Omega _e^2 y_{st}}$, $\Theta =\frac{1}{\Omega _e R_p C_p}$, $\Lambda =\frac{Q_0}{C_p \vartheta _0}$ and $N_1= C\cdot k_1$, $v_b=\frac{v_0}{\Omega _e y_{st}}$, ${\bar{\mu }}_1 = \mu _1\Omega _e y_{st}$, ${\bar{\mu }}_3 = \mu _3(\Omega _e y_{st})^3$. It should be noted that $\Lambda$ and $N_1$ are dimensionless with $N_1\le 1$ because the static deflection $y_{st}$ represents the static charge $Q_0$ while $k_1$ transforms into elastance ($\frac{1}{C}$) in electromechanical equivalence.

2.3 State space subdivision by Filippov method

The frictional term $\mu ({\bar{v}}_r)$ in Eq. (9) makes the vector field associated with the governing system of Eq. (9) discontinuous. Suppose the state space vector is defined as $\{\mathbf {y\}} = \{x, {\dot{x}}, y, {\dot{y}}, \phi \}^{T}$, the surface of discontinuity $\Sigma$ in the present case can be specified by the scalar function $\Sigma : D({\textbf{y}}) = v_b - {\dot{y}}$. Using this surface of discontinuity, the five-dimensional state space can be partitioned into three regions:

$$\begin{aligned} S_1= & {} \left\{ {\textbf{y}} \in \Re ^5:D({\textbf{y}})<0\right\} \\ S_2= & {} \left\{ {\textbf{y}}\in \Re ^5:D({\textbf{y}})>0\right\} \\ \Sigma= & {} \left\{ {\textbf{y}}\in \Re ^5:D({\textbf{y}})=0\right\} \end{aligned}$$

A pictorial representation of this partitioning is given in Fig. 3. As $sgn(v_b-{\dot{y}}) = -1$ when ${{\textbf{y}}} \in S_1$, and $sgn(v_b-{\dot{y}}) = +1$ when ${{\textbf{y}}} \in S_2$, the vector field is smooth in regions $S_1$ and $S_2$. These smooth vector fields are denoted as $F_1$ and $F_2$, respectively.

Fig. 3

Surface of discontinuity $\Sigma$ and the Filippov partitioning

According to the Filippov methodology for discontinuous systems [34], the vector field along the discontinuous surface $\Sigma$ is defined as a convex combination of the two smooth vector fields.

$$\begin{aligned}{} & {} \bar{co}\left( F_1({\textbf{y}}),F_2({\textbf{y}})\right) \nonumber \\{} & {} \quad = \left\{ F_D:{\textbf{y}}\in \Re ^5\rightarrow \Re ^5:F_D\right. \nonumber \\{} & {} \quad =\left. (1-\alpha _p)F_1+\alpha _p F_2,\alpha _p \in [0,1]\right\} \end{aligned}$$

(11)

When an orbit, starting out in one region of the state space, intersects with the surface of discontinuity $\Sigma$, it can either slide along the surface or transversally cross over to the other region. For illustration, a sliding orbit is shown in Fig. 3. This scheme allows one to formulate the analytical treatment of the discontinuous problem.

3 Analytical solution

The Filippov rendition enables us to solve the system in regions $S_1$ and $S_2$ separately by taking $sgn(v_b-{\dot{y}}) = -1,\ +1$ in Eq. (9). This way, we can identify the various resonant conditions present in the system. The solution in the region $\Sigma$, however, yields no such information since ${\dot{y}} = v_b$. It implies that the mass sticks to the belt until slipping occurs, and the convex combination in Eq. (11) applies. Hence, the approximate analytical solution is found only at $sgn(v_b-{\dot{y}}) = +1$ for simplicity and further analysis. This solution is valid for all cases since only the sign of $\mu _s$ (i.e., $\pm \mu _s$) can be changed without affecting the method. First, Eq. (9) is re–arranged as follows, introducing unit constants to separate the complex terms. We have

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} \ddot{x}+p_1^2 x-\lambda N_1 y-\alpha \left( 1-\eta x^2\right) {\dot{x}}\\ &{}\quad +\lambda \mu _p N_1 x \cos (2 \Omega \tau )-\lambda \mu _p N_1 y cos(2 \Omega \tau ){=}0\\ &{}\ddot{y}+p_2^2 y-\lambda x+\beta {\dot{y}}+\gamma y^3 +\chi \phi \\ &{}\quad -\rho \left( {\bar{\mu }}_s+{\bar{\mu }}_3 \left( v_b-\kappa {\dot{y}}\right) ^3-{\bar{\mu }}_1 \left( v_b-{\dot{y}}\right) \right) \\ &{}-\lambda \mu _p x cos(2 \Omega \tau )+\lambda \mu _p y cos(2 \Omega \tau ) =0, \\ &{}{\dot{\phi }} + \Theta \phi -\chi \Lambda \dot{y} = 0, \end{array}\right. } \end{aligned}$$

(12)

where $p_1^2=(1+\lambda N_1)$, $p_2^2=(1+ \lambda )$, $\eta =\kappa =1$. The initial conditions are

$$\begin{aligned}{} & {} x(0) = x_0, \ {\dot{x}}(0)=v_{x0}, \ y(0) = y_0, \ {\dot{y}}(0)=v_{y0},\nonumber \\{} & {} \ \phi (0) = \phi _0. \end{aligned}$$

(13)

The analytical solution is sought using the multiple scales method in the time domain (MSM). Awrejcewicz et al. [35] established the computational sequence of this method herein adopted. We introduce a book-keeping parameter $\varepsilon$, and use two-time scales on the dimensionless time $\tau$. The time-scales $\tau _0$, $\tau _1$ are related as

$$\begin{aligned} \tau _{r} =\varepsilon ^r\tau ,\ \ \ \ r=0,1 . \end{aligned}$$

(14)

Then, the solutions and auxiliary functions are approximated by the following asymptotic expansions

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}x(\tau ;\varepsilon )=\sum _{k=1}^{2}{\varepsilon ^k\xi _{k}(\tau _0,\ \tau _1)+O(\varepsilon ^3)}\\ &{}y(\tau ;\varepsilon )=\sum _{k=1}^{2}{\varepsilon ^k\varphi _{k}(\tau _0,\ \tau _1)+O(\varepsilon ^3)} \\ &{}\phi (\tau ;\varepsilon )=\sum _{k=1}^{2}{\varepsilon ^k\Phi _{k}(\tau _0,\ \tau _1)+O(\varepsilon ^3)} , \end{array}\right. } \end{aligned}$$

(15)

where the function $\xi _{k}(\tau _0,\ \tau _1)$, $\varphi _{k}(\tau _0,\ \tau _1)$ and $\Phi _{k}(\tau _0,\ \tau _1)$ are to be found. Those of order $O(\varepsilon ^3)$ and above are neglected. The differential operators relating to the non–dimensional time $\tau$ , and assumptions on the system’s parameters for non–resonant solutions are as follows.

$$\begin{aligned} \frac{d}{d\tau }= & {} D_0+\varepsilon D_1+\ldots ,\ \frac{d^2}{d\tau ^2}\nonumber \\= & {} D_0^2+2\varepsilon D_0D_1+\varepsilon ^2 D_1^2+\ldots ,\ D_r^j=\frac{\partial ^j}{\partial \tau _r^j}\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} &{}\alpha =\varepsilon \tilde{\alpha },\ \ \beta =\varepsilon \tilde{\beta },\ \ \lambda =\varepsilon \tilde{\lambda },\ \ \eta =\varepsilon ^{-2}\tilde{\eta }, \\ &{} \kappa =\varepsilon ^{-1}\tilde{\kappa },\ \ \gamma =\varepsilon ^{-1}\tilde{\gamma }, \\ &{}\Lambda =\varepsilon ^{-1}\tilde{\Lambda },\ \ \chi =\varepsilon \tilde{\chi },\ \ \rho =\varepsilon ^2\tilde{\rho }, \end{array}\right. } \end{aligned}$$

(17)

where $\tilde{\alpha }$, $\tilde{\beta }$, $\tilde{\lambda }$, $\tilde{\eta }$, $\tilde{\kappa }$, $\tilde{\gamma }$, $\tilde{\Lambda }$, $\tilde{\chi }$ and $\tilde{\rho }$ are of the order 1.

3.1 Non-resonant solution

Substituting the relations (17) into the modified Eqs. (12), and considering the asymptotic expansions (15), the time scaling (14) and the time derivatives (16), the following expressions are yielded according to the ordered powers of $\varepsilon$.

For order ”1” :

$$\begin{aligned}&D_0^2\xi _1+p_1^2\xi _1 =\ 0 \end{aligned}$$

(18)

$$\begin{aligned}&D_0^2\varphi _1+p_2^2\varphi _1 =\ 0 \end{aligned}$$

(19)

$$\begin{aligned}&D_0\Phi _1+\Theta \Phi _1-\tilde{\Lambda } \tilde{\chi }D_0\varphi _1 =\ 0 \end{aligned}$$

(20)

For order ”2”:

$$\begin{aligned}&D_0^2\xi _2+p_1^2\xi _2 = -\xi _1 N_1 \tilde{\lambda } \mu _p \cos \left( 2 \Omega \tau _0\right) \nonumber \\&+N_1 \varphi _1 \tilde{\lambda } \mu _p \cos \left( 2 \Omega \tau _0\right) -&\nonumber \\&D_0 \xi _1^3\tilde{\alpha } \tilde{\eta }+D_0 \xi _1 \tilde{\alpha }&\nonumber \\&+N_1 \varphi _1 \tilde{\lambda }-2 D_0 D_1 \xi _1 \end{aligned}$$

(21)

$$\begin{aligned}&D_0^2\varphi _2+p_2^2\varphi _2 = \nonumber \\&-3 D_0 \varphi _1 \bar{\mu }_3 \tilde{\kappa } \tilde{\rho } v_b^2\nonumber \\&+3 D_0^2 \varphi _1^2 \bar{\mu }_3 \tilde{\kappa }^2 \tilde{\rho } v_b+\bar{\mu }_3 \tilde{\rho } v_b^3-\bar{\mu }_1 \tilde{\rho } v_b-&\nonumber \\&D_0^3 \varphi _1^3 \bar{\mu }_3 \tilde{\kappa }^3 \tilde{\rho }+\tilde{\rho } \bar{\mu }_s+\xi _1 \tilde{\lambda } \mu _p \cos \left( 2 \Omega \tau _0\right) \nonumber \\&-\varphi _1 \tilde{\lambda } \mu _p \cos \left( 2 \Omega \tau _0\right) -\varphi _1^3 \tilde{\gamma }-&\nonumber \\&D_0 \varphi _1 \tilde{\beta }+\xi _1 \tilde{\lambda }\nonumber \\&-\Phi _1 \tilde{\chi }-2 D_0 D_1 \varphi _1 \end{aligned}$$

(22)

$$\begin{aligned}&D_0\Phi _2+\Theta \Phi _2-\tilde{\Lambda } \tilde{\chi }D_0\varphi _2 = D_1 \varphi _1 \tilde{\Lambda } \tilde{\chi }\nonumber \\&+D_0 \varphi _2 \tilde{\Lambda } \tilde{\chi }-D_1 \Phi _1 \end{aligned}$$

(23)

The solutions to Eqs. (18)–(20) are

$$\begin{aligned} \xi _1(\tau _0,\tau _1)=&B_1\left( \tau _1\right) e^{i p_1 \tau _0} + \tilde{B_1}\left( \tau _1\right) e^{-i p_1 \tau _0} \end{aligned}$$

(24)

$$\begin{aligned} \varphi _1(\tau _0,\tau _1)=&B_2\left( \tau _1\right) e^{i p_2 \tau _0} + \tilde{B_2}\left( \tau _1\right) e^{-i p_2 \tau _0}, \end{aligned}$$

(25)

$$\begin{aligned} \Phi _1(\tau _0,\tau _1)=&\frac{p_2 \tilde{\Lambda } \tilde{\chi } B_2\left( \tau _1\right) e^{i p_2 \tau _0}}{p_2-i\Theta }\nonumber \\&+ \frac{p_2 \tilde{\Lambda } \tilde{\chi } \tilde{B_2}\left( \tau _1\right) e^{-i p_2 \tau _0}}{p_2+ i \Theta }, \end{aligned}$$

(26)

where $B_j\left( \tau _1\right) (j=1,2)$ are unknown functions of slow time scale, and $\tilde{B_j}\left( \tau _1\right)$ are their complex conjugates. Substituting (24)–(26) into (21)–(23) leads to the emergence of secular terms. Eliminating the secular terms provides the following solvability conditions and their conjugate reflectors.

$$\begin{aligned}{} & {} -i B_1^2 p_1 \tilde{\alpha } {\tilde{B}}_1 \tilde{\eta }\nonumber \\{} & {} +i B_1 p_1 \tilde{\alpha }-2 i p_1 D_1 B_1 = 0 \end{aligned}$$

(27)

$$\begin{aligned}{} & {} -3 i B_2 p_2 \bar{\mu }_3 \tilde{\kappa } \tilde{\rho } v_b^2-3 i B_2^2 p_2^3 \bar{\mu }_3 {\tilde{B}}_2 \tilde{\kappa }^3 \tilde{\rho }\nonumber \\{} & {} -3 B_2^2 {\tilde{B}}_2 \tilde{\gamma }-i B_2 p_2 \tilde{\beta }- \nonumber \\{} & {} \frac{B_2 p_2 \tilde{\Lambda } \tilde{\chi }^2}{p_2-i \Theta }-2 i p_2 D_1 B_2 = 0 \end{aligned}$$

(28)

Removing the secular terms after substituting (24)–(26) into (21)–(23), one obtains

$$\begin{aligned}&\xi _2(\tau _0,\tau _1)\nonumber \\&\quad =\frac{B_1 N_1 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega +p_1\right) }}{8 \Omega \left( \Omega +p_1\right) }\nonumber \\&\qquad +\frac{B_2 N_1 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega +p_2\right) }}{2 \left( -2 \Omega +p_1-p_2\right) \left( 2\Omega +p_1+p_2\right) }&\nonumber \\&\qquad +\frac{N_1 {\tilde{B}}_1 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2\Omega -p_1\right) }}{8 \Omega \left( \Omega -p_1\right) }\nonumber \\&\qquad +\frac{N_1 {\tilde{B}}_2 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega -p_2\right) }}{2 \left( 2 \Omega +p_1-p_2\right) \left( -2 \Omega +p_1+p_2\right) }&\nonumber \\&\qquad +\frac{B_2 N_1 \tilde{\lambda } e^{i p_2 \tau _0}}{\left( p_1-p_2\right) \left( p_1+p_2\right) }\nonumber \\&\qquad +\frac{i B_1^3 \tilde{\alpha } \tilde{\eta } e^{3 i p_1 \tau _0}}{8 p_1} + \text {CC}, \end{aligned}$$

(29)

$$\begin{aligned}&\varphi _2(\tau _0,\tau _1)\nonumber \\&\quad = B_2^2 \bar{\mu }_3 \tilde{\kappa }^2 \tilde{\rho } v_b e^{2 i p_2 \tau _0}+6 B_2 \bar{\mu }_3 {\tilde{B}}_2 \tilde{\kappa }^2 \tilde{\rho } v_b\nonumber \\&\qquad -\frac{\bar{\mu }_3 \tilde{\rho } v_b^3+\bar{\mu }_1 \tilde{\rho } v_b+\tilde{\rho } \bar{\mu }_s}{p_2^2}\nonumber \\&\qquad -\frac{e^{3 i p_2 \tau _0} \left( -B_2^3 \tilde{\gamma }+i B_2^3 p_2^3 \bar{\mu }_3 \tilde{\kappa }^3 \tilde{\rho }\right) }{8 p_2^2}\nonumber \\&\qquad +\frac{B_2 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega +p_2\right) }}{8 \Omega \left( \Omega +p_2\right) }\nonumber \\&\qquad -\frac{B_1 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega +p_1\right) }}{2 \left( 2 \Omega +p_1-p_2\right) \left( 2 \Omega +p_1+p_2\right) }\nonumber \\&\qquad -\frac{{\tilde{B}}_1 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega -p_1\right) }}{2 \left( 2 \Omega -p_1-p_2\right) \left( 2 \Omega -p_1+p_2\right) }\nonumber \\&\qquad +\frac{{\tilde{B}}_2 \tilde{\lambda } \mu _p e^{i \tau _0 \left( 2 \Omega -p_2\right) }}{8 \Omega \left( \Omega -p_2\right) }\nonumber \\&\qquad -\frac{B_1 \tilde{\lambda } e^{i p_1 \tau _0}}{\left( p_1-p_2\right) \left( p_1+p_2\right) }+ \text {CC}, \end{aligned}$$

(30)

$$\begin{aligned} \Phi _2(\tau _0,\tau _1)=&\frac{2 B_2^2 p_2 \bar{\mu }_3 \tilde{\kappa }^2 \tilde{\Lambda } \tilde{\rho } \tilde{\chi } v_b e^{2 i p_2 \tau _0}}{2 p_2-i \Theta }-\frac{i e^{3 i p_2 \tau _0} \left( \frac{3}{8} B_2^3 p_2^2 \bar{\mu }_3\tilde{\kappa }^3 \tilde{\Lambda } \tilde{\rho } \tilde{\chi }+\frac{3 i B_2^3 \tilde{\gamma } \tilde{\Lambda } \tilde{\chi }}{8 p_2}\right) }{3 p_2-i \Theta }\nonumber \\&-\frac{i e^{i \tau _0 \left( 2 \Omega +p_1\right) } \left( -\frac{i \Omega B_1 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{4 \Omega ^2+4 \Omega p_1+p_1^2-p_2^2}-\frac{i B_1 p_1 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{2 \left( 4 \Omega ^2+4 \Omega p_1+p_1^2-p_2^2\right) }\right) }{2 \Omega -i \Theta +p_1}\nonumber \\&-\frac{i e^{i \tau _0 \left( 2 \Omega -p_1\right) } \left( \frac{i p_1 {\tilde{B}}_1 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{2 \left( 4 \Omega ^2-4 \Omega p_1+p_1^2-p_2^2\right) }-\frac{i \Omega {\tilde{B}}_1 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{4 \Omega ^2-4 \Omega p_1+p_1^2-p_2^2}\right) }{2 \Omega -i \Theta -p_1}\nonumber \\&-\frac{i e^{i \tau _0 \left( 2 \Omega +p_2\right) } \left( -\frac{i B_2 p_2^2 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{8 \Omega \left( \Omega -p_2\right) \left( \Omega +p_2\right) }-\frac{i B_2 p_2 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{8 \left( \Omega -p_2\right) \left( \Omega +p_2\right) }+\frac{i \Omega B_2 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{4 \left( \Omega -p_2\right) \left( \Omega +p_2\right) }\right) }{2 \Omega -i \Theta +p_2}\nonumber \\&-\frac{i e^{i \tau _0 \left( 2 \Omega -p_2\right) } \left( \frac{i {\tilde{B}}_2 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{4 \left( \Omega -p_2\right) }-\frac{i p_2 {\tilde{B}}_2 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } \mu _p}{8 \Omega \left( \Omega -p_2\right) }\right) }{2 \Omega -i \Theta -p_2} +\frac{B_1 p_1 \tilde{\lambda } \tilde{\Lambda } \tilde{\chi } e^{i p_1 \tau _0}}{\left( p_1^2-p_2^2\right) \left( p_1-i \Theta \right) }+ \text {CC}, \end{aligned}$$

(31)

where CC stands for the complex conjugate terms. The complex functions $B_j$, and $\tilde{B_j}$ are dependent on $\tau _1$, and are found from the solvability conditions (27)–(28) as follows;

$$\begin{aligned} \begin{aligned}&B_i(\tau _1) = \frac{1}{2} b_i(\tau _1) e^{i \psi _i(\tau _1)}, \\&\tilde{B_i}(\tau _1) = \frac{1}{2} b_i(\tau _1) e^{-i \psi _i(\tau _1)}, \ \ i=1,2 \end{aligned} \end{aligned}$$

(32)

where $a_i(\tau _1)$ and $\psi _i(\tau _1)$ are real-valued.

Putting (32) in (27)–(28), separating the imaginary and real parts,

$$\begin{aligned} b_1^\prime =&-\frac{1}{8} b_1 \tilde{\alpha } \left( b_1^2 \tilde{\eta }-4\right) , \end{aligned}$$

(33)

$$\begin{aligned} \psi _1^\prime =&0, \end{aligned}$$

(34)

$$\begin{aligned} b_2^\prime =&\frac{1}{8} b_2 \left( -3 \bar{\mu }_3 \tilde{\kappa } \tilde{\rho } \left( b_2^2 p_2^2 \tilde{\kappa }^2+4 v_b^2\right) \right. \nonumber \\&\left. -4 \tilde{\beta }-\frac{4 \Theta \tilde{\Lambda } \tilde{\chi }^2}{\Theta ^2+p_2^2}\right) , \end{aligned}$$

(35)

$$\begin{aligned} \psi _2^\prime =&\frac{3 b_2^2 \tilde{\gamma }}{8 p_2}+\frac{p_2 \tilde{\Lambda } \tilde{\chi }^2}{2 \left( \Theta ^2+p_2^2\right) } . \end{aligned}$$

(36)

The reconstitution of Eqs. (33)–(36) into the original time scale $\tau$ is carried out using $a_i(\tau )=\varepsilon b_i$, and the reverse assumptions in (17),

$$\begin{aligned}&a_1^\prime = -\frac{1}{8} a_1 {\alpha } \left( a_1^2 {\eta }-4\right) , \end{aligned}$$

(37)

$$\begin{aligned}&\psi _1^\prime = 0, \end{aligned}$$

(38)

$$\begin{aligned}&a_2^\prime = \frac{1}{8} a_2 \left( -3 \bar{\mu }_3 {\kappa } {\rho } \left( a_2^2 p_2^2 {\kappa }^2+4v_b^2\right) \right. \nonumber \\&\left. -4 {\beta }-\frac{4 \Theta {\Lambda } {\chi }^2}{\Theta ^2+p_2^2}\right) , \end{aligned}$$

(39)

$$\begin{aligned}&\psi _2^\prime = \frac{3 a_2^2 {\gamma }}{8 p_2}+\frac{p_2 {\Lambda } {\chi }^2}{2 \left( \Theta ^2+p_2^2\right) }. \end{aligned}$$

(40)

Eqs. (37)–(40) are the modulation equations in time $\tau$, with initial conditions

$$\begin{aligned} a_1(0)=a_{10}, \ a_2(0)=a_{20}, \ \psi _1(0)=\psi _{10}, \ \psi _2(0)=\psi _{20}.\nonumber \\ \end{aligned}$$

(41)

The quantities $a_{10}$, $a_{20}$, $\psi _{10}$, and $\psi _{20}$ are connected with the initial values $x_0$, $v_{v0}$, $y_0$, $v_{y0}$, and $\phi _0$ in (13). However, due to nonlinearity in (37)–(40), the solutions are found using the NDSolve function in Mathematica software. Combining all the solutions from (24)–(25), and (29)–(30) in a reconstituted form, the following analytical solutions are obtained.

$$\begin{aligned} x(\tau ) =&\frac{a_1 \lambda N_1 \mu _p \cos \left( \tau \left( 2 \Omega -p_1\right) -\psi _1\right) }{8 \Omega \left( \Omega -p_1\right) }\nonumber \\&+\frac{a_1 \lambda N_1 \mu _p \cos \left( \tau \left( p_1+2 \Omega \right) +\psi _1\right) }{8 \Omega \left( p_1+\Omega \right) }\nonumber \\&+\frac{a_2 \lambda N_1 \mu _p \cos \left( \tau \left( 2 \Omega -p_2\right) -\psi _2\right) }{2 \left( p_1-p_2+2 \Omega \right) \left( p_1+p_2-2 \Omega \right) }\nonumber \\&-\frac{a_2 \lambda N_1 \mu _p \cos \left( \tau \left( p_2+2 \Omega \right) +\psi _2\right) }{2 \left( -p_1+p_2+2 \Omega \right) \left( p_1+p_2+2 \Omega \right) }\nonumber \\&+\frac{a_2 \lambda N_1 \cos \left( p_2 \tau +\psi _2\right) }{\left( p_1-p_2\right) \left( p_1+p_2\right) }\nonumber \\&-\frac{\alpha a_1^3 \eta \sin \left( 3 \left( p_1 \tau +\psi _1\right) \right) }{32 p_1}\nonumber \\&+a_1 \cos \left( p_1 \tau +\psi _1\right) , \end{aligned}$$

(42)

$$\begin{aligned}&y(\tau )\nonumber \\&= a_2 \cos \left( p_2 \tau +\psi _2\right) +\frac{1}{2} a_2^2 \kappa ^2 \rho \bar{\mu }_3 v_b \cos \left( 2 \left( p_2 \tau +\psi _2\right) \right) \nonumber \\&\quad +\frac{3}{2} a_2^2 \kappa ^2 \rho \bar{\mu }_3 v_b\nonumber \\&\quad +\frac{a_2^3 \left( \kappa ^3 p_2^3 \rho \bar{\mu }_3 \sin \left( 3 \left( p_2 \tau {+}\psi _2\right) \right) {+}\gamma \cos \left( 3 \left( p_2\tau {+}\psi _2\right) \right) \right) }{32 p_2^2}\nonumber \\&\quad -\frac{\rho \left( \bar{\mu }_3 v_b^3+\bar{\mu }_1 v_b+\bar{\mu }_s\right) }{p_2^2}&\nonumber \\&\quad +\frac{a_2 \lambda \mu _p \cos \left( \tau \left( 2 \Omega -p_2\right) -\psi _2\right) }{8 \Omega \left( \Omega -p_2\right) }\nonumber \\&\quad +\frac{a_2 \lambda \mu _p \cos \left( \tau \left( p_2+2 \Omega \right) +\psi _2\right) }{8 \Omega \left( p_2+\Omega \right) }\nonumber \\&\quad -\frac{a_1 \lambda \cos \left( p_1 \tau +\psi _1\right) }{\left( p_1-p_2\right) \left( p_1+p_2\right) }\nonumber \\&\quad -\frac{a_1 \lambda \mu _p \cos \left( \tau \left( 2 \Omega -p_1\right) -\psi _1\right) }{2 \left( -p_1-p_2+2 \Omega \right) \left( -p_1+p_2+2 \Omega \right) }\nonumber \\&\quad -\frac{a_1 \lambda \mu _p \cos \left( \tau \left( p_1+2 \Omega \right) +\psi _1\right) }{2 \left( p_1-p_2+2 \Omega \right) \left( p_1+p_2+2 \Omega \right) }, \end{aligned}$$

(43)

$$\begin{aligned} \phi (\tau ) =&\frac{a_2^2 \kappa ^2 \Lambda p_2 \rho \chi \bar{\mu }_3 v_b \left( 2 p_2 \cos \left( 2 \left( p_2 \tau +\psi _2\right) \right) -\Theta \sin \left( 2 \left( p_2 \tau +\psi _2\right) \right) \right) }{\Theta ^2+4 p_2^2}\nonumber \\&+\frac{3 a_2^3 \Lambda \chi \left( \kappa ^3 p_2^3 \rho \bar{\mu }_3 \left( \Theta cn(\tau )+3 p_2 sn(\tau )\right) +\gamma \left( 3 p_2 cn(\tau )-\Theta sn(\tau )\right) \right) }{32 p_2 \left( \Theta ^2+9 p_2^2\right) }\nonumber \\&+\frac{a_2 R_3 \left( \left( p_2+2\Omega \right) \cos \left( \tau \left( p_2+2 \Omega \right) +\psi _2\right) -\Theta \sin \left( \tau \left( p_2+2 \Omega \right) +\psi _2\right) \right) }{8 \Omega \left( p_2+\Omega \right) \left( \Theta ^2+4 p_2 \Omega +p_2^2+4 \Omega ^2\right) }\nonumber \\&+\frac{a_2 R_4 \left( \left( 2 \Omega -p_2\right) \cos \left( \tau \left( 2 \Omega -p_2\right) -\psi _2\right) -\Theta \sin \left( \tau \left( 2 \Omega -p_2\right) -\psi _2\right) \right) }{8 \Omega \left( \Omega -p_2\right) \left( \Theta ^2-4 p_2 \Omega +p_2^2+4 \Omega ^2\right) }\nonumber \\&-\frac{a_1 R_2 \left( \left( 2 \Omega -p_1\right) \cos \left( \tau \left( 2 \Omega -p_1\right) -\psi _1\right) -\Theta \sin \left( \tau \left( 2 \Omega -p_1\right) -\psi _1\right) \right) }{2 \left( -4 p_1 \Omega +p_1^2-p_2^2+4 \Omega ^2\right) \left( \Theta ^2-4 p_1 \Omega +p_1^2+4 \Omega ^2\right) }\nonumber \\&-\frac{a_1 R_1 \left( \left( p_1+2 \Omega \right) \cos \left( \tau \left( p_1+2 \Omega \right) +\psi _1\right) -\Theta \sin \left( \tau \left( p_1+2 \Omega \right) +\psi _1\right) \right) }{2 \left( 4 p_1 \Omega +p_1^2-p_2^2+4\Omega ^2\right) \left( \Theta ^2+4 p_1 \Omega +p_1^2+4 \Omega ^2\right) }\nonumber \\&+\frac{a_1 \lambda \Lambda p_1 \chi \left( \Theta \sin \left( p_1 \tau +\psi _1\right) -p_1 \cos \left( p_1 \tau +\psi _1\right) \right) }{\left( p_1^2-p_2^2\right) \left( \Theta ^2+p_1^2\right) }\nonumber \\&+\frac{a_2 \Lambda p_2 \chi \left( p_2 \cos \left( p_2 \tau +\psi _2\right) -\Theta \sin \left( p_2 \tau +\psi _2\right) \right) }{\Theta ^2+p_2^2}, \end{aligned}$$

(44)

where

$$\begin{aligned} \begin{aligned}&cn(\tau ) = \cos \left( 3 \left( p_2 \tau +\psi _2\right) \right) ,\\&sn(\tau ) = \sin \left( 3 \left( p_2 \tau +\psi _2\right) \right) ,\\&R_1 = \lambda \Lambda \chi \mu _p \left( p_1+2 \Omega \right) , R_2= \lambda \Lambda \chi \mu _p \left( 2 \Omega - p_1 \right) , \\&R_3 = \lambda \Lambda \chi \mu _p \left( p_2+2 \Omega \right) , \ R_4 {=} \lambda \Lambda \chi \mu _p \left( 2 \Omega - p_2 \right) . \end{aligned} \end{aligned}$$

The time–dependent functions $a_j(\tau )$ and $\psi _j(\tau )$ are the amplitudes and phases of the modulation equations (37)–(40).

Fig. 4

Compared time histories of x-coordinate

Fig. 5

Compared time histories of y-coordinate

Fig. 6

Compared time histories of voltage ($\phi$-coordinate) and the RMS power

Using the following set of fixed parameters: $\eta =1$, $\kappa =1$, $\alpha =0.06$, $\beta = 0.03$, $\gamma =0.01$, $\lambda =0.179$, $\mu _p=0.12$, $N_1=-0.209$, $p_1=1.001$, $p_2 =1.4$, $\chi = 0.000002$, $\Lambda =5000000$, $\Theta =0.000003$, $\rho =1$, $\Omega =2.095$, $v_b =0.06$, $\mu _s =0.001$, ${\tilde{\mu }}_1 =0.02232$, ${\tilde{\mu }}_3 = 1.1191$, and the initial values: $a_{10} = -0.04$, $a_{20} = 0.0$, $\psi _{10} = 0.0$, $\psi _{20} = 0.0$, the initial conditions for the numerical simulation were estimated from (42)–(44) as $x_0 = -0.0399867$, $v_{x0} = -0.00119876$, $y_0 =-0.0087211$, $v_{y0} = -0.00022204$, $\phi _0=-0.074043$. Figures 4 and 5 compare the short-time and long-time histories for x and y, respectively, obtained by the analytical (MSM) with the corresponding numerical solutions. There is a high degree of compliance between the solutions methods. Though other sets of initial values could be used, the choice of the value of $a_{10}$, which represents the initial displacement of the mass, is crucial for the parametrically coupled oscillators to have immediate influences on each other. However, this value and those of the system parameters are assumed to be small in order to minimize computational errors.

On the harvested energy, Fig. 6 is added to show the generated dimensionless voltage time–histories (Fig. 6a) and the dimensional instantaneous root mean square (RMS) power (Fig. 6b), computed based on metrics established in Sect. 4. The results are also well-matched between the analytical and numerical solutions. The RMS power increases at the instance of time until the steady state, where it is fairly held constant. Additionally, the following resonances are identified from Eqs. (42)–(44) where the terms with negative operands in the denominators are equated to zero.

• (i) Primary parametric resonances at $\Omega \approx p_1$, $\Omega \approx p_2$;

• (ii) Combined parametric resonances at $\Omega \approx \frac{1}{2} (-p_1 + p_2)$, $\Omega \approx \frac{1}{2} (p_1 - p_2)$, $\Omega \approx \frac{1}{2} (p_1 + p_2)$;

• (iii) Internal resonance at $p_1 \approx p_2$.

Fig. 7

Frequency response of the system with identified parametric resonances

Table 1 Compliance errors

Figure 7 presents the frequency response of the y solution showing some identified primary and combined parametric resonance $w_{rj}, j=1, 2,\ldots ,5$. These resonant points were identified based on the fixed data set used. The greatest (combined) parametric resonance occurs at $w_{r4} \approx \frac{1}{2} (p_1 + p_2)$. It is closely guided by the primary resonance and its harmonic at $w_{r5}=p_2$ and $w_{r3}=\frac{1}{2}p_2$.

The approximate solutions presented here are valid only for the non-resonant case. At resonance, some modifications must be made to accommodate the resonance-causing terms, which are outside the aim of the present study. Furthermore, the computations are based on small identified parameter values to minimize errors. The assumptions in (14)–(17) truncate the asymptotic expansion of the assumed solution. However, they ensure that all the terms in the governing equations are captured in solution procedures. It implies that the compliance errors are only limited to the truncation of asymptotic solutions by two-time scales.

3.2 Compliance error

Compliance error is the difference between the analytical solution and the numerical solution computed based on two well-known metrics: the root mean square error (RMSE) and the mean absolute error (MAE) according to the following equations [36], where RMSE measures the robustness of the method, and MAE indicates the estimation accuracy of the analytical process.

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}RMSE = \sqrt{\frac{\sum _{j=1}^{N}E_j^2}{N}},\\ &{}MAE = \frac{\sum _{j=1}^{N}|E_j|}{N}, \end{array}\right. } \end{aligned}$$

(45)

where E is the difference between the numerical and approximate analytical solutions, evaluated at time interval j to N. For ease of calculation, N is fixed at 1010. Table 1 shows the compliance errors of the computations. The errors are of the order of $10^-5/10^-6$, which portends the solutions’ robustness and accuracy.

4 Numerical treatment

The Filippov rendition of the system in section 2.3 also allows one to obtain a smooth approximation of the surface of discontinuity in state-space by applying Eq. (11). This way, the system’s global dynamics can be investigated via the bifurcation analysis. The effects of these dynamics on harvested energy can also be numerically examined. The non-dimensional RMS voltage is computed by

$$\begin{aligned} V_{rms}= \sqrt{\frac{1}{n}\Sigma _j^n\phi _j^2}, \ j=1, 2, 3, ... n; \end{aligned}$$

(46)

and n is the approximate period (or its multiple) of the generated non–dimensional voltage $\phi$. The dimensional value of RMS voltage is, however, ${\tilde{V}}_{rms} = \vartheta _0 V_{rms}$. The value of $\vartheta _0$ can be found using the expression given in Sect. 2.2 as $\vartheta _0 = \frac{m_p g}{\Omega R_p C_p} = 4.314 mV$, adopted from our previous work [32]. The dimensional RMS power can also be computed from

$$\begin{aligned} {\tilde{P}}_{rms}=\frac{\vartheta _0 V_{rms}^2}{R_L}, \end{aligned}$$

(47)

where the value of load resistance is taken as $R_L = 10 k\Omega$ for calculation purposes. Other parameters are $\alpha =0.3$, $\beta = 0.03$, $\gamma =0.1$, $\lambda =0.2213$, $\mu _p=0.12$, $N_1=0.98$, $\chi = 0.0002$, $\Lambda =500000$, $\Theta =0.0003$, $\rho =1$, $\Omega =2.095$, $v_b =0.1$, $\mu _s =0.9$, except where it is explicitly stated. Additionally, the following relations hold for ${\bar{\mu }}_1$ and ${\bar{\mu }}_3$;

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}{\bar{\mu }}_1=\frac{3}{2}\frac{\mu _s-\mu _m}{v_m}, \\ &{}{\bar{\mu }}_3=\frac{1}{2}\frac{\mu _s-\mu _m}{v_m^3}, \end{array}\right. } \end{aligned}$$

(48)

where $v_m=f(v_b)$ and $\mu _m=f(\mu _s)$.

4.1 Bifurcation analysis

One of the critical components affecting the behavioral stability of the system is the belt speed $v_b$.

Fig. 8

Coexisting bifurcation diagram with $v_b$ as the control parameter. The blue curve corresponds to forward sweep, while the red corresponds to backward sweep. (Color figure online)

Fig. 9

Phase portraits with Poincaré sections showing the transition for the NS—bifurcation in (a) and NS-BMT in (b), both with reference to Fig. 8

It is responsible for injecting a variant form of energy into the structural dynamics as friction-induced self-excitation. Using this variable as the control parameter, a coexisting bifurcation diagram is constructed in Fig. 8. The blue curve is obtained during the forward sweep, while the red (underlaid) is obtained during the backward sweep, both on the hyperplane $x-y$. Three types of bifurcations are notable: the Neimark–Sacker (NS), Neimark–Sacker bifurcation to multiple tori (NS-BMT), and grazing–sliding (GS) bifurcation.

Figure 9a shows the transition for the NS bifurcation occurring at $v_b=[0.166, 0.177, 0.179]$ in which the limit cycle (inset) on the left-hand side (LHS)changes shape to one in the middle and is finally destroyed, giving birth to an entirely new attractor (inset) on the right-hand side (RHS). In Fig. 9b, the NS-BMT is one that gives birth to n-torus via NS bifurcation [37], and is demonstrated at $v_b=[0.466, 0.478]$ in which a single torus formed by the Poincaré section on the LHS bifurcates into 3-torus demonstrated by the inset of the attractor’s Poincaré on the RHS.

Finally, the GS bifurcation happens at $v_b=0.607$ as shown in Fig. 11a (middle). At $v_b=0.603$, the system is still characterized by stick-slip motion as seen on the LHS. But at grazing–sliding bifurcation (middle), the system’s speed $\dot{y}$ grazes the touchline belt speed $v_b$ before sliding back into motion. The attractor on the RHS shows clearly when the system is in pure slip motion as $\dot{y} < v_b$. The second principal influencer of the induced excitation is the coefficient of static friction $\mu _s$. This is critical because, over time, the belt surface loses some roughness and affects the stick-slip motion of the mass. Fig. 10 shows the coexisting bifurcation diagram of the system, with $\mu _s$ as the control parameter. Discontinuity-induced bifurcation of torus (DIB-T) and NS-BMT are identified at $\mu _s \approx 0.6630$, and $\mu _s \approx 0.7431$, or $\mu _s \approx 0.8276$, respectively. The DIB-T [38] is examined in Fig. 11b, where the limit cycle in Fig. 11b (i) is destroyed via the transition in Fig. 11b (ii) to give birth to the torus of the Poincaré section in Fig. 11b (iii) as the system’s speed $\dot{y}$ grazes the belt speed $v_b$ held constant at $v_b=0.45$. These dynamics have effects on energy harvesting, which are further investigated in the next subsection.

4.2 Effect of behavioral dynamics on energy

On the effects of qualitative changes occurring within the structural dynamics on energy harvesting, the bifurcation diagram of the system is constructed and plotted alongside the harvested energy to highlight the energy’s responses to certain types of bifurcation. The metric used for measuring energy harvesting is the root mean square voltage $V_{rms}$ according to Eq. (46).

Fig. 10

Coexisting bifurcation diagram with $\mu _s$ as the control parameter. The blue curve corresponds to forward sweep, while the red corresponds to backward sweep. (Color figure online)

Fig. 11

Phase portraits with Poincaré sections showing the transition for the GS–bifurcation in (a) and DIB-T in (b), with reference to Figs. 8 and 10, respectively

Fig. 12

Voltage generated ($V_{rms}$) in log scale (blue) and the bifurcation diagram (red), with $v_b$ as the control parameter of the system without coupling. (Color figure online)

We begin by examining the system without coupling the electrical subcircuit of the van der Pol oscillator. In this case, only the simple mechanical substructure is present as a 1 DoF system, and the governing equations in Eq. (9) reduce to

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\ddot{y}+\beta {\dot{y}}+y+\gamma y^3 + \chi \phi - \rho \mu ({\bar{v}}_r) +\lambda y =0,\\ &{}{\dot{\phi }} + \Theta \phi -\chi \Lambda \dot{y} = 0. \end{array}\right. }\nonumber \\ \end{aligned}$$

(49)

Using $v_b$ as the control parameter, Fig. 12 is constructed, showing the bifurcation diagram in red (axis on the right) overlaid with the generated voltage in blue (axis on the left). It can be seen that the harvested energy ($V_{rms}$) is characteristically low (i.e., $V_{rms}<1$) all through the system’s dynamics. The highest voltage is recorded at the GS bifurcation ($v_b \approx 0.6$) where $V_{rms} \approx 0.6$, after which the voltage falls to $V_{rms} = 0.53$ for $v_b \ge 0.64$. In comparison with the originally proposed design having the parametric coupling with the van der Pol oscillator whose dynamic model is given by Eq. (9), and using the same system parameters, Fig. 13a is constructed, with $v_b$ as the bifurcation parameter. It can be seen that the energy harvested in this case is much higher (i.e., $V_{rms} > 100$ for all $v_b>0.076$). Furthermore, this figure shows two kinds of bifurcation with significant changes in the level of harvested energy. First, the $V_{rms}$ increases exponentially from near zero value until it reaches $V_{rms}=207.4$ just before the NS bifurcation point ($v_b \approx 0.177$). At this point, $V_{rms}$ jumps to a lower level ($V_{rms} \approx 156$) before increasing further at a slow pace. The steady increase, though small, terminates at NS–BMT, after which a fairly steady and stable energy is harvested. At GS bifurcation ($v_b \in [0.603,0.611]$), another jump to a lower energy level ($V_{rms} \approx 149.7$) was recorded. After GS bifurcation, the system enters a pure slip motion, and this steady generated voltage level is maintained. Hence, the proposed model not only overcomes the limitation of low energy generation associated with the simple 1 DoF system but also generates higher (useful) energy over a wide range of belt speeds.

With $\mu _s$ as the bifurcation parameter, the harvested energy is fairly constant at $V_{rams} \approx 150$ until DIB-T as shown in Fig. 13b.

At DIB-T, there is a jump in harvested energy to a higher level. However, the new energy level is hard to maintain at a steady pace due to the underlying system’s dynamics for $\mu _s>0.731$. At NS–BMT, a further jump in $V_{rms}$ to a higher level is seen. However, the voltage is not smooth at this level but increases gradually for $\mu _s>0.852$.

Fig. 13

Voltage generated ($V_{rms}$) in log scale (blue) and the bifurcation diagram (red), with $v_b$ as the control parameter in a, and $\mu _s$ as the control parameter in b

Fig. 14

Voltage generated ($V_{rms}$) in log scale (blue) and the bifurcation diagram (red), with $\mu _p$ as the control parameter in a, and $\lambda$ as the control parameter in b. (Color figure online)

Examining the system’s dynamics and the energy harvested with respect to the variation of the internal parametric coupling strength $\mu _p$, Fig. 14a is constructed using $\mu _p$ as the control parameter. It can be seen from this figure that $\mu _p$ did not cause a distinctive bifurcation phenomenon, but one can identify the region of soft, intermediate, and hard coupling. In the soft coupling $\mu _p<0.1$, the energy $V_{rms}$ is mildly rough in the neighborhood of $V_{rms} \approx 131$. In the intermediate region $\mu _p \in [0.1,1.12)$, the degree of roughness in $V_{rms} \approx 132.5$ increases. Hard coupling at $\mu _p \ge 1.12$ shows a decline in the energy harvested.

For the external coupling strength $\lambda$, the system experienced rich dynamics. Fig. 14b shows the constructed bifurcation diagram with $\lambda$ as the control parameter. The energy $V_{rms}$ increases steadily until it approaches the neighborhood of NS bifurcation ($\lambda \approx 0.2231$). At NS bifurcation point, $V_{rms}$ jumps from about 160 to 220, and remains steady at this level until another behavioral change occurs at $\lambda \ge 0.4642$. Furthermore, a parametric study was conducted under the soft, intermediate, and hard internal parametric coupling to examine the harvested energy, and presented in Fig. 15.

Fixing the values of $\mu _p=0.05$, $\mu _p=0.12$, and $\mu _p=1.12$, respectively for the soft, intermediate, and hard coupling, Fig. 15a shows the $V_{rms}$ under these conditions with varying $v_b$. From this figure, the effect is slightly desirable under the soft and intermediate couplings. With $\mu _s$ as the varying parameter (Fig. 15b), the jumps to higher voltage levels under soft and intermediate couplings are desirable as they generate more energy. Finally, in the case of $\lambda$ as the varying parameter (Fig. 15c), the generated voltages under these conditions are quantified as follows. For $\lambda <0.2$, the highest energy is harvested at about $\tilde{V}_{rms}=726.9$ mV corresponding to dimensional RMS power $\tilde{P}_{rms}=12.25$ mW under soft and intermediate couplings. In the region $\lambda \in [0.2, 0.4]$, energy harvested under intermediate coupling is the highest, with ${{\tilde{P}}}_{rms}=20.86$ mW. However, for $\lambda > 0.4$, the hard coupling produced the highest energy with ${{\tilde{P}}}_{rms}=31.25$ mW.

Fig. 15

Voltage generated ($V_{rms}$) at soft, intermediate, and hard internal parametric coupling (strength with $\mu _p$), while varying $v_b$ in (a), $\mu _s$ in (b), $\lambda$ in (c)

Fig. 16

Experimental setup with whole system (a) and enlarged portion (b). 1—valve, 2—motor driver, 3—unbalanced rotor, 4—aerostatic bearing, 5—body frame with mass, 6—spring, 7—belt support and drive, 8—support frame, 9—NI DAQ, 10—motor driver 2, 11—Signal generators (1 and 2), 12—computer with LabVIEW

5 Experimental setup

An experiment is performed to qualitatively verify the model in this section. The experimental stand in Fig. 16 is a multipurpose rig configured to accommodate the major features of the conceptual framework in Fig. 1 without the energy harvester. In Fig. 16, the air preparation module (valve with gauge and filter) labeled 1 uses the air at set pressure from the compressor and controls the aerostatic bearing 4, to give the body frame with masses 3 and 5 a frictionless swing on the attached handle. The body frame is attached to springs 6 on both sides.

The mass 3 is a rotor, providing unbalanced rotation on the body frame, and it is controlled by the first stepper motor driver 2, which takes input from computer 12 running the real-time electrical subcircuit simulation diagram in LabVIEW. The speed of the belt 7 is controlled by the second motor driver 10, which also takes input from the second signal generator 11.

A PC–based National Instrument Data Acquisition (NI DAQ) module 9 is connected to the computer system 12, with LabVIEW software to capture the dynamic responses which are saved to Excel spreadsheet. It should be noted that label 8 provides the support for the mechanical part while label 3 provides the unbalanced rotation that incorporates the parametric coupling. This setup is without the energy harvesting component, which reduces complexities in the implementation.

When valve 1 is turned ON, and the speed of the belt 7 is set, the speed of the unbalanced mass 3 is provided from the van der Pol electrical subcircuit drawn in LabVIEW running on the computer 12. The frame with the masses 3 and 5 as one lumped mass experiences displacement, and it is captured by the computer system 12 via module 9. This way, the setup is used to qualitatively compare the results of the numerical simulations with the experimental results after minor preprocessing to remove dead zones and timing alignments. Figure 17 shows the sampled current generated by the van der Pol electrical subcircuit in LabVIEW as the driving signal for the unbalanced rotor 3, and the corresponding pulse width modulation (PWM) voltage signal from the first signal generator. This ensures that the speed of the rotor is not constant but varies based on the current generated from the electrical subcircuit.

Fig. 17

Driving current from the van der Pol electrical subcircuit and associated PWM signal for driving the unbalanced rotor at slow-fast speed from the experiment

Fig. 18

Quasiperiodic phase portrait of numerical (a) $v=0.045$, $\mu _s=0.517$ and experimental (b) $v_0=0.007$ m/s; during stick-slip phenomenon

Fig. 19

Phase portrait of numerical a $v=0.485$, $\mu _s=0.65$ and experimental b $v_0=0.147$ m/s; near the grazing–sliding phenomenon

Fig. 20

Phase portrait of numerical a $v=0.56$, $\mu _s=0.85$ and experimental b $v_0=0.15$ m/s; during pure-slip motion

Figures 18, 19 and 20 compare the results of the numerical simulations (a) and the experimental verifications (b) of the system under three scenarios, in which the experimental results were scaled to their respective non–dimensional values using the relations established in Sect. 2.2. In Fig. 18, the system is entirely in the stick-slip quasiperiodic motion; the phase portraits show this phenomenon in both the numerical (a) and experimental (b) results when the belt’s speed is kept at $v_0=0.007$ m/s. Increasing the belt’s peed to $v_0=0.147$ m/s brought the system close to the grazing–sliding in Fig. 19. It should be noted that due to the high sensitivity of the system to the belt’s speed and other assumptions and nonlinear effects present in the experimental setup, the exact grazing speed was hard to find. This is shown when the speed was increased to $v_0=0.15$ m/s, the system entered into pure-slip motion with two quasiperiodic orbits (I) and (II) respectively in Fig. 20 for both numerical (a) and experimental (b) results. All the parameter values are fixed as previously, except for those indicated in the figure captions. The experiment results verified the model qualitatively. However, some results are not the exact match due to the following assumptions and limitations:

• (i) The two linear springs estimate the nonlinear spring in the setup,

• (ii) The coefficient of static friction $\mu _s$ on the belt’s surface reduces from the actual value due to long usage.

6 Concluding remarks

The governing equations for the dynamics of the parametrically coupled electromechanical structure were established. The system was solved analytically using the multiple scales method and validated by numerical simulation. The analytical treatment reveals the various parametric resonances captured in the frequency response of the system. The global dynamics of the structure were investigated, and nonlinear behaviors such as Neimark–Sacker (NS) bifurcation, NS-bifurcation to multiple tori, grazing–sliding bifurcation, and discontinuity-induced bifurcation of torus were identified. The effects of these qualitative changes on harvested energy were also investigated. At these bifurcation points, there are changes in the level of harvested energy in the form of jumps. At the NS bifurcation point, the harvested energy jumps to a higher level, while at grazing–sliding, it decreases to a lower level. The effects of parametric couplings were also examined. The greatest energy was harvested under the hard coupling with a quantified RMS power of 31.25 mW. The investigated model overcomes the limitations of low energy harvesting associated with the simple uncoupled system of the same kind. Finally, the experimental verification of the model was carried out to qualitatively validate the numerical methods.