On $\frac{1}{2}$-DOF active dampers to suppress multistability vibration of a $2$-DOF rotor model subjected to simultaneous multiparametric and external harmonic excitations

Abstract

This article addresses the bifurcation characteristics and vibration reduction of a $2$-DOF dynamical system simulating the nonlinear oscillation of an asymmetric rotor model subjected to simultaneous multiparametric and external excitations. To suppress the system's vibrations, two $1/2$-DOF active dampers are attached to the system in linear and cubic nonlinear forms via a magnetic coupling actuator. The closed-loop system model is derived as two differential equations with multi-control terms, including cubic, quantic, and septic, coupled nonlinearly to two first-order systems. Applying perturbation theory, the system model is solved, and the autonomous system describing the closed-loop slow-flow dynamics is obtained. Through numerical algorithms, the motion bifurcation is analyzed using various tools such as 2D and 3D bifurcation diagrams, two-parameter stability charts, basins of attraction, orbit plots, and time response profiles. The analytical investigations confirm that the uncontrolled model behaves like a hardening Duffing oscillator with multistability characteristics, displaying simultaneous mono-stable, bi-stable, tri-stable, or quadri-stable periodic oscillations depending on both the asymmetric nonlinearities and angular velocity. Subsequently, the influence of different control parameters is analyzed to determine the threshold between mono and multi-stability conditions. Finally, optimal control parameters are designed to eliminate multistability characteristics and achieve minimum and safe vibration levels.

1 Introduction

Nonlinear vibration is an inherent and intricate phenomenon in rotating machinery, influenced by various factors acting independently or concurrently. These factors encompass the inherent nonlinearities of the shaft restoring force, leading to solution multiplicity and sensitivity in rotor models. Additionally, non-circular shafts and rotor cracks introduce asymmetric restoring forces, serving as parametric or multi-parametric excitation forces in the rotor dynamic model. Unbalanced weights during rotation generate centrifugal forces, becoming external harmonic excitations that significantly amplify machine vibrations. Misalignment in interconnected components results in axial or radial vibrations. Wear, characterized by the traversal of bearing balls over pitted roller bearing races, triggers machine vibrations. Looseness from lax bearings or insecure rotor attachment adds complexity to the system dynamics, inducing substantial vibrations, etc.

Approximately twenty years ago, Cveticanin [1] delved into the free oscillations analysis within a rotor model characterized by cubic nonlinear restoring force. Employing the Krylov-Bogolubov method, the author explored the rotor's sensitivity to initial conditions. Findings indicated that initiating the rotor with initial bending could result in oscillations along a straight line, while a non-zero initial velocity could induce circular whirling motion. Subsequent discussions on rotor dynamics extended to encompass both nonlinear restoring forces and external excitations. Adiletta et al. [2] conducted a comprehensive theoretical and experimental exploration, investigating the relationship between aperiodic oscillations and the nonlinear restoring force of a rotor model endowed with adjustable stiffness coefficients. Experimental results revealed that variations in both stiffness and excitation amplitude could lead to quasiperiodic oscillations. In a study by Ishida and Inoue [3], the Jeffcott model with minor gyroscopic effects was examined, taking into account internal resonance conditions between forward and backward whirling modes. Theoretical and experimental analyses unveiled increased complexity in resonance curves, the emergence of nearly periodic motions, and significant influences from asymmetrical nonlinearity and gyroscopic effects. Yabuno et al. [4] explored normal oscillation modes of a horizontally positioned nonlinear rotor. Through coordinate transformation, the authors derived an equivalent 2-DOF system with quadratic and cubic nonlinearities. Theoretical and experimental investigations demonstrated that the system could undergo localized and nonlocalized vibrations. Their work highlighted the small difference in natural frequencies between horizontal and vertical directions as the primary cause of such oscillations. In a recent contribution by Malgol et al. [5], the focus shifted towards elucidating the impact of hydrodynamic forces generated by lubricant oil and gyroscopic forces on a Jeffcott model previously studied in Ref. [4]. The primary inference drawn was those lubricants with high viscosity efficiently attenuate system vibrations.

Asymmetry in shaft stiffness is a common characteristic in specific rotating machinery, exemplified by the two-pole alternating current generator, where coils are oriented in opposite directions, resulting in asymmetric bending stiffness. These non-uniform shafts display dynamic behaviors distinct from their symmetrical counterparts. The investigation into the dynamics of asymmetric rotating machines has attracted researchers for a long time, Ardayfio and Frohrib [6] examined an asymmetric rotor system with symmetric elastic bearings, assessing the impact of bearing flexibility on the unstable speed range. Iwatsubo et al. [7] explored the vibrational behaviors of a rotor model having asymmetric bearings, utilizing the perturbation method to analyze the derived linear time-varying model. Park [8] analyzed the vibration of an asymmetric two-pole generator, revealing excessive lateral vibrations at twice the critical speed. Hsieh et al. [9] discussed lateral torsional vibrations in an asymmetric rotor-bearing system, utilizing a Timoshenko beam model. Shahgholi and Khadem [10] investigated nonlinear lateral vibrations in an asymmetrical shaft with stretching nonlinearity at the primary resonance case. Han and Chu [11, 12] explored the effect of a transverse crack on asymmetric shaft dynamics, noting that increased crack depth improves system stability. Meng et al. [13] proposed an efficient method, utilizing 3D finite element analysis, to study the stability and frequency characteristics of asymmetric rotor-bearing anisotropic model. Xiang et al. [14] delved into the dynamics of an asymmetric system, considering coupling faults of crack and rub-impact occurrence. Przybylowicz et al. [15] analyzed the stability of an asymmetric rigid system supported on two journal bearings, showcasing the avoidance of chaotic responses through appropriate damping and stiffness coefficient selection. Yu et al. [16] investigated the dynamics of a flexible asymmetrical rotor, reporting potential chaotic motions under Hamiltonian and dissipative perturbations. Srinath et al. [17, 18] explored the stability of an asymmetrical rotor, treating it as a continuous and lumped parameters model. The authors analyzed the systems as multi-degree of freedom Mathieu equations, employing perturbation analysis and Floquet theory. They provided stability conditions for the diverse system parameters. Yi et al. [19] deliberated on the dynamics of a rotor system with asymmetric cross-sectional features in both the disc and shaft when subjected to periodic base excitations. Their conclusion highlighted significant alterations in both the response spectra and external resonances when considering periodic base excitation. Bavi et al. [20, 21] investigated the behaviors of an asymmetric thin-walled unbalanced rotating shaft that incorporated both gyroscopic motion and unbalanced effect. Examining the nonlinear dynamics of a rotor model under primary resonance conditions, Saeed [22] investigated a system characterized by both linear and nonlinear asymmetric stiffness coefficients. The findings indicated the potential for the system to oscillate with either forward or backward whirling motion, depending upon the specified initial states. Furthermore, the author concluded that the studied model could manifest multistability characteristics and unsafe oscillation levels attributable to stiffness asymmetry, even in cases of negligible disc eccentricities.

To address hazardous oscillation levels in rotating machinery, a variety of vibration reduction approaches have been investigated in the literature. These include passive, semi-active, and advanced active control methods. Bab et al. [23, 24] employed the nonlinear energy sink (NES) as a passive controller to diminish undesired oscillations in a nonlinear Jeffcott model subjected to harmonic excitation from mass eccentricity. Taghipour et al. [25, 26] applied NES as a broadband vibration absorber to improve the oscillatory characteristics of a flexible rotor shaft with a longitudinally positioned eccentric disc. Taghipour et al. [27] and Tehrani and Dardel [28] employed a combination of a tuned mass damper (TMD) and NES to suppress undesired vibrations in two distinct rotor models. Abbasi et al. [29] designed an optimized suspension system having high-static low-dynamics stiffness behaviors as a passive vibration absorber. In contrast, Ishida and Inoue [30] implemented a semi-active dynamic damper (TMD) to control lateral oscillations in the Jeffcott rotor model with cubic stiffness. The authors utilized four electromagnetic poles to exert a push–pull control force on the rotating shaft. Furthermore, Awrejcewicz and Dzyubak [31, 32] explored the nonlinear oscillations of a high-speed rotor positioned within an asymmetrical magneto-hydrodynamic environment. They examined the dynamic responses of the system in the case of both soft and rigid magnetic materials. Employing the multiple-scale analysis, they derived an approximate analytical solution for the system in scenarios involving soft magnetic materials. Conversely, for cases involving rigid magnetic materials, the Bouc–Wen hysteretic model was employed to simulate the hysteresis in the system. Saeed et al. [33,34,35] utilized 4-pole, 8-pole, and 12-pole magnetic actuators to implement a fully active control strategy, employing various PD-control laws to reduce the oscillatory motion of rotor systems.

Within the current work, two $\frac{1}{2}$-DOF active dampers have been employed to alleviate undesired vibrations in an asymmetric rotor model featuring linear and nonlinear asymmetric stiffness coefficients. The proposed active dampers are modeled by two $\frac{1}{2}$-DOF systems coupled to the rotor model, implemented through electromagnetic force via a four-pole magnetic actuator. The coupling between the rotor and the active dampers, whether linear or nonlinear, is established based on the sensed lateral displacements of the rotor and the corresponding feedback control currents applied to the actuator. The mathematical model describing the dynamics of the closed-loop system is derived and analyzed using perturbation theory. The effectiveness of the control method is evaluated through various bifurcation diagrams, considering different control and feedback parameters as bifurcation parameters. Analytical and numerical simulations illustrate that coupling 1/2-DOF active dampers to the rotor model using magnetic poles as an actuator transforms the system's nonlinear characteristics from hardening to softening Duffing characteristics. Moreover, it is noted that linear coupling of the active dampers to the rotor system is more effective than cubic nonlinear coupling in both vibration reduction and multistability elimination. However, the optimal control strategy may involve combined coupling (i.e., linear and cubic).

2 System modeling and amplitude-phase autonomous equations

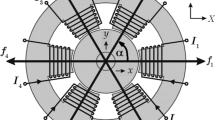
The mathematical model governing the lateral vibrations in the ${x}_{1}$ and ${x}_{2}$ directions of an asymmetric vertically supported rotor system illustrated in Fig. 1, is provided as follows [22, 36]:

$$ M\ddot{X}_{1} + C_{1} \dot{X}_{1} + F_{1} = M\,E_{D} \lambda^{2} \cos (\lambda t + \theta ), $$

(1.1)

$$ M\ddot{X}_{2} + C_{2} \dot{X}_{2} + F_{2} = M\,E_{D} \lambda^{2} \sin (\lambda t + \theta ), $$

(1.2)

where in the inertial cartesian coordinate system ${x}_{1}-{x}_{2}$ shown in Fig. 1c, ${X}_{1}(t)$ and ${X}_{2}(t)$ are the displacements of the rotor in ${x}_{1}$ and ${x}_{2}$ directions,$\dot{{X}_{1}}=\frac{d{X}_{1}}{dt}$, $\dot{{X}_{2}}=\frac{d{X}_{2}}{dt}, {\ddot{X}}_{1}=\frac{{d}^{2}{X}_{1}}{d{t}^{2}}$, ${\ddot{X}}_{2}=\frac{{d}^{2}{X}_{2}}{d{t}^{2}}$, $M$ refers to the mass of the rotating shaft, ${C}_{1}$ and ${C}_{2}$ denote the bearings' linear damping coefficients in ${x}_{1}$ and ${x}_{2}$ directions, respectively. ${F}_{1}$ and ${F}_{2}$ represent the rotor restoring forces in ${x}_{1}$ and ${x}_{2}$ directions, ${E}_{D}$ is the shaft eccentricity, $\lambda$ denotes the rotor angular velocity, ${\psi }_{1}-{\psi }_{2}$ is a rotational coordinate system that rotates with angular velocity$\lambda$, and $\theta$ is the angle between the rotational axis $\overrightarrow{O{\psi }_{1}}$ and the eccentricity direction.

Fig. 1

a Asymmetric rotor- general view, b cross-section through rotor body, and c schematic diagram of an asymmetric cross-section

As in the case of the two-pole electrical generators [4, 22, 36], the asymmetric linear and nonlinear restoring forces in ${\psi }_{1}$ and ${\psi }_{2}$ axis shown in Fig. 1c can be expressed as follows:

$$ f_{1} = (K_{L} - \Delta K_{L} )X_{{\psi_{1} }} + (K_{N} - \Delta K_{N} )X_{{\psi_{2} }}^{3} , $$

(2.1)

$$ f_{2} = (K_{L} + \Delta K_{L} )X_{{\psi_{2} }} + (K_{N} + \Delta K_{N} )X_{{\psi_{2} }}^{3} , $$

(2.2)

where ${f}_{1}$ and ${f}_{2}$ are the nonlinear restoring force in $\overrightarrow{{o\psi }_{1}}$ and $\overrightarrow{{o\psi }_{2}}$ directions, respectively, ${x}_{{\psi }_{1}}$ and ${x}_{{\psi }_{2}}$ are the shaft displacements in $\overrightarrow{{o\psi }_{1}}$ and $\overrightarrow{{o\psi }_{2}}$ directions. ${K}_{L}$ and ${K}_{N}$ are the linear and nonlinear stiffness coefficients, $\Delta {K}_{L}$ and ${\Delta K}_{N}$ denote the asymmetry in linear and nonlinear stiffness. Accordingly, the relationship between ${X}_{1},{X}_{2},{x}_{{\psi }_{1}}$, and ${x}_{{\psi }_{2}}$ can be expressed as follows:

$$ \left[ {\begin{array}{*{20}c} {x_{{\psi_{1} }} } \\ {x_{{\psi_{2} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos (\lambda t)} & {\sin (\lambda t)} \\ { - \sin (\lambda t)} & {\cos (\lambda t)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{1} } \\ {X_{2} } \\ \end{array} } \right] $$

(3)

Substituting Eq. (3) into Eqs. (2.1) and (2.2), we have

$$ \begin{aligned} f_{1} = & (K_{L} - \Delta K_{L} )\left( {X_{1} \cos (\lambda t) + X_{2} \sin (\lambda t)} \right) + (K_{N} - \Delta K_{N} )(X_{1}^{3} \cos^{3} (\lambda t) \\ & + 3X_{1}^{2} X_{2} \cos^{2} (\lambda t)\sin (\lambda t + 3X_{1} X_{2}^{2} \cos (\lambda t)\sin^{2} (\lambda t) + X_{2}^{3} \sin^{3} (\lambda t)), \\ \end{aligned} $$

(4.1)

$$ \begin{aligned} f_{2} = & (K_{L} + \Delta K_{L} )( - X_{1} \sin (\lambda t) + X_{2} \cos (\lambda t)) + (K_{N} + \Delta K_{N} )( - X_{1}^{3} \sin^{3} (\lambda t) \\ & + 3X_{1}^{2} X_{2} \cos (\lambda t)\sin^{2} (\lambda t - 3X_{1} X_{2}^{2} \cos^{2} (\lambda t)\sin (\lambda t) + X_{2}^{3} \cos^{3} (\lambda t)). \\ \end{aligned} $$

(4.2)

the relationship between ${F}_{1}, {F}_{2},{ f}_{1}$, and ${f}_{2}$ can be expressed such that:

$$ \left[ {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos (\lambda t)} & { - \sin (\lambda t)} \\ {\sin (\lambda t)} & {\cos (\lambda t)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \end{array} } \right] $$

(5)

Substituting Eqs. (4.1), (4.2), and (5) into Eqs. (1.1) and (1.2), we get the equations of motion governing the nonlinear vibrations of the controlled asymmetric rotor model as follows:

$$ \begin{aligned} M\ddot{X}_{1} + & C_{1} \dot{X}_{1} + K_{L} X_{1} + \frac{3}{4}K_{N} \left( {X_{1}^{3} + X_{1} X_{2}^{2} } \right) = M\,E_{D} \lambda^{2} \cos (\lambda t + \theta ) \\ & + \left( {\Delta K_{L} X_{1} + \Delta K_{N} X_{1}^{3} } \right)\cos \left( {2\lambda t + \left( {\Delta K_{L} X_{2} + \frac{1}{2}\Delta K_{N} X_{2}^{3} + \frac{3}{2}\Delta K_{N} X_{1}^{2} X_{2} } \right)} \right)\sin (2\lambda t) \\ & + \left( {\frac{3}{4}K_{N} X_{1} X_{2}^{2} - \frac{1}{4}K_{N} X_{1}^{3} } \right)\cos (4\lambda t) \\ & + \left( {\frac{1}{4}K_{N} X_{2}^{3} - \frac{3}{4}K_{N} X_{1}^{2} X_{2} } \right)\sin (4\lambda t) + U_{1} (t), \\ \end{aligned} $$

(6.1)

$$ \begin{aligned} M\ddot{X}_{2} + & C_{2} \dot{X}_{2} + K_{L} X_{2} + \frac{3}{4}K_{N} \left( {X_{2}^{3} + X_{1}^{2} X_{2} } \right) = M\,E_{D} \lambda^{2} \sin (\lambda t + \theta ) \\ & - \left( {\Delta K_{L} X_{2} - \Delta K_{N} X_{2}^{3} } \right)\cos (2\lambda t) \\ & + \left( {\Delta K_{L} X_{1} + \frac{1}{2}\Delta K_{N} X_{1}^{3} + \frac{3}{2}\Delta K_{N} X_{1} X_{2}^{2} } \right)\sin (2\lambda t) \\ & + \left( {\frac{3}{4}K_{N} X_{1}^{2} X_{2} - \frac{1}{4}K_{N} X_{2}^{3} } \right)\cos (4\lambda t) \\ & + \left( { - \frac{1}{4}K_{N} X_{1}^{3} + \frac{3}{4}K_{N} X_{1} X_{2}^{2} } \right)\sin (4\lambda t) + U_{2} (t), \\ \end{aligned} $$

(6.2)

where ${U}_{1}\left(t\right)$ and ${U}_{2}(t)$ are the proposed control force of the active dampers. To exert control force on a rotating system, a set of four electromagnetic poles is utilized as an actuator. The control force is applied in the form of an electromagnetic attractive force by regulating the electric current applied to the pole coils, as depicted in Fig. 2. The net electromagnetic attractive forces (${U}_{1}\left(t\right)$ and ${U}_{2}(t)$) in ${x}_{1}$ and ${x}_{2}$ directions can be expressed as follows [37, 38]:

$$ U_{1} = K\left[ {\left( {\frac{{I_{0} - I_{{X_{1} }} (t)}}{{R_{0} - X_{1} (t)}}} \right)^{2} - \left( {\frac{{I_{0} + I_{{X_{1} }} (t)}}{{R_{0} + X_{1} (t)}}} \right)^{2} } \right],\,\,\,\,U_{2} = K\left[ {\left( {\frac{{I_{0} - I_{{X_{2} }} (t)}}{{R_{0} - X_{2} (t)}}} \right)^{2} - \left( {\frac{{I_{0} + I_{{X_{2} }} (t)}}{{R_{0} + X_{2} (t)}}} \right)^{2} } \right], $$

(7)

where $K$ is the magneto-mechanical coupling constant as defined in Table 1, ${I}_{0}$ is a bias constant current, ${I}_{{X}_{1}}(t)$ and ${I}_{{X}_{2}}(t)$ are the control currents in ${x}_{1}$ and ${x}_{2}$ directions, ${R}_{0}$ is the nominal radial clearance between the rotor and the pole housing as shown in Fig. 2. Within this work, the currents ${I}_{{X}_{1}}(t)$ and ${I}_{{X}_{2}}(t)$ are designed to be proportional to the displacements (${X}_{3}(t)$ and ${X}_{4}(t)$) of the active dampers as follows:

$$ I_{{X_{1} }} = - \left( {K_{1} X_{3} (t) + K_{2} X_{3}^{3} (t)} \right),\,\,\,\,\,I_{{X_{2} }} = - \left( {K_{1} X_{4} (t) + K_{2} X_{4}^{3} (t)} \right), $$

(8)

where ${K}_{1}{X}_{3}$ and ${K}_{1}{X}_{4}$ are the linear part of the control signals, while ${K}_{2}{X}_{3}^{3}$ and ${K}_{2}{X}_{4}^{3}$ denote the nonlinear part. The equations of motion of the $\frac{1}{2}-$ DOF active dampers are proposed as follows [39,40,41]:

$$ \dot{X}_{3} + K_{3} X_{3} = K_{4} X_{1} , $$

(9.1)

$$ \dot{X}_{4} + K_{3} X_{4} = K_{4} X_{2} , $$

(9.2)

where ${K}_{3}$ and ${K}_{4}$ are the internal and feedback gains, respectively.

Fig. 2

Asymmetric rotor equipped with 4-pole magnetic actuator

Table 1 Rotor-actuator actual parameters

By expanding Eq. (7) using the third-order Maclaurin series in terms of ${X}_{1}, {X}_{2}, {I}_{{X}_{1}},$ and ${I}_{{X}_{2}}$, and then inserting Eq. (8) into the resulting equations [33], we have:

$$ \begin{aligned} U_{1} (t) = & \frac{4K}{{R_{0}^{4} }}\left( {R_{0}^{3} I_{0} K_{1} X_{3} + R_{0}^{3} I_{0} K_{2} X_{3}^{3} + R_{0}^{2} I_{0}^{2} X_{1} + 2I_{0}^{2} X_{1}^{3} + 3R_{0} I_{0} K_{1} X_{1}^{2} X_{3} + 3R_{0} I_{0} K_{2} X_{1}^{2} X_{3}^{3} } \right. \\ & + R_{0}^{2} K_{1}^{2} X_{1} X_{3}^{2} + 2R_{0}^{2} K_{1} K_{2} X_{1} X_{3}^{4} \left. { + R_{0}^{2} K_{2}^{2} X_{1} X_{3}^{6} } \right), \\ \end{aligned} $$

(10.1)

$$ \begin{aligned} U_{2} (t) = & \frac{4K}{{R_{0}^{4} }}\left( {R_{0}^{3} I_{0} K_{1} X_{4} + R_{0}^{3} I_{0} K_{2} X_{4}^{3} + R_{0}^{2} I_{0}^{2} X_{2} + 2I_{0}^{2} X_{2}^{3} + 3R_{0} I_{0} K_{1} X_{2}^{2} X_{4} + 3R_{0} I_{0} K_{2} X_{2}^{2} X_{4}^{3} } \right. \\ & + R_{0}^{2} K_{1}^{2} X_{2} X_{4}^{2} + 2R_{0}^{2} K_{1} K_{2} X_{2} X_{4}^{4} \left. { + R_{0}^{2} K_{2}^{2} X_{2} X_{4}^{6} } \right). \\ \end{aligned} $$

(10.2)

Inserting Eqs. (10.1) and (10.2) into Eqs. (6.1) and (6.2), one can obtain the whole mathematical models governing the nonlinear dynamics of the closed-loop control system as follows:

$$ \begin{aligned} M\ddot{X}_{1} + & C_{1} \dot{X}_{1} + K_{L} X_{1} + \frac{3}{4}K_{N} (X_{1}^{3} + X_{1} X_{2}^{2} ) = M\,E_{D} \lambda^{2} \cos (\lambda t + \theta ) \\ & + (\Delta K_{L} X_{1} + \Delta K_{N} X_{1}^{3} )\cos (2\lambda t) \\ & + (\Delta K_{L} X_{2} + \frac{1}{2}\Delta K_{N} X_{2}^{3} + \frac{3}{2}\Delta K_{N} X_{1}^{2} X_{2} )\sin (2\lambda t) \\ & + (\frac{3}{4}K_{N} X_{1} X_{2}^{2} - \frac{1}{4}K_{N} X_{1}^{3} )\cos (4\lambda t) \\ & + (\frac{1}{4}K_{N} X_{2}^{3} - \frac{3}{4}K_{N} X_{1}^{2} X_{2} )\sin (4\lambda t) \\ & + \frac{4K}{{R_{0}^{4} }}\left( {R_{0}^{3} I_{0} K_{1} X_{3} + R_{0}^{3} I_{0} K_{2} X_{3}^{3} + R_{0}^{2} I_{0}^{2} z_{1} + 2I_{0}^{2} X_{1}^{3} } \right. \\ & + 3R_{0} I_{0} K_{1} X_{1}^{2} X_{3} + 3R_{0} I_{0} K_{2} X_{1}^{2} X_{3}^{3} + R_{0}^{2} K_{1}^{2} X_{1} X_{3}^{2} \\ & + 2R_{0}^{2} K_{1} K_{2} X_{1} X_{3}^{4} \left. { + R_{0}^{2} K_{2}^{2} X_{1} X_{3}^{6} } \right), \\ \end{aligned} $$

(11.1)

$$ \begin{aligned} M\ddot{X}_{2} + & C_{2} \dot{X}_{2} + K_{L} X_{2} + \frac{3}{4}K_{N} (X_{2}^{3} + X_{1}^{2} X_{2} ) = M\,E_{D} \lambda^{2} \sin (\lambda t + \theta ) \\ & - \left( {\Delta K_{L} X_{2} - \Delta K_{N} X_{2}^{3} } \right)\cos (2\lambda t) + \left( {\Delta K_{L} X_{1} + \frac{1}{2}\Delta K_{N} X_{1}^{3} + \frac{3}{2}\Delta K_{N} X_{1} X_{2}^{2} } \right)\sin (2\lambda t) \\ & + \left( {\frac{3}{4}K_{N} X_{1}^{2} X_{2} - \frac{1}{4}K_{N} X_{2}^{3} } \right)\cos (4\lambda t) \\ & + \left( { - \frac{1}{4}K_{N} X_{1}^{3} + \frac{3}{4}K_{N} X_{1} X_{2}^{2} } \right)\sin (4\lambda t) \\ & + \frac{4K}{{R_{0}^{4} }}\left( {R_{0}^{3} I_{0} K_{1} X_{4} + R_{0}^{3} I_{0} K_{2} X_{4}^{3} } \right. \\ & + R_{0}^{2} I_{0}^{2} X_{2} + 2I_{0}^{2} X_{2}^{3} + 3R_{0} I_{0} K_{1} X_{2}^{2} X_{4} + 3R_{0} I_{0} K_{2} X_{2}^{2} X_{4}^{3} \\ & + R_{0}^{2} K_{1}^{2} X_{2} X_{4}^{2} + 2R_{0}^{2} K_{1} K_{2} X_{2} X_{4}^{4} \left. { + R_{0}^{2} K_{2}^{2} X_{2} X_{4}^{6} } \right), \\ \end{aligned} $$

(11.2)

$$ \dot{X}_{3} + K_{3} X_{3} = K_{4} X_{1} , $$

(11.3)

$$ \dot{X}_{4} + K_{3} X_{4} = K_{4} X_{2} , $$

(11.4)

To generalize the mathematical model given by Eqs. (11.1) to (11.4), the dimensionless variables ${y}_{1}=\frac{{X}_{1}}{{R}_{0}}, {y}_{2}=\frac{{X}_{2}}{{R}_{0}}, {y}_{3}=\frac{{X}_{3}}{{R}_{0}}, {y}_{4}=\frac{{X}_{4}}{{R}_{0}} ,$ and $\tau =\gamma t$ (where $\gamma =\sqrt{{K}_{L}/M}$ is the rotor linear natural frequency) are introduced into Eqs. (11.1) to (11.4) to obtain the following dimensionless nonlinear model:

$$ \begin{aligned} \ddot{y}_{1} + & \mu_{1} \dot{y}_{1} + y_{1} + \frac{3}{4}\alpha_{1} (y_{1}^{3} + y_{1} y_{2}^{2} ) = f\omega^{2} \cos (\omega \tau + \theta ) + \alpha_{2} y_{1} \cos (2\omega \tau ) \\ & + \alpha_{2} y_{2} \sin (2\omega \tau ) + \alpha_{3} y_{1}^{3} \cos (2\omega \tau ) + \frac{1}{2}\alpha_{3} (y_{2}^{3} + 3y_{1}^{2} y_{2} )\sin (2\omega \tau ) \\ & + \frac{1}{4}\alpha_{1} (3y_{1} y_{2}^{2} - y_{1}^{3} )\cos (4\omega \tau ) + \frac{1}{4}\alpha_{1} (y_{2}^{3} - 3y_{1}^{2} y_{2} )\sin (4\Omega \tau ) \\ & + \Delta \left( {y_{1} } \right. + \eta_{1} y_{3} + \eta_{1}^{2} y_{1} y_{3}^{2} + 3\eta_{1} y_{1}^{2} y_{3} + 2y_{1}^{3} + \eta_{2} y_{3}^{3} + 3\eta_{2} y_{1}^{2} y_{3}^{3} + 2\eta_{1} \eta_{2} y_{1} y_{3}^{4} \left. { + \eta_{2}^{2} y_{1} y_{3}^{6} } \right), \\ \end{aligned} $$

(12.1)

$$ \begin{aligned} \ddot{y}_{2} + & \mu_{2} \dot{y}_{2} + y_{2} + \frac{3}{4}\alpha_{1} (y_{2}^{3} + y_{1}^{2} y_{2} ) = f\omega^{2} \sin (\omega \tau + \theta ) + \alpha_{2} y_{1} \sin (2\omega \tau ) \\ & - \alpha_{2} y_{2} \cos (2\omega \tau ) + \alpha_{3} y_{2}^{3} \cos (2\omega \tau ) + \frac{1}{2}\alpha_{3} (y_{1}^{3} + 3y_{1} y_{2}^{2} )\sin (2\omega \tau ) \\ & + \frac{1}{4}\alpha_{1} (3y_{1}^{2} y_{2} - y_{2}^{3} )\cos (4\omega \tau ) + \frac{1}{4}\alpha_{1} (3y_{1} y_{2}^{2} - y_{1}^{3} )\sin (4\omega \tau ) \\ & + \Delta \left( {y_{2} + \eta_{1} y_{4} } \right. + \eta_{1}^{2} y_{2} y_{4}^{2} + 3\eta_{1} y_{2}^{2} y_{4} + 2y_{2}^{3} + \eta_{2} y_{4}^{3} + 3\eta_{2} y_{2}^{2} y_{4}^{3} + 2\eta_{1} \eta_{2} y_{2} y_{4}^{4} \left. { + \eta_{2}^{2} y_{2} y_{4}^{6} } \right), \\ \end{aligned} $$

(12.2)

$$ \dot{y}_{3} + \delta_{1} y_{3} = \delta_{2} y_{1} , $$

(12.3)

$$ \dot{y}_{4} + \delta_{1} y_{4} = \delta_{2} y_{2} , $$

(12.4)

where,$\dot{{y}_{1}}=\frac{d{y}_{1}}{d\tau }\dot{{y}_{2}}=\frac{d{y}_{2}}{d\tau }, \dot{{y}_{3}}=\frac{d{y}_{3}}{d\tau },$$\dot{{y}_{4}}=\frac{d{y}_{4}}{d\tau }, {\ddot{y}}_{1}=\frac{{d}^{2}{y}_{1}}{d{\tau }^{2}},$${\ddot{y}}_{2}=\frac{{d}^{2}{y}_{2}}{d{\tau }^{2}},$${\mu }_{1}=\frac{{C}_{1}}{\sqrt{{K}_{L}M}}, {\mu }_{2}=\frac{{C}_{2}}{\sqrt{{K}_{L}M}} , {\alpha }_{1}=\frac{{R}_{0}^{2}{K}_{N}}{{K}_{L}}, {\alpha }_{2}=\frac{\Delta {K}_{L}}{{K}_{L}}, {\alpha }_{3}=\frac{{R}_{0}^{2}\Delta {K}_{N}}{{K}_{L}}, {\eta }_{1}=\frac{{R}_{0}{K}_{1}}{{I}_{0}}, {\eta }_{2}=\frac{{R}_{0}^{3}{K}_{2}}{{I}_{0}} , {\delta }_{1}=\frac{{K}_{3}}{\sqrt{{K}_{L}/M}}, {\delta }_{2}=\frac{{K}_{4}}{\sqrt{{K}_{L}/M}}, f=\frac{{E}_{D}}{{R}_{0}} ,\Delta =\frac{4K{I}_{0}^{2}}{{R}_{0}^{2}{K}_{L}},$ and$\upomega =\frac{\lambda }{\gamma }$. To investigate the dynamics of the above system under the different control gains ${\eta }_{1}, {\eta }_{2} , {\delta }_{1},$ and${\delta }_{2}$, an approximate solution for Eqs. (12.1) to (12.4) is sought using the perturbation method as follows [42,43,44]:

$$ y_{n} (\tau ,\zeta ) = y_{n0} (\tau_{0} ,\tau_{1} ) + \zeta y_{n1} (\tau_{0} ,\tau_{1} ),\quad n = 1,2, $$

(13.1)

$$ y_{n} (\tau ,\zeta ) = \zeta y_{n0} (\tau_{0} ,\tau_{1} ) + \zeta^{2} y_{n1} (\tau_{0} ,\tau_{1} ),\quad n = 3,4. $$

(13.2)

where $\zeta$ is just a book-keeping parameter,${\tau }_{0}=\tau ,$ and ${ \tau }_{1}=\zeta \tau$. In terms of the time scales ${\tau }_{0}$ and ${\tau }_{1}$, the derivatives $\frac{d}{d\tau }$ and $\frac{{d}^{2}}{{d\tau }^{2}}$ could be expressed such that:

$$ \frac{d}{d\tau } = \frac{\partial }{{\partial \tau_{0} }} + \zeta \frac{\partial }{{\partial \tau_{1} }}, \, \,\,\,\,\frac{{d^{2} }}{{d\tau^{2} }} = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\zeta \frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }} $$

(14)

To adhere to the multiple scales solution procedure, the system parameters must be appropriately scaled in a manner that:

$$ \begin{gathered} \mu_{1} = \zeta \hat{\mu }_{1} \,,\,\,\mu_{2} = \zeta \hat{\mu }_{2} ,\,\,\alpha_{1} = \zeta \hat{\alpha }_{1} ,\,\,\alpha_{2} = \zeta \hat{\alpha }_{2} ,\,\,\alpha_{3} = \zeta \hat{\alpha }_{3} ,\,\,\Delta = \zeta \hat{\Delta }, \hfill \\ \eta_{1} = \zeta^{ - 1} \hat{\eta }_{1} ,\,\,\eta_{2} = \zeta^{ - 3} \hat{\eta }_{2} ,\,\,\delta_{2} = \zeta \hat{\delta }_{2} ,\,\,f = \zeta \hat{f} \hfill \\ \end{gathered} $$

(15)

Now, Inserting Eqs. (13.1), (13.2), (14), and (15) into Eqs. (12.1) to (12.4), yields:

O (${\zeta }^{0}$)

$$ \left( {\frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 1} \right)y_{11} = 0, $$

(16.1)

$$ \left( {\frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 1} \right)y_{21} = 0, $$

(16.2)

O (${\zeta }^{1}$):

$$ \left( {\frac{\partial }{{\partial \tau_{0} }} + \delta_{1} } \right)y_{31} = \hat{\delta }_{2} y_{11} , $$

(17.1)

$$ \left( {\frac{\partial }{{\partial \tau_{0} }} + \delta_{1} } \right)y_{41} = \hat{\delta }_{2} y_{21} , $$

(17.2)

$$ \begin{aligned} \left( {\frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 1} \right)y_{12} = & - 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }}y_{11} - \hat{\mu }_{1} \frac{\partial }{{\partial \tau_{0} }}y_{11} - \frac{3}{4}\hat{\alpha }_{1} (y_{11}^{3} + y_{11} y_{21}^{2} ) \\ & + \hat{f}\omega^{2} \cos (\omega \tau_{0} + \theta ) + \hat{\alpha }_{2} y_{11} \cos (2\omega \tau_{0} ) + \hat{\alpha }_{2} y_{21} \sin (2\omega \tau_{0} ) \\ & + \hat{\alpha }_{3} y_{11}^{3} \cos (2\omega \tau_{0} ) + \frac{1}{2}\hat{\alpha }_{3} (y_{21}^{3} + 3y_{11}^{2} y_{21} )\sin (2\omega \tau_{0} ) \\ & + \frac{1}{4}\hat{\alpha }_{1} (3y_{11} y_{21}^{2} - y_{11}^{3} )\cos (4\omega \tau_{0} ) + \frac{1}{4}\hat{\alpha }_{1} (y_{21}^{3} - 3y_{11}^{2} y_{21} )\sin (4\omega \tau_{0} ) \\ & + \hat{\Delta }(y_{11} + \hat{\eta }_{1} y_{31} + \hat{\eta }_{1}^{2} y_{11} y_{31}^{2} + 3\hat{\eta }_{1} y_{11}^{2} y_{31} + 2y_{11}^{3} + \hat{\eta }_{2} y_{31}^{3} \\ & + 3\hat{\eta }_{2} y_{11}^{2} y_{31}^{3} + 2\hat{\eta }_{1} \hat{\eta }_{2} y_{11} y_{31}^{4} + \hat{\eta }_{2}^{2} y_{11} y_{31}^{6} ), \\ \end{aligned} $$

(17.3)

$$ \begin{aligned} \left( {\frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 1} \right)y_{22} = & - 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }}y_{21} - \hat{\mu }_{2} \frac{\partial }{{\partial \tau_{0} }}y_{21} - \frac{3}{4}\hat{\alpha }_{1} (y_{21}^{3} + y_{11}^{2} y_{21} ) \\ & + \hat{f}\omega^{2} \sin (\omega \tau_{0} + \theta ) + \hat{\alpha }_{2} y_{11} \sin (2\omega \tau_{0} ) - \hat{\alpha }_{2} y_{21} \cos (2\omega \tau_{0} ) \\ & + \hat{\alpha }_{3} y_{21}^{3} \cos (2\omega \tau_{0} ) + \frac{1}{2}\hat{\alpha }_{3} (y_{11}^{3} + 3y_{11} y_{21}^{2} )\sin (2\omega \tau_{0} ) \\ & + \frac{1}{4}\hat{\alpha }_{1} (3y_{11}^{2} y_{21} - y_{21}^{3} )\cos (4\omega \tau_{0} ) + \frac{1}{4}\hat{\alpha }_{1} (3y_{11} y_{21}^{2} - y_{11}^{3} )\sin (4\omega \tau_{0} ) \\ & + \hat{\Delta }(y_{21} + 2y_{21}^{3} + \hat{\eta }_{1} y_{41} + 3\hat{\eta }_{1} y_{21}^{2} y_{41} + \hat{\eta }_{2} y_{41}^{3} + 3\hat{\eta }_{2} y_{21}^{2} y_{41}^{3} \\ & + \hat{\eta }_{1}^{2} y_{21} y_{41}^{2} + 2\hat{\eta }_{1} \hat{\eta }_{2} y_{21} y_{41}^{4} + \hat{\eta }_{2}^{2} y_{21} y_{41}^{6} ). \\ \end{aligned} $$

(17.4)

The solution of Eqs. (16.1), (16.2), (17.1), and (17.2) can be written as follows:

$$ y_{11} (\tau_{0} ,\tau_{1} ) = Q_{1} (\tau_{1} )e^{{i\tau_{0} }} + \overline{{Q_{1} }} (\tau_{1} )e^{{ - i\tau_{0} }} , $$

(18.1)

$$ y_{21} (\tau_{0} ,\tau_{1} ) = Q_{2} (\tau_{1} )e^{{i\tau_{0} }} + \overline{{Q_{2} }} (\tau_{1} )e^{{ - i\tau_{0} }} , $$

(18.2)

$$ y_{31} (\tau_{0} ,\tau_{1} ) = \frac{{(\delta_{1} - i)}}{{(\delta_{1}^{2} + 1)}}\hat{\delta }_{2} Q_{1} (\tau_{1} )e^{{i\tau_{0} }} + \frac{{(\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)}}\hat{\delta }_{2} \overline{{Q_{1} }} (\tau_{1} )e^{{ - i\tau_{0} }} , $$

(18.3)

$$ y_{41} (\tau_{0} ,\tau_{1} ) = \frac{{(\delta_{1} - i)}}{{(\delta_{1}^{2} + 1)}}\hat{\delta }_{2} Q_{2} (\tau_{1} )e^{{i\tau_{0} }} + \frac{{(\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)}}\hat{\delta }_{2} \overline{{Q_{2} }} (\tau_{1} )e^{{ - i\tau_{0} }} , $$

(18.4)

where$i=\sqrt{-1}$. The values of the coefficients ${Q}_{1}({\tau }_{1})$ and ${Q}_{2}({\tau }_{1})$ are currently unspecified and will be specified at a later stage. Furthermore, $\overline{{Q }_{1}}({\tau }_{1})$ and $\overline{{Q }_{2}}({\tau }_{1})$ represent the conjugate functions of ${Q}_{1}({\tau }_{1})$ and ${Q}_{2}({\tau }_{1})$ respectively. To investigate the system dynamics near the resonance condition (i.e. $\to 1$), let

$$ \omega = 1 + \sigma = 1 + \zeta \hat{\sigma }, $$

(19)

where $\sigma$ is a parameter representing the closeness of $\omega$ to the normalized natural frequency of the rotor system. Now, by inserting Eqs. (18.1), (18.2), (18.3), (18.4), and (19) into Eqs. (17.3) and (17.4), one can obtain the following secular term:

$$ \begin{gathered} - 2i\frac{{dQ_{1} }}{d\tau } - i\mu_{1} Q_{1} - \frac{9}{4}\alpha_{1} A^{2} \overline{Q}_{1} - \frac{3}{2}\alpha_{1} Q_{1} Q_{2} \overline{Q}_{2} - \frac{3}{4}\alpha_{1} \overline{Q}_{1} Q_{2}^{2} + \frac{1}{2}f\omega^{2} e^{i(\sigma \tau + \theta )} + \frac{1}{2}\alpha_{2} \overline{Q}_{1} e^{2i\sigma \tau } \hfill \\ - \frac{i}{2}\alpha_{2} \overline{Q}_{2} e^{2i\sigma \tau } + \frac{3}{2}\alpha_{3} Q_{1} \overline{Q}_{1}^{2} e^{2i\sigma \tau } + \frac{1}{2}\alpha_{3} Q_{1}^{3} e^{ - 2i\sigma \tau } - \frac{3i}{4}\alpha_{3} Q_{2} \overline{Q}_{2}^{2} e^{2i\sigma \tau } + \frac{i}{4}\alpha_{3} Q_{2}^{3} e^{ - 2i\sigma \tau } \hfill \\ - \frac{3i}{4}\alpha_{3} \overline{Q}_{1}^{2} Q_{2} e^{2i\sigma \tau } + \frac{3i}{4}\alpha_{3} Q_{1}^{2} Q_{2} e^{ - 2i\sigma \tau } - \frac{3i}{2}\alpha_{3} Q_{1} \overline{Q}_{1} \overline{Q}_{2} e^{2i\sigma \tau } + \frac{3}{8}\alpha_{1} \overline{Q}_{1} \overline{Q}_{2}^{2} e^{4i\sigma \tau } - \frac{1}{8}\alpha_{1} \overline{Q}_{1}^{3} e^{4i\sigma \tau } \hfill \\ - \frac{i}{8}\alpha_{1} \overline{Q}_{2}^{3} e^{4i\sigma \tau } + \frac{3i}{8}\alpha_{1} \overline{Q}_{1}^{2} \overline{Q}_{2} e^{4i\sigma \tau } + \Delta \left( {Q_{1} + \frac{{\eta_{1} \delta_{2} (\delta_{1} - i)}}{{(\delta_{1}^{2} + 1)}}} \right.Q_{1} + \frac{{2\eta_{1}^{2} \delta_{2}^{2} }}{{(\delta_{1}^{2} + 1)}}Q_{1}^{2} \overline{Q}_{1} + \frac{{\eta_{1}^{2} \delta_{2}^{2} (\delta_{1} - i)^{2} }}{{(\delta_{1}^{2} + 1)^{2} }}Q_{1}^{2} \overline{Q}_{1} \hfill \\ + \frac{{3\eta_{1} \delta_{2} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)}}Q_{1}^{2} \overline{Q}_{1} + \frac{{6\eta_{1} \delta_{2} (\delta_{1} - i)}}{{(\delta_{1}^{2} + 1)}}Q_{1}^{2} \overline{Q}_{1} + 6Q_{1}^{2} \overline{Q}_{1} + \frac{{3\eta_{2} \delta_{2}^{3} (\delta_{1} - i)^{2} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)^{3} }}Q_{1}^{2} \overline{Q}_{1} \hfill \\ + \frac{{9\eta_{2} \delta_{2}^{3} (\delta_{1} - i)(\delta_{1} + i)^{2} }}{{(\delta_{1}^{2} + 1)^{3} }}Q_{1}^{3} \overline{Q}_{1}^{2} + \frac{{18\eta_{2} \delta_{2}^{3} (\delta_{1} - i)^{2} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)^{3} }}Q_{1}^{3} \overline{Q}_{1}^{2} + \frac{{3\eta_{2} \delta_{2}^{3} (\delta_{1} - i)^{3} }}{{(\delta_{1}^{2} + 1)^{3} }}Q_{1}^{3} \overline{Q}_{1}^{2} \hfill \\ + \frac{{12\eta_{1} \eta_{2} \delta_{2}^{4} (\delta_{1} - i)^{2} (\delta_{1} + i)^{2} }}{{(\delta_{1}^{2} + 1)^{4} }}Q_{1}^{3} \overline{Q}_{1}^{2} + \frac{{8\eta_{1} \eta_{2} \delta_{2}^{4} (\delta_{1} - i)^{3} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)^{4} }}Q_{1}^{3} \overline{Q}_{1}^{2} + \frac{{20\eta_{2}^{2} \delta_{2}^{6} (\delta_{1} - i)^{3} (\delta_{1} + i)^{3} }}{{(\delta_{1}^{2} + 1)^{6} }}Q_{1}^{4} \overline{Q}_{1}^{3} \hfill \\ \left. { + \frac{{15\eta_{2}^{2} \delta_{2}^{6} (\delta_{1} - i)^{4} (\delta_{1} + i)^{2} }}{{(\delta_{1}^{2} + 1)^{6} }}Q_{1}^{4} \overline{Q}_{1}^{3} } \right) = 0, \hfill \\ \end{gathered} $$

(20.1)

$$ \begin{gathered} - 2i\frac{{dQ_{2} }}{d\tau } - i\mu_{2} Q_{2} - \frac{9}{4}\alpha_{1} Q_{2}^{2} \overline{Q}_{2} - \frac{3}{2}\alpha_{1} Q_{1} \overline{Q}_{1} Q_{2} - \frac{3}{4}\alpha_{1} Q_{1}^{2} \overline{Q}_{2} - \frac{i}{2}f\omega^{2} e^{i(\sigma \tau + \theta )} - \frac{i}{2}\alpha_{2} \overline{Q}_{1} e^{2i\sigma \tau } \hfill \\ - \frac{1}{2}\alpha_{2} \overline{Q}_{2} e^{2i\sigma \tau } + \frac{3}{2}\alpha_{3} Q_{2} \overline{Q}_{2}^{2} e^{2i\sigma \tau } + \frac{1}{2}\alpha_{3} Q_{2}^{3} e^{ - 2i\sigma \tau } - \frac{3i}{4}\alpha_{3} Q_{11} \overline{Q}_{1}^{2} e^{2i\sigma \tau } + \frac{i}{4}\alpha_{3} Q_{1}^{3} e^{ - 2i\sigma \tau } \hfill \\ - \frac{3i}{4}\alpha_{3} Q_{1} \overline{Q}_{2}^{2} e^{2i\sigma \tau } + \frac{3i}{4}\alpha_{3} Q_{1} Q_{2}^{2} e^{ - 2i\sigma \tau } - \frac{3i}{2}\alpha_{3} \overline{Q}_{1} Q_{2} \overline{Q}_{2} e^{2i\sigma \tau } + \frac{3}{8}\alpha_{1} \overline{Q}_{1}^{2} \overline{Q}_{2} e^{4i\sigma \tau } - \frac{1}{8}\alpha_{1} \overline{Q}_{2}^{3} e^{4i\sigma \tau } \hfill \\ + \frac{i}{8}\alpha_{1} \overline{Q}_{1}^{3} e^{4i\sigma \tau } - \frac{3i}{8}\alpha_{1} \overline{Q}_{1} \overline{Q}_{2}^{2} e^{4i\sigma \tau } + \Delta \left( {Q_{2} + \frac{{\eta_{1} \delta_{2} (\delta_{1} - i)}}{{(\delta_{1}^{2} + 1)}}} \right.Q_{2} + \frac{{2\eta_{1}^{2} \delta_{2}^{2} }}{{(\delta_{1}^{2} + 1)^{2} }}Q_{2}^{2} \overline{Q}_{2} + \frac{{\eta_{1}^{2} \delta_{2}^{2} (\delta_{1} - i)^{2} }}{{(\delta_{1}^{2} + 1)^{2} }}Q_{2}^{2} \overline{Q}_{2} \hfill \\ + \frac{{6\eta_{1} \delta_{2} (\delta_{1} - i)}}{{(\delta_{1}^{2} + 1)}}Q_{2}^{2} \overline{Q}_{2} + \frac{{3\eta_{1} \delta_{2} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)}}Q_{2}^{2} \overline{Q}_{2} + 6Q_{2}^{2} \overline{Q}_{2} + \frac{{3\eta_{2} \delta_{2}^{3} (\delta_{1} - i)^{2} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)^{3} }}Q_{2}^{2} \overline{Q}_{2} \hfill \\ + \frac{{9\eta_{2} \delta_{2}^{3} (\delta_{1} - i)(\delta_{1} + i)^{2} }}{{(\delta_{1}^{2} + 1)^{3} }}Q_{2}^{3} \overline{Q}_{2}^{2} + \frac{{18\eta_{2} \delta_{2}^{3} (\delta_{1} - i)^{2} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)^{3} }}Q_{2}^{3} \overline{Q}_{2}^{2} + \frac{{3\eta_{2} \delta_{2}^{3} (\delta_{1} - i)^{3} }}{{(\delta_{1}^{2} + 1)^{3} }}Q_{2}^{3} \overline{Q}_{2}^{2} \hfill \\ + \frac{{12\eta_{1} \eta_{2} \delta_{2}^{4} (\delta_{1} - i)^{2} (\delta_{1} + i)^{2} }}{{(\delta_{1}^{2} + 1)^{4} }}Q_{2}^{3} \overline{Q}_{2}^{2} + \frac{{8\eta_{1} \eta_{2} \delta_{2}^{4} (\delta_{1} - i)^{3} (\delta_{1} + i)}}{{(\delta_{1}^{2} + 1)^{4} }}Q_{2}^{3} \overline{Q}_{2}^{2} + \frac{{20\eta_{2}^{2} \delta_{2}^{6} (\delta_{1} - i)^{3} (\delta_{1} + i)^{3} }}{{(\delta_{1}^{2} + 1)^{6} }}Q_{2}^{4} \overline{Q}_{2}^{3} \hfill \\ \left. { + \frac{{15\eta_{2}^{2} \delta_{2}^{6} (\delta_{1} - i)^{4} (\delta_{1} + i)^{2} }}{{(\delta_{1}^{2} + 1)^{6} }}Q_{2}^{4} \overline{Q}_{2}^{3} } \right) = 0. \hfill \\ \end{gathered} $$

(20.2)

By substituting the polar representations of ${Q}_{1}\left(\tau \right)=\frac{1}{2}{z}_{1}(\tau ){e}^{i{\psi }_{1}\left(\tau \right)}$ and ${Q}_{2}\left(\tau \right)=\frac{1}{2}{z}_{2}\left(\tau \right) {e}^{i{\psi }_{2}\left(\tau \right)}$ into Eqs. (20.1) and (20.2) and then separating the real and imaginary components, we can deduce the following autonomous system:

$$ \begin{gathered} \frac{{dz_{1} }}{d\tau } = - \frac{1}{2}\left[ {\mu_{1} + \frac{{\Delta \eta_{1} \delta_{2} }}{{(1 + \delta_{1}^{2} )}}} \right]z_{1} - \left[ {\frac{{\Delta \eta_{1}^{2} \delta_{1} \delta_{2}^{2} }}{{4(1 + \delta_{1}^{2} )^{2} }} + \frac{{3\Delta \eta_{1} \delta_{2} }}{{8(1 + \delta_{1}^{2} )}} + \frac{{3\Delta \eta_{2} \delta_{2}^{3} }}{{8(1 + \delta_{1}^{2} )^{2} }}} \right]z_{1}^{3} \\ - \left[ {\frac{{9\Delta \eta_{2} \delta_{2}^{3} }}{{32(1 + \delta_{1}^{2} )^{2} }} - \frac{{3\Delta \eta_{2} \delta_{2}^{3} (1 - 3\delta_{1}^{2} )}}{{32(1 + \delta_{1}^{2} )^{3} }} + \frac{{3\Delta \eta_{1} \eta_{2} \delta_{1} \delta_{2}^{4} }}{{4(1 + \delta_{1}^{2} )^{4} }} + \frac{{\Delta \eta_{1} \eta_{2} \delta_{1} \delta_{2}^{4} }}{{2(1 + \delta_{1}^{2} )^{3} }}} \right]z_{1}^{5} \\ + \left[ {\frac{{5\Delta \eta_{2}^{2} \delta_{1} \delta_{2}^{6} (3 + \delta_{1}^{2} )}}{{16(1 + \delta_{1}^{2} )^{6} }} - \frac{{15\Delta \eta_{2}^{2} \delta_{1} \delta_{2}^{6} }}{{64(1 + \delta_{1}^{2} )^{4} }}} \right]z_{1}^{7} - \frac{{3\alpha_{1} }}{32}z_{1} z_{2}^{2} \sin (2\theta_{2} - 2\theta_{1} ) \\ - \frac{{\alpha_{2} }}{4}z_{1} \sin (2\theta_{1} ) - \frac{{3\alpha_{1} }}{64}z_{1} z_{2}^{2} \sin (2\theta_{2} + 2\theta_{1} ) - \frac{{\alpha_{2} }}{8}z_{1}^{3} \sin (2\theta_{1} ) + \frac{{\alpha_{1} }}{64}z_{1}^{3} \sin (4\theta_{1} ) \\ - \frac{{\alpha_{2} }}{4}z_{2} \cos (\theta_{2} + \theta_{1} ) - \frac{{3\alpha_{3} }}{32}z_{2}^{3} \cos (\theta_{2} + \theta_{1} ) + \frac{{\alpha_{3} }}{32}z_{2}^{3} \cos (3\theta_{2} - \theta_{1} ) \\ - \frac{{\alpha_{1} }}{64}z_{2}^{3} \cos (\theta_{1} + 3\theta_{2} ) - \frac{{3\alpha_{3} }}{32}z_{1}^{2} z_{2} \cos (\theta_{2} - 3\theta_{1} ) - \frac{{3\alpha_{3} }}{32}z_{1}^{2} z_{2} \cos (\theta_{2} + \theta_{1} ) \\ + \frac{{3\alpha_{1} }}{64}z_{1}^{2} z_{2} \cos (\theta_{2} + 3\theta_{1} ) + \frac{{f\omega^{2} }}{2}\sin (\theta - \theta_{1} ), \\ \end{gathered} $$

(21.1)

$$\begin{aligned} \frac{{dz_{2} }}{{d\tau }} = & - \frac{1}{2}\left[ {\mu _{2} + \frac{{\Delta \eta _{1} \delta _{2} }}{{(\delta _{1}^{2} + 1)}}} \right]z_{2} - \left[ {\frac{{\Delta \eta _{1}^{2} \delta _{1} \delta _{2}^{2} }}{{4(\delta _{1}^{2} + 1)^{2} }} + \frac{{3\Delta \eta _{1} \delta _{2} }}{{8(\delta _{1}^{2} + 1)}} + \frac{{3\Delta \eta _{2} \delta _{2}^{3} }}{{8(\delta _{1}^{2} + 1)^{2} }}} \right]z_{2}^{3} \\ & - \left[ {\frac{{9\Delta \eta _{2} \delta _{2}^{3} }}{{32(\delta _{1}^{2} + 1)^{2} }} - \frac{{3\Delta \eta _{2} (1 - 3\delta _{1}^{2} )\delta _{2}^{3} }}{{32(\delta _{1}^{2} + 1)^{3} }} + \frac{{3\Delta \eta _{1} \eta _{2} \delta _{1} \delta _{2}^{4} }}{{4(\delta _{1}^{2} + 1)^{4} }} + \frac{{\Delta \eta _{1} \eta _{2} \delta _{1} \delta _{2}^{4} }}{{2(\delta _{1}^{2} + 1)^{3} }}} \right]z_{2}^{5} \\ & + \left[ {\frac{{5\Delta \eta _{2}^{2} \delta _{1} (3 + \delta _{1}^{2} )\delta _{2}^{6} }}{{16(\delta _{1}^{2} + 1)^{6} }} - \frac{{15\Delta \eta _{2}^{2} \delta _{1} \delta _{2}^{6} }}{{64(\delta _{1}^{2} + 1)^{4} }}} \right]z_{2}^{7} - \frac{{3\alpha _{1} }}{{32}}z_{1}^{2} z_{2} \sin (2\theta _{1} - 2\theta _{2} ) \\ & + \frac{{\alpha _{2} }}{4}z_{2} \sin (2\theta _{2} ) - \frac{{3\alpha _{1} }}{{64}}z_{1}^{2} z_{2} \sin (2\theta _{2} + 2\theta _{1} ) - \frac{{\alpha _{2} }}{8}z_{2}^{3} \sin (2\theta _{2} ) + \frac{{\alpha _{1} }}{{64}}z_{2}^{3} \sin (4\theta _{2} ) \\ & - \frac{{\alpha _{2} }}{4}z_{1} \cos (\theta _{2} + \theta _{1} ) - \frac{{3\alpha _{3} }}{{32}}z_{1}^{3} \cos (\theta _{2} + \theta _{1} ) + \frac{{\alpha _{3} z_{1}^{3} }}{{32}}\cos (3\theta _{1} - \theta _{2} ) \\ & + \frac{{\alpha _{1} }}{{64}}z_{1}^{3} \cos (\theta _{2} + 3\theta _{1} ) - \frac{{3\alpha _{3} }}{{32}}z_{1} z_{2}^{2} \cos (\theta _{1} - 3\theta _{2} ) - \frac{{3\alpha _{3} }}{{32}}z_{1} z_{2}^{2} \cos (\theta _{2} + \theta _{1} ) \\ & - \frac{{3\alpha _{1} }}{{64}}z_{1} z_{2}^{2} \cos (\theta _{1} + 3\theta _{2} ) - \frac{{f\omega ^{2} }}{2}\cos (\theta - \theta _{2} ), \\ \end{aligned}$$

(21.2)

$$ \begin{aligned} \frac{{d\theta _{1} }}{{d\tau }} = & \left[ {1 - \frac{\Delta }{2} - \frac{{\eta _{1} \delta _{1} \delta _{2} }}{{2(\delta _{1}^{2} + 1)}} - \Omega } \right] + \frac{9}{{32}}\left[ {\alpha _{1} - \frac{{8\Delta }}{3} - \frac{{8\Delta \eta _{1}^{2} \delta _{2}^{2} }}{{9(\delta _{1}^{2} + 1)}} - \frac{{4\Delta \eta _{1}^{2} (\delta _{1}^{2} - 1)\delta _{2}^{2} }}{{9(\delta _{1}^{2} + 1)^{2} }} - \frac{{4\Delta \eta _{1} \delta _{1} \delta _{2} }}{{(\delta _{1}^{2} + 1)}}} \right. \\ & \left. { - \frac{{4\Delta \eta _{2} \delta _{1} \delta _{2}^{3} }}{{3(\delta _{1}^{2} + 1)^{2} }}} \right]z_{1}^{2} - \frac{3}{{32}}\left[ {\frac{{9\Delta \eta _{2} \delta _{1} \delta _{2}^{3} }}{{(\delta _{1}^{2} + 1)^{2} }} + \frac{{\Delta \eta _{2} (\delta _{1}^{3} - 3\delta _{1} )\delta _{2}^{3} }}{{(\delta _{1}^{2} + 1)^{3} }} + \frac{{4\eta _{1} \eta _{2} \delta _{2}^{4} }}{{(\delta _{1}^{2} + 1)^{2} }} + \frac{{8\Delta \eta _{1} \eta _{2} (\delta _{1}^{4} - 1)\delta _{2}^{4} }}{{3(\delta _{1}^{2} + 1)^{4} }}} \right]z_{1}^{4} \\ & - \frac{5}{{32}}\left[ {\frac{{\Delta \eta _{2}^{2} \delta _{2}^{6} }}{{(\delta _{1}^{2} + 1)^{3} }} + \frac{{3\Delta \eta _{2}^{2} (\delta _{1}^{6} + \delta _{1}^{4} - \delta _{1}^{2} - 1)\delta _{2}^{6} }}{{4(\delta _{1}^{2} + 1)^{6} }}} \right]z_{1}^{6} - \frac{{\alpha _{3} }}{4}z_{1}^{2} \cos (2\theta _{1} ) + \frac{{\alpha _{1} }}{{64}}z_{1}^{2} \cos (4\theta _{1} ) \\ & + \frac{{3\alpha _{1} }}{{32}}z_{2}^{2} \cos (2\theta _{2} - 2\theta _{1} ) - \frac{{3\alpha _{1} }}{{64}}z_{2}^{2} \cos (2\theta _{2} + 2\theta _{1} ) + \frac{{3\alpha _{1} }}{{16}}z_{2}^{2} - \frac{{\alpha _{2} }}{4}\cos (2\theta _{1} ) + \frac{{\alpha _{2} }}{{4z_{1} }}z_{2} \sin (\theta _{2} + \theta _{1} ) \\ & + \frac{{3\alpha _{3} }}{{32z_{1} }}z_{2}^{3} \sin (\theta _{2} + \theta _{1} ) + \frac{{\alpha _{3} }}{{32z_{1} }}z_{2}^{3} \sin (3\theta _{2} - \theta _{1} ) + \frac{{\alpha _{1} }}{{64z_{1} }}z_{2}^{3} \sin (\theta _{1} + 3\theta _{2} ) - \frac{{3\alpha _{3} }}{{32}}z_{1} z_{2} \sin (\theta _{2} - 3\theta _{1} ) \\ & - \frac{{9\alpha _{3} }}{{32}}z_{1} z_{2} \sin (\theta _{2} + \theta _{1} ) + \frac{{3\alpha _{1} }}{{64}}z_{1} z_{2} \sin (\theta _{2} + 3\theta _{1} ) - \frac{{f\omega ^{2} }}{{2z_{1} }}\cos (\theta - \theta _{1} ), \\ \end{aligned} $$

(21.3)

$$ \begin{aligned} \frac{{d\theta _{2} }}{{d\tau }} = & \left[ {1 - \frac{\Delta }{2} - \frac{{\Delta \eta _{1} \delta _{1} \delta _{2} }}{{2(\delta _{1}^{2} + 1)}} - \Omega } \right] + \frac{9}{{32}}\left[ {\alpha _{1} - \frac{{8\Delta }}{3} - \frac{{8\Delta \eta _{1}^{2} \delta _{2}^{2} }}{{9(\delta _{1}^{2} + 1)}} - \frac{{4\Delta \eta _{1}^{2} (\delta _{1}^{2} - 1)\delta _{2}^{2} }}{{9(\delta _{1}^{2} + 1)^{2} }} - \frac{{4\Delta \eta _{1} \delta _{1} \delta _{2} }}{{(\delta _{1}^{2} + 1)}}} \right. \\ & \left. { - \frac{{4\eta _{2} \delta _{1} \delta _{2}^{3} }}{{3(\delta _{1}^{2} + 1)^{2} }}} \right]z_{2}^{2} - \frac{3}{{32}}\left[ {\frac{{9\Delta \eta _{2} \delta _{1} \delta _{2}^{3} }}{{(\delta _{1}^{2} + 1)^{2} }} + \frac{{\Delta \eta _{2} (\delta _{1}^{3} - 3\delta _{1} )\delta _{2}^{3} }}{{(\delta _{1}^{2} + 1)^{3} }} + \frac{{4\Delta \eta _{1} \eta _{2} \delta _{2}^{4} }}{{(\delta _{1}^{2} + 1)^{2} }} + \frac{{8\Delta \eta _{1} \eta _{2} (\delta _{1}^{4} - 1)\delta _{2}^{4} }}{{3(\delta _{1}^{2} + 1)^{4} }}} \right]z_{2}^{4} \\ & - \frac{5}{{32}}\left[ {\frac{{\Delta \eta _{2}^{2} \delta _{2}^{6} }}{{(\delta _{1}^{2} + 1)^{3} }} + \frac{{3\Delta \eta _{2}^{2} (\delta _{1}^{6} + \delta _{1}^{4} - \delta _{1}^{2} - 1)\delta _{2}^{6} }}{{4(\delta _{1}^{2} + 1)^{6} }}} \right]z_{2}^{6} - \frac{{\alpha _{3} }}{4}z_{2}^{2} \cos (2\theta _{2} ) + \frac{{\alpha _{1} }}{{64}}z_{2}^{2} \cos (4\theta _{2} ) \\ & + \frac{{3\alpha _{1} }}{{32}}z_{1}^{2} \cos (2\theta _{1} - 2\theta _{2} ) - \frac{{3\alpha _{1} }}{{64}}z_{1}^{2} \cos (2\theta _{2} + 2\theta _{1} ) + \frac{{3\alpha _{1} }}{{16}}z_{1}^{2} + \frac{{\alpha _{2} }}{{4z_{2} }}z_{1} \sin (\theta _{2} + \theta _{1} ) + \frac{{\alpha _{2} }}{4}\cos (2\theta _{2} ) \\ & + \frac{{3\alpha _{3} }}{{32z_{2} }}z_{1}^{3} \sin (\theta _{2} + \theta _{1} ) + \frac{{\alpha _{3} }}{{32z_{2} }}z_{1}^{3} \sin (3\theta _{1} - \theta _{2} ) - \frac{{\alpha _{1} }}{{64z_{2} }}z_{1}^{3} \sin (3\theta _{1} + \theta _{2} ) - \frac{{3\alpha _{3} }}{{32}}z_{2} z_{1} \sin (\theta _{1} - 3\theta _{2} ) \\ & + \frac{{9\alpha _{3} }}{{32}}z_{2} z_{1} \sin (\theta _{2} + \theta _{1} ) + \frac{{3\alpha _{1} }}{{64}}z_{2} z_{1} \sin (\theta _{1} + 3\theta _{2} ) - \frac{{f\omega ^{2} }}{{2z_{2} }}\sin (\theta - \theta _{2} ), \\ \end{aligned} $$

(21.4)

where ${\theta }_{1}=\left[{\psi }_{1}-\upomega \tau +\tau \right]$ and ${\theta }_{2}=\left[{\psi }_{2}-\upomega \tau +\tau \right]$. Substituting Eqs. (18.1) to (18.4) into Eqs. (13.1) and (13.2), one can obtain the periodic solution of Eqs. (12.1) to (12.4) as follows:

$$ y_{1} (\tau ) = z_{1} (\tau )\cos (\omega \tau - \theta_{1} (\tau )), $$

(22.1)

$$ y_{2} (\tau ) = z_{2} (\tau )cos(\omega \tau - \theta_{2} (\tau )), $$

(22.2)

$$ y_{3} (\tau ) = \frac{{\delta_{2} z_{1} (\tau )}}{{\delta_{1}^{2} + 1}}\left[ {\delta_{1} \cos (\omega \tau - \theta_{1} (\tau )) + \sin (\omega \tau - \theta_{1} (\tau ))} \right] = z_{3} (\tau )\sin (\omega \tau - \theta_{3} (\tau )), $$

(22.3)

$$ y_{4} (\tau ) = \frac{{\delta_{2} z_{2} (\tau )}}{{\delta_{1}^{2} + 1}}\left[ {\delta_{1} \cos (\omega \tau - \theta_{2} (\tau )) + \sin (\omega \tau - \theta_{2} (\tau ))} \right] = z_{4} (\tau )\sin (\omega \tau - \theta_{4} (\tau )), $$

(22.4)

where ${z}_{3}=\frac{{\delta }_{2}}{\sqrt{{\delta }_{2}^{2}+1}}{z}_{1}, {z}_{4}=\frac{{\delta }_{2}}{\sqrt{{\delta }_{2}^{2}+1}}{z}_{2}, {\theta }_{3}={\theta }_{1}-{{\text{tan}}}^{-1}\left({\delta }_{1}\right)$, and ${\theta }_{4}={\theta }_{2}-{{\text{tan}}}^{-1}\left({\delta }_{1}\right)$. It is important to note from Eqs. (22.1) and (22.2) that ${z}_{1}\left(\tau \right), {z}_{2}\left(\tau \right), {\theta }_{1}\left(\tau \right),$ and ${\theta }_{2}\left(\tau \right)$ represent the oscillation amplitudes and phase angles of the rotor system in the ${y}_{1}$ and ${y}_{2}$ directions. These parameters (${z}_{1}\left(\tau \right), {z}_{2}\left(\tau \right), {\theta }_{1}\left(\tau \right),$ and ${\theta }_{2}\left(\tau \right)$) are governed by the derived dynamical system given by Eqs. (21.1) to (21.4), expressed in terms of the system and control parameters (i.e., $f, {\alpha }_{1}, {\alpha }_{2}, {\alpha }_{3}, {\eta }_{1}, {\eta }_{2}, {\delta }_{1}, {\delta }_{2}$). Additionally, it is evident from Eqs. (22.3) and (22.4) that ${z}_{3}, {z}_{4}, {\theta }_{3},$ and ${\theta }_{4}$ are linear functions of the rotor amplitudes and phases. Therefore, by analyzing the bifurcation characteristics of the system (21.1) to (21.4), one can explore the dynamics of the controlled rotor model given by Eqs. (12.1) to (12.4).

3 Stability analysis, bifurcation diagrams, and numerical simulations

At steady-state vibration, the rotor oscillation amplitudes and phase angles exhibit a zero rate of change (i.e., $d{z}_{1}\backslash d\tau =d{z}_{2}\backslash d\tau ={d\theta }_{1}\backslash d\tau ={d\theta }_{2}\backslash d\tau =0.0$). Consequently, the nonlinear algebraic system that dictates rotor vibrations under steady-state conditions can be expressed using Eqs. (21.1) to (21.4) as follows:

$$ G_{j} (z_{1} ,z_{2} ,\theta_{1} ,\theta_{2} ) = \frac{{dz_{k} }}{d\tau } = 0,\,\,\,\,\,\,\,\,\,\,\,\,j = k = 1,2 $$

(23.1)

$$ G_{j} (z_{1} ,z_{2} ,\theta_{1} ,\theta_{2} ) = \frac{{d\theta_{k} }}{d\tau } = 0,\,\,\,\,\,\,\,\,\,\,\,\,j = 3,4,\,\,\,k = 1,2. $$

(23.2)

By numerically solving for ${G}_{j}\left({z}_{1},{z}_{2}, {\theta }_{1}, {\theta }_{2} \right)=0$, where $j=\mathrm{1,2},\mathrm{3,4}$, concerning various parameters (i.e., $f, {\alpha }_{1}, {\alpha }_{2}, {\alpha }_{3}, {\eta }_{1}, {\eta }_{2}, {\delta }_{1}, {\delta }_{2}$), one can generate the system's bifurcation diagrams as detailed in Sects. 3.1 and 3.2. Additionally, to assess the solution stability of Eqs. (23.1) and (23.2), let the solution for ${G}_{j}\left({z}_{1},{z}_{2}, {\theta }_{1}, {\theta }_{2}\right)=0$ be ${z}_{1}={w}_{1}, {{z}_{2}=w}_{2}, {\theta }_{1}={w}_{3},$ and ${\theta }_{2}={w}_{4}$. Further, consider ${w}_{10}, {w}_{20}, {w}_{30}$, and ${w}_{40}$ are small infinitesimal increments of ${w}_{1}, {w}_{2}, {w}_{3},$ and ${w}_{4}$, respectively. Consequently, the perturbed solution of Eqs. (23.1) and (23.2) can be expressed as follows:

$$ \left\{ \begin{gathered} z_{1} = w_{1} + w_{10} , \, \,z_{2} = w_{2} + w_{20} ,\,\,\,\,\theta_{1} = w_{3} + w_{30} , \, \,\,\,\theta_{2} = w_{4} + w_{40} \,, \hfill \\ \frac{{dz_{1} }}{d\tau } = \frac{{dw_{10} }}{d\tau }, \, \,\,\,\,\frac{{dz_{2} }}{d\tau } = \frac{{dw_{20} }}{d\tau },\,\,\,\,\,\,\,\frac{{d\theta_{1} }}{d\tau } = \frac{{dw_{30} }}{d\tau }, \, \,\,\,\,\,\,\,\frac{{d\theta_{2} }}{d\tau } = \frac{{dw_{40} }}{d\tau }. \hfill \\ \end{gathered} \right. $$

(24)

By substituting Eqs. (24) into Eqs. (21.1) to (21.4) and linearizing the resulting nonlinear system around the equilibrium point (${w}_{1}, {w}_{2}, {w}_{3}, {w}_{4}$), the following linear variational system is obtained:

$$ \left( {\begin{array}{*{20}c} {\frac{{dw_{10} }}{d\tau }} \\ {\frac{{dw_{20} }}{d\tau }} \\ {\frac{{dw_{30} }}{d\tau }} \\ {\frac{{dw_{40} }}{d\tau }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{{\partial G_{1} }}{{\partial w_{1} }}} & {\frac{{\partial G_{1} }}{{\partial w_{2} }}} & {\frac{{\partial G_{1} }}{{\partial w_{3} }}} & {\frac{{\partial G_{1} }}{{\partial w_{4} }}} \\ {\frac{{\partial G_{2} }}{{\partial w_{1} }}} & {\frac{{\partial G_{2} }}{{\partial w_{2} }}} & {\frac{{\partial G_{2} }}{{\partial w_{3} }}} & {\frac{{\partial G_{2} }}{{\partial w_{4} }}} \\ {\frac{{\partial G_{3} }}{{\partial w_{1} }}} & {\frac{{\partial G_{3} }}{{\partial w_{2} }}} & {\frac{{\partial G_{3} }}{{\partial w_{3} }}} & {\frac{{\partial G_{3} }}{{\partial w_{4} }}} \\ {\frac{{\partial G_{4} }}{{\partial w_{1} }}} & {\frac{{\partial G_{4} }}{{\partial w_{2} }}} & {\frac{{\partial G_{4} }}{{\partial w_{3} }}} & {\,\frac{{\partial G_{4} }}{{\partial w_{4} }}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {w_{10} } \\ {w_{20} } \\ {w_{30} } \\ {w_{40} } \\ \end{array} } \right), $$

(25)

The coefficients $\frac{\partial {G}_{j}}{\partial {w}_{k}}$, where $\{j=1, 2, 3, 4;k=1, 2, 3, 4\}$, are provided in Appendix. Thus, the stability of the solution for Eqs. (23.1) to (23.2) can be assessed by examining the eigenvalues of Eq. (25) (see Ref. [45]). To investigate the dynamics of the asymmetric rotor model in terms of the original system parameters and control gains, the controlled system physical parameters have been selected as given in Table 1. In addition, the corresponding dimensionless coefficients are calculated and reported in Table 2. Employing the normalized parameters given in Table 2, one can investigate the motion bifurcation of the considered mathematical model governed by Eqs. (12.1) to (12.4) via solving the algebraic system given by Eqs. (23.1) and (23.2). Moreover, the solution stability can be checked by analyzing the eigenvalues of the linear system given by Eq. (25).

Table 2 Rotor-actuator dimensionless parameters

3.1 Nonlinear dynamics of the uncontrolled model

The nonlinear interaction of the rotor system with both linear and nonlinear asymmetric stiffness is discussed in this section before control (i.e. $\Delta ={\eta }_{1}={\eta }_{2}={\delta }_{1}={\delta }_{2}=0$). Before proceeding further, it is worth mentioning that the parameter ${\alpha }_{1}={R}_{0}^{2}{K}_{N}/{k}_{L}$ represents the nonlinear dimensionless stiffness coefficient of the system, ${\alpha }_{2}=\Delta {K}_{L}/{K}_{L}$ denotes the linear dimensionless asymmetric stiffness, and ${\alpha }_{3}=\Delta {K}_{N}/{K}_{L}$ is the nonlinear dimensionless asymmetric stiffness.

The nonlinear response of the rotor system, when neglecting stiffness asymmetry (i.e.${\alpha }_{2}={\alpha }_{3}=0.0$), is illustrated by plotting the steady-state amplitudes (${z}_{1}$ and${z}_{2}$) and the corresponding phase angles (${\theta }_{1}$ and${\theta }_{2}$) versus $\sigma$, as shown in Fig. 3. The figure is obtained by solving Eqs. (23.1) and (23.2) applying the Newton–Raphson algorithm [46], utilizing $\sigma$ as the parameter of bifurcation. Simultaneously, the stability of the solution is explored by analyzing the eigenvalues of the linear system given by Eq. (25). The stable solution is plotted as a solid line, and the unstable solution is shown as a dotted line. It is evident from Fig. 3a and b that in a symmetric model (i.e.${\alpha }_{2}={\alpha }_{3}=0.0$), two solution branches labeled S.B. (1) and S.B. (2) are observed. These solution branches may coexist, signifying the presence of a bi-stable solution for the rotor system, or they may exist individually, indicating mono-stable solutions. This distinction depends on the angular velocity$\omega$, which has been parameterized using $\sigma$ as defined by Eq. (19). In addition, the change of phase angles in terms of $\sigma$ are illustrated according to the S.B. (1) and S.B. (2), respectively, in Fig. 3c and d. Furthermore, Fig. 3c and d depict the variation of phase angles in terms of $\sigma$ for the solution branches S.B. (1) and S.B. (2) respectively. Building upon the established periodic solution provided by Eqs. (22.1) and (22.2), one can infer that when the phase angle ${\theta }_{1}$ is greater than ${\theta }_{2}$ (i.e. ${\theta }_{1}>{\theta }_{2}$), it indicates the forward whirling of the system. Conversely, if${\theta }_{1}<{\theta }_{2}$, it signifies the backward whirling of the system. Accordingly, Fig. 3c and d demonstrate that the considered rotor model can perform forward whirling only. Hence, the solution multiplicity as well as the associated oscillation amplitudes of the symmetric system as a function of $\sigma$ can be predicted utilizing bifurcation diagrams shown in Fig. 3a and b, while the whirling direction associated with each solution branch can be demonstrated from Fig. 3c and d. Consequently, Fig. 3c and d reveal that the analyzed rotor model exhibits exclusively forward whirling. Thus, the multiplicity of solutions and the corresponding oscillation amplitudes (${z}_{1}$ and${z}_{2}$), as a function of$\sigma$, can be anticipated using the bifurcation diagrams depicted in Fig. 3a and b. Simultaneously, the whirling direction linked to each solution branch (S.B. (1) and S.B. (2)) can be determined using Fig. 3c and d.

Fig. 3

Vibration amplitudes (${z}_{1}$ and ${z}_{2}$) and the phase angles (${\theta }_{1}$ and ${\theta }_{2}$) against $\sigma$ when ${\alpha }_{1}=0.05$ and ${\alpha }_{2}={\alpha }_{3}=0.0$

Figure 3a and 3b indicate that the system can exhibit one of two stable solutions for $\sigma >0$. For instance, the rotor model presents two periodic solutions at $\sigma =0.02$, each with oscillation amplitudes ${S}_{11}$ and ${S}_{12}$ as marked in the figure. The system will follow one of these solutions based on the rotor's initial positions (${y}_{1}\left(0\right)$ and ${y}_{2}\left(0\right)$) and velocities ($\dot{{y}_{1}}\left(0\right)$ and $\dot{{y}_{2}}\left(0\right)$). Similarly, at $\sigma =0.1$, the amplitudes for the two solutions are ${S}_{21}$ and ${S}_{22}$, while at at $\sigma =0.2$,, the amplitudes are ${S}_{31}$ and ${S}_{32}$. To numerically validate the accuracy of the bifurcation diagrams presented in Fig. 3, Eqs. (12.1) and (12.2) were solved using the MATLAB ODE45 solver, adhering to the parameters specified in Fig. 3 (i.e., ${\alpha }_{1}=0.05, {\alpha }_{2}={\alpha }_{3}=0.0$). Numerical solutions were computed for the three discrete values of $\sigma : 0.02, 0.1,$ and $0.2$. Subsequently, the corresponding basins of attraction were established, as illustrated in Fig. 4.

Fig. 4

Basins of attraction in the three different two-dimensional spaces according to Fig. 2 at $\sigma =0.02, 0.1$, and $0.2$: a, b, c basin of attraction in ${\dot{y}}_{1}\left(0\right)-{\dot{y}}_{2}\left(0\right)$ space when ${y}_{1}\left(0\right)={y}_{2}(0)=0.0$, d, e, f basin of attraction in ${y}_{1}\left(0\right)-{y}_{2}\left(0\right)$ space when ${\dot{y}}_{1}\left(0\right)={\dot{y}}_{2}\left(0\right)=0.0$, and (g, h, i) basin of attraction in $({y}_{1}\left(0\right)={\dot{y}}_{1}\left(0\right))-({y}_{2}\left(0\right)={\dot{y}}_{2}\left(0\right))$ space

To determine the basin of attraction for a 2-DOF system (i.e. Equations (12.1) and (12.2)), three distinct techniques were employed. First, the basins were constructed in the $\dot{{y}_{1}}\left(0\right)-\dot{{y}_{2}}\left(0\right)$ space, with a fixed initial position set to zero (${y}_{1}\left(0\right)={y}_{2}\left(0\right)=0.0$), as depicted in Fig. 4a to c. Second, the basins were illustrated in the ${y}_{1}\left(0\right)-{y}_{2}(0)$ space, assuming zero initial vibration velocities (i.e., $\dot{{y}_{1}}\left(0\right)-\dot{{y}_{2}}\left(0\right)=0$), as shown in Fig. 4d to f. Third, assuming ${y}_{1}\left(0\right)=\dot{{y}_{1}}\left(0\right)$ and ${y}_{2}\left(0\right)=\dot{{y}_{2}}\left(0\right)$, the basin of attraction was plotted, as presented in Fig. 4g to i. In all subfigures, the basin of attraction for the solution ${S}_{j1}$ is highlighted in magenta, while the basin of the solution ${S}_{j2}$ is illustrated in cyan, where $j=\mathrm{1,2},3.$

Based on the basin of attraction depicted in Fig. 4d (i.e. $\sigma =0.02,$ and $\dot{{y}_{1}}\left(0\right)=\dot{{y}_{2}}\left(0\right)=0.0$), the two periodic solutions corresponding to the attractors ${S}_{11}$ and ${S}_{12}$ were numerically verified by solving Eqs. (12.1) and (12.2) at two different initial positions, as illustrated in Fig. 5. The first position was chosen with ${y}_{1}\left(0\right)={y}_{2}\left(0\right)=0$ to fall within the attractor ${S}_{11}$, while the second position was selected to be within the attractor ${S}_{12}$ by setting ${y}_{1}\left(0\right)=0.0$ and ${y}_{2}\left(0\right)=-1.5$. The figure demonstrates that the rotor exhibits one of two periodic motions based on the initial conditions, with oscillation amplitudes strongly aligning with those presented in Fig. 3a and b at $\sigma =0.02$. Moreover, the system whirls forward, consistent with the observation in Fig. 3d.

Fig. 5

The bi-stable periodic solution of the rotor system according to the basin of attraction shown in Fig. 3d when ${\dot{y}}_{1}\left(0\right)={\dot{y}}_{2}\left(0\right)=0.0$

The impact of linear asymmetric stiffness on the system dynamics is depicted in Fig. 6. This figure illustrates the bifurcation of periodic motion in the nonlinear system (i.e. ${\alpha }_{1}=0.05$) with a linear asymmetric stiffness ${\alpha }_{2}=0.1$. By comparing Fig. 6a and b with Fig. 3a and b, one can infer that the presence of linear asymmetry in the rotor restoring forces may reduce the system's linear natural frequency, leading to pronounced oscillations and solution multiplicity at angular velocities below the rotor's first critical speed (i.e., when $\sigma <0$). This is in contrast to the behavior observed in the symmetric system shown in Fig. 3a and b. In addition, the bifurcation diagrams encompass three solution branches labeled S.B. (1), S.B. (2), and S.B. (3), which indicate the coexistence of both mono-stable and tri-stable stable periodic solutions on specific rotational speed intervals. Nevertheless, the bifurcation diagram reveals that the two stable solution branches, S.B. (1) and S.B. (2), seamlessly merge into a single solution branch when the rotor's angular speed reaches the point where the solution branch S.B. (3) emerges. To illustrate, at $\sigma =-0.02$, the system exhibits two periodic solutions labeled ${S}_{11}$ and ${S}_{12}$. However, as $\sigma$ increases to $0.1$, these two solutions, ${S}_{11}$ and ${S}_{12}$, appear to merge into a unified solution, ${S}_{22}$. Concurrently, a new branch, denoted as S.B. (3), emerges, giving rise to the solution ${S}_{21}$. Furthermore, upon scrutiny of Fig. 6c to e, it becomes evident that ${\theta }_{1}>{\theta }_{2}$ for all solution branches, indicating that the rotor can only whirl in the forward direction regardless of the initial values and the spinning speed.

Fig. 6

Vibration amplitudes (${z}_{1}$ and ${z}_{2}$) and the phase angles (${\theta }_{1}$ and ${\theta }_{2}$) against $\sigma$ when ${\alpha }_{1}=0.05, {\alpha }_{2}=0.1,$ and ${\alpha }_{3}=0.0$

To validate the accuracy of the bifurcation diagrams presented in Fig. 6, the basin of attraction was constructed in the ${y}_{1}\left(0\right)-{y}_{2}\left(0\right)$ space by numerically solving Eqs. (12.1) and (12.2), with the initial lateral velocities fixed at zero, as depicted in Fig. 7. Figure 7a showcases the basin of attraction for the bi-stable periodic solutions ${S}_{11}$ and ${S}_{12}$ reported at $\sigma =-0.02$ in Fig. 6. Figure 7b and c illustrate the basins of attraction for $\sigma =0.1$ and $0.2$, respectively. It is worth noting that although the attractors for both ${S}_{22}$ and ${S}_{32}$, as marked in Fig. 6, consist of two periodic solutions resulting from solution branches S.B. (1) and S.B. (2), they are treated as a single solution with one attractor, as shown in Fig. 7b and c.

Fig. 7

Basins of attraction in ${y}_{1}\left(0\right)-{y}_{2}(0)$ space when ${\dot{y}}_{1}\left(0\right)={\dot{y}}_{2}\left(0\right)=0.0$ according to Fig. 6: a $\sigma =-0.02$, b $\sigma =0.1$, c $\sigma =0.2$

To substantiate the presence of three periodic solutions resulting from the coexistence of three stable solution branches, a closer examination of the point ${S}_{22}$ marked in Fig. 6 is presented in Fig. 8a and b, where two distinct points, ${S}_{221}$ and ${S}_{222}$, are highlighted. Additionally, the basin of attraction, as depicted in Fig. 7b, is revisited in Fig. 8c with a reduced resolution to emphasize the attractors of the three periodic solutions ${S}_{21}, {S}_{221}$ and ${S}_{222}$. Ultimately, the three concurrent periodic solutions are depicted in Fig. 9, corresponding to the marked initial conditions highlighted in Fig. 8c.

Fig. 8

a, b A zoomed-in view of the marked point ${S}_{22}$ shown in Figs. 6, and c displays a low-resolution representation of the basin of attraction depicted in Fig. 7b

Fig. 9

The tri-stable periodic solution of the rotor system corresponds to the basin of attraction shown in Fig. 8c

The rotor dynamics, considering the simultaneous effect of linear and nonlinear asymmetric stiffness (i.e. ${\alpha }_{2}=0.1,$ and ${\alpha }_{3}=0.025$), are illustrated in Fig. 10. Comparing Fig. 10a and b with Fig. 6a and b, it is evident that the bifurcation behaviors of the rotor, under the influence of both linear and nonlinear asymmetric stiffness, are similar to those observed when only linear asymmetric stiffness is present, as shown in Fig. 6a and b. A noteworthy distinction is the appearance of the solution branch S.B. (4) when $\sigma >0$, suggesting the possibility of the rotor having mono-stable, bi-stable, tri-stable, and quadri-stable periodic solutions at the same spinning speed depending on the angular velocity. Additionally, the phase angle relationship presented in Fig. 10f indicates that ${\theta }_{1}> {\theta }_{2}$, signifying the initiation of backward whirling motion in the rotor when it follows S.B. (4). Conversely, the rotor will exhibit forward whirling, as demonstrated in Fig. 10c, d, and e, where ${\theta }_{1}< {\theta }_{2}$.

Fig. 10

Vibration amplitudes (${z}_{1}$ and ${z}_{2}$) and the phase angles (${\theta }_{1}$ and ${\theta }_{2}$) against $\sigma$ when ${\alpha }_{1}=0.05, {\alpha }_{2}=0.1,$ and ${\alpha }_{3}=0.025$

Consequently, the basins of attraction according to Fig. 10 when $\sigma =-0.02, 0.1,$ and $0.2$ have been established as illustrated in Fig. 11). Figure 11a visualizes the attractors of the bi-stable solution ${S}_{11}$ and ${S}_{12}$ reported in Fig. 10 when $\sigma =-0.02$. Figure 11b and c depict the basins of attraction corresponding to the quadri-stable solutions reported in Fig. 10 when $\sigma =0.1,$ and $0.2$, respectively. It is worth noting that the two periodic solutions (${S}_{23}$ and ${S}_{33}$), resulting from solution branches S.B. (1) and S.B. (2), are treated as a single solution attractor (cyan color attractor in Fig. 11b and c). This consolidation is due to the merging of branches S.B. (1) and S.B. (2) into one branch at $\sigma =0.1,$ and $0.2$. However, to substantiate the existence of quadri-stable periodic solutions resulting from the coexistence of four solution branches, a closer examination of the point ${S}_{33}$ marked in Fig. 10a is depicted in Fig. 12a and b, where two distinct solutions, ${S}_{331}$ and ${S}_{332}$, are highlighted. Additionally, the basin of attraction, as shown in Fig. 11c, is revisited in Fig. 12c with a reduced resolution to emphasize the attractors of the quadri-stable periodic solutions ${S}_{31}, {S}_{32}, {S}_{331}$ and ${S}_{332}$. Ultimately, four concurrent periodic solutions are illustrated in Fig. 13, corresponding to the marked initial conditions highlighted in Fig. 12c.

Fig. 11

Basins of attraction in ${y}_{1}\left(0\right)-{y}_{2}(0)$ space when ${\dot{y}}_{1}\left(0\right)={\dot{y}}_{2}\left(0\right)=0.0$ according to Fig. 10: a $\sigma =-0.02$, b $\sigma =0.1$, c $\sigma =0.2$

Fig. 12

a, b A zoomed-in view of the marked point ${S}_{33}$ shown in Figs. 10, and c displays a low-resolution representation of the basin of attraction depicted in Fig. 11c

Fig. 13

The quadri-stable periodic solution of the rotor system corresponds to the basin of attraction shown in Fig. 12c

3.2 Nonlinear dynamics of controlled model

This section discusses the impact of control parameters (${\eta }_{1}, {\eta }_{2}, {\delta }_{1},$ and ${\delta }_{2}$) on both the multistability behaviors and the vibration reduction of the asymmetric rotor model. The discussion is presented in the form of 3D bifurcation diagrams and two-parameter stability charts, as shown in Figs. 14, 15, 16, 17, 18, 19 and 20 when $f=0.01, {\alpha }_{1}=0.05, {\alpha }_{2}=0.1, {\alpha }_{3}=0.025,$ and $\Delta =0.1$.

Fig. 14

3D bifurcation analysis of the controlled asymmetric system: a, b 3D visualization of oscillation amplitudes (${z}_{1}$ and ${z}_{2}$) at different values of linear control gain (${\eta }_{1}$) versus the bifurcation parameter $\sigma$, and c multistable and monostable solutions boundaries in ${\eta }_{1}-\sigma$ plane

Fig. 15

3D bifurcation analysis of the controlled asymmetric system: a, b 3D visualization of oscillation amplitudes (${z}_{1}$ and ${z}_{2}$) at different values of nonlinear control gain (${\eta }_{2}$) versus the bifurcation parameter $\sigma$, and c multistable and monostable solutions boundaries in ${\eta }_{2}-\sigma$ plane

Fig. 16

3D bifurcation analysis of the controlled asymmetric system: a, b 3D visualization of oscillation amplitudes (${z}_{1}$ and ${z}_{2}$) at different values of linear and nonlinear control gains (${{\eta }_{1}=\eta }_{2}$) versus the bifurcation parameter $\sigma$, and c multistable and monostable solutions boundaries in ${{(\eta }_{1}=\eta }_{2})-\sigma$ plane

Fig. 17

3D bifurcation analysis of the controlled asymmetric system: a, b 3D visualization of oscillation amplitudes (${z}_{1}$ and ${z}_{2}$) at different values of the controller's internal gain ${(\delta }_{1}$) versus the bifurcation parameter $\sigma$, and c multistable and monostable solutions boundaries in ${\delta }_{1}-\sigma$ plane

Fig. 18

3D bifurcation analysis of the controlled asymmetric system: a, b 3D visualization of oscillation amplitudes (${z}_{1}$ and ${z}_{2}$) at different values of feedback gain ${(\delta }_{2}$) versus the bifurcation parameter $\sigma$, and c multistable and monostable solutions boundaries in ${\delta }_{2}-\sigma$ plane

Fig. 19

3D bifurcation diagrams of the system with the optimum control gains ${\eta }_{1}={\eta }_{2}=2.0, {\delta }_{1}=0.5,$ and ${\delta }_{2}=1.0$: a, b robustness of the controlled system against a wide spectrum of the excentricity $f$, c, d robustness of the controlled system against a wide spectrum of the stiffness nonlinearity ${\alpha }_{1}$, e, f robustness of the controlled system against a wide spectrum of the linear stiffness asymmetry ${\alpha }_{2}$, and g, h robustness of the controlled system against a wide spectrum of the nonlinear stiffness asymmetry ${\alpha }_{3}$

Fig. 20

a, b Vibration amplitudes (${z}_{1}$ and ${z}_{2}$) of the system before and after control, and c the phase angles (${\theta }_{1}$ and ${\theta }_{2}$) after control

The vibration amplitudes (${z}_{1}$ and ${z}_{2}$) are illustrated in the 3D bifurcation diagram, shown in Fig. 14a and b, across five different values of the linear control gain (${\eta }_{1}$), where the rotor's angular velocity ($\omega =1+\sigma ,-0.3\le \sigma \le 0.05$) serves as a continuous bifurcation parameter. A noteworthy observation from Fig. 14a and b is that coupling the asymmetric system to an active controller through a magnetic coupling actuator transforms the nonlinear characteristics of the system from hardening spring characteristics, as demonstrated in Figs. 3, 6 and 10, to soft spring characteristics. This transformation results in the occurrence of nonlinear resonance in the system below the first critical speed, a phenomenon absent in the uncontrolled model. Additionally, the figures reveal that the oscillation amplitudes are monotonically decreasing functions of ${\eta }_{1}$. At specific critical values of the gain ${\eta }_{1}$, the multistability behaviors of the nonlinear model may vanish, and the system responds with a mono-stable periodic solution, resembling a linear dynamical system. To pinpoint the threshold value of ${\eta }_{1}$ that distinguishes between the linear and nonlinear characteristics of the system along the $\sigma$ axis, a stability chart in the ${\eta }_{1}-\sigma$ plane is presented in Fig. 14c. It is evident that the system exhibits only a mono-stable periodic solution as long as ${\eta }_{1}>{\eta }_{critical}=1.56174$, irrespective of the angular velocity. Otherwise, it may display multistability behaviors depending on the angular velocity. On the other hand, rotor dynamics under various magnitudes of the nonlinear control gain (${\eta }_{2}$) are depicted in Fig. 15a and b, where ${z}_{1}$ and ${z}_{2}$ are plotted against $\sigma$ for ${\eta }_{2}$ values of $0.5, 1.0, 1.5, 2.0,$ and $2.5$. The figures illustrate that oscillation amplitudes are monotonically decreasing functions of ${\eta }_{2}$. However, upon comparing these results with Fig. 14a and b, one can deduce the comparatively lower efficiency of the nonlinear controller compared to the linear one. Furthermore, the stability chart in the ${\eta }_{2}-\sigma$ plane confirms that the rotor will exhibit a multistability solution within a specific range of angular velocity regardless of ${\eta }_{2}$ magnitude.

Accordingly, the linear and nonlinear control gains ( ${\eta }_{1}$ and ${\eta }_{2}$) are treated as a single control parameter. Rotor amplitudes (${z}_{1}$ and ${z}_{2}$) are plotted against $\sigma$ for values of ${\eta }_{1}={\eta }_{2}= 0.5, 1.0, 1.5, 2.0,$ and $2.5$, as shown in Fig. 16a and b. Additionally, the corresponding stability chart has been established in $\left({\eta }_{1}={\eta }_{2}\right)-\sigma$, as depicted in Fig. 16c. Comparing Fig. 16a and b with Figs. 14a, b and 15a, b, it becomes evident that the combined linear and nonlinear control strategy may be the most effective for suppressing multistability behaviors in the rotor model at small control gains. Conversely, the worst resonant control strategy appears to be the nonlinear feedback controller.

Moreover, the stability chart in Fig. 16c demonstrates that the threshold value of ${\eta }_{1}={\eta }_{2}$, distinguishing between the linear and nonlinear characteristics of the system along the $\sigma$ axis, is ${\eta }_{critical}=1.45081$. The rotor exhibits a mono-stable solution as long as ${\eta }_{1}={\eta }_{2}>{\eta }_{critical}$, irrespective of the angular velocity. Otherwise, the system may experience multistability behavior depending on the rotational speed.

The rotor dynamics concerning the internal feedback gain (${\delta }_{1}$) are presented in a 3D bifurcation diagram in Fig. 17. Here, ${z}_{1}$ and ${z}_{2}$ are plotted against $\sigma$ for ${\delta }_{1}$ values of $0, 0.5, 1, 1.5,$ and $2.0$, with the other control parameters fixed at ${\eta }_{1}={\eta }_{2}={\delta }_{2}=1.0$. Figure 17a and b reveal that the oscillation amplitudes are inversely proportional to ${\delta }_{1}$, with the most efficient suppression occurring at ${\delta }_{1}=0$. However, an increase in this gain beyond zero degrades controller efficiency, leading to multistability behavior and high oscillation amplitudes of the system.

To identify critical values (${\delta }_{1 \left(critical\right)}$) beyond which the rotor experiences multistability oscillations, a stability chart corresponding to Fig. 17a and b is presented in the ${\delta }_{1}-\sigma$ plane, as depicted in Fig. 17c. Examination of Fig. 17c illustrates that the asymmetric rotor model system exhibits mono-stable periodic motion irrespective of rotational speed as long as ${\delta }_{1}<{\delta }_{1 \left(critical\right)}=0.72409$. Otherwise, the system will undergo multistability motion based on the magnitudes of both ${\delta }_{1}$ and $\sigma$.

Finally, the rotor dynamics under the variation of the feedback gain δ₂ are visualized in Fig. 18 with ${\eta }_{1}={\eta }_{2}={\delta }_{1}=1.0$. Steady-state amplitudes ${z}_{1}$ and ${z}_{2}$ are plotted against $\sigma$ at five different levels of gain ${\delta }_{2}$ in a 3D bifurcation diagram, as shown in Fig. 18a and b. in addition, the corresponding stability chart in the ${\delta }_{2}-\sigma$ plane has been established, as depicted in Fig. 18c. Similar to the linear and nonlinear control gains (${\eta }_{1}$ and ${\eta }_{2}$), the oscillation amplitudes are monotonic decreasing functions of ${\delta }_{2}$. The critical value of ${\delta }_{2}$, as reported in Fig. 18c, is ${\delta }_{2 \left(critical\right)}=1.3747$. Below this critical value, the system undergoes multistability conditions.

Based on the discussions presented in Figs. 14, 15, 16, 17 and 18, the rotor dynamics are visualized in Fig. 19 over a wide range of rotor eccentricity ($f$), stiffness nonlinearity (${\alpha }_{1}$), linear stiffness asymmetry (${\alpha }_{2}$), and nonlinear stiffness asymmetry (${\alpha }_{3}$). The simulations are conducted at optimum control gains ${\eta }_{1}={\eta }_{2}=2.0, {\delta }_{1}=0.5,$ and ${\delta }_{2}=1.0$. In Fig. 19a and b, the system's lateral vibrations are simulated at different eccentricity levels ranging from $f=0.02$ to $f=0.1$, with fixed values of ${\alpha }_{1}=0.05, {\alpha }_{2}=0.1,$ and ${\alpha }_{3}=0.025$. Figures 19c and d depict ${z}_{1}$ and ${z}_{2}$ plotted against $\sigma$, where the stiffness nonlinearity ${\alpha }_{1}$ varies between $0.05$ and $0.25$, with other parameters fixed at $=0.01, {\alpha }_{2}=0.1,$ and ${\alpha }_{3}=0.025$. In Fig. 19e and f, the oscillation amplitudes are plotted versus $\sigma$, varying the linear stiffness asymmetry ${\alpha }_{2}$ between $0.05$ and $0.25$, with $f=0.01, {\alpha }_{1}=0.05,$ and ${\alpha }_{3}=0.025$ fixed. In Fig. 19g and h, the rotor amplitudes are plotted versus $\sigma$, varying the nonlinear stiffness asymmetry ${\alpha }_{3}$ from $0.1$ to $0.5$, with $f=0.01, {\alpha }_{1}=0.05,$ and ${\alpha }_{2}=0.1$ fixed. All subfigures confirm the high performance of the controller in eliminating multistability conditions in the complicated models of the asymmetric rotor given by Eqs. (12.1) and (12.2) for different values of the nonlinear parameters ${\alpha }_{1}, {\alpha }_{2},$ and ${\alpha }_{3}$, as well as the rotor eccentricity $f$. However, Fig. 19a, b, e and f demonstrate that increasing $f$ and/or ${\alpha }_{2}$ has a stronger influence on increasing the vibration of the controlled system compared to ${\alpha }_{1},$ and ${\alpha }_{3}$.

3.3 Controlled versus uncontrolled motion.

The bifurcation diagrams of the asymmetric model before and after control are compared in Fig. 20. Figure 20a and b depict the vibration amplitudes (${z}_{1}$ and ${z}_{2}$) of the asymmetric model before control and after optimal control (i.e. ${\eta }_{1}={\eta }_{2}=2.0, {\delta }_{1}=0.5$, and ${\delta }_{2}=1.0$) when $f=0.01, {\alpha }_{1}=0.05, {\alpha }_{2}=0.1,$ and ${\alpha }_{3}=0.025$. Meanwhile, Fig. 20c illustrates the relationship between the phase angles ${\theta }_{1}$ and ${\theta }_{2}$ of the controlled asymmetric model. It is evident from Fig. 20a and b that the strong oscillation amplitudes and multistability characteristics of the uncontrolled model (red line) have been effectively suppressed after control, resulting in a mono-stable periodic solution with an oscillation peak very close to zero (green line). This occurs irrespective of the rotor angular velocity. Additionally, Fig. 20c demonstrates the elimination of the backward whirling motion reported in Fig. 10f, where ${\theta }_{1}>{\theta }_{2}$ along the $\sigma -$ axis.

Finally, the steady-state time response of the system before and after control has been simulated according to Fig. 20 when $\sigma =0.2$ (i.e. the normalized angular speed is $\omega =1+0.2$) via solving the four coupled nonlinear differential equations given by Eqs. (12.1) to (12.4) using MATLAB ODE45 solver. As clear from the figure the uncontrolled model has four simultaneous periodic solutions at $\sigma =0.2$, where the system responds with one of these solutions at a time depending on the initial conditions, where the basins of attraction for these four solutions have been established before in Fig. 12c. Accordingly, Eqs. (12.1) to (12.4) have been solved numerically before and after control using the four initial conditions marked in Fig. 12c as shown in Fig. 21. By examining Fig. 21, one can deduce that the multistability characteristics as well as the backward whirling motion of the uncontrolled system have been eliminated after control.

Fig. 21

Motion profile of the rotor model before and after control according to Fig. 19 when $\sigma =0.2$ at zero initial velocities ${\dot{y}}_{1}\left(0\right)={\dot{y}}_{2}\left(0\right)=0.0$: (a, b, c) ${y}_{1}\left(0\right)={y}_{2}\left(0\right)=0.0$, (c, d, e) ${y}_{1}\left(0\right)=3.0, {y}_{2}\left(0\right)=0.0$, (f, g, h) ${y}_{1}\left(0\right)=-3.2, {y}_{2}\left(0\right)=0.0$, and (k, l, m) ${y}_{1}\left(0\right)=-2.4, {y}_{2}\left(0\right)=-5.0$

4 Concluded remarks

The nonlinear dynamics of the asymmetric rotor model have been investigated in this work using two $1/2$-DOF active dampers attached to the system via a magnetic actuator. The rotor includes stiffness nonlinearity, as well as linear and nonlinear asymmetric restoring forces, which manifest as multiparametric excitations alongside the external excitation caused by disc eccentricity. The whole dynamics have been modeled using a $2$-DOF system coupled to two $1/2$-DOF systems. Subsequently, the derived mathematical model has been investigated analytically using perturbation theory and validated numerically through suitable numerical techniques. The performance of the applied control method in reducing rotor vibrations and eliminating multistability characteristics has been assessed using various 3D bifurcation diagrams and two-parameter stability charts. Based on the discussions provided above, the following points can be noted:

• 1. The nonlinear symmetric rotor model behaves like a hardening Duffing oscillator, exhibiting either a mono-stable or bi-stable periodic solution depending on the angular velocity whether below or higher than the first critical speed.

• 2. Incorporating asymmetric linear stiffness in the system model results in the appearance of bi-stability behaviors below the first critical speed, as well as the emergence of a tri-stable periodic solution when the rotor angular speed is beyond the first critical speed.

• 3. The coexistence of both linear and nonlinear stiffness may result in a quadri-stable solution when the rotor rotational speed is higher than the first critical speed. One of these solutions represents backward whirling, while the other three solutions correspond to forward whirling.

• 4. Coupling the asymmetric system to two $1/2$-DOF active dampers through a magnetic coupling actuator has transformed the nonlinear characteristics of the system from hardening to softening Duffing characteristics.

• 5. The linear coupling of the $1/2$-DOF active dampers to the rotor system is more efficient than pure nonlinear coupling in both vibration reduction and multistability elimination. However, the combined coupling (i.e., linear and cubic) may be the best control strategy.

• 6. Properly selecting the control and feedback parameters can harness the considered complex nonlinear system to behave with a monostable solution, achieving minimum and safe vibration levels.

Appendix 1

$$ \begin{aligned} \frac{{\partial G_{1} }}{{\partial w_{1} }} = & \left( { - \frac{{\mu_{1} }}{2} - \frac{{3\alpha_{1} }}{32}w_{20}^{2} \sin (2w_{40} - 2w_{30} ) - \frac{{\alpha_{2} }}{4}\sin (2w_{30} ) - \frac{{3\alpha_{1} }}{64}w_{20}^{2} \sin (2w_{40} + 2w_{30} )} \right) \\ & - \left( {\frac{{\alpha_{3} }}{8}\sin (2w_{30} ) - \frac{{\alpha_{1} }}{64}\sin (4w_{30} )} \right)3w_{10}^{2} - \left( {\frac{{3\alpha_{3} }}{32}\cos (w_{40} - 3w_{30} ) + \frac{{3\alpha_{3} }}{32}\cos (w_{40} + w_{30} )} \right. \\ & \left. { - \frac{{3\alpha_{1} }}{64}\cos (w_{40} + 3w_{30} )} \right)2w_{10} w_{20} + \Delta \left( {\frac{ - 1}{2}\frac{{\eta_{1} \delta_{2} }}{{(1 + \delta_{1}^{2} )}} - \frac{3}{4}\frac{{\eta_{1}^{2} \delta_{1} \delta_{2}^{2} w_{10}^{2} }}{{(1 + \delta_{1}^{2} )^{2} }} - \frac{9}{8}\frac{{\eta_{1} \delta_{2} w_{10}^{2} }}{{(1 + \delta_{1}^{2} )}}} \right. - \frac{9}{8}\frac{{\eta_{2} \delta_{2}^{3} w_{10}^{2} }}{{(1 + \delta_{1}^{2} )^{2} }} \\ & - \frac{45}{{32}}\frac{{\eta_{2} \delta_{2}^{3} w_{10}^{4} }}{{(1 + \delta_{1}^{2} )^{2} }} + \frac{15}{{32}}\frac{{\eta_{2} (1 - 3\delta_{1}^{2} )\delta_{2}^{3} w_{10}^{4} }}{{(1 + \delta_{1}^{2} )^{3} }} - \frac{15}{4}\frac{{\eta_{1} \eta_{2} \delta_{1} \delta_{2}^{4} w_{10}^{4} }}{{(1 + \delta_{1}^{2} )^{4} }} - \frac{5}{2}\frac{{\eta_{1} \eta_{2} \delta_{1} \delta_{2}^{4} w_{10}^{4} }}{{(1 + \delta_{1}^{2} )^{3} }} + \frac{35}{{16}}\frac{{\eta_{2}^{2} \delta_{1} (3 + \delta_{1}^{2} )\delta_{2}^{6} w_{10}^{6} }}{{(1 + \delta_{1}^{2} )^{6} }} \\ & \left. { - \frac{105}{{64}}\frac{{\eta_{2}^{2} \delta_{1} \delta_{2}^{6} w_{10}^{6} }}{{(1 + \delta_{1}^{2} )^{4} }}} \right), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{1} }}{{\partial w_{2} }} = & - \frac{{\alpha _{2} }}{4}\cos (w_{{40}} + w_{{30}} ) + \left( {} \right)\left( { - \frac{{3\alpha _{3} }}{{32}}\cos (w_{{40}} + w_{{30}} ) + \frac{{\alpha _{3} }}{{32}}\cos (3w_{{40}} - w_{{30}} )} \right. \\ & \left. { - \frac{{\alpha _{1} }}{{64}}\cos (w_{{30}} + 3w_{{40}} )} \right)3w_{{20}}^{2} - \left( {\frac{{3\alpha _{3} }}{{32}}\cos (w_{{40}} - 3w_{{30}} ) + \frac{{3\alpha _{3} }}{{32}}\cos (w_{{40}} + w_{{30}} )} \right. \\ & \left. { - \frac{{3\alpha _{1} }}{{64}}\cos (w_{{40}} + 3w_{{30}} )} \right)w_{{10}}^{2} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{1} }}{{\partial w_{3} }} = & \left( {\frac{{3\alpha_{1} }}{16}w_{20}^{2} \cos (2w_{40} - 2w_{30} ) - \frac{{\alpha_{2} }}{2}\cos (2w_{30} ) - \frac{{3\alpha_{1} }}{32}w_{20}^{2} \cos (2w_{40} + 2w_{30} )} \right)w_{10} \\ & - \left( {\frac{{\alpha_{2} }}{4}\cos (2w_{30} ) - \frac{{\alpha_{1} }}{16}\sin (4w_{30} )} \right)w_{10}^{3} + \frac{{\alpha_{2} }}{4}w_{20} \sin (w_{40} + w_{30} ) + \left( {\frac{{3\alpha_{3} }}{32}\sin (w_{40} + w_{30} )} \right. \\ & \left. { + \frac{{\alpha_{3} }}{32}\sin (3w_{40} - w_{30} ) + \frac{{\alpha_{1} }}{64}\sin (w_{30} + 3w_{40} )} \right)w_{20}^{3} - \left( { - \frac{{9\alpha_{3} }}{32}\sin (w_{40} - 3w_{30} )} \right. - \frac{{3\alpha_{3} }}{32}\sin (w_{40} + w_{30} ) \\ & \left. { + \frac{{9\alpha_{1} }}{64}\sin (w_{40} + 3w_{30} )} \right)w_{10}^{2} w_{20} - \frac{{f\omega^{2} }}{2}\cos (\theta - w_{30} ), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{1} }}{{\partial w_{4} }} = & \left( { - \frac{{3\alpha _{1} }}{{16}}w_{{20}}^{2} \cos (2w_{{40}} - 2w_{{30}} ) - \frac{{3\alpha _{1} }}{{32}}w_{{20}}^{2} \cos (2w_{{40}} + 2w_{{30}} )} \right)w_{{10}} + \frac{{\alpha _{2} }}{4}w_{{20}} \sin (w_{{40}} + w_{{30}} ) \\ & + \left( {\frac{{3\alpha _{3} }}{{32}}\sin (w_{{40}} + w_{{30}} ) - \frac{{3\alpha _{3} }}{{32}}\sin (3w_{{40}} - w_{{30}} ) + \frac{{3\alpha _{1} }}{{64}}\sin (w_{{30}} + 3w_{{40}} )} \right)w_{{20}}^{3} \\ & - \left( { - \frac{{3\alpha _{3} }}{{32}}\sin (w_{{40}} - 3w_{{30}} ) - \frac{{3\alpha _{3} }}{{32}}\sin (w_{{40}} + w_{{30}} )} \right.\left. { + \frac{{3\alpha _{1} }}{{64}}\sin (w_{{40}} + 3w_{{30}} )} \right)w_{{10}}^{2} w_{{20}} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{2} }}{{\partial w_{1} }} = & - \frac{{\alpha _{2} }}{4}\cos (w_{{40}} + w_{{30}} ) \\ & + \left( { - \frac{{9\alpha _{3} }}{{32}}\cos (w_{{40}} + w_{{30}} ) + \frac{{3\alpha _{3} }}{{32}}\cos (3w_{{30}} - w_{{40}} ) + \frac{{3\alpha _{1} }}{{64}}\cos (w_{{40}} + 3w_{{30}} )} \right)w_{{10}}^{2} \\ & - \left( {\frac{{3\alpha _{3} }}{{32}}\cos (w_{{30}} - 3w_{{40}} ) + \frac{{3\alpha _{3} }}{{32}}\cos (w_{{40}} + w_{{30}} ) + \frac{{3\alpha _{1} }}{{64}}\cos (w_{{30}} + 3w_{{40}} )} \right)w_{{20}}^{2} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{2} }}{{\partial w_{2} }} = & \left( { - \frac{{\mu_{2} }}{2} - \frac{3\alpha }{{32}}w_{10}^{2} \sin (2w_{30} - 2w_{40} ) + \frac{{\beta_{1} }}{4}\sin (2w_{40} ) - \frac{3\alpha }{{64}}w_{10}^{2} \sin (2w_{40} + 2w_{30} )} \right) \\ & - \left( {\frac{{3\beta_{2} }}{8}\sin (2w_{40} )} \right.\left. { - \frac{3\alpha }{{64}}\sin (4w_{40} )} \right)w_{20}^{2} - \left( {\frac{{6\beta_{2} }}{32}\cos (w_{30} - 3w_{40} ) + \frac{{6\beta_{2} }}{32}\cos (w_{40} + w_{30} )} \right. \\ & \left. { + \frac{6\alpha }{{64}}\cos (w_{30} + 3w_{40} )} \right)w_{10} w_{20} + \Delta \left( {\frac{ - 1}{2}\frac{{\eta_{1} \delta_{2} }}{{(1 + \delta_{1}^{2} )}} - \frac{3}{4}\frac{{\eta_{1}^{2} \delta_{1} \delta_{2}^{2} w_{20}^{2} }}{{(1 + \delta_{1}^{2} )^{2} }} - \frac{9}{8}\frac{{\eta_{1} \delta_{2} w_{20}^{2} }}{{(1 + \delta_{1}^{2} )}}} \right. - \frac{9}{8}\frac{{\eta_{2} \delta_{2}^{3} w_{20}^{2} }}{{(1 + \delta_{1}^{2} )^{2} }} \\ & - \frac{45}{{32}}\frac{{\eta_{2} \delta_{2}^{3} w_{20}^{4} }}{{(1 + \delta_{1}^{2} )^{2} }} + \frac{15}{{32}}\frac{{\eta_{2} (1 - 3\delta_{1}^{2} )\delta_{2}^{3} w_{20}^{4} }}{{(1 + \delta_{1}^{2} )^{3} }} - \frac{15}{4}\frac{{\eta_{1} \eta_{2} \delta_{1} \delta_{2}^{4} w_{20}^{4} }}{{(1 + \delta_{1}^{2} )^{4} }} - \frac{5}{2}\frac{{\eta_{1} \eta_{2} \delta_{1} \delta_{2}^{4} w_{20}^{4} }}{{(1 + \delta_{1}^{2} )^{3} }} \\ & \left. { + \frac{35}{{16}}\frac{{\eta_{2}^{2} \delta_{1} (3 + \delta_{1}^{2} )\delta_{2}^{6} w_{20}^{6} }}{{(1 + \delta_{1}^{2} )^{6} }} - \frac{105}{{64}}\frac{{\eta_{2}^{2} \delta_{1} \delta_{2}^{6} w_{20}^{6} }}{{(1 + \delta_{1}^{2} )^{4} }}} \right), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{2} }}{{\partial w_{3} }} = & \left( { - \frac{{3\alpha _{1} }}{{16}}w_{{10}}^{2} \cos (2w_{{30}} - 2w_{{40}} ) - \frac{{3\alpha _{1} }}{{32}}w_{{10}}^{2} \cos (2w_{{40}} + 2w_{{30}} )} \right)w_{{20}} \\ & + \frac{{\alpha _{2} }}{4}w_{{10}} \sin (w_{{40}} + w_{{30}} ) \\ & + \left( {\frac{{3\alpha _{3} }}{{32}}\sin (w_{{40}} + w_{{30}} ) - \frac{{3\alpha _{3} }}{{32}}\sin (3w_{{30}} - w_{{40}} ) + \frac{{3\alpha _{1} }}{{64}}sin(w_{{40}} + 3w_{{30}} )} \right)w_{{10}}^{3} \\ & \left. { - \left( { - \frac{{3\alpha _{3} }}{{32}}\sin (w_{{30}} - 3w_{{40}} ) - \frac{{3\alpha _{3} }}{{32}}\sin (w_{{40}} + w_{{30}} )} \right. - \frac{{3\alpha _{1} }}{{64}}\sin (w_{{30}} + 3w_{{40}} )} \right)w_{{10}} w_{{20}}^{2} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{2} }}{{\partial w_{4} }} = & \left( {\frac{{3\alpha_{1} }}{16}w_{10}^{2} \cos (2w_{30} - 2w_{40} ) + \frac{{\alpha_{2} }}{2}\cos (2w_{40} ) - \frac{{3\alpha_{1} }}{32}w_{10}^{2} \cos (2w_{40} + 2w_{30} )} \right)w_{20} \\ & - \left( {\frac{{\alpha_{3} }}{4}\cos (2w_{40} )} \right.\left. { - \frac{{\alpha_{1} }}{16}\cos (4w_{40} )} \right)w_{20}^{3} + \frac{{\alpha_{2} }}{4}w_{10} \sin (w_{40} + w_{30} ) + \left( {\frac{{3\alpha_{3} }}{32}\sin (w_{40} + w_{30} )} \right. \\ & \left. { + \frac{{\alpha_{3} }}{32}\sin (3w_{30} - w_{40} ) - \frac{{\alpha_{1} }}{64}\sin (w_{40} + 3w_{30} )} \right)w_{10}^{3} - \left( {\frac{{9\alpha_{3} }}{32}\sin (w_{30} - 3w_{40} )} \right. \\ & \left. { - \frac{{3\alpha_{3} }}{32}\sin (w_{40} + w_{30} ) - \frac{{9\alpha_{1} }}{64}sin(w_{30} + 3w_{40} )} \right)w_{10} w_{20}^{2} - \frac{{f\omega^{2} }}{2}\sin (\theta - w_{40} ), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{3} }}{{\partial w_{1} }} = & \left( {\frac{{3\alpha_{1} }}{8} + \frac{{3\alpha_{1} }}{16}\cos (2w_{30} - 2w_{40} ) - \frac{{3\alpha_{1} }}{32}\cos (2w_{40} + 2w_{30} )} \right)w_{10} + \frac{{\alpha_{2} }}{{4w_{20} }}\sin (w_{40} + w_{30} ) \\ & + \left( {\frac{{9\alpha_{3} }}{{32w_{20} }}\sin (w_{40} + w_{30} ) + \frac{{3\alpha_{3} }}{{32w_{20} }}\sin (3w_{30} - w_{40} ) - \frac{{3\alpha_{1} }}{{64w_{20} }}\sin (3w_{30} + w_{40} )} \right)w_{10}^{2} \\ & - \left( {\frac{{3\alpha_{3} }}{32}\sin (w_{30} - 3w_{40} ) - \frac{{9\alpha_{3} }}{32}\sin (w_{40} + w_{30} ) - \frac{{3\alpha_{1} }}{64}\sin (w_{30} + 3w_{40} )} \right)w_{10} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{3} }}{{\partial w_{2} }} = & \left( {\frac{{9\alpha_{1} }}{32} - \frac{{\alpha_{3} }}{4}\cos (2w_{20} ) + \frac{{\alpha_{1} }}{64}\cos (4w_{20} )} \right)2w_{20} - \frac{{\alpha_{2} }}{{4w_{20}^{2} }}w_{10} \sin (w_{20} + w_{10} ) \\ & + \left( { - \frac{{3\alpha_{3} }}{{32w_{20}^{2} }}\sin (w_{20} + w_{10} ) - \frac{{\alpha_{3} }}{{32w_{20}^{2} }}\sin (3w_{10} - w_{20} ) + \frac{{\alpha_{1} }}{{64w_{20}^{2} }}\sin (3w_{10} + w_{20} )} \right)w_{10}^{3} \\ & - \left( {\frac{{3\alpha_{3} }}{32}\sin (w_{10} - 3w_{20} ) - \frac{{9\alpha_{3} }}{32}\sin (w_{20} + w_{10} ) - \frac{{3\alpha_{1} }}{64}\sin (w_{10} + 3w_{20} )} \right)w_{10} \\ & - \Delta \left( {\frac{1}{2}\frac{{\eta_{1}^{2} \delta_{2}^{2} w_{20} }}{{(1 + \delta_{1}^{2} )}}} \right. + \frac{1}{4}\frac{{\eta_{1}^{2} (\delta_{1}^{2} - 1)\delta_{2}^{2} w_{20} }}{{(1 + \delta_{1}^{2} )^{2} }} + \frac{18}{8}\frac{{\eta_{1} \delta_{1} \delta_{2} w_{20} }}{{(1 + \delta_{1}^{2} )}} + \frac{3}{2}w_{20} + \frac{3}{4}\frac{{\eta_{2} \delta_{1} \delta_{2}^{3} w_{20} }}{{(1 + \delta_{1}^{2} )^{2} }} + \frac{27}{8}\frac{{\eta_{2} \delta_{1} \delta_{2}^{3} w_{20}^{3} }}{{(1 + \delta_{1}^{2} )^{2} }} \\ & + \frac{3}{8}\frac{{\eta_{2} (\delta_{1}^{3} - 3\delta_{1} )\delta_{2}^{3} w_{20}^{3} }}{{(1 + \delta_{1}^{2} )^{3} }} + \frac{3}{2}\frac{{\eta_{1} \eta_{2} \delta_{2}^{4} w_{20}^{3} }}{{(1 + \delta_{1}^{2} )^{2} }} + \frac{{\eta_{1} \eta_{2} (\delta_{1}^{4} - 1)\delta_{2}^{4} w_{20}^{3} }}{{(1 + \delta_{1}^{2} )^{4} }} + \frac{15}{{16}}\frac{{\eta_{2}^{2} \delta_{2}^{6} w_{20}^{5} }}{{(1 + \delta_{1}^{2} )^{3} }} \\ & \left. { + \frac{45}{{64}}\frac{{\eta_{2}^{2} (\delta_{1}^{6} + \delta_{1}^{4} - \delta_{1}^{2} - 1)\delta_{2}^{6} w_{20}^{5} }}{{(1 + \delta_{1}^{2} )^{6} }}} \right) + \frac{{f\omega^{2} }}{{2w_{20}^{2} }}\sin (\theta - w_{40} ), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{3} }}{{\partial w_{3} }} = & \left( { - \frac{{3\alpha_{1} }}{16}\sin (2w_{30} - 2w_{40} ) + \frac{{3\alpha_{1} }}{32}\sin (2w_{40} + 2w_{30} )} \right)w_{10}^{2} + \frac{{\alpha_{2} }}{{4w_{20} }}w_{10} \cos (w_{40} + w_{30} ) \\ & + \left( {\frac{{3\alpha_{3} }}{{32w_{20} }}\cos (w_{40} + w_{30} )} \right.\left. { + \frac{{3\alpha_{3} }}{{32w_{20} }}\cos (3w_{30} - w_{40} ) - \frac{{3\alpha_{1} }}{{64w_{20} }}\cos (3w_{30} + w_{40} )} \right)w_{10}^{3} \\ & - \left( {\frac{{3\alpha_{3} }}{32}\cos (w_{30} - 3w_{40} )} \right.\left. { - \frac{{9\alpha_{3} }}{32}\cos (w_{40} + w_{30} ) - \frac{{3\alpha_{1} }}{64}\cos (w_{30} + 3w_{40} )} \right)w_{20} w_{10} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{3} }}{{\partial w_{4} }} = & \left( {\frac{{\alpha_{3} }}{2}\sin (2w_{40} ) - \frac{{\alpha_{1} }}{16}\sin (4w_{40} )} \right)w_{20}^{2} + \left( {\frac{{3\alpha_{1} }}{16}\sin (2w_{30} - 2w_{40} ) + \frac{{3\alpha_{1} }}{32}\sin (2w_{40} + 2w_{30} )} \right)w_{10}^{2} \\ & + \frac{{\alpha_{2} }}{{4w_{20} }}w_{10} \cos (w_{40} + w_{30} ) - \frac{{\alpha_{2} }}{2}\sin (2w_{40} ) + \left( {\frac{{3\alpha_{3} }}{{32w_{20} }}\cos (w_{40} + w_{30} ) - \frac{{\alpha_{3} }}{{32w_{20} }}\cos (3w_{30} - w_{40} )} \right. \\ & \left. { - \frac{{\alpha_{1} }}{{64w_{20} }}\cos (3w_{30} + w_{40} )} \right)w_{20}^{3} - \left( {\frac{{3\alpha_{3} }}{32}\cos (w_{30} - 3w_{40} ) - \frac{{9\alpha_{3} }}{32}\cos (w_{40} + w_{30} )} \right. \\ & \left. { - \frac{{9\alpha_{1} }}{64}\cos (w_{30} + 3w_{40} )} \right)w_{20} w_{10} + \frac{{f\omega^{2} }}{{2w_{20} }}\cos (\theta - w_{40} ), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{4} }}{{\partial w_{1} }} = & \left( {\frac{{3\alpha_{1} }}{8} + \frac{{3\alpha_{1} }}{16}\cos (2w_{30} - 2w_{40} ) - \frac{{3\alpha_{1} }}{32}\cos (2w_{40} + 2w_{30} )} \right)w_{10} + \frac{{\alpha_{2} }}{{4w_{20} }}\sin (w_{40} + w_{30} ) \\ & + \left( {\frac{{9\alpha_{3} }}{{32w_{20} }}\sin (w_{40} + w_{30} ) + \frac{{3\alpha_{3} }}{{32w_{20} }}\sin (3w_{30} - w_{40} ) - \frac{{3\alpha_{1} }}{{64w_{20} }}\sin (3w_{30} + w_{40} )} \right)w_{10}^{2} \\ & - \left( {\frac{{3\alpha_{3} }}{32}\sin (w_{30} - 3w_{40} ) - \frac{{9\alpha_{3} }}{32}\sin (w_{40} + w_{30} ) - \frac{{3\alpha_{1} }}{64}\sin (w_{30} + 3w_{40} )} \right)w_{10} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{4} }}{{\partial w_{2} }} = &\, \frac{9}{{32}}\left( {\alpha _{1} - \frac{{8\Delta }}{3} - - \frac{{4\Delta \eta _{1}^{2} (\delta _{1}^{2} - 1)\delta _{2}^{2} }}{{9(\delta _{1}^{2} + 1)^{2} }} - \frac{{4\Delta \eta _{1} \delta _{1} \delta _{2} }}{{(\delta _{1}^{2} + 1)}}\frac{{8\Delta \eta _{1}^{2} \delta _{2}^{2} }}{{9(\delta _{1}^{2} + 1)}}\left. { - \frac{{4\eta _{2} \delta _{1} \delta _{2}^{3} }}{{3(\delta _{1}^{2} + 1)^{2} }}} \right)2w_{{20}} } \right. \\ & - \frac{3}{{32}}\left( {\frac{{9\Delta \eta _{2} \delta _{1} \delta _{2}^{3} }}{{(\delta _{1}^{2} + 1)^{2} }} + \frac{{\Delta \eta _{2} (\delta _{1}^{3} - 3\delta _{1} )\delta _{2}^{3} }}{{(\delta _{1}^{2} + 1)^{3} }} + \frac{{4\Delta \eta _{1} \eta _{2} \delta _{2}^{4} }}{{(\delta _{1}^{2} + 1)^{2} }} + \frac{{8\Delta \eta _{1} \eta _{2} (\delta _{1}^{4} - 1)\delta _{2}^{4} }}{{3(\delta _{1}^{2} + 1)^{4} }}} \right)4w_{{20}}^{3} \\ & - \frac{5}{{32}}\left( {\frac{{\Delta \eta _{2}^{2} \delta _{2}^{6} }}{{(\delta _{1}^{2} + 1)^{3} }} + \frac{{3\Delta \eta _{2}^{2} (\delta _{1}^{6} + \delta _{1}^{4} - \delta _{1}^{2} - 1)\delta _{2}^{6} }}{{4(\delta _{1}^{2} + 1)^{6} }}} \right)6w_{{20}}^{5} - \left( {\frac{{\alpha _{3} }}{2}\cos (2\theta _{2} )} \right. \\ & \left. { - \frac{{\alpha _{1} }}{{64}}\cos (4\theta _{2} )} \right)w_{{20}} - \frac{{\alpha _{2} }}{{4w_{{20}}^{2} }}\sin (\theta _{2} + \theta _{1} ) - \left( {\frac{{3\alpha _{3} }}{{32w_{{20}}^{2} }}\sin (\theta _{2} + \theta _{1} )} \right. \\ & \left. { + \frac{{\alpha _{3} }}{{32w_{{20}}^{2} }}\sin (3\theta _{1} - \theta _{2} ) - \frac{{\alpha _{1} }}{{64w_{{20}}^{2} }}\sin (3\theta _{1} + \theta _{2} )} \right)w_{{10}}^{3} - \left( {\frac{{3\alpha _{3} }}{{32}}\sin (\theta _{1} - 3\theta _{2} )} \right. \\ & \left. { - \frac{{9\alpha _{3} }}{{32}}\sin (\theta _{2} + \theta _{1} ) - \frac{{3\alpha _{1} }}{{64}}\sin (\theta _{1} + 3\theta _{2} )} \right)w_{{10}} + \frac{{f\omega ^{2} }}{{2w_{{20}}^{2} }}\sin (\theta - \theta _{2} ), \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{4} }}{{\partial w_{3} }} = & \left( { - \frac{{3\alpha_{1} }}{16}sin(2w_{30} - 2w_{40} ) + \frac{{3\alpha_{1} }}{32}\sin (2w_{40} + 2w_{30} )} \right)w_{10}^{2} \\ & + \frac{{\alpha_{2} }}{{4w_{20} }}w_{10} \cos (w_{40} + w_{30} ) + \left( {\frac{{3\alpha_{3} }}{{32w_{20} }}\cos (w_{40} + w_{30} ) + \frac{{3\alpha_{3} }}{{32w_{20} }}\cos (3w_{30} - w_{40} ) - \frac{{3\alpha_{1} }}{{64w_{20} }}\cos (3w_{30} + w_{40} )} \right)w_{10}^{3} \\ & - \left( {\frac{{3\alpha_{3} }}{32}\cos (w_{30} - 3w_{40} ) - \frac{{9\alpha_{3} }}{32}\cos (w_{40} + w_{30} ) - \frac{{3\alpha_{1} }}{64}\cos (w_{30} + 3w_{40} )} \right)w_{20} w_{10} , \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial G_{4} }}{{\partial w_{4} }} = & \left( {\frac{{\alpha_{3} }}{2}\sin (2w_{40} ) - \frac{{\alpha_{1} }}{16}\sin (4w_{40} )} \right)w_{20}^{2} \\ & + \left( {\frac{{3\alpha_{1} }}{16}\sin (2w_{30} - 2w_{40} ) + \frac{{3\alpha_{1} }}{32}\sin (2w_{40} + 2w_{30} )} \right)w_{10}^{2} \\ & + \frac{{\alpha_{2} }}{{4w_{20} }}w_{10} \cos (w_{40} + w_{30} ) - \frac{{\alpha_{2} }}{2}\sin (2w_{20} ) \\ & + \left( {\frac{{3\alpha_{3} }}{{32w_{20} }}\cos (w_{40} + w_{30} ) - \frac{{\alpha_{3} }}{{32w_{20} }}\cos (3w_{30} - w_{40} ) - \frac{{\alpha_{1} }}{{64w_{20} }}\cos (3w_{30} + w_{40} )} \right)w_{10}^{3} \\ & - \left( {\frac{{ - 9\alpha_{3} }}{32}\cos (w_{30} - 3w_{40} ) - \frac{{9\alpha_{3} }}{32}\cos (w_{40} + w_{30} ) - \frac{{9\alpha_{1} }}{64}\cos (w_{30} + 3w_{40} )} \right)w_{20} w_{10} \\ & + \frac{{f\omega^{2} }}{{2w_{20} }}\cos (\theta - w_{40} ). \\ \end{aligned} $$