Towards efficient control synthesis for nonlinear wave energy conversion systems: impedance-matching meets the spectral-domain

Abstract

Existing studies within the literature that focus on designing parametric energy-maximizing controllers for Wave Energy Converter (WEC) systems predominantly rely on the impedance-matching (IM) principle, originally developed for linear time-invariant systems. Alternatively, iterative optimization routines are commonly employed for nonlinear WECs. However, these approaches often face a trade-off between effectiveness in maximizing energy extraction and computational efficiency. To address this limitation, this study proposes a computationally efficient controller tuning method for analogous synthesis in the case of nonlinear WECs. The proposed approach combines a statistical linearization technique known as spectral-domain modeling with the IM principle, to synthesize a Proportional–Integrative (PI) controller for a nonlinear WEC. Furthermore, a comparison is performed with two other synthesis methods: one based on a standard (i.e. linear) frequency-domain representation of the WEC that incorporates the IM principle, and the other employing a gradient-free optimization routine applied to the nonlinear time-domain model of the WEC for PI parameter tuning through exhaustive numerical search. A discussion on the effectiveness of each tuning method in maximizing energy absorption is provided, including an appraisal of their associated computational time requirements. Numerical analyses demonstrate that the proposed method, which integrates spectral-domain modeling and IM, can achieve (almost) optimal PI controller design for a nonlinear WEC. Furthermore, this study addresses the inaccuracies inherent in the frequency-domain approach and significantly reduces the computational time compared to the exhaustive search procedure. The findings of this research represent a significant advancement towards the development of simple, effective, and efficient IM-based techniques for synthesis of controllers in nonlinear WEC systems

1 Introduction

Over the past decade, the renewable energy sector has witnessed remarkable growth attributed to government support, financial incentives, and technological advancements, leading to cost reductions. Despite the challenges posed by the COVID-19 epidemic and the Russian-Ukraine conflict, resulting in a widespread financial and energy supply crisis, the demand for solar, wind, and renewable energies persists. According to the International Energy Agency [37], solar PV and wind turbines are currently considered the most effective means of reducing emissions in the power sector, and their global share of electricity generation is projected to increase from 10 (%) in 2021, to 40 (%) in 2030, and 70 (%) in 2050.

Against this backdrop, strides have been made in ocean energy research, with wave energy converter (WEC) technologies inching towards reliability and cost-effectiveness. Current research efforts are focused on reducing the energy cost of WEC systems through optimal design processes [6, 11, 30], ultimately aimed at minimizing the capital cost of WEC technologies, including optimal control techniques [16, 25, 47] to facilitate maximum energy harvesting capabilities. However, numerical simulations and optimization techniques alone are not sufficient to guarantee the real-world performance and reliability of WEC designs. Experimental tests and validation provide invaluable insights into the actual physical behavior of the system, ensuring that numerical models accurately represent the complexities of ocean dynamics [19, 44].

In the context of WEC design, the process involves intricate optimization stages covering each component of the conversion chain, such as the floater, internal mechanics, and energy conversion. Due to the numerous design factors linked to this process, and their interdependencies, global optimization routines are typically employed [9, 62], requiring significant computational efforts to evaluate numerous WEC architectures and components. Additionally, early consideration of energy-maximizing control has been shown to be crucial [54], as it has the potential to greatly enhance power generation throughout the operational lifespan, with multipliers suggested by a variety of wave energy researchers and technologists regarding the performance improvement (in captured energy varying from 2 to 4). Optimization informed by control considerations can influence the dynamic characteristics of the resulting WEC [32], as the system is optimized not only in terms of its physical characteristics but also with respect to control variables [24, 29], which inherently affect the system’s response. However, the process of tuning a WEC controller often relies on rather empirical approaches, involving multiple numerical tests to maximize energy harvesting capabilities in a set of pre-defined operating conditions [6]. In summary, the design of a WEC involves a delicate balancing between conflicting objectives [6], aiming to achieve both maximum energy absorption and optimal design within a reasonable (computational) time-frame. This trade-off can be pursued through the use of accurate and computationally efficient numerical models and optimal control design and tuning.

In the field of WEC modelling, time-domain (TD) frameworks are commonly preferred for predicting WEC performances [33, 53] and implementing optimal control strategies [28, 31, 47]. However, frequency-domain (FD) and spectral-domain (SD) models have also gained popularity as they offer a simple and efficient simulation tool [20]. In particular, SD models serve as an intermediate solution, incorporating nonlinear effects in a FD simulation (which is, by definition, fully linear) through the use of stochastic linearization methods [21, 57]. Recognizing the effectiveness of SD methods both in terms of accuracy and computational efficiency, studies leveraging this technique can be found in [4, 8, 58], to provide a numerical model for the ISWEC [51], a WEC developed by the Marine Offshore Renewable Energy Lab (MOREnergy Lab) at Politecnico di Torino (Italy). Main goal in these studies is that of reducing the simulation burden while maintaining reliable power extraction (i.e. performance) estimations. Furthermore, the universality of stochastic linearization has been demonstrated across a wide range of engineering fields [14], ensuring accurate results and computational efficiency when compared to other modelling techniques based on FD and TD models. In the offshore industry, the application of SD models can be traced back to 1983, when Gudmestad [34] used an SD model to analyze the dynamics of a floating offshore structure. More recent applications in the WEC domain can be found in [12, 57, 60, 61], where SD representations of widely studied WEC systems are discussed.

The availability of effective control systems for maximal energy harvesting is a critical milestone in the pathway towards commercialization of WECs, having a significant potential to reduce the associated levelised cost of energy. Various control methods have been proposed in the literature, encompassing both optimization-based approaches [17] and non-optimization-based strategies [16]. Focusing on the latter, a comprehensive review of ‘simple controllers’ based on the Impedance-Matching (IM) principle is presented in [25]. The IM principle is commonly employed to design stable energy-maximizing controllers using different architectures [10], encompassing both feedforward [22, 23, 26, 27] (which require knowledge of the so-called wave excitation force [5, 7]) and feedback structures [3, 59], some of which incorporate constraint handling mechanisms [22, 26, 27]. However, the existing non-optimization-based control methodologies in the literature primarily rely on the availability of a linear model of the WEC system, i.e. synthesis is performed under linearity assumptions. As a result, these studies fail to address how these controllers can be designed and synthesised in a more realistic case, that is considering nonlinear WEC models. As a matter of fact, typically, optimal control tuning and energy-maximizing control strategies are designed and applied to WECs represented in terms of linear approximations. Controllers applied to nonlinear WECs are often tuned through exhaustive search methods [6], which can be both time-consuming, and lack convergence guarantees towards a global solution. This approach can involve a ‘brute force’ search, where a subset of possible control parameters are systematically explored until an optimum solution is found, or by exploiting an optimization routine that employs gradient-based or gradient-free search methods. Overall, research on energy-maximizing controllers has been mostly restricted to LTI models, lacking of systematic and efficient control synthesis for nonlinear systems.

In this study, we propose a novel control synthesis procedure that leverages a SD representation of the nonlinear WEC dynamics in combination with the IM principle. The objective is to develop a method for control design, synthesis and tuning that achieves effectiveness in terms of energy maximization for predominantly nonlinear WEC systems, while showcasing efficiency in terms of computational burden. In particular, our approach utilizes the SD representation of the WEC dynamics to tune a Proportional–Integral (PI) feedback controller. The tuning process relies on the IM principle, which enables the derivation of optimal coefficients for the PI structure via frequency-based interpolation. To elaborate, the IM principle provides an optimal anti-causal transfer function that maps velocity to the corresponding energy-maximizing control action. However, since such an anti-causal condition cannot be implemented in practice, we perform an interpolation of the IM-based optimal response at a suitably defined point (frequency), to derive a causal PI controller based on the SD representation of the nonlinear WEC dynamics. Additionally, we present two other tuning methods in this study, for the sake of comparison. The first method uses a fully linear FD model of the WEC, and the IM principle is employed to synthesize the corresponding PI controller. The second method directly employs a nonlinear TD model controlled by a PI structure, which is tuned using an optimization routine to maximize power extraction for the specific sea state considered. We apply and provide a numerical appraisal of these three tuning methods using a conceptual point absorber (PA) WEC, taking into account various nonlinear effects. A critical comparison of the three methods is provided, considering the trade-off between energy-maximizing performance and computational burden required by each tuning approach. We demonstrate the effectiveness of the proposed control synthesis methodology based on SD modelling and the IM principle, showing a significant improvement in the design and synthesis of PI controllers for nonlinear WEC systems.

The structure of this article is as follows. Section 2 provides an introduction to the mathematical framework utilized in this study, including an overview of linear random vibration theory, the SD modelling technique, and the IM principle as applied to a single degree of freedom (DoF) WEC. Section 3 presents the novel control tuning procedure proposed in this study, along with the two additional numerical methods used for synthesizing a PI controller. In Sect. 4, a conceptual nonlinear PA is described, which serves as the case study for evaluating the performance of the control tuning methods considered. Section 5 provides a summary of the numerical models employed to tune the PI controller. The section also compares these models in terms of their accuracy in predicting WEC motion, and their computational requirements. The numerical comparison between the three control tuning methods, in terms of performance, is presented in Sect. 6. In particular, this section analyses and compares these strategies in terms of energy-maximizing capabilities and computational efficiency. Finally, Sect. 7 presents the conclusions drawn from the study, and discusses potential avenues for further research and development in the field.

2 Mathematical framework

This section elucidates the mathematical framework underpinning the research study. Firstly, it delves into the statistical (or stochastic) linearization process, which establishes a correlation between elements of linear random vibration theory and the analytical derivation of the SD model for a generic nonlinear dynamical system. Subsequently, the IM principle is introduced, offering a concise yet qualitative exposition of its principal properties and implications.

2.1 Elements of linear random vibration theory

Assuming ocean waves follow a Gaussian random phenomenon [64], the excitation and response of a WEC are modelled as stochastic processes [18]. In this study, we focus on a single DoF system, implicitly assuming Linearity Time Invariance (LTI) and input–output stability. Let us consider a lumped parameter LTI model that describes the system for $t \in \mathbb {R}^+$, given by the following equation:

$$\begin{aligned} \Sigma : \left\{ \begin{aligned}&{M}\ddot{ {q}}(t) + { B}\dot{ {q}}(t) + { K} {{q}}(t) = {f}(t), \\&v(t) = \dot{q}(t), \end{aligned} \right. \end{aligned}$$

(1)

where ${{q}}: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto {{q}}(t)$ is the device displacement, $\dot{ {q}}: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto \dot{q}(t)$ (equivalently $\dot{q} = v$) its first time-derivative, and $\ddot{ {q}}: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto \ddot{q}(t)$ its second time-derivative. ${ M} \in \mathbb {R}^{+}$ is the mass constant, ${ B} \in \mathbb {R}^{+}$ is the damping constant, ${ K} \in \mathbb {R}^{+}$ is the stiffness constant, and ${f}: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto {f}(t)$ represents the un-controllable external force, i.e the wave excitation force. Both FD and TD solutions for system (1) are recalled hereafter, alongside their fundamental properties associated to the Gaussian random process underlying f.

2.1.1 Frequency-domain response evaluation

To predict the steady-state response of a LTI system under stochastic loads, the FD may be used. Depending on the desired output, e.g. displacement q or velocity $\dot{q}$, the input–output responses are derived in FD as follows:

$$\begin{aligned} \begin{aligned}&H(\jmath \omega ) = \frac{Q(\jmath \omega )}{F(\jmath \omega )} = \frac{1}{-\omega ^2 M + \jmath \omega B + K}, \\&G(\jmath \omega ) = \jmath \omega H(\jmath \omega ), \end{aligned} \end{aligned}$$

(2)

where $H: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto H(\jmath \omega )$ and $G: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto G(\jmath \omega )$ denote the input–output dynamics between the system input, i.e. the wave excitation force f, to the WEC outputs, i.e. the WEC displacement q and velocity $\dot{q}$, respectively. $F: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto F(\jmath \omega )$ stands for the Fourier transform of the input force f, $Q: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto Q(\jmath \omega )$ for the Fourier transform of the displacement q, and $V: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto V(\jmath \omega )$ for the Fourier transform of the velocity v. If the stochastic nature of the input f can be described by its power spectral density (PSD) $S_{ff}: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$, $\omega \mapsto S_{ff}(\omega )$, that is derived by the wave PSD $S_{\eta \eta }: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$, $\omega \mapsto S_{\eta \eta }(\omega )$ via:

$$\begin{aligned} S_{ff}(\omega ) = |E(\jmath \omega )|^2 S_{\eta \eta } (\omega ), \end{aligned}$$

(3)

the PSD of the responses $S_{qq}: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$, $\omega \mapsto S_{qq}(\omega )$ and $S_{\dot{q}\dot{q}}: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$, $\omega \mapsto S_{\dot{q}\dot{q}}(\omega )$ can be computed as follows:

$$\begin{aligned} \begin{aligned}&S_{qq}(\omega ) = |H(\jmath \omega )|^2 S_{ff} (\omega ), \\&S_{\dot{q}\dot{q}}(\omega ) = |G(\jmath \omega )|^2 S_{ff} (\omega ), \end{aligned} \end{aligned}$$

(4)

where ${E}: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto {E}(\jmath \omega )$ collects the Froude–Krylov and diffraction coefficients that relate the wave excitation force to the wave profile [20, 63]. Please note that the Eq. (4) are applicable in the scalar case, though can be straightforwardly extended to multi-DoF systems accordingly. These equations provide a fundamental relationship in linear vibration theory, establishing a direct connection between input and output PSDs. Since the Gaussian process underlying f is fully specified in terms of its mean (which is assumed to be zero in this study) and variance, the variance of the output q, denoted as $m_q \in \mathbb {R}^{+}$, is sufficient to obtain a complete probabilistic characterization of the system response [55, 65]. For a single DoF system, the probability density function (PDF) $f_q: \mathbb {R} \rightarrow \mathbb {R}$ of a zero-mean displacement q, following a Gaussian distribution, can be expressed as:

$$\begin{aligned} f_q(q) = \frac{1}{\sqrt{2 \pi m_q}} e^{-\frac{1}{2}\frac{q^2}{m_q}}, \end{aligned}$$

(5)

where the zero-order moment $m_q$, namely variance, is computed with the auto-spectrum of q as follows:

$$\begin{aligned} m_q = \int _{\mathbb {R}^+}^{} S_{qq}(\omega ) \, d\omega . \end{aligned}$$

(6)

2.1.2 Time-domain response evaluation

To obtain a statistically consistent TD output for Eq. (1), we define the mathematical framework for analyzing experiments with f repeated $R \in \mathbb {N}$ times over $T \in \mathbb {R}^+$. As f follows a Gaussian distribution, a single realization $\tilde{f}(t)$ for $t \in [0; T]$ differs across experiments. The randomness and statistical properties of the signal in TD are appreciated through two procedures:

Procedure 1

• : generating a large number of finite-length signals, whereby ensemble statistics can be characterised.

Procedure 2

• : generating an infinitely-long time-horizon realization, whereby the time statistic can be obtained.

A concise but effective analysis of the influence of finite-length wave profiles can be found in [42]. Against this background, considering a zero-mean input signal $\tilde{f}$ with finite-time duration, the TD convolution integral relationships between $\tilde{f}$ and the outputs $\tilde{q}: \mathbb {R} \rightarrow \mathbb {R}$ and $\dot{\tilde{q}}: \mathbb {R} \rightarrow \mathbb {R}$, for $\tau \in \mathbb {R}^+$, can be expressed as:

$$\begin{aligned} \begin{aligned}&\tilde{q}(t) = \int _{0}^{T} h(\tau ) \tilde{f}(t-\tau ) \, d\tau , \\&\dot{\tilde{q}}(t) = \int _{0}^{T} g(\tau ) \tilde{f}(t-\tau ) \, d\tau , \end{aligned} \end{aligned}$$

(7)

where $h: \mathbb {R} \rightarrow \mathbb {R}$, $t \mapsto h(t)$ and $g: \mathbb {R} \rightarrow \mathbb {R}$, $t \mapsto g(t)$ denote the impulse response function between the system input $\tilde{f}$ to the WEC outputs $\tilde{q}$ and $\dot{\tilde{q}}$, respectively. Then, the variance of the system output, say $\tilde{q}$, is:

$$\begin{aligned} \tilde{m}_q = \frac{1}{T} \int _{0}^{T} \tilde{q}^2(t) \, dt. \end{aligned}$$

(8)

Note that $\tilde{m}_q \in \mathbb {R}$ computed with Eq. (8) is merely an estimate, which differs from the theoretical $m_q$ defined in Eq. (6). In particular, for large T, the standard deviation ${\sigma }_{m_q} \in \mathbb {R}^+$ of the $m_q$ estimator tends to zero, approximated as [52]:

$$\begin{aligned} {\sigma }_{m_q} \approx \sqrt{\frac{1}{T} \int _{\mathbb {R}^+}^{} S^2_{qq}(\omega ) \, d \omega }. \end{aligned}$$

(9)

This implies that generating a series of R finite-time traces $\tilde{f}$ or a single infinitely-long time trace f provides statistically consistent evaluations of WEC outputs as obtained through a single FD via (4).

2.2 Spectral-domain modelling

A SD model can be regarded as a statistical equivalent linear representation of a nonlinear model. The primary concept behind this approach is to employ a set of equivalent linear matrices that aim to replicate the time-averaged behavior of nonlinear effects in FD. Initially, we define the following nonlinear differential equation to describe the motion of a single DoF WEC system, based on a corresponding extension of Eq. (1), in TD:

$$\begin{aligned} \Xi : \left\{ \begin{aligned}&{M}\ddot{ {q}}(t) + { B}\dot{ {q}}(t) + { K} {{q}}(t) + { \Theta }( {q},\dot{ {q}},\ddot{ {q}}) = {f}(t), \\&v(t) = \dot{q}(t), \end{aligned} \right. \end{aligned}$$

(10)

where the nonlinear effects are grouped in ${ \Theta }( {q},\dot{ {q}},\ddot{ {q}}): \mathbb {R} \times \mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$, $( {q},\dot{ {q}},\ddot{ {q}}) \mapsto {{\Theta }}( {q},\dot{ {q}},\ddot{ {q}})$, as a function of the system motion q, velocity $\dot{{q}}$, and acceleration $\ddot{ {q}}$. A suitable linear element ${{ \Theta }}_0( {q},\dot{ {q}},\ddot{ {q}}): \mathbb {R} \times \mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$, $( {q},\dot{ {q}},\ddot{ {q}}) \mapsto {{\Theta }}_0( {q},\dot{ {q}},\ddot{ {q}})$ for the purpose of approximating the nonlinear term ${{\Theta }}$ is one which produces an output:

$$\begin{aligned} {{ \Theta }}_0( {q},\dot{ {q}},\ddot{ {q}}) = { M_0}\ddot{ {q}}(t) + { B_0}\dot{ {q}}(t) + { K_0} {{q}}(t), \end{aligned}$$

(11)

where ${ M_0} \in \mathbb {R}^{+}$, ${ B_0} \in \mathbb {R}^{+}$, and ${ K_0} \in \mathbb {R}^{+}$ are the equivalent linear mass, damping, and stiffness matrices, respectively. The parameters $M_0$, $B_0$, and $K_0$ can be chosen to minimize the difference between the nonlinear term ${{ \Theta }}$ and its linear approximation ${{ \Theta }}_0$:

$$\begin{aligned} \epsilon = {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}}) - {{ \Theta }}_0( {q},\dot{ {q}},\ddot{ {q}}). \end{aligned}$$

(12)

Various minimization criteria for $\epsilon$ are proposed in literature [38], but the following is considered to give, in general, the best accuracy [55]:

$$\begin{aligned} \begin{aligned} \min _{M_0, B_0, K_0} \quad&\langle \epsilon ^2 \rangle , \end{aligned} \end{aligned}$$

(13)

where the operator $\langle \bullet \rangle$ stands for the expected value of $\bullet$. This procedure leads to the following expressions, for the special case where q is a Gaussian process [55]:

$$\begin{aligned} \begin{aligned}&K_0 = \left\langle \frac{\partial {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}})}{\partial {q}}\right\rangle ,&B_0 = \left\langle \frac{\partial {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}})}{\partial \dot{ {q}}}\right\rangle , \\&M_0 = \left\langle \frac{\partial {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}})}{\partial \ddot{ {q}}}\right\rangle , \end{aligned} \end{aligned}$$

(14)

The expectations reported in Eq. (14) can be computed considering that variables q, $\dot{q}$, and $\ddot{q}$ are Gaussian process with zero-mean, zero-order moments $m_q$, $m_{\dot{q}}$, and $m_{\ddot{q}}$ computed as follows:

$$\begin{aligned} \begin{aligned}&m_q = \int _{\mathbb {R}^+}^{} S_{qq}(\omega ) \, d\omega ,&m_{\dot{q}} = \int _{\mathbb {R}^+}^{} S_{\dot{{q}}\dot{{q}}}(\omega ) \, d\omega , \\&m_{\ddot{q}} = \int _{\mathbb {R}^+}^{} \omega ^2 S_{\dot{{q}}\dot{{q}}}(\omega ) \, d\omega , \end{aligned} \end{aligned}$$

(15)

and PDFs derived as follows:

$$\begin{aligned} \begin{aligned}&f_q(q) = \frac{1}{\sqrt{2 \pi m_q}} e^{-\frac{1}{2}\frac{q^2}{m_q}},&f_{\dot{{q}}}(\dot{{q}}) = \frac{1}{\sqrt{2 \pi m_{\dot{{q}}}}} e^{-\frac{1}{2}\frac{\dot{{q}}^2}{m_{\dot{{q}}}}}, \\&f_{\ddot{q}}(\ddot{q}) = \frac{1}{\sqrt{2 \pi m_{\ddot{q}}}} e^{-\frac{1}{2}\frac{\ddot{q}^2}{m_{\ddot{q}}}}. \end{aligned} \end{aligned}$$

(16)

Then, Eq. (14) can be fully explicit:

$$\begin{aligned} \begin{aligned}&K_0 = \int _{\mathbb {R}^+}^{} \frac{\partial {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}})}{\partial {q}} f_q(q) \, d{q}, \\&B_0 = \int _{\mathbb {R}^+}^{} \frac{\partial {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}})}{\partial {\dot{q}}} f_{\dot{q}}(\dot{q}) \, d\dot{q}, \\&M_0 = \int _{\mathbb {R}^+}^{} \frac{\partial {{ \Theta }}( {q},\dot{ {q}},\ddot{ {q}})}{\partial {\ddot{q}}} f_{\ddot{q}}(\ddot{q}) \, d\ddot{q}. \end{aligned} \end{aligned}$$

(17)

The spectral-domain model can now be explicitly formulated by substituting expression (11) in Eq. (10), and deriving $M_0$, $B_0$ and $K_0$ via Eq. (17). The linearized system follows:

$$\begin{aligned} \Xi _{eq}: \left\{ \begin{aligned}&{M_{eq}}\ddot{ {q}}(t) + { B_{eq}}\dot{ {q}}(t) + { K_{eq}} {{q}}(t) = {f}(t), \\&v(t) = \dot{q}(t), \end{aligned} \right. \end{aligned}$$

(18)

where the scalars $M_{eq} \in \mathbb {R}$, $B_{eq} \in \mathbb {R}$, and $K_{eq} \in \mathbb {R}$ are defined as:

$$\begin{aligned} \begin{aligned}&M_{eq} = M + M_0,&B_{eq} = B + B_0,{} & {} K_{eq} = K + K_0. \end{aligned} \end{aligned}$$

(19)

As a result, the equivalent linear input–output responses between f and the outputs q and $\dot{q}$ can be written as:

$$\begin{aligned} \begin{aligned}&H_{eq}(\jmath \omega ) = \frac{Q(\jmath \omega )}{F(\jmath \omega )} = \frac{1}{-\omega ^2 M_{eq} + \jmath \omega B_{eq} + K_{eq}}, \\&G_{eq}(\jmath \omega ) = \jmath \omega H_{eq}(\jmath \omega ). \end{aligned} \end{aligned}$$

(20)

Then, the system output in terms of motion and velocity PSD can be obtained as follows:

$$\begin{aligned} \begin{aligned}&S_{qq}(\omega ) = |H_{eq}(\jmath \omega )|^2 S_{ff} (\omega ), \\&S_{\dot{q}\dot{q}}(\omega ) = |G_{eq}(\jmath \omega )|^2 S_{ff} (\omega ). \end{aligned} \end{aligned}$$

(21)

The purpose of an SD model is to calculate the equivalent linear terms, namely $M_0$, $B_0$, and $K_0$, to approximate the response of the nonlinear system (Eq. (10)) using the linearized equation (Eq. (1)). Since there is, in general, no analytical solution to this problem, an iterative procedure is employed:

• Step 1: Initialize the linearized transfer functions (20) with an initial guess of linearized matrices (17).

• Step 2: Evaluate the system responses $S_{qq}$ and $S_{\dot{q} \dot{q}}$ via Eq. (21).

• Step 3: Compute the system outputs in term of the PDF $f_q$, $f_{\dot{q}}$, and $f_{\ddot{q}}$, and variance $m_q$, $m_{\dot{q}}$, and $m_{\ddot{q}}$ via Eqs. (16) and (15), respectively.

• Step 4: Calculate the linearized matrices via Eq. (17) and update the equivalent linear models in (20).

• Step 5: Again, evaluate the spectral responses of the body $S_{qq}$ and $S_{\dot{q} \dot{q}}$ based on the new equivalent system via Eq. (21). Check the convergence of the new values compared with the values obtained at step 2. If convergence is not achieved, return to step 3.

Convergence is verified by comparing the spectral responses of the body $S_{qq}$ and $S_{\dot{q} \dot{q}}$ with the values generated in the previous iteration. Typically, the results are considered converged when the relative error is less than 1 (%) [12].

It is important to note that, despite the presence of nonlinearities in the system dynamics, the assumption of a Gaussian distribution of the WEC response (stated in Sect. 2.1) is considered valid as long as the nonlinear forces are not dominant [20]. However, strong nonlinearities may lead to non-Gaussian response distributions. Therefore, since the application of an energy-maximizing control action often amplifies WEC displacements and increases nonlinear behaviors, the validity of the SD model should also be verified under optimal control conditions, as per discussed in Sect. 6.3 of our study.

For a more in-depth understanding of statistical linearization and SD modeling, readers are encouraged to refer to [20, 55].

2.3 The impedance-matching principle in a nutshell

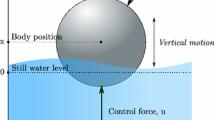
The IM principle involves designing or adjusting the impedance of an electrical device to optimize power transfer. Applied to wave energy control, it is used to synthesize an energy-maximizing controller, enhancing the WEC power extraction capabilities. We consider a single DoF WEC device described by the LTI operator G, which represents the input–output dynamics for a WEC affected by two distinct inputs: the wave excitation force f and the controlled action u. The output of the WEC, namely the WEC velocity v, can be computed using the following FD relation:

$$\begin{aligned} V(\jmath \omega ) = G(\jmath \omega ) \left[ F(\jmath \omega ) - U(\jmath \omega )\right] , \end{aligned}$$

(22)

where $U: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto U(\jmath \omega )$ is the Fourier transform of the controlled input u. We do identify the dynamical characteristics of G that are significant in the development of the IM: G is input–output stable, strictly proper, minimum-phase, and positive-real (see [15]).

Equation (22) can be rewritten in FD defining the so-called WEC intrinsic impedance [15] $I: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto I(\jmath \omega )$ as:

$$\begin{aligned} I(\jmath \omega ) = \frac{1}{G(\jmath \omega )}, \end{aligned}$$

(23)

where $\omega$ is the input frequency, so that the system (22) can be expressed in terms of I as:

$$\begin{aligned} V(\jmath \omega ) = \frac{1}{I(\jmath \omega )} \left[ F(\jmath \omega ) - U(\jmath \omega )\right] . \end{aligned}$$

(24)

With this, the IM principle dictates that the load impedance $I_u: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto I_u(\jmath \omega )$ for the control action U should coincide with the complex-conjugate of the intrinsic impedance:

$$\begin{aligned} I_u (\jmath \omega ) = I^{\star } (\jmath \omega ) = \frac{1}{G^{\star }(\jmath \omega )}. \end{aligned}$$

(25)

The IM closed-loop mapping $Z: \mathbb {C} \rightarrow \mathbb {R}^+$, $\jmath \omega \mapsto Z(\jmath \omega )$, can be fully written in terms of G as follows:

$$\begin{aligned} \begin{aligned} Z(\jmath \omega )&= \frac{V(\jmath \omega )}{F(\jmath \omega )} = \frac{G(\jmath \omega ) G^{\star }(\jmath \omega )}{G(\jmath \omega ) + G^{\star }(\jmath \omega )} = \\&= \frac{\Re (G(\jmath \omega ))^2 + \Im (G(\jmath \omega ))^2}{2 \Re (G(\jmath \omega ))}, \end{aligned} \end{aligned}$$

(26)

where Z is an ideal filter [46] and hence has zero-phase. Operators $\Re (\bullet )$ and $\Im (\bullet )$ stand for the real and imaginary part of $\bullet$, respectively. This results in a zero-phase condition between the system input f and output v. Another perspective on the mapping Z lies in seeing the output v as a scaled version of the input f. This statement can be hence split as two conditions, i.e. in terms of phase and amplitude:

• Amplitude condition Under optimal control conditions, the instantaneous amplitude of the velocity v is equal to the excitation force f scaled by the mapping |Z|.

• Phase condition The instantaneous phase of the velocity v under optimal control conditions is synchronised (instantaneously) with that of the wave excitation force f.

It is worth noting that the mapping Z can be used to obtain the system outputs $S_{qq}$ and $S_{\dot{ {q}}\dot{ {q}}}$ for a controlled system with optimal control action $U=I_u V$ as follows:

$$\begin{aligned} \begin{aligned}&S_{qq}(\omega ) = |\frac{1}{\jmath \omega } Z(\jmath \omega )|^2 S_{ff} (\omega ), \\&S_{\dot{q}\dot{q}}(\omega ) = |Z(\jmath \omega )|^2 S_{ff} (\omega ). \end{aligned} \end{aligned}$$

(27)

For a deeper understanding of the IM principle applied to WECs, the reader should refer to [15].

3 Control structures and tuning

We dedicate this section to illustrate a detailed explanation of the specific objectives of this study, which involve the comparison of three different numerical procedures for synthesizing an energy-maximizing controller for a nonlinear WEC modelled in TD. Special emphasis is placed on adapting the concept of an IM-based controller, originally developed for LTI systems, to the context of a nonlinear single-DoF WEC. The mathematical frameworks presented in Sect. 2 serve as the basis for this adaptation. Three distinct numerical procedures for tuning controllers in nonlinear WECs are described in this section. It is important to note that, throughout this section, we utilize the WEC representation and notation introduced in Sect. 2.

3.1 Control structure

As per the discussion provided in Sect. 2.3, IM-based controllers introduce a control action designed to induce zero-phase between the input f and the output v, with the aim to maximize power extraction. However, the resultant optimal control condition is inherently non-causal due to the complex conjugate operator in Eq. (25), and hence require future information of the corresponding device motion (in a feedback structure). An approximation is commonly performed to derive a causal and stable controller for LTI systems, delivering simplified control solutions that are straightforward to deploy in real-time. Figure 1 reports a feedback control structure, which we herein generalise to the single-DoF WEC case.

Fig. 1

Typical IM-based feedback control configuration for a sigle-DoF system

The control structure defined in Fig. 1 is of a feedback nature: output measurements are used directly in a feedback configuration, together with a dynamic stable and causal (i.e. implementable) controller. A classical feedback control structure, as depicted in Fig. 1, does not require any knowledge of the wave excitation force, which significantly reduces controller complexity and simplifies its implementation. This feedback controller is to be designed such that it approximates the corresponding IM condition for a specific wave frequency range $\omega \in \mathbb {W}$. In fact, the ‘true’ optimal condition reported in Eq. (25) cannot be achieved in this setting, since the associated optimal impedance $I_u$ is not implemented. We hence define the approximated feedback controller $I_c: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto I_c(\jmath \omega )$ such that the general approximating condition holds:

$$\begin{aligned} \begin{aligned} || I_c(\jmath \omega ) - I_u(\jmath \omega ) ||_2 \approx 0&,&\omega \in \mathbb {W}, \end{aligned} \end{aligned}$$

(28)

where the operator $|| \bullet ||_2$ denotes the 2-norm of $\bullet$. A typical design that fits the control structure of Fig. 1 is the so-called reactive controller, namely PI. These type of feedback controllers achieve the IM condition for a single wave frequency $\omega _i \in \mathbb {R}$ with a PI control structure with respect to the output velocity v. Following the derivation of the IM conditions presented in Sect. 2.3, such controller can be simply designed by fulfilling the interpolation condition:

$$\begin{aligned} I_{c}(\jmath \omega ) = \Re {(I_u(\jmath \omega _i))} - \frac{\omega _i \Im {(I_u(\jmath \omega _i))}}{\jmath \omega }. \end{aligned}$$

(29)

This procedure is proposed here to tune the PI feedback controller relying on a single-frequency approximation of the optimal anti-causal control impedance $I_u$ that is, in fact, not achievable in practice. Equation (26), defining the optimal mapping Z between the system input f and the corresponding output v, can be rewritten for the controller proposed in Eq. (29) as follows:

$$\begin{aligned} Z_c(\jmath \omega ) = \frac{V(\jmath \omega )}{F(\jmath \omega )} = \frac{G(\jmath \omega )}{1 + G(\jmath \omega )I_c(\jmath \omega )}. \end{aligned}$$

(30)

where the mapping $Z_c: \mathbb {C} \rightarrow \mathbb {C}$, $\jmath \omega \mapsto Z_c(\jmath \omega )$ is not an ideal filter, and hence has no zero phase for $\omega \in \mathbb {R}^+$. Despite this outcome makes $Z_c$ intrinsically suboptimal with respect to the optimal expression Z, the impedance $I_c$ allows obtaining a causal closed-loop transfer function that is achievable in practice. Then, Eq. (27) can be rewritten as:

$$\begin{aligned} \begin{aligned}&S_{qq}(\omega ) = |\frac{1}{\jmath \omega } Z_c(\jmath \omega )|^2 S_{ff} (\omega ), \\&S_{\dot{q}\dot{q}}(\omega ) = |Z_c(\jmath \omega )|^2 S_{ff} (\omega ). \end{aligned} \end{aligned}$$

(31)

A specific example case on how to use this interpolation condition is offered in Fig. 2. In particular, Fig. 2a depicts a typical optimal controller transfer function $I_u$ derived via IM-principle that is used to synthesize a PI controller with parameters tuned following Eq. (29). Moreover, Fig. 2b shows the corresponding closed-loop mapping Z and its causal approximation derived with a PI controller. It can be readily appreciated that $I_{c}$ derived with a PI structure effectively interpolates the optimal controller response $I_u$ and the transfer function Z at the wave frequency $\omega _i$=1 (rad/s) both in magnitude and phase.

Fig. 2

a Optimal feedback controller $I_u$ and b optimal closed-loop response Z (black solid), with the corresponding feedback PI controller $I_c$ and suboptimal closed-loop mapping $Z_c$ (light-blue dashed), achieved by interpolation at $\omega _i=$1 (rad/s)

Considering the TD formulation of the controller transfer function (29), the control action u can be expressed in TD as follows:

$$\begin{aligned} u(t) = \alpha \dot{q}(t) + \beta q(t), \end{aligned}$$

(32)

where $\alpha = \Re {(I_u(\jmath \omega _i))} \in \mathbb {R}$, and $\beta = - {\omega _i \Im {(I_u(\jmath \omega _i))}} \in \mathbb {R}$ are the controller parameters.

Alternatively, the controller proposed in this study could be designed in a feedforward fashion [10]. One key advantage of the feedforward configuration is that the stability of the control loop can be directly ensured by designing Z to be stable (and causal for practical implementation). However, it should be noted that the feedforward design requires knowledge of the wave excitation, which is not directly measurable in practice [49]. Furthermore, more advanced interpolation techniques could be employed, utilizing FD system identification algorithms [17] to approximate the optimal anti-causal controller $I_u$ within a specific frequency range, while employing the LiTe-Con [27] and the LiTe-Con+ [26] architectures.

3.2 Control tuning

The purpose of this study is to identify the most effective way to design a PI feedback controller for a nonlinear WEC. In particular, with effective we refer to (I) maximising the mean extracted power obtained with the nonlinear TD model system (10), while (II) minimising the computational time required to tune the control parameters $\alpha$ and $\beta$. These identified control parameters, obtained using various methodologies, are applied to the TD model of the WEC. By evaluating and comparing the mean extracted power, annual energy extraction, and computational time associated with each tuning method, we can determine which approach is the most effective and efficient for designing a PI controller for the nonlinear WEC.

Considering the controller derived in Sect. 3.1 (see Eqs. (29) and (32)), different methods are proposed here to identify $\alpha$ and $\beta$:

• FDm A straightforward control synthesis can be performed considering the FD model of the WEC system. First, the $I_u$ is derived via Eq. (25) by using the force-to-velocity transfer function G defined in Eq. (2). Then, the control coefficients $\alpha$ and $\beta$ are selected by interpolating the optimal anti-causal control impedance $I_u$ at the specific input frequency $\omega _i$ as reported in Eq. (29).

• SDm A more sophisticated identification relies on the SD of the WEC. $I_u$ is derived using the force-to-velocity transfer function $G_{eq}$ defined in Eq. (20). Again, $\alpha$ and $\beta$ are subsequently selected to interpolate $I_u$ at the specific input frequency $\omega _i$. The process traces the steps outlined in Sect. 2.2 with some modifications:

  • Step 1: Initialize the linearized transfer functions (20) with an initial guess of linearized matrices (17).

  • Step 2: Synthesize the controller via IM procedure to find the optimal control $I_u$, considering $G_{eq}$ computed via Eq. (20), and by replacing it into Eq. (25) accordingly. Then, derive a PI controller by interpolating $I_u$ at the angular frequency $\omega _i$ through Eq. (29). Implement the controller $I_c$ to obtain the mapping $Z_c$ via Eq. (30).

  • Step 3: Evaluate the system responses $S_{qq}$ and $S_{\dot{q} \dot{q}}$ via Eq. (31).

  • Step 4:Compute the system outputs in term of the PDF $f_q$, $f_{\dot{q}}$, and $f_{\ddot{q}}$, and variance $m_q$, $m_{\dot{q}}$, and $m_{\ddot{q}}$ via Eq. (16) and Eq. (15), respectively.

  • Step 5: Calculate the linearized matrices via Eq. (17), synthesize a new controller $I_c$, and update the closed-loop mapping function $Z_c$.

  • Step 6: Again, evaluate the spectral responses of the body $S_{qq}$ and $S_{\dot{q} \dot{q}}$ based on the new equivalent system $Z_c$ via Eq. (31). Check the convergence of the new values compared with the values obtained at step 3. If convergence is not achieved, return to step 4.

  The control coefficients $\alpha$ and $\beta$ to be considered as optimal are the values obtained at the last iteration of the SD simulation.

• TDm The last method directly uses the TD model controlled with a PI controller, tuned individually by varying its control parameters, with the aim to maximize the power extracted for the specific sea-state considered. The optimization is performed with a Nelder-Mead simplex method [39], that is implemented in MATLAB®with the native function fminsearch. This procedure aims to optimize the control parameters for a single sea-state defined by its PSD $S_{\eta \eta }$, using the TD model, and considering the following minimization problem:

  $$\begin{aligned} \begin{aligned}&\quad \quad \min _{\alpha ,\beta } \quad \overline{p}_u = \frac{1}{T}\int _{0}^{T} p_u(t) \, dt = \frac{1}{T}\int _{0}^{T} \dot{q}(t)u(t) \, dt \\&\quad \quad \text {s.t.} \quad u(t) = \alpha \dot{q}(t) + \beta q(t)&\\&\qquad \quad \text {System} \quad \Xi \quad (\text {see }(10)). \\ \end{aligned} \end{aligned}$$

  (33)

  where $\overline{p}_u \in \mathbb {R}$ is the mean extracted power and $p_u: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto p_u(t)$ is the instantaneous power produced by the PTO. The fminsearch routine has been set for a maximum of 25 function evaluation to limit its computational time. The influence of this limit on the control parameter search are based on sensitivity analyses carried out in previous studies by the authors [6, 30].

The control parameters $\alpha$ and $\beta$ obtained through the different tuning methodologies are applied to the time-domain model (10) of the WEC. Extracted power and annual energy production of the WEC using these control parameters is compared among the different tuning methods. Additionally, the computational time required for each tuning method is reported. All numerical simulations and calculations are carried out using MATLAB® 2022b, running on a computer equipped with a 2.8 (GHz) 8-core Intel® processor and 16 (GB) of RAM.

Table 1 summarizes the case studies that are addressed and compared in this paper in terms of: structure of the Controller (PI) with the correspondent Parameters ($\alpha$, and $\beta$), numerical Model (FD, SD or TD) used to tune the controller, and the Tuning approach (IM or fminsearch) used to derive the control coefficients.

4 Case study

In this section, we present a case study focusing on a PA WEC to provide a concrete illustration of optimal control synthesis and the design of an IM-based controller for a nonlinear WEC. The PA is a widely used technology in the WEC industry, suitable for both nearshore and offshore environments. While the real ocean environment induces multiple motions in WECs, such as surge, sway, heave, roll, pitch, and yaw, the PA typically allows for power production only in the heave DoF, while restraining other motions [56]. For our specific case study, we consider an articulated PA configuration, as shown in Fig. 3. This configuration enables the PA to harness wave energy efficiently in the heave motion. We provide a detailed description of the equations governing the PA in TD. We explicitly present the hydrodynamics of the floater and the internal mechanics, distinguishing between linear and nonlinear contributions.

Fig. 3

Illustrative picture of the PA studied in this work

4.1 Point absorber nonlinear equations

The basis of WEC modelling is the Newton’s Second Law, which relates the motion of moving parts to the forces exerted onto the WEC system. A numerical description of the PA WEC is presented here in terms of its vertical excursion, namely heave motion $z: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto z(t)$. Then, the governing equation can be generically expressed by:

$$\begin{aligned} \Pi : \left\{ \begin{aligned}&m\ddot{z}(t) = f(t) + f_i(t) - f_u(t), \\&f_i(t) = f_r(t) + f_h(t) + f_d(t) + f_{e}(t) \\ {}&\qquad + f_{s}(t) + f_{f}(t), \\&v(t) = \dot{z}(t), \end{aligned} \right. \end{aligned}$$

(34)

Table 1 Methods considered for tuning a PI controller for a nonlinear WEC

where $f_r: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_r(t)$ the radiation force, $f_h: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_h(t)$ the nonlinear hydrostatic restoring force, $f_d: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_d(t)$ the viscous drag force, $f_{e}: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_{e}(t)$ the end-stop force, $f_{s}: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_{s}(t)$ the snap-through mechanism force, $f_u: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_u(t)$ the control force acted by the PTO, and $m \in \mathbb {R}^{+}$ the device mass. $\dot{z}: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto \dot{z}(t)$ and $\ddot{z}: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto \ddot{z}(t)$ are the vertical velocity and acceleration of the PA, respectively. The term $f_i: \mathbb {R}^+ \rightarrow \mathbb {R}$, $t \mapsto f_i(t)$ collects all the internal forces acting on the system.

4.1.1 Wave excitation force

As stated in Sect. 2.1, the time-series of the wave excitation force f cannot be represented with a deterministic description [40]. In particular, the wave field is modelled at a fixed location in space and the wave PSD $S_{\eta \eta }$ is considered to be unidirectional and described through the JONSWAP (Joint North Sea Wave Project, [35]). A single wave profile realization $\tilde{\eta }: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto \tilde{\eta }(t)$ is supposed to be generated for a finite duration T and it is approximated locally following a random amplitude scheme [42]:

$$\begin{aligned} \tilde{\eta }(t) = \sum _{w=1}^{N} \eta _{0w} \cos (\omega _wt + \phi _w), \end{aligned}$$

(35)

where ${\eta }_{0w} \in \mathbb {R}^+$ is the wave amplitude, $\phi _w$ is the random phase, uniformly distributed in $[0,2\pi ]$, and $\omega _w \in \mathbb {R}^+$ is the w-th wave frequency. $N \in \mathbb {N}$ represents the total number of frequencies with which the wave elevation is approximated. Then, a single time-domain realization of the wave excitation force $\tilde{f}$ is derived from a single wave profile realization $\tilde{\eta }$ as follows:

$$\begin{aligned} \tilde{f}(t) = \sum _{w=1}^{M} |{E}(\jmath \omega _w)|{\eta }_{0w} \cos (\omega _w t + \phi _w + \angle {E}(\jmath \omega _w)). \end{aligned}$$

(36)

The complex coefficients E of our specific case study are reported in Fig. 12 in “Appendix A”. The operator $\angle \bullet$ represents the phase of $\bullet$.

4.1.2 Hydrodynamic model

The description of Eq. (34) underlines a mathematical representation of hydrodynamic loads based on Cummins’ equation [36] and linear potential flow theory [63], extended by the inclusion of a nonlinear hydrostatic restoring force and a viscous effect for a more reliable prediction of the hydrodynamic response.

The radiation force $f_{r}$ arises from the motion of the spherical floater through the water, that results in inertia and friction components [36] that can be obtained as:

$$\begin{aligned} f_r(t) = -A_{\infty } \ddot{z}(t) - \int _{\mathbb {R}^+}^{} h_{r}(\tau )\dot{z}(t-\tau ) \, d\tau , \end{aligned}$$

(37)

where $A_{\infty } \in \mathbb {R}^+$ is the added mass at infinite excitation frequency, and $h_{r}: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$, $t \mapsto h_{r}(t)$ is the (causal) radiation implulse response function [50]. As the computation of the convolution integral can be very time consuming, it is convenient to express this term with a state-space representation:

$$\begin{aligned} \begin{aligned} \dot{\varvec{\zeta }}(t) = \textbf{A}_r \varvec{\zeta }(t) + \textbf{B}_r{\dot{z}}(t), \\ \int _{\mathbb {R}^+}^{} h_{r}(\tau )\dot{z}(t-\tau ) \, d\tau = \textbf{C}_r \varvec{\zeta }(t) + \text {D}_r{\dot{z}}(t), \end{aligned} \end{aligned}$$

(38)

where the vector $\varvec{\zeta }: \mathbb {R}^{r+} \rightarrow \mathbb {R}^r$, $t \mapsto \varvec{\zeta }(t)$ represents the state vector that approximates the radiation force contributions and $r \in \mathbb {N}$ is the approximation order. The state-space matrices $\textbf{A}_r \in \mathbb {R}^{r \times r}$, $\textbf{B}_r \in \mathbb {R}^{r}$, $\textbf{C}_r \in \mathbb {R}^{1 \times r}$ and $\text {D}_r \in \mathbb {R}$ can be identified following the approach proposed in [48].

Considering the case of a spherical shaped floating PA, the nonlinear hydrostatic restoring force $f_h$ can be expressed as a sum between a linear $f_{h1}: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_{h1}(t)$ and a cubic $f_{h3}: \mathbb {R}^{+} \rightarrow \mathbb {R}$, $t \mapsto f_{h3}(t)$ term as follows [12]:

$$\begin{aligned} f_{h}(t) = f_{h1}(t) + f_{h3}(t) =- k_{h1} z(t) + k_{h3} z^3(t), \end{aligned}$$

(39)

where $k_{h1} \in \mathbb {R}^+$ and $k_{h3} \in \mathbb {R}^+$ are the linear and nonlinear restoring stiffness:

$$\begin{aligned} \begin{aligned}&k_{h1} = \pi \rho g R_s^2, \\&k_{h3} = \frac{\pi \rho g}{3}, \end{aligned} \end{aligned}$$

(40)

with $\rho \in \mathbb {R}^+$ the water density, $g \in \mathbb {R}^+$ the gravitational acceleration, and $R_s \in \mathbb {R}^+$ the floater radius.

Concerning the viscous drag force, the term $f_d$ models a nonlinear effect based on the Morison equation [43]:

$$\begin{aligned} f_d(t) = -\frac{1}{2} C_d \rho S \dot{z}(t) |\dot{z}(t)| \end{aligned}$$

(41)

where $C_d \in \mathbb {R}^+$ is the drag coefficient, derived experimentally as a function of geometry, roughness, flow regime and Reynolds number, and $S \in \mathbb {R}^+$ the cross-sectional area of the floater perpendicular to the z-axis.

4.1.3 Internal mechanics

An end-stop mechanism is considered to restrict motion of the WEC floater between upper and lower bounds, as shown in Fig. 3. The impact interaction between the moving part (namely slider) and the end of the PTO stator (namely stop) is assumed to be elastic, introducing a force linearly proportional to the relative penetration between the slider and the stop. Moreover, to account for non-elastic effects, a damping term is considered, making it possible to model energy losses. The basic end-stop model is described with the following equations:

$$\begin{aligned} f_{e}(t) = \left\{ \begin{aligned}&-k_{e}\left( z(t)-l_{e}\right) - b_{e} \dot{z}(t)&\text { if }&z(t) \ge l_{e}\\&0&\text { if }&|z(t)| < l_{e}\\&-k_{e}\left( z(t)+l_{e}\right) - b_{e} \dot{z}(t)&\text { if }&z(t) \le -l_{e}\\ \end{aligned} \right. \end{aligned}$$

(42)

where $l_{e} \in \mathbb {R}^+$ is the initial gap between the slider and both upper and lower bound, $k_{e} \in \mathbb {R}^+$ is the contact stiffness at the bounds, and $b_{e} \in \mathbb {R}^+$ is the damping coefficient at the bounds.

The snap-through mechanism is composed of two linear springs mounted as illustrated in Fig. 3. According to the expression proposed in [12], the expression of the snap-through action is obtained as:

$$\begin{aligned} f_{s}(t) = - 2 k_{s} \left( 1 - \frac{l_{s}}{\sqrt{z^2(t) + d_{s}^2}} \right) \end{aligned}$$

(43)

where $k_{s} \in \mathbb {R}^+$ is the spring stiffness, $l_{s} \in \mathbb {R}^+$ the un-stretched length of the spring, and $d_{s} \in \mathbb {R}^+$ the horizontal projection of $l_{s}$ measured between the stator wall and the vertical centre of it (see Fig. 3).

4.1.4 Power take-off and friction effects

The PTO considered in this study consists of a linear permanent-magnet synchronous machine connected to the PA as showed in Fig. 3 [1, 13]. The concept is to control the generator torque as follows:

$$\begin{aligned} f_u(t) = \left\{ \begin{aligned}&f_u(t){} & {} \text { if }\ -f_{sat} \le f_u(t) \le f_{sat} \\&f_{sat}{} & {} \text { if }\ f_u(t) > f_{sat} \\&-f_{sat}{} & {} \text { if }\ f_u(t) < -f_{sat} \\ \end{aligned} \right. , \end{aligned}$$

(44)

where $f_{sat} \in \mathbb {R}$ is the saturation force limit to avoid the generator overcoming its force limit.

A static friction is added due to the contact between slider and seals that are installed at the interface between the stator and the slider itself. Such an effect is modelled as a Coulomb-like force regulated by the speed direction:

$$\begin{aligned} f_f(t) = - {\text {sign}}(\dot{z}(t)) F_f , \end{aligned}$$

(45)

where $F_f \in \mathbb {R}$ stands for the friction force and the operator ${\text {sign}}(\bullet )$ computes the sign of $\bullet$.

5 Numerical models

In this section, we present a compact representation of the three models considered in this study: TD model, FD model, and SD model.

5.1 Time-domain model

Equation (34) can be rewritten in matrix form as:

$$\begin{aligned} \begin{aligned} \Xi : \quad&\textbf{M} \varvec{\ddot{x}}(t) + \textbf{B} \varvec{\dot{x}}(t) + \textbf{K} \textbf{x}(t) + \varvec{\Theta }(\textbf{x},\varvec{\dot{x}},\varvec{\ddot{x}})\\ {}&\quad = \textbf{f}(t) - \textbf{f}_(t), \end{aligned} \end{aligned}$$

(46)

including the kinematic variable of interest $\textbf{x}: \mathbb {R}^{n+} \rightarrow \mathbb {R}^{n}$, $t \mapsto \textbf{x}(t)$, $\varvec{\dot{x}}: \mathbb {R}^{n+} \rightarrow \mathbb {R}^n$, $t \mapsto \varvec{\dot{x}}(t)$ its first time-derivative, and $\varvec{\ddot{x}}: \mathbb {R}^{n+} \rightarrow \mathbb {R}^n$, $t \mapsto \varvec{\ddot{x}}(t)$ its second time-derivative. $\textbf{M} \in \mathbb {R}^{n \times n}$ denotes the mass matrix, $\textbf{B} \in \mathbb {R}^{n \times n}$ the damping matrix, $\textbf{K} \in \mathbb {R}^{n \times n}$ the stiffness matrix, the nonlinear function $\varvec{\Theta }: \mathbb {R}^{n} \times \mathbb {R}^{n} \times \mathbb {R}^{n} \rightarrow \mathbb {R}^{n}$, $( \textbf{x},\mathbf {\dot{x}},\varvec{\ddot{x}}) \mapsto {{\Theta }}( \textbf{x},\varvec{\dot{x}},\varvec{\ddot{x}})$, $\textbf{f}: \mathbb {R}^{n+} \rightarrow \mathbb {R}^{n}$, $t \mapsto \textbf{f}(t)$ the external forces, and $\textbf{f}_u: \mathbb {R}^{n+} \rightarrow \mathbb {R}^{n}$, $t \mapsto \textbf{f}_u(t)$ the control action. $n \in \mathbb {N}$ is the system dimension. The state vector $\textbf{x}$ contains the floater displacement and the radiation states:

$$\begin{aligned} \textbf{x}(t) = \begin{bmatrix} z(t) \\ \varvec{\zeta }(t) \end{bmatrix}. \end{aligned}$$

(47)

The nonlinear term $\varvec{\Theta }$ includes the nonlinear hydrostatic force, viscous damping, end-stop mechanism, snap-through mechanisms, and friction force:

$$\begin{aligned} \varvec{\Theta }(\textbf{x},\varvec{\dot{x}},\varvec{\ddot{x}}) = \begin{bmatrix} f_{h3} + f_d + f_{e} + f_{s} + f_{f}\\ {\textbf {0}} \end{bmatrix}. \end{aligned}$$

(48)

The linear terms, concerning the matrices $\textbf{M}$, $\textbf{B}$ and $\textbf{K}$, are defined as follows:

$$\begin{aligned} \begin{aligned}&\textbf{K} = \begin{bmatrix} {k}_{h1} &{} \textbf{C}_r \\ {\textbf {0}} &{} -\textbf{A}_r \end{bmatrix}&\textbf{B} = \begin{bmatrix} \text {D}_r &{} {\textbf {0}} \\ -\textbf{B}_r &{} \textbf{I} \\ \end{bmatrix}, \\&\textbf{M} = \begin{bmatrix} m +A_{\infty } &{} {\textbf {0}} \\ {\textbf {0}} &{} {\textbf {0}} \\ \end{bmatrix}. \end{aligned} \end{aligned}$$

(49)

For what regards the external force and control input, $\textbf{f}$ and $\textbf{f}_u$ read:

$$\begin{aligned} \begin{aligned} \textbf{f}(t) = \begin{bmatrix} f(t) \\ \textbf{0} \end{bmatrix}&,&\textbf{f}_u(t) = \begin{bmatrix} f_u(t) \\ \textbf{0} \end{bmatrix}. \end{aligned} \end{aligned}$$

(50)

The terms ${\textbf {0}}$ and $\textbf{I}$, used above, denote zeros and identity matrices of appropriate dimensions.

5.2 Frequency-domain model

With reference to the nonlinear model previously discussed, the following assumptions and linearizations are considered to obtain a FD model:

• The displacement z is considered small in magnitude.

• The added mass and radiation damping are defined in FD and not in TD.

• Nonlinear hydrostatic effects, viscous forces, end-stop and snap-through actions are considered to be zero.

• The PTO system is assumed ideal, hence excluding saturations and Coulomb friction from the model.

Under these assumptions, the kinematic variable of interest for the FD model framework becomes the heave displacement z and its first and second time derivatives $\dot{z}$ and $\ddot{z}$. Then, the system model can be represented in a scalar form following the notation of Eq. (2):

$$\begin{aligned} \begin{aligned}&H(\jmath \omega ) = \frac{1}{-\omega ^2 (m+\mathcal {A}(\omega )) + \jmath \omega \mathcal {B}(\omega ) + k_{h1}}, \\&G(\jmath \omega ) = \jmath \omega H(\jmath \omega ), \end{aligned} \end{aligned}$$

(51)

where $\mathcal {A}(\omega ) \in \mathbb {R}^+$ is the frequency-dependent added mass, and $\mathcal {B}(\omega ) \in \mathbb {R}^+$ the frequency-dependent radiation damping defined from Ogilvie’s relations [45] as:

$$\begin{aligned} \begin{aligned}&\mathcal {A}(\omega ) = A_{\infty } - \frac{1}{\omega } \int _{\mathbb {R}^+}^{} h_r(t)\sin (\omega t) \, dt,\\&\mathcal {B}(\omega ) = \int _{\mathbb {R}^+}^{} h_r(t)\cos (\omega t) \, dt. \end{aligned} \end{aligned}$$

(52)

The coefficients $\mathcal {A}$ and $\mathcal {B}$, for the considered PA device, are graphically represented in Fig. 12b, c in “Appendix A”.

5.3 Spectral-domain model

Following the procedure outlined in Sect. 2.2, the linearized matrices in (17) can be formulated by deriving the nonlinear term of Eq. (48) with respect to system states $({z},{\dot{z}},{\ddot{z}})$ as follows:

$$\begin{aligned} \begin{aligned}&\frac{\partial {\Theta }({z},{\dot{z}},{\ddot{z}})}{\partial {{z}}} = \frac{\partial f_h }{\partial { {z}}} + \frac{\partial f_e}{\partial { {z}}} + \frac{\partial f_s}{\partial { {z}}}, \\&\frac{\partial {\Theta }({z},{\dot{z}},{\ddot{z}})}{\partial {{\dot{z}}}} = \frac{\partial f_d }{\partial \dot{ {z}}} + \frac{\partial f_e}{\partial \dot{ {z}}} + \frac{\partial f_f}{\partial \dot{ {z}}}, \\&\frac{\partial {\Theta }({z},{\dot{z}},{\ddot{z}})}{\partial {{\ddot{z}}}} = 0. \end{aligned} \end{aligned}$$

(53)

Then, the explicit formulation of ${K}_0$, ${B}_0$, and ${M}_0$ concerning the PA under study are reported in Eq. (54). In the sake of clarification, Eq. (54) have been derived by substituting Eq. (53) in Eq. (17) and by applying Eq. (16) to the present case study. It is straightforward to see how each term depends on both the nature of a specific nonlinear effect and on the magnitude of the PA displacements and velocity, synthesised in terms of the zero-order moments $m_z \in \mathbb {R}^{+}$ and $m_{\dot{z}} \in \mathbb {R}^{+}$.

$$\begin{aligned} {K}_0&= -\pi \rho g m_{{z}} + k_{es} \left( 1 - {\text {erf}}\left( \frac{l_{es}}{\sqrt{2 m_z}}\right) \right) \nonumber \\&\quad + \int _{\mathbb {R}} \frac{2k_{st} ((z^2+d^2_{st})^\frac{3}{2}-d^2_{st}l_{st})}{(z^2+d^2_{st})^\frac{3}{2}} \frac{1}{\sqrt{2 \pi m_z}}\nonumber \\&\quad \textrm{e}^{-\frac{1}{2}\frac{z^2}{m_z}} \, dz, {B}_0 \nonumber \\&=\sqrt{\frac{8 m_{\dot{z}}}{4 \pi }} C_d \rho S + b_{es} \left( 1 - {\text {erf}}\left( \frac{l_{es}}{\sqrt{2 m_{\dot{z}}}}\right) \right) \nonumber \\&\quad + F_f \sqrt{\frac{2}{\pi m_{\dot{z}}}}, {M}_0 = 0. \end{aligned}$$

(54)

The results in Eq. (54) highlight a crucial aspect of statistical linearization. The linearized coefficients are sensitive to the magnitudes of motion, represented by the variances $m_z$ and $m_{\dot{z}}$. Essentially, as the amplitudes of motion, denoted by displacement z and velocity $\dot{z}$, increase, the corresponding linearized coefficients also increase (or decrease) in magnitude. Typically, nonlinear effects dominate when the system exhibits substantial oscillations, causing the system behavior to deviate from its linear representation. From a mathematical perspective, the terms ${K}_0$, ${B}_0$, and ${M}_0$ act as correction coefficients that adjust by a certain factor, depending on the extent of z and $\dot{z}$. This adjustment is made considering the expected value of the nonlinear function in Eq. (48).

The PA can be effectively represented in the SD using the following expressions:

$$\begin{aligned} \begin{aligned}&H_{eq}(\jmath \omega ) \\&\quad = \frac{1}{-\omega ^2 (m+\mathcal {A}(\omega ) + {M}_0) + \jmath \omega (\mathcal {B}(\omega ) + {B}_0) + k_{h1} {K0}}, \\&G_{eq}(\jmath \omega ) = \jmath \omega H_{eq}(\jmath \omega ). \end{aligned} \end{aligned}$$

(55)

5.4 Model comparison

Before delving into the primary focus of this study, we conduct a comparison among the three modelling techniques presented in this section. The aim is to verify the validity of the SD representation and assess its accuracy in predicting the PA motion. The buoy is considered to be excited by a typical sea from the Pantelleria test site (Italy) [41], in which waves are characterized by a JONSWAP spectrum, with peak period $T_p \in \mathbb {R}^+$, significant wave height $H_s \in \mathbb {R}^+$, and peak enhancement factor $\gamma \in \mathbb {R}^+$, as reported in Table 2. These specific wave conditions are considered to excite the PA with sea-states with increasing energy content $E_w \in \mathbb {R}^+$. In particular, sea states $s_1$, $s_2$ and $s_3$ are considered, low, medium and high energetic seas, respectively.

Table 2 Parameters of irregular wave conditions based on JONSWAP spectra

This work initiates simulating the PA in TD by solving Eq. (46) via Runge–Kutta 4th order scheme. R=50 realizations with a duration of¹T=600 (s) of the input force f are generated with both random phase and amplitude [42]. Then, the WEC is simulated in FD and SD by models (51) and (55), respectively. The PA is controlled with a PI controller, and the nominal parameters used for this comparison are summarized in Table 5 reported in Appendix A. This systematic procedure, repeated for each sea state reported in Table 2, allows for the verification of the accuracy of both FD and SD models with respect to the TD counterpart.

Figure 4 depicts the PDF of the heave motion obtained from a unique FD simulation (grey solid), a unique SD simulation (blue dashed), and averaging a serie of 50 TD simulations (black solid). The PDF obtained via SD simulation accurately traces the average PDF obtained through TD simulations for all considered sea states. A slight decrease in accuracy of the SD appears for sea state $s_3$, in which the motion of the PA is exaggerated. If the device is excited by severe wave conditions, experiencing large displacements, the SD model becomes less accurate, showing a small gap with respect to the TD model, albeit acceptable. Moreover, the TD results are fairly comparable with the Gaussian distribution obtained via SD technique. The similarity achieved enables one to rely on the Gaussian distribution assumption. On the other hand, the FD is not able to capture the PA behaviour, not even for the less energetic sea state ($s_1$).

Fig. 4

Comparison of different PDF of the heave motion, computed averaging R=50 TD simulations (black solid), obtained via FD model (grey solid), and obtained via SD model (blue dashed). The buoy is considered to be excited by the three waves reported in Table 2: a concerns sea state $s_1$, b sea state $s_2$, and c sea state $s_3$

Table 3 presents the zero-order moments of the PA vertical displacement and the mean CPU time required for a single simulation using different numerical models. The mean CPU time is calculated by averaging 1000 simulations for each model. The results demonstrate that the SD technique exhibits excellent agreement with the TD simulation in terms of $m_z$. This agreement is notable even in sea state $s_3$, where nonlinear contributions are expected to be significant compared to linear effects.

Regarding computational efficiency, there are significant differences among the three models. As anticipated, the FD model outperforms the other two, with an average simulation time of less than 1 (ms). The SD model is approximately one order of magnitude slower than the FD model but still two orders of magnitude faster than the TD technique. However, considering the accuracy achieved by the SD framework compared to its TD counterpart, the use of the SD technique for simulating the nonlinear PA is justified, despite the FD model being notably faster. It is important to note that the computational time associated with a single SD simulation remains relatively small compared to FD and TD models. Furthermore, note that the reported computational time for the TD model corresponds to a single wave realization, and to obtain accurate statistical results, such as the mean PDF of the heave motion shown in Fig. 4, 50 realizations (R=50) are required.

6 Performance analysis

The results and methodologies presented in Sect. 2 and 3 are applied to the specific case of the PA described in Sect. 4.1 and 5. The analysis aim to compare the tuning methods discussed in Sect. 3.2 in terms of mean extracted power and annual energy production, as computed using the nonlinear TD model. Additionally, the computational time required for tuning the controllers is compared to evaluate the computational burden of each tuning method.

6.1 Power extraction and CPU time

First, the PI parameters, i.e. $\alpha$ and $\beta$, are tuned via FDm, SDm, and TDm and applied to the nonlinear TD model. The PTO force can be expressed as a piecewise function depending on $\alpha$, $\beta$, and $f_{sat}$, as follows:

$$\begin{aligned} f_u(t) = \left\{ \begin{aligned}&f_u(t){} & {} \text { if }\ -f_{sat} \le \alpha \dot{z}(t) + \beta z(t) \le f_{sat} \\&f_{sat}{} & {} \text { if }\ f_u(t) > f_{sat} \\&-f_{sat}{} & {} \text { if }\ f_u(t) < -f_{sat} \\ \end{aligned} \right. . \end{aligned}$$

(56)

Then, the extracted power is derived from the nonlinear TD model controlled via Eq. (56), as computed integrating in time the product of the velocity component of the PA and the PTO force, as follows:

$$\begin{aligned} \overline{p} = \frac{1}{T}\int _{0}^{T} \dot{z}(t) f_u(t) \, dt. \end{aligned}$$

(57)

Table 3 Variance of the PA motion and velocity, and computational time required for simulations for each sea state and numerical model considered

Fig. 5

Extracted power (left) and CPU time (right) derived from the three tuning methods for the three example sea states. The red axis concern the ratio between the performances obtained with FDm and SDm w.r.t TDm

To begin with the corresponding performance assessment, Fig. 5 shows the extracted power for each of the tuning method (see Sect. 3.2), for the three irregular waves described by a JONSWAP spectrum with data summarized in Table 2. A number of conclusions can be directly elucidated from Fig. 5, which are discussed in the following. At first glance, it is clear that tuning the PI controller with SDm outperforms the use of FDm. This is, naturally, highly consistent with the quality of the approximating TD solutions of the SD model with respect to the FD one. In particular, as briefly demonstrated in Sect. 5.4, the accuracy of the SD is remarkably higher than the FD in modelling the TD solution in terms of output statistics. The ‘superiority’ of SDm with respect to FDm sits on the force-to-velocity response $G_{eq}$ (see Eq. (55)) used to identify the PI parameters, i.e. $\alpha$ and $\beta$ (see Eq. (32)), being capable to model the steady state behaviour of the nonlinear TD model. On the other hand, TDm is the most effective in adjusting $\alpha$ and $\beta$. Specifically, the use of an optimization routine, fminsearch in our concrete example, allows to further improve energy production, especially for high energetic seas (e.g. sea state $s_3$). This rationale is justified by the fact that the optimization process is conducted directly on the nonlinear plant to effectively locating an optimal condition. Additionally, FDm and SDm incorporate a single interpolation point $\omega _i = 2 \pi / T_p$, leading to suboptimal results when compared to TDm that optimises the extracted power via exhaustive search. The selection of $\omega _i = 2 \pi / T_p$ as interpolation point is herein motivated by the nature of the PA operating conditions, notwithstanding there is no theoretical reference that clearly asserts that this is the ideal decision. For instance, we assume in the following that the PA is subject to a stochastic sea-state, fully characterised in terms of a PSD with a peak period of $T_p$. An irregular sea state is composed of different frequencies and, depending on the broadness of the wave PSD, the resultant WEC motion will exhibit a certain range of frequency components, many of which differ from $\omega _i = 2 \pi / T_p$. Then, the interpolation point $\omega _i = 2 \pi / T_p$ could no longer be a proper and hence this choice must be done considering different spectrum parameters, e.g. peak enhancement factor $\gamma$, and others interpolation points, e.g. mean energy period or a series of selected frequencies [26, 27].

To further quantify the energy absorption differences, Fig. 5 reports the ratio between the extracted power achieved with FDm and SDm and the value obtained with TDm (dashed red line). It is shown how SDm approaches a unitary ratio since the extracted power is almost the same of TDm. On the other hand, the performances of FDm remarkably drop when the sea state becomes more energetic and the nonlinearities of the system are dominant, making the FD modelling inaccurate. Concerning the computational burden, Fig. 5 reports the CPU time to accomplish the control tuning for a single sea state. We can find that TDm ranks in ‘last position’ with respect to the CPU time being far from the CPU time guaranteed by FDm and SDm. It is straightforward to see that FDm is the most efficient from a computational perspective, allowing the calculation of the controller parameters $\alpha$ and $\beta$ in, almost, 10$^{-3}$ (s). SDm takes about 10$^{-2}$ (s) to tune the PI controller. Then, TDm gives the worst performance in terms of computational time by taking, on average, more than 10 (s) to optimise the control parameters. Figure 5 empathises the CPU time reduction of FDm and SDm with respect to TDm (dashed red line), showing that SDm are FDm are three to four order of magnitude faster than TDm, respectively.

6.2 Annual energy and CPU time

In order to expand the analysis on the effectiveness of each tuning method, the annual energy production of the PA is computed. The chosen installation site for the PA is located near Pantelleria island in the Mediterranean Sea (Italy). Based on the information provided in Fig. 6, the waves that are most representative for assessing the PA power generation capabilities have peak periods ranging from 3 to 10 (s), and significant wave heights ranging from 0.5 to 4 (m).

The three methods are tested across a broad spectrum of wave frequencies and heights, encompassing all possible sea conditions pertinent to the installation site of interest. The annual energy production of the PA is computed as follows:

$$\begin{aligned} E = \sum \overline{p} T. \end{aligned}$$

(58)

Equation (58) concerns the sum of the average powers extracted from each wave considered in the analysis.

The performance evaluation, focusing on the differences in energy extraction with respect to TDm, is depicted in Fig. 7. As anticipated, the percentage variations in terms of extracted energy between SDm and TDm are minimal, ranging from 0 to 10 ($\%$) for low-energy sea states and up to a maximum of 10–20 ($\%$) for more energetic sea states. Another anticipated outcome pertains to the performance disparity between FDm and TDm. From the figure, it is evident that TDm outperforms FDm by up to 70 ($\%$) in sea states where nonlinearities dominate. Specifically, FDm yields acceptable energy extraction differences (ranging from 0 to 20 ($\%$)) compared to TDm only in sea states characterized by peak periods between $T_p=4$ s and $T_p=6$ (s), and significant wave heights between $H_s=0.5$ (m) and $H_s=2$ (m). It should be noted that if the control action is not appropriately adapted to the prevailing sea state, the WEC motions may become exaggerated, causing a decrease in the accuracy of the FD representation and resulting in suboptimal control parameters and poor energy extraction performance

Fig. 6

Qualitative occurrences and energy scatter diagram for the reference site close to Pantelleria island (Italy)

Fig. 7

Percentage difference on annual energy extraction for all the Pantelleria sea states. TDm has been considered as the reference method

Quantitatively speaking, the annual energy produced by each method are reported in Table 4. SDm leads satisfactory results in term of energy extraction maximization, approaching the energy obtained through TDm that still remains the more effective to design a PI controller for the PA studied. In particular, SDm leads to a productivity 11 ($\%$) lower than TDm. On the contrary, FDm demonstrates its drawbacks in optimizing the energy extraction capabilities of the converter, underestimating the annual energy extracted of almost 41 ($\%$). The process of computing the annual energy produced by a WEC is (usually) carried out during the design of a WEC, involving a large number of evaluated individuals, which, in order to be compared, require the calculation of their potential in terms of extracted energy. From a CPU time perspective, Table 4 shows how the calculation of the annual extracted energy for an individual system through TDm requires a significant computational expenditure of approximately 286 (s). In contrast, SDm takes just over a tenth of second, precisely 0.160 (s), to complete the calculation of annual productivity. As expected, FDm is the most computationally efficient, as it outperforms SDm by (almost) one order of magnitude, performing the calculation of the energy produced by the PA in 0.022 (s). To illustrate the impracticality of using TDm in the design of the PA under study, consider the following example: suppose we aim to evaluate 11,250 individuals as part of an optimization problem with 12 free parameters, utilizing a single-objective genetic algorithm set to consider 150 generations in which 75 individual per generation are evaluated [6]. In such a scenario, FDm and SDm would require approximately 9.8 (s) and 72 (s), respectively, to complete the evaluations. In contrast, employing TDm would necessitate a staggering time of about 35.8 (h), assuming the optimization problem is solved on a high-performance computing (HPC) cluster-type computer equipped with 25 physical CPUs. This stark contrast in computational time highlights the infeasibility of utilizing TDm in practice, emphasizing the advantages of FDm and SDm in terms of computational efficiency.

Table 4 Annual energy produced and elapsed time to calculate it

6.3 Numerical models validity and controller design considerations

The observed effectiveness of SDm in maximizing annual productivity, and its computational efficiency, warrant further analysis to understand the reasons behind its success compared to FDm, and to justify the gap in performance compared to TDm.

The accuracy of the numerical model plays an important role, since the ability of a numerical representation in reproducing the realistic behaviour of a WEC naturally increases the optimality of the controller identification process. In our concrete example, the SD model ensures a remarkable accuracy in estimating the PA behaviour, both in low and high energetic sea conditions, as demonstrated previously (see Sect. 5.4). Aiming to demonstrate further the accuracy of the SD representation under optimal control conditions, numerical simulations has been conducted considering sea state $s_2$, while applying the optimal control parameters obtained via TDm to all the numerical models proposed, i.e. FD, SD and TD. The output, in terms of PDF of the heave motion (z) and heave rate ($\dot{z}$), are depicted in Fig. 8. It can be argued that the SD model accurately predict the statistical behaviour of the PA also under optimal control conditions, in which the WEC motion is exaggerated. Upon initial inspection, it is evident that the PDF of the heave motion, as shown in Fig. 8, is broader compared to the PDF depicted in Fig. 4. This observation is expected as the energy-maximizing control conditions induce larger motion amplitudes compared to sub-optimal control configurations. Additionally, the PDF obtained from the SD model closely follows the PDF derived from TD simulations, demonstrating the SD model ability to accurately capture the system response. A slight dissimilarity appears in the heave rate PDF if the SD and TD results are compared. In particular, the TD one diverges from a Gaussian distribution due to the high nonlinearities that appears in optimal control conditions.

Fig. 8

Pdf of the heave motion (left) and heave rate (right) obtained simulating the sea-state $s_2$ under optimal control consditions identified via TDm

Figure 9 reports stiffness and damping forces, depending on the heave motion and rate, respectively, with the aim to compare linear and nonlinear contributions. At a first glance, the nonlinear forces are of the same order of magnitude of the linear ones, specially for what concerns the damping contributions. The nonlinear components manifest themselves more as a damping contribution and, as can be seen in Fig. 9, the end-stop and viscous damping components are of the same magnitude as the radiation damping and about half the magnitude of the damping acted by the PTO. This result explains why the heave rate pdf diverges more from a Gaussian distribution than the heave motion pdf. Another important aspect to note in Fig. 9 concerns the sign of the stiffness component realised by the PTO. It can be seen that it is of different sign with respect to the hydrostatic stiffness, since the obtained $\beta$ coefficient is less than zero. Practically, the system’s resonance period is shifted to higher values, and its resonance frequency decreases. This result is due to the fact that the PA considered as a case study has a resonance frequency equal to 1.41 (rad/s), as can be seen in Fig. 12 in “Appendix A”, while the IM-principle tunes the PTO stiffness to make the WEC resonant at $2\pi / T_p$=1.04 (rad/s), for the case of sea state $s_2$. This result can be further appreciated in Fig. 10. This figure shows the optimal parameters $\alpha$ and $\beta$ identified by the three calibration methods. It can be seen that the stiffness coefficients $\beta$ are all of negative sign.

Fig. 9

Time traces of linear and nonlinear forces concerning both stiffness (up) and damping forces (down). The time traces refer to the sea state $s_2$ and a PI tuned with TDm

To further extend the analysis on the ability of each tuning method to identify optimal control parameters, Fig. 10 reports some iso-levels indicating the ratio between the extracted power obtained with a generic pair of $\alpha$ and $\beta$, and the maximum achievable power. The PI parameters obtained via TDm (pointed with a black dot) almost coincide with the optimal ones (indicated with a yellow marker and labelled as True maximum). The True maximum was obtained by testing a dense sequence of $\alpha$ and $\beta$ values around the point identified by the TDm. These exhaustive parametric simulations ensured a thorough exploration of the parameter space, allowing to accurately identify the absolute maximum for the sea state $s_2$. Concerning FDm and SDm, these are able to identify the $\beta$ coefficient better than the $\alpha$ coefficient, approaching the result achieved with TDm. This outcome demonstrates how the calibration principle based on IM theory provides satisfactory results in calibrating the resonance of a PA system. The same cannot be said for the identification of PTO damping, namely $\alpha$. It can be seen from Fig. 10 that the coefficients $\alpha$ identified with FDm and SDm differ profoundly from the optimal one identified with TDm. This inaccuracy can be explained by the fact that nonlinearities associated to the heave rate prevail over linear effects, as demonstrated by the time traces shown in Fig. 9, and thus the IM-based calibration process does not return the optimal damping coefficient. On the other hand, the sensitivity of the PA to the magnitude of the PTO damping seems to be very low since, while SDm synthesize a coefficient $\alpha$ equal to about half of the one obtained from TDm, the extracted power achieved is quite similar to the optimal one (see Fig. 5).

Fig. 10

Influence of the control parameters for the sea state $s_2$. The results of the three methods are reported with filled dot. The iso-level indicates the ratio between the extracted power obtained with a generic pair of $\alpha$ and $\beta$ and the extracted power achieved with TDm

Figure 11 shows a quantitative comparison of the coefficients $\alpha$ and $\beta$ identified by the three proposed methods. As already mentioned, FDm and SDm are excellent for identifying the stiffness coefficient of the PTO $\beta$ but not for choosing its damping parameter $\alpha$. In particular, SDm accurately design the stiffness coefficient $\beta$ with (almost) no error in respect to TDm for all the three sea-states. On the contrary, FDm and SDm lack in identifying the coefficient $\alpha$, giving error between 30 ($\%$) and 75 ($\%$) in respect to TDm. Overall, SDm gives lower error in identifying the control parameters for all the sea-states considered.

Fig. 11

Coefficient $\alpha$ (left) and coefficient $\beta$ (right) identified with the three tuning methods for the three example sea states. The red axis concerns the differences obtained with FDm and SDm w.r.t TDm

7 Conclusions

The problem of tuning a PI controller for a nonlinear WEC is solved with three different tuning methods. The first method (FDm) consists in deriving the (non-causal) IM energy-maximising controller via linear FD modelling and then interpolate it to derive a causal and implementable controller that satisfies the IM condition for one specific wave frequency. The second method (SDm) combines the use of the SD modelling technique and the IM-principle to find the controller parameters, relying on a more accurate PA representation in respect to the FD one. Concerning the third method (TDm), the controller is tuned via optimization: a cost function to be maximized is defined, i.e. extracted power, and different control parameters are imposed iteratively to the nonlinear TD model until the optimization process converges to a pre-described condition.

A critical comparison is provided not only in terms of power and annual energy absorption, but also in terms of CPU time needed to accomplish each tuning process. The results demonstrate how the novel method (SDm) outperforms the tuning provided by the FD model in terms of extracted energy, due to a better accuracy of the SD model, while approaching the power extraction performances of the tuning based on optimization routine. Moreover, the new technique abruptly reduces the computational burden since it need a single SD simulation to tune the controller, that is a specific purpose of this study, hence directly avoiding any numerical optimization routines. To sum up, despite a slightly lack in estimating the ‘true’ energy-maximizing control parameters, especially for energetic sea state, SDm is considered a valid method to synthesize a PI controller for nonlinear WEC in a computational efficient way.

The new methodology proposed is particularly suitable for the initial stages of WEC development, which (usually) employ global optimization routines that requires a high computational burden to evaluate many WEC architectures and components. Together, these results provide important insights towards an optimal and time-efficient control tuning, ideally enabling the use of nonlinear TD model also at early stage of designing WECs, thus avoiding computationally demanding optimization routines to solve for energy-maximizing control solution. It’s crucial to note that utilizing the SD model instead of the TD model leads to sub-optimal solutions in control parameter identification due to the inability to precisely replicate the nonlinear model. The SDm, which suggests using only one interpolating frequency to derive PI parameters, introduces an additional error in this identification. Moreover, the SDm operates without awareness of the maxima and minima attainable in the TD simulation. This lack can further contribute to sub-optimal calibration, as crucial information regarding the system’s dynamic range may be overlooked. These aspects collectively underscore the importance of carefully considering the choice of modeling approach and calibration methodology to ensure accurate control parameter identification.

Future works will apply the novel procedure to design controllers in broadband scenarios, using more advanced interpolation techniques to approximate the optimal IM-based controller within a frequency range, rather then at a specific frequency. In particular, future studies endeavours will delve into the study of both feedback and feedforward controllers employing the LiTe-Con and LiTe-Con+ architectures, further exploring their applicability in WEC systems.

Point-absorber parameters

In this work, a conceptual PA is used to prove the performances of different technique for tuning a PI controller intended to maximize the annual energy extraction. Table 5 gives the PA parameters used in the simulations, which follows the parameters reported in [12].

Table 5 Parameters of the point absorber under study

Fig. 12

Frequency-dependent a Froude–Krylov and diffraction complex coefficents reported in terms of magnitude |E| and phase $\angle E$, b added mass $\mathcal {A}$, c radiation damping $\mathcal {B}$, and d heave RAO reported in terms of magnitude |RAO| and phase $\angle RAO$

The hydrodynamic coefficients, that are derived via boundary element method (BEM) software, such as NEMOH [2], are reported in Fig. 12. In this figure, E represets Froude–Krylov and diffraction complex coefficents, $\mathcal {A}$ and $\mathcal {B}$ added mass and radiation damping coefficients, respectively. In Fig. 12, the response amplitude operator (RAO), referred to the heave DoF, has been reported in terms of magnitude and phase. The RAO is defined as:

$$\begin{aligned} RAO(\jmath \omega ) = \frac{E(\jmath \omega )}{-\omega ^2 (m+\mathcal {A}(\omega )) + \jmath \omega \mathcal {B}(\omega ) + k_{h1}}. \end{aligned}$$

(59)