Stochastic dynamics of mechanical systems with impacts via the Step Matrix multiplication based Path Integration method

Abstract

In this work we propose the Step Matrix Multiplication based Path Integration method (SMM-PI) for nonlinear vibro-impact oscillator systems. This method allows the efficient and accurate deterministic computation of the time-dependent response probability density function by transforming the corresponding Chapman–Kolmogorov equation to a matrix–vector multiplication using high-order numerical time-stepping and interpolation methods. Additionally, the SMM-PI approach yields the computation of the joint probability distribution for response and impact velocity, as well as the time between impacts and other important characteristics. The method is applied to a nonlinear oscillator with a pair of impact barriers, and to a linear oscillator with a single barrier, providing relevant densities and analysing energy accumulation and absorption properties. We validate the results with the help of stochastic Monte-Carlo simulations and show the superior ability of the introduced formulation to compute accurate response statistics.

1 Introduction

Vibro-impact oscillator systems have gained considerable attention in the scientific community due to their theoretical and practical significance in describing a wide range of problems in engineering. The impacts in such systems have been widely recognised to significantly influence system responses via various nonlinearities, such as grazing bifurcations [1, 2], chatter, sticking and chaos [3] with a profound effect on the performance and safety of mechanical structures. These nonlinear phenomena are mostly undesirable in applications, as they lead to complex behaviour, acoustic noise, increased maintenance, and even to system failures. Therefore, in most applications, we aim to avoid impacts, yet in many mechanical systems they inevitably occur due to tolerances e.g. in gears [4], ageing, wear, design-specific requirements (seismic mitigation gaps introduced to uncouple structure from the environment [5]) or the targeted applications involving impact interaction (hammer drills, jackhammers, deep drilling). There are also applications that utilise the nonlinearities introduced by intentionally designed impacts, e.g. in energy harvesting and vibration damping as they expand the operational bandwidth [6]. Therefore, accurately predicting and controlling the behaviour of vibro-impact systems is vital for optimising performance, ensuring reliability, and achieving desired system characteristics in practical engineering applications.

The inclusion of stochastic effects in mechanical systems is essential for capturing the inherent uncertainties present in real-world conditions. Uncertainties can arise from variations in system properties [7], external disturbances [8], or environmental factors [9], among others. The consideration of stochastic effects enables a more realistic representation of the system’s behaviour and facilitates the modelling and analysis of these uncertainties. In mechanical systems, stochastic effects can significantly influence the system’s stability [10], energy dissipation [11], energy harvesting [12] and dynamic response [13]. Understanding and quantifying these stochastic effects are crucial for robust design, risk assessment, and effective control strategies in engineering applications. In the context of vibro-impact systems, the significance of stochastic effects becomes particularly pronounced. The combination of intermittent impacts and stochastic influences introduces additional complexity and challenges in the analysis and prediction of system behaviour. Stochastic effects can give rise to phenomena such as stochastic resonance, amplification or suppression of vibrations, and transitions between different impact-induced behaviours. Investigating the role of stochastic effects in vibro-impact systems is essential for a comprehensive understanding of their dynamics under uncertain conditions, enabling more accurate predictions and improved control strategies in practical engineering scenarios.

One of the most important characteristics of the response statistics of a dynamical system to random effects is the time evolution of the probability density function (PDF) for the state variables [14]. By obtaining a response PDF, one can infer other important properties of the dynamical system, such as moments and reliability, and can improve the decision-making processes, where relevant. Concise and efficient tools for the description and the quantitative modelling of stochastic dynamical systems is stochastic differential equations (SDEs).

When modelling stochastic systems with impacts using SDEs there are several potential methods to obtain the PDF of the state variables. In the Monte-Carlo (MC) method, path-wise approximations are obtained through the numerical integration of the SDE [15, 16], even combined with stochastic averaging [17, 18] or with the method of multiple scales [19]. As it is a stochastic approach, and we need a large number of approximated realisations to obtain a good approximation for the PDF. The advantages of this method are its relative simplicity and its generalisation for a large set of problem classes. However, due to the stochastic nature of the MC method, we might need a large number of sample paths to properly characterise the statistics of the investigated system, and some uncertainty and noise remain in the results. There are also deterministic methods such as the Fokker–Planck equation, where we have to solve a corresponding partial differential equation to obtain the response PDF. In general, even for smooth systems, there is no explicit analytical solution for this equation, except for a small number of special cases. Thus we require a numerical approximations, such as finite element [20, 21] or finite difference [22] methods. However, due to the continuity conditions, the Fokker–Planck equation does not generalise well to non-smooth settings, such as time-varying impacts, except under certain special transformations [23].

Another formulation, based on the law of total probability, is the Chapman–Kolmogorov (CK) equation. Similarly to the Fokker–Planck equation, we have to rely on numerical methods to solve it. A possible approach to estimate the transitional probability density function (TPDF) is a generalised cell mapping (GCM), where the region of interest is divided into cells, and the probability of transitioning from one cell to another is computed through MC simulations [24, 25]. This method generalises well for a wide range of systems, but it introduces stochastic perturbations. Another approach, the Wiener Path Integral method, uses a variations formulation and the most probable path to approximate the TPDF [26,27,28,29]. This method is exceptionally efficient at approximating the TPDF and thus can be used directly to determine the steady-state PDF, however, it does not generalise to systems with impacts. The Path Integration (PI) method can address this gap while maintaining efficiency. This method utilises the PDF of explicit numerical time stepping schemes (e.g. Euler-Maruyama) to approximate TPDF. This consideration removes both the need for discrete cells and the negative effects of the stochastic perturbations, that is characteristic to the GCM, while not compromising on generality. With the help of the PDF of numerical schemes we can directly approximate the TPDF for a large number of system classes, including non-smooth dynamical systems. Most formulations of the numerical evaluation of PI solutions of the CK equations lead to a computationally expensive iterative method [30,31,32,33,34,35], where the integral in the CK is evaluated directly while using interpolation for the spatial discretisation of the PDF. There are efforts to accelerate this computation that maintain the general nature of the method. A computational approach uses GPUs [30, 36] to evaluate an iteration, greatly increasing the performance of the method as it is a highly parallelisable task without restrictions on the problem investigated. The step matrix multiplication-based path integration (SMM-PI) approach accelerates the computations algorithmically [37] by formulating the evaluation of the CK equation as a matrix–vector multiplication.

This work aims to expand the SMM-PI method for vibro-impact oscillators. This method was already shown to be able to uncover the response PDF of nonsmooth [38] linear vibro-impact systems [39], therefore it is an ideal candidate for the efficient analysis of nonlinear vibro-impact systems as well. We generalise the SMM-PI method for vibro-impact oscillators, and additionally, we use the resulting time-dependent response PDF to obtain important statistical characteristics of such oscillators, including the impact velocity distribution, the time between impacts, and the energy accumulated and absorbed by the system.

The paper is organised as follows. In Sec. 2 we describe the class of vibro-impact oscillators under consideration and give their equations of motion. Next, in Sec. 3 we derive the step matrix multiplication path integration (SMM-PI) method for the PDF of the vibro-impact oscillators and the impact velocity distribution. Furthermore, in this section, we use the SMM-PI formulation to obtain also the mean first impact time for such systems in order to compute the time between impacts. Then, in Sec. 5 we investigate the vibro-impact Van der Pol and linear oscillators and compare the results to Monte-Carlo simulations. The analysis includes the computation of the evolution of the response PDF, the impact velocity PDF, the energy accumulated within the system, the time between impacts and the energy absorbed by the impacts. Additionally, we discuss how to address a local error of the method through the simple example of a linear oscillator with a single impact barrier. Finally, in Sec. 6 we draw conclusions and summarise the results of this paper.

2 Stochastic vibro-impact oscillators

Fig. 1

Example mechanical model for the vibro-impact oscillator with two impact barriers. Here $f(x,v,t) = R(x,v) + F_{\textrm{det}}(x,v,t)$ and $g(x,v,t) = F_{\textrm{stoch}}(x,v,t)$

The governing equation of motion of a single-degree-of-freedom vibro-impact system (sketched in Fig. 1) is

(1)

if $x(t) \in {\mathcal {S}}$, and

$$\begin{aligned} v^+(\tau ) = -r\,v^-(\tau ) \end{aligned}$$

(2)

if $x(\tau ) \in \partial {\mathcal {S}}$. Here $x$ and $v$ denote the displacement and velocity of the oscillator, that evolve in time $t$, $v^-(\tau )$ and $v^+(\tau )$ are the velocities just before and after the impact at time $\tau$, $r$ is the coefficient of restitution (CoR), ${\mathcal {S}}$ denotes the region of smooth motion and $\partial {\mathcal {S}}$ denotes its boundaries, that we refer to as impact barriers. The functions $f$ and $g$ are smooth functions, where $f(x,v,t)$ incorporates nonlinear behaviour (e.g. in case of a mechanical oscillator this is the nonlinear restoring and damping forces) while $g$ is the state varying noise intensity. In this work we focus on vibro-impact oscillators of two types: with a single impacting barrier where ${\mathcal {S}} = (\xi _{\textrm{L}},\infty )$ and $\partial {\mathcal {S}} = \{\xi _{\textrm{L}}\}$, and with two impacting barriers, where ${\mathcal {S}} = (\xi _{\textrm{L}},\xi _{\textrm{R}})$ and $\partial {\mathcal {S}} = \{\xi _{\textrm{L}}, \xi _{\textrm{R}}\}$. Here $x=\xi _{\textrm{L}}$ is the location of the left boundary and $x = \xi _{\textrm{R}}$ is the right boundary.

3 Path integration method

To investigate the response statistics of the vibro-impact oscillator (1) first we compute the PDF $p(x,v,t)$. As the stochastic process (1) is Markovian, we describe the time evolution of $p(x,v,t)$ with the Chapman–Kolmogorov (CK) equation, that we solve with the help of the SMM-PI method. In the case of the vibro-impact oscillator (1) the CK equation has the form of

(3)

Here, $p(x,v,t_{n+1} \vert x_0,v_0,t_n)$ is the transitional joint PDF of the displacement $x$ and velocity $v$ of the vibro-impact oscillator at time $t_{n+1}$ given an initial state $x(t_n) = x_0$, $v(t_n) = v_0$. Note that the difference between (3) and the CK equation for a smooth oscillator is the integration interval; in case of (3) $x_0 \in {\mathcal {S}}$, while in case of a smooth oscillator $x_0 \in {\mathbb {R}}$.

The SMM-PI method approximates the time evolution of the PDF $p(x,v,t)$ by transforming the Eq. (3) into a matrix multiplication of the form

(4)

where is a matrix containing the values of the probability density function $q_{i,j,n} = p(x_{i},v_{j},t_n)$ at the discrete points $\{x_{i},v_{j} \vert i = 1,\ldots ,N_x, j= 1, \ldots , N_v\}$ over a finite region, and is the step matrix. The process of this transformation has three key components: the interpolation of the PDF $p(x,v,t_n)$, the approximation of the transitional probability density function $p(x,v,t_{n+1} \vert x_0,v_0,t_n)$ based on the PDF of numerical time stepping schemes and the computation of the integral in (3) using e.g. a Gauss-Legendre quadrature.

3.1 Interpolation

For the interpolation of the PDF $p(x,v,t_n)$ we use a fifth-order polynomial interpolation formulated as the linear combination of the elements of the matrix of the known points, i.e.,

(5)

where is an interpolation weight matrix constructed using the interpolation function $\phi _i(.)$ of the fifth order interpolation detailed in Appendix B.1.3. of [37]. In [37] a detailed analysis comparing different interpolation methods (linear, cubic, quintic, barycentric, trigonometric) show that the fifth-order polynomial (quintic) interpolation is remarkably efficient in the SMM-PI setting. The quintic interpolation has a high error convergence rate (up to $O(N_x^{-5})$), while it has a small constant number (i.e. 6) of interpolation functions, making it a computationally performant choice for interpolating $p(x,v,t_n)$.

The main advantage of the formulation in (5), is that we can detach the weight functions $\phi _{i}(x)\,\phi _{j}(v)$ from the values $q_{i,j,n}$, and evaluate the integral of the CK-equation only on these weight functions. To compute we evaluate the CK equation (3) for each interpolation value $q_{i,j,n+1}$, namely,

(6)

with

(7)

where ${\mathcal {I}}_v \subset {\mathbb {R}}$ is the velocity interval covered by the interpolation.

3.2 Transitional probability density function of non-smooth oscillators

For the approximation of the TPDF $p(x,v,t_{n+1} \vert x_0, v_0,t_n)$ we use a similar approach as in [37], however, we adjust it for the case of the vibro-impact systems, namely for the non-smooth impacting dynamics. In general, the TPDF is not available in a closed analytical form even for smooth systems. Thus, the basis of the approximation of the TPDF is the probability density function of a numerical time stepping scheme with $x(t_n) = x_0$ and $v(t_n) = v_0$:

$$\begin{aligned} \begin{aligned} x(t_{n+1})&\approx \eta _{x}(x_0,v_0,t_n,t_{n+1}),\\ v(t_{n+1})&\approx \eta _{v}(x_0,v_0,t_n,t_{n+1}) + g(x_0,v_0,t_n) \Delta W_n \end{aligned} \end{aligned}$$

(8)

for a time step between $t_n$ and $t_{n+1}$. Here $\eta _{x}$ and $\eta _{v}$ are the approximations of the drift term, while $\Delta W_n \sim {\mathcal {N}}(0,\sqrt{\Delta t})$ is the Maruyama approximation of the Wiener increment. At this point, we do not restrict this description to a particular numerical time-stepping scheme for the drift term. One potential candidate is the Euler step, which uses

(9)

However, we can opt for a higher order drift approximation, that captures the interactions between $x$ and $v$ with high accuracy (e.g. fourth-order Runge–Kutta approximation). In these cases the formulas for $\eta _{x}$ and $\eta _{v}$ are more complex and potentially too convoluted to write out. In this work we approximate the drift evolution with Ralston’s method (detailed in Appendix A), a second-order explicit time-stepping scheme, that has the minimal local error bound among the two-stage Runge–Kutta methods [40].

Furthermore, as we use a small time step $\Delta t = t_{n+1}-t_{n}$ when computing the TPDF, we assume that we have at most a single impact during the time interval $[t_{n},t_{n+1}]$ even for low velocities $v$. In both cases (with and without impact), the TPDF is approximated as

(10)

where $p_{{\mathcal {N}}}(v,v_1, \sigma _v )$ is the PDF of the normal distribution ${\mathcal {N}}(v_1,\sigma _v)$, i.e.

$$\begin{aligned} p_{{\mathcal {N}}}(v,v_1, \sigma _v ) = \frac{1}{\sqrt{2\pi }\sigma _v}e^{-\frac{(v-v_1)^2}{2 \sigma _v^2}}. \end{aligned}$$

(11)

To obtain $x_1$, $v_1$ for the smooth motion, i.e., when we start at $x(t) \notin \partial {\mathcal {S}}$, over $t\in [t_n,t_{n+1}]$, we solve

$$\begin{aligned} \begin{aligned} x_1 - \eta _x(x_0,v_0,t_n,t_{n+1})&= 0,\\ v_1 - \eta _v(x_0,v_0,t_n,t_{n+1})&= 0, \end{aligned} \end{aligned}$$

(12)

where $x_0$ and $v_1$ are the unknown variables. Note, that $x_1$ is fixed due to the term $\delta (x-x_1)$ in (11). The diffusion of the step without impact is

$$\begin{aligned} \sigma _v = g(x_0,v_0,t_n). \end{aligned}$$

(13)

Starting from an initial condition that results in an impact ($x(\tau ) \in \partial {\mathcal {S}}, \tau \in [t_n,t_{n+1}]$), we use an approximation where we first trace the time evolution of the drift $\eta _x$ and $\eta _v$ through the impact, and then approximate the diffusion. In this case, we solve the set of equations

$$\begin{aligned} \begin{aligned} \xi - \eta _{x}(x_0,v_0,t_n, \tau )&= 0,\\ v^- - \eta _{v}(x_0,v_0,t_n, \tau )&= 0,\\ v^+ + r\,v^-&= 0,\\ x_1 - \eta _{x}({\bar{x}},v^+, \tau ,t_{n+1})&= 0,\\ v_1 - \eta _{v}({\bar{x}},v^+, \tau ,t_{n+1})&= 0. \end{aligned} \end{aligned}$$

(14)

Here $\xi \in \partial {\mathcal {S}}$ denotes the location of the impact barrier, $\tau$ is the time of the impact, and $x_1$ and $v_1$ are the finishing position and velocity at time $t_{n+1}$. In (14) the unknown variables are $x_0$, $v_1$, $v^-$, $v^+$ and $\tau$.

Next, we approximate the diffusion $\sigma _v$. We assume, that each trajectories started at $x_0,v_0$ reach the barrier at $x=\xi$ approximately at time $\tau$ with a variance . Then the corresponding impact velocities $v^-(\tau )$ are multiplied by a factor of $-r$, i.e. $v^+(\tau ) = -r v^-(\tau )$. This leads to a contracted velocity variance $\sigma _{v,+}^2 = r^2 \sigma _{v,-}^2$, and as the trajectories continue according to (8), this variance further increases by leading to

(15)

Next, we substitute (11) into (3) and utilise (12)-(15) to compute the parameters $v_1$ and $\sigma _v$ of $p_{{\mathcal {N}}}(v,v_1,\sigma _v)$. When evaluating the resulting integral we integrate the Dirac delta function of the form $\delta (\gamma (x))$, that has the property

(16)

where

(17)

When applying this property to (3) combined with the approximated TPDF, the integral yields

(18)

Here $x_0^*$ denotes the initial condition $x_0 = x_0^*$ for which

$$\begin{aligned} \gamma _x(x_0^*) = (x-x_1(x_0^{*},v_0,t_n,t_{n+1})) = 0. \end{aligned}$$

(19)

In (18) and (19) we used the clarifying notations $v_1 = v_1(x_0^*,v_0,t_{n},t_{n+1})$, $\sigma _v = \sigma _v({x_0}^{*},v_0,t_{n},t_{n+1})$ and $x_1 = x_1({x_0}^{*},v_0,t_n,t_{n+1})$ to emphasise that these quantities depend on $x_0^*$, $v_0$, $t_n$ and $t_{n+1}$. Note that Eqs. (16)-(19) hold for both the non-impacting and impacting cases. The difference is that for the case without impact we use (12) for computing the states $v_1$ and $x_0^*$ in (19), and (13) for the diffusion $\sigma _v$. Meanwhile, for the case with impact we use (14) and (15) to obtain $x_0^*$, $v_1$ and $\sigma _v$, while as a side benefit we also obtain $\tau$, $v^+$, and $v^-$ as well.

3.3 Approximation of the integral

As the final key step of solving of the Chapman–Kolmogorov Eq. (3) we evaluate the integral

(20)

Here $x_0^*$ corresponds to the initial position that satisfies (19) for $x_1 = x_{i}$. We utilise the exponential decay of the Gaussian component of the TPDF, and only evaluate the integrale on the interval $v_0\in \bar{{\mathcal {I}}}_v \subset {\mathcal {I}}_v$ where the kernel of (20) significantly differs from zero. With this consideration we minimise the number of subnodes required for an accurate quadrature approximation of . To find the starting velocities $v_0 \in \bar{{\mathcal {I}}}_v:= [V_{\textrm{L},0},V_{\textrm{U},0}]$ that contribute to $p(x_1,v_1,t_{n+1})$ we trace back trajectories ending in the interval $\bar{{\mathcal {J}}}_v:=[V_{\textrm{L},1},V_{\textrm{U},1}]$ around $v_1$ using only the drift of (1). We choose the limits $V_{\textrm{L},1}$ and $V_{\textrm{U,1}}$ using the diffusion at $g(x_0,v_0,t_{n})$, e.g. $(V_{\textrm{L},1},V_{\textrm{U,1}}) = v_1 \pm k \; g(x_0,v_0,t_{n})\Delta t$, where we set $k\in {\mathbb {R}}_+$ large enough to find all initial states that contribute to $p(x_1,v_1,t_{n+1})$, e.g. $k = 4$ or $k = 6$.

For the final position $x_1$ and velocities $v_1 \in \bar{{\mathcal {J}}}_v$ that we reach without an impact this process is straightforward: we choose the limits $V_{\textrm{L},1}$ and $V_{\textrm{U},1}$ then use Eqs (12) to find the corresponding initial velocity interval $\bar{{\mathcal {I}}}_v = [V_{\textrm{L},0},V_{\textrm{U},0}]$. However, when we have a final position $x_1$ close to the impact barrier, we have to take into consideration that for some velocities within the interval $\bar{{\mathcal {J}}}_v$ we might have an impact. Figure 2 shows the sketch of this process for $x_1$ being close to $x = \xi _{\textrm{L}}$. We first find $V_{\textrm{I},1}$ by setting the time of impact to $\tau = t_n$ and substitute it back to (12) with $x_0^*= \xi _\textrm{L}$ and solve it for $v_1 =V_{\textrm{I},1}$ and $v_0 = V_{\textrm{I},0}$. In case $V_{\textrm{I},1} \in \bar{{\mathcal {J}}}_v$, then we split the interval $\bar{{\mathcal {J}}}_v$ into an interval $\bar{{\mathcal {J}}}_{v,1}$ (orange in Fig. 2) that consists of final velocities that are reached through smooth motion and to an interval $\bar{{\mathcal {J}}}_{v,1}$ (green in Fig. 2) that are final velocites that are reached after an impact. Finally, for the endpoints $V_{\textrm{L},1}$ and $V_{\textrm{I},1}$ of the interval $\bar{{\mathcal {J}}}_{v,1}$ we compute the corresponding initial velocity interval $[V_{\textrm{L},0}, V_{\textrm{I},0}]$ with the use of the Eqs (12) corresponding to the smooth motion. Similarly, for the velocities $V_{\textrm{I},1}$, $V_{\textrm{U},1}$ of $\bar{{\mathcal {J}}}_{v,2}$ we compute the initial velocity interval $[V_{-\textrm{I},0}/r, V_{\textrm{U},0}]$ by utilising the Eq. (14) describing the motion with impact. The resulting composite interval $\bar{{\mathcal {I}}}_v = [V_{\textrm{U},0},-V_{\textrm{I},0}/r] \cup [V_{\textrm{L},0},V_{\textrm{I},0}]$ gives us the initial velocities for the quadrature evaluation of the integral (20). For TPDFs $p(x_1,v_1,t_{n+1} \vert x_0,v_0,t_n)$ where $v_0 \in [V_{\textrm{U},0},-V_{\textrm{I},0}/r]$ we use (14) and (15) corrsponding to the dynamics with impacts compute the drift and diffusion of the trajectories, while for TPDFs where $v_0 \in [V_{\textrm{L},0},V_{\textrm{I},0}]$ we use (12) and (13) corresponding to the smooth dynamics. Note that in Fig 2 the position $x_1$ is fixed, while $x_0^{*}$ is the intial position corresponding to $x_1$ and $v_0$ and the dashed lines represent the the change in velocity during impact, i.e. the mapping that takes $v^-$ to $v^+ = -r v^-$.

Fig. 2

Sketch for the integration limits: the quantities $V_{\textrm{L}}$, $V_{\textrm{I}}$ and $V_{\textrm{U}}$ with the index 0 refer to states corresponding to $t_n$ and with the index 1 refer to states corresponding to $t_{n+1}$

Remark

In the models of mechanical systems where we describe impacts as instantaneous velocity changes, as the underlying deterministic system in (1), we encounter the so-called grazing phenomenon [41]: an impact with zero velocity, i.e. $x \in \partial {\mathcal {S}}$ and $v = 0$. In case of deterministic systems where we have periodic orbits, grazing can lead to bifurcations and other singular behaviour [1, 2, 41]. In this work we consider these zero velocity impacts as if there is no impact happening, therefore we use (12) to compute $v_1$ and $\sigma _v$ necessary for the TPDF approximation (11).

4 Derived statistics

4.1 Impact velocity distribution

Besides the joint PDF $p(x,v,t)$ another important statistic describing a stochastic vibro-impact process is the impact velocity distribution $p^{(\xi )}_{v^-}(v,t)$ at the impact barrier $x = \xi$. This distribution is essential when investigating the impact forces or the energy absorbed by impacts. First, we assume that the joint PDF $p(x,v,t)$ is available via e.g. the SMM-PI method. Next we use Bayes theorem, namely we write

(21)

The condition that an impact happens is satisfied when the velocity $v\in {\mathcal {V}}(\xi )$. This impact velocity interval ${\mathcal {V}}(\xi )$ depends on $\xi$, i.e.

(22)

In terms of probability density functions 21 translates for $v\in {\mathcal {V}}(\xi )$ as

(23)

where is the normalising constant. Here we utilise , that is an inherent relationship between the displacement $x$ and the velocity $v$ in case of oscillators. To summarise: the impact velocity distribution at $x = \xi$ is

$$\begin{aligned} p^{(\xi )}_{v^-}(v,t) = {\left\{ \begin{array}{ll} v \, p(\xi , v, t)/K &{} \text {if } v\in {\mathcal {V}}(\xi ),\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(24)

4.2 Expected time until next impact

In this section we formulate an approximation for the steady-state mean time ${\bar{T}}_{\partial S}(x,v,t)$ of impacting the barrier $\partial S$ starting from state $(x,v)$. The equation we use to estimate the mean first hitting time (MFHT) is

(25)

The Eq. (25) captures the expected time to the next impact starting from state ($x$, $v$): after taking a time step $t_{n+1}-t_n$ we end up in state ($x_1$, $v_1$) with probability density $p(x_1,v_1,t_{n+1} \vert x,v,t_n)$ (the TPDF corresponding to (1)), from where the expected time to next impact is ${\bar{T}}_{\partial S}(x_1,v_1, t_{n+1})$. The second term in (25) utilizes the law of total expectation to average the expected times to impact ${\bar{T}}_{\partial S}(x_1,v_1, t_{n+1})$ after the time step weighted by the TPDF $p(x_1,v_1,t_{n+1} \vert x,v,t_n)$. Throughout this process we assume that the time step is small, therefore, there is no impact for $t \in [t_n,t_{n+1}]$.

Using a numerical approximation analogous to that given for the PI method in Sec. 3, we transform (25) to the system of linear equations

(26)

where is the unknown matrix of interpolation values for ${\bar{T}}_{\partial S}(x,v,t_n)$, is the step matrix for the mean first hitting time, is a vector of ones of the appropriate size. In constructing (26) we use similar approximation steps as in case of the Chapman–Kolmogorov equation’s transformation to (4). Namely, we approximate the transitional probability density function $p(x_1,v_1,t_{n+1} \vert x,v,t_n)$ according to Sec. 3.2, we interpolate ${\bar{T}}_{\partial S}(x_1,v_1,t_{n+1})$ according to Sec. 3.1 and then evaluate the integral in (25) using e.g. a Gauss-Legendre quadrature. To solve system (26) we set the elements of to zero, that correspond to the boundary conditions ${\bar{T}}_{\partial S}(\xi _{\textrm{L}},v,t_{n+1}) = 0$ for all $v\le 0$ and ${\bar{T}}_{\partial S}(\xi _{\textrm{R}},v,t_{n+1}) = 0$ for all $v\ge 0$.

For a general time-variant vibro-impact oscillator (1) solving the system (26) for requires an initial , which is generally not available. However, when investigating the steady-state mean first hitting time of a periodic ($f(x,v,t) = f(x,v,t+\tau _p)$, $g(x,v,t) = g(x,v,t+\tau _p)$) or a time-invariant ($f(x,v,t) = f(x,v)$, $g(x,v,t) = g(x,v)$) vibro-impact oscillator, we can utilise that , $\tau _p = p \Delta t$ and , respectively. In these cases we have a well-defined system of linear equations for (26) that we solve to obtain the (periodic) steady-state mean first hitting time of the barriers.

5 Numerical examples

5.1 Stochastic Van der Pol oscillator with impacts

In this section, we use numerical experiments to test the SMM-PI method’s ability to estimate the time evolution of the PDF $p(x,v,t)$, the impact velocity PDF $p^{(\xi )}_{v^-}(v,t)$, the expected time ${\bar{T}}_{\partial S}$ between impacts, energy ${\bar{E}}_{\text {acc}}$ accumulated in the system and energy ${\bar{E}}_{\text {absorb}}$ absorbed by impacts in a nonlinear vibro-impact oscillator. Even though the definition in (27) and in the TPDF definitions through (8)-(19) we generalised the method for stochastic vibro-impact oscillators with state-dependent noise, in the examples we will focus on systems with additive noise, as it is the most frequently applied noise model in engineering problems. Therefore, in this section we consider the stochastically forced Van der Pol oscillator, the prototype for systems with self-excited limit cycle oscillations, with two, symmetric impact barriers. The Van der Pol oscillator is a well studied system, with several advantages that make it a good candidate to benchmark the PI method. It is autonomous, allowing a number of simplifications (discussed later) during the computation of the step matrix , the PDF $p(x,v,t)$ and the other statistics. Furthermore, it is also a nonlinear system, that not only makes this system ideal to demonstrate the SMM-PI method’s capabilities, but also it has a stable limit cycle allowing it to mimic some characteristics of a periodically forced stochastic vibro-impact system, e.g. the system that is used to describe vibro-impact energy harvester [2, 6].

The governing equations of motion for the Van der Pol oscillator subjected to additive noise is

(27)

when $x\in {\mathcal {S}}=(\xi _{\textrm{L}} = -d,\xi _{\textrm{R}} = d)$ with two symmetric impacting barriers at $x = \pm d$. The impact condition at $x(\tau )\in \partial S = \{-d,d\}$ is

$$\begin{aligned} v^+(\tau ) = -r\,v^-(\tau ). \end{aligned}$$

(28)

We use the SMM-PI method to capture the response probability function $p(x,v,t)$, the impact velocity distribution $p^{(\xi )}_{v^-}(v,t)$, the mean time between impacts ${\bar{T}}_{\partial S}(x,v,t)$ and the energy response of the system in the presence of additive white noise, and compare the results to Monte-Carlo simulations.

Since the Van der Pol oscillator is an autonomous system, the corresponding step matrix is time invariant as well, i.e. . Therefore we need to compute it only once, and the matrix–vector multiplication (4) representing a time step in the (3) for the PDF $p(x,v,t)$ reduces to

(29)

Additionally,when there is a single steady-state solution $p(x,v):= \lim _{t\rightarrow \infty } p(x,v,t)$ for (3), independent from the initial distribution $p(x,v,0)$, we can obtain the steady-state discretised representation using two main approaches. One is the successive evaluation of (29) until we reach a tolerance condition , for some norm (e.g. $L_2$). Alternatively, we can utilise the fact that the eigenvector of corresponding to the eigenvalue with the largest magnitude $\lambda _{(1)}\approx 1$ is the only surviving eigenvector following the successive multiplications in (29). In this case represents the steady state PDF $p(x,v)$, given that the time step $\Delta t$ and resolutions $N_x$ and $N_v$ are sufficient for the approximation of (3).

Throughout this section we use the parameters $\mu = 1/2$, $\sigma = 1/2$,$d = 1.25$ and $r = 0.7$, and initial distributions $x(0) \sim {\mathcal {N}}(0, \sqrt{0.3})$ and $v_0 \sim {\mathcal {N}}(3,\sqrt{0.3})$. Note that throughout this paper we use the notation $X\sim {\mathcal {N}}(\mu _X,\sigma _X)$ for a Gaussian random variable with mean and variance .

We test the SMM-PI method with a time step $\Delta t = 10^{-2}$ and a spatial discretisation $N_x = N_v = 151$ along each direction over the $(x,v)\in [-d,d]\times [-6,6]$ region, that is a sufficiently large to contain the non-zero values of the steady-state PDF. When choosing a time step $\Delta t$ and spatial discretisations $N_x$ and $N_v$, we rely on the results of [37], where we conducted an in-depth analysis on the effect of $\Delta t$, $N_x$ and $N_v$ on the mean absolute error and computational performance of the SMM-PI method by comparing the results to closed form solutions for smooth systems. As for the examples in this work there are no such benchmarks available, we do not conduct a formal analysis to choose suitable resolutions. Rather, we experimented with multiple temporal and spatial resolutions, and we decided to use such a combination that resulted in an accurate solution with acceptable computational requirements.

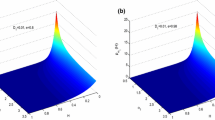
Figure 3 shows the response PDF $p(x,v,t)$ evolution as a surface for the above parameters. After a short transient, we see that the response PDF evolves to a steady-state distribution by $t \approx 7$. This is expected, as system (27) is time-invariant and the system is ergodic. Furthermore, the underlying deterministic system without impacts has a stable periodic orbit. Results show, that the property of having a stable periodic orbit carries over to the motion of the Van der Pol oscillator with impacts, and this new stable orbit dominates the stochastic dynamics as well, as illustrated in Fig. 4.

Fig. 3

Joint response probability distribution $p(x,v,t)$ evolution for the Van der Pol oscillator for parameters $\mu = 1/2$, $\sigma = 1/2$, $d = 1.25$ and $r = 0.7$, and initial conditions $x(0) \sim {\mathcal {N}}(0, \sqrt{0.3})$ and $v(0) \sim {\mathcal {N}}(3, \sqrt{0.3})$

Fig. 4

a) Stable limit cycle for the Van der Pol oscillator with parameter $\mu = 1/2$, b) stable limit cycle for the Van der Pol oscillator with impacts at $d = 1.25$ and c) contours of the steady state PDF $p(x,v)$ for the stochastic Van der Pol oscillator with impacts with parameters $\mu = 1/2$, $\sigma = 1/2$, $d = 1.25$ and $r = 0.7$. The dashed red line in panel c) shows the stable limit cycle from panel b)

Figure 5 shows the contour lines of the joint PDF $p(x,v,t)$ and the marginal PDFs $p_x(x)$ and $p_v(v)$ computed with the SMM-PI method, at different times $t$. We compare the results of the SMM-PI to histograms based on MC-simulations, that we conducted using the strong order 1 Runge-Kutta-Milstein method with time step $\Delta t_{\text {MC}} = 0.001$, combined with automatic impact detection from the DifferentialEquations.jl [42] numerical differential equation solver library. To construct the histograms we used $10^5$ trajectories. For the histogram we partioned each direction into 20 sections, and recorded the frequency of trajectories being in each bin. The resulting 400 bins leads to on average $\sim 250$ data points for each bin, meaning that in the case that the PDF $p(x,v,t)$ is spread over a larger area, then the histogram estimation is noiser due to the smaller sample sizes in each of the significant bins. In the case of the marginal PDF’s $p_x(x,t)$ and $p_v(v,t)$ we have an average of 5000 samples for each segment, therefore the histogram estimation has smaller variance, leading to a smoother estimation. We see that the contours obtained by the SMM-PI are in good agreement with the results of the corresponding MC results for each time instant, especially for the marginal PDF’s $p_x(x,t)$ and $p_v(v,t)$. This demonstrates, that the SMM-PI is capable of capturing the whole time evolution of the response PDF $p(x,v,t)$, and the marginal PDFs $p_x(x,t)$ and $p_v(v,t)$ (for $x$ and $v$) with high accuracy. Note, that the contours in Fig. 5 are rescaled for each time instant for visualisation purpose.

Fig. 5

Comparison of the joint PDF $p(x,v,t)$ and the marginal PDFs $p_x(x)$ and $p_v(v)$ for the Van der Pol oscillator at different time instances, obtained via the SMM-PI method and Monte-Carlo simulations. The parameters are $\mu = 1/2$, $\sigma = 1/2$, $d = 1.25$ and $r = 0.7$, and the initial conditions are $x(0) \sim {\mathcal {N}}(0, \sqrt{0.3})$ and $v_0 \sim {\mathcal {N}}(3,\sqrt{0.3})$

Next, we investigate the impact velocity distribution $p^{(\xi )}_{v^-}(v,t)$ defined by (24). Here $x = \pm d$ is the location of the impact, ${\mathcal {V}}(\xi )$ is the interval of impact velocities on the barriers, is the normalisation constant. For the Van der Pol oscillator (27) we have ${\mathcal {V}}(-d) = (-\infty , 0)$ and ${\mathcal {V}}(d) = (-\infty , 0)$.

By using the SMM-PI method we can obtain an impact velocity PDF $p^{(\xi )}_{v^-}(v,t)$ for a single time instant $t$. However, when comparing the results to MC simulations, we need to consider that the impacts are instantaneous events, thus it is impossible to observe the impact velocity distribution for that time instant $t$. Hence we take a finite length time interval $[t_1,t_2]$ and use the velocities of the observed impacts within that time interval to estimate the impact velocity distribution ${\bar{p}}^{(\xi )}_{v^-}(v,t_1,t_2)$ averaged over the interval $[t_1,t_2]$:

(30)

with $\xi \in \{-d,d\}$.

In Fig. 6 we see that the SMM-PI is capable of capturing the impact velocities as well, as we see good agreement between the results on both impact barriers for all time interval displayed. As the structure of the system (27) is time-invariant and symmetric, the impact velocity distribution converges to a symmetric steady-state distribution ${\bar{p}}^{(\xi )}_{v^-}(v) = \lim _{t \rightarrow \infty } {\bar{p}}^{(\xi )}_{v^-}(v,t)$, namely

$$\begin{aligned} {\bar{p}}^{(-d)}_{v^-}(v) = {\bar{p}}^{(d)}_{v^-}(-v). \end{aligned}$$

(31)

We can observe this symmetry in the righmost column of 6.

We emphasise that the SMM-PI method is capable of capturing the whole time evolution of the impact velocity distribution $p^{(\xi )}_{v^-}(v,t)$ with high accuracy, as well as the steady-state distribution ${\bar{p}}^{(\xi )}_{v^-}(v)$, while the MC simulations can only provide an averaged estimate of the impact velocity distribution.

Fig. 6

Comparison of the impact velocity distribution PDF ${\bar{p}}^{(\xi )}_{v^-}(v,t_1,t_2)$ for the Van der Pol oscillator at different time instances, obtained via the SMM-PI method and Monte-Carlo simulations. The parameters are $\mu = 1/2$, $\sigma = 1/2$, $d = 1.25$ and $r = 0.7$, and the initial conditions are $x(0) \sim {\mathcal {N}}(0,\sqrt{0.3})$ and $v_0 \sim {\mathcal {N}}(3,\sqrt{0.3})$ and the system reaches steady state at around $t\approx 7$

Next, we consider the steady-state MFHT ${\bar{T}}_{\partial S}(x,v)$ of the barriers $\partial S = \{-d,d\}$. In Fig. 7 we compare results obtained via solving (25)-(26) using the SMM-PI formulation to the MFHTs computed by MC simulations started from the impact barrier with different velocities $v$. As our aim is to use the MFHT to approximate the time between impacts, we only consider the MFHT ${\bar{T}}_{\partial S}(x,v)$ for the barrier $x \in \partial S$. In Fig. 7 we show the MFHT ${\bar{T}}_{\partial S}$ on the impact barriers, computed with the SMM-PI formulation compared to MC simulations for the parameters $\mu = \sigma = 1/2$, $\delta = 1.25$ and $r = 0.7$. To estimate ${\bar{T}}_{\partial S}(x,v)$, $x\in \{-d,d\}$ with MC simulations, we started $10^5$ trajectories for 21 different velocities $v$ on each barrier, and measured the time until the first impact occured. In Fig. 7 we see good agreement between these MC results and the results obtained through the SMM-PI formulation. However, we have to be aware a local interpolation error that occur at $v^+=0$ when using the SMM-PI formulation to obtain mean impact time ${\bar{T}}_{\partial S}$. This is due to the reason, that near $v^+=0$ where we go from velocities $v^+ = -r v^-$ with $v^- \notin {\mathcal {V}}(\xi )$ to velocities $v^+ = -r v^-$ with $v^- \in {\mathcal {V}}(\xi )$ the mean impact time ${\bar{T}}_{\partial S}$ makes a sudden transition from 0 to a finite positive value. This introduces high frequency components into the function ${\bar{T}}_{\partial S}(\xi ,v^+)$ describing the impact times, which the interpolation struggles to properly capture. This may leads to physically not meaningful negative impact times near $v^{+} = 0$, as in Fig. 7.

From Fig. 7 we also see, that as we increase the magnitude $\vert v^+ \vert$ of the initial velocity of the trajectory after impact, the effect of the nonlinear dynamics decreases. In this case the impact time $T(\xi ,v^+)$ converges to a behaviour as if the path has a constant velocity $v^+$ during the entire travel between the two barrers, i.e. we have an asymptotic impact time $\lim _{ \vert v^+ \vert \rightarrow \infty } T(\xi ,v^+) = 2d/v^+$ for $v^+ = -r v^-$ with $v^- \in {\mathcal {V}}(\xi )$, $\xi \in \{-d,d\}$.

Fig. 7

Expected time between impacts for the Van der Pol oscillator starting from the barrier located at $x = -d$ and $x = d$ for different $v^+$ after impact velocities

At this point, we have the framework to investigate the energy statistics of the vibro-impact Van der Pol oscillator driven by noise. We can compute the mean of the energy accumulated within the system in the steady state by

(32)

where $p(x,v):= \lim _{t \rightarrow \infty } p(x,v,t)$. The mean energy dissipated by a single impact during steady-state at barrier $x = \xi$ is given by

(33)

Here we utilised that for a trajectory the kinetic energy before the impact is $(v^-)^2/2$, while after the impact it is $(v^+)^2/2 = (r v^-)^2/2$.

As the system (27) is symmetric we can easily use (33), to compute the mean energy dissipated by a single impact during steady state as

(34)

Next, we compute the mean time between impacts during steady-state. We have a probability density ${\bar{p}}^{(\xi )}_{v^-}(v)$, $\xi \in \partial {\mathcal {S}} = \{-d,d\}$ of an impact happening with velocity $v$. After the impact the motion continues from the state $(\xi ,-r v)$, with a mean first hitting time $T(\xi ,-rv)$ of the barrier $\partial S$. Furthermore, due to the symmetric structure of system (27) after reaching steady state we hit each barrier with equal probability. Hence, the mean time between impacts is given by

(35)

During steady-state we have an impact with velocity $v$ with probability density ${\bar{p}}^{(\xi )}_{v^-}(v)$ at the barrier located at $\xi$. The impact absorbs $(1-r^2)v^2/2$ energy and then on average there is no next impact for $T(\xi ,v)$, thus we distribute the absorbed energy over this time period. Therefore the average energy absorption performance ${\bar{P}}_{\textrm{imp}}$ of the impacts is

(36)

Fig. 8

Steady-state a) mean time between impacts ${\bar{T}}_{\textrm{imp}}$, b) accumulated energy ${\bar{E}}_{\textrm{acc}}$ and c) energy absorption performance ${\bar{P}}_{\textrm{imp}}$ of the Van der Pol oscillator with impact with different barrier positions $d$ for the stochastic Van der Pol oscillator with parameters $\mu = 1/2$, $\sigma = 1/2$

Figure 8 shows the steady-state accumulated energy ${\bar{E}}_{\text {acc}}$, the impact time ${\bar{T}}_{\text {imp}}$ and the energy absorption performance ${\bar{P}}_{\textrm{imp}}$ for different barrier locations $d$ ($\partial {\mathcal {S}} = \{-d,d\}$). In Fig. 8a we see that as we increase the distance $2d$ between the barriers, and we begin to leave the domain affected by the limit cycle, the mean impact time ${\bar{T}}_{\textrm{imp}}$ begins to increase sharply, as there are an increasing number of impacts after which the trajectory does multiple (half) periods of oscillations before hitting either barrier. This is expected, since increasing $d$ beyond a value leads to a system where there is almost surely no interaction with the barriers, hence we converge to the stochastic Van der Pol oscillator without barriers.

Figure 8b presents that in case our aim is to increase the energy $E_{\textrm{acc}}$ accumulated within the system the introduction of barriers is beneficial. Furthermore, according to Fig. 8c, we can choose a barrier distance $d$ that maximises the energy absorption performance ${\bar{P}}_{\textrm{imp}}$, that is beneficial if we use the stochastic Van der Pol oscillator to model an application where impacts are utilised to harvest energy [6], as ${\bar{P}}_\textrm{imp}$ is proportional to the harvestable energy.

Next we discuss a local error in the PDF $p(x,v,t)$ at the barriers that is characteristic to the SMM-PI method, namely a local probability density accumulation near grazing (“impacts with zero velocity $v=0$”) velocities. This phenomenon is hard to present in case of the Van der Pol oscillator as its effect is significant only for a small set of parameters. The comparison in Fig. 9 shows the effect of the barrier location $d$ on this local error. In case $d = 1.25$ this local error is not that apparent, as near grazing velocities occur only with small probability densities. However, for $d = 2$, for which trajectories have a large probability density near grazing, this local error becomes significant. We note that the effect of this error is localised: its effect is contained by averaging, thus it does not show up in expected values or marginal probability densities. Nonetheless, in the next section we discuss the effect of the spatial resolution of the approximation of the PDF $p(x,v,t)$, focusing on the probability densities near $v=0$ at the barriers. We consider the stochastic linear oscillator with impacts, as the approximation of the response PDF $p(x,v,t)$ with SMM-PI produces this error for a wide range of parameters and barrier locations.

Fig. 9

Local error near grazing velocities for the Van der Pol oscillator with impacts for barrier locations $\partial S = \{-1.25,1.25\}$ (left) and $\partial S = \{-2,2\}$ (right)

5.2 Stochastic linear oscillator with impacts

In this section we consider a stochastically forced linear oscillator with a single impact barrier, that is described by

(37)

if $x\in {\mathcal {S}}=(-d,\infty )$. The system has a single impacting barrier at $x = -1$, i.e. $\partial S = \{-1\}$. The impact condition at $x(\tau )\in \partial S$ is again

$$\begin{aligned} v^+(\tau ) = -r\,v^-(\tau ), \end{aligned}$$

(38)

with $r = 0.7$. In case of the SMM-PI method we use a time step $\Delta t = 0.025$ and a spatial discretisation $N_x = N_v = 151$ along both directions over the $(x,v)\in [-1,6]\times [-6,6]$ region. This system’s steady-state PDF $p(x,v)$ has a large value of the probability density along $v=0$, thus it allows us to observe the influence of the spatial resolution on the joint PDF $p(x,v,t)$ near grazing.

Fig. 10

Joint response probability distribution $p(x,v,t)$ evolution for the linear oscillator with initial conditions $x(0) \sim {\mathcal {N}}(2.5, 7/12)$ and $v(0) \sim {\mathcal {N}}(0, 4/3)$

Fig. 11

Comparison of the joint PDF $p(x,v,t)$ and the marginal PDFs $p_x(x)$ and $p_v(v)$ for the linear oscillator at different time instances, obtained via the SMM-PI method and Monte-Carlo simulations. The initial conditions are $x(0) \sim {\mathcal {N}}(2.5, 7/12)$ and $v(0) \sim {\mathcal {N}}(0, 4/3)$

Figure 10 shows the response PDF $p(x,v,t)$ evolution as a surface for multiple time instances and Fig. 11 shows the comparison with MC simulations for multiple time instances, showing good agreement between the results. This system also converges to a steady-state, even though it has a slower rate than the Van der Pol oscillator, which is also suggested by inspecting the eigenvalues of the step matrix . We also see, that at the wall where grazing happens $x\in \partial {S} = \{-1\}$ near $v=0$, a local spike appears in the interpolated PDF $p(x,v,t)$. However, carefully inspecting the comparison in Fig. 11 we see, that this artifact near $(x,v)=(-1,0)$ is a characteristic only for the interpolated PDF $p(x,v,t)$ obtained with the SMM-PI, and not for the results MC simulations. Due to the inadequate resolution of the interpolation of $p(x,v,t)$, the SMM-PI accumulates probability density near $v=0$ at the barrier. One tool to reduce this error is to increase both the resolution $N_x$ and $N_v$ of the interpolation of the $p(x,v,t)$. Figure 12 demonstrates that this is indeed the case: increasing the resolution of the interpolation decreases this numerical singularity. However, increasing the interpolation resolution does come at a significant computational time cost with a complexity of $O(N^4)$ according to [37]: while computing the steady-state PDF with $N:= N_x = N_v = 101$ takes approximately $6.5$ s on a computer with an Intel i7 8565U CPU, it takes approx. $32.5$ s and $475$ s for $N:= N_x = N_v = 151$ and $N:= N_x = N_v = 301$, respectively.

With these observations in mind, one has to balance accuracy with computational time. As this error is local, its influence is limited when computing marginal PDFs or expectation values; therefore, a lower accuracy joint PDF is acceptable. Also, this error does not propagate into the impact velocity PDF, as it is outside the interval ${\mathcal {V}}(\xi )$ where the ${\bar{p}}_{v^-}^{(\xi )}(v,t)$ is nonzero. In Fig. 13 we see that despite the significant local error being present in the joint PDF $p(x,v,t)$ for $N_x = N_v = 151$, the results for the impact velocity distribution $p^{(-1)}(x,t_1,t_2)$ obtained through the SMM-PI method and MC simulations are in good agreement for multiple time intervals.

Note, here we have considered a linear oscillator, to facilitate illustrating the behaviour of the SMM-PI. We have also confirmed a similar phenomenon for bilateral impacts in the nonlinear Van der Pol model. Similar observations would follow in an asymmetric Van der Pol model with unilateral impacts as in the linear case.

Fig. 12

Effect of resolution on the interpolated steady-state PDF $\lim _{t\rightarrow \infty } p(x,v,t)$ of the linear oscillator near grazing

Fig. 13

Comparison of the impact velocity distribution PDF ${\bar{p}}^{(-1)}_{v^-}(v,t_1,t_2)$ for the linear oscillator at different time instances, obtained via the SMM-PI method and Monte-Carlo simulations. The initial conditions are $x(0) \sim {\mathcal {N}}(2.5, 7/12)$ and $v(0) \sim {\mathcal {N}}(0, 4/3)$

6 Conclusions

In this work, we provide a systematic formulation of the SMM-PI method to solve the Chapman–Kolmogorov (CK) Eq. (3) to obtain time evolution of the PDF for non-smooth dynamics of vibro-impact oscillator systems (1), and apply this formulation to conduct a detailed analysis of the response statistics. The three key elements in the construction of the SMM-PI method are the interpolation of the PDF $p(x,v,t)$, the approximation of the TPDF $p(x,v,t_{n+1} \vert x_0,v_0,t_n)$, and the evaluation of the integral [37]. For the discretisation of the PDF $p(x,v,t)$ we use the Euclidean inner product formulation of the fifth-order polynomial interpolation, for the approximation of the TPDF we use the PDF of a Runge–Kutta-Maruyama scheme, and for the evaluation of the integral (20) we use a Gauss-Lengendre quadrature on a restricted interval $v_0\in \bar{{\mathcal {I}}}_v$. Through this formulation we transform the CK equation into a multiplication by a step matrix that not only captures the full PDF evolution, but also contains the steady-state PDF in its eigenvectors. We also formulated two important quantities for vibro-impact systems within the framework of the SMM-PI method: the impact velocity PDF ${\bar{p}}_{v^-}^{(\xi )}$ and the mean first hitting time ${\bar{T}}_{\partial S}$.

We validate the SMM-PI method by applying it to the Van der Pol and the impacting linear oscillators and comparing the results for the joint response PDF $p(x,v,t)$ against Monte-Carlo simulations for the quantities the impact velocity distribution $p_{v^-}(v,t)$, and the expected time until next impact ${\bar{T}}_{\partial S}(x,v,t)$, the energy $E_{\textrm{acc}}$ accumulated within the system, the energy absorption performance ${\bar{P}}_{\textrm{imp}}$ and the mean time ${\bar{T}}_{\textrm{imp}}$ between impacts. For the Van der Pol oscillator with impacting barriers we analysed the non-stationary joint PDF $p(x,v,t)$, the impact velocity PDF ${\bar{p}}_{v^-}^{(d)}(v)$, the expected time until next impact ${\bar{T}}_{\partial S}(\xi ,v)$. We also demonstrated, that the results of the SMM-PI method reliably capture the mean time between impacts ${\bar{T}}_{\textrm{imp}}$, the energy ${\bar{E}}{\textrm{acc}}$ accumulated within the system, and the energy absorption performance ${\bar{P}}_{\textrm{imp}}$ of the impacts.

In the case of the linear oscillator with impacting barriers, we also investigated the non-stationary joint PDF $p(x,v,t)$ and the impact velocity PDF ${\bar{p}}_{v^-}^{(d)}(v)$. We used this simple example to demonstrate the effect of spatial resolutions $N_x$ and $N_v$ on the local error within the approximated joint PDF near grazing. We showed, that even though it is possible to reduce this error, this effort has high computational costs. We demonstrate that this highly localized error has little effect on the accuracy in calculating the averages and marginals, so that these extra costs may not be necessary. The results obtained through the SMM-PI method are confirmed by Monte-Carlo simulations.

Fig. 14

Comparison of the steady-state impact velocity distribution PDF $\lim _{t\rightarrow \infty }p^{(\xi )}_{v^-}(v,t)$ for the Van der Pol oscillator (27) for multiple coefficients of restitution $r$, obtained via the SMM-PI method. The parameters are $\mu = 1/2$, $\sigma = 1/2$, $d = 1.25$

Fig. 15

Comparison of the steady-state joint PDF $\lim _{t\rightarrow \infty }p(x,v,t)$ for the Van der Pol oscillator (27) for multiple coefficient of restitutions $r$, obtained via the SMM-PI method. The parameters are $\mu = 1/2$, $\sigma = 1/2$, $d = 1.25$

The method presented in this paper proved to be a high-performance deterministic computational solution to obtain the response statistics of stochastic nonlinear vibro-impact systems. Even though it is not demonstrated through examples, the formulation is generalised for stochastic systems with impacts with time-varying parameters as well. However for such systems, one has to consider the increased computational cost of computing the step matrix for each time step. Therefore, the SMM-PI method is most useful and efficient for time invariant or periodic system, when one needs to compute only a small set of step matrices, and use them to advance the probability density function.

Appendices

Ralston’s method

To increase the accuracy of the approximation of the TPDF $p(x,v,t_{n+1} \vert x_0,v_0,t_{n})$ for second order system’s of the form (1) we use a second order Runge–Kutta method, the Ralston’s method [40] for the drift term. In this case the approximations $\eta _x$ and $\eta _v$ of the drift term in (8) is

(A1)

where $\Delta t_n = t_{n+1}-t_n$. The Ralston approximation is

(A2)

where

(A3)

with

(A4)

Effect of the coefficient of restitution

Figure 14 shows the steady-state impact velocity distribution $\lim _{t\rightarrow \infty }p^{(\xi )}_{v^-}(v,t)$ and Fig. 15 shows the steady-state PDF $\lim _{t\rightarrow \infty } p(x,v,t)$ and the corresponding marginal PDFs $\lim _{t\rightarrow \infty } p_x(x,t)$ and $\lim _{t\rightarrow \infty }p_v(v,t)$ for the Van der Pol oscillator for multiple coefficients of restitution $r$.

A general observable trend is that in the case of lower $r$ values, the probability density tends to accumulate near the impact barriers. This is due to the increased velocity reduction, that makes it harder for the trajectories to escape the region near the impact barriers. Meanwhile, for larger coefficient of restitution values $r$ the motion is dominated with higher velocities, as less energy is absorbed by each impact, suggesting higher accumulated energy within the system. This is confirmed by the impact velocity distributions as well, i.e. for larger restitution coefficients the impacts velocities are larger.