Harmonic expansion and nonsmooth dynamics in a circular contact region with combined slip-spin motion

Abstract

We analyse a rigid body in planar motion while touching a rough plane at a finite-sized, circular contact area. Assuming Coulomb friction between the tangential and normal pressure distributions, the resultant forces and torques can be expressed formally with a nonsmooth dependence on the kinematic variables. In the literature, the exact form of the tangential forces is available for special pressure distributions expressed by transcendent functions; recently, an approximate linear model was introduced. Now, we present a nonlinear extension of the approximation, which can be used effectively to characterise slipping-sticking transitions between the bodies.

1 Introduction

During the modelling and analysis of mechanical systems, dry friction is often the source of uncertainty and complex dynamical behaviour. Besides unilateral normal contact of bodies, dry friction is another main source of nonsmooth effects in rigid body dynamics. At dry friction, it is essential to distinguish a dynamic (slipping) and static (sticking, rolling) contact states. During the motion, transitions of the system occur between these states.

Although the detailed modelling of the frictional contact leads to a complicated description (see [19]), it is a requirement to have compact macroscopic friction models in the analysis of rigid body systems. Originating from the Coulomb friction law, several friction models have been developed for different applications [39]. When applying these models in the mathematical analysis of multi-body systems, each model model causes a typical type of discontinuity in the state space of the system.

When modelling a planar (2-dimensional) mechanical system, we can use the classical Coulomb friction model, which leads to piecewise smooth differential equations (see [8, 18, 37] for an overview). In these systems, a codimension–1 discontinuity occurs in the state space. At a single contact point in spatial (3-dimensional) systems, the spatial formulation of the Coulomb friction model leads to codimension–2 discontinuities. There, from the continuously many directions of slipping, we can find certain limit directions [3, 4, 11], which are organizing objects or the trajectories nearby the discontinuity. In the case of multiple contact points, the nonsmooth effects of the contact points are coupled [5, 9, 17].

A further level of complexity arises when, instead of assuming contact point, a finite contact region is considered between the bodies caused by either contacting faces of the bodies or small local deformations. Still, there are possibilities to compress the mechanical effect of the continuous region to friction models applied as concentrated friction forces and torques at a theoretical contact point. The derivation of these friction force laws requires the integration of pressure fields over the finite contact region, which usually results in a complicated dependence on the kinematic variables (nonlinear, transcendent or even without an explicit form). In the literature, there are several possibilities for modelling the friction forces at a finite contact region between rigid bodies. In some cases, it is possible to derive the exact form of the resultant friction forces [12, 16, 36, 38, 47]. Even without the complete analytical solution, it is possible to obtain qualitative results at special motions [21, 22, 49]. For an approximate solution, several types of functions have been proposed, such as the Padé approximants [24,25,26,27, 50], implicit quadratic equations [17], tangent hyperbolic functions [31], piecewise applied expansions [36], different shape of force reservoirs [46]. A regularized variant of a square root function is used in [32,33,34,35, 52]. A review of different models can be found in [51]. Instead of Coulomb acting locally between rigid surfaces, viscoelastic foundations and viscous friction models are considered in [20, 40, 41, 53].

It can be important to find the simplest relevant friction model, which is appropriate to reproduce the qualitative behaviour of the system [44]. For an effective approximation, an ellipsoidal model was introduced [6, 42] and a similar model was presented in [28,29,30]. It was shown in [6] that by analysing the resulting nonsmooth system [45], this ellipsoidal model can be used effectively in dynamic analysis of rigid bodies. However, the linear-ellipsoidal model is not always accurate enough to find all qualitative details of the dynamics. This paper aims to apply a natural extension of the linear model by higher-order terms to find a compromise in accuracy and effective usage.

The structure of the paper is the following: In Sect. 2, the form of the dynamical equations is presented with friction forces from a finite circular contact region. In Sect. 3, we analyse the properties and form of the functions of friction forces and in Sect. 4, the exact solutions are presented from the literature. In Sect. 5, the linear-ellipsoidal friction model is presented. In Sect. 6, we present the improved nonlinear model. Finally, in Sect. 7, the nonlinear model is applied to the dynamics of some test problems.

2 Problem statement

2.1 General form of the analysed systems

Consider first a mechanical system consisting of mass points and rigid bodies, where the only nonsmooth effect is a single frictional contact ensured by a bilateral normal contact condition. Assume that by using the minimal number of variables for the system, the configuration is described by the generalised coordinates ${\textbf{q}}=(q_1,\dots q_n)\in {\mathbb {R}}^n$ and the velocity state is described by generalised velocities ${\textbf{u}}=(u_1,\dots u_m)\in {\mathbb {R}}^m$.

Then, in the slipping case, consider the equations of motion of the system can be expressed in the form

$$\begin{aligned} {\textbf{M}}({\textbf{q}})\dot{{\textbf{u}}}={\textbf{W}}{\textbf{Q}}({\textbf{x}})+{\textbf{Q}}_e({\textbf{u}},{\textbf{q}}) \end{aligned}$$

(1)

with

$$\begin{aligned} \dot{{\textbf{q}}}={\textbf{G}}({\textbf{q}}){\textbf{u}}. \end{aligned}$$

(2)

In (1), ${\textbf{M}}$ is the mass matrix, ${\textbf{Q}}$ is the vector of frictional force components and ${\textbf{Q}}_e$ contains all the other force terms. The matrix ${\textbf{W}}$ is used to connect the force directions of the friction forces and the directions of the generalised velocities, and ${\textbf{G}}$ contains the kinematic relationship between the variables.

Consider the state space ${\textbf{x}}=({\textbf{u}},{\textbf{q}})\in {\mathbb {R}}^{n+m}$ of the system. Then, (1)-(2) can be expressed as a system of first-order ordinary differential equations (ODEs),

$$\begin{aligned} \dot{{\textbf{x}}}={\textbf{F}}({\textbf{x}})=\begin{bmatrix} {\textbf{M}}({\textbf{q}})^{-1}\left( {\textbf{W}}{\textbf{Q}}({\textbf{x}})+{\textbf{Q}}_e({\textbf{u}},{\textbf{q}})\right) \\ {\textbf{G}}({\textbf{q}}){\textbf{u}} \end{bmatrix}. \end{aligned}$$

(3)

Let us decompose the state vector in the form ${\textbf{x}}=({\textbf{x}}_o,{\textbf{x}}_t)$ where ${\textbf{x}}_o=(u_1,\dots u_p)$, where $p\le m$ contains the variables involved in the nonsmooth terms from the friction. We assume that the dynamics (3) depends smoothly on all the other variables ${\textbf{x}}_t\in {\mathbb {R}}^{n+m-p}$. Then, the variables ${\textbf{x}}_o$ span an $n+m-p$ subspace of the state space, which we call the codimension-p discontinuity set. The subscripts ’o’ and ’t’ refers to orthogonal and tangential directions to the discontinuity set. Finally, we decompose the vector field in the form ${\textbf{F}}=({\textbf{F}}_o,{\textbf{F}}_t)$, where

$$\begin{aligned} \begin{aligned} \dot{{\textbf{x}}}_o&={\textbf{F}}_o({\textbf{x}}_o,{\textbf{x}}_t), \\ \dot{{\textbf{x}}}_t&={\textbf{F}}_t({\textbf{x}}_o,{\textbf{x}}_t). \end{aligned} \end{aligned}$$

(4)

This formulation implicitly contains the following assumptions:

• The contact is in slipping state, and the static states (sticking, rolling) are considered as limit cases of the slipping equations.

• The force system ensures the permanent bilateral normal contact between the plane and the body: The effects of detachment and impacts are excluded.

We assume that the effect of dry friction is considered in the rigid body model by different friction laws based on the Coulomb friction model. According to p, the important cases are the following:

• At $p=1$, we get the case of a planar (2D) mechanical system with single contact point.

• At $p=2$, we get the case of a spatial (3D) mechanical system with a single contact point.

• At $p=3$, we get the case of a spatial mechanical system with a finite contact region.

• At $p=5$, we get the case of a spatial mechanical system with a finite contact region, where the rolling resistance and friction are coupled.

In this paper, we focus on the case $p=3$ with a circular contact region. For these systems, a first-order approximate model was proposed in [6]. Now, we present an improved nonlinear approximation for circular contact regions.

Fig. 1

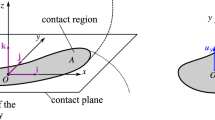
Sketch of the circular contact region and the corresponding quantities. Left panel: the circular contact region between a fixed plane and a moving body. Right panel: the slipping velocities (5) and the friction forces (6) in the plane of the contact region. The figure shows that in the paper, the directions of the friction forces $Q_x$, $Q_y$, $T_z$ are defined according to the coordinate axes, and the negative direction from the dissipation will be ensured from the formulae of the friction models

2.2 Circular contact region on a fixed, rigid plane

Consider a fixed, rigid plane and assume that one of the rigid bodies of the system is touching this plane in a circular contact region. The analysis is fully described in an inertial reference frame fixed to the plane, but we use two coordinate systems (see Fig. 1):

• Fixed coordinate system: The origin $O'$ and rectangular coordinate system $x'y'z'$ fixed to the plane; the axes $x'$ and $y'$ lie inside the plane and the axis $z'$ points vertically upwards.

• Co-moving coordinate system: The origin O is at the centre of the circular contact region; the coordinate axes x, y, z are parallel to the fixed coordinate system (not co-rotating).

Let R denote the radius of the contact region. The velocity components of the contacting body at O are denoted by $u_x$ and $u_y$, and $\omega _z$ denotes the angular velocity about the normal direction of the plane (spin). The resultant of the distributed frictional force field in the contact region is parametrised by the force components $Q_x$ and $Q_y$ acting at O and the torque $T_z$.

To match the units of the quantities and improve the numerical condition of the problem, let us introduce the parameter $\rho$ expressing the typical size of the contact region. For a first guess, one can take $\rho =R$, a detailed analysis of its appropriate choice is presented below. Then we can take the normalised angular velocity $\rho \omega _z$ and the normalised torque $T_z/\rho$. Then, the vector of the orthogonal (”nonsmooth”) variables become

$$\begin{aligned} {\textbf{x}}_o=(u_x,u_y,\rho \omega _z), \end{aligned}$$

(5)

and the vector of friction forces becomes

$$\begin{aligned} {\textbf{Q}}=(Q_x,Q_y,T_z/\rho ). \end{aligned}$$

(6)

Then, we assume that the friction law can be written in the form

$$\begin{aligned} {\textbf{Q}}({\textbf{x}}_o,P({\textbf{x}})), \end{aligned}$$

(7)

where P is the resultant normal force of the normal pressure distribution. As the dependence on P will be trivial (proportional) in the friction models, we will consider the friction forces in the form

$$\begin{aligned} {\textbf{Q}}({\textbf{x}}_o). \end{aligned}$$

(8)

Our goal is to determine the relationship (8) and investigate its effects on the dynamics of the system.

2.3 Test problems

To demonstrate the results through the paper, we introduce two test problems (see Fig. 2). These problems are minimal but non-trivial examples of two important cases:

• The disc on a rigid plane is an example for conforming contact where static friction state is stick without rolling. Here, the size of the contact region and the body are comparable.

• The ball on a rigid plane is an example for non-conforming contact where the static friction state is rolling. Here, the contact region is much smaller than the typical size of the body.

In these problems, we can get analytical and semi-analytical results. The obtained experiences can be useful for predicting the behaviour of more complicated systems.

In both problems, we consider a horizontal, rigid, fixed plane and a single rigid body on it. The body (homogeneous disc or ball) has a mass m, a radius ${\bar{R}}$ and the relevant component of the moment of inertia is J computed at the centre of gravity. In both problems, the external force is a single, constant force F pointing to the x direction at the centre of gravity of the body, and the gravity force characterised by the acceleration g pointing in the negative z direction. (This forcing is equivalent to an inclined plane, see [38].) In both problems, C denotes the centre of gravity of the body.

2.3.1 Disc on a plane

Consider a rigid disc slipping on a rigid plane, where the thickness of the disc is significantly smaller than its radius (see the left panel of Fig. 2). The generalised coordinates are

$$\begin{aligned} {\textbf{q}}=(x'_C,y'_C,\gamma ), \end{aligned}$$

(9)

where $x'_C$, $y'_C$ are the coordinates of the centre of gravity, and $\gamma$ measures the rotation of the disc about the $z'$ axis. The generalised velocities are

$$\begin{aligned} {\textbf{u}}=(u_x, u_y, \rho \omega _z), \end{aligned}$$

(10)

where the components have been defined at (5). Then, the mass matrix of the system is

$$\begin{aligned} {\textbf{M}}= \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ 0 &{} 0 &{} \frac{{\bar{R}}^2}{\rho ^2}jm \end{bmatrix}, \end{aligned}$$

(11)

where $j=J/m{\bar{R}}^2$ is the dimensionless moment of inertia. The value of this parameter is $j=1/2$ for a solid disc where $J=1/2\cdot m{\bar{R}}^2$. The choice of variables leads to the following expressions for the quantities in (1)-(2):

$$\begin{aligned} {\textbf{W}}=\begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix},{} & {} {\textbf{Q}}_e=\begin{bmatrix} F \\ 0 \\ 0 \end{bmatrix},{} & {} {\textbf{G}}({\textbf{q}})=\begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1}{\rho } \end{bmatrix}. \end{aligned}$$

(12)

Finally the orthogonal part of (3) becomes

$$\begin{aligned} \dot{{\textbf{x}}}_o={\textbf{F}}({\textbf{x}}_o)=\begin{bmatrix} \frac{1}{m}Q_x({\textbf{x}}_0)+\frac{1}{m}F \\ \frac{1}{m}Q_y({\textbf{x}}_0) \\ \frac{\rho }{jm{\bar{R}}^2}T_z({\textbf{x}}_0) \end{bmatrix}. \end{aligned}$$

(13)

In this text example, the right-hand side of (13) does not contain the tangential variables ${\textbf{x}}_t$, because the symmetries of the system eliminate the dependence on these variables. Thus, the system (13) itself is an ODE that can be analysed separately.

Fig. 2

Sketch of the test problems presented in Subsection 2.3. Left panel: a disc slipping on a rough rigid plane in the presence of an in-plane force F. Middle panel: a ball slipping on a rough plane in the presence of an in-plane force F. Right panel: the momentary replacement of the inertia of the ball by a pair of rigidly connected point masses

2.3.2 Ball on plane

Consider a rigid ball slipping on a rigid plane (see the middle panel of Fig. 2). The generalised coordinates are

$$\begin{aligned} {\textbf{q}}=(x'_C,y'_C,\gamma _1,\gamma _2,\gamma _3), \end{aligned}$$

(14)

where $x_C'$, $y_C'$ are the coordinates of the centre of gravity C and $\gamma _1$,$\gamma _2$,$\gamma _3$ are appropriately chosen Euler angles of the orientation of the ball. For the vector of generalised velocities, we choose

$$\begin{aligned} {\textbf{u}}=(u_x, u_y, \rho \omega _z, v_{Qx}, v_{Qy}), \end{aligned}$$

(15)

where the special point Q can be seen in the right panel of Fig. 2. It can be shown that this choice of variables simplifies the mass matrix into a diagonal form

$$\begin{aligned} {\textbf{M}}= \begin{bmatrix} \frac{j}{1+j}m &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \frac{j}{1+j}m &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \frac{{\bar{R}}^2}{\rho ^2}jm &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \frac{1}{1+j}m &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{1+j}m \end{bmatrix}. \end{aligned}$$

(16)

This choice of variables can be imagined as a momentary replacement of the inertia of the ball by a pair of rigidly connected point masses (”dumbbell”). Then, the further matrices become

$$\begin{aligned} {\textbf{W}}=\begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix},{} & {} {\textbf{Q}}_e=\begin{bmatrix} F\frac{j}{1+j} \\ 0 \\ 0 \\ F\frac{1}{1+j} \\ 0 \end{bmatrix}. \end{aligned}$$

(17)

The kinematic expression for ${\textbf{G}}({\textbf{q}})$ in (2) is not presented here for this problem. This expression is lengthy and depends on the specific choice of the Euler angles. However, neither the choice of the Euler angles nor ${\textbf{G}}({\textbf{q}})$ affects the dynamics of the other variables due to the spherical symmetry of the problem.

Then, the dynamics of the orthogonal variables becomes

$$\begin{aligned} \dot{{\textbf{x}}}_o={\textbf{F}}_o=\begin{bmatrix} \frac{1+j}{jm}Q_x({\textbf{x}}_0)+\frac{1}{m}F\\ \frac{1+j}{jm}Q_y({\textbf{x}}_0) \\ \frac{\rho }{jm{\bar{R}}^2}T_z({\textbf{x}}_0) \end{bmatrix}. \end{aligned}$$

(18)

The form of the equations (13) and (18) are very similar, and again, we get an independent system of ODEs because the other variables (the velocities $v_{Qx}$, $v_{Qy}$ and all generalised coordinates) are absent from (18).

The two problems differ from each other in the magnitude of the parameters $\rho$ and ${\bar{R}}$: Compared to the case of the disc with $\rho \approx R={\bar{R}}$, the ball has a small contact region with $\rho \approx R\ll {\bar{R}}$, thus, the effect of the pivoting torque $T_z$ is less significant here. The other difference originates from the friction laws due to the different pressure distributions analysed below.

Let us now present the analysis of the friction forces, and the results are applied to these test problems in Sect. 7.

3 Calculation of the resultant friction forces

3.1 General case

Consider a general - not necessarily circular - contact region with an area A. Assume that the distribution of the normal force between the surfaces is given by the function p(x, y). As a first step, the resultant force from this pressure can be obtained by

$$\begin{aligned} P=\int _Ap(x,y)\,\textrm{d}A. \end{aligned}$$

(19)

For the tangential forces, we need the velocity distribution in the contact region. We assume planar rigid body kinematics in the contact region. Then, the velocity components of a point in the contact region are expressed by the variable set (5):

$$\begin{aligned} \begin{aligned} v_x(x,y)&=u_x-\omega _z y, \\ v_y(x,y)&=u_y+\omega _z x. \end{aligned} \end{aligned}$$

(20)

This kinematic conditions (20) are valid for the conforming case (e.g. disc on the plane) and a good approximation for the non-conforming case (e.g. ball on the plane) with a small contact region. This assumption is usual in the literature (e.g. in [36]). An improved description would require the explicit analysis of the elastic deformations (see [19]), which is beyond the scope of this paper.

Then, we consider the Coulomb friction law locally between the distributed forces, and the components of the tangential distributed force ${\textbf{q}}_{xy}=(q_x,q_y)$ become

$$\begin{aligned} \begin{aligned} q_x(x,y)&=-\mu p(x,y)\cdot \frac{v_x(x,y)}{\sqrt{v_x^2(x,y)+v_y^2(x,y)}}, \\ q_y(x,y)&=-\mu p(x,y)\cdot \frac{v_y(x,y)}{\sqrt{v_x^2(x,y)+v_y^2(x,y)}}, \end{aligned} \end{aligned}$$

(21)

where $\mu$ is the friction coefficient. Then, the infinitesimal torque of ${\textbf{q}}_{xy}$ about the z axis of the point O is given by

$$\begin{aligned} t_z(x,y)=x\cdot q_y(x,y)-y\cdot q_x(x,y). \end{aligned}$$

(22)

Finally, the components of the friction forces in (6) can be obtained by surface integrals of (14)-(22) over the contact region:

$$\begin{aligned} \begin{aligned} Q_x&=\int _A q_x(x,y)\,\textrm{d}A, \\ Q_y&=\int _A q_y(x,y)\,\textrm{d}A, \\ T_z&=\int _A t_z(x,y)\,\textrm{d}A. \end{aligned} \end{aligned}$$

(23)

The sequential substitution of (20)-(22) into (23) leads to complicated integrals. In special cases such as circular contact with typical axisymmetric pressure distributions, these integrals can be evaluated algebraically (see Sect. 4.1-4.2 and the references there). Otherwise, numerical computation or approximations are necessary.

However, an important homogeneous property can be identified for the integrals (23) depending on the kinematic variables $u_x,u_y,\rho \omega _z$ (see e.g. [50]). By using the vector notation ${\textbf{Q}}({\textbf{x}}_o)$ (see (8)) for the friction law, we can state the following:

Proposition 1

The function ${\textbf{Q}}({\textbf{x}}_o)$ is positively homogeneous of degree zero, that is

$$\begin{aligned} {\textbf{Q}}(\lambda {\textbf{x}}_o)={\textbf{Q}}({\textbf{x}}_o) \end{aligned}$$

(24)

for any $\lambda \in {\mathbb {R}}^+$.

As a proof, we can compare (20)-(22) to find that the integrands of (23) is positively homogeneous in $u_x,u_y,\rho \omega _z$ (the denominators and numerators are both linear in these variables). Note, that for $\lambda <0$ in (21)-(22), the square root (norm) in the denominator does not change sign while the numerator does.

The homogeneity property (24) is known in the literature (see e.g. the numbered properties in [25, 50]). The fundamental idea in [45] and [6] was to formally decompose the magnitude of the slip (which does not effect the friction forces due the homogeneity) and the direction of the slip (which is essentially the dependent variable of the friction forces). In the next subsection, we present different formulations of this decomposition.

3.2 Different parametrisations of the slip direction

Let us decompose the variables for the contact kinematics (5) into magnitude and direction, which transformation plays a key role in the whole analysis of the paper. We present three kinds of parametrisations for the direction of the slip:

• Parametrisation 1 with the components of the unit direction vector: This is the main formulation of the friction models in the paper, leading to a polynomial form of expressions for the higher degree approximations.

• Parametrisation 2 with spherical angles: This is an intermediate formulation used for performing the harmonic expansion, leading to the truncated Fourier series form for the higher degree approximations.

• Parametrisation 3 with the ratio between the translational and rotational slip: This is the typical formulation in the literature for deriving both the exact friction models and their approximations. We use is as a reference for a comparison with the existing results.

3.2.1 Parametrisation 1: Direction vector

Let us decompose ${\textbf{x}}_o$ into spherical coordinates in the form

$$\begin{aligned} {\textbf{x}}_\textrm{o}=r{\textbf{w}}=r\cdot (w_1,w_2,w_3), \end{aligned}$$

(25)

where

$$\begin{aligned} r=\left\Vert {\textbf{x}}_\textrm{o}\right\Vert =\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2} \end{aligned}$$

(26)

measures the magnitude of slip (see the left panel of Fig. 3), and ${\textbf{w}}$ measures the direction of the slip with

$$\begin{aligned} \begin{aligned} w_1&=\frac{u_x}{r}=\frac{u_x}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ w_2&=\frac{u_y}{r}=\frac{u_y}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ w_3&=\frac{\rho \omega _z}{r}=\frac{\rho \omega _z}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}. \end{aligned} \end{aligned}$$

(27)

The vanishing of the magnitude ($r\rightarrow 0$) corresponds to the sticking state of the whole contact region. The components of the unit (direction) vector ${\textbf{w}}$ satisfy the condition $\sqrt{w_1^2+w_2^2+w_3^2}=1$, and consequently, ${\textbf{w}}$ is an element of the unit 2-sphere ${\mathbb {S}}^2\subset {\mathbb {R}}^3$ (see the middle panel of Fig. 3).

Fig. 3

Left panel: the spherical decomposition (25) of the slipping velocities into the magnitude r and the direction ${\textbf{w}}$. Middle panel: the unit sphere of the variable ${\textbf{w}}\in {\mathbb {S}}^2\in {\mathbb {R}}^3$. The location on the sphere can be measured by the redundant variables $(w_1,w_2,w_3)$ of (27), or, the two angles of (32). Right panel: a typical image of the mapping ${\textbf{w}}\rightarrow {\textbf{Q}}({\textbf{w}})$ onto the space of the friction forces (31)

Consider the inverse transformation of (27),

$$\begin{aligned} u_x=r w_1,{} & {} u_y=r w_2,{} & {} \omega _z=r w_3/\rho , \end{aligned}$$

(28)

and substitute it into the integrands of (23):

$$\begin{aligned} q_x(x,y){} & {} =-\mu p(x,y)\tfrac{w_1-w_3 y/\rho }{\sqrt{(w_1-w_3 y/\rho )^2+(w_2+w_3 x/\rho )^2}}, \nonumber \\ q_y(x,y){} & {} =-\mu p(x,y)\tfrac{w_2+w_3 x/\rho }{\sqrt{(w_1-w_3 y/\rho )^2+(w_2+w_3 x/\rho )^2}}.\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned} t_z(x,y)\!=\!-\mu p(x,y)\rho \tfrac{-w_1y/\rho +w_2x/\rho +w_3(x^2+y^2)/\rho ^2 }{\sqrt{(w_1-w_3 y/\rho )^2+(w_2+w_3 x/\rho )^2}}.\nonumber \\ \end{aligned}$$

(30)

We get that in accordance with (24) the magnitude $r>0$ of slipping is cancelling, and thus, the integrals (23) depend on only the direction ${\textbf{w}}$. Consequently, we can reformulate (6) in the form

$$\begin{aligned} {\textbf{Q}}({\textbf{w}})=(Q_x({\textbf{w}}),Q_y({\textbf{w}}),T_z({\textbf{w}})/\rho ). \end{aligned}$$

(31)

Note, that in physically realistic cases, the friction model (31) maps the unit sphere of the slipping direction ${\textbf{w}}$ onto a smooth closed surface (see the right panel of Fig. 3).

3.2.2 Parametrisation 2: Direction angles

In (27), the variables $w_3$, $\sqrt{w_1^2+w_2^2}$ express the relative amount of translational slip (of the centre point) and rotational slip. Instead of the redundant parametrisation of the unit sphere with $w_1,w_2,w_3$, we can introduce two angles in the form

$$\begin{aligned} \begin{aligned} w_1&=\cos \theta \cos \phi , \\ w_2&=\cos \theta \sin \phi , \\ w_3&=\sin \theta , \end{aligned} \end{aligned}$$

(32)

where $\phi \in [-\pi ,\pi )$ is the longitude and $\theta \in [-\pi /2,\pi /2]$ is the latitude on the unit sphere (see the middle panel of Fig. 3). As an inverse of (32), we get

$$\begin{aligned} \begin{aligned} \theta&=\arctan _2\left( w_3,\sqrt{w_1^2+w_2^2}\right) , \\ \phi&=\arctan _2(w_2,w_1). \end{aligned} \end{aligned}$$

(33)

In (33), $\arctan _2(y,x)$ denotes the two-parametric arcus tangent function defined by

$$\begin{aligned} \arctan _2(y,x)=2\arctan \tfrac{y}{\sqrt{x^2+y^2}+x}, \end{aligned}$$

(34)

with $\arctan _2(y,x)=\arctan (y/x)$ if $x>0$.

3.2.3 Parametrisation 3: Slip-spin ratio

Finally, let us introduce a third parameter $\epsilon$ expressing the normalised ratio between the magnitudes of translational and rotational slip velocities (slip-spin ratio) in the form:

$$\begin{aligned} \epsilon =\frac{\sqrt{u_x^2+u_y^2}}{R|\omega _z|}= \frac{\rho }{R}\frac{\sqrt{1-w_3^2}}{|w_3|}= \frac{\rho }{R}|\cot \theta |. \end{aligned}$$

(35)

This parametrisation of the direction is widely used in the literature (see e.g. [36, 47]) along with is reciprocal $1/\epsilon$ (spin-slip ratio, see e.g. [50]). As inverse expressions from (35), we get

$$\begin{aligned} \begin{aligned} |\theta |&=\arctan \frac{\rho }{\epsilon R},\\ |w_3|&=|\sin \theta |=\frac{1}{\sqrt{1+\epsilon ^2R^2/\rho ^2}},\\ \sqrt{w_1^2+w_2^2}&=|\cos \theta |=\frac{1}{\sqrt{1+\rho ^2/(\epsilon ^2R^2)}}. \end{aligned} \end{aligned}$$

(36)

As the single parameter $\epsilon$ replaces only the latitude $\theta$ to express the relation between slip and spin, the longitude $\phi$ is still required to use to express the relation of the velocity components $u_x$ and $u_y$.

Table 1 Different parametrisations of the unit sphere ${\mathbb {S}}\ni {\textbf{w}}$ presented in Sect. 3.2

3.3 Form of the solution in the axisymmetric case

Consider now the fully axisymmetric case where the contact region is circular and the pressure distribution is axisymmetric in the form

$$\begin{aligned} p(x,y)={\tilde{p}}\left( \sqrt{x^2+y^2}\right) . \end{aligned}$$

(37)

Then, let us consider the following integrals:

$$\begin{aligned} P&=2\pi \int _0^R\!\!{\tilde{p}}(\xi )\xi \,\textrm{d}\xi , \end{aligned}$$

(38)

$$\begin{aligned} \kappa&=\frac{2\pi }{P}\int _0^R\!\!{\tilde{p}}(\xi )\xi ^2\,\textrm{d}\xi , \end{aligned}$$

(39)

where (38) is just the application of (19) to the axisymmetric case (37), and (39) is a normalised first moment of the pressure distribution having a dimension of length.

3.3.1 Properties of the axisymmetric problem

For the special cases of pure translational ($\omega _z=0$) or pure rotational slip ($u_x^2+u_y^2=0$), the integrals (23) of the axisymmetric problem can be calculated:

Proposition 2

In the case of the pure translational slip ($\omega _z=0$), (23) leads to

$$\begin{aligned} \begin{aligned} Q_x&=-\mu P \tfrac{u_x}{\sqrt{u_x^2+u_y^2}},{} & {} \quad Q_y=-\mu P \tfrac{u_y}{\sqrt{u_x^2+u_y^2}}, \\ T_z&=0. \end{aligned} \end{aligned}$$

(40)

In the case of the pure rotational slip ($u_x^2+u_y^2=0$), (23) leads to

$$\begin{aligned} T_z=-\mu \kappa P\frac{\omega _z}{|\omega _z|},{} & {} \sqrt{Q_x^2+Q_y^2}=0. \end{aligned}$$

(41)

That is, due to the circular symmetry, the rotation-free motion induces a single friction force coinciding with the Coulomb law in 3D. In contrast, the pure rotational motion induces a single torque $T_z$ with a magnitude $-\mu \kappa P$, where the parameter $\kappa$ is calculated in (39).

In addition, it can be shown that the integrals (23) has the following reflectivity (anti)symmetries:

Proposition 3

The transformation $\omega _z\rightarrow -\omega _z$ gives

$$\begin{aligned} \begin{aligned} Q_x(u_x,u_y,-\omega _z)&=Q_x(u_x,u_y,\omega _z), \\ Q_y(u_x,u_y,-\omega _z)&=Q_y(u_x,u_y,\omega _z), \\ T_z(u_x,u_y,-\omega _z)&=-T_z(u_x,u_y,\omega _z). \end{aligned} \end{aligned}$$

(42)

The transformation $u_x\rightarrow -u_x$, $u_y\rightarrow -u_y$ gives

$$\begin{aligned} \begin{aligned} Q_x(-u_x,-u_y,\omega _z)&=-Q_x(u_x,u_y,\omega _z), \\ Q_y(-u_x,-u_y,\omega _z)&=-Q_y(u_x,u_y,\omega _z), \\ T_z(-u_x,-u_y,\omega _z)&=T_z(u_x,u_y,\omega _z). \end{aligned} \end{aligned}$$

(43)

Note, that the properties of the axisymmetric problem is discussed in details in the numbered Properties of [50] and [25]. In [50], Property 1 corresponds to the homogeneity (24), Properties 2-3 are related to (40)-(41), Property 6 corresponds to (42)-(43), while Properties 4, 5 and 7 are related to monotonicity and derivatives not considered here.

Moreover, the integrals (23) can be shown to have the following property:

Proposition 4

The components of the resultant force satisfy

$$\begin{aligned} Q_xu_y-Q_yu_x=0. \end{aligned}$$

(44)

That is, the resultant force is required to be opposite to the velocity, of the reference point.

Finally, it can be shown that the integrals (23) possess the following symmetries with respect to the rotation about the z axis:

Proposition 5

Consider the transformation given by $u_x'=u_x\cos \alpha -u_y\sin \alpha$, $u_y'=u_x\sin \alpha +u_y\cos \alpha$, which realises a rotation of the velocity of the reference point by an angle $\alpha$. Then, the friction forces become

$$\begin{aligned} \begin{aligned} Q_x(u_x',u_y',\omega _z)&=Q_x(u_x,u_y,\omega _z)\cdot \cos \alpha - \\&-Q_y(u_x,u_y,\omega _z)\cdot \sin \alpha , \\ Q_y(u_x',u_y',\omega _z)&=Q_x(u_x,u_y,\omega _z)\cdot \sin \alpha - \\&-Q_y(u_x,u_y,\omega _z)\cdot \cos \alpha , \\ T_z(u_x',u_y',\omega _z)&=T_z(u_x,u_y,\omega _z). \end{aligned} \end{aligned}$$

(45)

That is, for a constant rotation speed $\omega _z$, the resultant force has a constant magnitude and it is rotating together with the velocity of the reference point. In the meantime, the resultant torque is unaffected by this transformation. Note, that (42) can be obtained as a special case of (45) at $\alpha =\pi$.

Now, by utilizing the properties (40)–(45), we can write up the form of the friction laws of the axisymmetric problem in a simple form with parametrisations from Sect. 3.2.

3.3.2 Parametrisation 1 – Direction vector

Consider the integrals (23) in the form

$$\begin{aligned} \begin{aligned} Q_x&=-\mu P \tfrac{w_1}{\sqrt{w_1^2+w_2^2}}\cdot {\mathcal {Q}}_{w}(w_3), \\ Q_y&=-\mu P \tfrac{w_2}{\sqrt{w_1^2+w_2^2}}\cdot {\mathcal {Q}}_{w}(w_3), \\ T_z&=-\mu P\cdot \kappa \cdot {\mathcal {T}}_{w}(w_3). \end{aligned} \end{aligned}$$

(46)

where ${\mathcal {Q}}_{w}$ and ${\mathcal {T}}_{w}$ are functions on $[-1,1]\rightarrow {\mathbb {R}}$ satisfying

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{w}(0)&=1,&{\mathcal {Q}}_w(1)&=0, \\ {\mathcal {T}}_{w}(0)&=0,&{\mathcal {T}}_w(1)&=1, \end{aligned} \end{aligned}$$

(47)

and

$$\begin{aligned} {\mathcal {Q}}_{w}(-w_3)={\mathcal {Q}}_{w}(w_3),{} & {} {\mathcal {T}}_{w}(-w_3)=-{\mathcal {T}}_{w}(w_3). \end{aligned}$$

(48)

It can be checked by direct calculation that by using Parametrisation 1 of the unit vector (27), the expressions (46)-(48) provide the general form of the friction laws satisfying all the properties (40)-(45).

3.3.3 Parametrisation 2 – Direction angles

Consider the transformation (32) to replace the components $w_1,w_2,w_3$ of the direction vector to the direction angles $\phi$ and $\theta$. Then, (46) can be transformed into

$$\begin{aligned} \begin{aligned} Q_x&=-\mu P\cos \phi \cdot {\mathcal {Q}}(\theta ), \\ Q_y&=-\mu P\sin \phi \cdot {\mathcal {Q}}(\theta ), \\ T_z&=-\mu P\cdot \kappa \cdot {\mathcal {T}}(\theta ), \end{aligned} \end{aligned}$$

(49)

where the functions defined by

$$\begin{aligned} {\mathcal {Q}}(\theta )={\mathcal {Q}}_w(\sin \theta ),{} & {} {\mathcal {T}}(\theta )={\mathcal {T}}_w(\sin \theta ), \end{aligned}$$

(50)

on $[-\pi /2,\pi /2]\rightarrow {\mathbb {R}}$ satisfy

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}(0)&=1,&{\mathcal {Q}}(\pi /2)&=0, \\ {\mathcal {T}}(0)&=0,&{\mathcal {T}}(\pi /2)&=1. \end{aligned} \end{aligned}$$

(51)

and

$$\begin{aligned} {\mathcal {Q}}(-w_3)={\mathcal {Q}}(w_3),{} & {} {\mathcal {T}}(-w_3)=-{\mathcal {T}}(w_3). \end{aligned}$$

(52)

3.3.4 Parametrisation 3 – Slip-spin ratio

Finally, consider the transformation (35)-(36) to introduce the slip-spin ratio $\epsilon$. Then, (49) can be transformed into

$$\begin{aligned} \begin{aligned} \sqrt{Q_x^2+Q_y^2}&=\mu P\cdot {\mathcal {Q}}_\epsilon (\epsilon ), \\ T_z&=-\mu P\cdot \kappa \cdot {\mathcal {T}}_\epsilon (\epsilon ), \end{aligned} \end{aligned}$$

(53)

where the functions defined by

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}(\theta )&={\mathcal {Q}}_\epsilon \left( \frac{\rho }{R}|\cot \theta |\right) , \\ {\mathcal {T}}(\theta )&={\mathcal {T}}_\epsilon \left( \frac{\rho }{R}|\cot \theta |\right) , \end{aligned} \end{aligned}$$

(54)

on $[0,\infty )\rightarrow {\mathbb {R}}$ satisfy

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{\epsilon }(0)&=0,&\lim _{\epsilon \rightarrow \infty }{\mathcal {Q}}_\epsilon (\epsilon )&=1, \\ {\mathcal {T}}_{\epsilon }(0)&=1,&\lim _{\epsilon \rightarrow \infty }{\mathcal {T}}_\epsilon (\epsilon )&=0. \end{aligned} \end{aligned}$$

(55)

Finally, the friction forces in the axisymmetric case expressed by the three different parametrisations (46), (49), (53); each of them has different properties (see Table 1). In this paper, we prefer (46) for the dynamical equations, but the harmonic expansion of the new nonlinear model is based on (49). In the literature, we can find analytical solutions for the test problems in the form (53); these solutions are presented in the following section.

4 Exact solutions

In Sect. 2.3, two test problems were introduced. To fully define the ODEs (13) and (18), we need to express the friction model (31) from the assumption of the pressure distributions:

• For the disc with a significantly smaller height than its radius, we can assume uniform pressure distribution.

• For the ball, we can use the assumption of the Hertz contact theory suggesting a parabolic pressure distribution.

In this section, exact solutions for these cases are presented according to the literature.

4.1 Uniform pressure distribution

Consider first the case where the pressure distribution (37) is uniform,

$$\begin{aligned} {\tilde{p}}(\xi )=\frac{P}{R^2\pi }. \end{aligned}$$

(56)

From the literature [47] (see also [13]), we can find an exact analytical solution for the friction forces (53) in the form

$$\begin{aligned} {\mathcal {Q}}_\epsilon (\epsilon )={\left\{ \begin{array}{ll} {\mathcal {Q}}_{\epsilon 1}(\epsilon ), &{} \epsilon \le 1, \\ {\mathcal {Q}}_{\epsilon 2}(\epsilon ), &{} \epsilon \ge 1, \end{array}\right. } \end{aligned}$$

(57)

and

$$\begin{aligned} {\mathcal {T}}_\epsilon (\epsilon )={\left\{ \begin{array}{ll} {\mathcal {T}}_{\epsilon 1}(\epsilon ), &{} \epsilon \le 1, \\ {\mathcal {T}}_{\epsilon 1}(\epsilon ), &{} \epsilon \ge 1, \end{array}\right. } \end{aligned}$$

(58)

where the expressions are given by

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{\epsilon 1}(\epsilon )&=\tfrac{4}{3}\tfrac{(\epsilon ^2+1)E(\epsilon ^2)+(\epsilon ^2-1)K(\epsilon ^2)}{\epsilon \pi }, \\ {\mathcal {Q}}_{\epsilon 2}(\epsilon )&=\tfrac{4}{3}\tfrac{(\epsilon ^2+1)E(\epsilon ^{-2})-(\epsilon ^2-1)K(\epsilon ^{-2})}{\pi }, \end{aligned} \end{aligned}$$

(59)

and

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_{\epsilon 1}(\epsilon )&=\tfrac{2}{3}\tfrac{(4-2\epsilon ^2)E(\epsilon ^2)+(\epsilon ^2-1)K(\epsilon ^2)}{\pi }, \\ {\mathcal {T}}_{\epsilon 2}(\epsilon )&=\tfrac{2}{3}\tfrac{(4-2\epsilon ^2)E(\epsilon ^{-2})+(2\epsilon ^2-5+3\epsilon ^{-2})K(\epsilon ^{-2})}{\epsilon ^{-1}\pi }. \end{aligned} \end{aligned}$$

(60)

In (59)-(60), the functions K(m) and E(m) denote the incomplete elliptic integrals expressed by the elliptic parameter m. An alternative parametrisation of the elliptic integrals is the usage of the elliptic modulus $\sqrt{m}$ in the form ${\bar{E}}(\sqrt{m})=E(m)$, which can also be used to express the result (see [16]). For the definitions of the incomplete elliptic integrals and their parametrisations, see [1], p. 589 or [43] p. 637.

Although (59), (60) are given by different expressions for the regions $\epsilon <1$ and $\epsilon >1$, the functions are smoothly connected at $\epsilon =1$. Moreover, it is possible to express them by a single but more lengthy formula (see [47]). The solution (59), (60) is depicted in Fig. 4.

Fig. 4

Analytical solutions for the normalised friction forces ${\mathcal {Q}}$ and ${\mathcal {T}}$ in the case of the constant pressure distribution (56) (depicted by solid lines) and the parabolic pressure distribution (61) (depicted by dashed lines). In the first three panels: the analytical solutions (59)–(60) and (62)–(63) for the three parametrisations (53), (46) and (49). Fourth (rightmost) panel: the solutions as parametric curves showing a meridian curve of the friction disc (see the right panel of Fig. 3). These curves of the two distributions almost overlap each other, but they still have moderately different behaviour, shown in the other three diagrams

4.2 Parabolic pressure distribution

Consider now the case when the axisymmetric pressure distribution (53) is parabolic given by the Hertz contact theory [19],

$$\begin{aligned} {\tilde{p}}(\xi )=\frac{3P}{2 R^2 \pi }\sqrt{1-\frac{\xi ^2}{R^2}}. \end{aligned}$$

(61)

In (61), the maximum pressure in the middle of the contact region ($\xi =0$) is 3/2 times larger than that of the uniform distribution (56), and the pressure vanishes at the edge of the contact region ($\xi =r$).

For this case, the exact analytical solution for the friction forces (53) can be found in [48, 36] and [15]. This solution has the same piecewise definition (57), but the expressions are now given by

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{\epsilon 1}(\epsilon )&=\frac{3\pi }{32}\epsilon (4-\epsilon ^2), \\ {\mathcal {Q}}_{\epsilon 2}(\epsilon )&=\frac{3}{16\epsilon }\left( \epsilon ^2(4-\epsilon ^2)\arcsin (\epsilon ^{-1})+ \right. \\&\left. \quad +(\epsilon ^2+2)\sqrt{\epsilon ^2-1}\right) , \end{aligned} \end{aligned}$$

(62)

and

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_{\epsilon 1}(\epsilon )&=\frac{1}{8}(3\epsilon ^4-8\epsilon ^2+8), \\ {\mathcal {T}}_{\epsilon 2}(\epsilon )&=\frac{1}{4\pi }\left( (3\epsilon ^4-8\epsilon ^2+8)\arcsin (\epsilon ^{-1})+ \right. \\&\left. \quad +(6-3\epsilon ^2)\sqrt{\epsilon ^2-1}\right) . \end{aligned} \end{aligned}$$

(63)

The results (62)-(63) can be seen in Fig. 4.

Note, that analytical results exist for some other kinds of pressure distribution, see e.g. [14] for the Bussinesque distribution.

5 Linear-ellipsoidal approximate model

Our goal is to develop approximate models for the friction force (31), which can be used effectively for analytical and numerical calculations in rigid body models. In this section, we present a first-order approximation already presented in [6]. This is the basis of the improved nonlinear model introduced in the next section.

5.1 General case

Consider the approximation of (31) in the form

$$\begin{aligned} {\textbf{Q}}({\textbf{w}})\approx \hat{\varvec{\Pi }}{\textbf{w}}=-\mu P \varvec{\Pi }{\textbf{w}} \end{aligned}$$

(64)

where $\hat{\varvec{\Pi }},\varvec{\Pi }\in {\mathbb {R}}^{3\times 3}$ are the coefficient matrices of the linear mapping. This model has the advantage that

• it is algebraically simple (linear in ${\textbf{w}}$), and

• it results in a model which is a good approximation of the analytical results in several cases (see [6]).

We call (64) a linear model due to the linear dependence on the slip direction ${\textbf{w}}$, but note that it is still a nonlinear, nonsmooth function of the original slip velocities (6) (see the definition in (27)). We can also call it an ellipsoidal model because the unit sphere ${\mathbb {S}}^2\ni {\textbf{w}}$ is mapped by (64) into an ellipsoid in the space ${\mathbb {R}}^3\ni {\mathbb {Q}}$ of the friction forces. This model was proposed in [6]; a similar model was presented in [42].

To specify the value of the matrix $\hat{\varvec{\Pi }}$ in (64), we need some information about the analytical solution, at least at some points or numerically. We can think about at least two strategies:

• specifying the model from some global conditions on ${\textbf{w}}\in {\mathbb {S}}^2$;

• fitting the model at some specific points of ${\textbf{w}}$.

The first strategy will be applied at the harmonic expansion in Sect. 6. Now, according to [6], we fit the model to the special slip directions

$$\begin{aligned} \begin{aligned} {\textbf{w}}_i=(1,0,0),{} & {} \!\!{\textbf{w}}_{ii}=(0,1,0),{} & {} \!\!{\textbf{w}}_{iii}=(0,0,1), \end{aligned} \end{aligned}$$

(65)

which correspond to the elementary motions for each component of the slip velocity vector (5). In many cases, it is easy to compute the friction force for these motions, resulting in the forces ${\textbf{Q}}({\textbf{w}}_{i})$, ${\textbf{Q}}({\textbf{w}}_{ii})$, ${\textbf{Q}}({\textbf{w}}_{iii})$, respectively. Then, the coefficient matrix $\hat{\varvec{\Pi }}$ becomes

$$\begin{aligned} \hat{\varvec{\Pi }}=\begin{bmatrix} {\textbf{Q}}({\textbf{w}}_{i})&\,&{\textbf{Q}}({\textbf{w}}_{ii})&\,&{\textbf{Q}}({\textbf{w}}_{iii}) \end{bmatrix}. \end{aligned}$$

(66)

Based on the contact geometry and the pressure distribution, (66) can be a general matrix filled by non-zero components [6]. Now, we restrict ourselves to the axisymmetric case.

5.2 Axisymmetric case

It can be show by direct calculation from (29)-(30) and (37) that in the axisymmetric case, (66) has the form of of a diagonal matrix

$$\begin{aligned} \hat{\varvec{\Pi }}=\begin{bmatrix} -\mu P &{} 0 &{} 0 \\ 0 &{} -\mu P &{} 0 \\ 0 &{} 0 &{} -\mu P\cdot \kappa /\rho \end{bmatrix}, \end{aligned}$$

(67)

where the parameter $\kappa$ is given by

$$\begin{aligned} \kappa =\frac{2\pi }{P}\int _0^R{\tilde{p}}(\xi )\xi ^2\,\textrm{d}\xi , \end{aligned}$$

(68)

where the value $0<\kappa /R<1$ depends on the pressure distribution ${\tilde{p}}$. By substituting (67) into (64), we get the final form of the linear friction model in the axisymmetric case:

$$\begin{aligned} \begin{aligned} Q_x&=-\mu P w_1=-\mu P\frac{u_x}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ Q_y&=-\mu P w_2=-\mu P\frac{u_y}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ T_z&=-\mu P \kappa w_3=-\mu P\frac{\kappa \rho \omega _z}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}. \end{aligned} \end{aligned}$$

(69)

From (69), we can express the linear model by using the formulations (46), (49) and (53) of the three parametrisations:

$$\begin{aligned} {\mathcal {Q}}_w(w_3)&=\sqrt{1-w_3^2},{} & {} {\mathcal {T}}_w(w_3)=w_3, \end{aligned}$$

(70)

$$\begin{aligned} {\mathcal {Q}}(\theta )&=\cos \theta ,{} & {} {\mathcal {T}}(\theta )=\sin \theta , \end{aligned}$$

(71)

$$\begin{aligned} {\mathcal {Q}}_\epsilon (\epsilon )=\tfrac{\epsilon }{\sqrt{\epsilon ^2+(\rho /R)^2}},{} & {} {\mathcal {T}}_\epsilon (\epsilon )=\tfrac{\rho /R}{\sqrt{\epsilon ^2+(\rho /R)^2}}. \end{aligned}$$

(72)

Note that by introducing the variable

$$\begin{aligned} w_{12}=\sqrt{w_1^2+w_2^2}=\sqrt{1-w_3^2}, \end{aligned}$$

(73)

the normalised friction force ${\mathcal {Q}}_w$ in (70) can be transformed to a linear function

$$\begin{aligned} \bar{{\mathcal {Q}}}_w(w_{12})={\mathcal {Q}}_w\left( \sqrt{1-w_{12}^2}\right) =w_{12}. \end{aligned}$$

(74)

An important issue is to choose the value of $\rho$ in (69) appropriately. This parameter should express the typical size of the contact region, and there are two straightforward choices for it:

• If we choose $\rho =R$, it simplifies the expressions in (72) and the forms of the mass matrices such as (11) and (16).

• If we choose $\rho =\kappa$, it simplifies (67) into a unit matrix.

The decision between these choices can be judged according to the accuracy of the models, as we will check below.

In the limit case of a very small contact region ($R\rightarrow 0$), the parameters tend to $\rho \rightarrow 0$ and $\kappa \rightarrow 0$, and (69) reduces to

$$\begin{aligned} \begin{aligned} Q_x&=-\mu P w_1=-\mu P\frac{u_x}{\sqrt{u_x^2+u_y^2}}, \\ Q_y&=-\mu P w_2=-\mu P\frac{u_y}{\sqrt{u_x^2+u_y^2}}, \\ T_z&=0, \end{aligned} \end{aligned}$$

(75)

which is the Coulomb model in three dimensions for a single-point contact. In this degenerate case, no torque is generated because of $x\rightarrow 0$ and $y\rightarrow 0$ in the integrand (22) of the torque (23). Even in the general case of a finite contact region ($R>0$), the model (69) has a similar form to that of (75). That is, the linear-ellipsoidal model is a natural extension of the Coulomb model to finite circular contact regions.

Fig. 5

Results of the linear-ellipsoidal model for the constant pressure distribution. The results of the linear model (71) are denoted by solid lines. The thick dotted lines correspond to the transformed analytical solution (59), (60) with the choice $\rho =\kappa$. The thin dotted lines correspond to the transformed analytical solution with the choice $\rho =R$

Fig. 6

Results of the linear-ellipsoidal model for the parabolic pressure distribution. The notations are the same as those in Fig. 5

5.3 Test problems

Let us now apply the linear-ellipsoidal model (69) for the pressure distributions (56) and (61):

• For the uniform pressure distribution (56), the formula (37) leads to

  $$\begin{aligned} \kappa =\frac{2}{3}R\approx 0.667 R. \end{aligned}$$

  (76)

• For the parabolic pressure distribution (56), formula (37) results in

  $$\begin{aligned} \kappa =\frac{3\pi }{16}R\approx 0.589 R. \end{aligned}$$

  (77)

In both cases, the results are depicted in Figs. 5 and 6 for both choices $\rho =R$ and $\rho =\kappa$. We can have the following conclusions:

• The linear-ellipsoidal model gives a slightly better approximation for the constant pressure distribution compared to the parabolic one.

• The linear-ellipsoidal model gives a significantly better approximation with the choice $\rho =\kappa$ compared to the choice $\rho =R$. Thus, it seems more effective to include the typical magnitudes of the contact forces from (46) to the rescaling of the kinematic variables in (5).

The moderate accuracy of the linear model can be enough in many dynamical problems to grab the essence of the phenomenon. Moreover, the linear model in (64) makes it possible to obtain analytical results in several cases (see [6]). However, the accuracy of the linear model is not always enough to find all phenomena and bifurcations. Thus, let us introduce the nonlinear extension in the next section.

6 Nonlinear approximate models

In the general case of arbitrary contact geometry and pressure distribution, the nonlinear model would be based on the expansion of the friction forces (31) on the unit sphere ${\mathbb {S}}^2\ni {\textbf{w}}$. In this case, the linear-ellipsoidal model would be used as a leading-order term of the expansion. However, a spherical expansion such as the usage of the Laplace spherical harmonics (see [7, 10]) goes beyond the scope of the paper. Now, we consider the single-variable expansion of the friction models in the axisymmetric case presented above.

6.1 Nonlinear models for the axisymmetric case

In the axisymmetric description, we introduced the three parametrisations (46), (49) and (53) of the friction forces. From the characteristics of the functions, we can suggest different expansions to create nonlinear approximate models:

• For the parameter $w_3$ in (46), the leading-order linear-ellipsoidal model contain the linear functions (70) and (74). Thus, it seems to be effective to use a polynomial expansion by using the Legendre-polynomials.

• For the latitude parameter $\theta$ in (49), the linear-ellipsoidal model contains the harmonic functions (71). Thus, a harmonic Fourier expansion can be applied.

• For the parameter of the slip-spin ratio $\epsilon$ in (53), the linear-ellipsoidal model leads to the sigmoid functions (72). For these types of functions, it is useful to apply a piecewise-defined expansion for the two sections of (57) and (58).

For the last case, it is efficient to use a Taylor expansion around $\epsilon =0$ for $\epsilon <1$ and an asymptotic expansion around $\epsilon =0$ for $\epsilon >1$ (see [36, 18]). For the uniform pressure distribution, such expansion can be found in [36]. There, the approximation of (59)-(60) becomes

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{\epsilon 1}(\epsilon )&= \epsilon -\frac{\epsilon ^3}{8}-\frac{\epsilon ^5}{64}+{\mathcal {O}}(\epsilon ^7), \\ {\mathcal {Q}}_{\epsilon 2}(\epsilon )&= 1-\frac{1}{8\epsilon ^2}-\frac{1}{64\epsilon ^4}-\frac{5}{1024\epsilon ^6}+{\mathcal {O}}(\epsilon ^{-8}), \end{aligned} \end{aligned}$$

(78)

$$\begin{aligned} \begin{aligned} {\mathcal {T}}_{\epsilon 1}(\epsilon )&=\frac{3}{2}\cdot \left( \frac{2}{3}-\frac{\epsilon ^2}{2}+\frac{3\epsilon ^4}{32}+\frac{5\epsilon ^6}{584}+{\mathcal {O}}(\epsilon ^8)\right) , \\ {\mathcal {T}}_{\epsilon 2}(\epsilon )&=\frac{3}{2}\cdot \left( \frac{1}{4\epsilon }+\frac{1}{48\epsilon ^3}+\frac{1}{512\epsilon ^5}+{\mathcal {O}}(\epsilon ^{-7})\right) . \end{aligned} \end{aligned}$$

(79)

For the indicated number of terms in (78)-(79), we get a nonlinear model with very good quantitative accuracy; thus, the model can be used effectively for many further purposes of analysis. However, there is still a discontinuity in (78)-(79) at $\epsilon =1$. In some cases, it would be useful to have a single smooth approximate model for the whole interval. This motivates the other two types of expansions.

In this paper, we present and apply the harmonic Fourier expansion of the formulation (49). The author also tested the expansion (46) by using Legendre polynomials. It seems that the final results from the harmonic and Legendre expansions are very close to each other. Thus, only the harmonic expansion is presented in this paper.

Note that regardless of choice between the three parametrisations of the expansion, the obtained nonlinear model can be transformed to the other parametrisations by using (50)-(54).

6.2 Harmonic expansion of the axisymmetric case

In the axisymmetric model (49), the symmetry with respect to the sign of the rotation cause the properties

$$\begin{aligned} {\mathcal {Q}}(-\theta )={\mathcal {Q}}(\theta ),{} & {} {\mathcal {T}}(-\theta )=-{\mathcal {T}}(\theta ). \end{aligned}$$

(80)

Moreover, although the domain of the functions ${\mathcal {Q}}$ and ${\mathcal {T}}$ is $\theta \in [-\pi /2,\pi ]$, they can be extended to the interval $\theta \in [-\pi ,\pi )$ by requiring the symmetries

$$\begin{aligned} {\mathcal {Q}}(\pi -\theta )=-{\mathcal {Q}}(\theta ),{} & {} {\mathcal {T}}(\pi -\theta )&={\mathcal {T}}(\theta ). \end{aligned}$$

(81)

Now, we can perform the harmonic Fourier expansion of ${\mathcal {Q}}$ and ${\mathcal {T}}$. Due to the symmetries (80)-(81), the expansions contains only selected terms of the full Fourier series,

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}(\theta )&\approx \sum _{i=1}^{N}c_i\cos \big ((2i-1)\theta \big ), \\ {\mathcal {T}}(\theta )&\approx \sum _{i=1}^{N}s_i\sin \big ((2i-1)\theta \big ). \end{aligned} \end{aligned}$$

(82)

where N is the degree of the expansion, and the coefficients $c_i$ and $s_i$ are given by

$$\begin{aligned} \begin{aligned} c_i&=\frac{4}{\pi }\int _{0}^{\pi /2}{\mathcal {Q}}(\theta )\cos \big ((2i-1)\theta \big )\,\textrm{d}\theta , \\ s_i&=\frac{4}{\pi }\int _{0}^{\pi /2}{\mathcal {T}}(\theta )\sin \big ((2i-1)\theta \big )\,\textrm{d}\theta . \end{aligned} \end{aligned}$$

(83)

The solution (82) can be transformed to the variable $w_3$ by using (50). Then, we get

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_w(w_3)&\approx \sqrt{1-w_3^2}\cdot \sum _{i=1}^N C_i w_3^{2i-2}, \\ {\mathcal {T}}_w(w_3)&\approx w_3\cdot \sum _{i=1}^N S_i w_3^{2i-2}, \end{aligned} \end{aligned}$$

(84)

where the coefficients $C_i$, $S_i$ can be expressed from $c_i$ and $s_i$.

Let us introduce the notation

$$\begin{aligned} \begin{aligned} {\mathcal {C}}(w_3)=\sum _{i=1}^N C_i w_3^{2i-2}, \\ {\mathcal {S}}(w_3)=\sum _{i=1}^N S_i w_3^{2i-2}. \end{aligned} \end{aligned}$$

(85)

Then, by substituting (84) into (46), we get

$$\begin{aligned} \begin{aligned} Q_x&\approx -\mu P w_1\cdot {\mathcal {C}}(w_3), \\ Q_y&\approx -\mu P w_2\cdot {\mathcal {C}}(w_3), \\ T_z&\approx -\mu P \kappa w_3\cdot {\mathcal {S}}(w_3). \end{aligned} \end{aligned}$$

(86)

Finally, by comparing (86) and (64), the form of the nonlinear approximate model becomes

$$\begin{aligned} {\textbf{Q}}({\textbf{w}})\approx \hat{\varvec{\Pi }}{\textbf{N}}({\textbf{w}}){\textbf{w}}, \end{aligned}$$

(87)

where the multiplier matrix

$$\begin{aligned} {\textbf{N}}({\textbf{w}})=\begin{bmatrix} {\mathcal {C}}(w_3) &{} 0 &{} 0 \\ 0 &{} {\mathcal {C}}(w_3) &{} 0 \\ 0 &{} 0 &{} {\mathcal {S}}(w_3) \end{bmatrix} \end{aligned}$$

(88)

contains the nonlinear part of the model. Thus, we obtained the approximate model (87) of the friction forces (31) as a polynomial in the components of the slipping direction ${\textbf{w}}$. This model can be directly applied in mechanical systems such as (3).

Fig. 7

Results of the nonlinear approximate model for estimating the magnitude of normalised friction force ${\mathcal {Q}}$ (left panel) and the normalised friction torque ${\mathcal {T}}$ (right panel) at the uniform pressure distribution. The black dotted curves denote the analytical solution, while the coloured curves depict the nonlinear harmonic model for the degrees $N=1\dots 4$. As a reference, the fitted linear model (see Fig. 5) is depicted by dashed grey lines. All results are computed with the choice $\rho =\kappa$. (Color figure online)

6.3 Form of the model for low degrees

Before applying the model to these dynamical systems, let us show the expressions of the model in the simplest cases.

6.3.1 First-order approximation

In the case $N=1$, the model (82) simplifies to

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}(\theta )&\approx c_1\cos \theta , \\ {\mathcal {T}}(\theta )&\approx s_1\sin \theta . \end{aligned} \end{aligned}$$

(89)

Then, the polynomial form (84) becomes

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_w(w_3)&\approx \sqrt{1-w_3^2}\cdot C_1, \\ {\mathcal {T}}_w(w_3)&\approx w_3\cdot S_1 \end{aligned} \end{aligned}$$

(90)

with $C_1=c_1$ and $S_1=s_1$. The matrix of nonlinear factors becomes a constant matrix

$$\begin{aligned} {\textbf{N}}({\textbf{w}})=\tilde{{\textbf{N}}}=\begin{bmatrix} C_1 &{} 0 &{} 0 \\ 0 &{} C_1 &{} 0 \\ 0 &{} 0 &{} S_1 \end{bmatrix}. \end{aligned}$$

(91)

Thus, finally (87) reduces formally to the linear-ellipsoidal model (64) with the replacement $\hat{\varvec{\Pi }}\rightarrow \hat{\varvec{\Pi }}\tilde{{\textbf{N}}}$. Thus, the two linear models differ from each other due to the values in the matrix (91). To distinguish the two models, we call

• (64)-(66) a linear model from fitting, and

• (87)-(91) a linear model from harmonic expansion.

6.3.2 Second-order approximation

In the case $N=2$, the model (82) becomes

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}(\theta )&\approx c_1\cos \theta +c_2\cos (3\theta ), \\ {\mathcal {T}}(\theta )&\approx s_1\sin \theta +s_2\sin (3\theta ). \end{aligned} \end{aligned}$$

(92)

Then, in the polynomial form (84), we get

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_w(w_3)&\approx \sqrt{1-w_3^2}\cdot \left( C_1+C_2w_3^2\right) , \\ {\mathcal {T}}_w(w_3)&\approx w_3\cdot \left( S_1+S_2w_3^2\right) , \end{aligned} \end{aligned}$$

(93)

where

$$\begin{aligned} \begin{aligned} C_1=c_1+c_2,&\quad&C_2=-4c_2, \\ S_1=s_1+3s_2,{} & {} S_2=-4s_2. \end{aligned} \end{aligned}$$

(94)

Thus, we have

$$\begin{aligned} \begin{aligned} {\mathcal {C}}(w_3)&=C_1+C_2w_3^2, \\ {\mathcal {S}}(w_3)&=S_1+S_2w_3^2 \end{aligned} \end{aligned}$$

(95)

in the matrix (91) and in the final form (86) of the model. In the original variables, the model becomes

$$\begin{aligned} \begin{aligned} Q_x&=\frac{-\mu P C_1 u_x}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}+ \frac{-\mu P C_2 u_x \kappa ^2\rho ^2\omega _z^2}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}^3}\\ Q_y&=\frac{-\mu P C_1 u_y}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}+ \frac{-\mu P C_2 u_y \kappa ^2\rho ^2\omega _z^2}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}^3}, \\ T_z&=\frac{-\mu PS_1\kappa \rho \omega _z}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}+ \frac{-\mu P S_2 \kappa ^3\rho ^3\omega _z^3}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}^3}. \end{aligned} \end{aligned}$$

(96)

Compared to the linear-ellipsoidal model (69), the model is expanded by the first nonlinear term. By continuing the expansion (82) for degrees $N>2$, the sequence of nonlinear models can be generated.

Although the expressions in the full form (96) are algebraically complicated, they have a compact polynomial form when using the variable ${\textbf{w}}$. This makes the model useful for dynamical analysis if the dynamical equations are transformed by the spherical decomposition (25).

Fig. 8

Results of the nonlinear approximate model for estimating the magnitude of normalised friction force ${\mathcal {Q}}$ at the uniform pressure distribution. The notations are the same as those of Fig. 7. The results are computed with the choice $\rho =R$

Fig. 9

Results of the nonlinear approximate model for estimating the magnitude of normalised friction force ${\mathcal {Q}}$ at the parabolic pressure distribution. The notations are the same as those of Fig. 7. The results are computed with the choice $\rho =\kappa$

Finally, let us compare the results of the nonlinear harmonic model (96) to those of the Padé approximations can be found in the literature (see [50], similar models can be found in [26, 27]). In Fig. 10, we can see that in the endpoints (pure translation or pure rotation) the Padé model has an exact fit to the analytical results, including the derivatives at the second degree model. In comparison, the harmonic nonlinear models have a finite error for these special motions. However, the average accuracy of the harmonic models are significantly better for the whole interval, thus, they provide an improved accuracy for the combined slip-spin cases.

Fig. 10

Comparison of the nonlinear harmonic model (96) and the Padé model from [50]. For the same degree of approximation, the Padé models have a better fit at the endpoints of the interval, but the nonlinear harmonic model provide a better average approximation

6.4 Test problems

Let us calculate the nonlinear approximate model (82)-(83) for the uniform and parabolic pressure distributions. Some results can be seen in Figs. 7, 8, 9.

In Fig. 7, we can see both the normalised force ${\mathcal {Q}}(\theta )$ and torque ${\mathcal {T}}(\theta )$ for the uniform pressure distribution with the choice $\rho =\kappa$ of the rescaling parameter. We can see that the first-order harmonic term gives a linear-ellipsoidal model that differs from the fitted linear model (see Fig. 5). In the figure, we can observe the convergence of the nonlinear approximate model to the analytical solution.

In Fig. 8, we can see the results for ${\mathcal {Q}}(\theta )$ with uniform pressure distribution, but now, for the choice $\rho =R$ of the rescaling parameter. We experienced earlier (see Fig. 5) that this approximation is significantly worse than the case $\rho =\kappa$ in the case of the fitted linear model. For the nonlinear model, such a difference cannot be observed, and by increasing the degree N of the approximation, the nonlinear model seems to eliminate the accurate choice of $\rho$.

In Fig. 9, we can see the results for ${\mathcal {Q}}(\theta )$ with parabolic pressure distribution for the choice $\rho =\kappa$. The convergence of the approximation is similar to that of the uniform pressure distribution.

7 Dynamics of the test problems

After introducing the nonlinear approximate friction model (87) for combined slip and spin, let us apply this model for the analysis of the dynamics of rigid bodies.

7.1 Form of the dynamical equations

From (4), the dynamics of the orthogonal variables in the general equations (1) becomes

$$\begin{aligned} \dot{{\textbf{x}}}_o={\textbf{F}}_o({\textbf{x}})={\textbf{M}}({\textbf{q}})^{-1}{\textbf{W}}{\textbf{Q}}({\textbf{u}})+{\textbf{M}}({\textbf{q}})^{-1}{\textbf{Q}}_e({\textbf{x}}). \end{aligned}$$

(97)

In the two test problems (13) and (18), this dynamics simplifies to

$$\begin{aligned} \dot{{\textbf{x}}}_o={\textbf{M}}^{-1}{\textbf{Q}}({\textbf{w}})+{\textbf{M}}^{-1}{\textbf{Q}}_e \end{aligned}$$

(98)

due to the constant mass matrix, constant external forces and the trivial form of ${\textbf{W}}$. By substituting the nonlinear friction model (87) into (98), we get

$$\begin{aligned} \dot{{\textbf{x}}}_o={\textbf{M}}^{-1}\hat{\varvec{\Pi }}{\textbf{N}}({\textbf{w}}){\textbf{w}}+{\textbf{M}}^{-1}{\textbf{Q}}_e. \end{aligned}$$

(99)

By introducing

$$\begin{aligned} {\textbf{B}}({\textbf{w}})={\textbf{M}}^{-1}\hat{\varvec{\Pi }}{\textbf{N}}({\textbf{w}}),{} & {} {\textbf{c}}={\textbf{M}}^{-1}{\textbf{Q}}_e, \end{aligned}$$

(100)

the equation (99) can be written into the form

$$\begin{aligned} \dot{{\textbf{x}}}_o={\textbf{F}}_o({\textbf{x}}_o)={\textbf{B}}({\textbf{w}})\cdot {\textbf{w}}+{\textbf{c}}. \end{aligned}$$

(101)

7.2 Dynamics in the vicinity of codimension–3 discontinuities

Before the analysis, let us briefly present some concepts and results about the qualitative analysis of vector fields with codimension–3 discontinuities. For more details, see [45].

7.2.1 Discontinuity, limit vector field

Based on (4), let us consider the differential equation

$$\begin{aligned} \dot{{\textbf{x}}}={\textbf{F}}({\textbf{x}})=\begin{bmatrix} \dot{{\textbf{x}}}_o \\ \dot{{\textbf{x}}}_t \end{bmatrix}= \begin{bmatrix} {\textbf{F}}_o({\textbf{x}}_o,{\textbf{x}}_t) \\ {\textbf{F}}_t({\textbf{x}}_o,{\textbf{x}}_t) \end{bmatrix}. \end{aligned}$$

(102)

where the state variable ${\textbf{x}}\in {\mathbb {R}}^{n+m}$ is decomposed into the orthogonal variables ${\textbf{x}}_o=(x_1,x_2,x_3)\in {\mathbb {R}}^3$ and tangential variables ${\textbf{x}}_t\in {\mathbb {R}}^{n+m-3}$. The orthogonal and tangential property is defined with respect to the set

$$\begin{aligned} \Sigma =\{ {\textbf{x}}=({\textbf{x}}_o,{\textbf{x}}_t): {\textbf{x}}_o={\textbf{0}} \}. \end{aligned}$$

(103)

Physically, ${\textbf{x}}_o$ contains the variables associated to slip and nonsmooth dynamics, while ${\textbf{x}}_t$ contains all the other variables of the system. We assume that ${\textbf{F}}$ is a smooth vector field ${\textbf{F}}:{\mathbb {R}}^{n+m}\setminus \Sigma \rightarrow {\mathbb {R}}^{n+m}$, but it is not defined on $\Sigma$. Thus, $\Sigma$ is called a codimension–3 discontinuity set of ${\textbf{F}}$. We assume that the directional limit

$$\begin{aligned} {\textbf{F}}^\star (\bar{{\textbf{x}}},{\textbf{v}}):=\lim _{\epsilon \searrow 0}{\textbf{F}}(\bar{{\textbf{x}}}+\epsilon {\textbf{v}}) \end{aligned}$$

(104)

exists for all ${\bar{x}}\in \Sigma$ and for all ${\textbf{v}}\in {\mathbb {R}}^{n+m}$ orthogonal to $\Sigma$. We call ${\textbf{F}}^\star (\bar{{\textbf{x}}},{\textbf{v}})$ the limit vector field of ${\textbf{F}}$ at the point $\bar{{\textbf{x}}}$.

7.2.2 Spherical decomposition

Consider the spherical decomposition ${\textbf{x}}_o=r{\textbf{w}}$ from (25). Recall, that physically, r represents the magnitude (26) of the slip, while ${\textbf{w}}$ denotes the direction (27) of the slip. From formal differentiation of (25), the dynamics of the orthogonal variables is

$$\begin{aligned} {\textbf{F}}_o({\textbf{x}})=\dot{{\textbf{x}}}_o=\dot{(r{\textbf{w}})}=\dot{r}{\textbf{w}}+r\dot{{\textbf{w}}}. \end{aligned}$$

(105)

By multiplying (105) by ${\textbf{w}}^\top$ from the left, and utilizing that ${\textbf{w}}^\top {\textbf{w}}=1$ and ${\textbf{w}}^\top \dot{{\textbf{w}}}=0$, we get

$$\begin{aligned} \dot{r}={\textbf{w}}^\top {\textbf{F}}_o({\textbf{x}}), \end{aligned}$$

(106)

and by comparing (105) and (106), we obtain

$$\begin{aligned} \dot{{\textbf{w}}}=\frac{{\textbf{F}}_o({\textbf{x}})-\dot{r}{\textbf{w}}}{r}=\frac{{\textbf{F}}_o-{\textbf{w}}^\top {\textbf{F}}_o({\textbf{x}}){\textbf{w}}}{r}. \end{aligned}$$

(107)

Let us introduce the notation

$$\begin{aligned} \begin{aligned} R({\textbf{x}})&={\textbf{w}}^\top {\textbf{F}}_o({\textbf{x}}), \\ {\textbf{V}}({\textbf{x}})&={\textbf{F}}_o-{\textbf{w}}^\top {\textbf{F}}_o({\textbf{x}}){\textbf{w}}=\left( {\textbf{I}}-{\textbf{w}}{\textbf{w}}^\top \right) {\textbf{F}}_o. \end{aligned} \end{aligned}$$

(108)

The component R is the radial dynamics, and ${\textbf{V}}$ is the circumferential dynamics, both are understood with respect to the unit sphere ${\mathbb {S}}^2\ni {\textbf{w}}$. Physically, R represents the change of the magnitude of the slip, while V corresponds to the change of the direction of the slip. Finally, the dynamics (102) can be transformed into

$$\begin{aligned} \begin{aligned} \dot{r}&=R(r,{\textbf{w}},{\textbf{x}}_t), \\ \dot{{\textbf{w}}}&={\textbf{V}}(r,{\textbf{w}},{\textbf{x}}_t)/r, \\ \dot{{\textbf{x}}}_t&={\textbf{F}}_t(r,{\textbf{w}},{\textbf{x}}_t). \end{aligned} \end{aligned}$$

(109)

The discontinuity at ${\textbf{x}}_o=0$ in (102) was transformed to $r=0$ in (109).

7.2.3 Asymptotic dynamics

Let us investigate the dynamics in the vicinity of the discontinuity set, corresponding to the physical case of the small slip velocities with $r\rightarrow 0$. Consider the limits

$$\begin{aligned} \begin{aligned} R^\star ({\textbf{w}},{\textbf{x}}_t)&:=\lim _{r \searrow 0}R(r,{\textbf{w}},{\textbf{x}}_t), \\ {\textbf{V}}^\star ({\textbf{w}},{\textbf{x}}_t)&:=\lim _{r \searrow 0}{\textbf{V}}(r,{\textbf{w}},{\textbf{x}}_t), \\ {\textbf{F}}_t^\star ({\textbf{w}},{\textbf{x}}_t)&:=\lim _{r \searrow 0}{\textbf{F}}_t(r,{\textbf{w}},{\textbf{x}}_t), \end{aligned} \end{aligned}$$

(110)

depending smoothly on their variables, which property is inherited from (104). Then, the dynamics of r can be written as a series expansion around $r=0$ in the form

$$\begin{aligned} \dot{r}=R^\star ({\textbf{w}},{\textbf{x}}_t)+\sum _{i=1}^\infty R_i ({\textbf{w}},{\textbf{x}}_t)\cdot \frac{r^i}{i!}, \end{aligned}$$

(111)

where

$$\begin{aligned} R_i({\textbf{w}},\bar{{\textbf{x}}}_t)= \frac{\partial ^i R(r,{\textbf{w}},{\textbf{x}}_t)}{\partial r^i}\bigg |_{r=0}. \end{aligned}$$

(112)

In smooth systems, a leading-order approximation is usually obtained by linearisation (first-degree terms). However, as typical in many discontinuous systems, the leading-order term in (112) is the non-trivial zeroth-degree term $R^\star ({\textbf{w}},{\textbf{x}}_t)$. We can do the same expansion as (112) for the other components of (109) at $r=0$. A detailed justification of this process can be found in [45]. Finally, in the vicinity $r=0$ of the discontinuity set, we can define the asymptotic dynamics

$$\begin{aligned} \begin{aligned} \dot{r}&=R^\star ({\textbf{w}},{\textbf{x}}_t), \\ \dot{{\textbf{w}}}&={\textbf{V}}^\star ({\textbf{w}},{\textbf{x}}_t)/r, \\ \dot{{\textbf{x}}}_t&={\textbf{F}}_t^\star ({\textbf{w}},{\textbf{x}}_t) \end{aligned} \end{aligned}$$

(113)

associated to (109). Physically, this asymptotic dynamics (113) describes the behaviour of he system for infinitesimally small slip velocities.

7.2.4 Time rescaling

For small r, the systems (109) and (113) behave as multiple time scale dynamical systems where the dynamics of ${\textbf{w}}$ is fast and the dynamics of r and ${\textbf{x}}_t$ is slow. Moreover, the second component of (109) and (113) become singular at $r\rightarrow 0$. Let us transform the time to regularise the dynamics of the fast variable ${\textbf{w}}$ at $r=0$ and eliminate the discontinuity. For that, let us introduce a new time variable $\tau$ defined by $\text {d}/\text {d}t =r\cdot \text {d}/\text {d}\tau$. Then, (113) can be transformed into

$$\begin{aligned} \begin{aligned} r'&=rR^\star ({\textbf{w}},{\textbf{x}}_t), \\ {\textbf{w}}'&={\textbf{V}}^\star ({\textbf{w}},{\textbf{x}}_t), \\ {\textbf{x}}'_t&=r{\textbf{F}}_t^\star ({\textbf{w}},{\textbf{x}}_t), \end{aligned} \end{aligned}$$

(114)

where the dash denotes the time derivative with respect to the new time variable $\tau$. The singular time transformation created a smooth system (114) from (113) while keeping the trajectories unchanged.

7.2.5 Fast dynamics

At the limit case $r\rightarrow 0$ of the former discontinuity, we obtain the fast subsystem

$$\begin{aligned} \begin{aligned} r'&=0, \\ {\textbf{w}}'&={\textbf{V}}^\star ({\textbf{w}},\bar{{\textbf{x}}}_t), \\ {\textbf{x}}'_t&=0, \end{aligned} \end{aligned}$$

(115)

while $r(\tau )\equiv 0$ and ${\textbf{x}}_t(\tau )\equiv \bar{{\textbf{x}}}_t$. Therefore, for a chosen point $\bar{{\textbf{x}}}_t\in \Sigma$, the dynamics at the discontinuity reduces to the dynamics of ${\textbf{w}}$ on the unit sphere.

7.2.6 Limit directions – radial dynamics

Definition 1

Consider a fixed point $\hat{{\textbf{w}}}$ of (115) satisfying ${\textbf{V}}^\star (\hat{{\textbf{w}}},\bar{{\textbf{x}}}_t)={\textbf{0}}$. Then, we call $\hat{{\textbf{w}}}$ a limit direction of the system (102) at $\bar{{\textbf{x}}}_t$.

Definition 2

Consider a limit direction $\hat{{\textbf{w}}}$ at $\bar{{\textbf{x}}}_t$. We call the limit direction (radially) attracting if $R^\star (\hat{{\textbf{w}}},\bar{{\textbf{x}}}_t)<0$, and it is called (radially) repelling if $R^\star (\hat{{\textbf{w}}},\bar{{\textbf{x}}}_t)>0$.

The limit directions are not just the fixed points of the fast dynamics on the unit sphere, but they are important organising objects of the full dynamics in the vicinity of the discontinuity. This is stated in the next pair of theorems; for proof and an explanation, see [45].

Theorem 1

(from [45]) Consider an attracting limit direction $\hat{{\textbf{w}}}$ at $\bar{{\textbf{x}}}_t\in \Sigma$. Then, there exists a trajectory ${\textbf{x}}(t)$ of (113) with circumferential component ${\textbf{w}}(t)$, and ${\hat{t}}\in {\mathbb {R}}$ such that

$$\begin{aligned} \lim _{t\nearrow {\hat{t}}} {\textbf{x}}(t)=\bar{{\textbf{x}}}_t,{} & {} \lim _{t\nearrow {\hat{t}}}{\textbf{w}}(t)=\hat{{\textbf{w}}}. \end{aligned}$$

(116)

Theorem 2

(from [45]) Consider a repelling limit direction $\hat{{\textbf{w}}}$ at $\bar{{\textbf{x}}}_t\in \Sigma$. Then, there exists a trajectory ${\textbf{x}}(t)$ of (113) with circumferential component ${\textbf{w}}(t)$, and ${\hat{t}}\in {\mathbb {R}}$ such that

$$\begin{aligned} \lim _{t\searrow {\hat{t}}} {\textbf{x}}(t)=\bar{{\textbf{x}}}_t,{} & {} \lim _{t\searrow {\hat{t}}}{\textbf{w}}(t)=\hat{{\textbf{w}}}. \end{aligned}$$

(117)

That is, for each limit direction, there exists at least one trajectory of the dynamics which can reach the discontinuity in forward or backward time. The limit directions at higher codimensional discontinuities have similar behaviour to eigenvectors at smooth equilibria. However, there are two fundamental differences:

• An eigenvector corresponds to a line, and there are trajectories to two opposite directions (bi-directional). A limit direction corresponds to a half-line and to a single direction of trajectories.

• Along an eigenvector, the trajectories tend to the equilibrium exponentially, which requires infinite time to reach the equilibrium. Along a limit direction, trajectories reach the discontinuity in finite time (see ${\hat{t}}$).

7.2.7 Limit directions – dynamics on the sphere

The attracting or repelling property of a limit direction in Definition 2 characterises the evolution on the slow time scale t in the radial direction after the fast dynamics has settled to one of the fixed points $\hat{{\textbf{w}}}$. To analyse the fast dynamics on the fast time scale $\tau$, let us linearise (115) around a fixed point $\hat{{\textbf{w}}}$:

$$\begin{aligned} {\textbf{w}}'={\textbf{V}}^\star _{\textbf{w}}(\hat{{\textbf{w}}},\bar{{\textbf{x}}}_t)({\textbf{w}}-\hat{{\textbf{w}}})+{\mathcal {O}}^2. \end{aligned}$$

(118)

The expression (118) contains the modified Jacobian

$$\begin{aligned} {\textbf{V}}^\star _{\textbf{w}}({\textbf{w}},\bar{{\textbf{x}}}_t)=\frac{\partial {\textbf{V}}^\star ({\textbf{w}},\bar{{\textbf{x}}}_t)}{\partial {\textbf{w}}}-\frac{\partial {\textbf{V}}^\star ({\textbf{w}},\bar{{\textbf{x}}}_t)}{\partial {\textbf{w}}}{\textbf{w}}{\textbf{w}}^\top , \end{aligned}$$

(119)

which maps the dynamics onto the unit sphere. Then, we can calculate the three eigenvalues: A trivial zero eigenvalue $\lambda _1=0$ is not relevant, and the remaining two eigenvalues $\lambda _2, \lambda _3$ characterise the limit direction as a node, focus or saddle on the unit sphere.

To avoid the constrained dynamics and a zero eigenvalue in (118), an alternative method to calculate the eigenvalues is to derive the evolution equations of $\phi$ and $\theta$ on the fast time scale. From (27), (32) and (115), we get

$$\begin{aligned} \begin{aligned} \phi '&=-\dot{u}_1\sin \phi +\dot{u}_2\cos \phi , \\ \theta '&=-(\dot{u}_1\sin \phi +\dot{u}_2\cos \phi )\sin \theta +\dot{u}_3\cos \theta , \end{aligned} \end{aligned}$$

(120)

where ${\dot{u}}_1$, ${\dot{u}}_2$ and ${\dot{u}}_3$ are the first three components of (104). Then, a two-by-two Jacobian can be calculated at the fixed points of (120), which can also be used to characterise the fast dynamics around limit directions.

7.2.8 Bifurcations of limit directions

In the general case of a limit direction $\hat{{\textbf{w}}}$, the slow radial dynamics is either attracting or repelling ($R^\star (\hat{{\textbf{w}}},\bar{{\textbf{x}}}_t)\ne 0$), and the $\hat{{\textbf{w}}}$ is a hyperbolic fixed point of the fast dynamics (115). When one of these conditions is violated, special bifurcations of the limit directions occur. These bifurcations were defined in [2] for the codimension–2 case, but conceptionally, we can extend it to the codimension–3 case, as well:

• If $R^\star (\hat{{\textbf{w}}},\bar{{\textbf{x}}}_t)\ne 0$, a tangency bifurcation of limit directions occur. At this bifurcation event, a limit direction changes the attracting property to repelling, or vice versa.

• If $\hat{{\textbf{w}}}$ becomes a non-hyperbolic fixed point of (115), several types of bifurcation can occur on the unit sphere. The simplest case is the saddle-node bifurcation of limit directions.

Fig. 11

Generic arrangements of the limit directions in the case of the problem of the disc on the plane. The numbering of the cases corresponds to the bifurcation diagrams Figs. 13 and 14. The circle containing the limit directions is the invariant circle on the unit sphere of the slip directions (denoted by green colour in Fig. 12). The case numbered (4) appears only with the nonlinear friction model (compare Figs. 13 and 14). In Figs. 11, 12, 13, 14, the colour code of the limit directions are the following: purple–repelling direction with a stable node on the sphere, red–attracting direction with an unstable node on the sphere, green–attracting direction with a saddle on the sphere where the stable eigenvector lies in the invariant set, brown–attracting direction with a saddle on the sphere where the unstable eigenvector lies in the invariant set, blue–attracting direction with a stable node on the sphere. (Color figure online)

Fig. 12

Generic arrangements of the limit directions in the case of the problem of the disc on the plane. The numbering of the cases corresponds to the bifurcation diagrams Figs. 13 and 14. (Color figure online)

Fig. 13

Bifurcation diagram of the disc on the plane with the first-degree approximation (linear-ellipsoidal model). The curves denote the locations of the limit directions on the invariant set (see Figs. 11 and 12). The accuracy of the linear model is enough to reveal the pitchfork bifurcation (P) of the limit directions and the tangency bifurcations (T). However, some qualitative details remain hidden at low values of the loading force F. (Color figure online)

Fig. 14

Bifurcation diagram of the disc on the plane with the second-degree approximation (nonlinear model). The curves denote the locations of the limit directions on the invariant set (see Figs. 11 and 12). Compared to the linear model in Fig. 13, already the first nonlinear approximation reveals the fold bifurcations (F) of limit directions and gives the complete qualitative description of the problem. The quantitative difference between approximate models and the analytical solution can be seen in Figs. 17 and 18. (Color figure online)

7.3 Mechanical consequences

Let us now identify the different mathematical concepts with quantities and phenomena in the mechanical systems considered above.

• The discontinuity set corresponds to the kinematic case of static contact, where the slip velocities (3) vanish. This is a codimension–3 discontinuity because three variables vanish at the same time.

• The vector field ${\textbf{F}}$ corresponds to the dynamics of slipping. These equations are not defined at the discontinuity set due to the nonsmooth property of the friction models (31).

• By using different mathematical tools, the dynamics can be extended for the static contact case (stick or roll). For more details, see [36] for set-valued force laws and [45] for sliding dynamics. This topic is out of the scope of the present paper, where we focus on the dynamics of slip in the vicinity of the discontinuity.

• A trajectory connected to the discontinuity set corresponds to a motion where a transition occurs between slip and the static state (stick or roll).

• A limit direction $\hat{{\textbf{w}}}$ corresponds to a slip direction where slip-stick transitions occur. An attracting limit direction corresponds to a transition from slip to stick, while a repelling limit direction is related to a transition from stick to slip.

• Consequently, the number and types of limit directions characterise the possible stick–slip transitions of the rigid body.

Let us now implement these mathematical tools to the system (101) containing the nonlinear approximate friction model. By applying (108) to the system (101), we get

$$\begin{aligned} {\dot{r}}&=R^\star ({\textbf{w}},\bar{{\textbf{x}}}_t)={\textbf{w}}^\top \left( {\textbf{B}}({\textbf{w}}){\textbf{w}}+{\textbf{c}}\right) , \end{aligned}$$

(121)

$$\begin{aligned} \dot{{\textbf{w}}}&={\textbf{V}}^\star ({\textbf{w}},\bar{{\textbf{x}}}_t)=\left( {\textbf{I}}-{\textbf{w}}{\textbf{w}}^\top \right) \cdot \left( {\textbf{B}}({\textbf{w}}){\textbf{w}}+{\textbf{c}}\right) . \end{aligned}$$

(122)

One possibility to find the limit directions is to solve the nonlinear equation (122) for ${\textbf{w}}$ directly. Alternatively, we can first multiply (121) by ${\textbf{w}}$ from the left,

$$\begin{aligned} \dot{r}{\textbf{w}}= {\textbf{w}}{\textbf{w}}^\top \left( {\textbf{B}}({\textbf{w}}){\textbf{w}}+{\textbf{c}}\right) . \end{aligned}$$

(123)

Then, by considering a limit direction $\dot{{\textbf{w}}}={\textbf{0}}$, the sum of (122) and (123) becomes

$$\begin{aligned} \dot{r}{\textbf{w}}=\left( {\textbf{I}}- {\textbf{w}}{\textbf{w}}^\top +{\textbf{w}}{\textbf{w}}^\top \right) \left( {\textbf{B}}({\textbf{w}}){\textbf{w}}+{\textbf{c}}\right) . \end{aligned}$$

(124)

Finally, after rearranging (124), we get

$$\begin{aligned} \left( {\dot{r}}{\textbf{I}}-{\textbf{B}}({\textbf{w}})\right) {\textbf{w}}={\textbf{c}}. \end{aligned}$$

(125)

Instead of solving (122), we can solve (125) and $||{\textbf{w}}||=1$ simultaneously for the limit directions ${\textbf{w}}$ and the corresponding values of $\dot{r}$ characterising the radial behaviour through ${\dot{r}}=R^\star ({\textbf{w}},\bar{{\textbf{x}}}_t)$. Finally, we can obtain a qualitative description of the local dynamics at the discontinuity.

Fig. 15

A special bifurcation of the force-free case with $F=0$ with the linear model. The linear model predicts stable attracting limit directions at the poles (pure spin), which is not consistent with the solution of the exact model

Fig. 16

A special bifurcation of the force-free case with $F=0$ with the nonlinear model. The nonlinear model reveals the family of limit directions of combined slip and spin (denoted by blue circles)

7.4 Results for the disc on plane

Consider the test problem (13) with the parameters $j=1/2$, $\kappa =2/3\cdot R$, $\rho =\kappa$. Without loss of generality, we consider only the case $F\ge 0$. Then, by using the nonlinear approximate model in the form (86), the dynamics (13) becomes

$$\begin{aligned} \dot{{\textbf{x}}}_o=\begin{bmatrix} -\mu g w_1\cdot {\mathcal {C}}(w_3)+\frac{1}{m}F \\ -\mu g w_2\cdot {\mathcal {C}}(w_3) \\ -\frac{8}{9}\mu g w_3\cdot {\mathcal {S}}(w_3) \end{bmatrix}. \end{aligned}$$

(126)

Recall that (126) determines the dynamics on a unit sphere. On this sphere, the second component of (126) shows that the circle $w_2=0$ is an invariant set. From the properties of ${\mathcal {C}}(w_3)$, it can be checked that ${\mathcal {C}}(w_3)=0$ does not occur in the unit sphere. Thus, the invariant set $w_2=0$ is the only place when the second component of (126) vanishes. Consequently, all limit directions must be found in this invariant set $w_2=0$.

By using the formula (125), the limit directions are determined by the equations

$$\begin{aligned} \begin{aligned} (\dot{r}+\mu g {\mathcal {C}}(w_3))w_1&=F/m, \\ (\dot{r}+\mu g {\mathcal {C}}(w_3))w_2&=0, \\ (\dot{r}+8/9\cdot \mu g {\mathcal {S}}(w_3))w_3&=0. \end{aligned} \end{aligned}$$

(127)

From (127) and the condition $\sqrt{w_1^2+w_2^2+w_3^2}=1$, we can find two types of limit directions:

7.4.1 Trivial limit directions

Then, $w_3=(w_2=)0$, $w_1=\pm 1$, and we get two special points of the equator of the unit sphere,

$$\begin{aligned} \hat{{\textbf{w}}}_{1,2}=(\pm 1,0,0). \end{aligned}$$

(128)

Then, from the first component of (127), de radial dynamics is characterised by

$$\begin{aligned} R^\star (\hat{{\textbf{w}}}_{1,2},\bar{{\textbf{x}}}_t)=\dot{r}_{12}=-\mu g C_1\pm F/m, \end{aligned}$$

(129)

because ${\mathcal {C}}(0)=C_1$.

• Consequently, the limit direction $\hat{{\textbf{w}}}_{2}=(- 1,0,0)$ is always attracting, because $C_1>0$.

• The limit direction $\hat{{\textbf{w}}}_{1}=(1,0,0)$ can be attracting or repelling, and the bifurcation point between these cases is located at

  $$\begin{aligned} F=\mu m gC_1=:F_T. \end{aligned}$$

  (130)

  This parameter value $F=F_T$ corresponds to a tangency bifurcation.

7.4.2 Non-trivial limit directions

In this case, we require $\dot{r}=-8/9\cdot \mu g {\mathcal {S}}(w_3)$ from the third component of (127). By substituting it into the first component of (127), we get

$$\begin{aligned} \mu g \left( {\mathcal {C}}(w_3)-\frac{8}{9}{\mathcal {S}}(w_3)\right) w_1=\frac{F}{m}. \end{aligned}$$

(131)

By rearranging (131) and eliminating $w_1$, we obtain:

$$\begin{aligned} \left( {\mathcal {C}}(w_3)-\frac{8}{9}{\mathcal {S}}(w_3)\right) ^2(1-w_3^2)=\left( \frac{F}{\mu m g}\right) ^2. \end{aligned}$$

(132)

For a degree N of the harmonic approximation, ${\mathcal {C}}$ and ${\mathcal {S}}$ are $N-1$ degree polynomials in $w_3^2$. That is, the solution of (132) leads to finding roots of a polynomial with a degree $2N-1$.

Let us find the points where the trivial (128) and the non-trivial (131) limit directions coincide:

$$\begin{aligned} F=\pm \mu m g\left( C_1-\frac{8}{9}S_1\right) =:F_P. \end{aligned}$$

(133)

This point corresponds to a pitchfork bifurcation of limit directions.

It can be shown that for the non-trivial limit directions, ${\dot{r}}>0$; thus, they are all attracting. Non-trivial limit directions are denoted in Figs. 11, 12, 13 and 14 by $\hat{{\textbf{w}}}_5\dots \hat{{\textbf{w}}}_8$.

7.4.3 Results with the linear first-degree model

With the linear model (90), (131) becomes

$$\begin{aligned} \mu g \left( C_1-\frac{8}{9}S_1\right) w_1=\frac{F}{m}, \end{aligned}$$

(134)

which can be solved explicitly for a single pair of limit directions,

$$\begin{aligned} w_1=\frac{F}{\mu m g (C_1-8/9S_1)},{} & {} w_3=\pm \sqrt{1-w_1^2}. \end{aligned}$$

(135)

The two limit directions vanish at (133) in the pitchfork bifurcation.

From these results, we can categorize the structurally different cases (Figs. 11 and 12) and sketch the bifurcation diagram (Fig. 13). According to the value of the loading force F, the following cases occur:

• Case 1, $|F|>F_T$: There are two limit directions, one of them is repelling ($\hat{{\textbf{w}}}_1$, denoted by purple colour in Figs. 11, 12). This means that the stick of the disc is not realisable, and the disc instantaneously starts slipping in the direction of the force.

• Case 2, $F_T>|F|>F_P$: There are two limit directions, both are attracting, one of them is a stable node on the unit sphere ($\hat{{\textbf{w}}}_1$, denoted by blue colour in Figs. 11, 12). That is, the stick state is realizable, and almost all neighbouring trajectories reach the discontinuity along this direction (corresponds to pure translation).

• Case 3, $F_P>|F|>0$: After the pitchfork bifurcation, the pair of attracting, stable (non-trivial) limit directions appear ($\hat{{\textbf{w}}}_3,\hat{{\textbf{w}}}_4$ denoted by blue colour in Figs. 11, 12). Thus, there are two directions where slip-stick transitions occur (corresponding to combined slip-spin motion).

Let us check the prediction of the linear model at the force-free case $F=0$, which is itself a special bifurcation event (see Fig. 15). Instead of the isolated limit directions $\hat{{\textbf{w}}}_1$ and $\hat{{\textbf{w}}}_2$, the whole circle (”equator”) with $w_3=0$ is filled by limit directions, which are unstable fixed points on the unit sphere. At the same time, the stable limit directions $\hat{{\textbf{w}}}_3$ and $\hat{{\textbf{w}}}_4$ reach the ”poles” of the unit sphere. This means that the model predicts that the transition of the disc from slip to stick should occur along with a pure rotational motion. This phenomenon is not consistent with the analytical and numerical solutions (see, e.g. [23, 47]). This shows that the linear model is needed to be improved in this case.

Fig. 17

Dependence on the accuracy of the nonlinear approximate model on the degree of the approximation. The intersection of the curves with horizontal lines provides the limit direction in the case of the disc on the plane according to (131). We assume uniform pressure distribution and a rescaling parameter $\rho =\kappa$

7.4.4 Results with nonlinear second-degree model

With the linear model (93), (131) becomes

$$\begin{aligned} \mu g \left( k_1+k_2w_3^2\right) w_1=\frac{F}{m}, \end{aligned}$$

(136)

where

$$\begin{aligned} k_1=C_1-\frac{8}{9}S_1,{} & {} k_2=C_2-\frac{8}{9}S_2. \end{aligned}$$

(137)

From (136), one of the bifurcations corresponds to the pitchfork bifurcation at (133). Moreover, we can find a new bifurcation at

$$\begin{aligned} \begin{aligned} w_3&=\sqrt{\frac{2k_2-k_1}{3k_2}}, \\ F&=\mu m g\sqrt{\frac{4(k_1+k_2)^3}{27k_2}}=:F_F, \end{aligned} \end{aligned}$$

(138)

which is a fold (saddle-node) bifurcations of limit directions.

Table 2 Comparison of the slip directions of the force-free ($F=0$) case of the disc problem with different methods

The results can be seen in Fig. 14. Here, many of the phenomena are preserved from the linear model (see Fig. 14), including the tangency bifurcation, the pitchfork bifurcation and the Cases 1-3 of dynamics. Moreover, the tangency bifurcation creates a fourth region for low values of F:

• Case 4: $F_F>|F|>0$: After the (pair of) fold bifurcations, four new limit directions are born (denoted by $\hat{{\textbf{w}}}_5\dots \hat{{\textbf{w}}}_8$ in Figs. 11, 12). All of them are attracting, but none of them are stable. Thus, the structure of the trajectories does not change much from Case 3 in the sense that the slip-stick transitions will happen along $\hat{{\textbf{w}}}_3$ and $\hat{{\textbf{w}}}_4$, related to a combined slip-spin motion.

However, the appearance of the four new limit directions changes the structure of the dynamics at the force-free case with $F=0$ (see Fig. 16). Here, we can find two circles containing stable limit directions. Thus, the slip-stick transition can occur along one of these directions, which corresponds to combined slip-spin motion. From (136), the locations of these limit directions are determined by $w_3=\sqrt{-k_1/k_2}$.

Let us present a comparison about the force-free ($F=0$) case between the presented approximate method and some analytical results in the literature (see Tab. 2). It can be found in several works [24, 38, 50] that the disc has a combined slip-spin motion before the sliding stops. These results are consistent to the presented second-order model (see Fig. 16). Moreover, we can find numerical values for the constant pressure distribution [38] and the Galin-distribution [24] as a reference solution. Table 2 contains these values transformed to all three parametrisations $\epsilon ,w_3,\theta$. We can see that the values of the approximate model are close to [38], and even for a different type of pressure distribution [24], there is a qualitative agreement. All in these methods, the disc stops moving with the same order of magnitude of slip and spin motion.

With these phenomena, the second-degree nonlinear approximate model can provide a full qualitative description of the problem of the disc on the plane. To increase the accuracy, the degree of the nonlinear model can be increased. In Fig. 17, we can see the plot of (131) for different degrees of nonlinear expansion. We can see the convergence to the exact solution.

7.5 Results for the ball on the plane

The whole analysis of Sect. 7.4 can be repeated for the problem of the ball on the plane. We now present only the essential things to see the differences between the two cases.

Consider the test problem (18) with the parameters $j=2/5$, $\kappa =3\pi /16\cdot R$, $\rho =\kappa$. Moreover, let $\lambda ={\bar{R}}/R$ be the ratio between the sizes of the body and the contact region. By using the nonlinear approximate model (86), the dynamics (18) leads to

$$\begin{aligned} \dot{{\textbf{x}}}_o=\begin{bmatrix} -\frac{7}{2}\mu gw_1\cdot {\mathcal {C}}(w_3)+\frac{1}{m}F\\ -\frac{7}{2}\mu gw_2\cdot {\mathcal {C}}(w_3) \\ -\frac{45\pi ^2}{512\lambda ^2}\mu gw_3\cdot {\mathcal {S}}(w_3) \end{bmatrix}. \end{aligned}$$

(139)

Fig. 18

Dependence on the accuracy of the nonlinear approximate model on the degree of the approximation. The intersection of the curves with horizontal lines provides the limit direction in the case of the ball on the plane according to (131). We assume parabolic pressure distribution, a rescaling parameter $\rho =\kappa$, and a relative size $\lambda ={\bar{R}}/R=5$ of the body with respect to the contact region

Then, by applying (125) to (139), we get

$$\begin{aligned} \begin{aligned} (\dot{r}+7/2\cdot \mu g {\mathcal {C}}(w_3))w_1&=F/m, \\ (\dot{r}+7/2\cdot \mu g {\mathcal {C}}(w_3))w_2&=0, \\ (\dot{r}+45\pi ^2/(512\lambda ^2)\cdot \mu g {\mathcal {S}}(w_3))w_3&=0. \end{aligned} \end{aligned}$$

(140)

Finally, the equation for the non-trivial limit directions becomes

$$\begin{aligned} \mu g \left( \frac{7}{2}{\mathcal {C}}(w_3)-\frac{45\pi ^2}{512\lambda ^2}{\mathcal {S}}(w_3)\right) w_1=\frac{F}{m}. \end{aligned}$$

(141)

This has a similar form to that of (131); there are differences only in the parameters and in the coefficients $C_i, S_i$ inside the friction model. However, for physically realistic values, these differences have significant effects. In Fig. 18, we can see the plot of (141) for different degrees of nonlinear expansion. Even for the choice $\lambda =5$ used in the diagram – the contact region is just 5 times smaller than the ball – the fold bifurcation does not appear. Thus, the linear model is appropriate for the qualitative analysis, and the nonlinear models provide a higher accuracy compared to the case of the disc on the ball. By increasing the value of $\lambda$ – which is reasonable in practical cases – the linear and nonlinear model gets even closer to the exact solution. Consequently, in the problem of the ball on the plane, nonlinearity in the friction model has a less significant effect than that in the case of the disc on the plane.

8 Conclusion

By focusing on the nonsmooth friction laws, we presented the problem of contacting rigid bodies with a circular contact region and an axisymmetric pressure distribution. After presenting some exact solutions from the literature, we analysed the ways to create approximate friction models for rigid body dynamics. After choosing the appropriate parametrisation of the kinematic variables, the existing linear-ellipsoidal model was presented, and then, the new nonlinear model was introduced by harmonic expansion. Finally, the properties of the obtained nonlinear friction model were demonstrated on two test problems: By using the mathematical concept of codimension–3 discontinuities, the possible slip-stick transitions were determined analytically and semi-analytically. In the case of a disc slipping on a plane, the first nonlinear improvement was necessary to find all phenomena missing from the linear model and to get a complete qualitative description of the problem. In the case of the ball slipping on the plane, the linear model was enough for the qualitative description, but the nonlinear model achieved an improved accuracy.

Finally, we get an approximate friction model, which might be used effectively for the analysis and simulation of rigid bodies with a finite contact area. One of the further tasks would be to find more complicated test problems to explore the properties and limitations of the model. An important issue would be to find the possibilities to extend the method to contact regions which are not axisymmetric.