Abstract
We investigate the motion of rigid bodies subject to combined slipping and spinning over a rough flat surface in the presence of dry friction. Integration of Coulomb friction forces over the contact area gives rise to a dynamical system with an isolated discontinuity of codimension 3. Recent results about such vector fields are applied to the motion of flat bodies under the assumption of known, time-independent distributions of normal contact forces and to general bodies where kinematic constraints enforce a state-dependent normal contact force distribution with a discontinuity at the sticking state. In both cases, the equations of motion are transformed into a smooth slow–fast dynamical system. The fixed points of the fast flow indicate the possible directions of combined slip–spin motion immediately before a body stops. We also introduce an approximation of the frictional forces and moments by the leading-order term of a spherical harmonic expansion, which allows for an explicit formulation of the equations of motion. The approximate model captures important empirically observed features of the motion. It is proven analytically and illustrated by examples that the number of fixed points in the approximate model is 2, 4, or 6.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The presence of dry friction in mechanics often leads to dynamic (slipping) and static (sticking) contact states. In dynamic problems, these mechanical states can switch into each other. Slip–stick transitions bring about nonsmooth behaviour of the system. The conditions of transitions between stick and slip can be implemented in the models in different ways. If we focus on the sticking state, then the (static) friction forces are determined by the dynamical equations as constraint forces, and the transitions can be modelled to occur at the boundary of the set of admissible contact forces. Alternatively, if we focus on the slipping state at transitions, then the slipping dynamics can be analysed in the vicinity of the sticking states to determine the presence and type of transitions between stick and slip. The two approaches often complement each other, and they can be implemented in different ways in friction models.
Here, we focus on the latter, dynamic approach by analysing the state space of slipping dynamics to explore the stick–slip transitions. A two-dimensional model of two rigid bodies with a single contact point and Coulomb friction gives rise to a piecewise smooth dynamical system (often called Filippov system) containing a codimension-1 discontinuity set in the phase space. In this case, the stick–slip transitions can occur in two directions (”left” and ”right”), and the corresponding mathematical theories are well established in the literature (see Leine and Nijmeijer 2004; di Bernardo et al. 2008; Jeffrey 2018). In three-dimensional problems with a single contact point, the state space contains a codimension-2 discontinuity. Then, from the continuously many possible slipping directions, one can find the so-called limit directions where the slip–stick transitions are realized (Antali and Stepan 2018, 2019; Batlle 1996; Cheesman et al. 2021), and this analysis can be naturally extended for multiple contact points (Antali and Stepan 2021). In this paper, we consider finite contact regions with a combined slip and spin motion, where the integration of locally prescribed Coulomb friction forces leads to a codimension-3 discontinuity in the state space (Marques et al. 2016). Vector fields with higher-codimensional discontinuities have been recently analysed by the authors (Varkonyi and Antali 2021); those mathematical tools can be applied to the slip–stick transitions of bodies with a finite contact region.
As proposed by Varkonyi and Antali (2021), we transform the equations of slip motion to spherical coordinates, whereby the discontinuity is replaced by smooth dynamics with two characteristic time scales. The positions and the attractivity of fixed points of the fast dynamics—or limit directions in our terminology—determine the direction of terminal motion at slip–stick transitions, including the direction of slip and the ratio of velocity and angular velocity at the time of the transition. The limit directions of some simple mechanical systems have already been discovered (Goyal et al. 1991b); however, our work is the first one to describe their role in a systematic and general way.
In some simple cases, the resultant of frictional forces over the contact region can be given in terms of elliptic integral functions (Leine and Glocker 2003; Farkas et al. 2003; Weidman and Malhotra 2005, 2007; Dahmen et al. 2005; Wolf et al. 2007; Magyari and Weidman 2001). Another class of problem that lends itself for analytical investigation is the case when the contact forces are concentrated at points or along lines introducing new forms of nonsmoothness (Goyal et al. 1991a; Dahmen et al. 2005; Hammond 2010; Borisov et al. 2016). However in general, the resultant can only be evaluated numerically. In order to enable analytical investigation, several closed-form approximations of frictional forces and torques have been proposed. These include Padé approximations (Kireenkov 2002a, b, 2017; Zhuvarlev and Kireenkov 2005), hyperbolic tangent functions (Kudra and Awrejcewicz 2011, 2012), concatenated Taylor series (Leine and Glocker 2003) and implicit quadratic equations (Goyal et al. 1991a; Howe and Cutkosky 1996). In addition, some works have proposed a priori closed-form friction models, neither derived by integration of local Coulomb forces nor derived by approximations of such integrals (Zhou et al. 2018; Walker and Leine 2019). In this paper, we propose a new and natural approximation, which is found to be the leading-order term in a spherical harmonic expansion of the exact model. Our approximation is represented by a linear function in some appropriately chosen variables. The simple form of the approximate model allows us to find explicit algorithms for identifying limit directions, and we also establish upper and lower bounds for the number of limit directions.
The structure of the paper is the following: In Sect. 2, the kinematic and dynamic description of a finite contact region is presented, and we identify the properties of the discontinuity, which originates from the resultant of the distributed dry friction forces. In Sect. 3, we review some recent mathematical tools for analysing codimension-3 discontinuities of vector fields (Varkonyi and Antali 2021). In Sect. 4, we introduce an approximate ellipsoidal model for the mapping between the variables of the velocity state and the friction forces. Section 5 contains the detailed analysis of the nonsmooth dynamics of a single rigid body under the approximate friction model, focusing on the sticking–slipping transitions. The new methods and results are demonstrated through mechanical examples in Sect. 6.
2 Problem Statement
We assume that the motion of the bodies can be decomposed into rigid body motion of the bodies and small local elastic deformations in the contact region. Therefore, the global elastic deformations of the bodies are neglected, and the effect of the local deformations is included in the friction forces (and torques) applied to the dynamical model of rigid bodies. This approach is common in the literature (see, e.g. Leine and Glocker 2003).
Friction phenomena greatly depend on the geometry of the contacting surfaces of the bodies. From the several possible situations, we focus on two typical cases:
-
(regular) point contact In this case, we consider a single theoretical contact point, and at this point, the curvatures of the contacting bodies are substantially different (nonconforming surfaces). Then, by considering the elastic deformation, a finite-sized contact region is initiated around the theoretical contact point. We assume that the contact region is a plane shape, and its size is considered to be much less than the typical size of the bodies. A prototype example of this case is a ball moving on a plane.
-
plane contact In this case, we consider two bodies with contacting planar surfaces. Then, the contact region is the overlapping part of the planar surfaces of the two bodies. The prototype example of this case is a block moving on a plane.
There are other possible situations beyond the scope of the present analysis, such as:
-
(general) conforming contact If the surfaces have approximately the same curvatures at the theoretical contact point, then the contact region has comparable size to the typical size of the bodies, and it can be a significantly curved surface. (Plane contact is the special case of conforming contact where the curvatures of both surfaces vanish.)
-
(regular) line contact The contacting surfaces can be conforming in one direction and nonconforming in another direction at the theoretical contact point. Then, the initiating contact region is a thin stripe. A typical example of this type can be the contact of two cylinders with parallel symmetry axes.
-
degenerate point and line contact If the edges or vertices of the bodies are involved in the contact, then the deformations and the geometry of the contact region can be irregular compared to smooth surfaces.
Although the cases of point contact and the plane contact are substantially different from each other in several aspects, they have some similarities, which make it possible to analyse them in a common calculation framework. In both cases, we can find a well-defined contact plane tangential to both surfaces, and the contact region can be considered as a subset of this plane. Throughout this section, these two cases are considered together unless otherwise stated. When there are differences between the point contact and plane contact case, the analysis is shown parallel.
2.1 Resultant of the Friction Forces
Without loss of generality, we describe the relative motion of the bodies. That is, one of the bodies is considered as a fixed body, and the other one is referred to as a moving body.
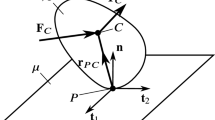
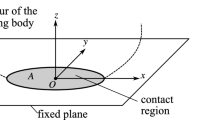
In the contact plane (tangential plane) between the bodies, a planar contact region A is initiated. The motion of the moving body is described in a steady reference frame attached to the fixed body but in a rotating coordinate system attached to the moving body. The origin of the coordinate system is located at a chosen reference point \(O\in A\). The coordinate axes are denoted by x, y, z where x, y lie in the contact plane and z points in the normal direction towards the moving body (see Fig. 1). The corresponding unit basis vectors are denoted by \(\mathbf {i},\mathbf {j},\mathbf {k}\), respectively. Then, the contact region is parametrized as a subset \(A=\left\{ (x,y)\right\} \subset \mathbb {R}^2\). During the motion, the coordinate system, the contact region A and all the contact forces may change in time. Time-dependence is not considered in this section (see, however, Sect. 5). Instead, we analyse a single time instant when the contact forces are calculated.
Left panel: Sketch of the contact region of two contacting bodies. One of the bodies is considered to be fixed. The coordinate direction z points into the normal direction towards the moving body. Right panel: The velocity components \(u_x,u_y\) of the reference point O and the angular velocity component \(\omega _z\) in the normal direction. With the assumption of planar rigid body motion in the contact plane, the velocity field can be calculated from these variables
We assume that after the initiation of the contact region, the tangential motion of the points of the moving body inside the contact region is planar rigid body motion. That is, from the velocity \(\mathbf {v}_O=u_x\mathbf {i}+u_y\mathbf {j}\) of the reference point O and the normal component \(\omega _z\) of the angular velocity of the moving body, we can express the tangential velocity distribution \(\mathbf {v}(x,y)\) in the contact region A as
Equation (1) includes the assumption that either the whole contact region is sticking (when \(u_x=u_y=\omega _z=0\)), or almost all points are slipping (when any components from \(u_x,u_y,\omega _z\) are nonzero). This assumption is widely used in the literature (see, e.g. Leine and Glocker 2003). To describe sticking and slipping zones in the contact region, a more detailed analysis of the deformations is necessary (see the details in, for example, Johnson 1985).
In this section, we assume that within the contact region, the normal pressure distribution is given, and it is denoted by p(x, y). Then, the total normal force \(P_z\mathbf {k}\) between the bodies is determined by
Moreover, the pressure distribution creates a resultant torque \(T_x\mathbf {i}+T_y\mathbf {j}\) about the point O, where the components are given by:
We assume spatial Coulomb friction locally at each point of the contact region, and the friction coefficient \(\mu \) is assumed to be the same for dynamic and static friction. Then, in the slipping case of the contact region, the distribution \(\mathbf {q}_{xy}(x,y)=q_x(x,y)\mathbf {i}+q_y(x,y)\mathbf {j}\) of the tangential contact forces is given by:
Then, by substituting (1) into (4), the components of the tangential pressures become:
Let us calculate the moment of the tangential force field with respect to the reference point O,
where \(\mathbf {r}=x\mathbf {i}+y\mathbf {j}\) and
Finally, the components of the resultant force and torque of the tangential force distribution are given by:
and the resultant of all contact forces with respect to the reference point O becomes:
It can be seen from formulae (5) and (7), that, in general, the integrals in (8) cannot be computed analytically. Analytical solutions are still possible in some special cases; a few of them are shown in Sect. 4.5.
2.2 Analysis of the Discontinuity
Equation (1) shows that the velocity distribution in the contact region is determined by the variables \(u_x\), \(u_y\) and \(\omega _z\). These three variables are considered in the vector form
where \(u_z=\rho \omega _z\) is the normalized angular velocity. The multiplier \(\rho \) is defined by:
i.e. \(\rho \) represents average distance from the reference point, or equivalently the characteristic length of the contact region. The rescaling of \(\omega _z\) by \(\rho \) makes the dimension of each component of (10) identical; furthermore, they also have a similar order of magnitude whenever \(u_x\), \(u_y\), and \(\omega _z\) are of the same order of magnitude [see the velocity reduction formula (1)].
In this paper, we use the boldface letters both for physical vectors such as \(\mathbf {P}\) and for general vectors and matrices such as \(\mathbf {x}_\mathrm {o}\). For the shorthand notation, the n-tuple (x, y, z) is considered to be equivalent to a column matrix \(\begin{bmatrix} x&y&z \end{bmatrix}^\top \). The notation \(\left\Vert .\right\Vert \) refers to the usual Euclidean 2-norm of vectors.
By the subscript ’o’ in the notation \(\mathbf {x}_\mathrm {o}\), we anticipate the fact that in the full state space of a dynamical system, the three variables in (10) correspond to the orthogonal subspace of the discontinuity set (for details, see Sect. 3).
The norm of \(\mathbf {x}_\mathrm {o}\) is:
which expresses the magnitude of slipping. In the limit case \(r=0\), the velocity of all points in the contact region becomes zero, and the bodies are sticking to each other. Let us transform the variables (10) into spherical coordinates in the form
where
The vector \(\mathbf {w}\) expresses the direction of slipping including information about the angular velocity, as well. Note that the variables \(w_1,w_2,w_3\) are not independent because they have to satisfy the equation \(\left\Vert \mathbf {w}\right\Vert =\sqrt{w_1^2+w_2^2+w_3^2}=1\). Thereby, \(\mathbf {x}_\mathrm {o}\) is decomposed into the magnitude \(r\ge 0\) of slipping and the direction \(\mathbf {w}\) of slipping in the space \((u_x,u_y,\rho \omega _z)\) (see the left panel of Fig. 2).
Left panel: spherical decomposition of the vector \(\mathbf {x}_\mathrm {o}=(u_x,u_y,\rho \omega _z)=r\mathbf {w}\) of velocities describing slipping of the contact region, where r is the magnitude of slipping and \(\mathbf {w}\) is the unit vector expressing the direction of the slipping. Right panel: parametrization of the unit sphere of the slipping directions \(\mathbf {w}\). In most part of the paper, we use the parameter set \(\mathbf {w}=(w_1,w_2,w_3)\), which is redundant due to \(\left\Vert \mathbf {w}\right\Vert =\sqrt{w_1^2+w_2^2+w_3^2}=1\). Sometimes, it is useful to transform to the usual longitude \(\phi \in [0,2\pi )\) (expressing the direction of the translational motion) and latitude \(\theta \in [-\pi /2,\pi /2]\) (expressing the ratio between the rotational and translational motion). Then, the ”equator” of the sphere corresponds to the pure translational motion, while the north and south ”poles” of the sphere corresponds to the pure rotational motion with respect to the reference point
The direction vector \(\mathbf {w}=(w_1,w_2,w_3)\) on the unit sphere \(\mathcal {S}^2\subset \mathbb {R}^3\) can be parametrized by two angles in the form:
In (15), \(\phi \in [0,2\pi )\) denotes the ”longitude” on the unit sphere, expressing the direction of the velocity of the reference point, and \(\theta \in [-\pi /2,\pi /2]\) denotes the ”latitude”, expressing the ratio between \(\omega _z\) and the velocity magnitude of the reference point (see the right panel of Fig. 2). The parametrization is singular at the ”poles” \(\mathbf {w}=(0,0,\pm 1)\), which states correspond to the pure rotating contact state with respect to the reference point (\(\mathbf {v}_O=\mathbf {0}\)).
It can be seen from (5) and (7) that the tangential force distribution and its resultant become discontinuous at the sticking state \(\mathbf {x}_\mathrm {o}=\mathbf {0}\) (equivalent to \(r=0\)). From (13), let us express \(u_x=r w_1\), \(u_y=r w_2\), \(\omega _z=r w_3/\rho \). By substituting these into (5)–(8), we get expressions, which depend formally on the direction \(\mathbf {w}\) only, and they are independent of the magnitude r of slipping velocity:
By using the vectorial form \(\mathbf {Q}=(P_x,P_y,T_z/\rho )\in \mathbb {R}^3\), formulae (16) of the tangential forces can be written as
Equation (17) maps the unit sphere \(\mathcal {S}^2\) onto \(\mathbb {R}^3\), and the image \(\mathcal {E}=\mathbf {Q}(\mathcal {S}^2)\) is the set of possible friction force resultants while slipping.
Now, let us highlight some properties of (16)–(17), which are crucial for our analysis:
-
The integrand of (17) is equivalent of the local form of the Coulomb friction law (5), which has codimension-2 discontinuities at each point \((x,y)\in A\). The integration in (17) usually eliminates these (zero-measure) discontinuities of the integrand, and hence, (17) becomes smooth. (A similar phenomenon occurs in the following elementary integral: \( \int _0^1(x-\xi )/|x-\xi |\mathrm {d}\xi =2x \) for \(0\le x\le 1\) where the integrand is discontinuous but the result is smooth.) Thus, by requiring some regularity of the pressure distribution p(x, y) and the geometry A of the contact region, the image \(\mathcal {E}=\mathbf {Q}(\mathcal {S}^2)\) forms a closed, smooth 2-surface in \(\mathbb {R}^3\).
-
As a notable exception, pressure distributions concentrated along lines (see Sect. 4.5.4) may result in nonsmooth function \(\mathbf {Q}(\mathbf {w})\), and pressure distributions concentrated in isolated points (see Goyal et al. 1991a; Dahmen et al. 2005; Hammond 2010; Borisov et al. 2016) may generate discontinuous \(\mathbf {Q}(\mathbf {w})\).
-
Despite smoothness of \(\mathbf {Q}(\mathbf {w})\), the friction force as a funtion of the velocity variables \(\mathbf {x}_\mathrm {o}=(u_x,u_y,u_z)\) has a codimension-3 discontinuity at \(\mathbf {x}_\mathrm {o}=\mathbf {0}\). This is caused by simultaneous discontinuity of the local friction force at all points in the trivial (motionless) state. Thus, mapping (17) itself is not discontinuous, but the discontinuity is included into the variable \(\mathbf {w}\) [see (14)].
-
The state \(\mathbf {x}_\mathrm {o}=\mathbf {0}\) cannot be directly substituted into (16). The limit \(\lim _{r\searrow 0} (r\mathbf {w})=\mathbf {x}_\mathrm {o}=\mathbf {0}\) gives the same (sticking) state independently from \(\mathbf {w}\); however, substituting this limit into (16) gives continuously many directional limits depending on \(\mathbf {w}\). The dynamics of vector fields in the vicinity of such discontinuities can be explored effectively by the mathematical tools developed recently in Varkonyi and Antali (2021), which we summarize briefly in Sect. 3.
3 Codimension-3 Discontinuities of Vector Fields
In a recent paper (Varkonyi and Antali 2021), the authors of the present work investigated the general properties of dynamical systems with an isolated codimension-n discontinuity. In this section, we review the main results related to the \(n=3\) case, which results are applied to slipping and spinning bodies in Sect. 5.
3.1 Codimension-3 Discontinuities
Consider the space \(\mathbb {R}^m\) where the vectors are denoted by \(\mathbf {x}=(x_1,x_2\dots x_m)\in \mathbb {R}^m\), and the following codimension-3 subspace of \(\mathbb {R}^m\):
Consider the differential equation
where \(\mathbf {F}\) is an \(\mathbf {R}^m\setminus \Sigma \rightarrow \mathbf {R}^m\) vector field with components \(\mathbf {F}=(F_1,F_2,\dots F_m)\). Dot means differentiation with respect to time t; the explicit time dependence \(\mathbf {x}(t)\) is not denoted except when it is necessary.
We assume that the vector field \(\mathbf {F}\) is undefined in \(\Sigma \), and it has the following properties:
-
1
\(\mathbf {F}\) is smooth everywhere in \(\mathbf {R}^m\setminus \Sigma \).
-
2
In all points \(\bar{\mathbf {x}}\in \Sigma \), the limit
$$\begin{aligned} \mathbf {F}^\star (\bar{\mathbf {x}},\mathbf {v}):=\lim _{\epsilon \searrow 0}\mathbf {F}(\bar{\mathbf {x}}+\epsilon \mathbf {v}) \end{aligned}$$(20)exists for any vector \(\mathbf {v}\in \mathbb {R}^m\) orthogonal to \(\Sigma \).
-
3
The limit (20) depends smoothly on \(\mathbf {v}\) and \(\bar{\mathbf {x}}\).
In this context, we call \(\Sigma \) a codimension-3 discontinuity set with respect to \(\mathbf {F}\). For a selected point \(\bar{\mathbf {x}}\in \Sigma \), we call \(\mathbf {F}^\star (\bar{\mathbf {x}},\mathbf {v})\) the limit vector field of \(\mathbf {F}\) at \(\bar{\mathbf {x}}\). Note that the linear spaces \(\mathbb {R}^m\) and \(\Sigma \) can be generalized to smooth manifolds if necessary.
In the case of contacting bodies, \(\mathbf {F}\) describes slipping motion, and the discontinuity set \(\Sigma \) corresponds to rolling or sticking states. The dynamics of \(\mathbf {F}\) can be extended to the discontinuity set \(\Sigma \), either by using the dynamical equation of sticking (or rolling) or by calculating the sliding dynamics (in the sense of Filippov theory) generated by F on \(\Sigma \) (see Varkonyi and Antali 2021).
Our goal is to investigate the behaviour of the differential equation (19) in a small neighbourhood of \(\Sigma \) with a focus on trajectories starting or ending at a point \(\bar{\mathbf {x}}\in \Sigma \). As we will see, such trajectories correspond to slip–stick and stick–slip transitions of the bodies in the mechanical model.
3.2 Reformulation of the Vector Field
To achieve an appropriate form of the equations, we reformulate the vector field in four steps.
3.2.1 Decomposition into Orthogonal and Tangential Parts
Let us separate the state variable \(\mathbf {x}\) into parts orthogonal and tangential to \(\Sigma \),
where \(\mathbf {x}_\mathrm {o}\in \mathbb {R}^3\) is the orthogonal part and \(\mathbf {x}_t\in \mathbb {R}^{m-3}\) the tangential part. Then, the vector field can be written in the form \(\mathbf {F}=(\mathbf {F}_o,\mathbf {F}_t)\) and (19) with \(\mathbf {F}_o=(F_1,F_2,F_3)\) and \(\mathbf {F}_t=(F_4,\dots F_m)\).
3.2.2 Spherical Decomposition of the Orthogonal Part
Next, a spherical decomposition of the orthogonal variable \(\mathbf {x}_\mathrm {o}\) is considered:
where \(r=\Vert \mathbf {x}_\mathrm {o} \Vert \) represents the distance of \(\mathbf {x}\) from \(\Sigma \), and \(\mathbf {w}=\mathbf {x}_\mathrm {o}/\Vert \mathbf {x}_\mathrm {o}\Vert =(w_1,w_2,w_3)\) is the unit vector showing the direction of \(\mathbf {x}\) around \(\Sigma \). This set of variables is redundant and subject to the constraint \(\left\Vert \mathbf {w}\right\Vert =1\). That is, \(\mathbf {w}\) is located on a unit sphere. Note that in (10)–(14), the same quantities were defined from mechanical point of view.
Transformations (21)–(22) allow us to identify \(\mathbf {x}\) with the variable set \((r,\mathbf {w},\mathbf {x}_t)\). Then, (19) can be rewritten into
In (23), the component \(R(\mathbf {x})=\mathbf {w}^\top \mathbf {F}_o(\mathbf {x})\) denotes the radial component of the vector field, and \(\mathbf {V}(\mathbf {x})=\mathbf {F}_o-\mathbf {w}^\top \mathbf {F}_o(\mathbf {x})\mathbf {w}\) is the circumferential component lying in the unit sphere of \(\mathbf {w}\).
3.2.3 Asymptotic Dynamics
Note that due to the requirement of the smooth dependence of (20) on the variables, the functions R, \(\mathbf {V}\) and \(\mathbf {F}_t\) depend smoothly on the variables \(r,\mathbf {w},\mathbf {x}_t\). Furthermore, they have well-defined limits
which are smooth functions in \(\mathbf {w}\) and \(\mathbf {x}_t\). Then, we can define the asymptotic dynamics
It was demonstrated in Varkonyi and Antali (2021) that in some important cases, the local dynamics (23) in an infinitesimal neighbourhood of a point \(\bar{\mathbf {x}}_t \in \Sigma \) can be described via investigation of the asymptotic dynamics (25).
3.2.4 Time Rescaling at the Singularity
The singularity associated with \(r=0\) is still present in the second equation of (25). This singularity can be removed by a singular rescaling of time,
rendering (25) into
where dash means derivation with respect to the transformed time variable \(\tau \). The new set of equations is a multiple time scale dynamical system for small r, where \(\mathbf {w}\) is a fast variable, and r and \(\mathbf {x}_t\) are slow variables.
Note that (27) does not fit into the standard form (see Kuehn 2015, p. 8), of multiple time scale systems. Standard slow–fast systems are written as:
where \(\mathbf {y}\) contains the fast variables, \(\mathbf {z}\) contains the slow variables, and \(0<\epsilon \ll 1\) is the so-called time-scale parameter. In (27), \(\mathbf {x}_t\) is a usual slow variable, but the slow variables r behave differently: We cannot see a time-scale parameter in (27), but the separation of the time scales is caused by variable r itself when \(0<r\ll 1\). Equation (27) appears to be outside the scope of (28); nevertheless, it has been found in Varkonyi and Antali (2021) that the overall behaviour of the system can be investigated via separation of fast and slow variables, similarly to the standard case.
3.3 Analysis of the Asymptotic Dynamics
In (27), the fast dynamics of \(\mathbf {w}\) fully decouples from the slow variables and the equation \(\mathbf {w}'=\mathbf {V}^\star (\mathbf {w},\bar{\mathbf {x}}_t)\) can be solved independently. According to the Poincaré–Bendixson theorem, trajectories of smooth dynamical systems over \(\mathbb {S}^2\) converge to fixed points, limit cycles, or polycycles (Lopez and Llibre 2007). By investigating a large number of cases, we found that trajectories corresponding to dynamics of slipping bodies always converge to fixed points, albeit this property is not proven here. In what follows, we only review results related to fast dynamics converging to fixed points. We begin by introducing the definition of limit directions:
Definition 1
Consider a fixed point \(\hat{\mathbf {w}}\) of the circumferential dynamics satisfying \(\mathbf {V}^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)=\mathbf {0}\). Then, we call \(\hat{\mathbf {w}}\) a limit direction of the system (19) at \(\bar{\mathbf {x}}_t\). In the cases \(R^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)<0\) or \(R^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)>0\), \(\hat{\mathbf {w}}\) is called an attracting or repelling limit direction, respectively.
The names defined above are inspired by the following pair of statements:
Theorem 1
(from Varkonyi and Antali 2021) Consider an attracting [repelling] limit direction \(\hat{\mathbf {w}}\) at \(\bar{\mathbf {x}}=\bar{\mathbf {x}}_t\in \Sigma \). Then, there exists a trajectory \(\mathbf {x}(t)\) of (25) with circumferential component \(\mathbf {w}(t)\), and \(\hat{t}\in \mathbb {R}\) such as
Theorem 1 states the existence of a single trivial trajectory at the fixed point \(\hat{\mathbf {w}}\) of the circumferential dynamics. The limit directions can be further classified based on the number and type of trajectories satisfying (29).
For this, let us linearize the circumferential dynamics at the limit direction \(\hat{\mathbf {w}}\):
where
The second term of (31) makes the linear term in (30) a projection on the unit sphere of \(\mathbf {w}\); we can check \(\mathbf {w}^\top \mathbf {V}^\star _\mathbf {w}\mathbf {w}=0\). (Note that alternatively for this analysis, the unit sphere \(\Vert \mathbf {w}\Vert =1\) could be considered as a smooth two-manifold.) Thus, in general, the \(3\times 3\) matrix \(\mathbf {V}^\star _\mathbf {w}\) has two nontrivial eigenvalues \(\lambda _1\) and \(\lambda _2\) and a trivial eigenvalue \(\lambda _3=0\), the latter correspond to the radial dynamics parallel to \(\mathbf {w}\). We call \(\hat{\mathbf {w}}\) a hyperbolic fixed point if \(\mathrm {Re}\lambda _1\ne 0\) and \(\mathrm {Re}\lambda _2\ne 0\). In this case, we can define the following types of limit directions:
Definition 2
Consider a limit direction \(\hat{\mathbf {w}}\) at \(\bar{\mathbf {x}}=(0,\mathbf {0},\bar{\mathbf {x}}_t)\in \Sigma \). Assume that \(\hat{\mathbf {w}}\) is a hyperbolic fixed point of (25) with corresponding nontrivial eigenvalues \(\lambda _1\) and \(\lambda _2\). The limit direction is called
-
dominant if
$$\begin{aligned} \min _{i\in 1,2} R^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)\mathrm {Re}\lambda _i>0; \end{aligned}$$(32) -
isolated if
$$\begin{aligned} \max _{i\in 1,2} R^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)\mathrm {Re}\lambda _i<0; \end{aligned}$$(33) -
saddle-type if
$$\begin{aligned} R^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)\mathrm {Re}\lambda _1 \cdot R^\star (\hat{\mathbf {w}},\bar{\mathbf {x}}_t)\mathrm {Re}\lambda _2<0. \end{aligned}$$(34)
In other words, a stable node or focus of \(\mathbf {w}'=\mathbf {V}^\star (\mathbf {w},\bar{\mathbf {x}}_t)\) corresponds to an attracting-dominant or a repelling-isolated limit direction; an unstable node or focus corresponds to an attracting-isolated or repelling-dominant limit direction, and a saddle corresponds to a saddle-type limit direction.
This categorization shows whether a limit direction attracts the nearby trajectories in the time direction of approaching the discontinuity set. At a dominant limit direction, the trivial trajectory from Theorem 1 has a neighbourhood where all trajectories are connected to \(\Sigma \) along the limit direction. At an isolated limit direction, there is a single isolated trajectory that is connected to \(\Sigma \). At a saddle-type limit direction, there is a mixed behaviour according to the stable and unstable directions of the saddle.
4 Ellipsoidal Approximation of the Slipping Friction Force Resultants
It can be seen from the integrals (16) that generally the expressions of the resultants of the friction forces cannot be computed analytically. Analytical solutions are still possible in some special cases; a few of them are shown as reference results in Sect. 4.5. For many purposes of dynamical analysis, it could be appropriate to calculate (8) numerically for the desired accuracy. Instead, in this section, we present a natural leading-order approximate model of (16), which makes it possible to apply the nonsmooth mathematical tools of Sect. 3 analytically in order to explore the different dynamical scenarios of nonsmooth behaviour of the contacting bodies (see Sect. 5).
4.1 Form of the Approximation
Let us approximate the closed surface \(\mathcal {E}=\mathbf {Q}(\mathcal {S}^2)\) to replace the exact integration of (16). A natural approximation of a closed surface is an ellipsoid. If \(\tilde{\mathcal {E}}=\tilde{\mathbf {Q}}(\mathcal {S}^2)\approx \mathbf {Q}(\mathcal {S}^2)\) is an ellipsoid, then \(\tilde{\mathbf {Q}}\) must be simply a linear function in \(\mathbf {w}\) in the form
where \(\hat{\varvec{\Pi }}\) is a \(3\times 3\) matrix.
The ellipsoidal approximation (35) can be considered as the leading term of a harmonic expansion of the function \(\mathbf {Q}(\mathbf {w})\) on the unit sphere, which is the higher-dimensional extension of the harmonic Fourier expansion on a unit circle. Such expansion would be achieved by using the Laplace spherical harmonics (see Brechbühler et al. 1995 and Arfken et al. 2013), which leads to higher-order terms of \(\mathbf {w}\) in (35). (Note that this is not a Taylor expansion because \(\mathbf {w}\) is located on the unit sphere, and it cannot have the value \(\mathbf {0}\).) In this paper, we focus on the first-order approximation (35) by an ellipsoid.
Note than in Howe and Cutkosky (1996) and (Arkadani et al. 2020), a similar ellipsoidal approximation of the surface \(\mathcal {E}\) is proposed. Those authors take a different approach: \(\mathcal {E}\) is generated as the boundary of the set of admissible static contact forces, and it is called limit surface (Goyal et al. 1991a). The relation between \(\mathbf {Q}\) and the corresponding slipping direction \(\mathbf {w}\) is established via an orthogonality assumption \(\mathbf {Q}^\top (\mathbf {w})\mathbf {w}=0\). Those authors also approximate \(\mathcal {E}\) by an ellipsoid; nevertheless, their orthogonality condition is not consistent with (35), and hence, our model and the model of Howe and Cutkosky (1996) and Arkadani et al. (2020) are not equivalent.
4.2 Fitting the Ellipsoid to Special Motions
There are several possibilities to fit the ellipsoidal approximation (35) onto the exact results (16)–(17). One possibility is to perform a proper harmonic expansion on the sphere and take the leading term. A second possibility would be to calculate (16) numerically at a sufficient number of points \(\mathbf {w}\in \mathcal {S}^2\), and the matrix \(\hat{\varvec{\Pi }}\) would be determined by, for example, the method of least squares. We follow a third way: we select those three special motions for which only one component of \(\mathbf {w}\) is nonzero and choose \(\hat{\varvec{\Pi }}\) to give exact results for these motions.
Let us first define the following integrals, which are used in the expressions below:
Note the connection with (3). The elements of \(\hat{\varvec{\Pi }}\) can be found by calculating the images of three linearly independent elements in \(\mathbb {R}^3\) corresponding to the special motions. In these cases, (16) leads to simple integrals expressed in terms of the quantities (36):
-
When \(u_y=\omega _z=0\), the reference point is moving into the x direction with a velocity \(u_x\) and the body is not rotating in the normal direction z. Then, we get \(\mathbf {x}_\mathrm {o}=(u_x,0,0)\), which leads to \(\Vert \mathbf {x}_\mathrm {o}\Vert =|u_x|\), \(w_1=u_x/|u_x|\), and \(\mathbf {w}=(w_1,0,0)\). By substituting these into (16), we get
$$\begin{aligned} P_x=-\mu P_zw_1,&P_y=0,&T_z=\mu P_z \pi _y w_1. \end{aligned}$$(37) -
When \(u_x=\omega _z=0\), the reference point is moving into the y direction with a velocity \(u_y\) and the body is not rotating in the normal direction z. Then, we get \(\mathbf {x}_\mathrm {o}=(0,u_y,0)\), which leads to \(\Vert \mathbf {x}_\mathrm {o}\Vert =|u_y|\), \(w_2=u_y/|u_y|\), and \(\mathbf {w}=(0,w_2,0)\). By substituting these into (16), we get
$$\begin{aligned} P_x=0,&P_y=-\mu P_z w_2,&T_z=-\mu P_z\pi _xw_2. \end{aligned}$$(38) -
When \(u_x=u_y=0\), the reference point is not moving but the body is rotating with an angular velocity \(\omega _z\). Then, we get \(\mathbf {x}_\mathrm {o}=(0,0,\rho \omega _z)\), which leads to \(\Vert \mathbf {x}_\mathrm {o}\Vert =\rho |\omega _z|\), \(w_3=\omega _z/|\omega _z|\), and \(\mathbf {w}=(0,0,w_3)\). By substituting these into (16), we get
$$\begin{aligned} P_x=\mu P_z \pi _{y0} w_3&P_y=-\mu P_z \pi _{x0} w_3&T_z=-\mu P_z \pi _{xy} w_3 \end{aligned}$$(39)
By comparing (35) with (37)–(39), the matrix \(\hat{\varvec{\Pi }}\) becomes:
where \(\varvec{\Pi }=\hat{\varvec{\Pi }}/(-\mu P_z)\). That is, we determined the matrix \(\hat{\varvec{\Pi }}\) in such a way that the ellipsoidal approximate model (35) provides an accurate result for the integrals (16) in the case of special motions described above.
4.3 The Proposed General Ellipsoidal Model
From (35), (40) and (36), the ellipsoidal approximation of the set of friction forces leads to the model
The components of (41) are given by:
If the region A and the pressure distribution p(x, y) do not change in time with respect to the co-moving coordinate system, then the elements of \(\varvec{\Pi }\) are parameters that can be calculated from different moments and averages (36) of the normal pressure distribution p(x, y). When the pressure distribution p(x, y) depends on other state variables of the system, then the elements of \(\varvec{\Pi }\) will change in time (see Sect. 5).
The resultant effect of the friction forces (16) is independent of the choice of the reference point O. However, the physical meaning of trivial motions \(\mathbf {x}_\mathrm {o}=(u_x,0,0)\) and \(\mathbf {x}_\mathrm {o}=(0,u_y,0)\), which are used for the fitting the ellipsoidal model (42), is changing with O. That is, the change of the reference point O modifies the ellipsoidal model (see the example in Sect. 4.5.5).
The components (42) are discontinuous at \(u_x=u_y=\omega _z\). That is, the application of this model in mechanical systems creates a codimension-3 discontinuity in the vector field (see Sect. 3).
4.4 Special Cases
Let us consider some important special cases of the ellipsoidal model:
-
If the region A is symmetric with respect to the reference point and \(p(-x,-y)=p(x,y)\), then, according to (36), \(\pi _x=\pi _y=\pi _{x0}=\pi _{y0}=0\). Thus, \(\varvec{\Pi }\) becomes diagonal and (42) leads to
$$\begin{aligned} \begin{aligned} P_x&=-\mu P_z w_1=-\mu P_z\frac{u_x}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ P_y&=-\mu P_z w_2=-\mu P_z\frac{u_y}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ T_z&=-\mu P_z \pi _{xy}w_3=-\mu P_z\frac{\pi _{xy}\rho \omega _z}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}. \end{aligned} \end{aligned}$$(43) -
The single-point contact is obtained as a limit case when A is very small; then, \(\rho \rightarrow 0\) and \(\pi _{xy}\rightarrow 0\). As the tiny contact region can be considered symmetric, (43) simplifies to
$$\begin{aligned} \begin{aligned} P_x&=-\mu P_z w_1=-\mu P_z\frac{u_x}{\sqrt{u_x^2+u_y^2}}, \\ P_y&=-\mu P_z w_2=-\mu P_z\frac{u_y}{\sqrt{u_x^2+u_y^2}}, \\ T_z&=0. \end{aligned} \end{aligned}$$(44)This contact model excludes the effect of drilling friction, and it leads to a codimension-2 discontinuity analysed in Antali and Stepan (2018, 2019).
-
When the pressure distribution p(x, y) does not change in time, it is useful to choose the reference point O and the coordinate directions x and y appropriately to make the form of \(\varvec{\Pi }\) as simple as possible. Assume now an initial choice of O for which \(\varvec{\Pi }\) has the general form (40). By a translation of O in the contact region, we can find a unique point when the resultant torques (3) vanish, and then, we get \(\pi _x=\pi _y=0\) [see (36)]. Then, by an appropriate rotation of the coordinate axes x and y, we can eliminate \(\pi _{x0}\) (or, alternatively \(\pi _{y0}\)). Finally, we get the model in the form
$$\begin{aligned} \begin{aligned} P_x&=-\mu P_z(w_1-\pi _{y0}w_3)=-\mu P_z\frac{u_x-\pi _{y0}\rho \omega _z}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ P_y&=-\mu P_z w_2=-\mu P_z\frac{u_y}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}, \\ T_z&=-\mu P_z \pi _{xy} w_3=-\mu P_z\frac{\pi _{xy}\rho \omega _z}{\sqrt{u_x^2+u_y^2+\rho ^2\omega _z^2}}. \end{aligned} \end{aligned}$$(45)
4.5 Case Studies
In this subsection, we calculate the ellipsoidal approximate model for some simple geometries and pressure distributions, where we can find analytical reference solutions for comparison.
4.5.1 The General Axisymmetric Case
Consider a circular contact region with a radius R with an axisymmetric pressure distribution \(p(x,y)=\tilde{p}(\sqrt{x^2+y^2})\). Assume that the reference point O is located in the centre of the circle. It can be shown from axisymmetric properties of the contact region and pressure distribution that in this special case, (16) can be written in the form
where \(\mathcal {P}\) and \(\mathcal {T}\) are \(2\pi \) periodic functions; \(\mathcal {P}_{w}\) and \(\mathcal {T}_{w}\) are scalar functions over the respective intervals (0, 1) and \((-1,1)\). From (11) and (36), the parameters \(\rho \) and \(\pi _{xy}\) are given by
Note that from transformation (15), the functions defined in (46) satisfy
In the literature, a further parametrization can be found (see, e.g., Leine and Glocker 2003; Farkas et al. 2003; Weidman and Malhotra 2005). Let \(\epsilon \) be a dimensionless ratio between the variables defined by
and consider the re-parametrized function \(\mathcal {P}_\epsilon (\epsilon )\) and \(\mathcal {T}_\epsilon (\epsilon )\) defined by
4.5.2 Circular Contact with Constant Pressure Distribution
Consider the uniform pressure distribution \(p(x,y)=\tilde{p}(\sqrt{x^2+y^2})\equiv P_z/(R^2\pi )\), which is a special case of (46). Then, (47)–(48) gives \(\rho =\pi _{xy}=2R/3\). The two parameters are equal due to the constant pressure distribution [compare (11) and (36)].
In Farkas et al. (2003), Weidman and Malhotra (2005), we can find the analytical formulae of (46) for the uniform pressure distribution. According to Weidman and Malhotra (2005), the functions \(\mathcal {P}_\epsilon (\epsilon )\) are given by:
where E(m) and K(m) are the incomplete elliptic integrals expressed by the elliptic parameter m (see Abramowitz and Stegun 1972, p. 589 or Oldham et al. 2009, p. 637). (Note that the elliptic integrals can be also defined by elliptic modulus \(\sqrt{m}\) in the form \(\bar{E}(\sqrt{m})=E(m)\)Abramowitz and Stegun 1972; Oldham et al. 2009, which parametrization in used, e.g., in Farkas et al. (2003).) The sections of the piecewise defined functions (52)–(53) are smoothly connected at \(\epsilon =1\), and each can be expressed by a single formula containing incomplete elliptic integrals (Weidman and Malhotra 2005).
Having this reference analytical solution, let us apply the approximate model in (41). From the symmetry of the problem with respect to the reference point, the conditions of (43) are satisfied. By comparing (46), (43), and (51), we get that the ellipsoidal approximation leads to
or, with the two types of parametrization from (46),
As \(\rho =\pi _{xy}\), the matrix \(\varvec{\Pi }\) from (40) becomes a unit matrix.
The dimensionless friction force (\(\mathcal {P}\)) and friction torque (\(\mathcal {T}\)) of a circular contact. On the three diagrams, the same quantities are shown by using different parametrizations (see (49) and (51) of the kinematic state. In each diagram, the dashed lines correspond to the exact solution of the constant pressure distribution [(52)–(53)]; the dotted lines correspond to the exact solution of the parabolic pressure distribution [(58)–(59)]; and the continuous lines correspond to the ellipsoidal approximation for both distributions [(54)–(56)]
The possible friction force and torque values at a circular contact. The diagrams are composed of the curves of Fig. 3. Due to the fitting method, the ellipsoidal approximation is accurate at pure translational and rotational motions with respect to the reference point. Left panel: the dimensionless friction force and torque values. We can see that these graphs for the constant and parabolic distributions are almost identical. Right panel: graph the friction force and torque components of the constant distribution, which we can call friction ball (Leine and Glocker 2003). The friction balls (exact and approximated) for the parabolic distribution have a very similar shape, but the axis of the ellipsoid in the direction of \(T_z\) is somewhat smaller (the value of \(\pi _{xy}\) is different)
The exact solution (52)–(53) and its ellipsoidal approximation (54)–(56) can be seen in Figs. 3 and 4. On the diagrams, we observe that the ellipsoidal model provides an acceptable approximation with a very simple algebraic formula, which is useful in dynamical calculations, for example, presented in Sect. 5.
4.5.3 Circular Contact with Parabolic Pressure Distribution
Consider the parabolic pressure distribution
for which (48) leads to \(\pi _{xy}=3\pi r/16\).
Based on Leine and Glocker (2003), the analytical solution to the problem is
When calculating the approximate solution (41), we get the same results as (54)–(56). It is not surprising as the exact dimensionless functions for constant and parabolic pressure distributions are close to each other (see Fig. 3).
4.5.4 Long, Thin Rectangular Contact
Consider a thin rectangular contact region \(A=[-L/2,L/2]\times [-\delta ,\delta ]\) with \(\delta /L\ll 1\) with a constant pressure distribution \(p(x,y)=P_z/(\delta L)\) (see Fig. 6). In the limit case \(\delta /L\rightarrow 0\), the integration in (16) leads to a single-variable integral. Then, the friction forces in (16) become
The integrals (60) have lengthy closed forms containing square root and area hyperbolic sine functions. As we did in (46), let us define the dimensionless friction force \(\mathcal {P}\) and friction torque \(\mathcal {T}\),
which quantities now depend on the angle \(\phi \) due to the anisotropic geometry of the contact region [see (14)–(15)]. In the two special cases when the velocity of the reference point is parallel (\(\phi =0\)) or perpendicular (\(\phi =\pi /2\)) to the x axis, we get simple analytical results from (60)–(61):
where \(\gamma =2\tan \theta \).
Let us calculate the ellipsoidal approximation according to (41). From (11), we get
and because of the uniform pressure distribution, (36) gives the same value for \(\pi _{xy}=L/4\). Then, matrix \(\varvec{\Pi }\) in (40) becomes a unit matrix, and the approximate model is given by (43) with the substitution \(\rho =\pi _{xy}=L/4\).
The results can be seen in Fig. 5. The exact friction law is anisotropic, and thus, the functions \(\mathcal {P}\) and \(\mathcal {T}\) depend on the angle \(\phi \), as well. However, the ellipsoidal model behaves isotropically here and gives the same approximation for each direction. The rectangle is assumed to be very thin (\(\delta \ll L\)), which tends to the case of line contact. Even in this singular case, the approximation is acceptable at \(\phi =0\); the error becomes significant at \(\phi =\pi /2\).
Friction force and torque of a thin rectangular contact. Left panel: the dimensionless force (\(\mathcal {P}\)) and torque (\(\mathcal {T}\)) depending on the parameter \(\theta \) [see (14)–(15)]. The exact solution is shown at \(\phi =0\) (dashed lines) and at \(\phi =\pi /2\) (dotted lines). The ellipsoidal approximation is denoted by continuous lines. Right panel: the dimensionless friction force and torque values
4.5.5 Long, Thin Rectangular Contact—Change of the Reference Point
Let us check the effect of the choice of the reference point O on the previous example. Let us consider the new reference point \(O'\) at \(x=L/8\) (see Fig. 6). The corresponding coordinate axes are \(x'\) and \(y'\), and the quantities with respect to \(O'\) are denoted by \(\mathbf {Q}'\), \(\mathbf {w}'\) and \(\varvec{\Pi }'\). Then, the form of the ellipsoidal model becomes
Dimensionless forces (\(\mathcal {P}_x,\mathcal {P}_y\)) and torque (\(\mathcal {T}_z\)) of a circular contact with linear pressure distribution. In each diagram, the solid lines denote the ellipsoidal approximation, and the dashed lines correspond to the numerically computed exact solution. Left panel: solutions for \(c_x=c_y=0\), which coincides with the constant pressure (see Fig. 3). Middle panel: solutions for \(c_x=p_0/R\) and \(c_y=0\), where the cross-directional force appears. Right panel: solutions for \(c_x=0\) and \(c_y=p_0/R\), where the characteristic curves are no more symmetric to the kinematic state \(\theta =0\). All diagrams are computed for \(\phi =0\) without loss of generality because of the circular symmetry of the geometry
By using the reduction formula of velocities and moments of rigid bodies, the relationship between the two sets of variables becomes
Then, (65) becomes
By calculating the components of the approximate model (40) at \(O'\), we get
Thus, although we transformed back the ellipsoidal model to the reference point O, the transformed model \(\mathbf {W}^\top \varvec{\Pi }'\mathbf {W}\) still slightly deviates from the unit matrix \(\varvec{\Pi }\) obtained in the previous case. This example demonstrates that the choice of the reference point modifies the fitting of the ellipsoidal approximate model.
4.5.6 Circular Contact with Linear Pressure Distribution
Consider now a circular contact region of radius R with a linear pressure distribution in the form
Then, from (2), we get
Compared to the previous examples, this pressure distribution has fewer symmetries, making both the exact and the approximate solution more irregular.
From the resulting friction force components (16), let us define the dimensionless friction components \(\mathcal {P}_x,\mathcal {P}_y,\mathcal {T}_z\) by
which are now available only from numerical computation.
In the ellipsoidal model, the integrals (36) can be calculated by using polar coordinates,
and the matrix from (40) becomes
Now, the matrix \(\varvec{\Pi }\) becomes nondiagonal; that is, the friction force characteristic is anisotropic.
The comparison of the ellipsoidal model and the numerically computed exact solution can be seen in Fig. 7. We can see that in several different cases, the ellipsoidal model provides an approximation that captures the qualitative behaviour of the friction forces.
5 Dynamic Equations of a Rigid Body in Conforming Contact with a Plane
Now, we demonstrate the application of the mathematical tools of Sect. 3 to the approximate model presented in Sect. 4.
In this section, we consider the case of plane contact from Sect. 2 when one of the objects is a fixed plane, and a flat face of a moving body is in conformal contact with this plane. In this section, the word body refers to the moving body.
5.1 Notation
Recall that the angular velocity of the body is \(\varvec{\omega }=\omega _z\mathbf {k}\) and the velocity of the reference point is \(\mathbf {v}_o=u_x\mathbf {i}+u_y\mathbf {j}\). Thus, the velocity state of the body is fully determined by the three variables \(u_x,u_y\) and \(\omega _z\).
Assume that the planar frictional contact is the only nonsmooth effect in the dynamics of the rigid body. Then, we expect that the state space of the body has the form (21), where \(\mathbf {x}_\mathrm {o}=(u_x,u_y,\rho \omega _z)\) [see (10)], and \(\mathbf {x}_t\) contains the other state variables, which has smooth effect on the dynamics. In the simplest case, \(\mathbf {x}_t\) contains the three generalized coordinates describing the configuration of the body.
Our goal is to obtain a set of first-order differential equations for \(\mathbf {x}_\mathrm {o}\) in the form
which is the basis of the analysis presented in Sect. 3. Then, it is useful to transform kinematic quantities with respect to the centre of gravity C of the body. Let the location of point C be \(\mathbf {r}_{c}=x_C\mathbf {i}+y_C\mathbf {j}+z_C\mathbf {k}\), where \(x_C,y_C,z_C\) are parameters because O, C, and the coordinate system are all fixed to the body. The velocity of C is given by:
Then, the velocity state of the rigid body can also be determined by
From (75), the relation between (76) and (10) becomes
where the transformation matrix \(\mathbf {W}\) is given by
It is assumed that an external force system is acting on the body whose resultant in O is described by the concentrated force and torque
respectively, which are assumed to depend smoothly on the variables \(\mathbf {x}_\mathrm {o}\) and \(\mathbf {x}_t\).
In addition to that, the body is subject to normal and frictional forces as described in Sect. 2. The resultant force and torque of the friction forces at the reference point O are given by \(\mathbf {P}=(P_x,P_y,P_z)\) and \(\mathbf {T}=(T_x,T_y,T_z)\), respectively.
5.2 Newton–Euler Equations of Motion
The angular momentum of the body with respect to the centre of gravity C can be written in the form:
where \(J_{xz}\), \(J_{yz}\) and \(J_{z}\) are the corresponding components of the mass moment inertia matrix of the body with respect to the point C. Note that the axes x, y, z are fixed to the body. The Newton–Euler equations of the body become
where m is the mass of the body.
The six scalar equations corresponding to (81) are
where the terms \(\omega _zv_{cy}\), \(\omega _zv_{cy}\), \(J_{yz}\omega _z^2\), \(J_{xz}\omega _z^2\) account for the rotating coordinate axes \(\mathbf {i}\), \(\mathbf {j}\) having the time derivatives \(\dot{\mathbf {i}}=\varvec{\omega }\times \mathbf {i}\) and \(\dot{\mathbf {j}}=\varvec{\omega }\times \mathbf {j}\).
5.3 Transformation of Variables
In matrix form, (82), (83), and (87) can be written as:
where
and \(\mathbf {W}\) is given by (78), and \(\mathbf {Q}=(P_x,P_y,T_z/\rho )\) was defined in (17). Now, we express the equation (88) in the variable \(\mathbf {x}_\mathrm {o}\). Let us multiply (88) by \(\mathbf {W}^\top \) from the left and substitute (77) to the equation:
Let \(\kappa \) denote the radius of gyration defined by \(J_z=m\kappa ^2\). Then, we can define the mass matrix
and the gyroscopic matrix
whereby (84) becomes
However, (93) is still not fully defined because we have to calculate the vector \(\mathbf {Q}\) of friction force components.
5.4 Calculation of the Contact Forces
In the ellipsoidal model (41), we proposed the approximation \(\mathbf {Q}=-\mu P_z\varvec{\Pi }\mathbf {w}\) where \(\mathbf {w}=\mathbf {x}_\mathrm {o}/\left\Vert \mathbf {x}_\mathrm {o}\right\Vert \). For the calculation of the elements of the matrix \(\varvec{\Pi }\), we used the integrals (36) containing the pressure distribution p(x, y).
In Sect. 2, the pressure distribution p(x, y) was declared to be known. However, in the case of conformal surface contact between quasi-rigid bodies, p(x, y) is determined by microscopic deformations of the objects involved in the contact; moreover, it depends extremely sensitively on geometric imperfections of the surfaces (Huang et al. 2017). Hence, we need to find p(x, y) and the acceleration of the moving body simultaneously.
Obviously, this problem is not tractable within the context of rigid body dynamics. One possible approach is considering detailed models of the material behaviour and geometric imperfection. To avoid the complexity of this approach, we make additional assumptions about p.
According to (2)–(3), p(x, y) has to satisfy the conditions
where \(P_z,T_x,T_y\) are determined by constraints of the motion. In particular, \(P_z\) is given by (84) as
and the torque components can be obtained from combining (85)–(87):
where
and \(j_{yz}=J_{yz}/J_z\), \(j_{xz}=J_{xz}/J_z\) are the dimensionless nondiagonal components of the inertia tensor.
For now, we restrict the analysis to the limit case \(\mathbf {N}=\mathbf {0}\) of flat bodies when the point C lies in the contact region (\(z_c=0\)) and the nondiagonal components of the inertia tensor vanish (\(j_{xy}=j_{yz}=0\)).
If \(\mathbf {N}=\mathbf {0}\), then \(T_x,T_y\) can be directly expressed from (96), and thus, the conditions (94) allow to identify three parameters of p(x, y). For example, one may assume that p is linear as in (69). Then, the parameters \(p_0,c_x,c_y\) are given by (94), and thus, p(x, y) becomes completely determined. Finally, we can calculate the elements of \(\varvec{\Pi }\) from (36), and model (41) provides the friction forces for the differential equation for (93).
In the more general case with \(\mathbf {N}\ne \mathbf {0}\), further complications occur because (96) already contains \(\varvec{\Pi }\) and \(\mathbf {w}\). This situation is analysed later in Sect. 5.6.
5.5 Analysis of the Discontinuous Dynamics
By considering the friction model \(\mathbf {Q}=-\mu P\varvec{\Pi }\mathbf {w}\) from (41), the time derivative \(\dot{\mathbf {x}}_o\) can be expressed from (93) in the form:
where
and
Based on the previous assumptions, \(\mathbf {B}\) and \(\mathbf {c}\) depend smoothly on \(\mathbf {x}=(\mathbf {x}_\mathrm {o},\mathbf {x}_t)\). Based on the decomposition (21), Eq. (98) is complemented with the dynamics of the smooth variables in the form \(\dot{\mathbf {x}}_t=\mathbf {F}_t(\mathbf {x})\).
The resulting vector field \(\mathbf {F}=(\mathbf {F}_o, \mathbf {F}_t)\) gives a differential equation of form (19), and thus, the analysis and results from Sect. 3 are applicable to the system.
5.5.1 Radial and Circumferential Dynamics
The discontinuity of the system is located at \(\mathbf {x}_\mathrm {o}=\mathbf {0}\), that is, \(\mathbf {x}_\mathrm {o}\) is the orthogonal subspace of variables according to the separation in (21). Consider the spherical decomposition \(\mathbf {x}=(r,\mathbf {w},\mathbf {x}_t)\) from (22) with \(\mathbf {x}_\mathrm {o}=r\mathbf {w}\). By using (23), the orthogonal dynamics (98) can be decomposed to the radial dynamics
and the circumferential dynamics
where \(\mathbf {I}\) is the identity matrix.
5.5.2 Limit Directions
Let us choose a point \(\bar{\mathbf {x}}=(0,\mathbf {w},\mathbf {x}_t)\) of the discontinuity set \(\Sigma \), and let \( \bar{\mathbf {B}}=\mathbf {B}(\bar{\mathbf {x}})\), \(\bar{\mathbf {c}}=\mathbf {c}(\bar{\mathbf {x}})\). Then, according to (25), the local approximation of the dynamics at \(\mathbf {x}=\bar{\mathbf {x}}\) becomes
It can be seen from (104) that \(\mathbf {w}\) evolves on a fast time scale in the vicinity \(r=0\) of the discontinuity.
At \(r=0\), the fixed points of (104) are determined by \(\mathbf {V}^\star (\mathbf {w},\bar{\mathbf {x}}_t)=0\), which are the limit directions of the dynamics at \(\mathbf {x}_t\) (see Definition 1). To obtain information about these fixed points, consider
By comparing (98) and (105) in the case \(\mathbf {x}=\bar{\mathbf {x}}\) and \(\dot{\mathbf {w}}=\mathbf {0}\), we get
The solution of equation (106) are pairs \((\mathbf {w}_i,\dot{r}_i)\), where \(\mathbf {w}_i\dots \mathbf {w}_k\) are the limit directions and \(\dot{r}_i\dots \dot{r}_k\) are the rate of evolution of the radial dynamics along the limit directions. From (106), we can draw consequences about the number of the limit directions.
5.5.3 Limit Directions Without External Accelerating Forces
Consider first the special case of \(\bar{\mathbf {c}}=\mathbf {0}\). As the gyroscopic matrix \(\mathbf {G}\) vanishes at \(r=0\) (\(\omega _z=0\)), the case \(\bar{\mathbf {c}}=\mathbf {0}\) is equivalent to \(\mathbf {Q}_e=0\), that is, there are no ”accelerating components” of the external forces. The other external force components \(P_{ez},T_{ex},T_{ey}\) can be nonzero, which affect the dynamics through modifying the pressure distribution.
If \(\bar{\mathbf {c}}=\mathbf {0}\), then (106) becomes
which is the eigenvalue–eigenvector problem of \(\bar{\mathbf {B}}\) leading to the following statement:
Proposition 1
Let \(\lambda \in \mathbb {R}\) be a real eigenvalue of \(\bar{\mathbf {B}}\) and let \(\varvec{\gamma }\) be an associated eigenvector satisfying \(\left( \lambda \mathbf {I}-\bar{\mathbf {B}}\right) \varvec{\gamma }=\mathbf {0}\). Then, the eigenvector determines \(\mathbf {w}=\pm \left\Vert \varvec{\gamma }\right\Vert ^{-1}\varvec{\gamma }\), which are two fixed points of (104) in the special case \(\bar{\mathbf {c}}=\mathbf {0}\). That is, in the number of limit directions is twice the number of the real eigenvectors of \(\bar{\mathbf {B}}\).
By direct calculation from (99), we can find one of the eigenvalues:
Proposition 2
\(\lambda _1=-\mu P/m\) is an eigenvalue of \(\bar{\mathbf {B}}\) and \(\varvec{\gamma }_1=(\pi _{x}-x_c,\pi _{y}-y_c,0)^\top \) is an associated eigenvector unless \(\pi _x-x_c=\pi _y-y_c=0\). Thus, the system has at least two limit directions \(\mathbf {w}_1=\left\Vert \varvec{\gamma }_1\right\Vert ^{-1}\varvec{\gamma }_1\) and \(\mathbf {w}_2=-\mathbf {w}_1\), and the corresponding rate of radial dynamics is \(\dot{r}_1=\dot{r}_2=-\mu P/m\).
Although the other two eigenvalues of \(\bar{\mathbf {B}}\) can be expressed explicitly, they are lengthy algebraic expressions, and it cannot be checked directly whether they are real or not. However, from the physical behaviour of the friction law, we expect that all three eigenvalues of \(\bar{\mathbf {B}}\) are real. Therefore, our conjecture is that in general, the body without external forces \(\mathbf {Q}_e\) has six limit directions.
Let us consider a singular case that was excluded from Proposition 2.
Proposition 3
Assume that \(\pi _x-x_c=\pi _y-y_c=0\). Then, \(\lambda _1=\lambda _2=-\mu P/m\) is a double eigenvalue of \(\bar{\mathbf {B}}\) with the eigenvectors \(\varvec{\gamma }_1=(1,0,0)\) and \(\varvec{\gamma }_2=(0,1,0)\). Then, \(\cos \phi \varvec{\gamma }_1+\sin \phi \varvec{\gamma }_2\) is also an eigenvector for all \(\phi \in [0,2\pi )\). That is, the system has continuously many limit directions in the form \(\mathbf {w}=(\cos \phi ,\sin \phi ,0)\).
5.5.4 Limit Directions with External Forces
In the general case when \(\mathbf {c}\ne \mathbf {0}\), (106) is a so-called inhomogeneous eigenvalue problem (Mattheij and Soderlind 1987) in the form
Assume that \(\dot{r}\) is not an eigenvalue of \(\bar{\mathbf {B}}\). Then, from (108), we can express
and we get the equation
From (109)–(110), we can reach some important conclusions:
Proposition 4
The system (104) has a maximum of six fixed points.
Proof
Equation (110) be rewritten into a 6\(^\text {th}\) degree polynomial in \(\dot{r}\). (Note that the inverse of a matrix can be expressed by the adjugate matrix and the determinant.) Consequently, it has maximum 6 real roots for \(\dot{r}\), and then, and the related fixed points \(\mathbf {w}\) are determined by (109). \(\square \)
Proposition 5
The system (104) has minimum two fixed points.
Proof
By varying \(\dot{r}\) along the set of real numbers, equation (109) generates a curve \(\mathbf {w}(\dot{r})\) in \(\mathbb {R}^3\). The condition \(\left\Vert \mathbf {w}\right\Vert =1\) determines that the solutions for \(\mathbf {w}\) are the intersection points with this curve with the unit sphere in \(\mathbb {R}^3\). Note that at \(\dot{r}\rightarrow \pm \infty \), equation (109) leads to \(\left\Vert \mathbf {w}\right\Vert \rightarrow 0\). Moreover, we know from Proposition 2 that \(\lambda _1=-\mu P/m\) is a real eigenvalue of \(\bar{\mathbf {B}}\). That is \(\dot{r}\rightarrow \lambda _1\) makes \(\left\Vert \mathbf {w}\right\Vert \rightarrow \infty \). Due to the continuity properties of the operations in (109), there must be two roots \(\dot{r}_1\in (-\infty ,\lambda _1)\) and \(\dot{r}_2\in (\lambda _1,\infty )\) such that \(\mathbf {w}(\dot{r}_1)\), \(\mathbf {w}(\dot{r}_2)\) satisfy \(\left\Vert \mathbf {w}\right\Vert =1\). \(\square \)
Note that in (109)–(110), we explicitly assumed that \(\dot{r}\) cannot be an eigenvalue of \(\bar{\mathbf {B}}\). We can use the following result from (Mattheij and Soderlind 1987), which includes these degenerate cases, as well.
Proposition 6
Consider the inhomogeneous eigenvalue problem (108) where \(\bar{\mathbf {B}}\) has at least one real eigenvalue. For the number k of the real solutions \(\dot{r}\in \mathbb {R}\) and \(\mathbf {w}\in \mathbb {R}^3\) (multiplicity counted), we have \(k=2\), \(k=4\) or \(k=6\).
Proof
Special case of Theorem 29 by Mattheij and Söderlind (Mattheij and Soderlind 1987). \(\square \)
It can also be found in Mattheij and Soderlind (1987) that for the real solutions, (108) can be transformed into
which is a usual eigenvalue–eigenvector problem in \(\mathbb {R}^6\) for the eigenvalues \(\dot{r}\) and eigenvectors \((\mathbf {w},\dot{r}\mathbf {w})\).
5.6 Case of Bodies with Significant Height
In Sect. 5.5, we assumed that the matrix \(\mathbf {N}\) vanishes in (96), which occurs when the height of the centre of gravity is negligible (\(z_c=0\)), and z is a principal axis of the inertia tensor (\(j_{xz}=j_{yz}=0\)).
If these conditions are not satisfied, then \(\mathbf {N}\ne \mathbf {0}\). Then, Eq. (96) cannot be used directly to express \(T_x\) and \(T_y\) because the matrix \(\varvec{\Pi }\) depends on the pressure distribution p(x, y) , which should be calculated from \(T_x\) and \(T_y\). Therefore, there is feedback from the dynamical equations, which makes the previous direct calculation impossible.
However, the problem can be resolved if we consider the assumed form (69) of the pressure distribution containing the parameters. In this case or for any other pressure distribution containing three parameters as linear coefficients, we can choose these three parameters as unknowns. Let us substitute (69) into the integrals in (36) and (94). Then, the parts of the integrals \(P_z,T_x,T_z\), and \(\varvec{\Pi }\) can be computed purely from the geometry of the contact region A, and the parameters \(p_0,c_x,c_y\) appear as unknown coefficients. Then, by substituting \(P_z,T_x,T_z\), and \(\varvec{\Pi }\) into (95)–(96), we get a set of three linear equations, which can be solved for the parameters \(p_0,c_x,c_y\).
Moreover, this solution depends on the slipping direction \(\mathbf {w}\), as well. Thus, we get solutions in the form \(p_0(\mathbf {w}),c_x(\mathbf {w}),c_y(\mathbf {w})\). Consequently, this case leads to a friction model in the form
This expression introduces nonlinearity in \(\mathbf {w}\) into the dynamics (98). Then, the results in Sect. 5.5 cannot be applied directly. However, we demonstrate in the example in Sect. 6.2 that several details can be explored about the limit directions even in this case.
6 Examples
In the previous section, we surveyed several cases of finding the limit directions of a moving body in planar contact with a plane. These limit directions express the specific directions where transitions can occur between the slipping and sticking states of the moving body. In what follows, we demonstrate the results on mechanical examples.
6.1 Thin Disk on a Flat Surface with an In-plane Loading Force
Consider a flat, circular disk of radius R with mass m and homogeneous mass density, implying radius of gyration \(\kappa =R/\sqrt{2}\), and \(J_{xz}=J_{yz}=0\). The disk moves on a horizontal plane, and the (vertical) gravitational acceleration is g (see the left panel of Fig. 8). The height of the disk is assumed to be much smaller than the radius, and the reference point is the midpoint of the base facet, that is, \(\mathbf {r}_c=\mathbf {0}\). An in-plane constant loading force is acting at the centre of gravity C of the disk; this force has a constant value F and a constant direction of the fixed plane. Then, the resultant of the external forces is \(\mathbf {P}_e=(F\cos \psi ,F\sin \psi ,-mg)\), \(\mathbf {T}_e=\mathbf {0}\), where \(\psi \) denotes the orientation of the disk on the plane with \(\dot{\psi }=\omega _z\). (Note that the coordinate system is fixed to the disk.) Then, (89)–(92) imply
From (84)–(86), the resultant of the normal contact forces becomes \(P_z=mg\), \(T_x=T_y=0\). We expect that the pressure distribution is constant with \(p(x,y)=p_0=mg/(R^2\pi )\). [This can be obtained by direct calculation of (69), as well.] From Sect. 4.5.2, the uniform pressure distribution implies that \(\varvec{\Pi }\) is a unit matrix.
Sketch of the examples analysed in Sect. 6. Left panel: thin disk on a flat surface with an in-plane loading force (see Sect. 6.1). Middle panel: thick disk on a flat surface with and in-plane loading force (see Sect. 6.2). Right panel: thin disk on a flat surface with an in-plane loading force and in-plane torque (see Sect. 6.3)
In addition to the orthogonal variables \(\mathbf {x}_\mathrm {o}=(u_x,u_y,\rho \omega _z)\), the only other state variable in the expressions is the orientation \(\psi \) of the disk, that is, \(\mathbf {x}_t=(\psi )\). As the problem is symmetric with respect to the rotation about the z axis, the dynamics is practically identical to any \(\psi \in [0,2\pi )\). Without loss of generality, we can take \(\psi =0\) and \(\bar{\mathbf {x}}_t=(0)\). Then, direct calculation of (98)–(105) yields:
By substituting (114) into (103)–(104), the radial and circumferential dynamics becomes

respectively.
The condition (106) of limit directions is recast as three scalar equations
In the nontrivial case \(F\ne 0\), we get two types of limit directions from the solution of (117):
-
There are two trivial limit directions
$$\begin{aligned} \mathbf {w}=\hat{\mathbf {w}}_{1,2}=(\pm 1,0,0)&\text {with}&\dot{r}=-\mu g \pm F/m. \end{aligned}$$(118)After computing the matrix (31), the eigenvalues with respect to the fast dynamics become \(\lambda =\mp F/m\) and \(\lambda =F/m \cdot (\mp 1+\mu m g/(9F))\)
-
There are two nontrivial limit directions
$$\begin{aligned} \mathbf {w}=\hat{\mathbf {w}}_{3,4}=\left( \frac{9F}{\mu m g},0,\pm \sqrt{1-\left( \frac{9F}{\mu m g}\right) ^2}\right)&\text {with}&\dot{r}=-\frac{8}{9}\mu g. \end{aligned}$$(119)where the eigenvalues of the fast dynamics are \(\lambda =-\mu g/9\) and \(\lambda =-\mu g/9\cdot (1-81F^2/(\mu ^2 m^2 g^2))\).
Sketch of the fast dynamics and limit directions on a unit sphere in the case of the thin disk with an in-plane loading force. Encircled numbers correspond to the three cases of behaviour identified in Sect. 6.1. The colour codes are the following: red and blue dots correspond to repelling and attracting behaviour, respectively. Red and blue arrows correspond to unstable and stable behaviour on the unit sphere, respectively. A limit direction is dominant if the colours of the dot and the corresponding arrows match, and otherwise, it is isolated (Color figure online)
Sketch of the fast dynamics and limit directions on the invariant circle in the case of the thin disk with an in-plane loading force. The invariant circle depicted to these sub-figures are denoted by green colour in Fig. 9. The circled numbers correspond to the three cases of behaviour identified in Sect. 6.1
The trivial limit directions \(\hat{\mathbf {w}}_1\) and \(\hat{\mathbf {w}}_2\) always exist, while the nontrivial \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\) exist for \(F<\mu m g/9\) only. Note that all limit directions are located on the circle \(w_2=0\) on the unit sphere (see Figs. 9, 10). Moreover, it can be seen from (116) that the circle \(w_2=0\) is an invariant set of the fast dynamics. Physically, \(\hat{\mathbf {w}}_1\) and \(\hat{\mathbf {w}}_2\) correspond to pure translational motions in the same direction (case of \(\hat{\mathbf {w}}_1\)) or the opposite direction of F (case of \(\hat{\mathbf {w}}_2\)). In contrast, \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\) are related to motions with a certain fixed ratio between the velocity \(u_x\) and the angular velocity \(\omega _z\). Consider the loading force \(F\in \mathbb {R}\) as a bifurcation parameter of the system. Then, according to the number and type of the limit directions, we can identify three structurally different regions:
Case 1 If \(|F|>\mu m g\), then there are two limit directions: \(\hat{\mathbf {w}}_1\) is repelling-isolated, \(\hat{\mathbf {w}}_2\) is attracting-isolated. As the only attracting limit direction \(\hat{\mathbf {w}}_2\) is isolated, there is a single trajectory characterized by \(u_x<0\) and \(u_y=\omega _z=0\), which reaches the discontinuity (the sticking state). Even in this case, the disk sticks for a moment and starts slipping immediately, prescribed by the repelling direction \(\hat{\mathbf {w}}_1\). All the other trajectories avoid the discontinuity, and thus, the sticking of the disk is practically unrealizable. The condition \(|F|>\mu m g\) of impossible sticking coincides with the trivial condition from elementary dynamics where only the velocity component \(u_x\) is considered without the transverse velocity or rotation. This case is depicted in the left sub-figures of Figs. 9 and 10.
Case 2 If \(\mu m g>|F|>\mu m g/9\), then there are two limit directions, \(\hat{\mathbf {w}}_1\) attracting-dominant, and \(\hat{\mathbf {w}}_2\) is attracting-isolated. As both limit directions are attracting, all nearby trajectories end at the discontinuity, and thus, sticking is a realizable long-term behaviour of the disk. A single trajectory exists—the same trajectory mentioned in the previous cases—which reaches the sticking state from the isolated direction \(\hat{\mathbf {w}}_2\). However, as \(\hat{\mathbf {w}}_1\) is a dominant limit direction, almost all trajectories approach the sticking state from this direction. Physically, it means that for almost all initial conditions of slipping, the disk reaches the sticking state in finite time, and just before sticking, the disk has a pure translational slipping with a positive velocity \(u_x\). This case is depicted in the middle sub-figures of Figs. 9 and 10.
Case 3 If \(\mu m g/9>|F|>0\), then there are four limit directions: \(\hat{\mathbf {w}}_1\) is attracting saddle type, \(\hat{\mathbf {w}}_2\) is attracting-isolated and \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\) are both attracting-dominant. The main difference from the previous case is that now, almost all trajectories tend to the discontinuity along \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\). On the unit sphere of the fast dynamics, the basins of attraction of these fixed points are separated by the ”equator” \(w_3=0\) of the unit sphere, which circle is an invariant set of the fast dynamics [see (116)]. Trajectories starting from this plane—without rotation—typically tend to the discontinuity along the saddle-type direction \(\hat{\mathbf {w}}_1\), except for the single trajectory of \(\hat{\mathbf {w}}_2\) mentioned before. However, the typical behaviour of the disk is reaching the sticking state along the nontrivial equilibria \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\). That is, just before coming to rest, the motion of the disk is a certain combination of simultaneous translational and rotational motion, where the ratio of the velocity \(u_x\) and the angular velocity \(\omega _z\) is prescribed by the limit directions in (119). This case is depicted in the right sub-figures of Figs. 9 and 10.
Bifurcation diagram of the limit directions when the loading force F is varied. The blue and red lines denote the attracting and repelling limit directions, respectively. The solid lines denote the dominant limit directions, while the dashed lines correspond to the isolated or saddle-type limit directions. The circled numbers of the regions correspond to Cases 1–3 identified in Sect. 6.3, and the corresponding phase portraits can be found in Figs. 9 and 10 (Color figure online)
In Magyari and Weidman (2001), a thin disk on a slope was analysed, which is analogous to the present example. The authors of Magyari and Weidman (2001) used a different approach analysing a reduced phase space implicitly assuming a zero transversal velocity \(u_y\), and the exact solution of the tangential force system was considered (see also Farkas et al. 2003; Weidman and Malhotra 2005). Our results about Cases 2 and 3 are consistent with the results of Magyari and Weidman (2001).
Let us take a look at the bifurcations occurring between the cases presented above (see Fig. 11). At \(|F|=\mu mg/9\), the trivial limit direction \(\hat{\mathbf {w}}_1\) interacts with the nontrivial ones \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\) in a way that we can call a pitchfork bifurcation of limit directions. At \(|F|=\mu mg\), neither the number, nor the fast eigenvalues of the limit direction change, but \(\hat{\mathbf {w}}_1\) turns from attracting into repelling.
A special degeneracy occurs at \(F=0\), which is the force-free motion of the disk on the plane. Then, (117) is satisfied by a continuous set of limit directions \(\hat{\mathbf {w}}_0(\zeta )=(\zeta ,\pm \sqrt{1-\zeta ^2},0)\) for any \(-1\le \zeta \le 1\) as well as the pair \(\hat{\mathbf {w}}_{3,4}=(0,0,\pm 1)\). The limit directions \(\hat{\mathbf {w}}_{3,4}=(0,0,\pm 1)\) are located at the ”north and south poles” of the unit sphere, corresponding to a pure rotational motion. These discrete limit directions are attracting-dominant, while the directions of the continuous set \(\hat{\mathbf {w}}_0(\zeta )\) are on the limit state between attracting-saddle and attracting-isolated. It can be shown that for initial conditions without rotation (\(\omega _z=0\)), the disk reaches the sticking state along one of these degenerate directions. Therefore, the model predicts that the typical behaviour of the force-free disc just before stopping is a pure rotational motion. However, this degenerate case is analysed in Farkas et al. (2003) with the exact contact forces, and it was found that the typical behaviour should be a combined motion with translational and rotational slipping (there, the \(\hat{\mathbf {w}}_{3,4}=(0,0,\pm 1)\) would not reach the ”poles” at \(F=0\)). This shows that for low values of F, higher-order terms of \(\mathbf {w}\), neglected in the ellipsoidal model (41), have a significant effect in this example.
6.2 Thick Disk on a Flat Surface with an In-plane Loading Force
Consider now an extension of the previous example, where the disk has a height 2h comparable to its radius R (see the middle panel of Fig. 8). Assume that the loading force acting at the centre of gravity, which is at the height \(z_c=h\) from the plane (uniform mass distribution is assumed). Then, \(\mathbf {r}_c=(0,0,h)\), and the external force system becomes \(\mathbf {P}_e=(F\cos \psi ,F\sin \psi ,-mg)\), \(\mathbf {T}_e=Fh(-\sin \psi ,\cos \psi ,0)\), where \(\psi \) is the orientation angle of the disk, again.
At \(\psi =0\), constraints (84)–(86) become
and from (36), we get
Then, (41), (70), (72), (120), and (121) form a system of 14 algebraic equations for the 14 variables \(P_x,P_y,P_z,T_x,T_y,T_z\) \(\pi _x,\pi _y,\pi _{x0},\pi _{y0}\) \(p_0,c_x,c_y\), which can be solved explicitly. For the parameters of the pressure distribution (69), we get \(p_0=mg/(R^2\pi )\),
where \(\eta =\mu h/R\) is the dimensionless height of the disk.
After sequential substitution into the system of equations above, condition (106) of limit directions in (117) now becomes
From (123), we can express
where \(\xi =F/(\mu g m)\) is the dimensionless force. By substituting (125) into the identity \(w_1^2+w_2^2+w_3^2=1\), we get an expression in the form
where the coefficients \(A_0\dots A_2\) depend on the dimensionless parameters \(\xi \) and \(\eta \). Expression (126) is a third-degree polynomial in \(w_3^2\), and we search for the nontrivial roots \(0<w_3^2<1\). We can investigate the roots by using the discriminant and Descartes’ Rule of Signs. Straightforward but lengthy calculations lead to the following result: Consider the critical value
of the loading force. In the case \(|F|>F_\text {crit}^{2/4}\), the polynomial (126) does not have a positive root. For \(0<|F|<F_\text {crit}^{2/4}\) (126) has a single positive root in the interval \(0<w_3^2<1\). Each root corresponds to two limit directions in the form \(\pm \sqrt{w_3^2}\).
Finally, the two types of limit directions are two trivial limit directions \(\mathbf {w}=\hat{\mathbf {w}}_{1,2}=(\pm 1,0,0)\) and two nontrivial limit directions nontrivial limit directions \(\mathbf {w}=\hat{\mathbf {w}}_{3,4}\) determined by (125). After checking the eigenvalues of the fast dynamics, we get similar cases of behaviour to those of the previous example:
Case 1 If \(|F|>\mu m g\), then there are two limit directions: \(\hat{\mathbf {w}}_1\) is repelling-isolated, \(\hat{\mathbf {w}}_2\) is attracting-isolated.
Case 2 If \(\mu m g>|F|>F_\text {crit}^{2/4}\), then there are two limit directions, \(\hat{\mathbf {w}}_1\) attracting-dominant, ans \(\hat{\mathbf {w}}_2\) is attracting-isolated.
Case 3 If \(F_\text {crit}^{2/4}>|F|>0\), then there are four limit directions: \(\hat{\mathbf {w}}_1\) is attracting-saddle type, \(\hat{\mathbf {w}}_2\) is attracting-isolated and \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\) are both attracting-dominant.
Thus, the dynamics of a thick disk is structurally similar to that of the thin disk. However, there are significant differences in Case 3 with relevant physical consequences:
-
In the limit case \(h/R\rightarrow 0\), formula (127) of the critical loading force gives the value previously determined to the thin disk. However, (127) shows a significant increase in the parameter value when we increase the height h. Thus, the thicker the disk is, the more typical it is that the motion will stop at the limit directions \(\hat{\mathbf {w}}_{3,4}\) corresponding to a combined translational—rotational motion.
-
In the case of the thin disk, the limit directions \(\hat{\mathbf {w}}_{3,4}\) are located on the invariant circle \(w_2=0\) (see the right panel of Fig. 9). Now, (125) shows that in general, these nontrivial limit directions move away from this circle, and the component \(w_2\ne 0\) grows with the increasing \(\eta =\mu h/R\). Therefore, at the stopping of the motion of the thick disk along the nontrivial limit directions \(\hat{\mathbf {w}}_{3,4}\), the velocity of the reference point is not parallel to the direction of the loading force, and the trajectory of the centre of the disk turns away from the direction of the loading force. This result is consistent with the heuristic estimation of Farkas et al. (2003) and with numerical results of Penner (2001).
The results are summarized in Fig. 12. We close the analysis of this example by checking whether the pressure distribution (69) gives a nonnegative pressure value at all points of the contact region. For the circular contact with this linear pressure distribution, the pressure is always nonnegative if \(p_0^2-R^2(c_x^2+c_y^2)\ge 0\). By direct calculation from (122), this is equivalent to \(160\eta ^2w_3^2-144\eta ^2+9\ge 0\). If it is satisfied for all \(0\le w_3\le 1\), we should prescribe \(\eta \le 1/4\). Therefore, the analysis is valid below a certain thickness given by \(\mu h/R<1/4\); otherwise, the assumption of the linear pressure distribution could give negative normal pressure at some points.
6.3 Thin Disk on a Flat Surface with an In-plane Loading Force and an In-plane Torque
Consider the problem of the thin disk again, but now, apply an additional torque T parallel to the loading force F. That is, the resultant of the external forces is \(\mathbf {P}_e=(F\cos \psi ,F\sin \psi ,-mg)\), \(\mathbf {T}_e=(T\cos \psi ,T\sin \psi ,0)\), where \(\psi \) denotes the orientation of the disk.
Left panel: Sketch of the fast dynamics and limit directions on a unit sphere in the case of the thick disk on a flat surface. Cases 1 and 2 are the same as those in the previous example (see Fig. 9). In Case 3, the attracting-dominant limit directions leave the circle \(w_2=0\), and the former invariant circle becomes a twisted invariant curve between the limit directions (denoted by the dashed green line). Physically this effect causes the rotating thick disk to stop slipping after turning away from the direction of the loading force by a certain angle (see the right panel). This angle can be read from the unit sphere of slipping directions (see the projected unit sphere in the middle panel) (Color figure online)
In this case, constraints (84)–(86) read as \(P_z=mg\), \(T_x=-T\cos \psi \), and \(T_y=-T\sin \psi \). At \(\psi =0\), (70), (72) and (121) imply \(p_0=mg/(R^2\pi )\); \(c_x=0\), and \(c_y=4T/(\pi R^4)\), and the matrix (73) becomes
By repeating the calculation done in (114)–(117), we get
Note, that the circle \(w_2=0\) is an invariant set, as it was in (117). From trying to solve (129), we get the following consequences:
-
It can be shown by direct calculation that on the invariant circle \(w_2=0\), the roots of (117) satisfy
$$\begin{aligned} (576\zeta ^2+1)w_3^4+432\xi \zeta w_3^3+(81\xi ^2-576\zeta ^2-1)w_3^2-216\xi \zeta w_3+144\zeta ^2=0, \end{aligned}$$(130)where \(\zeta =T/(mgR)\) is the dimensionless loading torque and \(\xi =F/(\mu mg)\) is the dimensionless friction force. In the special case \(\zeta =0\), (130) becomes \(w_3^2(w_3^2+81\xi ^2-1)=0\), which gives back the limit directions \(\hat{\mathbf {w}}_1\dots \hat{\mathbf {w}}_4\) we found in (118)–(119). In the general case \(\zeta \ne 0\), consider the critical force
$$\begin{aligned} F_\text {crit}^{2/4}=\mu m g \tilde{\xi }(\zeta ), \end{aligned}$$(131)where \(\xi =\tilde{\xi }(\zeta )\) makes the discriminant of (130) zero. It can be checked that (130) has four roots for \(|F|<F_\text {crit}^{2/4}\), and it has two roots for \(|F|>F_\text {crit}^{2/4}\).
-
It can be shown from direct calculation that the roots outside the \(w_2=0\) circle are
$$\begin{aligned} \hat{\mathbf {w}}_{5,6}=\left( \frac{\xi }{16\zeta ^2},\pm \sqrt{1-\left( \frac{\xi }{16\zeta ^2}\right) ^2-\left( \frac{3\xi }{4\zeta }\right) ^2},-\frac{3\xi }{4\zeta }\right) . \end{aligned}$$(132)These roots exist only if \(|F|<F_\text {crit}^{\,4/6}=16\zeta ^2/\sqrt{1+144\zeta ^2}\). It can be checked that \(F_\text {crit}^{\,4/6}<F_\text {crit}^{2/4}\).
-
The condition \(\mathbf {F}_o=\mathbf {0}\) shows the boundary case between the attracting and repelling limit directions (see Def. 1). By direct substitution, we get the critical force \(F_\text {crit}^{2/2}=1-2\zeta ^2\). It can be checked that at \(|F|=F_\text {crit}^{2/2}\), the limit direction \(\hat{\mathbf {w}}_1\) turns from attracting into repelling.
Left panel: sketch of the fast dynamics and limit directions on a unit sphere in the case of the thin disk with an in-plane loading force and an in-plane torque. Compared to the thin disk without the loading torque (see Fig. 9, a new, fourth scenario appears with six limit directions. Right panel: The four different dynamical cases depicted on the parameter space of the loading force and torque. On the coloured lines, bifurcations occur involving the limit directions (Color figure online)
After summarizing the results, we get the following structurally different regions:
Case 1 If \(|F|>F_\text {crit}^{2/2}\), we get a similar behaviour that of Case 1 in Sect. 6.1 without the loading torque.
Case 2 If \(F_\text {crit}^{2/2}>|F|>F_\text {crit}^{2/4}\), we get a similar behaviour that of Case 2 in Sect. 6.1 without the loading torque.
Case 3 If \(F_\text {crit}^{2/4}>|F|>F_\text {crit}^{4/6}\), we get a similar behaviour that of Case 3 in Sect. 6.1 without the loading torque.
Case 4 If \(F_\text {crit}^{4/6}>|F|>0\), we obtain a new type of behaviour, which was not present in the example without the loading torque. It can be checked that at \(|F|=F_\text {crit}^{\,4/6}\), the limit directions \(\hat{\mathbf {w}}_{5,6}\) are born from \(\hat{\mathbf {w}}_1\) through a pitchfork bifurcation. Thus, we get six limit directions: \(\hat{\mathbf {w}}_1\) and \(\hat{\mathbf {w}}_2\) are attracting-isolated, \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\) are attracting-dominant, \(\hat{\mathbf {w}}_5\) and \(\hat{\mathbf {w}}_6\) are attracting saddle-type. The fundamental qualitative behaviour does not change much compared to Case 3; the body typically stops slipping along the limit directions \(\hat{\mathbf {w}}_3\) and \(\hat{\mathbf {w}}_4\). However, the birth of the new two limit directions changes the structure of the fast dynamics around these special motions. The different regions in the parameter space can be seen in Fig. 13.
Finally, let us check the validity of the linear pressure distribution. As we showed in the previous example in Sect. 6.2, we can use the condition \(p_0^2-R^2(c_x^2+c_y^2)\ge 0\) to check whether the normal pressure is nonnegative everywhere in the contact region. In this example, this condition is equivalent to \(|\zeta |=|T|/(mgr)\le 1/4\).
7 Conclusion
We considered a finite planar contact region between two contacting bodies, where the (relative) velocity distribution in the contact region is assumed to be described by planar rigid body motion. By integrating the Coulomb friction model applied locally to the normal and tangential pressure distributions, the resultant force and torque components depend on three kinematic variables of the slip and spin motion in the contact region. When applied to problems with rigid body dynamics, the resultant friction force and torque characteristics lead to a codimension-3 discontinuity in the vector field of slipping, which discontinuity set corresponds to the case of static (sticking or rolling) contact. By utilizing recently developed mathematical tools, the dynamics of this vector field at the discontinuity was investigated by spherical decomposition of the variables and by using the blow-up method. It was shown that the resulting multiple time scale system can be decomposed into fast and slow dynamics at the discontinuity, which revealed the structure of transitions between slipping and sticking states. Although kinematically, the stick–slip transitions could occur in any direction, the fixed points of the fast subsystem generate specific limit directions, where the transitions are dynamically realized. By finding the number and type of limit directions, we can explore the typical types of behaviour of the contacting bodies.
We created an ellipsoidal approximate model in the space of frictional force and torque components. This leading-order approximation is realized as linear formulae in the fast variables containing the discontinuity. The model was compared with several analytical reference solutions for simple geometries. By applying the ellipsoidal friction model for rigid body dynamics of a flat body moving on a rough plane, we could prove that the number of limit directions is 2, 4 or 6 in the generic cases. The results were demonstrated through mechanical examples where the different types of behaviour were explored.
For further research work, it would be useful to select some special benchmark problems and create detailed numeric and experimental studies to check the analytical results. A further major goal would be to include the coupled discontinuous effect from the rolling resistance at nonconforming bodies.
Finally, the ellipsoidal model could be developed by adding nonlinear terms in order to improve the accuracy. Some examples showed that nonlinear terms can have a significant effect on the bifurcation scenarios. Therefore, appropriate forms of nonlinear extensions are indeed useful.
Data availability statement
The manuscript has no associated data.
References
Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions. U.S. GPO, Washington, DC (1972)
Antali, M., Stepan, G.: Sliding and crossing dynamics in extended Filippov systems. SIAM J. Appl. Dyn. Syst. 17(1), 823–858 (2018)
Antali, M., Stepan, G.: Nonsmooth analysis of three-dimensional slipping and rolling in the presence of dry friction. Nonlinear Dyn. 97(3), 1799–1817 (2019)
Antali, M., Stepan, G.: Slipping-rolling transitions of a body with two contact points. Nonlinear Dyn. online first, 1–18 (2021)
Arfken, G.B., Weber, H.J., Harris, F.E.: Mathematical Methods for Physicists, 7th edn. Academic Press, Cambridge (2013)
Arkadani, M.M.G., Bimbo, J., Prattichizzo, D.: Quasi-static analysis of planar sliding using friction patches. Int. J. Rob. Res. 39(14), 1775–1795 (2020)
Batlle, J.A.: The sliding velocity flow of rough collisions in multibody systems. J. Appl. Mech. 63(3), 804–809 (1996)
Borisov, V.A., Mamaev, S.I., Erdakova, N.: Dynamics of a body sliding on a rough plane and supported at three points. Theor. Appl. Mech. 43(2), 169–190 (2016)
Brechbühler, C., Gerig, G., Kübler, O.: Parametrization of closed surfaces for 3-d shape description. Comput. Vis. Image Und. 61(2), 154–170 (1995)
Cheesman, N., Kristiansen, K.U., Hogan, S.J.: Regularisation of isolated codimension-2 discontinuity sets. SIAM J. Appl. Dyn. Syst. 20(4), 2630–2670 (2021)
Dahmen, S.R., Farkas, Z., Hinrichsen, H., Wolf, D.: Macroscopic diagnostics of microscopic friction phenomena. Phys. Rev. E 71(6), 066602 (2005)
Dahmen, S.R., Hinrichsen, H., Lysov, A., Wolf, D.: Coupling between static friction force and torque for a tripod. J. Stat. Mech. 2005(03), P03004 (2005)
di Bernardo, M., Budd, C.J., Champneys, A.R., Kowalczyk, P.: Piecewise-smooth Dynamical Systems. Springer, London (2008)
Farkas, Z., Bartels, G., Unger, T., Wolf, D.E.: Frictional coupling between sliding and spinning motion. Phys. Rev. Lett. 90(24), 248302 (2003)
Goyal, S., Ruina, A., Papadopoulos, J.: Planar sliding with dry friction part 1. Limit surface and moment function. Wear 143(2), 307–330 (1991a)
Goyal, S., Ruina, A., Papadopoulos, J.: Planar sliding with dry friction part 2. Dynamics of motion. Wear 143(2), 331–352 (1991b)
Hammond, R.T.: Spin and translation, the equation of motion. Open Appl. Phys. J. 3, 6–9 (2010)
Howe, R.D., Cutkosky, M.R.: Practical force-motion models for sliding manipulation. Int. J. Rob. Res. 15(6), 557–572 (1996)
Huang, E., Bhatia, A., Boots, B., Mason, M.: Exact bounds on the contact driven motion of a sliding object, with applications to robotic pulling. In: Proceedings of Robotics: Science and Systems. Cambridge, Massachusetts (2017). https://doi.org/10.15607/RSS.2017.XIII.010
Jeffrey, M.R.: Hidden Dynamics. Springer, Cham (2018)
Johnson, K.L.: Contact Mechanics. Cambridge University Press, Cambridge (1985)
Kireenkov, A.A.: Combined model of sliding and rolling friction in dynamics of bodies on a rough plane. Mech. Solids 43(3), 412–425 (2002)
Kireenkov, A.A.: On the motion of a homogeneous rotating disk along a plane in the case of combined friction. Mech. Solids 37(1), 47–53 (2002)
Kireenkov, A.A.: Coupled dry friction models in problems of aviation pneumatics’ dynamics. Int. J. Mech. Sci. 127, 198–203 (2017)
Kudra, G., Awrejcewicz, J.: Tangens hyperbolicus approximations of the spatial model of friction coupled with rolling resistance. Int. J. Bifurcat. Chaos 21(10), 2905–2917 (2011)
Kudra, G., Awrejcewicz, J.: Bifurcational dynamics of a two-dimensional stick-slip system. Differ. Equ. Dyn. Sys. 20, 301–322 (2012)
Kuehn, C.: Multiple Time Scale Dynamics. Springer, Berlin (2015)
Leine, R.I., Glocker, C.: A set-valued force law for spatial Coulomb-Contensou friction. Eur. J. Mech. A 22(2), 193–216 (2003)
Leine, R.I., Nijmeijer, H.: Dynamics and Bifurcations of Non-Smooth Mechanical Systems. Springer, Berlin (2004)
Lopez, V.J., Llibre, J.: A topological characterization of the \(\omega \)-limit sets for analytic flows on the plane, the sphere and the projective plane. Adv. Math. 216(2), 677–710 (2007)
Magyari, E., Weidman, P.: Frictionally coupled sliding and spinning on an inclined plane. Physica D 413, 132647 (2001)
Marques, F., Flores, P., Claro, J.C.P., Lankarani, H.M.: A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 86(3), 1407–1443 (2016)
Mattheij, R.M.M., Soderlind, G.: On inhomogeneous eigenvalue problems. Linear Algebra Appl. 88–89, 507–531 (1987)
Oldham, K.B., Myland, J.C., Spanier, J.: An Atlas of Functions, 2nd edn. Springer, New York (2009)
Penner, A.R.: The physics of sliding cylinders and curling rocks. Am. J. Phys. 69(3), 332–339 (2001)
Varkonyi, P.L., Antali, M.: On differential equations with codimension-\(n\) discontinuity sets. J. Appl. Dyn. Syst. (2021). Accepted in publication
Walker, S.V., Leine, R.I.: Set-valued anisotropic dry friction laws: formulation, experimental verification and instability phenomenon. Nonlinear Dyn. 96(2), 885–920 (2019)
Weidman, P.D., Malhotra, C.P.: Regimes of terminal motion of sliding spinning disks. Phys. Rev. Lett. 95(26), 264303 (2005)
Weidman, P.D., Malhotra, C.P.: On the terminal motion of sliding spinning disks with uniform Coulomb friction. Physica D 233(1), 1–13 (2007)
Wolf, D., Dahmen, S.R., Hinrichsen, H.: Solid friction: spinning at the onset of sliding. Int. J. Mod. Phys. B 21(23), 4158–4163 (2007)
Zhou, J., Mason, M.T., Paolini, R., Bagnell, D.: A convex polynomial model for planar sliding mechanics: theory, application, and experimental validation. Int. J. Rob. Res. 37(2–3), 249–265 (2018)
Zhuvarlev, V.P., Kireenkov, A.A.: Pade expansions in the two-dimensional model of coulomb friction. Mech. Solids 40(2), 1–10 (2005)
Acknowledgements
The research leading to these results has been supported by the Eotvos Lorand Research Network in the Premium Postdoctoral Fellowship Programme under the Grant No. PPD2018-014/2018 (first author) and by the National Research, Development, and Innovation Office under the Grant No. K124002 (second author).
Funding
Open access funding provided by Széchenyi István University (SZE).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alan R. Champneys.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Antali, M., Varkonyi, P.L. The Nonsmooth Dynamics of Combined Slip and Spin Motion Under Dry Friction. J Nonlinear Sci 32, 58 (2022). https://doi.org/10.1007/s00332-022-09812-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-022-09812-x