Recurrence-based analysis and controlling switching between synchronous silence and bursting states of coupled generalized FitzHugh-Nagumo models driven by an external sinusoidal current

Abstract

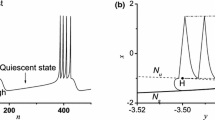
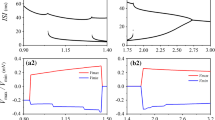
We investigate the response characteristics of a generalized FitzHugh-Nagumo model under an external sinusoidal current and the synchronization of two neurons coupled with a gap junction. In the autonomous case, we find analytically by the Lindsted’s method that the system can admit tristable activities in silence, subthreshold, and nerve pulse; depending on the conductance parameters and the state of ionic conductance. In the presence of an external sinusoidal current, we find by numerical simulations that neurons can exhibit a coexistence between different spiking patterns and periodic waves, which are well observed in the structure of the recurrence plot. We further study the synchronization between coupled neurons each admitting bistable activities, such as a coexistence between chaotic (active) and silence (inactive) regimes. We apply recurrence analysis tool to reveal the range of the coupling parameter where synchronization occurs, as well as the dynamical transitions between the synchronous coexisting states (hysteresis phenomenon). The coupling strength is an indicator of the phenomenon of synchronization that can also bring the system to any of the desired synchronous attractors. These phenomena of synchronization and the control between synchronous states can be improved by the presence of an external electrical field. The switching of the coupled neurons to bursting patterns or to periodic waves explains the well-known properties of excitatory (switching on) or inhibitory (switching off) synaptic coupling, respectively; while the unstable signal separating the two stable synchronous signals can be taken as the synaptic threshold. Rather, this study adds to our theoretical understanding of the topic and poses new challenges for investigation. Experimental investigations are required to validate these conclusions in real-world settings, and biological implications must be evaluated within the particular framework of the modeling that was done.

Appendix A: Exact solutions of the amplitude equation 17

Let us rewrite Eq. (17) in the following form:

$$\begin{aligned} x^4+a_3x^3+a_2x^2+a_1x+a_0=0, \end{aligned}$$

(A1)

where,

$$\begin{aligned} a_0= & {} \dfrac{128}{7}\dfrac{\gamma _0}{\gamma _4}, \quad a_1=\dfrac{-32}{7}\dfrac{\gamma _1}{\gamma _4}, \quad a_2=\dfrac{16}{7}\dfrac{\gamma _2}{\gamma _4}, \\ a_3= & {} \dfrac{-10}{7}\dfrac{\gamma _3}{\gamma _4}, \quad x=A^2.\\ \end{aligned}$$

Equation (A1) can be given in the following form:

$$\begin{aligned} y^4+p_1y^2+p_2y+r=0, \end{aligned}$$

(A2)

where,

$$\begin{aligned} r= & {} -\dfrac{3}{256}a_3^4+\dfrac{1}{16}a_3^2a_2-\dfrac{1}{4}a_3a_1+a_0,\\ p_2= & {} \dfrac{1}{8}a_3^3-\dfrac{1}{2}a_2a_3+a_1, \\ p_1= & {} -\dfrac{3}{8}a_3^2+a_2, \quad x=y-\dfrac{a_3}{4}. \end{aligned}$$

Equation (A2) can be transformed in the following form:

$$\begin{aligned} (y^2+\theta y+\beta _1)(y^2-\theta y+\beta _2)=0, \end{aligned}$$

(A3)

where,

$$\begin{aligned} 2\beta _2= & {} \theta ^2+p_1+\dfrac{p_2}{\theta },\nonumber \\ 2\beta _1= & {} \theta ^2+p_1-\dfrac{p_2}{\theta },\nonumber \\ 4\beta _1\beta _2= & {} 4r=(\theta ^2+p_1)^2-\dfrac{p_2^2}{\theta ^2}. \end{aligned}$$

(A4)

The last equation of the system (A4) lead to a following third degree equation with $\theta ^2$ as solution:

$$\begin{aligned} \eta ^3+b_2\eta ^2+b_1\eta +b_0=0, \end{aligned}$$

(A5)

where,

$$\begin{aligned} b_0 =-p_2^2, \quad b_1=p_1^2-4r, \quad b_2=2p_1, \quad \eta =\theta ^2. \end{aligned}$$

With the following change of variable: $\eta =\xi -\dfrac{b_2}{3}$, we obtain the cubic equation:

$$\begin{aligned} \xi ^{3} + p\xi +q = 0, \end{aligned}$$

(A6)

where,

$$\begin{aligned} p= & {} b_1-\dfrac{1}{3}b_2^2,\\ q= & {} b_0-\dfrac{1}{3}b_2b_1+\dfrac{2}{27}b_2^3. \end{aligned}$$

Let $\Delta$ the discriminant of Eq. (A6) define as:

$$\begin{aligned} \Delta = q^{2} + \dfrac{4}{27}p^{3}, \end{aligned}$$

(A7)

The number of solutions depend on the sign of $\Delta$, then we distingued many following case:

-if $\Delta$ > 0, Eq. (A5) has one real solution and two complex conjuguate solutions,

$$\begin{aligned} \eta =\root 3 \of {\dfrac{-q+\sqrt{\Delta }}{2}} + \root 3 \of {\dfrac{-q-\sqrt{\Delta }}{2}} -\dfrac{b_2}{3}, \end{aligned}$$

(A8)

-if $\Delta$ = 0, Eq. (A5) has one real solution and two double real solutions,

$$\begin{aligned} \begin{array}{ll} \eta =2\root 3 \of {\dfrac{-q}{2}}-\dfrac{b_2}{3}, \end{array}\qquad \begin{array}{ll} \eta =-\root 3 \of {\dfrac{-q}{2}}-\dfrac{b_2}{3}, \end{array} \end{aligned}$$

(A9)

-if $\Delta$ < 0, Eq. (A5) has three real solutions,

$$\begin{aligned}{} & {} \begin{array}{ll} \eta =U + V -\dfrac{b_2}{3};\\ \end{array} \quad \begin{array}{ll} \eta =jU + \bar{j}V -\dfrac{b_2}{3}\\ \end{array} \quad and\nonumber \\{} & {} \quad \begin{array}{ll} \eta =\bar{j}U + jV -\dfrac{b_2}{3}\\ \end{array} \end{aligned}$$

(A10)

with

$$\begin{aligned} j= & {} -\dfrac{1}{2} +\dfrac{i\sqrt{3}}{2}=e^{i\dfrac{2\pi }{3}}, U=\root 3 \of {\dfrac{-q+i\sqrt{-\Delta }}{2}}, \\ V= & {} \root 3 \of {\dfrac{-q-i\sqrt{-\Delta }}{2}}. \end{aligned}$$

Knowing $\theta ^2=\eta$, we can deduce from Eq. (A4), the parameters $\beta _1$, $\beta _2$. The solution y of Eq. (A2) is given by solving the following two second degree equations:

$$\begin{aligned}{} & {} y^2+\theta y+\beta _1=0,\nonumber \\{} & {} y^2-\theta y+\beta _2=0. \end{aligned}$$

(A11)

The existence and the number of solutions of Eq. (A11) depend on the sign of their discriminants $\Delta _1=\theta ^2-4\beta _1$ and $\Delta _2=\theta ^2-4\beta _2$. $\Delta _1$ and $\Delta _2$ are ensured from the two first equations of (A4) to be non zero. The number and values of y are sumarized in Table 2.

Table 2 Table summarizing the number and values of the possible solutions of Eq. (A11)

The exact solutions of Eq. (17) are found for $A^2=y+\dfrac{5}{14}\dfrac{\gamma _3}{\gamma _4}>0$.