Analysis of discontinuous dynamical behaviors for a 3-DOF friction collision system with dynamic vibration absorber

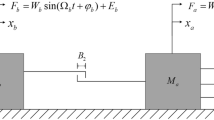
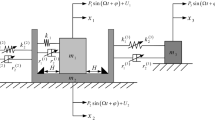
Abstract

In this work, the discontinuous dynamic behavior of a 3-DOF (three-degree-of-freedom) friction collision system with dynamic vibration absorber is studied by the flow transformation theory. This paper aims to explore the conversion of movement in the friction collision system with discontinuous and non-smooth properties. The global dynamics of the 3-DOF system are reflected by separately studying the movement of each target. The different motion states and equations are defined by the force of each target and the mode of model connection. The flow barriers at the boundary/edge are defined by the characteristics of the friction model. The domains are divided in the two-dimensional phase space of each object, and the continuous vector field and G-function are defined in each domain. Based on this, the motion switching criteria at the separation boundary/edge are researched. Finally, some classical motion states and periodic phenomena are drawn by MATLAB software to simulate the global movement of the system. The study of the 3-DOF model enriches the theoretical basis for the mechanical devices with dynamic vibration absorbers.

Appendices

Appendix A

The specific division of the phase space of the three objects is as follows.

Firstly, the movement phase space partition of the object $m _{a }$ in the absolute coordinates with its zero velocity as the boundary is expressed as

$$\begin{aligned} \left\{ \begin{array}{lll} D _{1}^{(a )}=\bigl \{(u _{a },\dot{u }_{a })\; |\;\dot{u }_{a }\in (0,+\infty ),\;u _{a }\in (-\infty , +\infty )\},\\ D _2^{(a )}=\bigl \{(u _{a },\dot{u }_{a })\; |\;\dot{u }_{a }\in (-\infty ,0),\;u _{a }\in (-\infty , +\infty )\},\\ \end{array}\right. \end{aligned}$$

(58)

and the horizontal axis as the boundary of the two domains is interpreted as

$$\begin{aligned} \left. \begin{array}{lll} \partial D _{12}^{(a )}=\partial D _{21}^{(a )}=\bigl \{(u _{a },\dot{u }_{a })\;|\;\rho _{12}^{(a )}=\rho _{21}^{(a )}\equiv \dot{u }_{a }=0,\; \\ \quad u _{a }\in (-\infty , +\infty )\bigr \}.\\ \end{array}\right. \end{aligned}$$

(59)

The specific classification is shown in Fig. 13. The gray area $D _{1}^{(a )}$ and the pink area $D _{2}^{(a )}$ represent the areas of free motion where the object $m _{a }$’s velocity is positive and negative, respectively. The two areas are separated by a velocity boundary $\partial D _{12}^{(a )}$ represented on a horizontal axis, which is depicted by a black dotted curve.

Secondly, the divisions of domains/boundaries/edges about the two objects $m _{b }$ and $m _{c }$ in the absolute coordinates are more complex than that of the object $m _{a }$. For the two masses $m _{b }$ and $m _{c }$, the partial divisions are described in detail as

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} D _{1}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\; |\;\dot{u }_{b }\in (0,+\infty ),\\ \qquad \qquad \;u _{b }\in (-\infty , u _{c }+L _{0})\},\\ D _{2}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\; |\;\dot{u }_{b }\in (-\infty ,0),\\ \qquad \qquad \;u _{b }\in (-\infty , u _{c }+L _{0})\},\\ D _{3}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })|\;\dot{u }_{b }\in (0,+\infty ),\\ \qquad \qquad \;u _{b }\in (u _{c }^{(cr) }+L _{0},+\infty ),\;u _{b }=u _{c }+L _{0}\},\\ D _{4}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\; |\;\dot{u }_{b }\in (-\infty ,0),\\ \qquad \qquad \;u _{b }\in ( u _{c }^{(cr) }+L _{0}, +\infty ),\\ \qquad \qquad \;u _{b }=u _{c }+L _{0}\},\\ \end{array}\right. \end{aligned}$$

(60)

$$\begin{aligned}{} & {} \quad \left\{ \begin{array}{lll} \partial D _{12}^{(b )}=\partial D _{21}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\;|\;\rho _{12}^{(b )}\\ \qquad =\rho _{21}^{(b )}\equiv \dot{u }_{b }=0,\;u _{b }\in (-\infty , u _{c }+L _{0})\bigr \},\\ \partial D _{34}^{(b )}=\partial D _{43}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\;|\;\rho _{34}^{(b )}\\ \qquad =\rho _{43}^{(b )}\equiv \dot{u }_{b }=0,\;u _{b }= u _{c }+L _{0}\bigr \},\\ \partial D _{13}^{(b )}=\partial D _{31}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\;|\;\rho _{13}^{(b )}\\ \qquad =\rho _{31}^{(b )}\equiv \dot{u }_{b }-\dot{u }_{c }^{(cr)}=0,\\ \qquad \;u _{b }= u _{c }^{(cr)}+L _{0},\;\dot{u }_{b }\in (0,+\infty )\bigr \},\\ \partial D _{24}^{(b )}=\partial D _{24}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\;|\; \rho _{24}^{(b )}\\ \qquad \, =\rho _{42}^{(b )}\equiv \dot{u }_{b }-\dot{u }_{c }^{(cr)}=0,\\ \qquad u _{b }= u _{c }^{(cr)}+L _{0},\;\dot{u }_{b }\in (-\infty ,0)\bigr \},\\ \end{array}\right. \end{aligned}$$

(61)

$$\begin{aligned}{} & {} \quad \left. \begin{array}{lll} \angle D _{5}^{(b )}=\partial D _{12}^{(b )}\cap \partial D _{13}^{(b )}=\partial D _{12}^{(b )}\cap \partial D _{24}^{(b )}\\ \quad =\partial D _{34}^{(b )}\cap \partial D _{13}^{(b )}=\partial D _{34}^{(b )}\cap \partial D _{24}^{(b )}=\bigl \{(u _{b },\dot{u }_{b })\;|\\ \quad \;\rho _{12}^{(b )}=\rho _{34}^{(b )}\equiv \dot{u }_{b }=0,\;\rho _{13}^{(b )}=\rho _{24}^{(b )}\\ \quad \equiv \dot{u }_{b }-\dot{u }_{c }^{(cr)}=0,\\ \quad \;u _{b }= u _{c }^{(cr)}+L _{0}\bigr \},\\ \end{array}\right. \end{aligned}$$

(62)

Fig. 13

Absolute domains and boundaries divisions of object $m _{a }$

and

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} D _{1}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\; |\; \\ \quad \dot{u }_{c }\in (0,+\infty ),\;u _{c }\in (u _{b }-L _{0}, +\infty )\},\\ D _{2}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\; |\; \\ \qquad \dot{u }_{c }\in (-\infty ,0),\;u _{c }\in (u _{b }-L _{0}, +\infty )\},\\ D _{3}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\; |\;\dot{u }_{c }\in (0,+\infty ),\; \\ \qquad u _{c }\in (-\infty , u _{b }^{(cr) }-L _{0})\},\\ \qquad \;u _{c }=u _{b }-L _{0}\},\\ D _{4}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\; |\;\dot{u }_{c }\in (-\infty ,0),\\ \qquad \;u _{b }\in (-\infty , u _{b }^{(cr) }-L _{0})\},\\ \qquad \;u _{c }=u _{b }-L _{0}\},\\ \end{array}\right. \end{aligned}$$

(63)

$$\begin{aligned}{} & {} \quad \left\{ \begin{array}{lll} \partial D _{12}^{(c )}=\partial D _{21}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\;|\;\rho _{12}^{(c )}\\ \qquad =\rho _{21}^{(c )}\equiv \dot{u }_{c }=0,\;u _{c }\in (u _{b }-L _{0}, +\infty )\bigr \},\\ \partial D _{34}^{(c )}=\partial D _{43}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\;|\;\rho _{34}^{(c )}\\ \qquad =\rho _{43}^{(c )}\equiv \dot{u }_{c }=0,\;u _{c }= u _{b }-L _{0}\bigr \},\\ \partial D _{13}^{(c )}=\partial D _{31}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\;|\;\rho _{13}^{(c )}\\ \qquad =\rho _{31}^{(c )}\equiv \dot{u }_{c }-\dot{u }_{b }^{(cr)}=0,\;u _{c }= u _{b }^{(cr)}\\ \qquad -L _{0},\;\dot{u }_{c }\in (0,+\infty )\bigr \},\\ \partial D _{24}^{(c )}=\partial D _{24}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\;|\;\rho _{24}^{(c )}\\ \qquad =\rho _{42}^{(c )}\equiv \dot{u }_{c }-\dot{u }_{b }^{(cr)}=0,\;u _{c }= u _{b }^{(cr)}\\ \qquad -L _{0},\;\dot{u }_{c }\in (-\infty ,0)\bigr \},\\ \end{array}\right. \end{aligned}$$

(64)

$$\begin{aligned}{} & {} \quad \left. \begin{array}{lll} \angle D _{5}^{(c )}=\partial D _{12}^{(c )}\cap \partial D _{13}^{(c )}=\partial D _{12}^{(c )}\\ \quad \cap \partial D _{24}^{(c )}=\partial D _{34}^{(c )}\cap \partial D _{13}^{(c )}=\partial D _{34}^{(c )}\\ \quad \cap \partial D _{24}^{(c )}=\bigl \{(u _{c },\dot{u }_{c })\;| \rho _{12}^{(c )}=\rho _{34}^{(c )}\\ \quad \equiv \dot{u }_{c }=0,\;\rho _{13}^{(c )}=\rho _{24}^{(c )}\equiv \dot{u }_{c }-\dot{u }_{b }^{(cr)}=0,\\ \quad \;u _{c }= u _{b }^{(cr)}-L _{0}\bigr \},\\ \end{array}\right. \end{aligned}$$

(65)

where $\dot{u }_{i }^{(cr)}$ and $u _{i }^{(cr)}$ $(i \in \{b , c \})$ are interpreted as the corresponding velocity and displacement of the object $m _{i }$ at the time when stick motion occurs or disappears.

Fig. 14

Absolute domains and boundaries divisions: a object $m _{b }$ and b object $m _{c }.$

The phase space partitions of two masses $m _{b }$ and $m _{c }$ are shown in Fig. 14 under the precondition that collision is not considered. The non-stick free motion domains ($D _{1}^{(i )}$, $D _{2}^{(i )}$, $i \in \{b , c \}$) with positive and negative velocity values are also filled in gray and pink, respectively. The stick free motion domains ($D _{3}^{(i )}$, $D _{4}^{(i )}$, $i \in \{b , c \}$) are filled in blue and purple, respectively. The velocity boundaries without stick state ($\partial D _{12}^{(b )}$, $\partial D _{12}^{(c )}$) and the velocity boundaries with stick state ($\partial D _{34}^{(b )}$, $\partial D _{34}^{(c )}$) are depicted by black and green dotted curves, and the stick displacement boundaries ($\partial D _{13}^{(b )}$, $\partial D _{24}^{(b )}$, $\partial D _{13}^{(c )}$ $\partial D _{24}^{(c )}$) are depicted by yellow dashed curves. The edges ($\angle D _{5}^{(b )}$, $\angle D _{5}^{(c )}$) are marked with solid red dots.

Considering the collision of two objects $m _{b }$ and $m _{c }$ requires comparing the relative velocities and displacements of this two objects, so the following definitions are listed as

$$\begin{aligned} \left\{ \begin{array}{lll} z _{b }=u _{b }-u _{c },\; \dot{z }_{b }=\dot{u }_{b }-\dot{u }_{c },\; \ddot{z }_{b }=\ddot{u }_{b }-\ddot{u }_{c },\\ z _{c }=u _{c }-u _{a },\; \dot{z }_{c }=\dot{u }_{c }-\dot{u }_{a },\; \ddot{z }_{c }=\ddot{u }_{c }-\ddot{u }_{a }.\\ \end{array}\right. \end{aligned}$$

(66)

In order to facilitate the research of stick motion and collision motion, the relative coordinates of the object $m _{b }$ are established for phase space division. The specific analysis is expressed as:

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} D _{1}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\; |\; \\ \quad \dot{z }_{b }\in (-\dot{z }_{c },+\infty ),\;z _{b }\in (-\infty , u _{c }+L _{0})\},\\ D _{2}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })|\; \\ \quad \dot{z }_{b }\in (-\infty , -\dot{z }_{c }),\;z _{b }\in (-\infty , u _{c }+L _{0})\},\\ D _{3}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\; | \\ \quad \;\dot{z }_{b }\in (-\dot{z }_{c },+\infty ),\;z _{b }=L _{0}\},\\ D _{4}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\; |\\ \quad \;\dot{z }_{b }\in (-\infty , -\dot{z }_{c }),\;z _{b }=L _{0}\},\\ \end{array}\right. \end{aligned}$$

(67)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} \partial D _{12}^{(b )}=\partial D _{21}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\;\rho _{12}^{(b )}=\rho _{21}^{(b )}\\ \quad \equiv \dot{z }_{b }+\dot{u }_{c }=0,\;z _{b }\in (-\infty , L _{0})\bigr \},\\ \partial D _{34}^{(b )}=\partial D _{43}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\;\rho _{34}^{(b )}=\rho _{43}^{(b )}\\ \quad \equiv \dot{z }_{b }+\dot{u }_{c }=0,\;z _{b }=L _{0}\bigr \},\\ \partial D _{13}^{(b )}=\partial D _{31}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\;\rho _{13}^{(b )}=\rho _{31}^{(b )}\\ \quad \equiv \dot{z }_{b }^{(cr)}=0,\; z _{b }^{(cr)}=L _{0},\;\dot{z }_{b }\in (-\dot{u }_{c },+\infty )\bigr \},\\ \partial D _{24}^{(b )}=\partial D _{24}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\;\rho _{24}^{(b )}=\rho _{42}^{(b )}\\ \quad \equiv \dot{z }_{b }^{(cr)}=0,\; z _{b }^{(cr)}=L _{0},\;\dot{z }_{b }\in (-\infty , -\dot{u }_{c })\bigr \},\\ \partial D _{1\infty }^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\;\rho _{1\infty }^{(b )}\\ \quad \equiv z _{b }-L _{0}=0,\; \dot{z }_{b }\in (0, +\infty )\bigr \},\\ \partial D _{2\infty }^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\;\rho _{2\infty }^{(b )}\\ \quad \equiv z _{b }-L _{0}=0,\; \dot{z }_{b }\in (-\infty , 0)\bigr \},\\ \end{array}\right. \end{aligned}$$

(68)

$$\begin{aligned}{} & {} \left. \begin{array}{lll} \angle D _{5}^{(b )}=\partial D _{12}^{(b )}\cap \partial D _{13}^{(b )}\\ \quad =\partial D _{12}^{(b )}\cap \partial D _{24}^{(b )}=\partial D _{34}^{(b )}\cap \partial D _{13}^{(b )}\\ \quad =\partial D _{34}^{(b )}\cap \partial D _{24}^{(b )}=\bigl \{(z _{b },\dot{z }_{b })\;|\\ \quad \;\rho _{12}^{(b )}=\rho _{34}^{(b )} \equiv \dot{z }_{b }+\dot{u }_{c }=0,\;\rho _{13}^{(b )}\\ \quad =\rho _{24}^{(b )}\equiv \dot{z }_{b }^{(cr)}=0,\; z _{b }^{(cr)}=L _{0}\bigr \},\\ \end{array}\right. \end{aligned}$$

(69)

where $\dot{z }_{b }^{(cr)}$ and $z _{b }^{(cr)}$ are interpreted as the corresponding velocity and displacement of the object $m _{b }$ at the time when stick motion occurs or disappears.

Fig. 15

Relative domains and boundaries divisions of object $m _{b }$

The partitioned phase space is shown in Fig. 15 for the object $m _{b }$. The dashed black curve is interpreted as the negative of the velocity for the other object $m _{c }$. After establishing coordinates with relative displacement $z _{b }$ and relative velocity $\dot{z }_{b }$ as horizontal and vertical axes, the non-stick free motion domains ($D _{3}^{(b )}$, $D _{4}^{(b )}$) and related boundaries and edges ($\partial D _{34}^{(b )}$, $\partial D _{13}^{(b )}$, $\partial D _{24}^{(b )}$, $\angle D _{5}^{(b )}$) can be marked with the same orange solid dot. The boundaries ($\partial D _{1\infty }^{(b )}$, $\partial D _{2\infty }^{(b )}$) where the object $m _{b }$ collides with $m _{c }$ is depicted by a thick solid red line.

Appendix B

According to Luo [47] and the normal vectors in Eqs. (31) $\sim$ (33), combined with the force and the derivative of the force in Sect. 3, the $\textrm{G}$-functions definitions and computational expressions are listed as follows.

The zero-order and first-order $\textrm{G}$-functions at the point ${\textbf{u}}_{i {} m }=(u _{i {} m },\,\dot{u }_{i {} m })\in \partial D _{\xi \sigma }^{(i )}$ are interpreted as

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi \sigma }^{(i )}}^{(0,\eta )}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi \sigma }^{(i )}}^{(0,\eta )}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi \sigma }^{(i )}}^\textrm{T}\\ \quad \cdot {\textbf{F}}_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm })={F }_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm }), \end{array}\right. \end{aligned}$$

(70)

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi \sigma }^{(i )}}^{(1,\eta )}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi \sigma }^{(i )}}^{(1,\eta )}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi \sigma }^{(i )}}^\textrm{T}\\ \quad \cdot D {{\textbf{F}}_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}=D {{F }_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}, \end{array}\right. \end{aligned}$$

(71)

where $\xi \ne \sigma \in \{1,2\},\,\,\,i \in \{a ,b ,c \},\,\,\,\eta \in \{1,2\}$;

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi \sigma }^{(i )}}^{(0,\eta )}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi \sigma }^{(i )}}^{(0,\eta )}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi \sigma }^{(i )}}^\textrm{T}\\ \quad \cdot {\bar{\textbf{F}}}_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm })={\bar{F }}_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm }), \end{array}\right. \end{aligned}$$

(72)

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi \sigma }^{(i )}}^{(1,\eta )}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi \sigma }^{(i )}}^{(1,\eta )}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi \sigma }^{(i )}}^\textrm{T}\\ \quad \cdot D {{\bar{\textbf{F}}}_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}=D {{\bar{F }}_{i }^{(\eta )}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}, \end{array}\right. \end{aligned}$$

(73)

where $\xi \ne \sigma \in \{3,4\},\,\,\,i \in \{b ,c \},\,\,\,\eta \in \{3,4\}$.

The zero-order and first-order $\textrm{G}$-functions at the point ${\textbf{z}}_{b {} m }=(z _{b {} m },\,\dot{z }_{b {} m })\in \partial D _{\delta \tau }^{(b )}\,(\delta \ne \tau \in \{1,3\}\,\,\textrm{or}\,\,\delta \ne \tau \in \{2,4\})$ are interpreted as

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\delta \tau }^{(b )}}^{(0,\eta )}({ t _{m }}_\pm )\equiv G _{\partial D _{\delta \tau }^{(b )}}^{(0,\eta )}({\textbf{z}}_{b {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\delta \tau }^{(b )}}^\textrm{T}\\ \quad \cdot {\textbf{W}}_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm })={W }_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm }),\\ G _{\partial D _{\delta \tau }^{(b )}}^{(0,\bar{\eta })}({ t _{m }}_\pm )\equiv G _{\partial D _{\delta \tau }^{(b )}}^{(0,\bar{\eta })}({\textbf{z}}_{b {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\delta \tau }^{(b )}}^\textrm{T}\\ \quad \cdot {\bar{\textbf{W}}}_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm })={\bar{W }}_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm }); \end{array}\right\} \end{aligned}$$

(74)

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\delta \tau }^{(b )}}^{(1,\eta )}({ t _{m }}_\pm )\equiv G _{\partial D _{\delta \tau }^{(b )}}^{(1,\eta )}({\textbf{z}}_{b {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\delta \tau }^{(b )}}^\textrm{T}\\ \quad \cdot {D \textbf{W}}_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm })={D {} W }_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm }),\\ G _{\partial D _{\delta \tau }^{(b )}}^{(1,\bar{\eta })}({ t _{m }}_\pm )\equiv G _{\partial D _{\delta \tau }^{(b )}}^{(1,\bar{\eta })}({\textbf{z}}_{b {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\delta \tau }^{(b )}}^\textrm{T}\\ \quad \cdot {D \bar{\textbf{W}}}_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm })={D {\bar{W }}}_{b }^{(\bar{\eta })}(\textbf{z}_{b {} m },{t _{m }}_{\pm }); \end{array}\right\} \end{aligned}$$

(75)

where $(\eta ,\bar{\eta })=(1,3)\,\,\,\textrm{if}\,\,\,\delta \ne \tau \in \{1,3\},\,\,\,(\eta ,\bar{\eta })=(2,4)\,\,\,\textrm{if}\,\,\,\delta \ne \tau \in \{2,4\}$.

The zero-order and first-order $\textrm{G}$-functions at the point ${\textbf{u}}_{i {} m }=(u _{i {} m },\,\dot{u }_{i {} m })\in \partial D _{\xi \tau }^{(i )}$ where the flow barrier exists are defined as

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi \tau }^{(i )}}^{(0,0\succ 0_{\eta })}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi \tau }^{(i )}}^{(0,0\succ 0_{\eta })}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi \tau }^{(i )}}^\textrm{T}\\ \quad \cdot {\textbf{F}}_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm })={F }_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm }), \end{array}\right. \end{aligned}$$

(76)

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi \tau }^{(i )}}^{(1,0\succ 0_{\eta })}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi \tau }^{(i )}}^{(1,0\succ 0_{\eta })}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi \tau }^{(i )}}^\textrm{T}\\ \quad \cdot D {{\textbf{F}}_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}=D {{F }_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}, \end{array}\right. \end{aligned}$$

(77)

where $\xi \ne \sigma \in \{1,2\},\,\,\,i \in \{a ,b ,c \},\,\,\,\eta \in \{1,2\}$;

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi j }^{(i )}}^{(0,0\succ 0_{\eta })}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi j }^{(i )}}^{(0,0\succ 0_{\eta })}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi j }^{(i )}}^\textrm{T}\\ \quad \cdot {\bar{\textbf{F}}}_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm })={\bar{F }}_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm }), \end{array}\right. \end{aligned}$$

(78)

$$\begin{aligned} \left. \begin{array}{lll} G _{\partial D _{\xi j }^{(i )}}^{(1,0\succ 0_{\eta })}({ t _{m }}_\pm )\equiv G _{\partial D _{\xi j }^{(i )}}^{(1,0\succ 0_{\eta })}({\textbf{u}}_{i {} m },{ t _{m }}_\pm )={\textbf{n}}_{\partial D _{\xi j }^{(i )}}^\textrm{T}\\ \quad \cdot D {{\bar{\textbf{F}}}_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}=D {{\bar{F }}_{i }^{(0\succ 0_{\eta })}(\textbf{u}_{i {} m },{t _{m }}_{\pm })}, \end{array}\right. \end{aligned}$$

(79)

where $\xi \ne \sigma \in \{3,4\},\,\,\,i \in \{b ,c \},\,\,\,\eta \in \{3,4\}$.

Appendix C

According to the description of the discontinuous boundary in Eq. (59), the two-dimensional transformation sets of the object $m _{a }$ are expressed as

$$\begin{aligned} \left\{ \begin{array}{lll} {}^{0}\sum ^{(a )}_{12}=\{(u _{a {} k },\dot{u }_{a {} k },t _k )|\\ \quad u _{a {} k }\in (-\infty ,+\infty ),\dot{u }_{a {} k }=0^0\},\\ {}^{+}\sum ^{(a )}_{12}=\{(u _{a {} k },\dot{u }_{a {} k },t _k )|\\ \quad u _{a {} k }\in (-\infty ,+\infty ),\dot{u }_{a {} k }=0^+\},\\ {}^{-}\sum ^{(a )}_{12}=\{(u _{a {} k },\dot{u }_{a {} k },t _k )|\\ \quad u _{a {} k }\in (-\infty ,+\infty ),\dot{u }_{a {} k }=0^-\};\\ \end{array}\right. \end{aligned}$$

(80)

where $u _{a {} k }=u _{a }(t _k )$ and $\dot{u }_{a {} k }=\dot{u }_{a }(t _k )$ ($k \in {\textbf{N}}$) represent the transformation displacement and transformation velocity of the object $m _{a }$ at the corresponding $t _k$ moment, respectively.

Considering the stick motion and collision motion of the system, the two-dimensional transformation sets of the two objects $m _{b }$ and $m _{c }$ are denoted as

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} {}^{0}\sum ^{(b )}_{12}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|\\ \quad u _{b {} k }\in (-\infty ,u _{c {} k }+L _{0}),\dot{u }_{b {} k }=0^0\},\\ {}^{+}\sum ^{(b )}_{12}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|\\ \quad u _{b {} k }\in (-\infty ,u _{c {} k }+L _{0}),\dot{u }_{b {} k }=0^+\},\\ {}^{-}\sum ^{(b )}_{12}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|\\ \quad u _{b {} k }\in (-\infty ,u _{c {} k }+L _{0}),\dot{u }_{b {} k }=0^-\},\\ {}^{0}\sum ^{(c )}_{12}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|\\ \quad u _{c {} k }\in (u _{b {} k }-L _{0},+\infty ),\dot{u }_{c {} k }=0^0\},\\ {}^{+}\sum ^{(c )}_{12}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|\\ \quad u _{c {} k }\in (u _{b {} k }-L _{0},+\infty ),\dot{u }_{c {} k }=0^+\},\\ {}^{-}\sum ^{(c )}_{12}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|\\ \quad u _{c {} k }\in (u _{b {} k }-L _{0},+\infty ),\dot{u }_{c {} k }=0^-\};\\ \end{array}\right. \end{aligned}$$

(81)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} {}^{0}\sum ^{(b )}_{34}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|\\ \quad u _{b {} k }=u _{c {} k }+L _{0},\dot{u }_{b {} k }=0^0\},\\ {}^{+}\sum ^{(b )}_{34}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|\\ \quad u _{b {} k }=u _{c {} k }+L _{0},\dot{u }_{b {} k }=0^+\},\\ {}^{-}\sum ^{(b )}_{34}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|\\ \quad u _{b {} k }=u _{c {} k }+L _{0},\dot{u }_{b {} k }=0^-\},\\ {}^{0}\sum ^{(c )}_{34}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|\\ \quad u _{c {} k }=u _{b {} k }-L _{0},\dot{u }_{c {} k }=0^0\},\\ {}^{+}\sum ^{(c )}_{34}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|\\ \quad u _{c {} k }=u _{b {} k }-L _{0},\dot{u }_{c {} k }=0^+\},\\ {}^{-}\sum ^{(c )}_{34}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|\\ \quad u _{c {} k }=u _{b {} k }-L _{0},\dot{u }_{c {} k }=0^-\};\\ \end{array}\right. \end{aligned}$$

(82)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} {}^{0}\sum ^{(b )}_{5}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{c {} k }+L _{0},\dot{u }_{b {} k }=0^0,\dot{u }_{b {} k }-\dot{u }_{c {} k }=0\},\\ {}^{+}\sum ^{(b )}_{5}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{c {} k }+L _{0},\dot{u }_{b {} k }=0^+,\dot{u }_{b {} k }-\dot{u }_{c {} k }=0\},\\ {}^{-}\sum ^{(b )}_{5}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{c {} k }+L _{0},\dot{u }_{b {} k }=0^-,\dot{u }_{b {} k }-\dot{u }_{c {} k }=0\},\\ {}^{0}\sum ^{(c )}_{5}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{b {} k }-L _{0},\dot{u }_{c {} k }=0^0,\dot{u }_{b {} k }-\dot{u }_{c {} k }=0\},\\ {}^{+}\sum ^{(c )}_{5}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{b {} k }-L _{0},\dot{u }_{c {} k }=0^+,\dot{u }_{b {} k }-\dot{u }_{c {} k }=0\},\\ {}^{-}\sum ^{(c )}_{5}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{b {} k }-L _{0},\dot{u }_{c {} k }=0^-,\dot{u }_{b {} k }-\dot{u }_{c {} k }=0\}.\\ \end{array}\right. \end{aligned}$$

(83)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} \sum ^{(b )}_{13}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{c {} k }+L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }=0,\dot{u }_{b {} k }\in (0,+\infty )\},\\ \sum ^{(b )}_{24}=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{c {} k }+L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }=0,\dot{u }_{b {} k }\in (-\infty ,0)\},\\ \sum ^{(c )}_{13}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{b {} k }-L _{0},\dot{u }_{c {} k }-\dot{u }_{b {} k }=0,\dot{u }_{c {} k }\in (0,+\infty )\},\\ \sum ^{(c )}_{24}=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{b {} k }-L _{0},\dot{u }_{c {} k }-\dot{u }_{b {} k }=0,\dot{u }_{c {} k }\in (-\infty ,0)\};\\ \end{array}\right. \end{aligned}$$

(84)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} \sum ^{(b )}_{1\infty }=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{b {} k }-u _{c {} k }=L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }>0\},\\ \sum ^{(b )}_{2\infty }=\{(u _{b {} k },\dot{u }_{b {} k },t _k )|u _{b {} k }\\ \quad =u _{b {} k }-u _{c {} k }=L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }<0\},\\ \sum ^{(c )}_{1\infty }=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{c {} k }-u _{b {} k }=L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }>0\},\\ \sum ^{(c )}_{2\infty }=\{(u _{c {} k },\dot{u }_{c {} k },t _k )|u _{c {} k }\\ \quad =u _{c {} k }-u _{b {} k }=L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }<0\};\\ \end{array}\right. \end{aligned}$$

(85)

where $u _{i {} k }=u _{i }(t _k )$ and $\dot{u }_{i {} k }=\dot{u }_{i }(t _k )$ ($i \in \{b ,c \}$,$k \in {\textbf{N}}$) represent the transformation displacement and transformation velocity of the object $m _{i }$ ($i \in \{b ,c \}$ at the corresponding $t _k$ moment, respectively.

According to the above two-dimensional transformation sets, the four-dimensional transformation sets that treat the two objects $m _{b }$ and $m _{c }$ as a whole can be defined as

$$\begin{aligned}{} & {} \left. \begin{array}{lll} {}^{(\mu \nu )}\sum ^{(b {} c )}_{12}={}^{(\mu )}\sum ^{(b )}_{12}\bigotimes {}^{(\nu )}\sum ^{(c )}_{12}\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }<u _{c {} k }\\ \quad +L _{0}, u _{c {} k }>u _{b {} k }-L _{0},\\ \quad \dot{u }_{b {} k }=0^{\mu },\dot{u }_{c {} k }=0^{\nu }\},\\ \end{array}\right. \end{aligned}$$

(86)

$$\begin{aligned}{} & {} \left. \begin{array}{lll} {}^{(\xi )}\sum ^{(b {} c )}_{34}={}^{(\xi )}\sum ^{(b )}_{34}\bigotimes {}^{(\xi )}\sum ^{(c )}_{34}\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }-u _{c {} k }=L _{0},\\ \quad \dot{u }_{b {} k }=0^{\xi },\dot{u }_{c {} k }=0^{\xi }\},\\ \end{array}\right. \end{aligned}$$

(87)

$$\begin{aligned}{} & {} \left. \begin{array}{lll} {}^{(\zeta )}\sum ^{(b {} c )}_{5}={}^{(\zeta )}\sum ^{(b )}_{5}\bigotimes {}^{(\zeta )}\sum ^{(c )}_{5}\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }-u _{c {} k }=L _{0},\\ \quad \dot{u }_{b {} k }=0^{\zeta },\dot{u }_{c {} k }=0^{\zeta }\},\\ \end{array}\right. \end{aligned}$$

(88)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} \sum ^{(b {} c )}_{13}=\sum ^{(b )}_{13}\bigotimes \sum ^{(c )}_{13}\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }-u _{c {} k }\\ \quad =L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }=0,\\ \quad \dot{u }_{b {} k }>0,\dot{u }_{c {} k }>0\},\\ \sum ^{(b {} c )}_{24}=\sum ^{(b )}_{24}\bigotimes \sum ^{(c )}_{24}\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }-u _{c {} k }\\ \quad =L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }=0,\\ \quad \dot{u }_{b {} k }<0,\dot{u }_{c {} k }<0\};\\ \end{array}\right. \end{aligned}$$

(89)

$$\begin{aligned}{} & {} \left\{ \begin{array}{lll} \sum ^{(b {} c )}_{1\infty }=\sum ^{(b )}_{1\infty }\bigotimes \sum ^{(c )}_{1\infty }\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }-u _{c {} k }\\ \quad =L _{0},\dot{u }_{b {} k }-\dot{u }_{c {} k }>0\},\\ \sum ^{(b {} c )}_{2\infty }=\sum ^{(b )}_{2\infty }\bigotimes \sum ^{(c )}_{2\infty }\\ \quad =\{(u _{b {} k },\dot{u }_{b {} k },u _{c {} k },\dot{u }_{c {} k },t _k )|u _{b {} k }-u _{c {} k }\\ \quad =L _{0}, \dot{u }_{b {} k }-\dot{u }_{c {} k }<0\};\\ \end{array}\right. \end{aligned}$$

(90)

where $\bigotimes$ represents the direct product of two transformation sets, the symbols $\mu ,\nu ,\xi ,\zeta \in \{0,+,-\}$.

Appendix D

As shown in Fig. 16, the corresponding two-dimensional basic mappings of the object $m _{a }$ are represented as

$$\begin{aligned} \left. \begin{array}{lll} P_1^{(a )}:{}^{0}\sum _{12}^{(a )}\rightarrow {}^{0}\sum _{12}^{(a )},\,\, P_2^{(a )}:{}^{+}\sum _{12}^{(a )}\rightarrow {}^{+}\sum _{12}^{(a )},\,\, \\ P_3^{(a )}:{}^{-}\sum _{12}^{(a )}\rightarrow {}^{-}\sum _{12}^{(a )}. \end{array}\right. \nonumber \\ \end{aligned}$$

(91)

Fig. 16

Switching sets and two-dimensional mapping structures of object $m _{a }$

Fig. 17

Switching sets and two-dimensional mapping structures: a object $m _{b }$ and b object $m _{c }$

Based on the two-dimensional transformation sets in Eqs. (81)–(85), the corresponding two-dimensional basic mappings can be given. All two-dimensional mappings (including local mappings and global mappings) of two objects $m _{i }$ $(i =b ,c )$ are

$$\begin{aligned} \left\{ \begin{array}{lll} P_4^{(i )}:{}^{0}\sum _{12}^{(i )}\rightarrow {}^{0}\sum _{12}^{(i )},\,\, P_5^{(i )}:{}^{+}\sum _{12}^{(i )}\rightarrow {}^{+}\sum _{12}^{(i )},\,\, \\ P_6^{(i )}:{}^{-}\sum _{12}^{(i )}\rightarrow {}^{-}\sum _{12}^{(i )},\\ P_7^{(i )}:{}^{0}\sum _{34}^{(i )}\rightarrow {}^{0}\sum _{34}^{(i )},\,\, P_8^{(i )}:{}^{+}\sum _{34}^{(i )}\rightarrow {}^{+}\sum _{34}^{(i )},\,\, \\ P_9^{(i )}:{}^{-}\sum _{34}^{(i )}\rightarrow {}^{-}\sum _{34}^{(i )},\\ P_{10}^{(i )}:{}^{0}\sum _{5}^{(i )}\rightarrow {}^{0}\sum _{5}^{(i )},\,\, P_{11}^{(i )}:{}^{+}\sum _{5}^{(i )}\rightarrow {}^{+}\sum _{5}^{(i )},\,\, \\ P_{12}^{(i )}:{}^{-}\sum _{5}^{(i )}\rightarrow {}^{-}\sum _{5}^{(i )},\\ P_{13}^{(i )}:{}^{+}\sum _{12}^{(i )}\rightarrow \sum _{13}^{(i )},\,\, \\ P_{14}^{(i )}:\sum _{13}^{(i )}\rightarrow {}^{+}\sum _{34}^{(i )},\,\, P_{15}^{(i )}:\sum _{13}^{(i )}\rightarrow {}^{+}\sum _{5}^{(i )},\\ P_{16}^{(i )}:{}^{-}\sum _{34}^{(i )}\rightarrow \sum _{24}^{(i )},\,\, P_{17}^{(i )}:\sum _{24}^{(i )}\rightarrow {}^{-}\sum _{12}^{(i )},\,\, \\ P_{18}^{(i )}:\sum _{24}^{(i )}\rightarrow {}^{-}\sum _{5}^{(i )},\\ P_{19}^{(i )}:{}^{+}\sum _{12}^{(i )}\rightarrow \sum _{1\infty }^{(i )},\,\, P_{20}^{(i )}:\sum _{1\infty }^{(i )}\rightarrow \sum _{2\infty }^{(i )},\,\, \\ P_{21}^{(i )}:\sum _{2\infty }^{(i )}\rightarrow \sum _{12}^{(i )}.\\ \end{array}\right. \end{aligned}$$

(92)

All the mapping structures of the two objects $m _{i }$ $(i =b ,c )$ without taking collision into account are depicted in Fig. 17, and the mapping structures with collision are shown in Fig. 18.

Based on the four-dimensional transformation sets in Eqs. (86)–(90), the corresponding four-dimensional basic mappings can be given. All four-dimensional mappings (including local mappings and global mappings) of two objects $m _{i }$ $(i =b ,c )$ are

$$\begin{aligned} \left\{ \begin{array}{lll} P_{rs }^{(bc )}=(P_{r }^{(b )},P_{s }^{(c )}):{}^{(\mu \nu )}\sum _{12}^{(bc )}\rightarrow {}^{(\mu \nu )}\sum _{12}^{(bc )},\\ P_{e }^{(bc )}=(P_{e }^{(b )},P_{e }^{(c )}):{}^{(\xi )}\sum _{34}^{(bc )}\rightarrow {}^{(\xi )}\sum _{34}^{(bc )},\\ P_{q }^{(bc )}=(P_{q }^{(b )},P_{q }^{(c )}):{}^{(\zeta )}\sum _{5}^{(bc )}\rightarrow {}^{(\zeta )}\sum _{5}^{(bc )},\\ P_{13}^{(bc )}=(P_{13}^{(b )},P_{13}^{(c )}):{}^{+}\sum _{12}^{(bc )}\rightarrow \sum _{13}^{(bc )},\\ P_{14}^{(bc )}=(P_{14}^{(b )},P_{14}^{(c )}):\sum _{13}^{(bc )}\rightarrow {}^{+}\sum _{34}^{(bc )},\\ P_{15}^{(bc )}=(P_{15}^{(b )},P_{15}^{(c )}):\sum _{13}^{(bc )}\rightarrow {}^{+}\sum _{5}^{(bc )},\\ P_{16}^{(bc )}=(P_{16}^{(b )},P_{16}^{(c )}):{}^{-}\sum _{34}^{(bc )}\rightarrow \sum _{24}^{(bc )},\\ P_{17}^{(bc )}=(P_{17}^{(b )},P_{17}^{(c )}):\sum _{24}^{(bc )}\rightarrow {}^{-}\sum _{12}^{(bc )},\\ P_{18}^{(bc )}=(P_{18}^{(b )},P_{18}^{(c )}):\sum _{24}^{(bc )}\rightarrow {}^{-}\sum _{5}^{(bc )},\\ P_{19}^{(bc )}=(P_{19}^{(b )},P_{19}^{(c )}):{}^{+}\sum _{12}^{(bc )}\rightarrow \sum _{1\infty }^{(bc )},\\ P_{20}^{(bc )}=(P_{20}^{(b )},P_{20}^{(c )}):\sum _{1\infty }^{(bc )}\rightarrow \sum _{2\infty }^{(bc )},\\ P_{21}^{(bc )}=(P_{21}^{(b )},P_{21}^{(c )}):\sum _{2\infty }^{(bc )}\rightarrow {}^{-}\sum _{12}^{(bc )},\\ \end{array}\right. \end{aligned}$$

(93)

where $r =4$ corresponds to $\mu =0$, $r =5$ corresponds to $\mu =+$, $r =6$ corresponds to $\mu =-$; $s =4$ corresponds to $\nu =0$, $s =5$ corresponds to $\nu =+$; $s =6$ corresponds to $\nu =-$; $e =7$ corresponds to $\xi =0$, $e =8$ corresponds to $\xi =+$, $e =9$ corresponds to $\xi =-$; $q =10$ corresponds to $\zeta =0$, $q =11$ corresponds to $\zeta =+$, $q =12$ corresponds to $\zeta =-$.

Fig. 18

Switching sets and two-dimensional mapping structures of object $m _{b }$ with collision motion

From the above analysis, the six-dimensional total mappings $P_{\Delta }$ $(\Delta =\theta \tau ,\tau \in \{rs ,e ,q ,13,14,15,16,17,18, 19,20,21\})$ (including local mappings and global mappings) of the 3-DOF system can be obtained as

$$\begin{aligned} \left\{ \begin{array}{lll} P_{\theta rs }=(P_{\theta }^{(a )},P_{rs }^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{(\mu \nu )}\sum _{12}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes {}^{(\mu \nu )}\sum _{12}^{(bc )},\\ P_{\theta e }=(P_{\theta }^{(a )},P_{e }^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{(\xi )}\sum _{34}^{(bc )} \\ \quad \rightarrow {}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{(\xi )}\sum _{34}^{(bc )},\\ P_{\theta q }=(P_{\theta }^{(a )},P_{q }^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{(\zeta )}\sum _{5}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{(\zeta )}\sum _{5}^{(bc )},\\ P_{\theta 13}=(P_{\theta }^{(a )},P_{13}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{+}\sum _{12}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{13}^{(bc )},\\ P_{\theta 14}=(P_{\theta }^{(a )},P_{14}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{13}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes {}^{+}\sum _{34}^{(bc )},\\ P_{\theta 15}=(P_{\theta }^{(a )},P_{15}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{13}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes {}^{+}\sum _{5}^{(bc )},\\ P_{\theta 16}=(P_{\theta }^{(a )},P_{16}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{-}\sum _{34}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes \sum _{24}^{(bc )},\\ P_{\theta 17}=(P_{\theta }^{(a )},P_{17}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{24}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes {}^{-}\sum _{12}^{(bc )},\\ P_{\theta 18}=(P_{\theta }^{(a )},P_{18}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{24}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes {}^{-}\sum _{5}^{(bc )},\\ P_{\theta 19}=(P_{\theta }^{(a )},P_{19}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{+}\sum _{12}^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes \sum _{1\infty }^{(bc )},\\ P_{\theta 20}=(P_{\theta }^{(a )},P_{20}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{1\infty }^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )} \sum _{12}^{(a )}\bigotimes \sum _{2\infty }^{(bc )},\\ P_{\theta 21}=(P_{\theta }^{(a )},P_{21}^{(bc )}):{}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes \sum _{2\infty }^{(bc )}\\ \quad \rightarrow {}^{(\varepsilon )}\sum _{12}^{(a )}\bigotimes {}^{-}\sum _{12}^{(bc )},\\ \end{array}\right. \nonumber \\ \end{aligned}$$

(94)

where the symbols $\theta \in \{1,2,3\}$, $\varepsilon \in \{0,+,-\}$. When $\theta =1$, $\varepsilon =0$; when $\theta =2$, $\varepsilon =+$; when $\theta =3$, $\varepsilon =-$.