1 Introduction

Vibration-based energy harvesting, a technique converting vibration energy into electrical energy, has attracted substantial attention, given its wide application potential [1,2,3]. The vibration sources include, but are not limited to, vibrations of vehicle suspensions [4], railway tracks [5], and civil structures [6] caused by different environmental loads. A typical configuration of the vibration-based energy harvester consists of a linear or nonlinear oscillator, an energy transducer (such as electromagnetic [7], piezoelectric [8], electrostatic transducers [9]), and an energy harvesting circuit (e.g., buck–boost converter [10]). These vibration-based energy harvesters share a very similar concept with wave energy converters (WECs) that generate energy from ocean waves-induced motions. They are often tuned to match excitation frequencies to achieve optimal output power.

However, in practice, environmental vibrations are usually broadband and time-variant. To enhance output power, the frequency-matching strategies by using either nonlinear broadband harvesters [11, 12] or frequency-tunable harvesters [13] are the classical approaches, wherein the nonlinear frequency bandwidth or tunable frequency range is expected to cover vibration frequencies. Particularly, corresponding to typical low-frequency vibration scenarios, such as human motions (≈ 1 Hz), ocean wave-induced vibrations (< 1 Hz), and civil structural vibrations (< 10 Hz) [14], a number of low-frequency linear or nonlinear energy harvesters have been reported with different structural configurations, such as the clips-pendulum structure [15], X-shape structure [16], and sprung eccentric rotor structure [17]. Among them, beam-like configurations or their variants are a well-known family.

Meanwhile, pendulum-type energy harvesters have been granted relatively less attention, although they show superiority in some aspects. For example, they are free from fracture issues under large amplitudes because of limited interior stress, and they possess relatively lower frequencies than beam-like structures. In recent years, the concept of beam-pendulum configuration emerged, demonstrating more or less success in numerical and experimental studies for specific targets. The coupled device can harvest multi-direction vibration energy by adding a simple pendulum to the tip of a piezoelectric cantilever-beam energy harvester [18]. The prototype was successfully tested in the frequency range of approximately 3–10 Hz. Similar structural versions were reported as an inverted beam with a simple pendulum [19] and a cantilever beam with a double pendulum [20].

In addition to the beam-pendulum configurations, pendulum-only configurations are investigated [21, 22]. Abbas Hassan et al. [23] presented a self-tuning, variable-length simple pendulum for energy harvesting, realizing a tunable frequency range from 0.47 Hz to 0.68 Hz. Dai [24] proposed a rotary pendulum-based energy harvester that consisted of two symmetric sector masses on the two sides of the bearing. The strong nonlinearity resulted in a 3 dB bandwidth of 3.2 Hz at 0.5 g root-mean-square (RMS) acceleration. Marszal et al. [25] analyzed the energy harvesting performance of an oscillation-motion simple pendulum-based energy harvester in 2:1 resonance. They found energy harvesting performance was more efficient for the shorter reduced pendulum length. Kumar et al. [26] investigated the dynamics of a double pendulum-based energy harvester subjected to base excitations. They claimed that the pendulum that exhibited chaotic motions could considerably increase the harvested power. Malaji and Ali [27] investigated a pendulum-type energy harvester that consists of two coupled simple pendulums connected by a spring, experimentally demonstrating that such a configuration enhances the energy harvesting performance in terms of magnitude and bandwidth. Other case studies on pendulum-type energy harvesters included, but were not limited to, Ma et al. [28] and Jia et al. [29]. In some studies, pendulum-type energy harvesters were also regarded as vibration control devices, forming dual-function dampers [1, 30,31,32].

Furthermore, attempting to reduce the direct effect of pendulum length on its natural frequencies, Yurchenko and Alevras [33] proposed the concept of the N-mass pendulum. They experimentally studied the dynamic responses of a tri-mass pendulum [21, 34] and numerically presented the stochastic dynamics of a parametric rotating pendulum under realistic wave profiles [35]. They designed the parametrically excited pendulums for WECs. However, whether such a pendulum version benefits energy harvesting performance is unanswered. Cai and Zhu [13] developed a new surge–pitch-type WEC, wherein a novel double-mass pendulum (DMP) energy harvester was proposed and employed as an oscillator in WEC. The experimental frequency was tunable in the range from 0.2 Hz to 1.4 Hz, much lower than most low-frequency devices. In the wave flume test, the output voltage could be dramatically improved by up to 170% with frequency tuning; meanwhile, the DMP exhibited softening nonlinearity under large wave heights. Therefore, the systematic nonlinear analysis of the DMP will be inevitable to guide the frequency tuning techniques in the nonlinear conditions. In addition, the advantages and disadvantages associated with the nonlinearity of the DMP structure for energy harvesting are worthy of discussion. Particularly, how the rotating motions of the pendulum-type energy harvesters affect the energy harvesting performance largely remains unknown. The conditions for realizing the rotating motions of the DMP also need to be investigated.

This study aims to systematically analyze the nonlinear dynamics and energy harvesting performance of the emerging DMP structure, which is necessary to address the aforementioned unanswered questions. The contributions of this study are reflected by the following works that were done for the first time: (1) analytically investigating the frequency characteristics of the undamped DMP and numerically investigating the nonlinear characteristics of the damped DMP; and (2) illustrating the benefits of rotating motions in DMP energy harvesters and revealing the corresponding conditions for realizing rotating motions. Although the nonlinear analysis was conducted for the DMP structure, the methodology and the conclusions can be easily extended to other pendulum-type energy harvesters in the future. The study is organized as follows: after the introduction, Sect. 2 analytically introduces the frequency characteristic of undamped DMP and highlights the merits compared with the traditional simple pendulum. Section 3 reports the nonlinear dynamics of the DMP energy harvester through a bifurcation diagram, phase diagram, and Poincaré map. Subsequently, Sects. 4 and 5 present the power analysis and matching conditions of the rotating motions for the DMP energy harvester, respectively. Then, Sect. 6 discusses the parametric analysis of the DMP energy harvester by considering different influencing factors. Section 7 shows shake table tests of a scaled DMP model to partially validate nonlinear dynamics and energy harvesting analysis. Section 8 discusses randomly excited DMP energy harvesters. Finally, the major conclusions are summarized.

2 Theoretical formulation

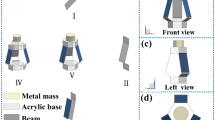
Figure 1a presents the structural configuration of a DMP consisting of two mass blocks. Despite their similar names, the DMP studied in this paper is completely different from traditional double pendulums. A DMP is a single-degree-of-freedom (SDOF) structure, while a double pendulum is a 2DOF structure. By adjusting the locations of double masses, a DMP can realize remarkably low frequency in the case of limited space. Thus, it is highly suitable for low-frequency energy harvesting.

Fig. 1
figure 1

Introduction of DMP

Full size image

By utilizing DMP’s ultra-low frequency characteristic that matches fairly with the wave frequencies, Cai and Zhu [13] designed and tested a DMP-based WEC, wherein the DMP energy harvester was regarded as an energy-extraction unit. Figure 1b shows the DMP energy harvester prototype developed by Cai and Zhu [13], which will also be used in the experimental tests presented in this study. The DMP energy harvester is essentially a damped DMP structure.

2.1 Undamped DMP

An undamped DMP structure is analyzed first in this subsection. If two identical masses mup = mlow = mm are used, the governing equation of the DMP without considering the damping effect and bar mass is as follows:

$$ m_{{\text{m}}} \left( {l_{1}^{2} + l_{2}^{2} } \right)\ddot{\theta } + m_{\text{m}} g\left( {l_{1} - l_{2} } \right)\sin \theta = 0 $$
(1)

where l1 and l2 are the distances from the pivot to the lower and upper masses, respectively. Evidently, l2 < l1. mm is the mass of each block. Although two mass blocks are used, the DMP is an SDOF pendulum (i.e., rotation angle θ). The initial frequency ω0 of the DMP under small vibration amplitude is as follows:

$$ \omega_{0} = \sqrt {\frac{{g\left( {1 - \alpha } \right)}}{{l_{1} \left( {1 + \alpha^{2} } \right)}}} $$
(2)

where α is the ratio of the upper- and lower-mass locations, as follows:

$$ \alpha = {{l_{2} } \mathord{\left/ {\vphantom {{l_{2} } {l_{1} }}} \right. \kern-0pt} {l_{1} }},\quad 0 \le \alpha \le 1 $$
(3)

According to Eq. (2), when α = 1, DMP becomes a zero-frequency device; when α = 0, it becomes a traditional simple pendulum. By setting the vertical position (θ = 0) as the zero potential energy plane, the total system energy can be obtained as the sum of the kinetic energy and potential energy of two masses, as follows:

$$ E = \frac{1}{2}m_{{\text{m}}} l_{1}^{2} \left( {1 + \alpha^{2} } \right)\dot{\theta }^{2} + m_{{\text{m}}} gl_{1} \left( {1 - \alpha } \right)\left( {1 - \cos \theta } \right) $$
(4)

In the undamped free vibration cases, the system vibration energy E is constant, and thus the angular velocity can be represented as follows:

$$ \dot{\theta }^{2} = \frac{{2E - 2m_{{\text{m}}} gl_{1} \left( {1 - \alpha } \right)\left( {1 - \cos \theta } \right)}}{{m_{{\text{m}}} l_{1}^{2} \left( {1 + \alpha ^2} \right)}} $$
(5)

If the DMP vibrates within θ \(\in \)(− π, π), the angular velocity becomes zero in the case of θ = θmax.

$$ E = m_{{\text{m}}} gl_{1} \left( {1 - \alpha } \right)\left( {1 - \cos \theta_{\max } } \right) $$
(6)

where E < 2mmgl1(1 − α). Combining Eqs. (5) and (6) yields

$$ \dot{\theta }^{2} = 2\omega_{0}^{2} \left( {\cos \theta - \cos \theta_{\max } } \right) $$
(7)

By using the trigonometric identity, Eq. (7) can be further rewritten as follows:

$$ \dot{\theta } = 2\omega_{0} \sqrt {\sin^{2} \left( {\frac{{\theta_{\max } }}{2}} \right) - \sin^{2} \left( {\frac{\theta }{2}} \right)} $$
(8)

Setting

$$ \sin \frac{\theta }{2} = \sin \frac{{\theta_{\max } }}{2}\sin \varphi $$
(9)
$$ k = \sin \left( {\frac{{\theta_{\max } }}{2}} \right) < 1 $$
(10)

where φ is a variable defined to facilitate the integration by substitution. Subsequently, an integral equation is formed by separating the variables:

$$ t_{0} = \frac{K(k)}{{\omega_{0} }} = \frac{1}{{\omega_{0} }}\int_{0}^{\pi /2} {\frac{{{\text{d}}\varphi }}{{\sqrt {1 - k^{2} \sin^{2} \varphi } }}} $$
(11)

where t0 = T/4 represents one-quarter of the period, and K(k) is the elliptic integral of the first kind. The period of the DMP can be obtained as follows:

$$ T = \frac{4K\left( k \right)}{{\omega_{0} }} = \frac{4}{{\omega_{0} }}\int_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {\frac{{{\text{d}}\varphi }}{{\sqrt {1 - k^{2} \sin^{2} \varphi } }}} $$
(12)

If the DMP swings over the vertical upright position corresponding to the maximum potential energy (i.e., E > 2mmgl1(1 − α)), the rotational motions occur, which means that (1) the angular velocity does not decay to zero, and (2) the maximum rotation angle θmax does not exist. Therefore, the maximum angular velocity \(\dot{\theta }\)0 at the vertical position θ = 0 is applied to estimate the dynamics of the DMP. In this study, the rotating motions are defined as the behavior that the DMP swings over the vertical upright position (i.e., θ exceeds π or − π). Such rotation motions can be either periodic or chaotic, where the former are termed periodic rolling motions, and the latter are termed chaotic motions that are unpredictable.

$$ \dot{\theta } = \sqrt {\dot{\theta }_{0}^{2} - 4\omega_{0}^{2} \sin^{2} \left( {\frac{\theta }{2}} \right)} $$
(13)

A new parameter κ is defined as follows:

$$ \kappa = \frac{{2\omega_{0} }}{{\dot{\theta }_{0} }} < 1 $$
(14)

According to Eqs. (13) and (14), the DMP period is derived as follows:

$$ T = \frac{2\kappa K\left( \kappa \right)}{{\omega_{0} }} = \frac{2\kappa }{{\omega_{0} }}\int_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {\frac{{{\text{d}}\varphi }}{{\sqrt {1 - \kappa^{2} \sin^{2} \varphi } }}} $$
(15)

Notably, if E = 2mmgl1(1 − α), the period becomes ∞. The corresponding energy E = 2mmgl1(1 − α) is referred to as the critical system energy that determines whether the swing-over rotational motions will occur or not.

The circular frequency of the undamped DMP ωd is summarized as follows:

$$ \omega_{{\text{d}}} = \left\{ {\begin{array}{*{20}c} {\frac{{\omega_{0} \pi }}{2K\left( k \right)}} & {if\;E < 2m_{{\text{m}}} gl_{1} \left( {l_{1} - \alpha } \right)} \\ 0 & {if\;E = 2m_{{\text{m}}} gl_{1} \left( {l_{1} - \alpha } \right)} \\ {\frac{{\omega_{0} \pi }}{\kappa K\left( \kappa \right)}} & {if\;E > 2m_{{\text{m}}} gl_{1} \left( {l_{1} - \alpha } \right)} \\ \end{array} } \right. $$
(16)

The frequency expression in Eq. (16) is similar to that of a simple pendulum; thus, the DMP structure evidently shows some similar features to a simple pendulum.

Figure 2 shows the frequency features of the DMP with a variation of the system energy (i.e., the sum of the potential and kinetic energy in Eq. (4)), wherein the frequencies are normalized by the initial frequency ω0, and the system energy is normalized by the critical energy threshold 2mmgl1(1 − α). The system parameters are set as the same as those in the following numerical analysis. The variation trend of the DMP frequency is a piecewise function. If the system energy E is less than the critical energy threshold, the DMP is in an oscillation state, i.e., θ \(\in \)(− π, π), and the DMP frequency decreases with the increase in normalized energy. A zero frequency appears at the critical energy. When the system energy is larger than the critical energy threshold, the DMP essentially is in the periodic rolling-motion state, and the DMP frequency increases with the increase in system energy. In the vicinity of the critical energy threshold, a very wide frequency bandwidth appears. Such a frequency trend confirms that DMP is, to some extent, similar to a simple pendulum.

Fig. 2
figure 2

Frequency of DMP with a variation of system energy

Full size image

2.2 Damped DMP

The DMP structures were originally proposed for low-frequency energy harvesting scenarios, such as WECs [13]. As shown in Fig. 1b, an electromagnetic transducer is connected to the rotating shaft of the DMP to realize the energy transduction function, forming a DMP energy harvester. The DMP energy harvester is essentially a damped DMP from the view of structural dynamics, wherein the damping effects are jointly contributed by the structural inherent damping, and the parasitic and electromagnetic damping of the transducer. Depending on the energy efficiency, part of the damping power is converted to the output power in the energy harvesting applications. Therefore, in this study, the DMP damping power is analyzed as approximate gross output power to evaluate energy harvesting performance, which is also a common practice in the field of vibration-based energy harvesting [36]. The energy conversion efficiency is influenced by multiple factors, and its discussion is out of the scope of the current study.

The governing equation of the DMP energy harvester is as follows:

$$ m_{{\text{m}}} l_{1} \left( {1 + \alpha^{2} } \right)\ddot{\theta } + c_{{\text{t}}} \left( {1 + \alpha^{2} } \right)\dot{\theta } + m_{{\text{m}}} g\left( {1 - \alpha } \right)\sin \theta = 0 $$
(17)

where ct is the total damping coefficient (unit: N·s/m), including the DMP inherent damping and transducer damping.

If the DMP is subjected to a horizontal base excitation (or ground motion), the corresponding governing equation is derived as follows:

$$ m_{{\text{m}}} l_{1} \left( {1 + \alpha^{2} } \right)\ddot{\theta } + c_{{\text{t}}} \left( {1 + \alpha^{2} } \right)\dot{\theta } + m_{m} g\left( {1 - \alpha } \right)\sin \theta = - m_{{\text{m}}} \ddot{x}_{g} \left( {1 - \alpha } \right)\cos \theta $$
(18)

Assuming the horizontal base acceleration as follows:

$$ \ddot{x}_{g} = A_{g} \cos \left( {\omega t} \right) $$
(19)

where Ag is the harmonic motion amplitude, and ω is the excitation frequency. Then, Eq. (18) can be rewritten as follows:

$$ \ddot{\theta } + 2\xi \omega_{0} \dot{\theta } + \omega_{0}^{2} \sin \theta = - \omega_{0}^{2} \gamma \cos \left( {\omega t} \right)\cos \theta $$
(20)

Without loss of generality, Eq. (20) is further nondimensionalized, as follows:

$$ \ddot{\tilde{\theta }} + 2\xi \dot{\tilde{\theta }} + \sin \tilde{\theta } = - \gamma \cos \left( {\lambda \tau } \right)\cos \tilde{\theta } $$
(21)

where

$$ \xi = {{c_{{\text{t}}} } \mathord{\left/ {\vphantom {{c_{{\text{t}}} } {2m_{{\text{m}}} \omega_{0} }}} \right. \kern-0pt} {2m_{{\text{m}}} \omega_{0} }} $$
(22)
$$ \gamma = {{A_{g} } \mathord{\left/ {\vphantom {{A_{g} } g}} \right. \kern-0pt} g} $$
(23)
$$ \lambda = {\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} $$
(24)
$$ \tau = \omega_{0} t $$
(25)
$$ \tilde{\theta }\left( \tau \right) = \theta \left( t \right) $$
(26)
$$ \dot{\tilde{\theta }} = {{\dot{\theta }} \mathord{\left/ {\vphantom {{\dot{\theta }} {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} $$
(27)
$$ \ddot{\tilde{\theta }} = {{\ddot{\theta }} \mathord{\left/ {\vphantom {{\ddot{\theta }} {\omega_{0}^{2} }}} \right. \kern-0pt} {\omega_{0}^{2} }} $$
(28)

where λ and γ are the normalized excitation frequency (the ratio of the excitation frequency to the initial frequency) and normalized excitation amplitude (the ratio of the excitation amplitude to the gravitational acceleration), respectively. The dimensionless governing equation of the DMP harvester, i.e., Eq. (21), is nearly identical to that of a damped simple pendulum. Notably, the parameters θ and its derivatives, as calculated in Eq. (20), are time variants with respect to t; whereas the corresponding dimensionless parameter \(\widetilde{\theta }\) and its derivatives in Eq. (21) are with respect to τ.

The average DMP damping power (treated as the gross output power) is computed as follows:

$$ P_{{\text{d}}} = \frac{1}{{t_{{\text{e}}} - t_{{\text{s}}} }}\int_{{t_{{\text{s}}} }}^{{t_{{\text{e}}} }} {c_{{\text{t}}} } \left( {l_{1}^{2} + l_{2}^{2} } \right)\dot{\theta }^{2} dt = \frac{1}{{t_{{\text{e}}} - t_{{\text{s}}} }}\int_{{t_{{\text{s}}} }}^{{t_{{\text{e}}} }} {2\xi \omega_{0} m_{{\text{m}}} } l_{1}^{2} \left( {1 + \alpha^{2} } \right)\dot{\theta }^{2} dt $$
(29)

where ts and te are the start and end measurement time, respectively. Correspondingly, the dimensionless power form is defined as follows:

$$ \tilde{P}_{{\text{d}}} = \frac{1}{{\tau_{{\text{e}}} - \tau_{{\text{s}}} }}\int_{{\tau_{{\text{s}}} }}^{{\tau_{{\text{e}}} }} {2\xi \sqrt {\frac{{\left( {1 - \alpha } \right)^{3} }}{{\left( {1 + \alpha^{2} } \right)}}} } \dot{\tilde{\theta }}^{2} d\tau $$
(30)

where the α-related items are retained in the dimensionless power expression. The power item in this study refers to the average value unless otherwise stated.

2.3 Unique DMP characteristics

Although the DMP and the traditional simple pendulum share similar dynamic equations, the DMP possesses the following unique characteristics, especially for the related dynamics with varying l1 and α (i.e., l1 and l2):

(1) DMP can effectively eliminate frequency dependence on pendulum length, realizing low frequency. Based on Eqs. (2) and (3), the DMP can easily realize extremely low initial natural frequency (even zero frequency) by tuning the l1 and α. However, a traditional simple pendulum requires an extremely long pendulum length (often become impractical) to realize a low initial frequency.

Figure 3 shows the normalized natural frequency of the DMP with a variation of dimensionless upper-mass position α and vibration amplitude, given a fixed lower-mass position l1. The DMP natural frequency is normalized by using (g/l1)1/2 in this figure. When α is increased from 0.2 to 0.96, the initial frequency decreases from 0.88 to 0.14, demonstrating that the additional upper mass could effectively reduce the pendulum frequency. The natural frequency of DMP decreases further with the increased vibration amplitude, considering the effect of softening nonlinearity. Given the vibration amplitude θmax = 0.95π, close to the critical energy threshold, the natural frequency can even decrease to 40% of the initial frequency setting. The possible low-frequency coverage demonstrates that the DMP is highly suitable for low-frequency energy harvesting or vibration control applications. As shown in Eq. (16) and Fig. 2, the frequency will be different once the rolling motion occurs, which will be discussed in the later section.

Fig. 3
figure 3

Natural frequency of DMP with a variation of upper-mass position and vibration amplitude. The calculated parameters are selected from the DMP prototype in the experimental test, adopted in Fig. 4 as well

Full size image

(2) The critical energy threshold (i.e., the potential energy barrier) of the DMP and simple pendulum are as follows:

$$ E_{{{\text{dmp}}}} = 2m_{{\text{m}}} gl_{1} \left( {1 - \alpha } \right) $$
(31)
$$ E_{{{\text{sp}}}} = 2m_{{\text{m}}} gl $$
(32)

where l is the pendulum length of the simple pendulum.

A low-frequency simple pendulum requires a long pendulum length, resulting in a high critical energy threshold. In contrast, a low-frequency DMP can be achieved by keeping a small l1 value and increasing α. Consequently, a lower-frequency DMP has a lower potential well. Figure 4 shows the normalized potential energy of the DMP with the variations in dimensionless upper-mass position α and rotation angle θ. The potential energy is normalized by using 2mmgl1.

Fig. 4
figure 4

Potential function of DMP with a variation of upper-mass position and rotation angle

Full size image

(3) A DMP energy harvester possesses more controllable parameters. The gross output power of a simple pendulum can be represented as follows:

$$ P_{{{\text{sp}}}} = \frac{1}{{t_{{\text{e}}} - t_{{\text{s}}} }}\int_{{t_{{\text{s}}} }}^{{t_{{\text{e}}} }} {c_{{\text{t}}} } l^{2} \dot{\theta }^{2} {\text{d}}t = \frac{1}{{t_{{\text{e}}} - t_{{\text{s}}} }}\int_{{t_{{\text{s}}} }}^{{t_{{\text{e}}} }} {2\xi \omega_{0} m_{{\text{m}}} } l^{2} \dot{\theta }^{2} {\text{d}}t $$
(33)

Considering Eqs. (21) and (29), if the parameters λ, γ, ξ, and ω0 are identical for damped simple pendulum and DMP, their corresponding angular velocities would be identical as well. In this scene, the power item of the simple pendulum is determined by the mass block mm only because the pendulum length has been determined by the initial natural frequency.

On the contrary, as indicated in Eq. (29), the DMP gross output power can be optimized by mm and α, considering the different combinations of l1 and α to achieve the same ω0. For example, parameters l1 = 0.10 m and α = 0.454 can realize an initial frequency of 1.06 Hz, the same as that of l1 = 0.125 m and α = 0.36.

Equation (34) presents the basic calculation of α to obtain a target ω0 value by varying l1,

$$ \alpha = {{\left( { - g + \sqrt {g^{2} - 4\omega_{0}^{4} l_{1}^{2} + 4\omega_{0}^{2} l_{1} g} } \right)} \mathord{\left/ {\vphantom {{\left( { - g + \sqrt {g^{2} - 4\omega_{0}^{4} l_{1}^{2} + 4\omega_{0}^{2} l_{1} g} } \right)} {2\omega_{0}^{2} l_{1} }}} \right. \kern-0pt} {2\omega_{0}^{2} l_{1} }} $$
(34)

The condition of β2 ≥ 1, wherein β = g/l1ω0, should be satisfied to obtain a positive α. The following analysis is based on a constant l1.

3 Nonlinear dynamics

The exact solution of the period (or frequency) cannot be obtained analytically after introducing the damping effect. Although some approximate analytical methods (e.g., harmonic balance method) enable solving the periodic steady-state responses of dynamic systems, they can hardly be applied to obtain high-precision results of complex nonlinear responses (e.g., chaotic behavior); therefore, efficient numerical methods are often adopted for nonlinear analyses [37]. In this section, the fourth-order Runge–Kutta method with a time step of 0.002 s is applied to obtain the numerical solution representing the nonlinear dynamics of the DMP energy harvester. Correspondingly, the numerical precision of this study is limited to O(0.0025). The parameters of the experimental DMP model, as shown in Table 1, are used in the numerical simulations in this section.

Table 1 DMP prototype parameters
Full size table

Angular velocity is often used to exhibit the period results of the pendulum-type structures, considering that the rotating motion achieves complete revolutions [38]. Figure 5a shows the bifurcation diagram of the dimensionless angular velocity \(\dot{\widetilde{\theta }}\) by setting the dimensionless upper-mass position α = 0.36 (the corresponding damping ratio ξ ≈ 8.71%), the normalized excitation frequency λ = 1/1.06, \(\dot{\widetilde{\theta }}\) = 0, and \(\widetilde{\theta }\)0 =  − 1/2π. With increase in excitation amplitude ratio γ, the DMP exhibits single-period, multiple-period, and chaotic behavior. Figure 5b shows a small range of excitation amplitude ratio γ (from 0.95 to 1.5) in detail. Under the given conditions: (1) if γ < 0.968, the DMP harvester is in a single-period oscillation state; (2) when 0.967 ≤ γ ≤ 1, a multiple-period vibrating structure is observed, wherein the multiple-period cascade is defined as the striking multiple-period (> 1) behavior in this study; (3) when 1 < γ < 1.038, the DMP harvester returns to vibrate in a single-period state; (4) near γ = 1.04, chaotic behavior is exhibited; (5) with increasing γ, the DMP harvester becomes a periodic vibrating structure until γ increases to approximately 1.22. These alternate occurrences of single-period, multiple-period, and chaotic vibrations demonstrate the complicated nonlinear dynamics of the DMP energy harvester. Besides, it is noted that when the initial conditions vary, the bifurcation results may be very different [39].

Fig. 5
figure 5

Bifurcation diagram of angular velocity with excitation amplitude ratio: λ = 1/1.06

Full size image

Correspondingly, Fig. 6 shows the bifurcation diagram of the maximum rotation angle \(\widetilde{\theta }\)max that is redefined to lie between − π and π to avoid the indecipherable infinite y-axis space. It not only exhibits similar vibrating period results to that of rotation velocity (i.e., Fig. 5), but also indicates the threshold of γ = 1.04 entering the rotating-motion state (see the red spot) in this special case.

Fig. 6
figure 6

Bifurcation diagram of rotation angle with excitation amplitude ratio: λ = 1/1.06

Full size image

Considering γ = 0.5, 0.98, 1.4, and 1.5 as representative examples, Fig. 7 presents the corresponding phase diagrams. Under the excitation amplitude ratio γ = 0.5, the rotation angle–velocity relationship shape spirals like an approximate ellipse. When γ = 0.98 and 1.4, the vibration behavior becomes multiple-period oscillation and rolling motion, respectively. Furthermore, the DMP energy harvester is like a chaotic system at γ = 1.5. The red dots in Fig. 7 represent the Poincaré map (also known as the state-space orbit), indicating the successive points over a certain time interval to show the stability. The Poincaré map of a chaotic system is fractal.

Fig. 7
figure 7

Phase diagram and Poincaré map of the DMP energy harvester under different excitation amplitude ratios γ

Full size image

4 Gross output power

4.1 Power FRF

Figure 8 shows the power frequency response function (FRF) under small-to-medium excitation amplitude ratios γ, when the dimensionless upper-mass position is α = 0.36. The y-axis herein is the DMP gross output power. It confirms that the DMP energy harvester exhibits rather softening nonlinearity with the increase in excitation amplitude ratios. Notably, the nonlinearity may be effectively reduced when the oscillation amplitude is mitigated by introducing a high-damping effect [14].

Fig. 8
figure 8

Dimensionless gross output power FRF of DMP energy harvester

Full size image

4.2 Rotating-motion benefits

The nonlinear behaviors typically depend on the initial conditions, especially for a chaotic system. Figure 9 presents the power variation by setting various initial rotation angles and zero initial angular velocity. Only the numerical response of time duration from 1000 to 2000 s is used to capture the steady-state gross output power. The results show that under small excitation amplitude ratios (0.5 < γ < 1), the output power level almost increases with the increment of γ, and the initial rotation angle \(\widetilde{\theta }\)0 has no influence on the steady-state output power. However, if the excitation amplitude ratio γ is sufficiently large (γ > 1), the initial conditions might affect the power generation, although the vibration is not chaotic. This result confirms that different initial conditions result in a change in the bifurcation analysis. Another interesting observation is an apparent power leap near γ ≈ 1, indicating the potential benefits of nonlinear energy harvesting, which has not been reported in typical linear energy harvesters.

Fig. 9
figure 9

Power analysis in different initial conditions and excitation amplitude ratios

Full size image

With a zoom-in plot of γ = 1.1–1.5 in Fig. 9b, increasing the excitation amplitude ratio γ does not correspond to a monotonous power increment in this specific range, and alternate power jumps and drops occur in the numerical analysis. Furthermore, considering the varying initial conditions-induced power difference in γ = 1.1, the corresponding phase diagrams depict the vibration behavior for two specific scenarios, namely, \(\widetilde{\theta }\)0 =  − 0.45π and − 0.5π, respectively, as shown in Fig. 9c and d. The DMP energy harvester performs a periodic rolling motion when \(\widetilde{\theta }\)0 =  − 0.5π, while it is in an oscillation state when \(\widetilde{\theta }\)0 =  − 0.45π; the corresponding power performances are marked by two red-cross points in Fig. 9b. To some extent, the finding indicates that rolling motion benefits power generation. As for the scenarios at γ = 1.3 and 1.5, the DMP energy harvester becomes a chaotic system, in which the initial conditions significantly influence the power generation. The chaotic behavior also includes unpredictable rotating motions; thus, their output power levels are above the power leap, demonstrating that the chaotic rotating motion improves power generation. It is noted that this observation is inconsistent with the findings by Daqaq et al. [40], who investigated a bi-stable beam-type piezoelectric energy harvester connecting to a buck circuit and observed the battery charging efficiency under chaotic inputs was less efficient than that under periodic inputs. The different observation in this study is likely due to the chaotic rotating motion of the DMP, which was not present in the beam-type structure.

As mentioned, the DMP damping power represents the potential harvestable power, often termed gross output power. Only part of the gross output power could be really harvested and stored in energy storage elements. The net output power of the DMP energy harvester is the product of the gross output power and the power efficiency, where the power efficiency is determined by the characteristics of an energy transducer and a specific energy harvesting circuit [36]. The power performance of the DMP structure connecting to a specific energy harvesting circuit should be quantified in future work.

5 Conditions of rotating motion

In view of the fact that rotating motions would benefit the energy harvesting performance, the realization conditions of rotating motions are investigated. According to Eq. (21), the influencing factors on the DMP dynamics are the excitation frequency ratio λ, excitation amplitude ratio γ, and damping ratio ξ. Figure 10 shows the parameter space plots calculated with different damping ratios ξ. Considering that the initial conditions may influence the DMP dynamic responses, vibration responses of the DMP energy harvester with initial rotation angles ranging in [− π, π] with an interval of 0.05π are calculated and averaged. The target of this figure is to identify the conditions that would result in the rolling or chaotic motion of a DMP energy harvester under horizontal ground motions. Five colors are used to classify the vibrating conditions of the DMP energy harvester: orangey-red colors represent the parameter regions, where the DMP energy harvester is always in a rolling motion or chaotic state (> 90% cases); cyan colors represent the parameter regions, where rotating motions can be observed in approximately 50%–70% of cases; and gray colors indicate those regions with less than 10%, treated as oscillations scenarios. The rolling and chaotic motions are not separately displayed in the figure. The analyzed case in Figs. 5 and 6 for a given excitation frequency ratio λ = 1/1.06 and excitation amplitude ratio γ = 0 − 3 is marked in Fig. 10b but for an initial condition of \(\widetilde{\theta }\)0 =  − 0.5π.

Fig. 10
figure 10

Parameter space plots indicating the thresholds for rotating motion

Full size image

Figure 10a–c illustrates that the boundaries separating the oscillation and the rotating motions show similar shapes, although the damping ratios are different. However, the corresponding excitation amplitude ratio γ to realize rotating motion generally increases as the damping ratio ξ increases. The parameter space plots can effectively indicate the conditions for rolling or chaotic motions that lead to attractive power leaps. In general, the rotating motions do not occur at low excitation amplitude ratios γ; with the increase in excitation amplitude ratio γ, the rotating motions may occur in a wider excitation frequency ratio λ. The tips of the orangey-red and cyan areas show the lowest excitation amplitude ratio γ required by rotating motions, which typically occurs when the excitation frequency ratio λ is slightly less than 1. For example, in the analyzed DMP energy harvester with a damping ratio ξ = 3.96%, the threshold for entering the rotating-motion state is approximately γ = 0.8 when λ = 0.78. Considering that the DMP has a tunable frequency to realize any desirable frequency ratio if necessary, the rotating motion can be realized as long as the excitation amplitude ratio γ > 0.8. Such excitation conditions are feasible in practical scenarios. For example, ocean waves with a period of 3 s and a height of 1.8 m approximately correspond to γ = 0.8.

Although the rotating-motion parameter space plots of the DMP harvester are nearly the same as those of a simple pendulum, the feasibilities of realizing rotating motions are very different. The results in Fig. 10 imply that the pendulum frequency should be tuned close to or even significantly lower than the excitation frequency to facilitate rotation motions. Given a low excitation frequency (e.g., ocean wave frequencies), frequency matching by a traditional simple pendulum is remarkably challenging as an impractically long pendulum length may be required. Moreover, the power performance of the DMP and single-pendulum energy harvesters should be significantly different, given that the individual pendulum lengths are different.

6 Parametric analysis

This section presents the parametric analysis of dimensionless upper-mass position α with frequency ratio λ and amplitude ratio γ.

6.1 Upper-mass position and excitation frequency

Figure 11 shows the dimensionless gross output power results with variations of upper-mass position α and frequency ratio λ, wherein the excitation amplitude ratio γ is fixed, and an averaging process for different initial conditions is adopted, as done in Fig. 10. Given a fixed α value, the corresponding horizontal line in Fig. 10 essentially represents a gross output power FRF, similar to Fig. 8. The following results are observed: (1) the maximum power occurs at the shift-left locations of excitation frequency ratio λ = 1 due to the softening nonlinearity. The result, to some extent, confirms that the approximate frequency matching leads to optimal output power; (2) the effective harvesting bandwidth at γ = 1.4 is much broader than that of γ = 0.2, and such a wide plateau in the harvesting performance is believed as a result of rotating motions; (3) higher output power is generated at smaller α corresponding to a higher natural frequency for both amplitude scenarios; (4) when γ = 1.4, the discrete power peaks or valleys occur alternately around λ = 1–1.5, which is believed as results of alternating nonlinear frequency matching and mismatching.

Fig. 11
figure 11

Gross output power with a variation of α and λ

Full size image

6.2 Upper-mass position and excitation amplitude

By selecting an excitation frequency equal to the initial natural frequency corresponding to α = 0.41, Fig. 12 presents the dimensionless gross output power results with variations of upper-mass position α and excitation amplitude ratio γ. A monotonous power increase is observed in the small γ range; subsequently, alternate power peaks and valleys occur with increasing γ; in the case of relatively larger γ, a rotating motion-induced higher-level power zone is observed as expected; the large power occurs at α = 0.2–0.4, smaller than 0.41 because of the softening nonlinearity.

Fig. 12
figure 12

Gross output power with a variation of α and γ: initial frequency matching at α = 0.41

Full size image

7 Experimental test

7.1 Experimental setup

Shake table tests were conducted to validate the DMP energy harvester simulations. The DMP energy harvester, as shown in Fig. 1, was the same as that used by Cai and Zhu [13], who conducted the proof-of-concept tests of a DMP oscillator in WEC but ignored its nonlinearity characteristic. Figure 13 shows the schematic of the experimental setup, wherein a 3D displacement measurement system (model no. XTDIC-CONST-SD23M) was used to record the DMP rotation angle, and a data acquisition system (model no. KYOWA EDX-100A) was used to measure the output voltage of the DMP energy harvester. The sampling frequency of the two devices was set to 100 Hz. The 3D displacement measurement system based on the digital-image-correlation technology consists of two BASLER cameras with a maximum of 160 fps and a lens focal length of 12 mm. The theoretical precision of the displacement measurement can be up to 0.01 pixel after calibrations. The rotation angle was measured by setting the encoded points in the vertical bar and the bearing support plate (see Fig. 13). The shake table (model no. MTC-6DOF-2000KG) generated harmonic or sweep horizontal ground motion for the DMP structure. The shake table has a maximum payload of 2000 kg and enables low-frequency motions (as low as 0.1 Hz). The suggestive maximum horizontal excursion, velocity, and acceleration are 190 mm, 400 mm/s, and 0.5 g, respectively. Figure 14 shows the photographs of the experimental setup. Through free vibration tests, the natural frequency and the inherent damping ratio of the DMP without an electromagnetic transducer were estimated as 1 Hz and 0.002, respectively, when α = 0.36 (i.e., l2 = 0.045 m). This DMP is referred to as a low-damping DMP, whereas the DMP connected with an electromagnetic transducer is called a high-damping DMP in this section. Table 1 lists the DMP prototype parameters, where the upper-mass position l2 = 0.035–0.125 m corresponds to α = 0.28–1, and the bar mass is ignorable. In addition, due to the performance limitation of the 3D measurement system, only approximately 60 s videos could be recorded if a 100 Hz sampling frequency was applied. Thus, to obtain the steady state of the DMP, the 3D system was set to begin recording the responses after 10 min of DMP vibrations. This experimental study aims to provide a preliminary validation of the numerical modeling of the DMP structure. More comprehensive experimental investigations of the DMP energy harvesting performance considering different load resistances, excitation frequencies, and frequency tuning are out of the scope of this paper and will be reported in future studies.

Fig. 13
figure 13

Schematic of the experimental setup for the DMP test

Full size image
Fig. 14
figure 14

Photograph of the experimental setup

Full size image

7.2 Experimental results

7.2.1 Low-damping DMP

Figure 15a and b shows the bifurcation diagram of the maximum rotation angle of the low-damping DMP subjected to the horizontal ground motions with excitation frequency ratios λ = 0.9 and 1, respectively (corresponding to 0.9 and 1 Hz). In the case of λ ≈ 0.9, the low-damping DMP vibrated in the single-period state under relatively small vibration amplitudes, but it exhibited multiple-period and chaotic behavior in the case of relatively larger vibration amplitudes. A sudden jump of the rotation degree was observed at the excitation amplitude ratio of approximately γ ≈ 0.08 because of the nonlinear resonance, where the amplitude-dependent natural frequency decreased to nearly 0.9 Hz. However, such a rotation angle jump occurred at approximately γ ≈ 0.15 in the case of numerical modeling. The discrepancy might be caused by the discrepancies in the estimated inherent damping and natural frequency between numerical and experimental conditions. When the frequency ratio λ ≈ 1, only a single-period behavior was observed in the experiment. The result was quite consistent with the analyzed rotating-motion conditions: the excitation-amplitude-ratio condition undertaking rotating motion at the shift-left region of λ ≈ 1 is smaller than that at exactly λ = 1. In general, the experimental results agreed fairly with the numerical modeling in the two excitation scenarios. Note that the applied horizontal velocity reached the maximum allowable value of 400 mm/s, so higher γ values could not be tested.

Fig. 15
figure 15

Bifurcation diagram of the rotation angle of low-damping DMP

Full size image

Considering γ = 0.16, 0.28, and 0.29, Fig. 16 shows the corresponding phase diagrams of low-damping DMP, where the red dots represent the Poincaré map. The phase diagrams were not very smooth due to the noise amplification effect in the finite difference calculation of angular velocities from rotation angles.

Fig. 16
figure 16

Phase diagram and Poincaré map of low-damping DMP: λ ≈ 0.9

Full size image

7.2.2 High-damping DMP

Figure 17 shows the maximum–rotation–angle bifurcation diagram of the high-damping DMP. In both frequency scenarios, only single-period behavior was observed for the high-damping DMP. Furthermore, due to the transducer damping, the maximum rotation angles of the high-damping DMP were relatively smaller than the low-damping case under the same excitation conditions. Similar to the low-damping DMP case, the maximum excitation amplitude ratio γ was capped by the testing capability of the shake table. In the case of λ ≈ 0.9, the shapes of the numerical modeling agreed with that of the experimental results, but the amplitude threshold entering the nonlinear resonance was quite different. On the contrary, the numerical modeling of the cases with λ ≈ 1 matched consistently with the experimental results. Results in Figs. 15, 16, and 17 demonstrated the effectiveness and fair accuracy of the DMP numerical modeling.

Fig. 17
figure 17

Bifurcation diagram of the rotation angle of high-damping DMP

Full size image

Figure 18 shows the open-circuit voltage of the high-damping DMP in the sweep tests with an excitation amplitude ratio of γ = 0.125 and a frequency sweep rate of 1/600 Hz/s. The backward and forward sweep tests were conducted. Such different profiles of the two sweep results demonstrated the nonlinear dynamics of DMP. Note that when higher transducer damping is considered, the vibration amplitude is reduced and the corresponding nonlinear dynamics are weakened.

Fig. 18
figure 18

Open-circuit voltage of high-damping DMP in the sweep test

Full size image

Figure 19 shows the estimated gross output power by using the measured rotation degrees. The power trend with increase in excitation amplitudes was similar to the corresponding response in Fig. 17. The DMP power performance under an excitation frequency of 0.9 Hz is smaller than that of 1 Hz at small excitation amplitudes. However, a sudden power jump at nearly γ ≈ 0.12 was shown due to the approximate nonlinear resonance and became superior to that of 1 Hz. The gross output power was estimated as approximately 0.6 W in the case of λ ≈ 0.9 and γ ≈ 0.28. Considering the theoretical and practical upper bounds of the energy harvesting efficiency [41], the DMP is potentially an excellent energy harvesting design.

Fig. 19
figure 19

Gross output power estimation of high-damping DMP

Full size image

8 Discussions

Random excitation is another common type of environmental load. This section will briefly discuss the performance of a randomly excited DMP energy harvester. Without loss of generality, the random excitation was modeled as white noise with a constant power spectrum density (PSD) [42]. The Monte Carlo simulation is performed to assess the DMP gross output power. The frequency bandwidth of the excitation is 0–500 Hz, the DMP dimensionless upper-mass position is α = 0.36, and the initial condition is set as \(\widetilde{\theta }\)0 = 0. Figure 20a shows the PSD example of one simulation, wherein the RMS amplitude ratio is γ = 3.16. The PSD generally meets the constant PSD assumption. Figure 20b presents the DMP gross output power under white noise excitation with different RMS excitation amplitude ratios γ. With the increase in excitation amplitude, the gross output power increases. Given the same excitation amplitude, the average power of each simulation is quite steady.

Fig. 20
figure 20

Results of DMP structure under random excitation

Full size image

It is not surprising to observe that the gross output power of a randomly excited DMP is considerably lower than that in resonant conditions. Notably, the DMP structure was initially designed as an energy-extraction unit for WEC [13]. The DMP can tune its frequency within the typical range (0.1–1 Hz) of ocean waves and resonate with regular waves (like harmonic input) to offer favorable energy harvesting performance. The wave profiles can provide sufficiently large excitations to realize rotating motions. In contrast, the DMP power performance is expected to be relatively lower under irregular waves associated with random and broadband features. The wave profiles at specific ocean regions are typically characterized by a wave spectrum with a dominant frequency (e.g., the JONSWAP wave spectrum [43]). The DMP frequency can be tuned to track the variable dominant frequency of irregular waves in this scenario.

9 Conclusions

This study systematically analyzes the nonlinear dynamics and energy harvesting performance of the DMP, a recently emerging tunable low-frequency device. The analytical derivation of the DMP frequency characteristic is conducted. The differences between DMP and simple pendulum are elaborated analytically through the potential energy functions, the realization of low natural frequency, and the controllable parameters influencing gross output power. The nonlinear dynamics and output power performance of the DMP energy harvester are analyzed numerically and experimentally. The results suggest the benefits of utilizing the rotating motions of the pendulum-type energy harvester for energy harvesting; the DMP is a good energy-extraction device for low-frequency energy harvesting scenarios, such as ocean waves energy harvesting. The specific results are remarked as follows:

  1. (1)

    The natural frequency characteristic of the undamped DMP is similar to that of the undamped simple pendulum. If the system energy is less than the critical system energy threshold, the DMP natural frequency decreases with increase in system energy. If the energy input is larger than the energy threshold, the DMP natural frequency increases with increase in system energy. The DMP is a zero-frequency device at the critical energy threshold and shows a broad bandwidth in the vicinity of the critical energy.

  2. (2)

    The DMP structure exhibits several unique characteristics compared with a simple pendulum. Lower-frequency DMP owns a lower potential well. The DMP can realize ultra-low frequency in limited space, even zero-frequency theoretically. The DMP energy harvester has more controllable parameters for the gross output power.

  3. (3)

    When the DMP energy harvester suffers from horizontal ground motion, only the damping ratio, frequency ratio, and excitation amplitude ratio influence the DMP dynamics.

  4. (4)

    The DMP energy harvester has complicated nonlinear dynamics, exhibiting alternate single-period, multiple-period, and chaotic vibration behavior with increasing excitation amplitude ratio. Such results are also observed in the parametric analysis of gross output power.

  5. (5)

    DMP rotating motions enhance the energy harvesting performance, regardless of chaotic or rolling motions. A remarkable power leap and a broader harvesting bandwidth can be observed in the rotating-motion state.

  6. (6)

    The rotating motions first occur near the excitation frequency ratio of 1 when the excitation amplitude ratio is small. A lower damping ratio corresponds to a lower amplitude ratio for realizing rotating motions.

  7. (7)

    The gross output power generally decreases with increasing upper-mass positions (a lower initial natural frequency). A wide power plateau corresponding to a broader harvesting bandwidth is observed under a relatively large excitation amplitude ratio.

  8. (8)

    The single-period, multiple-period, and chaotic behavior of the low-damping DMP was observed in the shake table test, which matched fairly with the numerical modeling. In the case of high-damping DMP, only single-period behavior was observed due to the limited testing capability of the used shake table and relatively large transducer damping.

Although the analysis is conducted explicitly for the DMP, the methodology and conclusions can be easily extended to other pendulum-type structures. The DMP was initially intended for WECs. The DMP will work efficiently under regular waves or irregular waves with dominant frequencies. The power performance analysis of large-scale DMP-based WEC under realistic wave profiles will be included in future work.