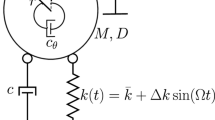Optimized and robust orbit jump for nonlinear vibration energy harvesters

Abstract

This paper introduces an optimized orbit jump strategy for nonlinear vibration energy harvesters (VEHs). Nonlinear VEHs are a promising alternative to linear VEHs due to their broadband characteristics. However, they exhibit complex dynamical behaviors, including not only high-power inter-well orbits but also low-power intra-well orbits and chaos. The existence of low-power orbits in their dynamics can restrict their energy harvesting performance. In order to overcome this issue, this study investigates an orbit jump strategy that allows the VEH to transition from low-power intra-well orbits to high-power inter-well orbits. The orbit jump strategy, which is based on varying the buckling level of a bistable VEH, has been previously studied but not yet optimized. In this study, we optimize this orbit jump strategy to ensure practical reproducibility and robustness against variations in parameters or excitation. Through the combination of thorough experimental identification and high-performance computing of the complex transients during orbit jumps, we achieved high numerical accuracy in orbit jump modeling. This was possible by a developed Python CUDA code using GPU parallel computing to handle a large number of numerical resolutions of the nonlinear VEH model. These simulations facilitate the optimization of both the robustness and the energy cost of orbit jumps, based on a novel numerical criterion. Experimental tests were performed on a bistable VEH over a frequency range of 30 Hz, validating the numerical results obtained with the optimized orbit jump strategy. Experimental results show an average success rate of 48%, despite a variation of $\pm 15\%$ in the starting and ending times of the jump, leading to a robust and optimized orbit jump strategy. The proposed optimization procedure can be applied to other orbit jump strategies, and other types of nonlinear VEHs. The results indicate that the energy consumption required for a successful orbit jump ranges between 0.2 and 1 mJ, and can be restored within 0.2 s in the worst case.

1 Introduction

Energy harvesting is seen as a viable alternative to the use of batteries for supplying low-power electronic systems. The sources of energy that can be harvested are diverse and numerous, including solar radiations, fluid flows, electromagnetic waves and mechanical vibrations. In particular, vibration energy is naturally ubiquitous even in confined environments with little solar and thermal energies available. This study focuses on energy harvesters that convert vibrational energy from ambient sources into electricity [1].

Vibration energy harvesters (VEHs) can be divided into two categories: linear VEHs, which rely on linear oscillators, and nonlinear VEHs that exploit nonlinear oscillators. Historically, linear VEHs have been studied because their behavior is easier to predict and because they can be more easily manufactured. However, linear VEHs have a narrow frequency bandwidth, and as a result, their energy harvesting performance drastically decreases when there is a mismatch between the driving frequency and their natural frequency [2, 3]. This makes linear VEHs unsuitable for applications with a time-varying spectrum, limiting their use in most environments. This has led to an increased interest in the development of nonlinear VEHs, especially bistable VEHs.

Fig. 1

Orbit jump strategy using buckling level adjustments of bistable VEH to switch from intra-well to inter-well orbits. Illustration inspired from [4]

The study of bistable VEHs started in 2008–2009 with the works of Shahruz et al. [5] and Cottone et al. [6]. Nonlinear VEHs have the advantage of exhibiting broadband behavior [7, 8], but their complex dynamics with multiple orbits can result in a drastic difference in power for a given driving frequency. Indeed, as illustrated in Fig. 1, bistable VEHs exhibit low-power intra-well orbits (in red), as well as high-power inter-well orbits (in blue). Many studies have aimed to better understand the underlying dynamics of multi-stable energy harvesters [9,10,11] (for reviews, see [12,13,14]). In particular, intra-well orbits can lead to poor energy harvesting performance, which hinders the advantages of nonlinear VEHs, and is a major limitation of this type of energy harvester.

To enhance the performance of nonlinear VEHs, researchers have developed methods called orbit jump strategies. As shown in Fig. 1, orbit jump strategies enable nonlinear VEHs to transition from low-power orbits (in red) to higher power orbits (in blue), maximizing energy harvesting performance and exploiting their full potential (for review in multi-stable VEHs control, see [13] and for broader review of nonlinear dynamical system control, see [15]). The concept of orbit jump strategies in energy harvesting was first introduced a decade ago, with early studies conducted by Erturk et al.  [16], Sebald et al.  [7, 17] and Masuda et al. [18]. Erturk et al.  [16] applied a “hand impulse” to impart enough velocity to a piezomagnetoelastic energy harvester, causing the nonlinear VEH to transition to the high-power orbit. To the best of our knowledge, this is the first experimentally and numerically demonstrated orbit jump strategy in the literature, using an additional velocity input to enhance the performance of nonlinear VEH. Sebald et al.  [7] proposed a method, Fast Burst Perturbation (FBP), which consists in adding an external sinusoidal excitation during a few cycles. This perturbation is added to either the ambient excitation or the voltage of the electromechanical transducer in order to use the latter as an actuator (which is limited by the maximum amplitude that can be injected into the electromechanical transducer before it undergoes a dielectric breakdown). The authors validated the FBP method through numerical simulations [7] and experimental measurements [17]. Thereafter, Masuda et al. [18] investigated an orbit jump strategy by theoretically and numerically analyzing the variations in the load resistance value as a function of the displacement amplitude. They implemented negative resistance, acting as a negative damping, to destabilize low-power orbits during periods of low displacement amplitude. Once the nonlinear VEH stabilizes on a high-power orbit, with a large amplitude of displacement, the load resistance returns to its initial positive value. However, the study is limited to numerical simulations and requires further experimental validation. Moreover, this orbit jump strategy is only valid for a specific range of accelerations and frequencies.

Subsequently, as illustrated in Table 1, the manner in which the nonlinear VEH is perturbed permits the classification of orbit jump strategies into two distinct categories:

• (i) Orbit jump strategies that add a temporary external force to the nonlinear VEH (e.g., a pulse on the voltage across the electromechanical transducer) [7, 16, 17];

• (ii) Orbit jump strategies which involve temporarily modifying the dynamic characteristics of the nonlinear VEH (e.g., its damping or stiffness) [18].

Furthermore, subsequent studies have placed increased emphasis on analyzing the energy expenditure associated with orbit jump strategies, which is a critical factor to consider. Indeed, if the energy required to realize the orbit jump is not quickly recovered, the effectiveness of this approach is questionable. With regard to orbit jump strategies which introduce an external signal to disturb the system, Mallick et al. [19] used the FBP technique by superimposing a sinusoidal signal on the voltage across the electromechanical transducer over 15 cycles to use the transducer as an actuator.

Table 1 Main properties associated to the both groups of orbit jump strategies defined in the current state of literature

They pointed out the effect of the phase shift between the ambient excitation and the resulting excitation¹ on the success of the orbit jump. That means, the success of the orbit jump strategy depends both on the nature of the perturbation and on the control of its timing. Their work is also among the first to consider the energy cost of the orbit jump strategy and gives the time needed to recover the energy consumed during the orbit jump (${2}\,\hbox {s}$), as shown in Table 1.

Udani et al. [4] added an artificial excitation to the ambient excitation creating a new excitation phase-shifted from the original ambient excitation. They demonstrated that the resulting modification of the dynamics and the basins of attraction of the orbits could facilitate escaping from the potential well. However, modifying the ambient excitation is not easy to implement in practice, limiting the applicability of their study. In a previous study [28], they developed a search algorithm in order to design an efficient attractor selection strategy. Notably, their approach was the first to search for the parameters of the perturbing signal that make their orbit jump strategy efficient.

On the other hand, a number of orbit jump strategies that involve temporarily modifying the nonlinear VEH’s dynamic characteristics have been developed. Lan et al.  [21] employed a method that emulates negative resistance using a negative impedance converter, similar to the approach taken by Masuda et al.  [18]. They highlighted that the primary factor that disrupts the system is the increase in piezoelectric voltage resulting from negative resistance emulation, rather than damping modification, since the duration of orbit jump is brief.

Similarly, Ushiki et al.  [23] defined a self-powered stabilization method using a negative impedance converter. Although they successfully destabilized low-power orbits across a frequency band of ${23}\,\hbox {Hz}$, the process of achieving positive energetic balance takes between 10 and ${100}\,\hbox {s}$, indicating that there is room for improvement in this aspect of the study.

Wang et al. [22] defined a load perturbation method based on the electrical load effects on the dynamics to attain high-power orbits. They disconnected the electrical load by opening a switch that was in series connection with the load and driven by an integrated circuit chip. This resulted in a reduction of the total damping rate of the VEH. However, this orbit jump strategy is only applicable for a specific combination of driving frequencies and amplitudes, making it non-robust and non-reproducible. Later, in order to decrease the energy injection of the orbit jump, Wang et al.  [24] used a Bidirectional Energy Conversion Circuit (BECC) that includes the energy extraction circuit. The experimental test shows a jump duration of ${10.9}\,\hbox {s}$, which requires an energy of ${22}\,\hbox {mJ}$. The corresponding recovery time of ${2}\,\hbox {min}$ suggests that the orbit jump strategy could benefit from optimization.

Several recent studies have investigated the modification of the buckling level in nonlinear VEHs as illustrated in Fig. 1. Huguet et al. [25] introduced the buckling level modification technique, using an additional electromechanical transducer² to alter the buckling level of the VEH. Figure 1 provides a summary of the orbit jump strategy process. In particular, the left part of Fig. 1 shows how the orbit jump strategy works: (i) initially, the system (represented by a green dot) oscillates in its potential wells, then (ii) the buckling level of the VEH increases, which modifies its potential wells shape, represented by a dashed curve. This modification propels the mass into this deeper potential, giving it a certain amount of potential energy. Subsequently, (iii) the buckling level returns to its original value and the system transitions to high-power orbit. The study of Huguet et al.  demonstrated the effectiveness and reproducibility of this orbit jump through numerous experimental tests, computing jumping probabilities across six tested driving frequencies. Furthermore, the study demonstrated that the energy consumed by the orbit jump strategy was quickly restored (in approximately 1 s), as shown in Table 1. Although this orbit jump strategy has been partially empirically optimized, a complete optimization has not yet been conducted, which could further enhance its robustness and effectiveness.

Huang et al. [27] introduced a new Voltage Inversion Excitation (VIE) method, which reverses the voltage of the piezoelectric actuator at specific times to provide additional excitation to nonlinear VEH. However, this method consumes a significant amount of energy. To address this issue, they developed a more complex combination of two orbit jump strategies, which generally involve longer jump durations, as depicted in Table 1.

Yan et al. [26] used a stiffness modulation circuit to temporarily adjust the stiffness of a monostable softening VEH and experimentally demonstrated the VIE technique at three frequencies, which can be expanded to more frequencies.

Although there is a large pool of research on designing orbit jump strategies, in general, very few strategies are optimized (i.e., a comprehensive optimization of the orbit jump parameters) in the literature as can be seen from Table 1. In most articles, the orbit jump parameters are determined through a preliminary numerical study or intuitive reasoning, rather than effective optimization. This hinders the performance of orbit jumps in the literature because they generally exhibit poor reproducibility, low robustness to parameters or excitation variations, and thus cannot be used in most application cases.

In this paper, we propose optimizing an orbit jump strategy in order to maximize its robustness, enhance reproducibility and ensure successful orbit jumps even when parameters or excitations vary. We focus our analysis on orbit jump strategies based on the buckling level modification (as illustrated in Fig. 1), originally introduced and partially optimized in [25]. Based on a thorough experimental identification, combined with high performance in the numerical simulation of transients, we have validated the possibility of accurately modeling orbit jumps numerically. From these simulations, we have been able to optimize the robustness, as well as the invested energy of the orbit jumps. This has been made possible thanks to the definition of a new numerical criterion assessing the harvested energy and the robustness of the orbit jumps. The obtained optimized orbit jumps have been experimentally validated and show better performance both in terms of jumping time, recovery time and robustness among the literature. This article is organized as follows: Section 2 gives the electromechanical model of the bistable VEH and an overview of its dynamics. Then, Sect. 3 presents the orbit jump strategy and its optimization based on a criterion which takes into account both the effectiveness and the robustness of the orbit jump strategy. Finally, Sect. 4 presents experimental validation of the optimized orbit jump strategy and proves its effectiveness under excitation amplitude variations.

2 Electromechanical dynamics of bistable VEH

This section introduces the electromechanical model of a bistable VEH, along with a summary of the underlying dynamics with multiple behaviors, highlighting the interest of introducing orbit jump strategies.

2.1 Bistable VEH model

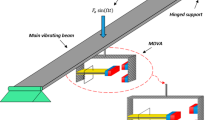
This paper studies a Duffing-type bistable VEH shown in Fig. 2.

Fig. 2

a Schematic structure of the bistable VEH. b Experimental bistable VEH studied in this article from [29]

This VEH (for more details on its design, see [29]) consists of buckled steel beams of length L to which a proof mass M is attached that can oscillate between two stable equilibrium positions, $-x_w$ and $x_w$. The VEH is driven by a sinusoidal excitation with a driving frequency $f_d=\omega _d/2 \pi$ and a constant acceleration amplitude A. Two amplified piezoelectric actuators (APA) are employed, with the smaller—Energy harvesting APA—having a force factor $\alpha$, a clamped capacitance $C_p$ and the capacity to extract energy from the mechanical oscillator.

The electrodes of the energy harvesting APA are connected to a resistance R. The second and stiffer APA—Tuning APA— acts as an actuator to implement the orbit jump strategy by temporarily modifying the buckling level of the nonlinear VEH. Therefore, this orbit jump strategy belongs to the category of orbit jump strategies that modulate the nonlinear VEH characteristics. The energy harvesting APA is the APA120S, and the tuning APA is the APA100M manufactured by Cedrat Technologies (France). The model of bistable VEH [25] is given in Eq. (1),

Where x denotes the mass displacement, $\dot{x}$ its velocity and $\ddot{x}$ its acceleration. The voltage in the energy harvesting APA is noted v. Note that the equations of the model (1) do not contain any term related to the tuning APA due to its higher stiffness compared to the harvesting APA, and thus does not have any significant influence on the dynamics of the VEH. The natural angular frequency $\omega _0$ and the quality factor Q of the considered symmetrical bistable VEH are determined by the underlying equivalent linear model [30], which is obtained by considering small oscillations of the mass around one of its two stable equilibrium positions. The tuning APA voltage, denoted $v_w$, is used to modulate the buckling level of the bistable VEH and facilitate transitions from low-power to high-power orbits. Table 2 shows the parameter values of the bistable VEH studied in this paper, which were determined experimentally through low-power orbit characterizations using weak sinusoidal vibrations (see Appendix 5.5 for more details on the characterization of the experimental prototype). Note that for simplicity, we assumed that the force factor of the bistable VEH was the same as that of the energy harvesting APA.

Table 2 Parameter values for the buckled-beam nonlinear VEH [25]

2.2 Bistable VEH behaviors

The dynamics of a bistable VEH may exhibit multiple behaviors for a given driving frequency, including low-power intra-well orbits, high-power inter-well orbits and chaotic orbits. In this study, we define an orbit as robust if it is less sensitive to perturbations and easily attainable. In order to detect all possible behaviors in the frequency range of $[{20}\,\hbox {Hz}, {100}\,\hbox {Hz}]$ and $A={4}\,\hbox {m/s}^{2}$, the nonlinear ordinary differential equations (ODEs) system (1) was solved for a large number of initial conditions using the Dormand–Prince method [31].

Since the nonlinear ODEs (1) can be solved independently across multiple resolutions, this problem is well suited to parallel computing that can greatly enhance computational performance. For this task, a custom Python CUDA code was executed on an NVIDIA RTX A5000 GPU featuring $8 \, 192$ CUDA cores, enabling the resolution of (1) with $80 \, 000$ distinct initial conditions for each driving frequency. In symmetric bistable VEH, the elastic potential energy is a quartic function of (t, x) whose expression is given in (2). Note that the natural angular frequency $\omega _0$ depends on the value of $x_w$ and will therefore be influenced during the orbit jump. The mean harvested power (for a given orbit) of the bistable VEH is the mean power dissipated in R and is expressed by (3),

$$\begin{aligned} E_p(t)= & {} \dfrac{M \omega _0^2}{8x_w^2} \left( x + x_w \right) ^2 \left( x - x_w \right) ^2 \end{aligned}$$

(2)

$$\begin{aligned} P_h= & {} \dfrac{1}{T} \int _0^{T} \dfrac{v^{2}}{R}{\text {d}}t \end{aligned}$$

(3)

where T is the period of the displacement x.

Fig. 3

a Mean harvested power $P_h$ as a function of the driving frequency $f_d$, b–d basins of attraction, attractors and orbits of coexisting behaviors in the dimensionless phase plane $(x/x_w,\dot{x}/x_w \, \omega _0)$ for $f_d={{40}\,}\hbox {Hz}$, $f_d={50}\,\hbox {Hz}$ and $f_d={65}\,\hbox {Hz}$, respectively. The denomination “Other” (in gray) regroups all the orbits not indicated in the legend (i.e., sub-harmonic orbits and chaos). For example, at ${65}\,\hbox {Hz}$, the highest orbits (whose basins are given in (d)) are sub-harmonic three inter-well orbits, which are characterized by a mass motion frequency three times lower than the driving frequency. The basins of attraction in (b–d) were obtained after $80 \, 000$ resolutions of the ODE system (1)

Figure 3a shows the mean harvested power associated with existing orbits as a function of driving frequency $f_d$ in [${20}\,\hbox {Hz}$, ${100}\,\hbox {Hz}$] when $R=1/2 C_p \omega _d$ for each driving frequency (which corresponds to the resistance value maximizing electrically induced damping [32] whose formula is valid for a harmonic excitation). Note that “Other” gathers sub-harmonic orbits and chaos [8, 33]. Producing Fig. 3a requires $80 \, \times \, 80 \, 000$ numerical computations, which can be completed in just a few minutes using parallel computing instead of the several hours required for sequential computing on CPU. It is worth mentioning that both power and existence of orbits vary with the driving frequency. As seen in Fig. 3a, the bistable VEH dynamics exhibits multiple orbits with various powers. As a matter of example, the high-power inter-well orbit allows to harvest 102 times more power than low-power intra-well orbits for $f_d={30}\,\hbox {Hz}$.

The high-power inter-well orbits see their power increases with the driving frequency while they stop existing beyond a particular frequency (the cutoff frequency). As shown in Fig. 3a, the cutoff frequency of high-power inter-well orbits occurs at ${55}\,\hbox {Hz}$. The power gap between intra-well and inter-well orbits becomes larger for frequencies near the cutoff frequency of the inter-well orbit, as seen in Fig. 3a. Therefore, as the driving frequency approaches the cutoff frequency of the inter-well orbits, it becomes increasingly difficult to attain inter-well orbits. The green, orange and red rectangles in Fig. 3a highlight the driving frequencies $f_d={{40}\,}\hbox {Hz}$, $f_d={50}\,\hbox {Hz}$ and $f_d={65}\,\hbox {Hz}$ whose orbits, basins of attraction³ and attractors⁴ are plotted in the dimensionless phase plane $(x/x_w,\dot{x}/x_w \, \omega _0)$ in Fig. 3b–d.

The basins of the intra-well orbits are in light blue, while the basins of the inter-well orbits are in dark blue. Note that Fig. 3d shows the basins of attraction of the sub-harmonic three inter-well orbits (in gray), which correspond to mass oscillations with a frequency three times lower than the driving frequency.

The narrowing of the orbit basins indicates reduced robustness, meaning that the system is more susceptible to transition into other orbits under small perturbations. As shown in Fig. 3b, c, the inter-well orbit basins get thinner as the driving frequency increases. Therefore, while the power of inter-well orbits increases with the driving frequency (Fig. 3), their robustness decreases, making them hard to reach and to sustain.

Thus, the primary challenges stem from:

• 1. There are multiple orbits with different harvested powers for a given driving frequency;

• 2. The harvested power gap between intra-well and inter-well orbits tends to increase with the driving frequency (particularly when $\omega _d > \omega _0$), with a maximum at the cutoff frequency of the inter-well orbits;

• 3. The inter-well orbits are less robust with larger driving frequencies.

The larger the power gap between intra-well and inter-well orbits, the greater the benefit in defining an orbit jump strategy. However, as the inter-well orbits become less robust with frequency, this task becomes increasingly difficult. All of these aforementioned difficulties are challenging to overcome and motivate the design of a robust orbit jump strategy in order to facilitate nonlinear VEHs to operate in high-power inter-well orbit as often as possible.

3 Orbit jump strategy: numerical modeling and optimization

This section introduces the orbit jump strategy [25] studied in this paper and its optimization using an evolutionary strategy algorithm.

3.1 Strategy description

The considered orbit jump strategy is based on the modification of the buckling level of bistable VEH. This orbit jump strategy has already been studied and experimentally validated in multiple studies [25, 34], with promising results. However, in most of these studies, the ending time of the jump has been fixed to the instant when the mass reaches its maximum displacement which may not be the optimal time to minimize the energy cost of the orbit jump and maximize its robustness. Therefore, in this study, we chose to optimize this ending time. The orbit jump strategy adjusts the buckling level of the bistable VEH from $x_w$ to $k_w\, x_w$ at a starting time $t_0$ for a (relatively short) duration $\varDelta t$.

Fig. 4

Different steps of the aforementioned orbit jump strategy using buckling level modifications. From the left to the right: potential wells, the APA-mass system and the displacement of the mechanical oscillator. Colored frames give corresponding equilibrium position and instant in the orbit jump strategy. It is worth noting that the mass motions in the central diagram are deliberately large in order to highlight the consequences of the variation of the buckling level on the mass

Figure 4 illustrates the important steps of the aforementioned orbit jump strategy. For each step (before, during and after the orbit jump), the potential wells, the evolution of the tuning APA-mass system and the displacement waveform of the mass are shown. As seen in Fig. 4a, at the beginning of the orbit jump process (when $t<t_0$, denoted $t_0^-$ in Fig. 4a) the mass oscillates around one of the two stable equilibrium positions at $x=x_w$ (low-power intra-well orbit oscillations). The gray dot in Fig. 4 illustrates the mass position in the potential well curve. Thereafter, between $t_0$ and $t_0+\varDelta t$ (when $t_0 \le t \le t_0 + \varDelta t$, denoted $t_0^+$ in Fig. 4b), the voltage of the tuning APA $v_w$ changes and the buckling level increases⁵ to $k_w \, x_w$ (with $k_w>1$). It is worth noting that, while the buckling level theoretically increases instantaneously, a certain amount of time is required in practice. As seen in Fig. 4b, the potential well changes: equilibrium positions are greater ($x=\pm k_w \, x_w$) and the potential energy barrier is also larger. Thus, the gray dot which was in the previous potential well (in gray dashed line) is now in a higher position, meaning that the inertial mass received potential energy during the buckling level modification. Finally, at $(t_0+\varDelta t)^+$ (that is, when $t>t_0+\varDelta t$), the initial buckling level is restored, reintroducing potential energy to the mass and setting both equilibrium positions back to $x= \pm x_w$. As illustrated in Fig. 4, if the values of the orbit jump parameters $(t_0, \varDelta t, k_w)$ are properly set, the bistable VEH should operate in its high-power inter-well orbit. For the sake of generality, we considered $t_0$ and $\varDelta t$ multiples of the driving period $T_d$ and used the both following dimensionless times:

• $\tau _0 = t_0/T_d$, the dimensionless starting time;

• $\varDelta \tau = \varDelta t/T_d$, the dimensionless orbit jump duration.

Figure 5 shows an example of application of this orbit jump strategy for $f_d={50}\,\hbox {Hz}$ (we intentionally chose orbit jump parameters that make possible to jump on high-power inter-well orbit in order to illustrate the approach).

Fig. 5

Example of a successful orbit jump strategy for $f_d={50}\,\hbox {Hz}$ with $(\tau _0, \varDelta \tau , k_w)=(0.46, 1.01, 2.00)$: a time displacement signal, b trajectories in the phase plane $(x,\dot{x}/x_w \, \omega _0)$, c evolution of the left stable equilibrium position before (in blue), during (in orange) and after (in green) the application of the orbit jump strategy and d the both elastic potential energy curves associated to the both buckling levels

Figure 5c, d shows the impact of orbit jump parameters $(\tau _0,\varDelta \tau , k_w)$ on stable equilibrium positions and potential wells during the orbit jump strategy. Blue dots in Fig. 5a, b, d represent the instant when starting the orbit jump process, denoted by $t_\text {ref}$. Triangle up (resp. down) markers represent the instants when the buckling level of the bistable VEH increases (resp. decreases) at $t-t_\text {ref}=t_0$ (resp. $t-t_\text {ref}=t_0+\varDelta t$ ). As illustrated in Fig. 5d, when the buckling level is increased, then decreased, the inertial mass acquires potential energy that comes from the APA actuating system. This energy, called invested energy $E_{\text {inv}}$, consists in the potential energy (2) difference between $t_0$ and $t_0+\varDelta t$. As shown by (4), $E_{\text {inv}}$ can be computed from the potential energy expression given by (2). The total harvested energy $E_{\text {tot}}$ (5) is the invested energy subtracted from the harvested energy over a duration of 100 $T_d$ from the instant $t_\text {ref}$. Note that we arbitrary take a duration of 100 $T_d$ for the evaluation of the orbit jump strategy in the rest of the paper, as it is long enough to yield significant total energy if we successfully jump to a high orbit, while also being short enough to account for the invested energy during the orbit jump.

$$\begin{aligned} E_{\text {inv}}(t_0, \varDelta t, k_w)&= E_p\left[ t_0^+\right] - E_p\left[ t_0^-\right] \nonumber \\&\quad + E_p\left[ (t_0+\varDelta t)^+ \right] \nonumber \\&\quad - E_p\left[ (t_0+\varDelta t)^- \right] \nonumber \\&= \varDelta E_0 + \varDelta E_1 \end{aligned}$$

(4)

$$\begin{aligned} E_{\text {tot}}(t_0, \varDelta t, k_w)&{=} \int _{t_\text {ref}}^{t_\text {ref} {+} 100 \, T_d } \dfrac{v^2}{R} {\text {d}}t {-} E_{\text {inv}}(t_0, \varDelta t, k_w) \end{aligned}$$

(5)

As a matter of example, (4) and (5) allow to estimate the invested energy ($E_{\text {inv}} \simeq {1.27}\,\hbox {mJ}$) and the total harvested energy over a duration of $100 \ T_d$ ($E_{\text {tot}} \simeq {5.54}\,\hbox {mJ}$) in the orbit jump shown in Fig. 5. The harvested power in high orbit (after the jump) is about 45 times larger than the power in low orbit (before the jump), for this driving frequency.

On the other hand, inherent experimental imprecision exists due to the non-ideal experimental setup (such as delays and parasitics effects) and imperfect experimental identification (with uncertainties regarding the values of $\omega _0$ or $x_w$). All of these possible variations in parameters must be considered, which emphasizes the need to optimize the orbit jump strategy to reduce its sensitivity to parameter variations (i.e., its robustness) and enhance its performance. In the rest of the paper, we will investigate the optimization of the orbit jump strategy (for several driving frequencies) that can enhance its effectiveness based on its energy cost and its robustness against variations.

3.2 Optimization of the orbit jump strategy

As noticed in the previous subsection, the success of an orbit jump strategy depends drastically on the values of its parameters $(\tau _0,\varDelta t, k_w)$ (which then depend on the driving frequency or the starting intra-well orbit for example). Properly defining both time parameters ($\tau _0, \varDelta _{\tau }$) is crucial to the success of the orbit jump, regardless of the buckling factor ($k_w$). For example, setting the starting time of the orbit jump $\tau _0$ to 0.9 renders the orbit jump strategy in Fig. 5 ineffective, meaning that the VEH remains in low-power intra-well orbit even after the orbit jump. To ensure an effective orbit jump strategy, we conduct a numerical investigation of the optimal values of the orbit jump parameters which:

($\mathcal {C}_1$):

Maximize the total harvested energy over 100 cycles, $E_{\text {tot}}$;

($\mathcal {C}_2$):

Maximize the success rate of the orbit jump within a neighborhood of the orbit jump parameter values, with a variation of $\pm 15\%$.

The criterion ($\mathcal {C}_1$) allows to select orbit jump parameters that maximize the harvested energy while minimizing the invested energy. This criterion allows to evaluate effectiveness of the orbit jump strategy, while the criterion ($\mathcal {C}_2$) makes it possible to anticipate potential experimental deviations in the characteristics of the VEH or in the parameters of the orbit jump strategy. This criterion allows to evaluate robustness of the orbit jump strategy. Then, the optimization of the orbit jump parameters according both ($\mathcal {C}_1$) and ($\mathcal {C}_2$) criteria is performed by means of an evolutionary strategy algorithm [35] implemented in our in-house Python CUDA code. Evolutionary strategy algorithm has been selected due to its robustness in handling multi-extremal and discontinuous fitness functions, as well as its ability to benefit from GPU parallel computing. For that we define the average total harvested energy in (6) which is the fitness function⁶ to maximize,

$$\begin{aligned}{} & {} \overline{E_{\text {tot}}}(\tau _0, \varDelta \tau , k_w)\nonumber \\{} & {} \quad = \sum _{i=0}^{N-1} E_{\text {tot}}(\tau _0^i, \varDelta \tau ^i, k_w^i) \Big / N, \; \, \forall N > 1, \ N \in \mathbb {N} \; \nonumber \\ \end{aligned}$$

(6)

where $N>1$ is the number of parameter combinations tested (e.g., $N= 8 \, 000$) and for all $i \in \llbracket 0, N-1 \rrbracket$, $\left( \tau _0^i, \varDelta \tau ^i, k_w^i\right) \in \mathcal {V}\left( \tau _0, \varDelta \tau , k_w\right)$, the neighborhood of a given parameters combination $\left( \tau _0, \varDelta \tau , k_w\right)$ with a variation of $\pm 15\%$. Therefore, the optimization problem to solve is formulated as (7).

$$\begin{aligned} \begin{aligned} \mathcal {S} : \max \left\{ \overline{E_{\text {tot}}}(\tau _0, \varDelta \tau , k_w) \Big | \left( \tau _0, \varDelta \tau , k_w \right) \in \mathcal {D}\right\} \\ \text {where} \quad \mathcal {D} = [0.2,1.2] \times [0.2,1.5] \times [1,2] \end{aligned} \end{aligned}$$

(7)

Note that we only consider $\tau _0$ and $\varDelta \tau$ larger than 0.2 for the ease of experimental implementations. Moreover, the maximum mechanical constraints that can be supported by the considered prototype of bistable VEH have been taken into account by limiting the $k_w$ to 2. $k_w > 1$ was chosen due to the prototype’s reference buckling level $x_w$ being close to the estimated minimum value, and optimization results showed no interesting solutions for $k_w < 1$.

The detailed optimization procedure is described in Appendix 1.

Fig. 6

Comparison between optimal (a, c) and suboptimal (b,d) of time displacement signals and trajectories in the phase plane ($x, \dot{x}/x_w \, \omega _0$) for $f_d={50}\,\hbox {Hz}$ before (in blue), during (in orange) and after (in green) the application of the orbit jump strategy. Blue dots correspond to the beginning of the orbit jump process, triangle up (resp. down) markers refer to the instant when the buckling level increased (resp. returned to its initial value). Optimal orbit jump parameter values $(\tau _0^{\text {opt}}, \varDelta \tau ^{\text {opt}}, k_w^{\text {opt}}) = (0.23, 0.46, 1.81)$. Suboptimal orbit jump parameter values $(\tau _0^{\text {sub}}, \varDelta \tau ^{\text {sub}}, k_w^{\text {sub}})=(0.46,1.01,2.00)$

Figure 6 presents a comparison between the optimized and suboptimized ${50}\,\hbox {Hz}$ orbit jump strategy (as shown previously in Fig. 5). The optimized orbit jump strategy requires an invested energy of ${0.49}\,\hbox {mJ}$ and yields a total harvested energy of ${6.06}\,\hbox {mJ}$ over 100 oscillation cycles. It is worth noting that the end of the optimized orbit jump is defined slightly after the maximum displacement of the mass, in contrast to previous studies where the end time was generally defined at the instant of maximum displacement. The next section will investigate optimal orbit jump parameters combination $(\tau _0, \varDelta \tau , k_w)$ satisfying (7) for [${30}\,\hbox {Hz}, {60}\,\hbox {Hz}$], and the optimization results will be presented jointly with the experimental results.

4 Optimized orbit jump strategy: experimental validation and energy analysis

This section compares experimental and numerical results of the optimized orbit jump strategy.

4.1 Experimental validation

In order to experimentally validate the aforementioned optimized orbit jump strategy, experimental tests have been made around each optimal orbit jump parameters combination for driving frequency in $[{30}\,\hbox {Hz}, {60}\,\hbox {Hz}]$. Figure 7 shows the experimental setup. The bistable VEH prototype shown in Fig. 2b is fixed on an electromagnetic shaker driven by a power amplifier. The acceleration amplitude A of the shaker is measured by an accelerometer and sent to the control board. As illustrated in Fig. 7b, the amplitude of the signal driving the power amplifier ($v_A$) is regulated in order to maintain a constant acceleration amplitude $A={4}\,\hbox {m/s}^2$ by means of an internal proportional integral (PI) controller. The piezoelectric electrodes of the energy harvesting APA (in blue) are connected to:

• A voltage follower in order to prevent the control board’s impedance impacting the piezoelectric element and to avoid the control board to be exposed to a voltage strictly higher than ${10}\,\hbox {V}$ which could damage it;

• A resistive decade box whose resistive value can be adjusted with a signal sent from the control board.

Displacement and velocity $(x, \dot{x})$ of the inertial mass are sensed with a laser differential vibrometer. At given times, when modifying the buckling level of the bistable VEH, the control board sends a signal to the high speed bipolar amplifier which controls the voltage across the tuning APA, $v_w$.

Fig. 7

a Experimental setup used to test the optimized orbit jump strategy and b its schematic representation

In order to smooth the variation of the buckling level and avoid to damage the VEH prototype, we implemented in the control board a second-order filter that reduces the sharpness of $v_w$ variations. The rise time of the buckling level is approximately one-twentieth of a cycle, which is acceptable. Before any runs, the acceleration amplitude is gradually increased to $A={4}\,\hbox {m/s}^2$ and the buckling level is decreased to obtain $x_w={0.71}\,\hbox {mm}$. It is worth noting that the parameters of the VEH prototype have been identified in low-power orbit characterization and given in Table 2.

In order to experimentally validate the model described in Eq. (1) and the numerical orbit jump modeling, $2 \, 000$ experimental results are launched with several values⁷ of $\tau _0$ and $\varDelta \tau$ ($k_w=1.5, \tau _0 \in [0.2, 1.2], \varDelta \tau \in [0.2, 1.5]$) for $f_d={40}\,\hbox {Hz}$ and arbitrary resistor $R={20}\,\hbox {k}\Omega$. Identical simulations are performed with $8 \, 000$ parameters combinations.

Fig. 8

Experimental (a) and numerical (b) maps $(\tau _0, \varDelta \tau )$ with $k_w=1.5$, $f_d={40}\,\hbox {Hz}$ and $R={20}\,\hbox {k}\Omega$

Fig. 9

Comparison between experimental (a, c) and numerical (b, d) of time displacement signals and trajectories in the phase plane ($x, \dot{x}/x_w \, \omega _0$) for $f_d={50}\,\hbox {Hz}$ before (in blue), during (in orange) and after (in green) the application of the orbit jump strategy. Blue dots correspond to the beginning of the orbit jump process, triangle up (resp. down) markers refer to the instant when the buckling level increased (resp. returned to its initial value). Experimental orbit jump parameter values $(\tau _0^{\text {exp}}, \varDelta \tau ^{\text {exp}}, k_w^{\text {exp}}) = (0.26, 0.44, 1.81)$. Numerical orbit jump parameter values $(\tau _0^{\text {num}}, \varDelta \tau ^{\text {num}}, k_w^{\text {num}})=(0.23,0.46,1.81)$

Figure 8 shows corresponding experimental and numerical scatter plots $(\tau _0, \varDelta \tau )$ with each point associated to its final orbit after the jump and gives comparison between experimental and numerical structures of the basins for $f_d={40}\,\hbox {Hz}$ and $R={20}\,\hbox {k}\Omega$. As shown in Fig. 8, there are three possible behaviors: low-power intra-well orbit (in light blue), high-power inter-well orbit (in dark blue) and chaos (in dark salmon). As an example, for experimental data in Fig. 8a), increasing the buckling level from $x_w$ to $1.5 \, x_w$ over a duration of $0.3 \, T_d$ starting at $t-t_{\text {ref}}=0.7 \, T_d$ will result in the bistable VEH operating on the high-power inter-well orbit. The ranges of parameter values where the VEH jumps are approximately the same, although more chaos is observed experimentally. This may be attributed to an insufficient waiting time for the nonlinear VEH to reach steady-state conditions in the experimental setup. However, the experimental and numerical basins’ structures given in Fig. 8 are almost identical which validates the numerical model of the bistable VEH and numerical model of the orbit jump application. Additionally, Fig. 8 shows the pseudo-periodicity of the inter-well orbit’s basin in $\tau _0$ (described with the two basins in the middle of Fig. 8a, b). Therefore, since the starting orbit is $T_d$–periodic, the values of $\tau _0$ can be restricted to a semi-open interval of length 1 without loss of information and justifies the values of $\tau _0$.

Fig. 10

Orbital mean harvested power $P_h$ obtained numerically (dots) and experimentally (stars) as a function of the driving frequency $f_d$ for a sinusoidal excitation of amplitude $A={4}\,\hbox {m/s}^2$ with resistance $R=1/2C_p\omega _d$. The experimental data (stars) were obtained through the implementation of the optimized orbit jump strategy

Fig. 11

The optimal numerical values (blue dots) and the optimal experimental values (red stars) of a the amplification coefficient $k_w$, b the starting time $\tau _0$, c the orbit jump duration $\varDelta \tau$ and d the corresponding dimensionless recovery time $t_{\text {rec}}/T_d$ for successful orbit jumps as a function of the driving frequency

In order to validate the model of the bistable VEH and the orbit jump strategy effect, we perform experimental tests around the optimized orbit jump parameters (obtained with the evolutionary strategy algorithm introduced in Sect. 3.2, and detailed in Appendix 1) for $f_d={50}\,\hbox {Hz}$. Figure 9 compares experimental (Fig. 9a, c) and numerical (Fig. 9b, d) time displacement signals and trajectories in the phase plane respectively before, during and after the application of the orbit jump strategy. Note that the transient trajectory for optimal successful jumps remains almost identical over the frequency range 30–${60}\,\hbox {Hz}$. Experimental orbits are asymmetric, as shown in Fig. 9a, c, which can be attributed to mechanical irregularities resulting from the manufacturing process of the bistable VEH. Moreover, the experimental transient just after the jump in Fig. 9a, c (in green) shows excitation from higher modes of the VEH prototype due to the quick buckling level variation. The corresponding experimental trajectory in the 3D plane ($t,x,\dot{x}/x_w \, \omega _0$) is presented in Fig. 19 in Appendix 5.5.

In quantitative terms, the mean harvested power is 26.5 times higher after the orbit jump in Fig. 9, while the experimental invested energy required is equal to ${0.65}\,\hbox {mJ}$ and can be recovered in ${0.21}\,\hbox {s}$. Then, we optimize the orbit jump strategy in the frequency range $[{30}\,\hbox {Hz}, {60}\,\hbox {Hz}]$ and obtain an optimal triplet $(\tau _0^{\text {opt}}, \varDelta \tau ^{\text {opt}}, k_w^{\text {opt}})$ satisfying the criterion $\mathcal {S}$ (7) for each driving frequency. Subsequently, we launch experimental maps around each optimal triplet and driving frequency in order to evaluate the robustness of the approach. It is worth mentioning that experimental maps are defined with 49 parameters values and a variation rate of $\pm 15\%$. Specifically, we take seven values in $\left[ 0.85 \times \tau _0^{\text {opt}}, 1.15 \times \tau _0^{\text {opt}}\right]$ for $\tau _0$, 7 values in $\left[ 0.85 \times \varDelta \tau ^{\text {opt}}, 1.15 \times \varDelta \tau ^{\text {opt}}\right]$ for $\varDelta \tau$ and $k_w=k_w^{\text {opt}}$.

Fig. 12

Experimental success rate with $\pm 15\%$ variations around each optimal times parameter as a function of the driving frequency

Fig. 13

a Invested energy and b Total harvested energy over 100 cycles for the numerical optimal orbit jump parameters (in blue dotted curve) and the experimental orbit jump parameters that allowed to jump (green star-shaped markers) as a function of the driving frequency with optimal load resistor. The dotted orange curve represents the minimum mechanical energy difference (8) between the highest inter-well orbit and the lowest intra-well orbit

Figure 10 compares numerically (dots) and experimentally (stars) mean harvested power (3) as a function of the driving frequency. Note that experimental power (stars) plotted in Fig. 10 comes from experimental results of the orbit jump. The VEH starts in an intra-well orbit at each driving frequency. Then, the optimal jump is applied, and the power is measured in order to evaluate the inter-well orbit power. Through optimization of the orbit jump strategy, the highest orbit was achieved at each driving frequency both experimentally and numerically, as illustrated in Fig. 10. Differences between experimental and numerical data may result from the mismatch between the numerical model and our experimental prototype. It is worth mentioning that applying an orbit jump strategy always yields a significant increase in power in this frequency range. As a matter of example, for $f_d={55}\,\hbox {Hz}$ the experimental mean harvested power of the intra-well orbit is ${0.044}\,\hbox {mW}$ despite of ${4.44}\,\hbox {mW}$ for the inter-well orbit leading to a power gain of 100 after a successful orbit jump. Then, as shown in Figs. 8, 9, 10, experimental results are consistent with numerical results and allow to validate the model and the proposed orbit jump strategy.

4.2 Energy harvesting performance analysis

Figure 11a–c shows the optimal orbit jump parameter combinations (blue dots) along with successful experimental parameters closest to the optimal (red stars) for each driving frequency. The corresponding recovery times up to ${55}\,\hbox {Hz}$⁸ are shown in Fig. 11d. Note that the automated pre-characterization of the relationship between $x_w$ and $v_w$ allows the experimental determination of the modified buckling level $k_w \, x_w$ with good accuracy (for more details on obtaining the experimental relationship between $v_w$ and $x_w$, see the Appendix 5.5). As shown in Fig. 11a–c, experimental data with a variation of $\pm 15\%$ around the optimal times parameters and fixed $k_w=k_w^{\text {opt}}$ are in good agreement with the optimized data except for $f_d={40}\,\hbox {Hz}$. The discrepancy between experimental and numerical models observed at $f_d={40}\,\hbox {Hz}$ can be attributed to the sudden change in behavior of the intra-well orbit due to softening nonlinearity of the potential wells for this particular acceleration amplitude (which equals ${4}\,\hbox {m/s}^{2}$), as seen in Fig. 10. Similarly, the variations between the numerical and experimental models (Fig. 3) may explain the observed differences in the recovery times.

The experimental success rate associated with tested $(\tau _0, \varDelta \tau )$ pairs, distributed with a variation of ±15%, is shown in Fig. 12. It is worth noting that despite the relatively large variation around the optimal times parameters, the average experimental success rate is about 48 %, which demonstrates the robustness of the optimized orbit jump strategy. However, the highest inter-well orbit ceases to exist beyond ${55}\,\hbox {Hz}$ (both numerically and experimentally), resulting in the sub-harmonic 3 [8] becoming the highest inter-well orbit. Nonetheless, this orbit is challenging to reach and highly unlikely, leading to a decline in success rate between 55 and ${60}\,\hbox {Hz}$.

Table 3 Comparison between the optimized orbit jump strategy developed in this paper and other previous orbit jump strategies in literature.

Figure 13 shows invested energy (4) and total harvested energy (5) over 100 cycles as a function of the driving frequency for both successful experimental data and optimal numerical data. The dotted orange curve corresponds to the minimum difference in mechanical energy between the high-power inter-well orbit and the low-power intra-well orbit, $\varDelta E_{\text {min}}$, whose expression is given by (8).

$$\begin{aligned} \small \varDelta E_{\text {min}}= & {} \min _{\forall t \in [0, T_d[} \left( \left[ E_p(t) + \dfrac{1}{2} m \dot{x}(t)^2\right] _{{\text {inter-well}}} \right. \nonumber \\{} & {} - \left. \left[ E_p(t) + \dfrac{1}{2} m \dot{x}(t)^2\right] _{\text {intra-well}}\right) \end{aligned}$$

(8)

As shown in Fig. 13, the invested energy required for the orbit jump does not exceed ${1}\,\hbox {mJ}$, even experimentally. For example, at $f_d={50}\,\hbox {Hz}$, the numerical optimum has an invested power of ${3.5}\,\hbox {mW}$ (see Fig. 10) and an invested energy of approximately ${0.5}\,\hbox {mJ}$ (Fig. 13), leading to a recovery time of about ${0.15}\,\hbox {s}$. Moreover, the invested energy associated with the optimal parameters is close to the minimum energy limit $\varDelta E_{\text {min}}$, validating the optimization of the orbit jump strategy. Note that a portion of the electrical energy injected into the system is currently lost as electrostatic energy in the tuning APA. For example, at $f_d={50}\,\hbox {Hz}$, the experimental mechanical energy injected into the system is equal to 0.45 mJ (as shown in Fig. 13a), while the electrostatic energy lost in the tuning APA is 4.16 mJ (which is not shown in Fig. 13). As a result, the total invested energy is 4.61 mJ with an invested power of about 3.1 mW (see Fig. 10 at $f_d={50}\,\hbox {Hz}$). Even when considering the electrostatic energy in the tuning APA, the recovery time does not exceed ${2}\,\hbox {s}$. Note that a power electronic converter could be used to store the lost electrostatic energy in the tuning APA and reintroduce it into the system at the appropriate time, although this approach was not implemented in this study.

As illustrated in Fig. 13, the driving frequency increases, achieving a high-power orbit becomes more challenging. This leads to an increase in the amplification factor, the invested energy and the total harvested energy over 100 cycles.

Fig. 14

Numerical maps $(f_d, A_d)$ a of the success and b the probability of success of the optimal jumps obtained for $A_d={4}\,\hbox {m/s}^{2}$

Fig. 15

Evolutionary strategy algorithm for optimizing orbit jump strategy. This flowchart illustrates different steps that allow to determine optimal orbit jump parameters for each driving frequency. Here, $(\tau _0, \varDelta \tau , k_w) \in \mathcal {D}$ denotes the individuals sequence for a given population in $\mathcal {D}$

The evaluation of the invested energy for orbit jumping is a major parameter for analyzing the quality of an orbit jump strategy. Additionally, the recovery time to achieve a positive energy balance allows the evaluation of the interest of jumping and the assessment of the cost-effectiveness ratio. Table 3 compares orbit jump strategies from the literature with results presented in this paper based on these aforementioned parameters (the jump duration, the invested energy and the recovery time), but also whether they are optimized or robust to parameter shifts and if they were experimentally tested over a wide frequency range. It can be noted that very few strategies are optimized in the literature and that the only reference where a complete optimization of an orbit jump strategy has been considered (Udani et al.  [4]) has only been tested for a single driving frequency, which does not validate its robustness, nor the generality of the optimization method. Wang’s et al.  [24] orbit jump strategy requires a high amount of energy which can be optimized. On the other hand, Huang et al.  [27] have defined an innovative orbit jump strategy that combines two other strategies (buckling level modification and VIE) and is therefore more complex. However, the jump duration is high (${90}\,\hbox {s}$), increasing the difficulties of implementation and decreasing both the robustness and efficiency of the orbit jump strategy with a long recovery time equals to ${120}\,\hbox {s}$. Huguet et al.  [25] introduced the orbit jump strategy considered in this paper and examined two orbit jump parameters: the starting time of the jump (tested in four different values) and the amplification factor of the buckling level (tested in six different values). They fixed the ending time as the instant when the mass reaches its maximum displacement. However, using the optimization criterion defined in our study, results show that the optimal ending time for the jump occurs slightly after the maximum displacement. Nonetheless, their study has the merit of presenting numerous experimental trials, which allowed them to partially evaluate the robustness of the approach through statistical analysis of the jumps (with a 0% variation around each combination). The evolutionary strategy algorithm as well as the new optimization criterion proposed in this paper enable the achievement of performant orbit jumps, combining the shortest time duration (${8.3}\,\hbox {ms}$), lowest energy cost (${0.6}\,\hbox {mJ}$), shortest recovery time (${0.1}\,\hbox {s}$) while being robust to large parameters shifts ($\pm 15 \%$ variation).

4.3 Effectiveness of optimized orbit jumps under excitation amplitude perturbations

In the previous sections, the robustness of the proposed orbit jump strategy has been assessed with variations of the jump parameters $(\tau _0, \varDelta \tau )$. In this section, a numerical analysis has been performed to evaluate the effectiveness of the optimized jump parameter combinations $\left( \tau _0^{\text {opt}}, \varDelta \tau ^{\text {opt}}, k_w^{\text {opt}}\right)$, obtained for $A_d={4}\,\hbox {m/s}^2$, under perturbations of the excitation amplitude. Numerical tests of optimal orbit jumps⁹ are computed for various acceleration amplitudes, ranging from ${2}\,\hbox {m/s}^2$ to ${6}\,\hbox {m/s}^2$, in the frequency range 30–${60}\,\hbox {Hz}$. Figure 14a shows the success of optimal parameters for each $(f_d, A_d)$ combination: whether successful (in green), or unsuccessful (in red) or when intra-well orbits do not exist under large acceleration amplitudes (in gray). The hatched area in Fig. 14a indicates combinations of $(f_d, A_d)$ where the highest inter-well orbit does not exist and the yellow line highlights the excitation amplitude $A_d={4}\,\hbox {m/s}^2$ used for the orbit jumps optimization. Figure 14b shows the success probability of optimal parameters for each $(f_d, A_d)$ combination tested. To calculate this probability, for a given pair of $(f_d, A_d)$, a grid of uniformly distributed jump parameters with a variation of $\pm 15\%$ centered around the associated optimal jump parameters, is tested.

Figure 14a, b demonstrates that optimal jumps remain robust under acceleration amplitude perturbations. Remarkably, their effectiveness improves further at higher acceleration amplitudes, as highlighted by the increased probability of success in Fig. 14b. For example, at ${45}\,\hbox {Hz}$, the success probability of optimal jumps is 62% for $A_d={4}\,\hbox {m/s}^2$, whereas it is 87% for $A_d={5.5}\,\hbox {m/s}^2$. Note that around ${40}\,\hbox {Hz}$, for excitation amplitudes less than ${3.5}\,\hbox {m/s}^{2}$, the optimal jumps are unsuccessful due to the amplitude-dependent softening resonance of intra-well orbits when $f_d={40}\,\hbox {Hz}$ for $A_d={4}\,\hbox {m/s}^2$ (Fig. 10), which occurs slightly above ${40}\,\hbox {Hz}$ for lower excitation amplitudes. This shift of softening resonance of intra-well orbits explains, for $A_d \le {3.5}\,\hbox {m/s}^2$, the ineffectiveness of the optimal jumps around ${40}\,\hbox {Hz}$. Note that for small excitation amplitudes, the highest inter-well orbit has a lower cutoff frequency than at high excitation amplitudes, as shown by the hatched area in Fig. 14a. For instance, at $f_d={50}\,\hbox {Hz}$, the highest inter-well orbit does not exist (in dark blue in Fig. 3) at $A_d={2}\,\hbox {m/s}^2$, but it does exist at $A_d={4}\,\hbox {m/s}^2$. Overall, optimal orbit jumps remain robust to variations in the excitation amplitude

5 Conclusion

Due to the existence of low-power orbits in nonlinear VEHs dynamics, robust and effective orbit jump strategies are essential to ensure good energy harvesting performance by enabling transition from low-power to high-power orbits. To achieve this, orbit jump parameters can be optimized. This paper presents the optimization of an existing orbit jump strategy using an evolutionary strategy algorithm. The development of an in-house Python CUDA code for GPU computations allows precise numerical simulations of complex transients involved during orbit jumps. The experimental results consistently demonstrate that the optimized orbit jump parameters generated high-power inter-well orbits, while maintaining their performance even under potential fluctuations in the VEH bistable environment. By considering the experimental amplification factor at its optimal value, and adjusting both the starting and duration times within a range of $\pm 15\%$ from their optimal values, the robustness of the optimized orbit jump strategy was demonstrated with an average success rate of 48%. Finally, the energy required for the orbit jump does not exceed ${1}\,\hbox {mJ}$, even in experimental conditions. The proposed optimization of the orbit jump strategy enhances the robustness of an orbit jump despite fluctuations in the environment of the VEH. In the last section of this paper, the effectiveness of the optimal jumps under perturbations in the excitation acceleration amplitudes is numerically demonstrated. The proposed optimization approach can be applied to other types of multi-stable VEHs to design robust optimized orbit jump strategies. In the future, the practical implementation of self-powered optimized orbit jumps will be realized using ultra-low-power integrated power management circuits and algorithms [36,37,38], where the optimized parameters of the orbit jump can be stored in an on-chip memory.

Appendices

A Evolutionary strategy algorithm methodology

Figure 15 illustrates the various steps involved in the evolutionary algorithm for optimizing the considered orbit jump strategy for frequencies between 30 and ${60}\,\hbox {Hz}$.

1.1 Initialization

First, we generate the initial population, which is randomly distributed in the optimization domain $\mathcal {D}$. The number of individuals in each population was arbitrarily set to $8 \, 000$. An individual corresponds to a combination of orbit jump parameters $(\tau _0, \varDelta \tau , k_w)$. An example of such an initial population is plotted¹⁰ in the 3D space $\mathcal {D}$ in Fig. 16 (blue dots).

1.2 Evaluation

The corresponding orbit jumps are simulated and evaluated based on their fitness function value, which is the average total harvested energy over 100 cycles by (9).

$$\begin{aligned}{} & {} \overline{E_{\text {tot}}}\left( \tau _0, \varDelta \tau , k_w\right) = \sum _{i=0}^{N-1} E_{\text {tot}}\left( \tau _0^i, \varDelta \tau ^i, k_w^i\right) \Big / N, \nonumber \\{} & {} \quad \forall N > 1, \ N \in \mathbb {N} \end{aligned}$$

(9)

Where $N=7^3=343$, since we considered 7 elements per direction, defining the neighborhood uniformly distributed around the given jump parameter combination $(\tau _0, \varDelta \tau , k_w)$. Figure 16 shows an example of such a neighborhood (green dots) used to evaluate the robustness of the associated orbit jump (with respect to the jump parameter values represented by the red dot). Consequently, 343 additional orbit jump simulations are launched to compute (9) for each individual. This means that for each generation, we simulate $2,\, 744, \, 000$ orbit jumps using parallel GPU computation.

Fig. 16

An example of a neighborhood (green dots) around a given parameter combination represented by a red dot in the initial population (blue dots) in the 3D plane $(\tau _0, \varDelta \tau , k_w)$

1.3 Selection and crossover

Individuals are classified based on their fitness function value. The top 10% of individuals are parents in the next generation (and are also in the next generation). Then, we used a whole arithmetic recombination as a crossover operation to produce children for the next generation. This consists of taking a percentage of each parent gene (or orbit jump parameter) and combining them linearly to create the child. We randomly chose two different parents, $P_1 = \left( \tau _0^1, \varDelta \tau ^1, k_w^1\right)$ and $P_2 = \left( \tau _0^2, \varDelta \tau ^2, k_w^2\right)$ among the top 10% of the current generation. We generate a random ratio $r \in [0,1]$ and the corresponding child $C = \left( \tau _0^C, \varDelta \tau ^C, k_w^C\right)$ is calculated as follows:

$$\begin{aligned} {C = rP_1 + (1-r)P_2 \iff \left\{ \begin{array}{lll} \tau _0^C = r\tau _0^1 + (1-r)\tau _0^2\\ \varDelta \tau ^C = r\varDelta \tau ^1 \\ + (1-r)\varDelta \tau ^2\\ k_w^C = rk_w^1 + (1-r)k_w^2 \end{array}\right. } \end{aligned}$$

(10)

Fig. 17 shows the crossover operation used to create new individuals.

Fig. 17

Schematic illustration of the crossover operation used in this paper

1.4 Mutation

The mutation operator, analogous to biological mutation, is used to explore the search space by introducing diversity into the population of genes and avoiding convergence to local minima. Each individual is selected for mutation with a probability of 0.1. Individuals which are selected for mutation will see their genes changed using a Gaussian distribution $\mathcal {N}(0, \sigma )$ with a standard deviation of $\sigma =1/3$. For example, suppose the individual $\left( \tau _0^i, \varDelta \tau ^i, k_w^i\right)$ is selected for mutation, its amplification factor mutated, ${k_w^i}^{\prime }$, is obtained from:

$$\begin{aligned} {{k_w^i}^{\prime } = k_w^i + \delta k_w^i, \quad \text {where} \ \delta k_w^i \sim \mathcal {N}(0, \sigma )} \end{aligned}$$

(11)

If one of the mutated genes, for example ${k_w^i}^{\prime }$, falls outside the search space, specifically, ${k_w^i}^{\prime } \notin [1,2]$, the mutated individual is not accepted. Consequently, the mutation process is repeated until a mutated individual falls within the acceptable search space, $\mathcal {D}$.

1.5 Convergence error

To evaluate the performance of the algorithm, we computed a convergence ratio (for each individual) based on the ratio between the fitness value of the individual, $\overline{E_{\text {tot}}}$, and the final fitness value of the best individual, $\overline{E_{\text {tot}}}^*$, found in the last generation. The convergence error was then calculated by subtracting the convergence ratios of individuals from the final convergence ratio of 1 (convergence ratio of the best individual in the last generation). Figure 18 illustrates the evolution of the convergence error over successive generations for $f_d={50}\,\hbox {Hz}$. Star markers represent the convergence error of the best individual of the respective generation, while orange dots indicate the convergence error of other (lower-ranked) individuals. The results show that even at the initialization of the algorithm, the solution found is notably close to the optimal solution, with a convergence error of about $10^{-1}$. This is due to the high performance of GPU parallel computing, which allows for the consideration of a significant number of individuals within each population. As generations advance, the algorithm refines the solution, minimizing the convergence error of the final solution by a factor of $10^3$ compared to the error of the initial solution. It should be noted that the optimization method used in this paper is computationally intensive and requires the utilization of parallel GPU computing. An alternative to this high numerical cost would be to implement the cross-entropy method [39] which has fast convergence and reduced computational cost.

Fig. 18

Evolution of the convergence error over 10 generations for $f_d={50}\,\hbox {Hz}$

B Experimental trajectory

See Fig. 19.

C Details of the processes for identifying the key parameters of the experimental prototype

Fig. 19

Experimental trajectory in ($t, x, \dot{x}/x_w \omega _0)$ 3D plane for $f_d={50}\,\hbox {Hz}$ before (in blue), during (in orange) and after (in green) the application of the orbit jump

This appendix describes the various processes used to characterize the experimental prototype, ensuring the closest possible agreement between the numerical and experimental models. This alignment is vital before optimizing any orbit jump strategies.

${{\underline{Prototype \; characteristics}}}$

Some parameters can be measured directly, such as the total inertial mass $M={6}\,\hbox {g}$ and the horizontal distance from the mass to the frame $L={35}\,\hbox {mm}$. The stiffness of the energy harvesting APA (APA120S), $K={0.342}\,\hbox {N}/\upmu \hbox {m}$, was sourced from the Cedrat Technologies data sheet. Note that the stiffness of the tuning APA (APA100M), $K_{\text {tuning}} = {1.859}\,\hbox {N}/\upmu \hbox {m}$, is larger than that of the energy harvesting APA. For this reason, we have assumed that the tuning APA stiffness has negligible impact on the harvester dynamics.

${{\underline{Impedance \; analysis \; tests}}}$

Impedance analysis has been performed on the experimental prototype to identify the values of its electromechanical coupling, $k_m^2$, the quality factor, Q, the linearized natural pulsation, $\omega _0$, the capacitance, $C_p$, or the original buckling level, $x_w$. By applying a low sinusoidal voltage, with a constant amplitude of ${5}\,\hbox {mV}$, to the energy harvesting APA, the mass oscillates with low amplitude around one of its two equilibrium positions. From current measurements, the impedance amplitude and phase can be obtained. From this impedance analysis, the identification of the theoretical model parameters, makes it possible to identify the values of $k_m^2=0.071$, $Q=290$, $\omega _0={295}\,\hbox {rad}/\hbox {s}$ and $C_p={1}\,\upmu \hbox {F}$, as detailed in [40]. Then, the equilibrium position $x_w={0.7}\,\hbox {mm}$ is deduced from the relation (12) (see [41] for details):

$$\begin{aligned} \omega _0 = \dfrac{x_w}{L} \sqrt{\dfrac{4 K}{M}} \end{aligned}$$

(12)

Furthermore, it is important to note that the quality factor value decreases with large oscillation amplitudes. Therefore, the value of Q identified by the impedance analysis, derived from low amplitude excitations, will not be representative of its value in high orbit operation. Orbit jumps will involve high-power orbit operation (with high displacement amplitude), requiring a refinement of the quality factor value.

${{\underline{Frequency \; sweep}}}$

A frequency sweep was performed at an acceleration of ${5}\,\hbox {m/s}^2$ over the ${30}\,\hbox {Hz}$ – ${60}\,\hbox {Hz}$ frequency range, enabling the measurement of voltage, displacement amplitude, velocity and acceleration of the experimental prototype operating in inter-well orbits. From these measurements, the adjusted value of the quality factor $Q=160$ is derived. This value was used in the numerical simulations performed throughout this study.

${{\underline{Precise \; matching \; of \; the \;original \; x_w \; value}}}$

To accurately model the orbit jump strategy, additional refinements to the initially identified value of $x_w$ were necessary, ensuring enhanced alignment between the experimental and theoretical orbital structure. We experimentally performed orbit jumps at ${40}\,\hbox {Hz}$ with various combinations¹¹ of $(\tau _0, \varDelta \tau )$, while maintaining the amplification coefficient¹²$k_w=1.5$ fixed. From these experimental results, the experimental map shown in Fig. 8 was plotted. The adjusted $x_w$ value was determined by selecting the value that produced a numerical jump map most similar to the one obtained experimentally. This leads to the final equilibrium position value $x_w={0.71}\,\hbox {mm}$, which is used to optimize the orbit jump strategy.

Fig. 20

Diagram illustrating the various processes involved in identifying key parameter values of the experimental prototype

The buckling level of the prototype can be fine-tuned using the tuning APA. This adjustment is crucial for implementing the studied orbit jump strategy. We have experimentally characterized the relationship between $v_w$ (the voltage across the tuning APA) and $x_w$. Details are given in the Appendix 5.5.

The whole identification methodology used in this paper is visually summarized in Fig. 20.

D Experimental measurement of the $(v_w, x_w)$ relation

Fig. 21

Experimental evolution of the equilibrium position $x_w$ as a function of the voltage applied to the tuning APA $v_w$

This appendix outlines the approach used to establish the experimental relationship between the equilibrium position $x_w$ and the voltage applied to the tuning APA, denoted as $v_w$. Precise characterization of this experimental relationship is essential for improving the reproducibility of the optimized orbit jump strategy. Using a downward tuning voltage sweep ranging from ${80}\,\hbox {V}$ to ${10}\,\hbox {V}$, the stable position of the mass was measured using a laser vibrometer. Figure 21 illustrates the evolution of the equilibrium position $x_w$ as a function of the voltage applied in the tuning APA. Using this experimentally derived relationship, $v_w$ was fine-tuned to set $x_w$ to its optimal value (obtained numerically), ensuring the successful implementation of the orbit jumps presented in this paper.