Dynamics of nonlinear beam-propeller system with different numbers of blades

Abstract

The dynamics of elastic systems coupled with rotating bladed-rotors is rich and complex, and the blade number may have an influence on the in-vacuo system dynamics. This paper aims to model its nonlinear dynamics in-vacuo and study the effects of blade number on its dynamics. To this end, a nonlinear model consisting of a nonlinear inextensible beam, a motor assembly and a rotating propeller is developed. This model is linearized, and modal analyses are performed with different blade numbers. It is validated numerically and experimentally that a two-bladed propeller introduces time-varying characteristics, while the system is time-invariant with more than two blades. For the two-bladed case, frequencies in the non-rotating condition split into two frequency loci with increasing rotational speed; while with more than two blades, one frequency in the non-rotating condition increases and the other in the same pair decreases with increasing speed. A structural instability due to frequency lock-in is identified in two-bladed configuration, while not identified with more than two blades. The static deformation using the nonlinear model is calculated and validated against the experiment. In the stable speed range, the frequency response functions calculated using the nonlinear and linearized models do not show notable differences. In the unstable speed range with two-bladed propeller, the nonlinear model is consistent with the experiment in terms of unstable frequencies and bounded steady-state oscillations. The system vibration in the unstable speed range features forward whirling pattern, in which the beam vibration is close to the first bending pattern.

1 Introduction

An elastic structure coupled with one or more rotors is a common configuration in novel means of aerial transport [1, 2]. Especially, in the aerospace field, a nacelle or a wing coupled with propellers or rotors is a typical propulsion system seen in many turboprop aircraft, tiltrotors and modern electric VTOL concepts. While this system can provide a number of performance and design advantages, it may introduce some dynamic and aeroelastic challenges such as whirl flutter instabilities at high forward speed or undesirable vibratory loads at certain flight conditions. These challenges can severely limit the performance of tiltrotor or propeller-driven aircrafts, so numerous relevant studies have been carried out to address them in the past few decades [3, 4]. This research investigates a novel simplified beam-propeller test system which highlights the nonlinear characteristics in the structural responses and enables focus on the modeling, analytical and experimental challenges.

Even without considering the aerodynamic effects, the structural dynamics of an elastic structure coupled with rotors should be studied in detail. Due to the rotation of the rotor, the gyroscopic effect and the possible time-varying characteristics are introduced in the system. The former results in the coupling of vibrations in two orthogonal directions, and the change of vibration frequencies with the change of rotational speed as well as whirling vibration pattern whose associated mode shapes are known as forward or backward whirl modes. The latter makes the dynamics richer and more complicated, e.g., the occurrence of frequency split, which is the split of a frequency in the non-rotating condition into two or more frequencies with the increasing rotational speed [5,6,7]. It may also lead to self-excited instability, which is a kind of structural/mechanical instability that is similar to ‘ground resonance’ in the helicopter field [8] and is frequently reported in the studies concerning the dynamics of spinning wind turbine [9] and helicopter blades [10,11,12]. However, the time-dependency arising from the rotation of propeller is usually ignored in the studies of whirl flutter.

The study of the influence of the number of hinged helicopter rotor blades dates back to 1940s [13]. It was reported that a rotor with two blades does not have polar symmetry while a rotor with three or more blades does. Such a difference results in the qualitative difference in the dynamics for rotors with different numbers of blades. A rotor with two blades presents a self-excited instability speed region due to this asymmetry, while no associated instability region was observed in the case with three blades. This research only takes into account the displacement of the hub in the plane of rotation and the angular displacements of the blades. For wind turbines, the modal dynamics with two- and three-bladed rotors show several similarities but also significant differences. The blades can be modeled as beams while the nacelle and tower as a rigid body [14]. Through experiments and numerical analysis using software HAWC2, the Campbell diagrams for two-bladed and three-bladed turbines show different characteristics, which is ascribed to the asymmetric inertial property of the two-bladed turbine [15]. In addition, some studies on the influence of blade number on the aerodynamic performance of wind turbines have been carried out both theoretically and experimentally [16,17,18]. All these studies are different from the configuration in this paper, where the support is modeled as an inextensible beam, while the propeller and motor as rigid bodies. The influence of the number of propeller blades on the structural dynamic characteristics of propeller-driven system, e.g., Campbell diagram, has not been investigated in the open literature.

A cantilevered beam can represent a simplified system for the flexible support structure of the propeller, e.g., nacelle and engine. The geometrically nonlinear response of an isolated cantilevered beam has been studied extensively. The beam is usually assumed to be inextensible, satisfying an inextensibility constraint. The two-dimensional nonlinear beam models were developed to study the nonlinear response when undergoing large deformation in [19, 20], the change of resonance under harmonic excitations [21, 22], as well as the dynamic stability subject to follower force [23]. In addition, three-dimensional nonlinear inextensible beam model with flexural–flexural–torsional coupling was put forward in [24] and the force response is studied in [25]. Recently, a three-dimensional geometrically exact inextensible beam model was developed by Farokhi and Erturk in [26]. However, in all these studies, the beam is the only component constituting the investigated system. The coupling of the nonlinear inextensible beam with a rotating rotor poses more challenges, e.g., the satisfaction of the dynamic constraints, and generates rich and interesting dynamics phenomena. To the best of authors’ knowledge, relevant studies have never been carried out in the open literature.

Motivated by the above background, a simplified system mainly consisting of an elastic cantilevered beam in connection with a rotating propeller at the tip is studied to progress understanding of the nonlinear dynamics of an elastic structure coupled with one or more rotors, originally within the framework of the UK EPSRC funded MENtOR project [27]. Previous studies were focused on the linear modeling of an elastic beam coupled with a rotating propeller [28]. It was found analytically that the number of blades had an influence on the time-dependency of the rotor rig system; however, no experimental validation or systematical analyses of dynamic characteristics with different numbers of blades were carried out. The linear model showed a good prediction capability manifested by the agreement observed in the frequency-speed diagram and the unstable speed range in the case of a two-bladed propeller. However, when the system exhibited the unstable behavior due to the time-varying characteristics, the vibration response in the linear model increased without limit, while it was observed as being constrained and entered a bounded oscillation in the experiments. These insufficiency and limitations directed this systematic study into the influence of blade numbers, nonlinear modeling and simulation of the beam-propeller system.

The rest of the paper is organized as follows: First, the experimental setup is presented in Sect. 2; then, the nonlinear modeling of the beam-propeller system is given in Sect. 3. The nonlinear model is linearized and the methods for modal analysis and calculating frequency response function (FRF) are presented in Sect. 4. The influence of the number of blades on the system time-dependency and the resultant dynamics is introduced in Sect. 5. The analyses of the nonlinear model in terms of the static deformation and dynamic time-domain responses are carried out in Sect. 6. Finally, a discussion is given in Sect. 7 and conclusions are drawn in Sect. 8.

2 Experimental setup

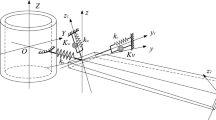
The detailed experimental setup is shown in Fig. 1. An aluminum beam with symmetric square cross section which represents a flexible propeller support is fixed to a frame using a steel support. The frame is strengthened to avoid any resonance in the frequency range of 0–150 Hz. A three-bladed propeller and motor is linked with the beam using an aluminum adaptor. The propeller has a diameter of 9 inches (= 22.86 cm) and pitch of 9 inches (= 22.86 cm). This geometric measure of blade pitch is taken as the theoretical distance a propeller moves forward when it makes a complete revolution. It is driven by an electric brushless motor (type: MN2806 KV400) whose rotational speed is controlled by RCbenchmark system and can be read from RCbenchmark interface. The motor is linked with the beam via an aluminum adaptor. While the effective length of beam is adjustable by controlling the length clamped between the support and the adaptor, its length was kept constant as 300 mm during these tests.

Fig. 1

Experimental setup. a Full picture b Enlarged picture of the propeller and adaptor c RCbenchmark motor control unit and modal hammer

Modal tests were carried out for the beam-propeller system in both the non-rotating and rotating conditions. The purpose of the modal test in the non-rotating condition was to identify the baseline modal frequencies and system mode shapes. The beam was excited transversally at 9 locations that divide the beam into 10 equal segments in y–z plane and x–z plane, respectively, using a modal hammer (PCB 086C03) (Fig. 1). The acceleration responses were measured by two single-axis accelerometers (PCB 352A25) that were attached onto the adaptor in y direction (acc1) and x direction (acc2). The modal test was performed when one of the blades was aligned in the y–z plane and directed toward + y direction.

The purpose of the modal tests in the rotating conditions was to study the influence of the rotational speed on the modal frequencies of the system. In the modal test, the beam was excited at location 6 in the x–z plane using a modal hammer (PCB 086C01) while the acceleration responses were measured in the same way as in the non-rotating condition. The test was done at a number of rotational speeds in the range of 0–246 rad/s. To confirm the influence of aerodynamics on the modal frequencies, the test was conducted when the propeller was rotating in both the ‘positive rotation’ (air flow starting from the leading edge) and the ‘reverse rotation’ (air flow starting from the trailing edge) while the propeller was kept in the same configuration as shown in Fig. 1.

In both the non-rotating and rotating conditions, NI 9234 module was used to acquire the input hammer force and the output accelerations. The FRFs from the hammer force to the accelerations were calculated and the modal properties were identified using the PolyMAX method [29].

To research into the influence of the number of blades, the results were compared with the test using a two-bladed propeller which was carried out in a very similar way and introduced in [28]. The difference lies in the position of the two accelerometers and the propeller. The test was conducted in the ‘nominal case’ where the propeller was spinning in the nominal thrust generating orientation and creating the tensile thrust force on the beam, and in the ‘revered case’ where the propeller worked in the reverse orientation and generated the compressive thrust force on the beam. In both cases, the air flow started from the leading edge, but the orientation of the propeller in the former case was the same as in Fig. 1 while that in the latter case was reversed to ensure the required leading edge first air flow conditions. With the two-bladed propeller, the acceleration responses were also acquired when the system exhibited instability.

3 Nonlinear modeling

The conventional commercial tools have their limitation when addressing the problem posed above. For example, the inextensibility constraint of the beam cannot be satisfied easily; for nonlinear modeling, the stability usually can only be determined through time-domain simulation; and it is difficult to couple the structural and aerodynamic models. To analyze the dynamics of the test rig rigorously and to enable future coupling with the propeller aerodynamics, a reduced-order analytical modeling approach is adopted. To study the underlying dynamics, the modeling only considers the essential characteristics while others are simplified or idealized. The developed nonlinear model of the test rig consists of a beam, the motor and adaptor (collectively called “motor assembly”), and the propeller. The beam is modeled using large deformation Euler–Bernoulli theory with an inextensibility constraint, while the motor assembly and propeller are modeled as rigid bodies. Thus, the geometric nonlinearity of the system is considered. The propeller rotates with a constant speed. To maintain the focus on the structural dynamics, the aerodynamics is neglected in the current modeling.

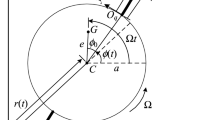
To better describe the vibration, three coordinate systems are introduced. The first one is the absolute coordinate system denoted as ${{\mathbf{S}}}_O = ({{\mathbf{i}}}_O ,{{\mathbf{j}}}_O ,{{\mathbf{k}}}_O )^T$, where ${{\mathbf{i}}}_O$, ${{\mathbf{j}}}_O$ and ${{\mathbf{k}}}_O$ represent the unit column basis vectors. The second coordinate system ${{\mathbf{S}}}_1 = ({{\mathbf{i}}}_1 ,{{\mathbf{j}}}_O ,{{\mathbf{k}}}_1 )^T$ is a relative one that is derived by rotating the coordinate system ${{\mathbf{S}}}_O$ around ${{\mathbf{j}}}_O$ by an angle $\gamma_1$, and the third coordinate system ${{\mathbf{S}}}_2 = ({{\mathbf{i}}},{{\mathbf{j}}},{{\mathbf{k}}})^T$ is derived by rotating the coordinate system ${{\mathbf{S}}}_1$ around ${{\mathbf{i}}}_1$ by an angle $\gamma_2$. The transformation between ${{\mathbf{S}}}_O$ and ${{\mathbf{S}}}_1$ is given by

$$ {{\mathbf{S}}}_O = {{\mathbf{T}}}_y (\gamma_1 ){{\mathbf{S}}}_1 ,{\text{where}}\,{{\mathbf{T}}}_y (\gamma_1 ) = \left[ {\begin{array}{*{20}l} {\cos \gamma_1 } \hfill & 0 \hfill & {\sin \gamma_1 } \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill \\ { - \sin \gamma_1 } \hfill & 0 \hfill & {\cos \gamma_1 } \hfill \\ \end{array} } \right] $$

(1)

The transformation between ${{\mathbf{S}}}_1$ and ${{\mathbf{S}}}_2$ is given by

$$ {{\mathbf{S}}}_1 = {{\mathbf{T}}}_x (\gamma_2 ){{\mathbf{S}}}_2 ,{\text{where}}\,{{\mathbf{T}}}_x (\gamma_2 ) = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \gamma_2 } & { - \sin \gamma_2 } \\ 0 & {\sin \gamma_2 } & {\cos \gamma_2 } \\ \end{array} } \right] $$

(2)

The rotational angles $\gamma_1$ and $\gamma_2$ differ at different locations along the beam and for the different modeled objects. Specifically, the coordinate system $({{\mathbf{i}}}_p ,{{\mathbf{j}}}_p ,{{\mathbf{k}}}_p )^T$, which is fixed with the motor assembly (denoted by subscript a) and non-rotating propeller (denoted by subscript p) and whose origin is the hub of the propeller, is derived by rotating the coordinate system ${{\mathbf{S}}}_O$ by the rotational angles $\varphi_a$ (or $\varphi_p$) and $- \theta_a$ (or $- \theta_p$) around ${{\mathbf{j}}}_O$ and ${{\mathbf{i}}}_1$ in sequence.

The modeling of the beam, the motor assembly and the propeller as well as the constraints in the system is introduced in the following subsections, respectively.

3.1 Modeling of the beam

The beam is modeled as a nonlinear inextensible Euler–Bernoulli beam that is fixed at one and free at the other end [30]. The inextensibility constraint is consistent with the physical property of the beam, i.e., the axial length of the beam on the neutral line is unchangeable during deformation [22]. And this constraint simplifies the mathematical expressions [30]. Different from the linear modeling by the authors in [28], the axial vibration of the beam is taken into account in this study. Therefore, its deformation is characterized by the transverse displacements (denoted by $w$ and $v$) in two orthogonal directions and axial displacement $u$ (Fig. 2). The torsion of the beam is not considered because its natural frequencies are higher than 1 kHz for the considered beam-propeller system. The transverse and axial displacements of the beam are expressed as the summation of the multiplication of the normalized function basis polynomials and the generalized time-dependent coordinates as

$$ w = \sum_{i = 1}^{N_w } {W_i (s)q_{wi} (t)} = {{\mathbf{q}}}_w^T {{\mathbf{W}}}(s) $$

(3)

$$ v = \sum_{i = 1}^{N_v } {V_i (s)q_{vi} (t)} = {{\mathbf{q}}}_v^T {{\mathbf{V}}}(s) $$

(4)

$$ u = \sum_{i = 1}^{N_u } {U_i (s)q_{ui} (t)} = {{\mathbf{q}}}_u^T {{\mathbf{U}}}(s) $$

(5)

where $s$ is the arc length along the deformed beam, $N_w$, $N_v$ and $N_u$ are the numbers of terms used in the summation, ${{\mathbf{W}}}(z) = \left[ {\begin{array}{*{20}c} {W_1 } & {W_2 } & \cdots & {W_{N_w } } \\ \end{array} } \right]^{\text{T}} \in {\mathbb{R}}^{N_w \times 1}$, ${{\mathbf{V}}}(z) = \left[ {\begin{array}{*{20}c} {V_1 } & {V_2 } & \cdots & {V_{N_v } } \\ \end{array} } \right]^{\text{T}} \in {\mathbb{R}}^{N_v \times 1}$ and ${{\mathbf{U}}}(z) = \left[ {\begin{array}{*{20}c} {U_1 } & {U_2 } & \cdots & {U_{N_u } } \\ \end{array} } \right]^{\text{T}} \in {\mathbb{R}}^{N_u \times 1}$ are the vectors consisting of the Chebyshev polynomials satisfying the ‘fixed-free’ geometric boundary conditions of $w(0) = v(0) = w^{\prime} (0) = v^{\prime} (0) = u(0) = 0$ generated as described in [28]; ${{\mathbf{q}}}_w = \left[ {\begin{array}{*{20}c} {q_{w1} } & {q_{w2} } & \cdots & {q_{wN_w } } \\ \end{array} } \right]^T \in {\mathbb{R}}^{N_w \times 1}$, ${{\mathbf{q}}}_v = \left[ {\begin{array}{*{20}c} {q_{v1} } & {q_{v2} } & \cdots & {q_{vN_v } } \\ \end{array} } \right]^T \in {\mathbb{R}}^{N_v \times 1}$ and ${{\mathbf{q}}}_u = \left[ {\begin{array}{*{20}c} {q_{u1} } & {q_{u2} } & \cdots & {q_{uN_u } } \\ \end{array} } \right]^T \in {\mathbb{R}}^{N_u \times 1}$ are the generalized coordinate vectors. ${{\mathbf{q}}}_b = \left[ {\begin{array}{*{20}c} {{{\mathbf{q}}}_u^T } & {{{\mathbf{q}}}_w^T } & {{{\mathbf{q}}}_v^T } \\ \end{array} } \right]^T \in {\mathbb{R}}^{(N_w + N_v + N_u ) \times 1}$ is the total generalized coordinate vector of the beam. The vibrations of the motor assembly and propeller are described by an axial displacement $u_a$, two transverse displacements $w_a$ and $v_a$, and two rotations $\varphi_a$ and $\theta_a$, so the generalized coordinate vector of the motor assembly and propeller is expressed as ${{\mathbf{q}}}_{mp} = \left[ {\begin{array}{*{20}c} {u_a } & {w_a } & {v_a } & {\varphi_a } & {\theta_a } \\ \end{array} } \right]^T \in {\mathbb{R}}^{5 \times 1}$, and ${{\mathbf{q}}}_{nl} = \left[ {\begin{array}{*{20}c} {{{\mathbf{q}}}_b^T } & {{{\mathbf{q}}}_{mp}^T } \\ \end{array} } \right]^T \in {\mathbb{R}}^{N_t \times 1}$ is the generalized coordinate vector of the entire model, and $N_t = N_w + N_v + N_u + 5$ is the total number of generalized coordinates.

Fig. 2

Nonlinear model of the test rig. The inset shows the geometric relation between the undeformed and deformed differential beam elements

The geometric relation between the undeformed and deformed differential elements is shown in Fig. 2. The axial strain of the beam on the neutral line is given by

$$ e = \sqrt {{(1 + u^{\prime} )^2 + v^{{\prime} 2} + w^{{\prime} 2} }} - 1 $$

(6)

where $o^{\prime} = \frac{\partial \left( o \right)}{{\partial s}}$.

Applying the inextensibility constraint $e = 0$ gives

$$ 2u^{\prime} + u^{{\prime} 2} + v^{{\prime} 2} + w^{{\prime} 2} = 0 $$

(7)

Because this constraint is dependent on the position, it is transformed into the following integral form in order to satisfy the constraint at any position:

$$ \Phi_b = \int_0^L {(2u^{\prime} + u^{{\prime} 2} + v^{{\prime} 2} + w^{{\prime} 2} )^2 {{\rm d}}s} = 0 $$

(8)

Two consecutive angles $\varphi$ and $\theta$ are used to describe the rotation from the undeformed position to the deformed one (Fig. 2). According to Fig. 2, the geometric relation for the two rotational angles, after simplification using the inextensibility constraint, is

$$ \sin \varphi = \frac{{w^{\prime} }}{{\sqrt {{(1 + u^{\prime} )^2 + w^{{\prime} 2} }} }} = \frac{{w^{\prime} }}{{\sqrt {{1 - v^{{\prime} 2} }} }},\cos \varphi = \frac{{1 + u^{\prime} }}{{\sqrt {{(1 + u^{\prime} )^2 + w^{{\prime} 2} }} }} = \frac{{1 + u^{\prime} }}{{\sqrt {{1 - v^{{\prime} 2} }} }} $$

(9)

$$ \sin \theta = v^{\prime} ,\cos \theta = \sqrt {{(1 + u^{\prime} )^2 + w^{{\prime} 2} }} = \sqrt {{1 - v^{{\prime} 2} }}$$

(10)

The approximate expressions for the two angles are derived from Eqs. (9)–(10) as

$$ \varphi = \arcsin \frac{{w^{\prime}}}{{\sqrt {{1 - v^{{\prime} 2} }} }} = w^{\prime} + \frac{1}{6}w^{{\prime} 3} + \frac{1}{2}v^{{\prime} 2} w^{\prime} + \frac{3}{8}v^{{\prime} 4} w^{\prime} + \frac{1}{4}w^{{\prime} 3} v^{{\prime} 2} + \frac{3}{{40}}w^{{\prime} 5} + O(\varepsilon ^6 ) $$

(11)

$$ \theta = \arcsin v^{\prime} = v^{\prime} + \frac{1}{6}v^{{\prime} 3} + \frac{3}{40}v^{{\prime} 5} + O(\varepsilon^6 ) $$

(12)

The curvature vector consisting of the curvatures of the beam about ${{\mathbf{i}}}$, ${{\mathbf{j}}}$ and ${{\mathbf{k}}}$ is derived from

$$ \left[ {\begin{array}{*{20}c} {\rho_1 } & {\rho_2 } & {\rho_3 } \\ \end{array} } \right] = \left( {\left[ {\begin{array}{*{20}c} 0 & {\varphi^{\prime}} & 0 \\ \end{array} } \right]{{\mathbf{T}}}_y (\varphi ) + \left[ {\begin{array}{*{20}c} { - \theta^{\prime}} & 0 & 0 \\ \end{array} } \right]} \right){{\mathbf{T}}}_x ( - \theta ) = \left[ {\begin{array}{*{20}c} { - \theta^{\prime}} & {\varphi^{\prime}\cos \theta } & {\varphi^{\prime}\sin \theta } \\ \end{array} } \right] $$

(13)

The potential energy of the beam due to bending deformation is given by

$$ \begin{aligned} U_b = & \frac{1}{2}EI_1 \int_0^L {\rho _1^2 {\text{d}}s} + \frac{1}{2}EI_2 \int_0^L {\rho _2^2 {\text{d}}s} = \frac{1}{2}EI_1 \int_0^L {v^{{\prime} {\prime} 2} (1 + v^{{\prime} 2} + v^{{\prime} 4} {\text{)d}}s} \\ & + \frac{1}{2}EI_2 \int_0^L {\begin{array}{*{20}l} {{\text{(}}w^{{\prime} {\prime} 2} + 2w^{{\prime} {\prime} } w^{\prime} v^{\prime} v^{{\prime} {\prime} } + w^{{\prime} {\prime} 2} w^{{\prime} 2} + w^{{\prime} {\prime} 2} w^{{\prime} 4} + w^{{\prime} {\prime} 2} w^{{\prime} 2} v^{{\prime} 2} } \hfill \\ { + 2w^{{\prime} {\prime} } w^{\prime} v^{{\prime} 3} v^{{\prime} {\prime} } + 2w^{{\prime} {\prime} } w^{{\prime} 3} v^{\prime} v^{{\prime} {\prime} } + w^{{\prime} 2} v^{{\prime} 2} v^{{\prime} {\prime} 2} {\text{)d}}s} \hfill \\ \end{array} } + O(\varepsilon ^7 ) \\ = & \frac{1}{2}{\mathbf{q}}_b^{\text{T}} {\mathbf{K}}_b {\mathbf{q}}_b + U_{bNL} \\ \end{aligned} $$

(14)

where ${{\mathbf{K}}}_b = {\text{diag}}\left( {\begin{array}{*{20}c} {{{\mathbf{O}}}_{N_u \times N_u } } & {{{\mathbf{K}}}_w } & {{{\mathbf{K}}}_v } \\ \end{array} } \right) \in {\mathbb{R}}^{(N_w + N_v + N_u ) \times (N_w + N_v + N_u )}$ is linear stiffness matrix of the beam, ${{\mathbf{K}}}_w = EI_2 \int_0^L {{\mathbf{W^{\prime \prime}}}} {\mathbf{W^{\prime \prime}}}^{\text{T}} {\text{d}}s \in {\mathbb{R}}^{N_w \times N_w }$, ${{\mathbf{K}}}_v = EI_1 \int_0^L {{\mathbf{V^{\prime \prime}V^{\prime \prime}}}^{\text{T}} {\text{d}}s} \in {\mathbb{R}}^{N_v \times N_v }$; $U_{bNL}$ is the nonlinear part of the potential energy expression due to bending of the beam.

The Kelvin–Voigt constitutive material model [31, 32] is chosen to represent the dissipation energy of the beam due to bending. The corresponding dissipation energy functional is given by

$$ \begin{aligned} D_b = & \frac{1}{2}c_s I_1 \int_0^L {\dot{\rho }_1^2 {\text{d}}s} + \frac{1}{2}c_s I_2 \int_0^L {\dot{\rho }_2^2 {\text{d}}s} \\ = & \frac{1}{2}c_s I_1 \int_0^L {\left( {\dot{v}^{{\prime} {\prime} 2} + \dot{v}^{{\prime} {\prime} 2} v^{{\prime} 2} + 2\dot{v}^{{\prime} {\prime} } v^{{\prime} {\prime} } \dot{v}^{\prime} \dot{v} + \dot{v}^{{\prime} {\prime} 2} v^{{\prime} 4} + v^{{\prime} {\prime} 2} v^{{\prime} 2} \dot{v}^{{\prime} 2} + 4\dot{v}^{{\prime} {\prime} } v^{{\prime} {\prime} } v^{{\prime} 3} \dot{v}^{\prime} } \right){\text{d}}s} \\ & + \frac{1}{2}c_s I_2 \int_0^L {\begin{array}{*{20}l} {{\text{(}} \dot{w}^{{\prime} {\prime} 2} + 2\dot{w}^{\prime} w^{{\prime} {\prime} } w^{\prime} \dot{w}^{{\prime} {\prime} } + w^{{\prime} 2} \dot{w}^{{\prime} {\prime} 2} + 2v^{{\prime} {\prime} } w^{\prime} \dot{w}^{{\prime} {\prime} } \dot{v}^{\prime} + 2v^{\prime} w^{\prime} \dot{w}^{{\prime} {\prime} } \dot{v}^{{\prime} {\prime} } + 2\dot{w}^{\prime} v^{{\prime} {\prime} } v^{\prime} \dot{w}^{{\prime} {\prime} } } \hfill \\ { + 6v^{{\prime} {\prime} } v^{{\prime} 2} {w}^{\prime} \dot{w}^{{\prime} {\prime} } \dot{v}^{\prime} + 2v^{{\prime} 3} {w}^{\prime} \dot{w}^{{\prime} {\prime} } \dot{v}^{{\prime} {\prime} } + 2\dot{w}^{\prime} v^{{\prime} {\prime} } v^{{\prime} 3} \dot{w}^{{\prime} {\prime} } + 2\dot{w}^{\prime} w^{{\prime} {\prime} } v^{{\prime} 2} w^{\prime} \dot{w}^{{\prime} {\prime} } + v^{{\prime} 2} w^{{\prime} 2} \dot{w}^{{\prime} {\prime} 2} } \hfill \\ { + 2w^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} \dot{w}^{{\prime} {\prime} } \dot{v}^{\prime} + 4\dot{w}^{\prime} v^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} \dot{w}^{{\prime} {\prime} } + 2v^{{\prime} {\prime} } w^{{\prime} 3} \dot{w}^{{\prime} {\prime} } \dot{v}^{\prime} + 2v^{{\prime} } w^{{\prime} 3} \dot{w}^{{\prime} {\prime} } \dot{v}^{{\prime} {\prime} } } \hfill \\ { + 4\dot{w}^{\prime} w^{{\prime} {\prime} } w^{{\prime} 3} \dot{w}^{{\prime} {\prime} } + w^{{\prime} 4} \dot{w}^{{\prime} {\prime} 2} + \dot{w}^{{\prime} 2} w^{{\prime} {\prime} 2} w^{{\prime} 2} + v^{{\prime} {\prime} 2} w^{{\prime} 2} \dot{v}^{{\prime} 2} + \dot{w}^{{\prime} 2} v^{{\prime} {\prime} 2} v^{{\prime} 2} } \hfill \\ { + v^{{\prime} 2} w^{{\prime} 2} \dot{v}^{{\prime} {\prime} 2} + 2v^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} \dot{v}^{{\prime} {\prime} } \dot{v}^{\prime} + 2\dot{w}^{\prime} v^{{\prime} {\prime} } w^{{\prime} {\prime} } w^{{\prime} 2} \dot{v}^{\prime} + 2\dot{w}^{\prime} v^{{\prime} {\prime} } v^{{\prime} 2} w^{\prime} \dot{v}^{{\prime} {\prime} } + 2\dot{w}^{\prime} w^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} \dot{v}^{{\prime} {\prime} } } \hfill \\ { + 2\dot{w}^{\prime} v^{{\prime} {\prime} 2} v^{\prime} w^{\prime} \dot{v}^{\prime} + 2\dot{w}^{{\prime} 2} v^{{\prime} {\prime} } w^{{\prime} {\prime} } v^{\prime} w^{\prime} ){\text{d}}s} \hfill \\ \end{array} } + O(\varepsilon ^7 ) \\ = & \frac{1}{2}{\dot{{\mathbf{q}}}}_b^{\text{T}} {\mathbf{C}}_b {\dot{{\mathbf{q}}}}_b + D_{bNL} \\ \end{aligned} $$

(15)

where $\dot{o} = \frac{{{\text{d}}\left( o \right)}}{{{\text{d}}t}}$, $c_s$ is the material coefficient of internal damping for bending, $\eta_s = c_s /E$ is the proportionality constant of internal damping in bending. ${{\mathbf{C}}}_b \in {\mathbb{R}}^{(N_w + N_v + N_u ) \times (N_w + N_v + N_u )}$ is the linear damping matrix of the beam; $D_{bNL}$ is the nonlinear part of the dissipation energy functional due to the beam bending activity.

The kinetic energy of the beam is given by

$$ T_b = \frac{1}{2}m\int_0^L ( \dot{u}^2 + \dot{v}^2 + \dot{w}^2 ){{\rm d}}s = \frac{1}{2}{\dot{\mathbf{q}}}_b^T {{\mathbf{M}}}_b {\dot{\mathbf{q}}}_b $$

(16)

where $m$ is the mass per unit length of the beam, ${{\mathbf{M}}}_b = {\text{diag}}\left( {\begin{array}{*{20}c} {{{\mathbf{M}}}_u } & {{{\mathbf{M}}}_w } & {{{\mathbf{M}}}_v } \\ \end{array} } \right) \in {\mathbb{R}}^{(N_w + N_v + N_u ) \times (N_w + N_v + N_u )}$ is the mass matrix of the beam, ${{\mathbf{M}}}_u = m\int_0^L {{{\mathbf{UU}}}^T {\text{d}}s} \in {\mathbb{R}}^{N_u \times N_u }$, ${{\mathbf{M}}}_w = m\int_0^L {{{\mathbf{WW}}}^T {\text{d}}s} \in {\mathbb{R}}^{N_w \times N_w }$, ${{\mathbf{M}}}_v = m\int_0^L {{{\mathbf{VV}}}^T {\text{d}}s} \in {\mathbb{R}}^{N_v \times N_v }$.

3.2 Modeling of motor assembly

The motor assembly is modeled as a rigid body. It has displacements in the axial direction (denoted by $u_a$) and two transverse directions (denoted by $w_a$ and $v_a$) as well as rotational angle $\varphi_a$ and $- \theta_a$ about ${{\mathbf{j}}}_O$ and ${{\mathbf{i}}}_1$ in sequence.

The angular velocity vector of the motor assembly about ${{\mathbf{i}}}_p$, ${{\mathbf{j}}}_p$ and ${{\mathbf{k}}}_p$ is derived from the following equation

$$ \begin{aligned} {{\varvec{\omega}}}_{{\mathbf{a}}} = & \left[ {\begin{array}{*{20}c} {\omega_{ax} } & {\omega_{ay} } & {\omega_{az} } \\ \end{array} } \right] \\ { = } & \left( {\left[ {\begin{array}{*{20}c} 0 & {\dot{\varphi }_a } & 0 \\ \end{array} } \right]{{\mathbf{T}}}_y (\varphi_a ) + \left[ {\begin{array}{*{20}c} { - \dot{\theta }_a } & 0 & 0 \\ \end{array} } \right]} \right){{\mathbf{T}}}_x ( - \theta_a ) \\ = & \left[ {\begin{array}{*{20}c} { - \dot{\theta }_a } & {\dot{\varphi }_a \cos \theta_a } & {\dot{\varphi }_a \sin \theta_a } \\ \end{array} } \right] \\ \end{aligned} $$

(17)

The kinetic energy of the motor assembly is then given by

$$ \begin{aligned} T_a = & \frac{1}{2}m_a \left( {\dot{u}_a^2 + \dot{v}_a^2 + \dot{w}_a^2 } \right) + \frac{1}{2}I_a \left( {\omega_{ax}^2 + \omega_{ay}^2 } \right) \\ = & \frac{1}{2}m_a \left( {\dot{u}_a^2 + \dot{v}_a^2 + \dot{w}_a^2 } \right) + \frac{1}{2}I_a \left( {\dot{\theta }_a^2 + \dot{\varphi }_a^2 \cos^2 \theta_a } \right) \\ \end{aligned} $$

(18)

where $m_a$ is the mass of the motor assembly, and $I_a$ is the moment of inertia of the motor assembly about its mass center around x or y axis.

3.3 Propeller modeling

It is assumed the rotor is isotropic, which means all the blades are the same. The propeller is modeled as a rigid body with the center of mass at the hub, and it has displacements in the axial direction (denoted by $u_p$) and two transverse directions (denoted by $w_p$ and $v_p$) as well as rotational angles $\varphi_p$ and $- \theta_p$ about ${{\mathbf{j}}}_O$ and ${{\mathbf{i}}}_1$, respectively.

The rotating propeller is in rigid connection with the motor assembly, so their displacements and rotational angles satisfy the following geometric relationships

$$ \left\{ {\begin{array}{*{20}l} {u_p = u_a - z_{pc} (1 - \cos \theta_a \cos \varphi_a )} \hfill \\ {w_p = w_a + \cos \theta_a \sin \varphi_a z_{pc} } \hfill \\ {v_p = v_a + \sin \theta_a z_{pc} } \hfill \\ {\theta_p = \theta_a } \hfill \\ {\varphi_p = \varphi_a } \hfill \\ \end{array} } \right. $$

(19)

where $z_{pc} = z_p - 0.5L_a$ is the distance from the center of the motor assembly to the propeller.

The angular velocity vector of the propeller about ${{\mathbf{i}}}_p$, ${{\mathbf{j}}}_p$ and ${{\mathbf{k}}}_p$ is obtained from the following equation

$$ \begin{aligned} {{\varvec{\omega}}}_p = & \left[ {\begin{array}{*{20}c} {\omega_{px} } & {\omega_{py} } & {\omega_{pz} } \\ \end{array} } \right] \\ { = } & \left( {\left[ {\begin{array}{*{20}c} 0 & {\dot{\varphi }_p } & 0 \\ \end{array} } \right]{{\mathbf{T}}}_y (\varphi_p ) + \left[ {\begin{array}{*{20}c} { - \dot{\theta }_p } & 0 & 0 \\ \end{array} } \right]} \right){{\mathbf{T}}}_x ( - \theta_p ) + \left[ {\begin{array}{*{20}c} 0 & 0 & \Omega \\ \end{array} } \right] \\ = & \left[ {\begin{array}{*{20}c} { - \dot{\theta }_a } & {\dot{\varphi }_a \cos \theta_a } & {\dot{\varphi }_a \sin \theta_a + \Omega } \\ \end{array} } \right] \\ \end{aligned} $$

(20)

The moment of inertia matrix of the propeller about ${{\mathbf{i}}}_p$ and ${{\mathbf{j}}}_p$ is then given by

$$ \left[ {\begin{array}{*{20}c} {I_{py} (t)} & {I_{pxy} (t)} \\ {I_{pxy} (t)} & {I_{px} (t)} \\ \end{array} } \right] = \sum_{i = 1}^{N_b } {{{\mathbf{T}}}_z (\alpha_i )\left[ {\begin{array}{*{20}c} {I_{py0} } & {I_{pxy0} } \\ {I_{pxy0} } & {I_{px0} } \\ \end{array} } \right]{{\mathbf{T}}}_z (\alpha_i )^{\text{T}} } $$

(21)

where $I_{px0} { = }\int {y^2 {\text{d}}m}$ and $I_{py0} = \int {x^2 {\text{d}}m}$ are the initial moments of inertia of each propeller blade about ${{\mathbf{i}}}_p$ and ${{\mathbf{j}}}_p$ axes, respectively; $I_{pxy0} = \int {xy{\text{d}}m}$ is the initial xy product of inertia. ${{\mathbf{T}}}_z (\alpha ) = \left[ {\begin{array}{*{20}c} {\cos \alpha } & { - \sin \alpha } \\ {\sin \alpha } & {\cos \alpha } \\ \end{array} } \right]$ is the transformation matrix. $\alpha_i = \Omega t + \alpha_{i0}$ is the azimuth angle of the ith blade of the propeller around ${{\mathbf{k}}}_p$. $\Omega$ is the rotational speed of the propeller, which is positive if the rotation is clockwise when viewing in + z direction, and vice versa.

The kinetic energy of the propeller [33] is given by

$$ T_p = \frac{1}{2}m_p \left( {\dot{u}_p^2 + \dot{v}_p^2 + \dot{w}_p^2 } \right) + \frac{1}{2}{{\varvec{\omega}}}_p {{\mathbf{I}}}_p (t){{\varvec{\omega}}}_p^T $$

(22)

where $m_p$ is the mass of the propeller, and ${{\mathbf{I}}}_p (t) = \left[ {\begin{array}{*{20}c} {I_{px} (t)} & { - I_{pxy} (t)} & 0 \\ { - I_{pxy} (t)} & {I_{py} (t)} & 0 \\ 0 & 0 & {I_{pz} } \\ \end{array} } \right]$ is the moment of inertia tensor, $I_{pz}$ is the moment of inertia of the propeller about ${{\mathbf{k}}}_p$ axis.

3.4 External work

The gravity of the motor assembly and the propeller is considered and there is an applied external force F_im at the location of $z_{ext}$ from the beam root with an angle of $\gamma$ with respect to positive x direction in the case of impulse response (Fig. 2), so the variation of the work done by the external force is given by

$$ \delta W_{{\text{ext}}} = m_a g\delta u_a + m_p g\delta u_p + F_{im} \cos \gamma \delta w(z_{{\text{ext}}} ) + F_{im} \sin \gamma \delta v(z_{{\text{ext}}} ) = \delta {{\mathbf{q}}}_{nl}^T {{\mathbf{f}}}_{{\text{ext}}} ({{\mathbf{q}}}_{mp} ) $$

(23)

where ${{\mathbf{f}}}_{{\text{ext}}} ({{\mathbf{q}}}_{mp} ) \in {\mathbb{R}}^{N_t \times 1}$ is the external force vector.

3.5 Motor assembly-beam dynamic constraint

The tip of the beam is in rigid connection with the motor assembly, so their displacements and rotations are nominally equal. The displacement and rotation continuity leads to the following constraint equations:

$$ {{\varvec{\varPhi}}}_c = \left[ {\begin{array}{*{20}c} {u(L,t) - u_a - 0.5L_a (1 - \cos \theta_a \cos \varphi_a )} \\ {w(L,t) - (w_a - 0.5L_a \sin \varphi_a \cos \theta_a )} \\ {v(L,t) - (v_a - 0.5L_a \sin \theta_a )} \\ {\varphi (L,t) - \varphi_a } \\ {\theta (L,t) - \theta_a } \\ \end{array} } \right] = {{\mathbf{0}}} $$

(24)

3.6 Equations of motion

To perform the time-domain simulations using the full nonlinear model, Udwadia-Kalaba method [34] is used to enforce the constraints in Eqs. (8), (24). To apply this method, the equation of motion without the constraints is derived first. The total kinetic, potential and dissipation energies of the system are given, , by

$$ T = T_b + T_a + T_p $$

(25)

$$ U = U_b $$

(26)

$$ D = D_b $$

(27)

The equation of motion without the constraints is obtained by substituting the total kinetic energy and total potential energy into Lagrange’s equation of the second kind as follows:

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial {\dot{\mathbf{q}}}_{nl}^T }}} \right) - \frac{\partial T}{{\partial {{\mathbf{q}}}_{nl}^T }} + \frac{\partial U}{{\partial {{\mathbf{q}}}_{nl}^T }} + \frac{\partial D}{{\partial {\dot{\mathbf{q}}}_{nl}^T }} = {{\mathbf{f}}}_{{\text{ext}}} $$

(28)

The equation of motion of the nonlinear system without the constraints, summarized in Eqs. (8), (24), expressed in matrix form is given by

$$ \underbrace {\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_b } & {\,} \\ {\,} & {{\mathbf{M}}_2 } \\ \end{array} } \right]}_{{\mathbf{M}}_{nl} }{\ddot{\mathbf{q}}}_{nl} + \underbrace {\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_b {\mathbf{q}}_b + {\mathbf{b}}_{nl} ({\mathbf{q}}_b ) + {\mathbf{C}}_b {\dot{\mathbf{q}}}_b + {\mathbf{c}}_{nl} ({\mathbf{q}}_b ,{\dot{\mathbf{q}}}_b )} \\ {{\mathbf{g}}_{nl} ({\mathbf{q}}_{mp} ,{\dot{\mathbf{q}}}_{mp} )} \\ \end{array} } \right]}_{{\mathbf{f}}_{nl} } = {\mathbf{f}}_{{\text{ext}}} ({\mathbf{q}}_{mp} ) $$

(29)

where ${{\mathbf{M}}}_2 \in {\mathbb{R}}^{5 \times 5}$ is the mass matrix of the motor assembly and propeller; thus, ${{\mathbf{M}}}_{nl} \in {\mathbb{R}}^{N_t \times N_t }$ is the mass matrix of the whole system; ${{\mathbf{b}}}_{nl} ({{\mathbf{q}}}_b ) \in {\mathbb{R}}^{(N_w + N_v + N_u ) \times 1}$ and ${{\mathbf{c}}}_{nl} ({{\mathbf{q}}}_b ,{\dot{\mathbf{q}}}_b ) \in {\mathbb{R}}^{(N_w + N_v + N_u ) \times 1}$ are the nonlinear structural force vector of the beam due to the nonlinear potential energy term $U_{bNL}$ and the dissipation force vector due to the nonlinear dissipation energy term $D_{bNL}$; ${{\mathbf{g}}}_{nl} ({{\mathbf{q}}}_{mp} ,{\dot{\mathbf{q}}}_{mp} ,t) \in {\mathbb{R}}^{5 \times 1}$ is the nonlinear structural force vector of the motor assembly and propeller due to the kinetic energy; thus, ${{\mathbf{f}}}_{nl} \in {\mathbb{R}}^{N_t \times 1}$ is the internal force vector of the whole system. The detailed expressions are provided in Appendix A.

Then, to satisfy the constraints in Eqs. (8), (24) in the spirit of the Udwadia-Kalaba method [34], the final equation of motion in the state-space form is given by

$$ \left\{ {\begin{array}{*{20}l} {{\dot{\mathbf{h}}}_1 = {{\mathbf{h}}}_2 } \hfill \\ {{\dot{\mathbf{h}}}_2 = {{\mathbf{a}}} + {{\mathbf{M}}}_{nl}^{ - 1/2} ({{\mathbf{AM}}}_{nl}^{ - 1/2} )^+ ({{\mathbf{b}}}_v - {{\mathbf{Aa}}})} \hfill \\ \end{array} } \right. $$

(30)

where ${{\mathbf{a}}} = {{\mathbf{M}}}_{nl}^{ - 1} ({{\mathbf{f}}}_{{\text{ext}}} - {{\mathbf{f}}}_{nl} )$, and the generalized coordinate vector in state space is $\left[ {\begin{array}{*{20}c} {{\mathbf{h}}_1 } \\ {{\mathbf{h}}_2 } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{nl} } \\ {{\dot{\mathbf{q}}}_{nl} } \\ \end{array} } \right]$. ${{\mathbf{A}}} = \frac{{\partial {{\varvec{\varPhi}}}}}{{\partial {{\mathbf{q}}}_{nl} }}$, ${{\mathbf{b}}}_v = - {\dot{\mathbf{q}}}_{nl}^{\text{T}} \frac{{\partial^2 {{\varvec{\varPhi}}}}}{{\partial {{\mathbf{q}}}_{nl}^2 }}{\dot{\mathbf{q}}}_{nl} - 2\frac{{\partial^2 {{\varvec{\varPhi}}}}}{{\partial {{\mathbf{q}}}_{nl} \partial t}}{\dot{\mathbf{q}}}_{nl} - \frac{{\partial^2 {{\varvec{\varPhi}}}}}{\partial t^2 }$ and ${{\varvec{\varPhi}}}({{\mathbf{q}}}_{nl} ) = \left[ {\begin{array}{*{20}c} {{{\varvec{\varPhi}}}_c } \\ {\Phi_b } \\ \end{array} } \right]$ is the constraint vector. The detailed expressions are provided in Appendix A.

However, given the differential nature in which the constraints are introduced in the above formulation, the direct use of Eq. (30) may lead to the error accumulation and constraint drift, ultimately leading to the divergent behavior during the simulation. To eliminate this drift in the numerical simulation, the equation of motion is corrected according to the method proposed in [35] as follows

$$ \left\{ {\begin{array}{*{20}l} {{\dot{\mathbf{h}}}_1 = {{\mathbf{h}}}_2 + {{\mathbf{M}}}_{nl}^{ - 1/2} ({{\mathbf{AM}}}_{nl}^{ - 1/2} )^+ ({{\mathbf{b}}}_q - {{\mathbf{Ah}}}_2 - {{\varvec{\varPhi}}}/{\text{d}}t)} \hfill \\ {{\dot{\mathbf{h}}}_2 = {{\mathbf{a}}} + {{\mathbf{M}}}_{nl}^{ - 1/2} ({{\mathbf{AM}}}_{nl}^{ - 1/2} )^+ ({{\mathbf{b}}}_v - {{\mathbf{Aa}}} - {\dot{\varvec{\Phi }}}/{\text{d}}t)} \hfill \\ \end{array} } \right. $$

(31)

where ${{\rm d}}t$ is the integration time step, ${{\mathbf{b}}}_q = - \frac{{\partial {{\varvec{\varPhi}}}}}{\partial t} = {{\mathbf{0}}}$, ${\dot{\varvec{\Phi}}}$ is the time derivative of the constraint vector. The detailed expressions are provided in Appendix A. The drawback of the correction approach is that it tends to generate the high-frequency oscillations in the first and second derivatives of the state variables and the correction terms do not have physical meaning.

4 Linearized model

To complete the analysis directly in the frequency domain, the nonlinear model in Sect. 3 is linearized in this section. The methods of performing modal analysis and calculating the FRFs for both the time-invariant and time-varying systems based on the linearized model are also introduced in this section.

4.1 Equation of motion

This section shows how the nonlinear model with inextensibility constraint introduced in Sect. 3 is transformed into the linearized model, and the relationship between the nonlinear model in this paper and the linear model in the previous paper [28]. To proceed with the linear analysis, the nonlinear model is linearized around the equilibrium position in the vertical orientation under the influence of gravity.

Since the axial displacements (i.e., $u$, $u_a$ and $u_p$) are assumed to be of higher order than the transverse displacements $w$ and $v$, they are neglected in the present linearized model. Adopting the original inextensibility constraint Eq. (7), the axial displacement of the beam is written in the following approximate form

$$ u^{\prime} \approx - \frac{1}{2}\left( {v^{{\prime} 2} + w^{{\prime} 2} } \right) $$

(32)

Considering the constraints in Eqs. (19), (24), (32), the external work due to the gravity in the axial direction in Eq. (23) becomes

$$ \delta W_{{\text{ext}}} = (m_a + m_p )g\delta u(L,t) = (m_a + m_p )g\delta \int_0^L { - \frac{1}{2}\left( {v^{{\prime} 2} + w^{{\prime} 2} } \right){\text{d}}s} = - \delta U_{ba} $$

(33)

Consequently, the potential energy of the beam due to the axial force is written as

$$ U_{ba} = \frac{1}{2}(m_a + m_p )g\int_0^L {(v^{{\prime} 2} + w^{{\prime} 2} ){{\rm d}}s} = (m_a + m_p )g\left[ {\begin{array}{cc} {{{\mathbf{q}}}_w^T } & {{{\mathbf{q}}}_v^T } \\ \end{array} } \right]\left[ {\begin{array}{cc} {\int_0^L {{\mathbf{W^{\prime}}}} {\mathbf{W^{\prime}}}^T {{\rm d}}s} & {{\mathbf{O}}} \\ {{\mathbf{O}}} & {\int_0^L {{\mathbf{V^{\prime}}}} {\mathbf{V^{\prime}}}^T {{\rm d}}s} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{{\mathbf{q}}}_w } \\ {{{\mathbf{q}}}_v } \\ \end{array} } \right] $$

(34)

The generalized coordinate vector of the linearized model is ${{\mathbf{q}}} = \left[ {\begin{array}{*{20}c} {{{\mathbf{q}}}_w^T } & {{{\mathbf{q}}}_v^T } & {w_a } & {v_a } & {\varphi_a } & {\theta_a } \\ \end{array} } \right]^T \in {\mathbb{R}}^{(N_w + N_v + 4) \times 1}$.

The small angle approximation is made, so that $\sin \alpha = \alpha$, $\cos \alpha = 1$, where $\alpha$ represents any angle.

In the previous study [28], it was shown that adding the large artificial springs in the frequency domain is analogous to applying Udwadia-Kalaba method in the time domain in terms of satisfying the constraints. Thus, for the purposes of the linear analysis, the constraint in Eq. (24) is enforced by adding large artificial springs. Under the above linearization assumptions, the corresponding potential energy is given by

$$ U_c = \frac{1}{2}{{\varvec{\varPhi}}}_{cL}^T {\text{diag}}\left( {\begin{array}{*{20}c} {k_l } & {k_l } & {k_r } & {k_r } \\ \end{array} } \right){{\varvec{\varPhi}}}_{cL} = \frac{1}{2}{{\mathbf{q}}}^T {{\mathbf{K}}}_c {{\mathbf{q}}} $$

(35)

where $k_l$ and $k_r$ are the stiffness values of the translational and rotational artificial springs, respectively; and ${{\mathbf{K}}}_c = {{\mathbf{A}}}^T {\text{diag}}\left( {\begin{array}{*{20}c} {k_l } & {k_l } & {k_r } & {k_r } \\ \end{array} } \right){{\mathbf{A}}} \in {\mathbb{R}}^{(N_w + N_v + 4) \times (N_w + N_v + 4)}$ is the stiffness matrix due to the beam-motor connection using these artificial springs, and ${{\mathbf{A}}} = \frac{{\partial {{\varvec{\varPhi}}}_{cL} }}{{\partial {{\mathbf{q}}}}} \in {\mathbb{R}}^{4 \times (N_w + N_v + 4)}$, ${{\varvec{\varPhi}}}_{cL} = \left[ {\begin{array}{*{20}c} {w(L,t) - (w_a - 0.5L_a \varphi_a )} \\ {v(L,t) - (v_a - 0.5L_a \theta_a )} \\ {\varphi (L,t) - \varphi_a } \\ {\theta (L,t) - \theta_a } \\ \end{array} } \right]$ is the linearized form of the kinematic constraints.

The variation of the work done by the external force ($F_{im}$) is then given by

$$ \delta W_{{\text{ext}}L} = F_{im} \sin \gamma \delta w(z_{{\text{ext}}} ) + F_{im} \cos \gamma \delta v(z_{{\text{ext}}} ) = \delta {{\mathbf{q}}}^{\text{T}} F_{im} {{\mathbf{B}}}(z_{{\text{ext}}} ,\gamma ) $$

(36)

where ${{\mathbf{B}}}(z_{{\text{ext}}} ,\gamma ) = \left[ {\begin{array}{*{20}c} {{{\mathbf{W}}}(z_{{\text{ext}}} )^T \cos \gamma }\;\; {{{\mathbf{V}}}(z_{{\text{ext}}} )^T \sin \gamma } & {{{\mathbf{0}}}_{1 \times 4} } \\ \end{array} } \right]^{\text{T}} \in {\mathbb{R}}^{(N_w + N_v + 4) \times 1}$ is the polynomial vector.

Substituting the kinetic energy, dissipation energy, potential energy and external force vector into the Lagrange’s equation, the equation of motion for the linearized model is written as

$$ {\mathbf{M}}_L {\ddot{\mathbf{q}}} + {\mathbf{C}}_L {\dot{\mathbf{q}}} + {\mathbf{K}}_L {\mathbf{q}} = F_{im} {\mathbf{B}}(z_{{\text{ext}}} ,\gamma ) $$

(37)

where ${{\mathbf{M}}}_L \in {\mathbb{R}}^{(N_w + N_v + 4) \times (N_w + N_v + 4)}$, ${{\mathbf{C}}}_L \in {\mathbb{R}}^{(N_w + N_v + 4) \times (N_w + N_v + 4)}$ and ${{\mathbf{K}}}_L \in {\mathbb{R}}^{(N_w + N_v + 4) \times (N_w + N_v + 4)}$ are the mass, damping and stiffness matrices of the linearized model, respectively. ${{\mathbf{C}}}_L$ includes the skew-symmetric gyroscopic damping matrix and the structural damping matrix for the beam. After this linearization, the nonlinear system actually adopts the form identical to the linear model developed in the previous study [28] with an exception for the additional structural damping terms of the beam in ${{\mathbf{C}}}_L$.

4.2 Modal analysis

As it will be discussed in more detail later, due to the rotation of the propeller and depending on the number of blades, the studied system can be either time-invariant or time-varying. Consequently, modal analysis is performed using the linearized model according to one of the method introduced in this subsection.

4.2.1 Time-invariant system

When the system is time-invariant, modal analysis is performed using the traditional approach. The equation of motion in Eq. (37) for free vibration is transformed into the state space as follows

$$ {\mathbf{A}}_1 {\dot{\mathbf{y}}} + {{\mathbf{B}}}_1 {{\mathbf{y}}} = {{\mathbf{0}}} $$

(38)

where ${\mathbf{y}} = \left[ {\begin{array}{*{20}c} {\mathbf{q}} \\ {{\dot{\mathbf{q}}}} \\ \end{array} } \right] \in \mathbb{R}^{2(N_w + N_v + 4) \times 1}$, ${{\mathbf{A}}}_1 = \left[ {\begin{array}{*{20}c} {{{\mathbf{C}}}_L } & {{{\mathbf{M}}}_L } \\ {{{\mathbf{M}}}_L } & {{\mathbf{O}}} \\ \end{array} } \right] \in {\mathbb{R}}^{2(N_w + N_v + 4) \times 2(N_w + N_v + 4)}$, and ${{\mathbf{B}}}_1 = \left[ {\begin{array}{*{20}c} {{{\mathbf{K}}}_L } & {{\mathbf{O}}} \\ {{\mathbf{O}}} & { - {{\mathbf{M}}}_L } \\ \end{array} } \right] \in {\mathbb{R}}^{2(N_w + N_v + 4) \times 2(N_w + N_v + 4)}$.

Then, ${{\mathbf{y}}} = {{\mathbf{Y}}}e^{\lambda t}$ is substituted into Eq. (38), and the eigenvalues $\lambda_i = - \zeta_i \omega_i + {\text{j}}\omega_i \sqrt {1 - \zeta_i^2 }$ and its corresponding eigenvectors ${{\mathbf{Y}}}_i$ are solved, where $\omega_i = 2\pi f_i$ is the ith undamped natural circular frequency, $f_i$ is the ith undamped natural frequency, and $\zeta_i$ is the ith damping ratio.

4.2.2 Time-varying system

When the system is time-varying, modal analysis is conducted using the coordinate transform method [5]. While the detailed procedure with equations can be found in the previous study [28], it is summarized briefly as follows:

• (1) The equation of motion Eq. (37) defined in the real coordinate system is transformed into that in the complex coordinate system by performing a coordinate transform which leads to the time-varying equation of motion with the complex valued matrices;

• (2) The resultant time-varying equation of motion with the complex valued coefficient matrices is expanded into an equivalent time-invariant equation of motion with the infinite coefficient matrices;

• (3) Finally, the equation of motion with the infinite coefficient matrices is truncated into a finite size and a state-space eigenvalue problem is formed from this truncated formulation. Note that ‘xN’ truncation denotes the case where the finite submatrices are of the size xN, starting from the center and $2N = N_w + N_v + 4$.

4.3 Frequency response function

For the same reason, the calculation of the FRFs also takes into account the time-dependency nature of the system. The FRFs are calculated using the linearized model, and the methods are introduced in this subsection.

4.3.1 Time-invariant system

When the system is time-invariant, the FRF is calculated using the traditional approach. The receptance from the applied force to the displacement response at the location of $z_{{\text{res}}}$ from beam root at an angle of $\beta_0$ from the positive x direction is calculated as follows

$$ H(\omega ) = {{\mathbf{B}}}(z_{{\text{res}}} ,\beta_0 )^{\text{T}} ( - \omega^2 {{\mathbf{M}}}_L + {\text{j}}\omega {{\mathbf{C}}}_L + {{\mathbf{K}}}_L )^{ - 1} {{\mathbf{B}}}(z_{{\text{ext}}} ,\gamma ) $$

(39)

4.3.2 Time-varying system

When the system is time-varying, the FRFs are calculated with the help of the coordinate transform method. The procedure is described as follows while the details can be found in the previous study [28]:

• (1) Following Step 3 in Sect. 4.2.2, the frequency response matrix (FRM) is calculated using the truncated time-invariant equation of motion;

• (2) The 2N × 2N block in the center of the FRM is used, where 2N equals N_w + N_v + 4, and then the receptance is calculated using Eq. (40) as follows

  $$ H(\omega ) = {\mathbf{B}}(z_{{\text{res}}} ,\beta _0 )^T {\mathbf{J}}^{ - 1} \overline{{\textbf{H}}}_{{\text{tr}}} (\omega ){\mathbf{JB}}(z_{{\text{ext}}} ,\gamma ) $$

  (40)

  where ${{\mathbf{H}}}_{{\text{tr}}} (\omega )$ is the 2N × 2N truncated FRM, and ${{\mathbf{J}}}$ is the transformation matrix from the real generalized coordinate vector to complex generalized coordinate vector.

5 Comparative analysis between 2- and more-bladed configurations

As discussed in introduction to this research, there are qualitative differences between the rotors with two and more numbers of blades. The attention in this section is paid to these differences. Initially, the influence of blade number on the time-dependency of the system is shown mathematically. Then, two specific instances of the two-bladed and three-bladed propeller configurations are compared, numerically and experimentally, considering both non-rotating and rotating operating conditions.

5.1 Time-dependency

The simple proof of the time-dependency is given here while the details can be found in the previous study [28]. Due to the rotation of the propeller, the system with the rigid rotor can be time-varying or time-invariant depending on the number of blades. Under the assumption of a rigid isotropic propeller and evenly-distributed blades, the moments of inertia of the propeller ($I_{px}$, $I_{py}$ and $I_{pxy}$) are the only source of potential time-dependency. From Eq. (21), the moments of inertia of a propeller with N_b blades about ${{\mathbf{i}}}_p$ and ${{\mathbf{j}}}_p$ and the xy product of inertia are derived as follows:

$$ \left\{ {\begin{array}{*{20}l} {I_{px} = \sum_{i = 1}^{N_b } {\frac{{I_{px0} + I_{py0} }}{2} - \frac{{I_{px0} - I_{py0} }}{2}\cos 2\alpha_i + I_{pxy0} \sin 2\alpha_i } = \left\{ {\begin{array}{*{20}l} {N_b \left( {I_{px0} + I_{py0} } \right)/2,} \hfill & {N_b \ge 3} \hfill \\ {(I_{px0} + I_{py0} ) - (I_{px0} - I_{py0} )\cos 2\beta + 2I_{pxy0} \sin 2\beta ,} \hfill & {N_b = 2} \hfill \\ \end{array} } \right.} \hfill \\ {I_{py} = \sum_{i = 1}^{N_b } {\frac{{I_{px0} + I_{py0} }}{2} + \frac{{I_{px0} - I_{py0} }}{2}\cos 2\alpha_i - I_{pxy0} \sin 2\alpha_i } = \left\{ {\begin{array}{*{20}l} {N_b \left( {I_{px0} + I_{py0} } \right)/2,} \hfill & {N_b \ge 3} \hfill \\ {(I_{px0} + I_{py0} ) + (I_{px0} - I_{py0} )\cos 2\beta - 2I_{pxy0} \sin 2\beta ,} \hfill & {N_b = 2} \hfill \\ \end{array} } \right.} \hfill \\ {I_{pxy} = \sum_{i = 1}^{N_b } {\frac{{I_{px0} - I_{py0} }}{2}\sin 2\alpha_i + I_{pxy0} \cos 2\alpha_i } = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {N_b \ge 3} \hfill \\ {(I_{px0} - I_{py0} )\sin 2\beta + 2I_{pxy0} \cos 2\beta ,} \hfill & {N_b = 2} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right. $$

(41)

where $\beta = \Omega t + \alpha_0$, and $\alpha_i = 2\pi i/N_b + \beta$ is the azimuth angle for ith blade of the propeller around ${{\mathbf{k}}}_p$, $\sum_{i = 1}^{N_b } {\cos 2\alpha_i } = \left\{ {\begin{array}{*{20}l} {2\cos 2\beta ,} \hfill & {N_b = 2} \hfill \\ {0,} \hfill & {N_b \ge 3} \hfill \\ \end{array} } \right.$, $\sum_{i = 1}^{N_b } {\sin 2\alpha_i } = \left\{ {\begin{array}{*{20}l} {2\sin 2\beta ,} \hfill & {N_b = 2} \hfill \\ {0,} \hfill & {N_b \ge 3} \hfill \\ \end{array} } \right.$ [28].

Equation (41) implies that the two-bladed propeller differs from the propellers with more than two blades. The former has the time-varying moments of inertia, which makes the overall beam-propeller system time-varying, while the latter is time-invariant. In addition, the propeller with more than two blades possesses the moments of inertia with the following symmetric properties $I_{px} = I_{py}$ and $I_{pxy} = 0$.

5.2 Modal analysis using linearized model

In this section, modal analyses using the linearized model in the non-rotating and rotating conditions with two-bladed and three-bladed propellers are performed. The computed results are validated against the experiment. The differences in the dynamic characteristics for the cases with the different numbers of blades are analyzed. Due to the small observed modal damping values, the structural damping of the beam is not considered in these analyses. The parameters listed in Table 1 were derived by trial and error via a judicious adjustment around their baseline values until a good agreement between the model and experiment was reached.

Table 1 The parameters of the beam-propeller model

5.2.1 Non-rotating condition

In the non-rotating condition, the system is time-invariant, so the modal analysis is performed using the traditional approach (Sect. 4.2.1). It is seen from Table 2 that with both two-bladed and three-bladed propellers, there are four modes in the considered frequency range, among which two modes (mode 1 and 3) feature first and second beam bending in x–z plane, while the other two modes (mode 2 and 4) feature first and second beam bending in y–z plane. The blue and the red lines represent the beam and the motor assembly, and the green dots indicate the trajectory of the propeller hub. The main found qualitative difference, when comparing the two propeller cases, is that the bending modes of the same order in x–z and y–z planes have clearly distinct modal frequencies in the two-bladed propeller case. This is caused by the inertial asymmetry of the propeller. In the two-bladed case, the bending shapes of the beam in modes 1 and 3 are localized in the same plane as the propeller, where the mass moment of inertia of the propeller about the bending direction is at its maximum. On the contrary, the bending shapes of the beam in modes 2 and 4 are perpendicular to the propeller, where the mass moment of inertia of the propeller about the bending direction is at its minimum. A counterintuitive observation in this study, however, is that the system becomes symmetric with the use of the three-bladed propeller. This is consistent with Eq. (41) where the moments of inertia of the propeller are shown to be symmetric. It can also be anticipated that the symmetry or asymmetry of the propeller is independent of the initial azimuth angle.

Table 2 The comparison of the modal properties (including mode shape, modal frequency and damping ratio) of the system in the non-rotating condition between two-bladed propeller and three-bladed propeller

In addition, the achieved agreement between the model and experiment is satisfactory in terms of both the modal frequencies and mode shapes in the non-rotating condition. This means the asymmetry in the two-bladed configuration and the symmetry in the three-bladed configuration are validated against the experiment. The small differences in the experimental modal frequencies between modes 1 and 2 and between modes 3 and 4 in the three-bladed configuration are thought to be caused by the slight asymmetry in the experimental setup, non-ideal propeller blade structure, the influence of the sensors and the impact of the measurement and modal identification errors. From Sect. 5.1, the asymmetry in the moments of inertia of the propeller will introduce the time-varying characteristics of the system in the rotating condition, which will lead to qualitatively different dynamic characteristics for the two-bladed and three-bladed configurations.

5.2.2 Rotating condition

In the rotating conditions, modal analysis is performed during different rotational speeds of the propeller in order to compare the frequency-speed diagrams for the two-bladed and three-bladed propellers. With the three-bladed propeller, the system is time-invariant, and modal analysis is performed using the traditional method (Sect. 4.2.1); while with the two-bladed propeller, modal analysis is performed using the coordinate transform method because of the time-varying characteristics (Sect. 4.2.2).

The variation of the modal frequencies with the increasing rotational speed (the so-called Campbell diagram) is plotted to study the influence of the propeller rotational speed. The rotational speed range in the simulation ends slightly higher than the speed when the instability appears in the two-bladed propeller case. The comparison of these diagrams between the systems with the two-bladed and the three-bladed propellers is illustrated in Fig. 3, and the calculated mode shapes at the rotational speed of 8 rad/s are shown in Table 3.

Fig. 3

The Campbell diagrams for a two-bladed propeller with model size of ‘4N,’ and b three-bladed propeller, both with symmetric support. The experimental configurations are described in Sect. 2. The superscript F or B denotes forward or backward whirl mode. For two-bladed case, the subscript k(m) indicates the kth eigensolution in cluster m. For three-bladed case, the subscript k indicates the kth eigensolution

Table 3 The modal property comparison between the two-bladed and three-bladed propeller cases with symmetric support when the rotational speed is 8 rad/s (the arrow indicates the direction of the propeller hub trajectory). The rotation of the propeller is clockwise when viewing in +z direction

With the two-bladed propeller and the chosen model truncation order 4N, each mode in the non-rotating condition splits into two branches with the increasing rotational speed. The branches with higher frequency correspond to the forward whirl modes (whirling direction same as the rotational direction), while the branches with lower frequency correspond to the backward whirl modes (whirling direction opposite to the rotational direction). The frequency difference between the two branches originating from the same source is twice the rotational speed. The mode shapes during the rotating conditions feature these forward or backward whirling characteristics, in which the bending of the beam is consistent with those in the non-rotating condition before the split (see Table 3). In this case, the whirling trajectory (green dots) for all the mode shapes forms a circle. The frequency splits are also dependent on the model truncation order. Higher order frequency splits will appear as the model order is increased [28].

As is known for the classical theory of rotating systems, e.g. [36], with the three-bladed propeller and the symmetric beam support, when increasing the rotational speed, the frequency branches display split-like frequency changes. Owing to the symmetry of the system, there are initially two coalescent modal frequencies in the non-rotating condition. With the increase in the rotational speed, one of the modal frequencies increases in value (forward whirl mode, $\lambda_2^F$, $\lambda_4^F$), while the other one decreases (backward whirl mode, $\lambda_1^B$, $\lambda_3^B$). Furthermore, the frequency difference between the forward and backward modes in one pair does not exhibit the previous specific relationship with the rotational speed. The mode shapes in the rotating condition feature backward or forward whirling characteristics, in which the bending of the beam is consistent with those in the corresponding non-rotating condition (see Table 3). The whirling trajectory (green dots) for all the mode shapes forms a circle. As shown in the following diagrams, while the frequency branches in this case also appear to be like the frequency splitting, this process is qualitatively different from the process observed in the two-bladed scenario. Instead, a pair of coalescent frequencies initially belonging to this symmetric non-rotating system is subjected to the symmetry breaking action of the propeller rotation whereby frequencies in this pair further evolve in the manner with, respectively, softening and stiffening influence from the rotating rigid propeller.

The agreement between the modal frequencies calculated by the model and measured in the experiment is satisfactory with the maximum frequency difference less than 1 Hz. Due to the slight unbalance of the propeller, some rotor harmonics (1/rev, 2/rev, etc.) are also visible in the experiment. The good consistency between the nominal case and reversed case with the two-bladed propeller and between the positive rotation and reverse rotation cases with the three-bladed propeller indicates that the influence of still-air aerodynamics on the structural dynamics is minor. Therefore, this test configuration is accepted as a sufficiently good approximation of the in-vacuo model introduced earlier. There are two frequencies close to each other in the enlarged regions for both cases. Owing to their magnitude and proximity, reliable modal identification of this frequency pair from the measured FRFs was challenging. Hence, typically, only a single frequency was identified and presented at each rotational speed in the Campbell diagrams.

With the two-bladed propeller, there are two vertically-separated unstable regions in the speed range of 247.5–260 rad/s due to the frequency lock-in phenomenon [37, 38]. Such instability was also observed in the experiment [28]. This self-excited instability can be explained as a parametric instability and similar phenomena were reported before, e.g., [39, 40]. In this case, the asymmetric property of the moment of inertia of the propeller generates self-excitation at the frequency equal to the twice the rotational speed. The energy supplied to the system through this route allows the instability to arise. Specifically, owing to the properties and structure of the problem, the first instability region arises from the coalescence between $\lambda_{1(0)}^F$ and $\lambda_{ - 3(0)}^B$, while the second from the coalescence between $\lambda_{3(0)}^F$ and $\lambda_{ - 1(0)}^B$. They occur in the same speed range because the frequency differences between $\lambda_{3(0)}^F$ and $\lambda_{3(0)}^B$ and between $\lambda_{ - 1(0)}^F$ and $\lambda_{ - 1(0)}^B$ are both twice the rotational speed, which makes the notional $\lambda_{ - 1(0)}^B$ crossing $\lambda_{3(0)}^F$ at the same speed as $\lambda_{3(0)}^B$ crossing $\lambda_{ - 1(0)}^F$ (the mirror image of $\lambda_{ - 3(0)}^B$ crossing $\lambda_{1(0)}^F$).

In contrast with the above case, the three- or more-bladed propeller’s moments of inertia are time-invariant. This makes the system do not feature the rotational speed dependent energy supply mechanism. Furthermore, neglecting the structural and aerodynamic damping in this numerical study, the system is conservative since the dissipation work done by the gyroscopic force is zero and no instability is found in the model or experiment when the rotational speed is increased up to 246 rad/s. Fundamentally speaking, a conservative linear system cannot be made unstable by gyroscopic forces [41], so the undamped linearized system will always be stable even when the rotational speed is increased further.

5.2.3 Influence of the beam support

In the previous analyses, the beam support is symmetric. To investigate the influence of the support on the system dynamics with different numbers of blades, its second moment of cross-sectional area about y axis (I₂) is increased by 1.3 times, creating an asymmetric support for the propeller. The Campbell diagrams with this asymmetric support are illustrated in Fig. 4. With a two-bladed propeller, because of the asymmetry of both the beam and moments of inertia of the propeller, the modal frequencies in the non-rotating condition change with the initial azimuth angle of the blades. Thus, instead of splitting from the same frequency, the frequency branches originate from their respective sources at the two different neighboring frequencies in the non-rotating condition. The frequency difference between the two branches associated with the same source pair is still approximately twice the rotational speed, except in the low-speed range (< 30 rad/s). The two unstable regions in the speed range of 266–279 rad/s due to the frequency lock-in phenomenon are still present. Different from the case of symmetric support, however, there are additional veering regions found between certain frequency branches, e.g., between $\lambda_{4(0)}^B$ and $\lambda_{3(0)}^F$, which indicates conditional inter-modal mixing in the case of asymmetric support.

Fig. 4

The Campbell diagrams for a two-bladed propeller, model size is ‘4N’. b three-bladed propeller, both cases using asymmetric support

With a three-bladed propeller, due to the asymmetry of the beam support, the two originally coalescent modal frequencies in the non-rotating condition of symmetric support become different. With the increasing rotational speed, one of the modal frequencies still increases in value (forward whirl mode, $\lambda_2^F$, $\lambda_4^F$), while the other one decreases (backward whirl mode, $\lambda_1^B$, $\lambda_3^B$). The frequency difference between the forward and backward modes in one pair still does not exhibit a specific relationship with the rotational speed. The whirling trajectory of the propeller hub is no longer a circle, but an ellipse instead.

5.2.4 Summary of the blade number effects

According to Sect. 5.1, when there are more than two blades in a propeller, the system does not exhibit the time-varying characteristics, so its dynamic characteristics will be qualitatively equivalent to the case with the three-bladed propeller. The influence of blade number on the system dynamics is summarized in Table 4.

Table 4 Summary of the influence of blade number on the undamped linearized system dynamics

The analysis in this section is based on the linearized model, which is only valid in the limited small deformation region. When vibrating about the equilibrium position, the linear terms dominate over the nonlinear terms. When the system loses stability in the case of two-bladed propeller, the vibration amplitude will increase beyond the linear region, which necessitates the use of the nonlinear model. The following study is focused on the dynamics of the nonlinear model and its comparison with the linearized model in the stable speed region.

6 Analysis of nonlinear model

In this section, the nonlinear model is analyzed in terms of its equilibrium deformation in the non-rotating condition, the FRFs in the stable rotational speed region and dynamic response in the unstable rotational speed region. In contrast with the previous sections, the beam’s structural damping is included here since this setup will enable realistic free vibration analysis in the time domain.

6.1 Analysis of nonlinear static responses

First, the nonlinear model is validated by comparing the numerically calculated static equilibrium deformation of the system with the two-bladed propeller with the experimental measurement. The experiment was conducted by measuring the static deformation of the system in the initial horizontal orientation under gravity when the beam was clamped at the left end and free at the right end (Fig. 5a). The deformation was measured by a ruler.

Fig. 5

Static deformation with the two-bladed propeller: a the experimental setup; b the comparison between the nonlinear model and experiment

The equilibrium deformation is calculated by setting all the time derivative equal to zero in Eq. (29), while the nonlinear constraints in Eqs. (8) and (24) are satisfied by adding stiff artificial springs. The nonlinear equation to be solved is given by

$$ \left[ {\begin{array}{*{20}c} {{{\mathbf{K}}}_b {{\mathbf{q}}}_b + {{\mathbf{b}}}_{nl} ({{\mathbf{q}}}_b )} \\ {{{\mathbf{0}}}_{5 \times 1} } \\ \end{array} } \right] + \frac{{\partial U_{cnl} }}{{\partial {{\mathbf{q}}}_{nl}^{\text{T}} }} = {{\mathbf{f}}}_g ({{\mathbf{q}}}_{mp} ) $$

(42)

where $U_{cnl} = \frac{1}{2}{{\varvec{\varPhi}}}_c^{\text{T}} {\text{diag}}\left( {\begin{array}{*{20}c} {k_l } & {k_l } & {k_l } & {k_r } & {k_r } \\ \end{array} } \right){{\varvec{\varPhi}}}_c + \frac{1}{2}k_l \Phi_b$ is the potential energy associated with the artificial springs. ${{\mathbf{f}}}_g ({{\mathbf{q}}}_{mp} ) = \left[ {\begin{array}{*{20}c} {{{\mathbf{0}}}_{1 \times N_u } } & { - mg\int_0^L {{{\mathbf{W}}}^{\rm{T}} {\rm{d}}s} } & {{{\mathbf{0}}}_{1 \times N_v } } \;\; 0 & { - (m_a + m_p )g} \;\; 0 \;\; { - m_p gz_{pc} \cos \theta_a \cos \varphi_a } \;\; {m_p gz_{pc} \sin \theta_a \sin \varphi_a } \\ \end{array} } \right]^{\rm{T}}$ is the external force vector due to gravity which is applied in the transversal direction relative to the horizontally placed undeformed beam.

The nonlinear equation Eq. (42) is solved using ‘fsolve’ function in Matlab. The equilibrium deformation of the system loaded by the two-bladed propeller under the influence of gravity is shown in Fig. 5a, from which the deformation of the real system is extracted given that the displacement of the beam tip is measured by a ruler and compared with the results calculated by the nonlinear model in Fig. 5b. The agreement between the model and experiment is good with the maximum displacement difference less than 1 mm while the tip deflection of the beam reaches nearly 20 mm. This agreement evidences the correctness of the nonlinear model in terms of elastic and boundary condition characteristics.

Then, in the vertical orientation, a horizontal transverse force is applied at the tip of the beam in the positive x direction, and the equilibrium deflection of the system is calculated in the same way, as shown in Fig. 6. This computational experiment is set up so that the beam exhibits clear geometric nonlinearity with the increasing force. When the force exceeds 3 N, and the beam tip displacement exceeds 5 cm, the tip displacement starts to deviate from the linear relationship and the displacement-force slope becomes smaller (Fig. 6b), indicating, in this coordinate format, the hardening nonlinear characteristics. This analysis gives us a rough idea at what amplitudes of deformation the system manifests notably nonlinear behavior.

Fig. 6

The equilibrium deflection of the system with applied transverse force in x direction from 1 to 14 N: a stroboscopic system deflection plot, b beam tip displacement-force characteristic

6.2 Nonlinear response of the rotating system

This section is to compare the nonlinear model with the linearized model in the stable speed region and validate the nonlinear response of the system with the experiment in the case of instability.

In the stable speed region, the purpose is to compare the FRFs between the linear and nonlinear models. For the nonlinear model, a force impulse F_im of 10 and 100 N, respectively, with a duration of 2 × 10⁻³ s is applied on the beam at the location of 0.12 m (same as experiment) from the root at the angle of π/4 with positive x axis. The nonlinear model developed in Sect. 3 is simulated in the time domain in Matlab’s Simulink environment using the ‘ode4’ solver with a fixed step size of 5 × 10⁻⁵ s. After obtaining the time-marched response of the system, the driving-point displacement response of the beam is calculated. The simulation lasts for 30 s. The driving-point receptance is calculated from the impulse force to the displacement response. For the linearized model, the driving-point receptance is calculated in the frequency domain using the method introduced in Sect. 4.3. The resonance peaks in the receptances are also compared with the natural frequencies of the linearized system calculated by modal analysis using the methods introduced in Sect. 4.2 with the structural damping considered. Table 5 illustrates the comparison of the driving-point receptances between the linearized model and the nonlinear model with 2-bladed and 3-bladed propellers at two different rotational speeds. As expected, it can be seen that the receptances calculated using the linearized model and nonlinear model do not differ significantly, and the natural frequencies calculated using the linearized model are also consistent with the peaks of the nonlinear model except that some peaks are not clearly visible in the receptances. The higher impulse force of 100 N triggers the nonlinearity more than the 10 N impulse. The receptances of the nonlinear model deviate from those of the linear model more significantly. The change of the resonances with the rotating speed can also be seen by comparing the receptances from across these two speeds. This indicates that, in the stable speed region, the use of the developed linearized model is appropriate to approximate the nonlinear system’s behavior.

Table 5 The comparison of the driving-point receptances between the linearized model and nonlinear model using impulse forces of 10 N and 100 N in the stable speed region

In what follows, the nonlinear response of the system is qualitatively validated against the experiment in the unstable speed region. As shown in Sect. 5.2, the unstable speed region only exists when the two-bladed propeller is used in the present test setup. Here, to enhance the influence of the nonlinear modeling terms, the nonlinear model is compared with the experimental measurement completed at the rotational speed of 259 rad/s where the system loses stability. This scenario is presented in Fig. 7. In both the simulation and experiment, the accelerations in two transverse directions initially increase, while the dominant frequencies are the two unstable frequencies that are consistent with the frequency-speed diagram in Fig. 3a, e.g., 3.8 Hz and 77 Hz in the model, 3.6 Hz and 77.4 Hz in the experiment.

Fig. 7

The comparison between a the nonlinear model and b experiment in terms of accelerations in two transverse directions (upper row) and the spectrograms of $\ddot{w}$ (lower row) at the location of 27 cm from beam root at the rotational speed of 259 rad/s (within unstable speed region) with a two-bladed propeller

After the transient build-up stage, the vibration levels in both the simulation and experiment reach bounded values. This behavior primarily emerges in response to the increasing presence of the geometric nonlinear terms. Furthermore, these bounded oscillations manifest richer frequency content compared to the build-up stage which is effectively dominated only by the two unstable frequencies. By way of inspecting the spectrograms included in Fig. 7, after reaching the bounded and steady-state oscillations, there appear frequencies of 70.2 Hz and 84.4 Hz in the experiment while 67 Hz and 85.4 Hz components are found in the simulation. At the time instant of around 58 s, the simulated displacement at the beam tip reaches 5 cm (Fig. 8b), after which the nonlinearity starts to take effect (see Fig. 6b). This is consistent with the evidence provided by the spectrogram (Fig. 7a), where the additional frequencies appear approximately after 58 s. These dynamic characteristics show a good agreement between the model and experiment.

Fig. 8

The vibration behavior of the system at the rotational speed of 259 rad/s during the first 150 s calculated by the nonlinear model. a Perspective view, b Top view. Green dots represent the trajectory of the propeller hub. The rotation of the propeller is clockwise when viewing in + z direction

The predicted vibration behavior between 0 and 150 s is visualized in Fig. 8. It can be seen that the vibration response of the system resembles that of the first forward whirl vibration pattern within which the beam’s modal activity is close to the first bending. This is also consistent with the findings in the previous linear study [28] which showed that the first forward whirling mode, within which the beam vibration features the first bending pattern, is unstable. However, contrary to the linear cases, the nonlinear system realizations presented here reach and remain in the bounded oscillation regime.

The differences between the experiment and model include: (1) the transient vibration build-up rate in the initial stage is different, i.e., the acceleration increases faster in the experiment than the model; (2) when reaching the steady-state and bounded oscillation regime, the acceleration magnitudes in the experiment and model are notably different, i.e., approximately 200 m/s² in the model and about 750 m/s² in the experiment; (3) after reaching the bounded oscillations, the additional frequency content in the experiment and model is not exactly the same. These differences imply that the underlying nonlinear dynamics of the system may be more complicated due to other unaccounted factors, e.g., material and interface nonlinearity of the beam, the in-air induced aerodynamics in the experiment and other types of damping since only Kelvin–Voigt type beam damping is considered. Despite these differences, the model demonstrates sufficient correspondence with the experiment, and it helps to elucidate the phenomena encountered after entering the zones of linear instability.

7 Discussion

7.1 Methods of constraint application

In this paper, the Udwadia-Kalaba method is used in the time-domain simulations to satisfy the constraints. Other methods that can be applied include Lagrange multiplier method [20] and large artificial springs. However, Lagrange multiplier method will increase the number of solved unknown functions, thereby increasing computational effort. In addition, its application will lead to a system of differential–algebraic equations that are subject to the numerical issues such as drift [42]. Some methods were proposed to address these problems, e.g., [43], but long simulation time still poses challenge. Large artificial springs are used in the linearized model and the frequency domain simulation to satisfy the constraints. This method is particularly suitable for frequency domain analyses but it can generate high-frequency oscillation in the time domain and thus results in the reduced step size and more demand on computational time. Udwadia-Kalaba method addresses these disadvantages, e.g., it does not increase the dynamic order of the system or generate differential-algebraic equation; it does not require particularly reduced step size, so the simulations are generally significantly faster. Further, in combination with the constraint drift correction method in [35], the long-time simulations are no longer a problem. The example from Figs. 7 to 8 is further expanded in Fig. 9, in which the first derivative and inextensibility constraint at the beam tip are illustrated. It can be seen that with the drift correction using Eq. (33), the inextensibility constraint Eq. (7) fluctuates around zero, so the constraint is always approximately satisfied and the stable progression of the calculation is ensured. The drawback is that the correction terms have no physical meaning and result in high-frequency oscillation in the first and second derivatives of the state variables.

Fig. 9

The first derivative and inextensibility constraint at the beam tip at the rotational speed of 259 rad/s with a two-bladed propeller

7.2 Influence of nonlinearity order

The previous simulation is conducted using the nonlinear model with the 5th order approximations. The comparison of the displacements calculated using the 5th order and 3rd order models is performed in Fig. 10. The 3rd order model is derived by ignoring all the higher terms than the 3rd order in the original 5th order model. It can be seen that there is a slight difference in the vibration frequency calculated using these different nonlinearity orders, so as to cause the varying phase difference in their results. There is also a slight difference in the vibration magnitudes, e.g., in the region of increasing vibration magnitudes (50–70 s) and in the region of the bounded oscillations (> 75 s). The difference in their results can be considered acceptable when the 3rd order model offers reduced analytical complexity or calculational time compared to the original 5th order model.

Fig. 10

The comparison of the displacements at the beam tip calculated using a 3rd order model and 5th order model at the rotational speed of 259 rad/s with a two-bladed propeller

7.3 Emergence of instability

With more than two blades, the rotating propeller does not introduce the time-varying characteristics into the system, and the moments of inertia about the two in-plane axes are the same. In this case, the classical Reed’s model [3] and Johnson’s model [44] with the time-invariant moments of inertia can be used. However, the two-bladed propeller is a special case, where its rotation introduces both the time-varying characteristics and gyroscopic effects into the system. Consequently, a self-excited instability can emerge even in the case of isotropic rotor. Furthermore, owing to its mathematical structure, the analytical treatment of this case is different.

Fundamentally speaking, the structural/mechanical instability studied in this paper is a self-excited instability, similar to the ‘ground resonance’ in the helicopter field. The principle in the studied case is that given an initial perturbation, the propeller generates the periodic moments with the frequency of twice the rotational speed in the propeller's pitch and yaw directions (i.e., propeller in-plane axes), which then excite the bending vibrations of the supporting beam. In return, the bending of the beam excites further the pitch and yaw motion of the propeller. In the specific propeller speed range where the natural frequencies of the beam-propeller system satisfy a specific relationship with the rotational speed, the vibration of the propeller exacerbates that of the beam and vice versa. In the linear setting, this interaction makes the system vibration amplitudes grow without bounds, thus leading to instability. The energy in this case is extracted from the motor (or rotation). This phenomenon is different from whirl flutter which, in effect, is an aeroelastic instability where the energy is extracted from the airstream through the motion of the structure and the role of the oscillatory aerodynamic forces along with the gyroscopic effects is crucial. On the one hand, while the in-air aerodynamic influences were inevitably part of the present study too, their impact on the qualitative attributes of the instability phenomenon studied here were shown to be minor. On the other hand, the absence of perfect in-vacuo conditions is seen as one of the main sources of the observed quantitative discrepancies, e.g., in terms of the achieved response amplitudes and the exact positioning of the instability boundaries.

This study is focused on a propeller with isotropic characteristics and the conclusions are drawn on this basis. While not within the scope of this paper, an anisotropic propeller may lead to instability even with more than two blades [12, 40].

7.4 Further model improvement

In the nonlinear modeling, the only nonlinearity that is taken into account is the geometric nonlinearity. Based on the observation in the experiment that the beam was prone to break at the root when operating in the unstable speed region, it can be speculated that the material was working in the plastic deformation region where the material nonlinearity needs to be considered as well. The discrepancy between the model and experiment can be partly ascribed to the absence of the material nonlinearity. To take into account the material nonlinearity, the linear strain–stress relationship can be replaced by a nonlinear one, e.g., Ludwick or modified Ludwick relation in [45,46,47].

All the experiments were carried out in air with no imposed airflow. Although the influence of the aerodynamics on the frequencies was shown to be minor, this factor was found to influence primarily the unstable speed region. The aerodynamic loads may have an important influence on the nonlinear response of the system when the rotational speed of the propeller is high or where the system responses become significant. This effect was not considered in this paper since our main focus was on the structural dynamics and induced interactions.

The intention behind developing this test rig and its nonlinear model is to study the whirl flutter phenomenon which is a classical aeroelastic instability typically associated with tiltrotor or propeller-driven aircraft. When the aerodynamics is considered and the imposed airflow speed reaches a certain critical value, the system will lose stability [48]. However, in these practical conditions, the vibration magnitude will be constrained by the effect of the system nonlinearity and the system is expected to enter a limit-cycle/bounded oscillation regime. Therefore, this nonlinear model will be used further to study the nonlinear dynamics in future research.

8 Conclusion

To study the interactional dynamics of rotating propellers with different numbers of blades mounted on elastic supports, a rotor rig is proposed, which consists of a beam, a motor assembly, and a propeller. The corresponding nonlinear model consisting of a nonlinear inextensible beam, a motor assembly and a rotating propeller is developed, in which the dynamic constraints are satisfied using the Udwadia-Kalaba method. Simulations in the frequency domain, using the linearized model, and the time domain, using the nonlinear model, are conducted. The key conclusions are summarized as follows:

• (1) Two-bladed propeller introduces time-varying characteristics into the system due to the time-varying moments of inertia, while the system is time-invariant for propellers with more than two blades.

• (2) With two blades, as observed in the frequency-speed diagrams, there are frequency splits originating from the non-rotating condition with increasing rotational speed. The frequency difference between the frequency splits in one pair is approximately twice the rotational speed. In the cases of more than two blades, from the pairs of the coalescent frequencies in the symmetric non-rotating case, one frequency increases and the other decreases with increasing rotational speed. In this case, there is no specific relationship between the frequency difference and the rotational speed.

• (3) With asymmetric support, the frequency splits in one modal pair do not originate from the same frequency in the non-rotating condition in the case of two-bladed propeller, and there is stronger coupling between the frequency loci (e.g., veering). The whirling trajectories in the mode shapes are elliptically shaped rather than the circles observed in the case of symmetric support.

• (4) There is a structural instability found due to the frequency lock-in phenomenon when a two-bladed propeller configuration is considered. However, there is no comparable instability identified when more than two-bladed propeller is considered.

• (5) The static equilibrium deformation using the nonlinear model is calculated and validated against the experiment. The beam starts to exhibit nonlinearity when the beam tip displacement reaches 5 cm.

• (6) In the stable speed range, the receptances calculated using the nonlinear model and linearized model do not show notable differences. This indicates that using the linearized model to approximate the nonlinear system response in the stable speed region is acceptable.

• (7) In the unstable speed range with the two-bladed propeller, the nonlinear model is consistent with the experiment in terms of the unstable frequencies and the overall qualitative behavior primarily manifested in terms of the reached steady-state bounded oscillations. Further, in both cases, the system vibration in the unstable speed range features the forward whirling pattern, in which the vibration of the beam is close to the first bending mode shape.

Further study will be focused on the influence of aerodynamics and the nonlinearity on the dynamic characteristics of the coupled flexible structure-rotor system.

Appendices

Appendix A

Detailed expressions

$$ {{\mathbf{M}}}_2 = \left[ {\begin{array}{*{20}c} {m_a + m_p } & 0 & 0 & { - m_p z_{pc} \cos \theta_a \sin \varphi_a } & { - m_p z_{pc} \sin \theta_a \cos \varphi_a } \\ 0 & {m_a + m_p } & 0 & {m_p z_{pc} \cos \theta_a \cos \varphi_a } & { - m_p z_{pc} \sin \theta_a \sin \varphi_a } \\ 0 & 0 & {m_a + m_p } & 0 & {m_p z_{pc} \cos \theta_a } \\ { - m_p z_{pc} \cos \theta_a \sin \varphi_a } & {m_p z_{pc} \cos \theta_a \cos \varphi_a } & 0 & \begin{gathered} I_a \cos^2 \theta_a + m_p z_{pc}^2 \cos^2 \theta_a \hfill \\ + I_{py} \cos^2 \theta_a + I_{pz} \sin^2 \theta_a \hfill \\ \end{gathered} & {I_{pxy} \cos \theta_a } \\ { - m_p z_{pc} \sin \theta_a \cos \varphi_a } & { - m_p z_{pc} \sin \theta_a \sin \varphi_a } & {m_p z_{pc} \cos \theta_a } & {I_{pxy} \cos \theta_a } & {I_a + m_p z_{pc}^2 + I_{px} } \\ \end{array} } \right] $$

$$ {{\mathbf{b}}}_{nl} ({{\mathbf{q}}}_b ) = \left[ {\begin{array}{*{20}c} {\frac{{\partial U_{bNL} }}{{\partial {{\mathbf{q}}}_u^T }}} \\ {\frac{{\partial U_{bNL} }}{{\partial {{\mathbf{q}}}_w^T }}} \\ {\frac{{\partial U_{bNL} }}{{\partial {{\mathbf{q}}}_v^T }}} \\ \end{array} } \right],{{\mathbf{c}}}_{nl} ({{\mathbf{q}}}_b ,{\dot{\mathbf{q}}}_b ) = \left[ {\begin{array}{*{20}c} {\frac{{\partial D_{bNL} }}{{\partial {\dot{\mathbf{q}}}_u^T }}} \\ {\frac{{\partial D_{bNL} }}{{\partial {\dot{\mathbf{q}}}_w^T }}} \\ {\frac{{\partial D_{bNL} }}{{\partial {\dot{\mathbf{q}}}_v^T }}} \\ \end{array} } \right],\frac{{\partial U_{bNL} }}{{\partial {{\mathbf{q}}}_u^T }} = {{\mathbf{0}}}_{N_u \times 1} ,\frac{{\partial D_{bNL} }}{{\partial {\dot{\mathbf{q}}}_u^T }} = {{\mathbf{0}}}_{N_u \times 1} $$

$$ \frac{{\partial U_{bNL} }}{{\partial {\mathbf{q}}_w ^T }} = \frac{1}{2}EI_2 \int_0^L {\left( \begin{gathered} 2w^{\prime} v^{\prime} v^{{\prime} {\prime} } {\mathbf{W}}^{{\prime} {\prime} } + 2w^{{\prime} {\prime} } v^{\prime} v^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2w^{{\prime} {\prime} } w^{{\prime} 2} {\mathbf{W}}^{{\prime} {\prime} } + 2w^{{\prime} {\prime} 2} w^{\prime} {\mathbf{W}}^{\prime} + 2w^{{\prime} {\prime} } w^{{\prime} 4} {\mathbf{W}}^{{\prime} {\prime} } + 4w^{{\prime} {\prime} 2} w^{{\prime} 3} {\mathbf{W}}^{\prime} + \hfill \\ 2w^{{\prime} {\prime} } w^{{\prime} 2} v^{{\prime} 2} {\mathbf{W}}^{{\prime} {\prime} } + 2w^{{\prime} {\prime} 2} w^{\prime} v^{{\prime} 2} {\mathbf{W}}^{\prime} + 2w^{\prime} v^{{\prime} 3} v^{{\prime} {\prime} } {\mathbf{W}}^{{\prime} {\prime} } + 2w^{{\prime} {\prime} } v^{{\prime} 3} v^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2w^{{\prime} 3} v^{\prime} v^{{\prime} {\prime} } {\mathbf{W}}^{{\prime} {\prime} } + \hfill \\ 6w^{{\prime} {\prime} } w^{{\prime} 2} v^{\prime} v^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2w^{\prime} v^{{\prime} 2} v^{{\prime} {\prime} 2} {\mathbf{W}}^{\prime} \hfill \\ \end{gathered} \right){{\rm d}}s} $$

$\begin{aligned} \frac{{\partial U_{bNL} }}{{\partial {\mathbf{q}}_v ^T }} = & \frac{1}{2}EI_1 \int_0^L {\left( {2v^{{\prime\prime} } v^{{\prime} 2} {\mathbf{V}}^{{\prime\prime} } + 2v^{\prime} v^{{\prime\prime} 2} {\mathbf{V}}^{\prime} + 2v^{{\prime\prime} } v^{{\prime} 4} {\mathbf{V}}^{{\prime\prime} } + 4v^{^{{\prime\prime} }2} v^{{\prime} 3} {\mathbf{V}}^{\prime} } \right){{\rm d}}s} \\ & + \frac{1}{2}EI_2 \int_0^L {\left( \begin{gathered} 2w^{{\prime\prime} } w^{\prime} v^{{\prime\prime} } {\mathbf{V}}^{\prime} + 2w^{{\prime\prime} } w^{\prime} v^{\prime} {\mathbf{V}}^{{\prime\prime} } + 2w^{{\prime\prime} 2} w^{{\prime} 2} v^{\prime} {\mathbf{V}}^{\prime} + 6w^{{\prime\prime} } w^{\prime} v^{{\prime} 2} v^{{\prime\prime} } {\mathbf{V}}^{\prime} + 2w^{{\prime\prime} } w^{\prime} v^{{\prime} 3} {\mathbf{V}}^{{\prime\prime} } + 2w^{{\prime\prime} } w^{{\prime} 3} v^{{\prime\prime} } {\mathbf{V}}^{\prime} \hfill \\ + 2w^{{\prime\prime} } w^{{\prime} 3} v^{\prime} {\mathbf{V}}^{{\prime\prime} } + 2w^{{\prime} 2} v^{\prime} v^{{\prime} {\prime} 2} {\mathbf{V}}^{\prime} + 2w^{{\prime} 2} v^{{\prime} 2} v^{{\prime\prime} } {\mathbf{V}}^{{\prime\prime} } \hfill \\ \end{gathered} \right){{\rm d}}s}, \\ \end{aligned}$,

$$ \frac{{\partial D_{bNL} }}{{\partial {{\dot{{\mathbf{q}}}}_{w}} {^{T}}}} = \frac{1}{2}EI_2 \int_0^L {\left( \begin{gathered} 2w^{{\prime} 2} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{{\prime} {\prime} } + 2\dot{v}^{{\prime} {\prime} } v^{\prime} w^{\prime} {\mathbf{W}}^{{\prime} {\prime} } + 2v^{{\prime} {\prime} } v^{\prime} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2v^{{\prime} {\prime} } v^{\prime} \dot{w}^{\prime} {\mathbf{W}}^{{\prime} {\prime} } + 2w^{{\prime} {\prime} } w^{\prime} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2w^{{\prime} {\prime} } w^{\prime} \dot{w}^{\prime} {\mathbf{W}}^{{\prime} {\prime} } \hfill \\ + 2\dot{v}^{\prime} v^{{\prime} {\prime} } w^{\prime} {\mathbf{W}}^{{\prime} {\prime} } + 2w^{{\prime} 4} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{{\prime} {\prime} } + 4v^{\prime} w^{\prime} v^{{\prime} {\prime} } w^{{\prime} {\prime} } \dot{w}^{\prime} {\mathbf{W}}^{\prime} + 2\dot{v}^{\prime} v^{{\prime} {\prime} } w^{{\prime} 3} {\mathbf{W}}^{{\prime} {\prime} } + 4v^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 4v^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} \dot{w}^{\prime} {\mathbf{W}}^{{\prime} {\prime} } \hfill \\ + 2w^{{\prime} {\prime} } w^{\prime} v^{{\prime} 2} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2w^{{\prime} {\prime} } w^{\prime} v^{{\prime} 2} \dot{w}^{\prime} {\mathbf{W}}^{{\prime} {\prime} } + 2\dot{v}^{{\prime} {\prime} } v^{{\prime} {\prime} } w^{\prime} v^{{\prime} 2} {\mathbf{W}}^{\prime} + 2\dot{v}^{{\prime} {\prime} } w^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} {\mathbf{W}}^{\prime} + 2v^{{\prime} 2} w^{{\prime} 2} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{{\prime} {\prime} } \hfill \\ + 6\dot{v}^{\prime} v^{{\prime} {\prime} } w^{\prime} v^{{\prime} 2} {\mathbf{W}}^{{\prime} {\prime} } + 2\dot{v}^{\prime} w^{{\prime} {\prime} } v^{\prime} w^{{\prime} 2} {\mathbf{W}}^{{\prime} {\prime} } + 2\dot{v}^{\prime} v^{{\prime} {\prime} } w^{{\prime} {\prime} } w^{{\prime} 2} {\mathbf{W}}^{\prime} + 2v^{{\prime} {\prime} 2} v^{{\prime} 2} \dot{w}^{\prime} {\mathbf{W}}^{\prime} + 2w^{{\prime} {\prime} 2} w^{{\prime} 2} \dot{w}^{\prime} {\mathbf{W}}^{\prime} + 2\dot{v}^{\prime} v^{{\prime} {\prime} 2} v^{\prime} w^{\prime} {\mathbf{W}}^{\prime} \hfill \\ + 2\dot{v}^{{\prime} {\prime} } v^{\prime} w^{{\prime} 3} {\mathbf{W}}^{{\prime} {\prime} } + 2\dot{v}^{{\prime} {\prime} } w^{\prime} v^{{\prime} 3} {\mathbf{W}}^{{\prime} {\prime} } + 2v^{{\prime} {\prime} } v^{{\prime} 3} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 2v^{{\prime} {\prime} } v^{{\prime} 3} \dot{w}^{\prime} {\mathbf{W}}^{{\prime} {\prime} } + 4w^{{\prime} {\prime} } w^{{\prime} 3} \dot{w}^{{\prime} {\prime} } {\mathbf{W}}^{\prime} + 4w^{{\prime} {\prime} } w^{{\prime} 3} \dot{w}^{\prime} {\mathbf{W}}^{{\prime} {\prime} } \hfill \\ \end{gathered} \right)} {{\rm d}}s $$

$$ \begin{aligned} \frac{{\partial D_{bNL} }}{{\partial {\dot{\mathbf{q}}}_v^T }} = & \frac{1}{2}EI_1 \int_0^L {\left( {2{\dot v^{\prime \prime}}v^{{\prime} 2} {\mathbf{V^{\prime \prime}}} + 2v^{\prime \prime}v^{\prime}{\dot v^{\prime}}{\mathbf{V^{\prime \prime}}} + 2{\dot v^{\prime \prime}}v^{\prime \prime}v^{\prime}{\mathbf{V^{\prime}}} + 2{\dot v^{\prime \prime}}v^{{\prime} 4} {\mathbf{V^{\prime \prime}}} + 2v^{{\prime} {\prime} 2} v^{{\prime} 2} {\dot v}^{\prime}{\mathbf{V^{\prime}}} + 4v^{\prime \prime}v^{{\prime} 3} {\dot v}^{\prime}{\mathbf{V^{\prime \prime}}} + 4{\dot v^{\prime \prime}}v^{\prime \prime}v^{{\prime} 3} {\mathbf{V^{\prime}}}} \right){{\rm d}}s} \\ & + \frac{1}{2}EI_2 \int_0^L {\left( \begin{gathered} 2v^{\prime}w^{\prime}{\dot w^{\prime \prime}}{\mathbf{V^{\prime \prime}}} + 2v^{\prime \prime}w^{\prime}{\dot w^{\prime \prime}}{\mathbf{V^{\prime}}} + 2v^{\prime \prime}w^{{\prime} 3} {\dot w^{\prime \prime}}{\mathbf{V^{\prime}}} + 2v^{\prime}w^{{\prime} 3} {\dot w^{\prime \prime}}{\mathbf{V^{\prime \prime}}} + 2v^{{\prime} 3} w^{\prime}{\dot w^{\prime \prime}}{\mathbf{V^{\prime \prime}}} + 2v^{{\prime \prime} 2} w^{{\prime} 2} {\dot v^{\prime}}{\mathbf{V^{\prime}}} \hfill \\ + 2v^{{\prime} 2} w^{{\prime} 2} {\dot v^{\prime \prime}}{\mathbf{V^{\prime \prime}}} + 2{\dot w^{\prime}}v^{\prime \prime}v^{{\prime} 2} w^{\prime}{\mathbf{V^{\prime \prime}}} + 2{\dot w^{\prime}}v^{\prime \prime}v^{\prime}w^{{\prime} 2} {\mathbf{V^{\prime \prime}}} + 2{\dot w^{\prime}}v^{{\prime} {\prime} 2} v^{\prime}w^{\prime}{\mathbf{V^{\prime}}} + 6v^{\prime \prime}v^{{\prime} 2} w^{\prime}{\dot w^{\prime \prime}}{\mathbf{V^{\prime}}} \hfill \\ + 2w^{\prime \prime}v^{\prime}w^{{\prime} 2} {\dot w^{\prime \prime}}{\mathbf{V^{\prime}}} + 2v^{\prime \prime}v^{\prime}w^{{\prime} 2} {\dot v^{\prime \prime}}{\mathbf{V^{\prime}}} + 2v^{\prime \prime}v^{\prime}w^{{\prime} 2} {\dot v^{\prime}}{\mathbf{V^{\prime \prime}}} + 2{\dot w}^{\prime}v^{\prime \prime}w^{\prime \prime}w^{{\prime} 2} {\mathbf{V^{\prime}}} \hfill \\ \end{gathered} \right){{\rm d}}s} \\ \end{aligned} $$

$$ {{\mathbf{g}}}_{nl} ({{\mathbf{q}}}_{mp} ,{\dot{\mathbf{q}}}_{mp} ) = \left[ {\begin{array}{*{20}c} { - m_p z_{pc} \left( {\cos \theta_a \dot{\theta }_a^2 \cos \varphi_a - 2\sin \theta_a \dot{\theta }_a \sin \varphi_a \dot{\varphi }_a + \cos \theta_a \cos \varphi_a \dot{\varphi }_a^2 } \right)} \\ {m_p z_{pc} \left( { - \cos \theta_a \dot{\theta }_a^2 \sin \varphi_a - 2\sin \theta_a \dot{\theta }_a \cos \varphi_a \dot{\varphi }_a - \cos \theta_a \sin \varphi_a \dot{\varphi }_a^2 } \right)} \\ { - m_p z_{pc} \sin \theta_a \dot{\theta }_a^2 } \\ \begin{gathered} - 2\sin \theta_a \cos \theta_a \dot{\theta }_a I_a \dot{\varphi }_a + m_p \left( \begin{gathered} z_{pc} \dot{u}_a \sin \theta_a \sin \varphi_a \dot{\theta }_a - \dot{u}_a z_{pc} \cos \theta_a \cos \varphi_a \dot{\varphi }_a - \dot{w}_a z_{pc} \dot{\theta }_a \sin \theta_a \cos \varphi_a \hfill \\ - \dot{w}_a z_{pc} \dot{\varphi }_a \cos \theta_a \sin \varphi_a - 2z_{pc}^2 \cos \theta_a \sin \theta_a \dot{\theta }_a \dot{\varphi }_a \hfill \\ \end{gathered} \right) \hfill \\ - 2I_{py} \dot{\varphi }_a \dot{\theta }_a \cos \theta_a \sin \theta_a + I_{pz} \dot{\varphi }_a \dot{\theta }_a \cos \theta_a \sin \theta_a + I_{pz} \left( {\dot{\varphi }_a \sin \theta_a + \Omega } \right)\cos \theta_a \dot{\theta }_a - I_{pxy} \dot{\theta }_a^2 \sin \theta_a \hfill \\ - m_p \left( {\dot{w}_a z_{pc} \left( { - \dot{\theta }_a \cos \varphi_a \sin \theta_a - \dot{\varphi }_a \cos \theta_a \sin \varphi_a } \right) - \dot{u}_a z_{pc} \left( { - \dot{\theta }_a \sin \theta_a \sin \varphi_a + \dot{\varphi }_a \cos \theta_a \cos \varphi_a } \right)} \right) \hfill \\ \end{gathered} \\ \begin{gathered} m_p \left( \begin{gathered} - \dot{u}_a z_{pc} \dot{\theta }_a \cos \theta_a \cos \varphi_a + z_{pc} \dot{u}_a \sin \theta_a \sin \varphi_a \dot{\varphi }_a - \dot{w}_a z_{pc} \dot{\theta }_a \cos \theta_a \sin \varphi_a \hfill \\ - \dot{w}_a z_{pc} \dot{\varphi }_a \sin \theta_a \cos \varphi_a - \dot{v}_a z_{pc} \dot{\theta }_a \sin \theta_a \hfill \\ \end{gathered} \right) \hfill \\ - m_p \left( \begin{gathered} - z_{pc}^2 \dot{\varphi }_a^2 \sin \theta_a \cos \theta_a - \dot{u}_a z_{pc} \left( {\dot{\theta }_a \cos \theta_a \cos \varphi_a - \dot{\varphi }_a \sin \theta_a \sin \varphi_a } \right) \hfill \\ + \dot{w}_a z_{pc} \left( { - \cos \theta_a \dot{\theta }_a \sin \varphi_a - \sin \theta_a \cos \varphi_a \dot{\varphi }_a } \right) - \dot{v}_a z_{pc} \sin \theta_a \dot{\theta }_a \hfill \\ \end{gathered} \right) - I_{pxy} \dot{\varphi }_a \sin \theta_a \dot{\theta }_a \hfill \\ + I_a \dot{\varphi }_a^2 \cos \theta_a \sin \theta_a + I_{py} \dot{\varphi }_a^2 \cos \theta_a \sin \theta_a - I_{pz} \left( {\dot{\varphi }_a \sin \theta_a + \Omega } \right)\dot{\varphi }_a \cos \theta_a + I_{pxy} \dot{\theta }_a \dot{\varphi }_a \sin \theta_a \hfill \\ \end{gathered} \\ \end{array} } \right] $$

$$ \begin{aligned} & {{\mathbf{f}}}_{{\text{ext}}} ({{\mathbf{q}}}_{mp} ) = \left[ {\begin{array}{*{20}c} {{{\mathbf{0}}}_{1 \times (N_u + N_w + N_v )} } & {m_p g + m_a g} & 0 & 0 & { - m_p gz_{pc} \sin \varphi_a \cos \theta_a } & { - m_p gz_{pc} \sin \theta_a \cos \varphi_a } \\ \end{array} } \right]^T \\ & \quad + F_{im} \left[ {\begin{array}{*{20}c} {{{\mathbf{0}}}_{1 \times N_u } } & {{{\mathbf{W}}}^T (z_{{\text{ext}}} )\cos \gamma } & {{{\mathbf{V}}}^T (z_{{\text{ext}}} )\sin \gamma } & {{{\mathbf{0}}}_{1 \times 5} } \\ \end{array} } \right]^T \\ \end{aligned} $$

${\mathbf{A}} = \frac{{\partial {\mathbf{\Phi }}}}{{\partial {\mathbf{q}}_{nl} }} = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}(L)^T } & {\mathbf{0}} & {\mathbf{0}} & { - 1} & 0 & 0 & { - 0.5L_a \sin \varphi _a \cos \theta _a } & { - 0.5L_a \cos \varphi _a \sin \theta _a } \\ {\mathbf{0}} & {{\mathbf{W}}(L)^T } & {\mathbf{0}} & 0 & { - 1} & 0 & {0.5L_a \cos \varphi _a \cos \theta _a } & { - 0.5L_a \sin \varphi _a \sin \theta _a } \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{V}}(L)^T } & 0 & 0 & { - 1} & 0 & {0.5L_a \cos \theta _a } \\ {\mathbf{0}} & {\frac{{\partial \varphi (L)}}{{\partial {\mathbf{q}}_w }}} & {\frac{{\partial \varphi (L)}}{{\partial {\mathbf{q}}_v }}} & 0 & 0 & 0 & { - 1} & 0 \\ {\mathbf{0}} & {\mathbf{0}} & {\frac{{\partial \theta (L)}}{{\partial {\mathbf{q}}_v }}} & 0 & 0 & 0 & 0 & { - 1} \\ {\frac{{\partial \Phi _b }}{{\partial {\mathbf{q}}_u }}} & {\frac{{\partial \Phi _b }}{{\partial {\mathbf{q}}_w }}} & {\frac{{\partial \Phi _b }}{{\partial {\mathbf{q}}_v }}} & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$,

$\begin{gathered} {\mathbf{b}}_v = - {\dot{\mathbf{q}}}_{nl}^T \frac{{\partial ^2 {\varvec{\Phi }}}}{{\partial {\mathbf{q}}_{nl} ^2 }}{\dot{\mathbf{q}}}_{nl} - 2\frac{{\partial ^2 {\varvec{\Phi }}}}{{\partial {\mathbf{q}}_{nl} \partial t}}{\dot{\mathbf{q}}}_{nl} - \frac{{\partial ^2 {\varvec{\Phi }}}}{{\partial t^2 }} \hfill \\ = \left[ {\begin{array}{*{20}c} {0.5L_a \left[ {\dot{\theta }_a^2 \cos \theta _a \cos \varphi _a - 2\dot{\theta }_a \dot{\varphi }_a \sin \theta _a \sin \varphi _a + \dot{\varphi }_a^2 \cos \theta _a \cos \varphi _a } \right]} \\ {0.5L_a \left[ {\dot{\varphi }_a^2 \sin \varphi _a \cos \theta _a + 2\dot{\theta }_a \dot{\varphi }_a \cos \varphi _a \sin \theta _a + \dot{\theta }_a^2 \sin \varphi _a \cos \theta _a } \right]} \\ {0.5L_a \dot{\theta }_a^2 \sin \theta _a } \\ \begin{gathered} - w^{\prime}(L){\dot w^{\prime}}(L)^2 - w^{\prime}(L){\dot v^{\prime}}(L)^2 - 2v^{\prime}(L){\dot v^{\prime}}(L){\dot w^{\prime}}(L) - 4.5v^{\prime}(L)^2 {\dot v^{\prime}}(L)^2 w^{\prime}(L) - 3v^{\prime}(L)^3 {\dot v^{\prime}}(L){\dot w^{\prime}}(L) \hfill \\ - 1.5w^{\prime}(L){\dot w^{\prime}}(L)^2 v^{\prime}(L)^2 - 1.5w^{\prime}(L){\dot w^{\prime}}(L)v^{\prime}(L){\dot v^{\prime}}(L) - 1.5w^{\prime}(L)^2 {\dot w^{\prime}}(L)v^{\prime}(L){\dot v^{\prime}}(L) - 0.5w^{\prime}(L)^3 {\dot v^{\prime}}(L)^2 \hfill \\ - 1.5w^{\prime}(L)^3 {\dot w^{\prime}}(L)^2 \hfill \\ \end{gathered} \\ { - v^{\prime}(L){\dot v^{\prime}}(L)^2 - 1.5v^{\prime}(L)^3 {\dot v^{\prime}}(L)^2 } \\ { - \int_0^L {(2{\dot u^{\prime}} + 2u^{\prime}{\dot u^{\prime}} + 2v^{\prime}{\dot v^{\prime}} + 2w^{\prime}{\dot w^{\prime}})^2 {\text{d}}s} - \int_0^L {(2u^{\prime} + u^{{\prime} 2} + w^{{\prime} 2} + v^{{\prime} 2} )(2\dot{u}^{{\prime} 2} + 2\dot{v}^{{\prime} 2} + 2\dot{w}^{{\prime} 2} ){\text{d}}s} } \\ \end{array} } \right] \hfill \\ \end{gathered},$, where

$$ \frac{\partial \varphi (L)}{{\partial {{\mathbf{q}}}_w }} = \left[ {1 + 0.5w^{\prime}(L)^2 + 0.5v^{\prime}(L)^2 + \frac{3}{8}v^{\prime}(L)^4 + \frac{3}{4}w^{\prime}(L)^2 v^{\prime}(L)^2 + \frac{3}{8}w^{\prime}(L)^4 } \right]{\mathbf{W^{\prime}}}(L) $$

$$ \frac{\partial \varphi (L)}{{\partial {{\mathbf{q}}}_v }} = \left[ {v^{\prime}(L)w^{\prime}(L) + 1.5v^{\prime}(L)^3 w^{\prime}(L) + 0.5w^{\prime}(L)^3 v^{\prime}(L)} \right]{\mathbf{V^{\prime}}}(L) $$

$$ \frac{\partial \theta (L)}{{\partial {{\mathbf{q}}}_v }} = \left[ {1 + 0.5v^{\prime}(L)^2 + \frac{3}{8}v^{\prime}(L)^4 } \right]{\mathbf{V^{\prime}}}(L) $$

$$ \begin{aligned} \frac{\partial \Phi_b }{{\partial {{\mathbf{q}}}_u }} = & \int_0^L {(2u^{\prime} + u^{{\prime} 2} + w^{{\prime} 2} + v^{{\prime} 2} )(2{\mathbf{U^{\prime}}} + 2u^{\prime}{\mathbf{U^{\prime}}}){\text{d}}s} , \\ \frac{\partial \Phi_b }{{\partial {{\mathbf{q}}}_w }} = & \int_0^L {(2u^{\prime} + u^{{\prime} 2} + w^{{\prime} 2} + v^{{\prime} 2} )2w^{\prime}{\mathbf{W^{\prime}}}{\text{d}}s} , \\ \frac{\partial \Phi_b }{{\partial {{\mathbf{q}}}_v }} = & \int_0^L {(2u^{\prime} + u^{{\prime} 2} + w^{{\prime} 2} + v^{{\prime} 2} )2v^{\prime}{\mathbf{V^{\prime}}}{\text{d}}s} \\ \end{aligned} $$

$$ {\dot{\varvec{\Phi} }} = \left[ {\begin{array}{lllll} {\dot{u}(L) - \dot{u}_a - 0.5L_a \left( {\dot{\theta }_a \sin \theta_a \cos \varphi_a + \dot{\varphi }_a \cos \theta_a \sin \varphi_a } \right)} \\ {\dot{w}(L) - \dot{w}_a + 0.5L_a \dot{\varphi }_a \cos \varphi_a \cos \theta_a - 0.5L_a \dot{\theta }_a \sin \varphi_a \sin \theta_a } \\ {\dot{v}(L) - \dot{v}_a + 0.5L_a \dot{\theta }_a \cos \theta_a } \\ \begin{gathered} \dot{w}^{\prime}(L) + 0.5w^{\prime}(L)^2 {\dot w^{\prime}}(L) + v^{\prime}(L){\dot v^{\prime}}(L)w^{\prime}(L) + 0.5v^{\prime}(L)^2 {\dot w^{\prime}}(L) + 1.5v^{\prime}(L)^3 {\dot v^{\prime}}(L)w^{\prime}(L) \hfill \\ + 3/8v^{\prime}(L)^4 {\dot w^{\prime}}(L) + 3/4w^{\prime}(L)^2 {\dot w^{\prime}}(L)v^{\prime}(L)^2 + 0.5w^{\prime}(L)^3 v^{\prime}(L){\dot v^{\prime}}(L) + 3/8w^{\prime}(L)^4 {\dot w}^{\prime}(L) - \dot{\varphi }_a \hfill \\ \end{gathered} \\ {\dot v^{\prime}(L) + 0.5v^{\prime}(L)^2 {\dot v^{\prime}}(L) + 3/8v^{\prime}(L)^4 {\dot v^{\prime}}(L) - \dot{\theta }_a } \\ {\int_0^L {\left( {2u^{\prime} + u^{{\prime} 2} + w^{{\prime} 2} + v^{{\prime} 2} } \right)\left( {2\dot{u}^{\prime} + 2u^{\prime}{\dot u^{\prime}} + 2v^{\prime}\dot{v}^{\prime} + 2w^{\prime}\dot{w}^{\prime}} \right){\text{d}}s} } \\ \end{array} } \right] $$