1 Introduction

The level-crossing problem is a challenging and essential aspect of the theory of random processes, encompassing various related issues such as first-passage and escape problems and the theory of extreme values [1, 2]. While the level-crossing problem is usually formulated within a probabilistic framework, the solution of its deterministic counterpart can also be non-trivial in many cases.

The escape from a potential well is a classic problem that arises in numerous fields of engineering and natural sciences [3,4,5,6,7]. It has applications in chemical reactions [8, 9], the physics of Josephson junctions [10], micro-electro-mechanical systems (MEMS) [11,12,13,14,15,16], energy harvesting [17], celestial mechanics, and gravitational collapse.

Different types of excitation, such as appropriate ICs, harmonic excitation [5], stochastic noise [18,19,20], and impact loading, can cause a particle to escape.

Thompson [4] investigated escape under constant forcing and found that potentially slow variations of the system parameters can lead to bifurcations of the steady-state response regimes. The semi-analytic approach in [5] approximates the steady-state motion using primary harmonic balance. An escape occurs when the steady-state solution’s total energy reaches the potential well’s height. However, the results of this approach often need to be corrected by additional empirical factors to better agree with numerically or experimentally obtained results. Under harmonic excitation, a typical result in various papers [5, 14, 15] is the sharp minimum of the forcing amplitude depicted against the excitation frequency. Gendelman et al. [21] explained the two underlying mechanisms responsible for the sharp minimum of the curve near the 1:1 resonance: the maximum and the saddle mechanisms. These two mechanisms compete; thus, a sharp minimum occurs when both are equally important. Gendelman et al. [22] extended this investigation to the problem of forced damped escape from a potential well with weak nonlinearity and found that the sharp minimum of the critical forcing amplitude of the undamped system becomes smooth as a consequence of damping in the case of a quadratic potential well. However, the sharp minimum persists in the case of a potential with a cubic–quartic disturbance.

In engineering applications, damping is a ubiquitous phenomenon that plays a crucial role in numerous systems. It leads to the decay of transient motion, allowing the system to settle into a steady-state behavior. To study particle escape dynamics, researchers often use steady-state solution-based techniques, such as the harmonic balance method, which are justified by the damping in the system [5, 6]. Nonetheless, these methods commonly disregard the influence of the ICs, which can have substantial effects in some instances. Specifically, when the damping is small, the decay of transient motion becomes slower, making ICs a pivotal factor in the escape process.

As in any technical problem, model inaccuracies, simplifications, non-modeled noise, and measurement errors also affect escape problems. Due to these uncertainties, it is common in practical applications to prescribe a safety margin from the boundary of the SBs. Virgin [6] defined the safe region in terms of the total energy \(E_T\) using the safety factor \(\rho \in [0,1]\), which describes how close the total energy of the particle gets to the energy corresponding to the energy of the separatrix \(E_S\). All the points with total energy less than \(\rho E_S\) are within the safe region.

This concept can be extended to any suitable functional (or observable) of the system, denoted as \(f(\textbf{x};\textbf{p}) \in \mathbb {R}\). A scalar \(\rho \in [0,1]\) can act as a safety factor, segmenting the combined space of system parameters and initial conditions into two distinct regions: the safe zone, where \(f(\textbf{x}(t);\textbf{p})<\rho \quad \forall t>0\), and the unsafe zone, defined by \(f(\textbf{x}(t);\textbf{p}) > \rho \) at some \(t>0\). For instance, in the context of Virgin, the functional is represented by \(f=E_T/E_S\). However, this concept can also be adapted to metrics such as critical displacement, velocity, acceleration, or stress values.

Since model uncertainties and the consequences of a failure are always problem-specific, so is the value of an appropriate safety factor \(\rho \). It is important to note that while larger safety margins (small \(\rho \)) increase the system’s robustness against escape, they also reduce the usable area within the SBs. Therefore, determining the optimal safety margin is a delicate balance between ensuring system safety and maximizing operational efficiency. In this context, the escape problem reduces to a level-crossing one, namely finding the smallest positive value for t (first-passage time), which fulfills \(f(\textbf{x}(t);\textbf{p})=\rho \). Those sets of ICs and parameters for which no positive, real solution exists are part of the safe region.

After fixing the parameter values, ICs can be analyzed using the concept of SBs of escape (or SBs of level-crossing). These SBs refer to ICs where the particle remains within the potential well (or does not cross a critical level) [23]. Various measures and methods have been introduced to characterize the size and shape of SBs in oscillatory problems [4, 18, 23, 24]. The global integrity measure (GIM), defined as the normalized hypervolume (or area, in 2D cases) of the SB, is a standard metric used to quantify the appropriate size of SBs. Although GIM is easy to obtain numerically, it often includes fractal tentacles of the SB that are irrelevant from an engineering perspective.

Determining and understanding the impact of system parameters on the SB are paramount in engineering design to ensure the development of robust systems and applications. Karmi et al. derived a conservation law for a forced escape by utilizing action-angle variables and averaging for a truncated quadratic–quartic potential well at different energy levels [25]. However, fully analytic treatment of SBs is rarely feasible due to the complexity of the problem. In the following, we present an exceptional case study of the escape of a weakly damped particle from a truncated quadratic potential well under harmonic excitation. The harmonically excited linear oscillator with viscous damping is arguably the simplest possible model for describing one-degree-of-freedom vibrations. Several engineering curricula in introductory mechanics courses teach and consider it well understood. However, this model might also be the most advanced for many engineers without further specialization in vibrations theory. Despite the simplicity of the equation of motion and its known analytic solution, the model’s transient dynamics still offer novelties for researchers. This study demonstrates how the above model explains the “Dover cliff” integrity curve, found by numerical simulations in [4, 26]. The integrity curve describes the integrity measure of SBs of escape (or level-crossing) depending on the excitation amplitude. In damped cases, the curve has a particular shape. It has a plateau for small excitation values, but after the excitation reaches a critical level, the SBs start to erode quickly, and the GIM rapidly drops to zero. After reaching a second critical excitation amplitude value, no SB exists anymore.

Escape and level-crossing problems are closely connected as the criteria for escape often involve the particle’s displacement or energy, which needs to reach a critical value [5, 6, 27]. While they are not identical, level-crossing problems frequently arise in escape problems, as the particle almost surely escapes from its potential well after achieving a certain distance or energy level [6, 21]. This study initially formulated the level-crossing problem based on displacement, but the “energy criterion” is later introduced to aid analytic calculations. Thus, the study seeks to identify a set of ICs for which the particle never reaches the critical distance \(r_B\).

This problem has practical applications, such as in ship engineering, where a safety region for the roll angle can be specified to prevent unwanted outcomes like cargo loss or ship capsize due to overshooting the critical roll angle [6]. Such examples justify the application of escape models based on the truncation of the potential well. Indeed, in such problems, truncation-based escape models and level-crossing problems become interchangeable. The critical level value in engineering also denotes a precarious state that machines must evade. Therefore, the rapid erosion of SBs becomes critical in noisy settings, where machines operating near the “cliff” become unsafe. The proposed mechanical model has numerous potential applications owing to its simplicity. It can simulate brittle material behavior where failure transpires at a critical stress level. Moreover, it can describe the motion of a harmonically excited body with linear damping and restoring force in a symmetric clearance, where collisions with the wall must be avoided for acoustic or safety reasons.

The paper’s structure is as follows: Sect. 2 outlines the mathematical model for the deterministic level-crossing problem and presents a solution to the equation of motion in the general case. In Sect. 3, appropriate level-crossing criteria are defined and applied to the equation of motion. Section 4 offers a semi-analytic approximation of the SBs’ area. In Sect. 5, the numerical model is validated. Finally, Sect. 6 summarizes the findings and highlights areas for further research.

2 Problem setting

We investigate the SBs of level-crossing of a classical particle m with the linear spring force of stiffness k and viscous damping c. The absolute value of the critical displacement is given by \(r_B\). We define the undamped natural frequency

$$\begin{aligned} \varOmega _0=\sqrt{\frac{k}{m}}. \end{aligned}$$
(1)

The particle is excited with a sinusoidal force of amplitude F, frequency \(\varOmega \), and initial phase \(\beta \), and its motion starts with the ICs \((\tilde{x}_0,\tilde{u}_0)\). The problem setting is depicted in Fig. 1.

Fig. 1
figure 1

Problem settings. a Homologous mechanical model of the problem, b symmetrically truncated quadratic potential. (Color figure online)

Full size image

2.1 Equation of motion

The equation of motion is given by

$$\begin{aligned}{} & {} m\tilde{x}''+c \tilde{x}'+m \varOmega _0^2 \tilde{x}=F \sin (\varOmega t+\beta ), \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \tilde{x}(t=0) =\tilde{x}_0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \tilde{x}'(t=0) =\tilde{u}_0, \end{aligned}$$
(4)

with \(\square ':=\text {d} \square /\text {d} t\). Dividing by m and introducing the dimensionless displacement \(x:=\tilde{x}/r_B\) and the dimensionless time \(t:=\varOmega _0 \tau \), we have

$$\begin{aligned}{} & {} \ddot{x}+\frac{c}{\varOmega _0 m} \dot{x}+x =\frac{F}{r_Bm} \sin \left( \frac{\varOmega }{\varOmega _0} \tau +\beta \right) , \end{aligned}$$
(5)
$$\begin{aligned}{} & {} x(\tau =0) =x_0:=\frac{\tilde{x}_0}{r_B}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \dot{x}(\tau =0) =u_0:=\frac{\tilde{u}_0}{\varOmega _0 r_B}, \end{aligned}$$
(7)

where \(\dot{\square }\) is the derivative with respect to dimensionless time \(\tau \). After defining

$$\begin{aligned} D:=\frac{c}{2\varOmega _0m}, \qquad f:=\frac{F}{r_Bm}, \qquad \omega :=\frac{\varOmega }{\varOmega _0}, \end{aligned}$$
(8)

we have the non-dimensional equation of motion

$$\begin{aligned}{} & {} \ddot{x}+2D\dot{x}+x =f \sin (\omega \tau +\beta ),\nonumber \\{} & {} x(\tau =0) =x_0,\nonumber \\{} & {} \dot{x}(\tau =0) =u_0 , \end{aligned}$$
(9)

which is the equation of a damped harmonic oscillator.

The steps to obtain the solution of Eq. (9) are well known and not presented in detail here. The solution is

$$\begin{aligned} x(\tau )=R \text {e}^{-D\tau } \sin (\omega _0 \tau +\alpha )+P\sin (\omega \tau +\beta +\gamma ),\nonumber \\ \end{aligned}$$
(10)

with

$$\begin{aligned} \omega _0:= & {} \sqrt{1-D^2}, \end{aligned}$$
(11)
$$\begin{aligned} P:= & {} \frac{f}{\sqrt{(1-\omega ^2)^2+4D^2\omega ^2}}, \end{aligned}$$
(12)
$$\begin{aligned} \gamma:= & {} \text {atan2}(-2D\omega ,1-\omega ^2), \end{aligned}$$
(13)
$$\begin{aligned} C_1:= & {} x_0-P \sin (\beta +\gamma ), \end{aligned}$$
(14)
$$\begin{aligned} C_2:= & {} u_0-P\omega \cos (\beta +\gamma ), \end{aligned}$$
(15)
$$\begin{aligned} R:= & {} \sqrt{\frac{C_1^2+2DC_1C_2+C_2^2}{1-D^2}}, \end{aligned}$$
(16)
$$\begin{aligned} \alpha:= & {} \text {atan2}(\omega _0 C_1,DC_1+C_2), \end{aligned}$$
(17)

where \(\text {atan2}(y,x)\) denotes the “2-argument arctangent.” Assuming that the excitation frequency is in the vicinity of \(\omega _0\), the small parameter

$$\begin{aligned} \varepsilon :=\omega -\omega _0 \end{aligned}$$
(18)
Fig. 2
figure 2

Two different types of level-crossing (\(D=0.02\), \(f=0.15\), \(\omega =1.1\), \(\beta =\pi \)). a “Fast” level-crossing (\(x_0=0.86\), \(u_0=0.045\)). b “Slow” level-crossing (\(x_0=-0.665\), \(u_0=0.945\)). (Color figure online)

Full size image

can be introduced. One can obtain the level-crossing time by finding the smallest positive \(\tau _\text {LC}\) that fulfills the equation

$$\begin{aligned} x(\tau _\text {LC})\overset{!}{=}\pm 1. \end{aligned}$$
(19)

Considering Eq. (10), two different level-crossing scenarios are possible: “fast” and “slow” level-crossing. In the “fast” case, the particle reaches the critical distance in the first excitation period. This means that the level-crossing is mainly due to the ICs since a small excitation amplitude cannot significantly affect the particle’s motion in such a short amount of time. If the second scenario, the particle’s initial total energy is insufficient for the level-crossing. However, due to the harmonic force acting upon it, the particle gradually gets closer to the critical value of the displacement until it finally reaches it (cf. Fig. 2).

In both scenarios, the plane of the ICs is divided into the safe (\(S_F,\) \(S_S\)) and unsafe regions (\(U_F,\) \(U_S\)) according to the type of the level-crossing. The particle will not cross the critical distance if it belongs to \(S_F\) and \(S_S\); thus, the final safe region is the intersection of the sets defined by the two conditions (\(S:=S_F \cap S_S\)).

3 Level-crossing criteria

In the following, we determine the shapes of the SBs given by both the “fast” and “slow” crossing mechanisms.

3.1 “Fast” level-crossing

First, let us investigate the “fast” level-crossing mechanism caused mainly by the ICs. At the boundary of the “fast” safe region \(S_F\), it holds that the first local extremum of the particle’s motion \(x(\tau _F)\) has the absolute value one:

$$\begin{aligned} \partial S_F:=\lbrace (x_0,u_0) \in \mathbb {R}^2| x(\tau _F;x_0,u_0)=\pm 1\rbrace , \end{aligned}$$
(20)

with

$$\begin{aligned} \tau _F(x_0,u_0):= \lbrace \min \tau |\dot{x}(\tau ;x_0,u_0)=0 \qquad \text {with } \tau \ge 0 \rbrace .\nonumber \\ \end{aligned}$$
(21)

To get the exact value and time instance of the first local extremum of \(x(\tau )\), the transcendental equation \(\dot{x}(\tau )=0\) has to be solved, which is not possible analytically in general. However, the regular perturbation method for algebraic expressions can be applied to obtain a good approximation for \(\tau _F\): a series expansion in the small parameter \(\varepsilon \) yields equations that can be solved successively to get estimates for the time where Eq. (10) takes its first local extrema. A first-order estimate in \(\varepsilon \) yields sufficient accuracy (cf. green line in Figs. 4 and 5); thus, we rewrite the time as

$$\begin{aligned} \tau =\tau _0+\varepsilon \tau _1+\mathcal {O}(\varepsilon ^2). \end{aligned}$$
(22)

In addition, \(x(\tau )\) has to be rewritten as

$$\begin{aligned} x(\tau )=x_0(\tau )+\varepsilon x_1(\tau )+\mathcal {O}(\varepsilon ^2). \end{aligned}$$
(23)

Writing \(D=D^*|\varepsilon |\), where \(D^* =\mathcal {O}(1)\), and \(\omega =\omega _0+\varepsilon \), we are left with the only small parameter \(\varepsilon \). Taylor expansion up to the first order in \(\varepsilon \) yields

$$\begin{aligned}&x(\tau )\approx R \sin (\omega _0 \tau _0+\alpha )+P\sin (\omega _0 \tau _0+\beta +\gamma )\nonumber \\&\quad + ( R \left[ \cos (\omega _0 \tau _0+\alpha )\omega _0 \tau _1-\sin (\omega _0\tau _0+\alpha )D^*\tau _0\right] \nonumber \\&\quad + P \cos (\omega _0 \tau _0+\beta +\gamma ) (\tau _0 +\omega _0\tau _1) ) \varepsilon . \end{aligned}$$
(24)

By defining

$$\begin{aligned} Q&:=\sqrt{R^2+2RP\cos (\alpha -\beta -\gamma )+P^2}, \end{aligned}$$
(25)
$$\begin{aligned} \nu&:=\text {atan2}(R\sin \alpha +P\sin (\beta +\gamma ),R\cos \alpha + \nonumber \\&\quad +P \cos (\beta +\gamma )), \end{aligned}$$
(26)

we can write Eq. (24) as

$$\begin{aligned} x(\tau )&=Q \sin (\omega _0 \tau _0+\nu )\nonumber \\&\quad +\varepsilon ( \tau _0(P\cos (\omega _0 \tau _0+\beta +\gamma ) \nonumber \\&\quad -D^*R\sin (\omega _0\tau _0+\alpha ))\nonumber \\&\quad +Q \tau _1 \omega _0 \cos (\omega _0 \tau _0+\nu ) ). \end{aligned}$$
(27)

At local extrema, the condition \(\dot{x}(\tau )=0\) is fulfilled. The time derivative with respect to \(\tau \) (as in the method of multiple scales) becomes

$$\begin{aligned} \frac{\text {d}\square }{\text {d}\tau }=\frac{\partial \square }{\partial \tau _0}+\varepsilon \frac{\partial \square }{\partial \tau _1}, \end{aligned}$$
(28)

which, after neglecting the terms of order higher than \(\mathcal {O}(\varepsilon )\), results in

$$\begin{aligned} \dot{x}(\tau )&=Q \omega _0 \cos (\omega _0 \tau _0+\nu )+\nonumber \\&\quad \varepsilon \big ( -Q \tau _1 \omega _0^2 \sin (\omega _0 \tau _0+\nu )+P(\cos (\omega _0\tau _0+\beta +\gamma )\nonumber \\&\quad -\tau _0\omega _0 \sin (\omega _0 \tau _0+\beta +\gamma ))-D^*R(\sin (\omega _0\tau _0+\alpha )\nonumber \\&\quad +\tau _0 \omega _0 \cos (\omega _0\tau _0+\alpha )) \big ). \end{aligned}$$
(29)

Based on condition (21), the terms with \(\varepsilon ^0\) and of \(\varepsilon ^1\) should disappear. There are infinitely many solutions, but we are interested in the smallest positive solution, which is

$$\begin{aligned}{} & {} \tau _0^*(x_0,u_0)=\frac{\text {mod}\left( \frac{\pi }{2}-\nu ,\pi \right) }{\omega _0}, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \tau _1^*(x_0,u_0)\nonumber \\{} & {} \quad =\frac{P(\cos (\omega _0\tau _0^*+\beta +\gamma )-\tau _0^*\omega _0 \sin (\omega _0 \tau _0^*+\beta +\gamma ))}{Q \omega _0^2 \sin (\omega _0 \tau _0^*+\nu )} \nonumber \\{} & {} \qquad -\frac{D^*R(\sin (\omega _0\tau _0^*+\alpha )+\tau _0^* \omega _0 \cos (\omega _0\tau _0^*+\alpha ))}{Q \omega _0^2 \sin (\omega _0 \tau _0^*+\nu )}, \nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned}{} & {} \tau _F(x_0,u_0):=\tau _0^*+\varepsilon \tau _1^*. \end{aligned}$$
(32)

Now, it is possible to insert the value of \(\tau _F(x_0,u_0)\) back into Eq. (20) and plot the boundary of the “fast” safe region \(\partial S_F\) as an implicit function of (\(x_0,u_0\)) (see Fig. 5 and 4). Equation (20) defining the “fast” boundary \(\partial S_F\) is still too complicated to evaluate analytically. However, its numerical evaluation is orders of magnitude faster (cf. Sec. 5) than the direct numerical simulation of Eq. (9).

Fig. 3
figure 3

Exact solution and its envelope calculated using Eq. (36) for \(D=0.02\), \(f=0.15\), \(\omega =1.1\), \(\beta =\pi \), \(x_0=0\), and \(u_0=1\). (Color figure online)

Full size image

The green line in Figs. 5 and 4 represents the “fast” level-crossing boundary. Without excitation (cf. Fig. 4a), level-crossing is only possible due to the ICs. Since the motion is damped and one-dimensional (due to coupling terms, this must not be true for two-dimensional motions), its global maximum is already taken during the first half period of the motion. In other words, the “fast” boundary \(\partial S_F\) entirely determines the particle’s SB. As the damping increases, the size of the SB expands. For moderate values of D, the analytic estimate shows an excellent agreement with the numerically obtained data.

With excitation and without damping (cf. Fig. 4b), the transient motion does not decay. Thus, the particular and homogeneous solution’s interaction (beating motion) determines the SB. In this case, the “slow” boundary \(\partial S_S\) entirely determines the SB. The resulting basin is a circular disk for an irrational frequency ratio of the particular and homogeneous solutions. However, the SB will have a different shape if the above frequency ratio is rational, as shown in [28]. Nonetheless, even in this case, for moderate forcing amplitudes, the “fast” boundary accurately describes the set of ICs where level-crossing happens in the first half period of the excitation (see the deep blue region in Fig. 4b).

With damping and with excitation (cf. Fig. 5), both the “fast” and the “slow” boundaries become relevant and define a section of the SB’s circumference.

3.2 “Slow” level-crossing

To determine the boundary of the safe region given by the “slow” crossing mechanism, we analyze the envelope of \(x(\tau )\), which we can estimate with the use of the total energy of the particle. First, we calculate

$$\begin{aligned} 2E=x^2+\dot{x}^2. \end{aligned}$$
(33)

Taking the derivative of Eq. (10) and inserting it into Eq. (33), the following expression is obtained:

$$\begin{aligned}{} & {} \!\!\!2E{=}R^2 \text {e}^{-2D\tau }{+}P^2{+}2RP\text {e}^{-D\tau }\cos (\varepsilon \tau {-}\alpha {+}\beta {+}\gamma )\nonumber \\{} & {} \quad +(\omega _0^2-1)R^2\text {e}^{-2D\tau }\cos ^2(\omega _0\tau +\alpha )\nonumber \\{} & {} \quad +P^2(\omega ^2-1)\cos ^2(\omega \tau +\beta +\gamma )\nonumber \\{} & {} \quad +2RP(\omega \omega _0-1)\text {e}^{-D\tau }\!\cos (\omega _0\tau {+}\alpha )\cos (\omega \tau {+}\beta {+}\gamma )\nonumber \\{} & {} \quad +D^2R^2\text {e}^{-2D\tau }\sin ^2(\omega _0 \tau +\alpha )\nonumber \\{} & {} \quad -2DR^2\omega _0\text {e}^{-2D\tau }\sin (\omega _0+\tau )\cos (\omega _0\tau +\alpha )\nonumber \\{} & {} \quad -2DRP\omega \text {e}^{-D\tau }\sin (\omega _0\tau +\alpha )\cos (\omega \tau +\beta +\gamma ).\nonumber \\ \end{aligned}$$
(34)

Note that from the second row onwards in Eq. (34), every term is of \(\mathcal {O}(\varepsilon )\). Thus, by neglecting them, we obtain

$$\begin{aligned} 2\tilde{E}:=R^2 \text {e}^{-2D\tau }{+}P^2{+}2RP\text {e}^{-D\tau }\cos (\varepsilon \tau {-}\alpha {+}\beta {+}\gamma ), \end{aligned}$$
(35)

and the envelope can be estimated by

$$\begin{aligned} A(\tau )=\pm \sqrt{2\tilde{E}}. \end{aligned}$$
(36)
Fig. 4
figure 4

Effects of the damping and the excitation on the “fast” level-crossing boundary in the IC plane. We neglect both effects in the analytic calculations. The color scale shows the time necessary to level-crossing (\(\infty \) means no crossing). a The area of the SB increases (yellow surface) compared to the area of the unit circle (solid magenta line) if damping is increased (\(D=0.1\)) and no excitation is applied (\(f=0\), \(\omega \) and \(\beta \) are irrelevant). The “slow” level-crossing mechanism does not apply here since the envelope (cf. Eq. (36)) has no other local maximum than the one at zero. b Impact of the exciting force (\(f=0.08\)) on the shape of the boundary predicted by the “fast” level-crossing mechanism (solid green line) when no damping is present (\(D=0\)), \({\omega =0.95}\) and \(\beta =0\). Since \(D=0\), the logarithmic spiral does not grow and degenerates into a circle. (Color figure online)

Full size image

A graphical representation of the envelope defined by Eqs. (35–36) can be seen in Fig. 3. The maximum of the envelope \(A_{\text {max}}\) cannot be found explicitly, either the time instance of the first level-crossing. (For numerical examples see Figs. 5, 4b, and 6.) However, for the envelope’s maximum, a reasonable estimate can be given considering that it is either taken at the beginning of the motion (“fast” level-crossing) or around the time point where the cosine term takes the value 1 for the first time in Eq. (35) (“slow” level-crossing), i.e.,

$$\begin{aligned} \tau _S=\text {mod}\left( \frac{\alpha -\beta -\gamma }{\varepsilon }, \frac{2 \pi }{|\varepsilon |}\right) . \end{aligned}$$
(37)

Thus,

$$\begin{aligned} A_\text {max}^2=(P+R\text {e}^{-D\tau _S})^2. \end{aligned}$$
(38)

So, the boundary of the “slow” safe region is given by

$$\begin{aligned} \partial S_S:=\lbrace (x_0,u_0) \big | A_\text {max}(x_0,u_0)=1 \rbrace . \end{aligned}$$
(39)

The interior of \(S_S\) (see Fig. 5) is described by

$$\begin{aligned} -1<P+R \text {e}^{-D\tau _S}&<1. \end{aligned}$$
(40)

The left-hand side of the inequality is fulfilled trivially. The right-hand side yields

$$\begin{aligned} R \text {e}^{-D\tau _S}&<1-P, \end{aligned}$$
(41)

which immediately implies the existence of a condition for a non-escaping set:

$$\begin{aligned} P\overset{!}{<}1. \end{aligned}$$
(42)

Considering that we can bring the exponential factor to the other side and take the square of both sides in Eq. (41) leads to

$$\begin{aligned} R^2&<\text {e}^{2D\tau _S}(1-P)^2. \end{aligned}$$
(43)

Substituting the value for \(R^2\) (see Eq. 16) and rearranging the terms, we have

$$\begin{aligned} \frac{C_1^2+2DC_1C_2+C_2^2}{(1-D^2)(1-P)^2}<\text {e}^{2D\tau _S}. \end{aligned}$$
(44)

The left-hand side of this equation describes level sets of ellipses rotated by \(45^{\circ }\) and centered at \((P\sin (\beta +\gamma )\),

\(P \omega \cos (\beta +\gamma ))\). The right-hand side is a function that depends on the ICs through \(\tau _S(x_0,u_0)\). We shall determine what kind of curves are the level sets of \(\text {e}^{ 2D\tau _S(x_0,u_0)}\). To this end, first, we consider the ranges of the parameters \(\alpha \in (-\pi ,\pi ]\), \(\beta \in (-\pi ,\pi ]\) and \(\gamma \in (-\pi ,0]\). We have

$$\begin{aligned} \tau _S= {\left\{ \begin{array}{ll} \frac{\alpha -\beta -\gamma +2\pi }{\varepsilon } &{} \text { if }\alpha -\beta -\gamma<0,\\ \frac{\alpha -\beta -\gamma }{\varepsilon } &{} \text { if } 0\le \alpha -\beta -\gamma \le 2\pi ,\\ \frac{\alpha -\beta -\gamma -2\pi }{\varepsilon } &{} \text { if }2 \pi <\alpha -\beta -\gamma , \end{array}\right. } \end{aligned}$$
(45)

where only \(\alpha \) depends on the ICs. The domain length of \(\tau _S\) is greater than \(2 \pi \) if all parameters are allowed to vary, but in case we only vary the ICs (by plotting the time of level-crossing in the IC plane, cf. Fig. 5) and the values of f, D, \(\omega \), and \(\beta \) are fixed, the only non-constant term is \(\alpha \). Since the range of \(\alpha \) is \((-\pi ,\pi ]\) and the values of \(\beta \) and \(\gamma \) are fixed, at most only two definition domains of Eq. (45) can be active. For some region of \(x_0\) and \(u_0\) values, the middle case of Eq. (45) will always become active irrespective of f, D, \(\omega \), and \(\beta \); however, only the first or third case can occur for the remaining values of \(x_0\) and \(u_0\).

Next, we find the subsets, where \(\tau _S\) has a constant value since these sets are the level sets of the right-hand side of the equation. This observation immediately implies that along these sets, \(\alpha \) also has a constant value, \(\alpha _0\). Thus, by the definition of \(\alpha \) given in Eq. (17), we have

$$\begin{aligned}&\alpha _0 =\text {atan2}\left( C_1 \sqrt{1-D^2},DC_1+C_2\right) =\text {const.} \end{aligned}$$
(46)
$$\begin{aligned}&C_2 =\left( \frac{\sqrt{1-D^2}}{\tan \alpha _0} -D\right) C_1. \end{aligned}$$
(47)
Fig. 5
figure 5

Numerically obtained level-crossing time (color scale) and SB (yellow region, \(\infty \) means no crossing) on the \(x_0-u_0\) IC plane with \(D=0.02\), \(f=0.15\), \(\omega =1.1\), and \(\beta =\pi \). The analytic estimation of the SB is given by the intersection of the curves \(\partial S_S\) and \(\partial S_F\). Rays of \(\tau _S=\text {const.}\) start at point \(\tilde{C}\) and \(\tau _S\) grows linearly with the angle in the clockwise direction. Every change in the color shade corresponds to a peak in the solution \(x(\tau )\) (cf. Fig. 2b). (Color figure online)

Full size image

By substituting the values of \(C_1\) and \(C_2\) defined in Eqs. (14–15), we have

$$\begin{aligned}&u_0-P\omega \cos (\beta +\gamma ))\nonumber \\&\quad =\left( \frac{\sqrt{1-D^2}}{\tan \alpha _0} -D\right) \left( x_0-P\sin (\beta +\gamma )\right) . \end{aligned}$$
(48)

From Eq. (48), it is obvious that the curves along which \(\tau _S\) takes constant values are rays (not entire lines because of the atan2 function) starting at the point \((P\sin (\beta +\gamma ), P \omega \cos (\beta +\gamma ))\). From Eq. (45), it follows that the ray along which \(\tau _S=0\) holds has slope

$$\begin{aligned} \frac{\varDelta u_0}{\varDelta x_0}=\frac{\sqrt{1-D^2}}{\tan (\beta +\gamma )}-D, \end{aligned}$$
(49)

and the direction of the ray is such that if \(\beta +\gamma \in [-\frac{\pi }{2},\frac{\pi }{2}]\), then the ray lies in the half plane fulfilling

$$\begin{aligned} C_2> & {} -DC_1, \end{aligned}$$
(50)
$$\begin{aligned} u_0> & {} -Dx_0+P(\sin (\beta +\gamma )+\omega \cos (\beta +\gamma ));\nonumber \\ \end{aligned}$$
(51)
Fig. 6
figure 6

Numerically obtained level-crossing time (color scale) and SB (yellow region, \(\infty \) means no crossing) on the \(x_0-u_0\) IC plane with \(D=0.02\), \(f=0.15\), \(\omega =1.1\), and \(\beta =\lbrace \pi /4, \pi /2 \rbrace \). Rays of \(\tau _S=\text {const.}\) start at point \(\tilde{C}\) and \(\tau _S\) grows linearly with the angle in the clockwise direction. The graphs together with Fig. 5 suggest that the initial phase of the excitation \(\beta \) has a negligible effect on the size of the SBs, and it affects their orientation solely. (Color figure online)

Full size image

otherwise, if \(\beta +\gamma \not \in [-\frac{\pi }{2},\frac{\pi }{2}]\), the ray lies in the opposite half plane, as given by

$$\begin{aligned} C_2<-DC_1. \end{aligned}$$
(52)

Starting along the ray corresponding to \(\tau _S=0\) and turning in the clockwise direction for \(\varepsilon >0\) or counterclockwise direction for \(\varepsilon <0\), the increment of \(\tau _S\) is proportional to the rotation angle. After a whole turn, the maximal level-crossing time takes the value

$$\begin{aligned} \tau _\text {S,max}=\frac{2 \pi }{|\varepsilon |}. \end{aligned}$$
(53)

When we plot the value of \(\text {e}^{2D\tau _S}\) (in Eq. (44)) as a function of the rotation angle around the point \((P\sin (\beta +\gamma ),P \omega \cos (\beta +\gamma ))\), we observe an increasing logarithmic spiral (cf. red curve in Fig. 4b and Fig. 5 and blue curve in Fig. 7). Regarding Eq. (41), the above observation implies that the predicted non-escaping set lies within an ellipse rotated by \(45^{\circ }\) with the major axis

$$\begin{aligned} a=\sqrt{1+D}(1-P) \end{aligned}$$
(54)

and minor axis

$$\begin{aligned} b=\sqrt{1-D}(1-P) \end{aligned}$$
(55)

stretched exponentially along the rotation angle.

4 The area of the SB

Estimating the SB area can be achieved through analytic means. Specifically, to perform the calculations, we substitute the boundary of the “fast” escaping set \(\partial S_F\) with the unit circle representing the SB of a truncated quadratic potential without damping and excitation. Regarding the damping, this simplification is a lower estimate of the safe region area since a part of the safe region is excluded from the possible set of SBs by neglecting the damping effect. Due to damping, the particle is sufficiently slowed not to reach the boundary (cf. Fig. 4a). However, the substitution of \(S_F\) by the unit disk is not restrictive regarding the excitation effect. Still, the difference between the two sets remains small for sufficiently small excitation amplitude values. Thus, the analytic estimate can remain sufficiently accurate (cf. Fig. 4b).

Fig. 7
figure 7

Shifted and rotated polar coordinate system after some simplifying assumptions. The black unit circle replaces \(\partial S_F\), while the blue logarithmic spiral depicts \(\partial S_S\). The beige region determined by the curves is the analytic estimate of the SB (here \(\varepsilon <0\)). (Color figure online)

Full size image
Fig. 8
figure 8

The solutions of \((1-P) \text {e}^{D^* \varphi }=-P \cos \varphi +\sqrt{1-P^2 \sin ^2 \varphi }\) depend on the parameters \(D^*\) and P. For values \(D^*>D_\text {crit}\), the only real solution \(\varphi _0=0\) exists

Full size image

The “slow” safe region \(S_S\) is also slightly simplified. Instead of treating the interior of the rotated ellipse given in Eq. (44), we neglect D on the left-hand side of the inequality, leading to a circle centered at

$$\begin{aligned} {\tilde{C}:=(P \sin (\beta +\gamma ),P \omega \cos (\beta +\gamma ))}. \end{aligned}$$
(56)

To simplify further, we neglect the effect of \(\omega \) in the position of the circle, and we define the point

$$\begin{aligned} C:=(P \sin (\beta +\gamma ),P \cos (\beta +\gamma )) \end{aligned}$$
(57)

as the center of origin of a new polar coordinate system (\(r,\varphi \)) which is rotated by

$$\begin{aligned} \angle (\overrightarrow{OC},\vec {e}_{x_0})=\frac{\pi }{2}-\beta -\gamma \end{aligned}$$
(58)

compared to the original coordinate system of \((x_0,u_0)\). Based on Eqs. (57) and (58), it is clear that the center and the orientation of the logarithmic spiral depend on \(\beta \) (rotation angle). However, in the new coordinate system \((r,\varphi )\), the excitation phase \(\beta \) does not play a role (cf. Fig. 6). The slope of the line along which \(\tau _S=0\) is given in Eq. (49). Neglecting D in Eq. (49), we find that this direction also corresponds to the same angle \(\frac{\pi }{2}-\beta -\gamma \). Thus, \(\varphi =0\) corresponds to the angle where the spiral starts (see Fig. 7). The following describes the calculation for \(\varepsilon <0\). Note that for \(\varepsilon >0\), the procedure is analogous but mirrored to the line \(\varphi =0\).

The unit circle with its center shifted to \((-P,0)\) is given by the equation

$$\begin{aligned} R_C(\varphi )=-P \cos \varphi +\sqrt{1-P^2 \sin ^2 \varphi }. \end{aligned}$$
(59)

The equation of the logarithmic spiral is given by

$$\begin{aligned} R_S(\varphi )=(1-P) \text {e}^{\frac{D}{|\varepsilon |} \varphi }. \end{aligned}$$
(60)

We can recognize that the effect of the independent parameters D and \(\varepsilon \) can be given by using only their ratio, \(D^*=D/|\varepsilon |\). There are two different scenarios regarding the number of solutions to the equation

$$\begin{aligned}&R_C(\varphi )=R_S(\varphi ) \nonumber \\&(1-P) \text {e}^{D^* \varphi }=-P \cos \varphi +\sqrt{1-P^2 \sin ^2 \varphi }. \end{aligned}$$
(61)

In the more straightforward case, i.e., when the growth of the spiral \(D^*\) is sufficiently large, the only real solution is at \(\varphi _0=0\). For some smaller value \(D^*_\text {crit}\), there are exactly two solutions of Eq. (61), \(\varphi =0\) and \(\varphi _1=\varphi _2=\varphi _\text {crit}\). For even smaller \(D^*\) values, there are three real-valued, distinct roots of Eq. (61), \(0=\varphi _0< \varphi _1<\varphi _2<2 \pi \). Unfortunately, Eq. (61) cannot be solved in a closed form for \(\varphi \). Instead, we give a graphical solution in Fig. 8. It is not possible to obtain the value of \(D^*_\text {crit}\) in an explicit form, but an accurate heuristic estimate can be given for it by

$$\begin{aligned} D^*_\text {crit}\approx \frac{3}{4}\text {atanh} (P). \end{aligned}$$
(62)

To determine the size of the SB, the integral

$$\begin{aligned} GIM=\frac{1}{2}\int _0^{2 \pi } (\min \lbrace R_C(\varphi ), R_S(\varphi ) \rbrace )^2 \text {d} \varphi \end{aligned}$$
(63)

has to be calculated. If \(D^*>D_\text {crit}\), then \(R_S(\varphi )>R_C(\varphi ) \quad \forall \varphi \in [0,2\pi )\). Thus, the integral always equals the area of the unit circle \(\pi \). Otherwise, the integral is given by

$$\begin{aligned} GIM=&\frac{1}{2} \left( \int _0^{\varphi _1} R_C^2(\varphi ) \text {d} \varphi +\int _{\varphi _1}^{\varphi _2} R_S^2(\varphi ) \text {d} \varphi \right. \nonumber \\&\qquad \left. +\int _{\varphi _2}^{2 \pi } R_C^2(\varphi ) \text {d} \varphi \right) . \end{aligned}$$
(64)

Without providing the details of the calculation, the indefinite integral of \(R_C^2(\varphi )\) is given by

$$\begin{aligned} I_C(\varphi ):=&\int R_C^2(\varphi ) \text {d} \varphi = \frac{P^2}{2} \sin (2 \varphi )+\varphi \nonumber \\&\quad {-}P \sin \varphi \sqrt{1{-}(P \sin \varphi )^2} {-}\text {arcsin}(P \sin \varphi ). \end{aligned}$$
(65)

The indefinite integral of \(R_S^2(\varphi )\) is given by

$$\begin{aligned} I_S(\varphi ):=\frac{(1-P)^2}{2 D^*}\text {e}^{2 D^* \varphi }. \end{aligned}$$
(66)

Thus, the size of the SB is

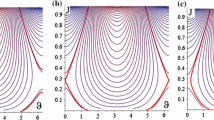
$$\begin{aligned} GIM=\frac{I_C(\varphi _1)+I_S(\varphi _2)-I_S(\varphi _1)+2\pi -I_C(\varphi _2)}{2}. \end{aligned}$$
(67)

Based on these calculations, we can also visually represent the area of the SBs (GIM) against \(D^*\) and P (cf. Fig. 9 and the right-hand side of Fig. 10a). It is worth noting that for nonzero damping, the size of the SB does not immediately decrease when the excitation amplitude, and consequently, the value of P increases.

Below a critical amplitude value of the forced excitation \(P_\text {crit}\), the SB remains entirely determined by the “fast” mechanism given by Eq. (20). This critical value of \(P_\text {crit}\) corresponds to the “cliff” and can be approximated using Eq. (62) as

$$\begin{aligned} P<P_\text {crit}=\text {tanh}\left( \frac{4}{3} D^* \right) . \end{aligned}$$
(68)

However, above the critical forced response amplitude \(P_\text {crit}\), both mechanisms play a role in the level-crossing process. As P increases, the “slow” level-crossing process gradually becomes more important, and a more significant proportion of the arc length of the SB’s boundary is defined by \(\partial S_S\).

In Fig. 9, the so-called “Dover cliff” erosion profiles (P increases at constant \(D^*\)) of the SBs can be observed. “Dover cliff” profiles were first observed in nonlinear, damped escape problems with external harmonic excitation [4, 26]. In the present case, where P is a linear function of the excitation amplitude f, we can interpret the plot in a classical way by depicting the size of the SBs against f while keeping D, \(\omega \), and \(\beta \) constant. There are two critical values of P: one at \(P_\text {crit}\), where the “fast” erosion of the SB begins, and another at \(P=1\) when the SB disappears. The sudden erosion at \(P_\text {crit}\) is often related to the homoclinic tangency of the particle’s orbit [29]; however, this current study has demonstrated that sudden erosion of the safe region can also occur in linear systems. Indeed, the erosion profile is not a matter of fact of nonlinearity but the transient motion’s decay. Through this study, we have accurately estimated the size and location of the SBs in the archetypical example of a harmonically forced damped linear oscillator, which can serve as a benchmark for investigating the effects of system nonlinearities.

Fig. 9
figure 9

The size of the SBs (GIM) is depicted against the parameters P (amplitude of the forced response) and \(D^*\) (damping–frequency perturbance ratio). Thick curves represent values \(D^*=0,0.2,0.4,\ldots ,2\). The erosion profiles (starting at \(P_\text {crit}\)) for fixed \(D^*>0\) are often called “Dover cliff” profiles. Above \(P=1\) no SBs exist

Full size image

5 Numerical results and model validation

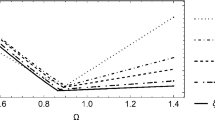
In this section, we validate the analytic model by comparing it to direct numerical results. In Fig. 10, the total SB area (GIM) is depicted depending on the values of \(D^*\) and P. On the left of Fig. 10a, the numerically obtained contour plot is shown for \(\omega =1.1\) and \(\beta =\frac{\pi }{3}\). The red line estimates the parameter combination where the logarithmic spiral is tangential to the unit circle. The analytic model works quite well, even though the value of \(\varepsilon =0.1-0.1056\) is not particularly small (\(\varepsilon \) cannot be held constant since \(\varepsilon =\omega -\omega _0(D)\); thus, it depends on D, and so on \(D^*\)). In Fig. 10b, the numerically obtained GIM is depicted for \(\omega =0.95\) and \(\omega =1.02\). In both cases, \(\beta =0\). The match with the analytic estimate is less exact here than for \(\omega =1.1\); nevertheless, it is still quite accurate. The discrepancy between the numerically obtained values and the analytic prediction increases with increasing \(D^*\), which is mainly due to the error caused by the false positioning of \(\partial S_S\) from the estimation of the maximum of Eq. (35) by Eq. (38). An error of 5–6 % in magnitude may occur, which can significantly affect the augmentation of the spiral. Applying Poincaré’s small parameter method to obtain a more accurate result for the maximum of Eq. (35) would probably work. However, it would also greatly complicate the equations, and the analytic continuation of the calculation would be impossible.

Direct numerical simulations require a large number of calculations. Due to the curse of dimensionality, the grids shown on the left side of Fig. 10a or in Fig. 10b consist of only 21\(\times \)21 nodes, since to find the GIM to each grid point, 101\(\times \)101 simulations on the IC plane were performed, resulting in 4 498 641 individual simulations.

Fig. 10
figure 10

Size of the safe basin (GIM) depending on the parameters \(D^*\) and P. The red line (\(P_\text {crit}\)) corresponds to the estimate of the critical forced vibration amplitude defined by Eq. (68). One can observe that for values \(P<P_\text {crit}\), the area of the safe basin continues to increase in the numerically obtained figures due to incremental damping (cf. Fig. 4a). For parameter values \(P<P_\text {crit}\), i.e., below the red line, the excitation seems to have a negligible effect on the size of the safe basin when computed directly by numerical means: Essentially, it is only influenced by \(D^*\). The SB’s increment in \(D^*\) is not taken into account when estimating \(\partial S_F\) by the unit circle. a On the left: numerically calculated values of the GIM for \(\omega =1.1\) and \(\beta =\pi /3\). On the right: analytically calculated values of the GIM. b On the left: numerically calculated values of the GIM for \(\omega =0.95\) and \(\beta =0\). On the right: numerically calculated values for \(\omega =1.02\) and \(\beta =0\). (Color figure online)

Full size image

To evaluate the reduction in computational cost by computing \(\partial S_S\) and \(\partial S_F\) over direct numerical integration of Eq. (9), we conducted simulations using the parameters: \(F=\lbrace 0.05, 0.1, 0.15 \rbrace \), \(\varOmega =1.1\), \(D=0.02\), and \(\beta =\pi /2\). These simulations utilized a 401\(\times \)601 grid spanning the ICs on \([-1,1] \times [-1.5,1.5]\). The results showed a 200–350-fold decrease in computational cost when using \(\partial S_S\) and \(\partial S_F\) as opposed to direct integration of Eq. (9).

6 Conclusions and future research scope

The stabilizing effect of viscous damping on the SBs of level-crossing from a symmetrically truncated quadratic potential well under harmonic excitation has been described in this article for the case when the excitation frequency is near the system’s natural frequency.

The analysis reveals that two competing mechanisms, the “fast” and “slow” level-crossing mechanisms, define the SBs: “Fast” level-crossing is related to the initial energy of the particle, whether it is sufficiently large to drive the particle from the potential well.

This mechanism is vital if the damping is significant compared to the difference between the potential well’s excitation and natural frequencies.

The mechanism of “slow” level-crossing is a beat-like phenomenon. It has an important role when the decay of the transient motion is slow, enabling the buildup of a large amplitude resonant oscillation.

The competition between the two mechanisms has a curious effect on the size of the SB. Until a particular value of the forced amplitude (\(P_\text {crit}\)), only the “fast” mechanism dominates. Up to this point, the size of the SB remains nearly unchanged. However, for stronger excitation resulting in steady-state amplitudes \(P>P_\text {crit}\), the “slow” mechanism gains more and more importance resulting in the rapid erosion of the SB. When the amplitude of the force reaches the value 1, level-crossing inevitably takes place for any ICs. In other words, the SB disappears.

Fig. 11
figure 11

Numerically obtained level-crossing time (color scale, \(\infty \) means no crossing) and SB (yellow region) on the \(x_0-u_0\) IC plane with \(D=0.02\), \(f=0.4\), \(\omega =0.5\), and \(\beta =0\). (Color figure online)

Full size image

Although the investigated model is linear, the identification of the two different mechanisms also has a significant implication for nonlinear systems: The typical, so-called “Dover cliff” erosion profile [23, 26], observed in many cases of damped, nonlinear escape problems is not a consequence of the system nonlinearities. It results from the two competing mechanisms: the interplay of the decaying motion caused by the ICs and the system’s forced response.

In the case of strong damping, the transient motion decays quickly, unable to create the beat-like vibration responsible for the “slow” mechanism. Thus, in the case of strong damping, the shape of the SB is determined mainly by the “fast” mechanism, at least when the oscillation amplitude of the particular solution P is less than one. In the case of \(P>1\), the forced oscillation is sufficiently strong: It swings into the critical region, and no SB exists.

Similarly, the “slow” mechanism, being beat-based, loses importance if the excitation frequency is further away from the resonant frequency of the well: The superposition of the transient and steady-state motion does not lead to prominent peaks in the envelope, leaving the “fast” mechanism the primary cause for level-crossing. To see this, in Fig. 11, the level-crossing time is depicted in the IC plane with excitation frequency \(\omega =0.5\). The time period of the excitation is \(4\pi \approx 12.57\), limiting the time of level-crossing by this value. Indeed, level-crossing does not occur after the first excitation period.

For large differences between the excitation and natural frequency, the boundaries of the “fast” and “slow” mechanisms defined by \(\partial S_F\) and \(\partial S_S\) are not described well by Eqs. (20) and (39), since both assume a small perturbance in the excitation frequency. However, the SB shows similarity to those found by Genda et al. [28] with zero damping, for which analytic estimates are available.

Furthermore, numerical evidence suggests that the initial phase of the excitation is not significant regarding the size of the SB; however, the SB’s location is strongly related to it (cf. Figs. 7 and  6). Therefore, the analytic model described in Sect. 4 dismisses any dependence on the excitation’s initial phase \(\beta \).

This study also gives a semi-analytic formula for calculating the SB area depending on the system parameters. Indeed, using Fig. 9, the size of the SB can be easily obtained.

These findings offer a valuable starting point for designing physical systems similar to those examined in this study. The results could have potential applications in existing technical systems. For instance, they could reduce the impact of oscillations in clearances under noisy excitation, where an extended SB is desirable. Pursuing \(P<P_\text {crit}\) is recommended in such cases. Similarly, the findings can be applied to prevent the failure of brittle materials under harmonic load, where the ICs should not significantly affect the system’s integrity. Furthermore, several other applications may require avoiding a specific range of operations. If a linear, one-degree-of-freedom model can describe the system, this study could be a starting point for designing the system’s safe operation.

The reader might formulate several questions about how damping affects the SBs. Such questions might be whether the SBs can be estimated accurately using analytic techniques in the case of other potentials. For small, polynomial-type nonlinearities of the system, obtaining an analytic expression for the boundaries of “fast” and “slow” level-crossing might still be viable. The Poincaré–Linstedt method might be adequate for the “fast” one, while using the averaging method, a differential equation for the slowly changing amplitude could be obtained. With nonlinearities like Coulomb friction or a constant restoring force, the system retains a (piecewise) integrability. This makes it possible to derive an exact analytic solution, providing a means to explore the two level-crossing mechanisms discussed in this paper.

Although intuitively, it seems correct, can we prove that damping always stabilizes escape and level-crossing? And what about nonlinear damping?

The shape of the SBs and escape (or level-crossing) probabilities in noisy dynamics are undoubtedly important in practical applications. Depending on the type of noise (e.g., Gaussian white noise), escape might even have a nonzero probability for any choice of the IC. However, intuition suggests that proper SBs with zero escape probability might occur when the noise amplitude is bounded. These basins might have extensions where escape has a certain probability, transitioning to the region of sure escape.

The authors hope this article contributes toward a better understanding of the mechanisms of escape (or level-crossing) and serves in the safer construction of devices and applications.