Escape of a harmonically forced particle from an infinite-range potential well: a transient resonance

Abstract

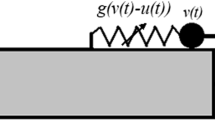
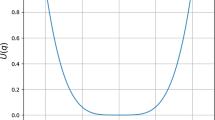
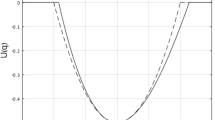
The paper considers a transient process of escape of a classical particle from a one-dimensional potential well. We address a particular model of the infinite-range potential well that allows independent adjustment of the well depth and of the frequency of small oscillations. The problem can be conveniently reformulated in terms of action-angle variables. Further averaging provides a nontrivial conservation law for the slow flow. Then, one can consider the problem in terms of averaged transient dynamics on primary 1:1 resonance manifold. This simplification allows efficient analytic exploration of the escape process. As a result, one obtains a theoretical prediction for minimal forcing amplitude required for the escape, as a function of the excitation frequency. This function exhibits a single sharp minimum for a certain intermediate frequency value, below the frequency of small free oscillations. This result conforms to earlier numeric and semi-analytic estimations for similar escape models, considered, in particular, in connection with problems of ship capsize and dynamic pull-in in microelectromechanical systems. The results presented in the paper allow conjecturing the generic dynamical mechanism, responsible for these regularities. In particular, the aforementioned sharp minimum in the frequency–amplitude domain is related to formation of heteroclinic connection between the saddle points on the resonance manifold. Numeric simulations are in complete qualitative and reasonable quantitative agreement with the theoretical predictions.

Appendix

This appendix presents the derivation details for expressions (12) and (14). In accordance with definition (3), the action variable is expressed as follows:

$$\begin{aligned} I(E)= & {} \frac{1}{2\pi }\oint {p(q,E)\mathrm{d}q=} \frac{1}{2\pi }\oint \sqrt{2E+\frac{1}{{\cos }\mathrm{h} ^{2}q}}\mathrm{d}q\nonumber \\= & {} \frac{1}{2\pi }\oint {\sqrt{2E+1-{\tan }\mathrm{h} ^{2}q}\mathrm{d}q} \nonumber \\= & {} \left| {_{a=\sqrt{1+2E},{\tan }\mathrm{h} q=z} } \right| =\frac{2}{\pi }\int _0^a {\frac{\sqrt{a^{2}-z^{2}}}{1-z^{2}}} \mathrm{d}z\nonumber \\= & {} 1-\sqrt{1-a^{2}}=1-\sqrt{-2E} \end{aligned}$$

(A1)

The last integral is easily evaluated with standard methods of contour integration. Inversion of (A1) yields the expression for $H_0 (I)$ from (12). Expression for the coordinate is calculated as follows:

$$\begin{aligned} \theta= & {} \frac{\partial }{\partial I}\int _0^q {p(q,I)\mathrm{d}q} =\frac{\partial }{\partial I}\int _0^q {\sqrt{2E+\frac{1}{{\cos }\mathrm{h} ^{2}q}}\mathrm{d}q} \nonumber \\= & {} \frac{\partial }{\partial I}\int _0^q {\sqrt{\frac{1}{{\cos }\mathrm{h} ^{2}q}-(1-I)^{2}}\mathrm{d}q} \nonumber \\= & {} -(1-I)\int _0^q {\frac{\mathrm{d}q}{\sqrt{\frac{1}{{\cos }\mathrm{h} ^{2}q}-(1-I)^{2}}}}\nonumber \\= & {} -(1-I)\int _0^q {\frac{\mathrm{d}({\sin }\mathrm{h} q)}{\sqrt{2I-I^{2}-(1-I)^{2}{\sin }\mathrm{h} ^{2}q}}} \nonumber \\= & {} -\arcsin \left( {\frac{(1-I){\sin }\mathrm{h} q}{\sqrt{2I-I^{2}}}} \right) . \end{aligned}$$

(A2)

Then, we obtain the second expression of (12), with insignificant change of sign. By symmetry considerations, Expression (12) for $q(I,\theta )$ can be expanded in sine-Fourier series:

$$\begin{aligned} q(I,\theta )= & {} {\arcsin }\mathrm{h}\left( {\frac{\sqrt{2I-I^{2}}}{1-I}\sin \theta } \right) \nonumber \\= & {} \sum _{m=1}^\infty {a_m \sin m\theta } \end{aligned}$$

(A3)

From (8) it is obvious that it is necessary to compute only the coefficient $a_1$. One obtains:

$$\begin{aligned} a_1= & {} \frac{1}{\pi }\int _{-\pi }^\pi {\arcsin }\mathrm{h} (c\sin \theta )\sin \theta \mathrm{d}\theta \nonumber \\= & {} \left. {-\frac{1}{\pi }{\arcsin }\mathrm{h}(c\sin \theta )\cos \theta } \right| _{-\pi }^\pi \nonumber \\&+\frac{4c}{\pi }\int _0^{\pi /2} {\frac{\cos ^{2}\theta }{\sqrt{1+c^{2}\sin ^{2}\theta }}} \mathrm{d}\theta \nonumber \\= & {} \left| {_{\cos \theta =\xi ,k=\frac{c}{\sqrt{1+c^{2}}}} } \right| =\frac{4}{\pi }\int _0^1 {\frac{\xi ^{2}\mathrm{d}\xi }{\sqrt{1-\xi ^{2}}\sqrt{1/{k^{2}}-\xi ^{2}}}} \nonumber \\= & {} \frac{4}{\pi k}\left( {\mathbf{K}(k)-\mathbf{E}(k)} \right) \end{aligned}$$

(A4)

Here $c=\frac{\sqrt{2I-I^{2}}}{1-I}$, and, consequently, $k=\sqrt{2I-I^{2}}$, as stated above. Substituting (A3–A4) into (5) and (8), one obtains $q_1 =-\frac{ia_1 }{2}$ and then—expression (13). Further coefficients $a_m ,m>1$ also are combinations of rational functions and complete elliptic integrals, but become quite awkward even for small m.