Prediction and suppression of chaos following flutter in wind turbines

Abstract

Chaotic motion in a fluttering wind turbine blade is investigated by the development of an efficient analytical predictive model that is then used to suppress the phenomenon. Flutter is a dynamic instability of an elastic structure in a fluid, such as an airfoil section of a wind turbine blade. It is presently modelled using generalised two degree of freedom coupled modes of a blade airfoil section (pitch and plunge) combined with local unsteady aerodynamics, based on flutter derivatives and a continuous bilinear lift curve under damping. The mode coupling causes instability and limit cycle flutter due to a Hopf bifurcation. Following the critical flutter speed, the response can transition to chaos through successive other bifurcations like period doubling. New closed-form conservative analytical conditions for chaos following blade flutter are identified and discussed for the wind turbine section taking into account the blade geometry and optimal design of the wind turbine. These predictions are numerically verified for a range of conditions including stall slope and damping. The results confirm that chaos following blade flutter can occur due to nonlinearities in the aerodynamics, i.e. due to a bilinear lift law. This phenomenon is then suppressed to unrealistically high wind speeds and/or eliminated by quantified variation of system parameters using the predictive model. The results show that small changes in tip speed ratio (−15%), and stall slope factor (−17%) can eliminate or suppress chaos following flutter, while, in general, larger magnitude changes in dynamic parameters (i.e. mass, inertia > 81%, stiffness > 97%, damping > 100%) are required to achieve the same, by detuning the coupled plunge and pitch natural frequencies or damping out overlapping parametric resonances. These results also highlight that the analytical predictions can remarkably be generalized to any parameter set and provide almost instantaneous calculations representing many thousands of numerical simulations from many bifurcation diagrams (computational acceleration factor of 10⁷ times). General insight is also provided into the occurrence and suppression of airfoil chaos following flutter in aeroelastic structures like wind turbines.

1 Introduction

Flutter is a vibration instability of an elastic structure interacting with a fluid, such as an airfoil section of a wind turbine blade. Its onset is characterized by a lower critical rotor or wind speed, while its amplitude is determined by the aerodynamic and/or structural nonlinearities. Since its identification in World War One aircraft, flutter remains an important design issue for aircraft and wind engineering industries such as to avoid wind turbine blade fatigue failure. Although not of great design importance in the past, flutter in wind turbines is more likely to occur as their size continues to increase with desired power output. This is because the local wind velocity on rotating blade airfoil sections is more likely to exceed critical limits, as blade lengths increase. Hence, presently, flutter is an important problem to solve as the world’s use of wind energy exponentially grows to avoid excessive impacts of climate change.

The investigation of flutter in many structures continues to grow since Theodorsen developed general theory for modelling and experiments of the instability in an airfoil, under unsteady subsonic conditions [1, 2]. Classical flutter (without structural damping in [3]), was shown to occur via an unstable aerodynamic coupling of the airfoil pitching and plunging dynamics [1, 2], such as for a wind turbine blade section. An immense body of other flutter research has been performed since then as comprehensively reviewed in [4], but here there is a necessary focus on reviewing wind turbine and nonlinear flutter behavior.

Generic analysis of airfoil flutter cannot be applied directly (without adaption) to wind turbines due to the added complexities of rotational effects, varying blade geometry and real optimal wind turbine design constraints. There has been much concentrated research on flutter in wind turbines in recent years as blades are becoming longer and slenderer. For instance, the effect of compressibility on wind turbine flutter was determined in [52] using the full blade geometry. Their numerical analysis showed that compressibility decreased the classical flutter speed by around 5%. An investigation of flutter performance of bend–twist coupled large-scale wind turbine blades was performed due to nonuniform material laminates and showed that they may also decrease the flutter speed by 5%, although this was still well above the local tip wind speed [54]. More recent analysis on this has been performed in [57]. A detailed investigation of the effects of experimental error on the aerodynamic properties of wind turbine blades also showed they may result in approximately ± 5% variation in the classical flutter speed due to mainly variations in the lift slope [56], which in turn are much larger around stall. A detailed finite element (FE) model for a large wind turbine system has been developed with elastic coupling between blade, tower and drivetrain oscillations, which found the critical rotor flutter speed was 60% higher than the nominal rotational speed. An internal torsional viscous blade damper was simulated and shown to increase this speed to 3.6 × the nominal [43], which exceeds the previous optimal performance in [58]. Recently, modelling and blade structural force measurements were used to forecast the critical flutter speed of a large wind turbine blade [59]. Due to the complexity of the blade geometry and associated models, this previous research has been necessarily restricted to numerical results, only pertaining to specific cases, i.e. flutter results, and parameter investigations pertaining to optimal wind turbine blade design (rather than specified blade geometries) appears to be lacking.

Research on the nonlinear dynamics of flutter has understandably focused on the generic wing airfoil initially. The onset of flutter requires an instability, but the amplitudes of flutter limit cycle oscillations are bounded by aerodynamic and/or structural nonlinearities. These include boundary layer separation and transitions, stall flutter and shock wave aerodynamics requiring computational fluid dynamics (CFD) [4, 7, 8] and integrated finite element analysis (FEA) depending on structure/shape complexity [9, 10]. Flutter instability types and limit cycles of a wing with quadratic and cubic pitching structural nonlinearities were predicted using unsteady aerodynamics in [11]. Similarly, structural geometric nonlinear coupling in a cantilevered wing caused limit cycle oscillations to grow after flutter onset [12]. A small amount of this research has been focused on wind turbines, i.e. the nonlinear dynamic response of a wind turbine blade revealed sustained limit cycle flutter below the classical flutter speed for large disturbances [55]. Much more recently, large deflection effects of geometrical nonlinearities on a rotating wind turbine blade has been investigated in [53] and showed nonlinear coupling between the torsion and bending deformations, and a decrease in the flutter frequency of up to 20%.

Nonlinearity can also lead to chaos and was first numerically found in an airfoil with cubic pitching stiffness [15] and then coupled cubic stiffnesses [16] under incompressible flow. This chaos following flutter (termed throughout this paper) is characterized by a transition to chaos following the instability of a Hopf bifurcation to self-sustained flutter limit cycle oscillations. Chaos following flutter has also been identified in a piezo-aeroelastic airfoil energy harvester supported by nonlinear springs [60] as well as nonlinear motion coupling, inertial and aerodynamic nonlinearity [62] and in panel flutter under thermal loads, supersonic flow [18] and experimental turbulent flow [19]. Nonlinear flutter of variable stiffness composite plates in supersonic flow has also shown limit cycle oscillations, quasi-periodic or chaotic solutions depending on fibre path orientation [61]. Chaos following stall flutter has been shown to occur under aerodynamic, structural and kinematic nonlinearities [20, 21]. Similarly, fin vibration chaos has been shown to occur under aerodynamic, thermal and structural nonlinearities in hypersonic flow [22]. Recent numerical simulation research on the transitions to chaos in general aeroelastic systems include [62,63,64]. This includes numerical work on freeplay in the pitch degree of freedom [65] and a flapping aerofoil [66]. Also, recently, chaos following flutter was identified in an airfoil without the need for structural or thermal nonlinearity [42]. This was identified based on interesting analogies between bilinear lift aerodynamics and friction under mode coupled structural dynamics causing chaos in railway wheel squeal and brake squeal [23,24,25,26, 33]. No research could be found on chaos following flutter or its control in wind turbines.

Although much has been contributed in the area of nonlinear phenomena in aeroelastic systems and flutter in wind turbines, there are some gaps in the literature. In particular, although classical coupled mode flutter has been identified in wind turbines, there is a gap in the literature on the investigation of chaos following blade flutter and its control. The previous research has also ultimately relied upon numerical simulation to predict chaos in general aeroelastic systems, which is necessarily restricted to parameter conditions and is computational expensive compared to closed-form solutions. In particular, the closed-form analytical prediction of chaos following flutter in a wind turbine has not been investigated previously. Also, the effect of constraining nonlinear dynamic investigations to real optimal wind turbine design conditions has not been performed. The present research aims to contribute to these gaps by identifying and controlling chaos following flutter in optimally designed wind turbines by developing closed-form analytical criteria for flutter onset and chaos and using them for suppression. In achieving this, the major contributions include:

• 1. Development and verification of analytical closed-form predictions of chaos following flutter, in optimally designed wind turbines, under general unsteady aerodynamic conditions and an approximate bilinear lift law, providing computational acceleration in the order of 10⁷ times compared to nonlinear numerical simulation.

• 2. Identification of, and insight into, the conditions under which classical flutter and chaos following flutter occur in optimal wind turbine blades, such as size, blade tip speed, structural damping and blade section stall behaviour.

• 3. Identification and efficient quantification of a range of parametric methods to eliminate or suppress chaos following flutter.

The optimal design of a wind turbine blade is first described to maximise energy generation. Then, a binary mode mathematical model for wind turbine blade flutter is detailed, including approximate bilinear lift aerodynamics. Closed-form solutions for flutter onset are described and corresponding new conservative analytical criteria for the occurrence of chaos following flutter are then derived. These predictions are then verified using full numerical simulations of the equations of motion for an optimally designed wind turbine and nonlinear dynamics analysis tools. The verified criteria are then used to efficiently investigate a range of typical wind turbine parameters under which chaos following flutter can be eliminated or suppressed.

2 Methodology

An optimally designed wind turbine blade flutter model is first described in Sect. 2.1, representing two degrees of freedom and generalized unsteady aerodynamics. The modelling is first based on the optimal design of a wind turbine to maximise energy efficiency. The binary airfoil model, for each local blade section, includes generalized flutter derivatives and an optimal offset angle of attack. The method for determining the onset and growth of flutter is then detailed in Sect. 2.2. In Sect. 2.3, analytical conservative criteria for predicting the onset of chaos following blade flutter are provided based on nonlinear dynamics theory.

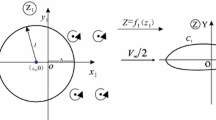
Figure 1 describes a conceptual nonlinear model for wind turbine blade flutter, due to an unstable interaction between the aerodynamics and coupled pitching and plunging dynamics for a blade section.

Fig. 1

a Wind turbine blade airfoil section and b conceptual model of flutter vibrations based on [42, 44]

The wind turbine blades are designed from airfoil sections that change in size and twist along the blade length for optimal aerodynamic performance [44]. The lift forces and pitching moments on each blade section are from aerodynamics simplified to flutter derivative components, H_1-4 and A_1-4, and also determined by the local wind velocity, W, at an optimal offset angle of attack, α_o. The dynamic response of the coupled pitching and plunging dynamics of each blade section is determined by the effective system modal damping and natural frequency, c_effi and ω_i. If unstable, a flutter limit cycle grows, which may break up into chaos depending on nonlinearities and local phase space expansion. The following methodology has been summarised to contain only the necessary theory to repeat the results while being self-contained.

2.1 Optimal wind turbine flutter modelling

It is important to summarise the optimal wind turbine parameter theory as this enables airfoil sectional theory to be incorporated as part of solving the aerodynamic complexities of the wind turbine blade rotation and varying geometry and hence forms one of the main contributions of the analysis and results. The geometry of a wind turbine blade depicted in Fig. 1a) needs to be optimally designed to maximise the power that can be harnessed from the wind. This is determined by how much the free stream wind speed slows as it passes through the blades and is detailed in many publications such as [44]. In particular, Lanchester—Betz used mass flow and momentum theory over a control volume of air, passing through the blades, to show that maximum efficiency is achieved when the velocity at the blades is two thirds of the freestream entry velocity infinitely far away, ${U}_{\infty }$. A variable speed turbine can maintain a constant tip speed ratio λ (between the blade tip rotation speed and the free stream wind velocity) required to achieve this maximum power output regardless of wind speed. This means the local wind speed W along the blade varies, due to its rotation under these optimal conditions, according to,

$$ W/U_{\infty } = \left[ {\left( \frac{2}{3} \right)^{2} + \lambda_{r}^{2} \left( {1 + \frac{2}{{9\lambda_{r}^{2} }}} \right)^{2} } \right]^{\frac{1}{2}} , \lambda_{r} = \lambda r/R $$

(1)

where $U_{\infty }$ is the freestream wind velocity entering the wind turbine infinitely far away, $\lambda_{r}$ is the local speed ratio between the blade rotation and the local wind speed at a radius, r and R is the blade length. To achieve optimal conditions, the blade geometry must also vary along its radius so that the torque generated at each blade section is maximised according to the blade geometry parameter [44],

$$ \left\langle {{\upsigma }_{r} \lambda_{r} {\text{C}}_{l} } \right\rangle = \frac{8}{9}\left[ {\left( \frac{2}{3} \right)^{2} + \lambda_{r}^{2} \left( {1 + \frac{2}{{9\lambda_{r}^{2} }}} \right)^{2} } \right]^{{ - \frac{1}{2}}} $$

(2)

where ${\upsigma }_{r}$ is the chord solidity defined as the total blade chord length, ${\text{n}}_{B} B$, divided by the circumferential length at a given radius, r, as,

$$ {\upsigma }_{r} = \left( {{\text{n}}_{B} B} \right)/2\pi r $$

(3)

and ${\text{C}}_{l}$ is the optimum lift coefficient to minimize drag. To achieve this the blade must be twisted by angle ${\upbeta }$ along its length, r, so each section has the same optimal (or offset) angle of attack, $\alpha_{o}$, according to,

$$ \beta = \phi - \alpha _{0} = {\text {a}}\tan \left[ {{{\frac{2}{{3\lambda _{r} }}} \mathord{\left/ {\vphantom {{\frac{2}{{3\lambda _{r} }}} {\left( {1 + \frac{2}{{9\lambda _{r}^{2} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + \frac{2}{{9\lambda _{r}^{2} }}} \right)}}} \right] $$

(4)

where, $\upphi$, is the local blade section inflow angle. By solving Eqs. (2) and (3), the optimal blade geometry parameter dictates how the blade section size varies along the length according to,

$$ {\text{B}}/{\text{R}} = 2\pi \left\langle {{\upsigma }_{r} \lambda_{r} {\text{C}}_{l} } \right\rangle /\left( {{\text{n}}_{B} \lambda {\text{C}}_{l} } \right) $$

(5)

Hence Eqs. (2), (4) and (5) analytically define the optimal geometry of a wind turbine blade determined by the optimal airfoil lift, ${\mathrm{C}}_{l}$, ${\mathrm{\alpha }}_{o}$, number of blades, ${\mathrm{n}}_{B}$ and tip speed ratio, $\uplambda$. The geometry and material properties of the blade determine its bending and torsional natural frequencies and modes shapes, which are required to model binary mode flutter of each blade section. For a tapered, twisted, NACA airfoil blade the fundamental (flap) bending natural frequency, ${\upomega }_{b1}$, may be approximated analytically as [45],

$$ {\upomega }_{b1} = \lambda_{b1}^{2} \sqrt {{\text{E I}}_{xc} /\left( {{\uprho }_{b} {\text{A}}} \right)} /R^{2} ,\;\lambda_{b1} = \lambda_{b1ta} {\text{f}}_{b1tw} ,$$

(6)

where E, ${\uprho }_{b}$, ${\text{I}}_{xc}$ and ${\text{A}}$ are the (axial) Young’s modulus and density, the second moment of area about the centroid and area of the airfoil cross section of the blade. The effect of a truncated taper on the blade, $\lambda_{b1ta}$, and formulae for ${\text{I}}_{xc}$ and $A$ for a NACA airfoil 4-digit profile are also conveniently available in [45]. The effect of blade twist on the fundamental bending frequency, ${\text{f}}_{b1tw}$, has been shown to be very small [67, 68] such that it is assumed to be ~ 1 for the present analysis. This is most likely because the effects of shear deformation and rotary inertia are small for relatively small twist (typical for wind turbine blades) for the first mode shape. The fundamental bending mode shape of the blade, $\phi_{b1}$, has also been assumed to be approximately that of a truncated cantilever plate,

$$ \phi_{b1} = \left( {{\text{r}}/{\text{R}}} \right)^{2} $$

(7)

Similarly, the fundamental torsional natural frequency of the blade, ${\upomega }_{t1}$, can be approximated as [45],

$$ {\upomega }_{t1} = \lambda_{t1} \sqrt {{\text{G C}}/\left( {{\uprho }_{b} I_{pc} } \right)} /{\text{R,}}\;\lambda_{t1} = \lambda_{t1ta} {\text{f}}_{t1tw} $$

(8)

where G, ${\text{I}}_{pc}$ and $C$ are the (axial) shear modulus, the polar moment of area about the centroid and torsion constant of the airfoil cross section of the blade. The effect of a truncated taper on the blade $\lambda_{t1ta}$ and formulae for ${\text{I}}_{pc}$, and ${\text{C}}$ for an airfoil are also conveniently available analytically in [45]. The effect of blade twist on the fundamental torsional frequency ${\text{f}}_{t1tw}$ can be significant. The fundamental torsion mode shape of the blade, $\phi_{t1}$, has also been assumed to be approximately that of a uniform rod,

$$ \phi_{t1} = {\text{sin}}({\pi r}/\left( {2{\text{R}}} \right) $$

(9)

The modal characteristics of the blade described by (6)-(9) may also be simply modified with a mode factor, to approximate higher modes than the fundamental [45], however, the effect of taper and twist are more difficult to predict. Also, it is important to highlight that they are approximate due to the real complex geometry, internal support structure and typically composite material behaviour of the turbine blade and can alternatively be more accurately determined using experimental measurements and/or complex finite element analysis. However, in the spirit of determining approximate blade flutter characteristics without complex numerical analysis, they are provided here in analytical form.

Blade element theory (i.e. assuming the flow may be described in 2D airfoil sections) may now be used to determine the aerodynamics and coupled modal dynamics of the wind turbine blade in Fig. 1b. In particular, Fig. 2, describes the pitching (with angle of attack), α, and plunging, h, of a wind turbine blade section with total chord length, B = 2b. These are caused by a moment, M and lift, L,(defined according to [27]) due to local aerodynamic flow speed, W (that includes a blade rotational velocity component). The wind turbine blade section has effective structural vertical and torsional stiffnesses, k_h and k_α, determined by the natural frequencies and sectional mass, m. The pitching and plunging occurs about the elastic support centre O at distance, ba, from the midchord and is coupled by, S_x, which is dependent upon the displacement, S_x/m, of the centre of gravity from CG to O. Mass balancing or no coupling occurs when S_x = 0.

Fig. 2

Binary (two degree of freedom) coupled wind turbine blade section under local aerodynamic flow

The equations of motion of the wind turbine blade section described in Fig. 2, may be determined as [4, 5],

$$ m\mathop {\ddot {h}}\limits \left( t \right) + c_{h} \dot{h}\left( t \right) + S_{x} \ddot{\alpha }\left( t \right) + k_{h} h\left( t \right) = L,\;J_{\alpha } \ddot{\alpha }\left( t \right) + c_{\alpha } \dot{\alpha }\left( t \right) + S_{x} \mathop {\ddot {h}}\limits \left( t \right) + k_{\alpha } \left( {\alpha \left( t \right) - \alpha_{o} } \right) = M $$

(10)

where, J, m, k, c, are the mass moment of inertia, mass, stiffnesses and damping constants with reference to the elastic centre, O, and the subscripts, h and α refer to the degrees of freedom. In this case, we can approximate them analytically using the results of the optimal blade geometry analysis of Eqs. (1) to (9), applied to each section of the blade, as,

$$ m = \rho _{b} A,c_{h} = 2\zeta _{b} \omega _{{b1}} m,k_{h} = \omega _{{b1}}^{2} m,\;J = \rho _{b} I_{{pc}} ,c_{\alpha } = 2\zeta _{t} \omega _{{t1}} J_{\alpha } ,k_{\alpha } = \omega _{{t1}}^{2} J_{\alpha } $$

(11)

where $\zeta _{b}$ and $\zeta _{t}$ are the damping ratios with respect to the bending (plunging) and torsional (pitching) degrees of freedom. Alternatively, experimental measurements [2] and/or finite element and modal analysis can be used. The aerodynamics acting at the centre of pressure, CP, are shifted and expressed as a modal plunging force and pitching moment at O, determined by the blade section shape flutter derivatives [27] and mode shape at the position of the blade section r/R, as,

$$ L = \frac{1}{2}\rho W^{2} B\phi _{{b1}}^{2} {\text{ }}\left( {KH_{1}^{*} \frac{{\dot{h}}}{W} + KH_{2}^{*} \frac{{B\mathop \alpha \limits^{{}} }}{W} + K^{2} \left( {H_{3\alpha}^{*} (\alpha ) - H_{3\alpha}^{*} \left( {\alpha _{o} } \right)} \right) + K^{2} H_{4}^{*} \frac{h}{B}} \right) $$

$$ \begin{gathered} M = \frac{1}{2}\rho W^{2} B^{2} \phi _{{t1}} ^{2} \hfill \\ \left( {KA_{1}^{*} \frac{{\dot{h}}}{W} + KA_{2}^{*} \frac{{B\dot{\alpha }}}{W} + K^{2} A_{3}^{*} \left( {\alpha - \alpha _{o} } \right) + K^{2} A_{4}^{*} \frac{h}{B}} \right) \hfill \\ \end{gathered} $$

(12)

where $\rho$ is the air density and K = Bω/W is a reduced frequency, varying with, ω, the frequency of vibration. Appendix A [1, 27] details the flutter derivatives, $H_{1 - 4}^{*}$ and $A_{1 - 4}^{*}$, for a thin airfoil (flat plate flow). Note they are general in that they can be obtained numerically or experimentally, e.g. [28, 29] for any section shape. The optimal (or offset) angle of attack ${\mathrm{\alpha }}_{o}$ is defined by the optimal wind turbine design in (4) and is where the steady structural and aerodynamic forces are in equilibrium. The lift coefficient function, ${H}_{3\mathrm{\alpha }}^{*}(\mathrm{\alpha })$, dominates the flutter limit cycle and can be conveniently defined as a continuous approximate bilinear function as [42],

$$ H_{{3\alpha }}^{*} (\alpha ) = H_{3}^{*} \left( {\alpha ( - k_{{stall}} + (1 + k_{{stall}} - \alpha _{c} \left( {1 + k_{{stall}} } \right)/\left| \alpha \right|)(1 - \tanh (\beta (\left| \alpha \right| - \alpha _{c} )))/~2) + sgn(\alpha )\alpha _{c} \left( {1 + k_{{stall}} } \right)} \right) $$

(13)

In Eq. (13), ${k}_{stall}$ is the absolute stall slope factor, i.e. the lift coefficient used in ${H}_{3\mathrm{\alpha }}^{*}(\mathrm{\alpha }$) becomes negatively sloped to -${k}_{stall}{H}_{3}^{*}$ if the critical angle of attack at stall, ${\alpha }_{c}$, is exceeded. Also, a smoothing factor, $\beta$, can be tuned between the pre- and post-stall conditions. A plot of the continuous bilinear lift coefficient curve of (13) for an airfoil, based on measurements in [30] and Appendix A, is provided subsequently in Fig. 3. In summary, the details of the aerodynamic load calculation are provided by Eqs. (12), (13) and (A.1–3). The structural elements and lift and moment components are all linear except for the approximate bilinear lift function (13), therefore, there is no coupling of nonlinear effects.

Fig. 3

The approximate bilinear lift (nonlinear) coefficient curve for NACA 4412 section of a wind turbine blade; simulated using Eq. (13) (-) with smoothing factor β = 9, k_stall = 0.81 and offset of 1 and experimentally measured in wind tunnel for Re = 1.2 × 10⁶(_{Blue shade sqaure}) and Re = 2.3 × 10⁶ (_{Red round}) [30]. The exact bilinear curve is also shown for comparison (- -)

The full nonlinear equations of motion for a wind turbine blade section (10)-(13) can be solved by numerical integration to verify flutter onset and chaos predictions as shown in Sect. 3. Prior to this, they can be solved analytically under appropriate approximations to predict flutter onset, efficiently, as follows.

2.2 Predicting flutter onset in a wind turbine

A summary of the closed-form analytical predictions for flutter is provided as these also form part of the new closed-form criteria for predicting chaos following flutter in a wind turbine, provided in 2.3. Typically the critical flutter speed at which the onset of flutter (local instability) occurs needs to be determined numerically using complex eigenvalue analysis (or other stability methods) on the coupled equations of motion (10)-(13), i.e. [1, 2]. However, recently in [42] an approximate analytical solution with damping was provided, assuming small non-proportional damping [23, 42]. The main results are summarised here with the inclusion of the effect of blade mode shapes for convenience. First, the equations of motion (10)-(13) in mass decoupled form are,

$$ {\mathbf{M}}{\ddot{{\bf X}}} + {\mathbf{C}}{\dot{{\bf X}}} + {\mathbf{KX}} = 0,\quad \quad \mathbf{X} = \left[ {x_{{h~}} \begin{array}{*{20}c} { = h} & {x_{{_{\alpha } }} = {\alpha } ~S_{x} /m} \\ \end{array} } \right]^{T} $$

(14)

where ${x}_{\alpha }$ is the displacement at CG due to the angle of attack, $\alpha$, as part of the degrees of freedom vector, X. The mass, damping and stiffness matrices M, C and K of the equations of motion may be determined as,

$$ {\mathbf{M}} = \left[ {\begin{array}{*{20}c} {m_{h} } & 0 \\ 0 & {m_{\alpha } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {m + m_{ae} - S_{x}^{2} /J_{\alpha } } \hfill & 0 \hfill \\ 0 \hfill & {(J_{\alpha } + J_{ae} )\left( {m/S_{x} } \right)^{2} - m} \hfill \\ \end{array} } \right] $$

$$ \begin{gathered} {\mathbf{C}} = \left[ {\begin{array}{*{20}c} {c_{{11}} } & {c_{{12}} } \\ {c_{{21}} } & {c_{{22}} } \\ \end{array} } \right] = \hfill \\ \left[ {\begin{array}{*{20}l} {c_{h} - \frac{1}{2}\rho WKB\left( {\phi _{{b1}} ^{2} H_{1}^{*} - \phi _{{t1}} ^{2} A_{1}^{*} BS_{x} /J_{\alpha } } \right)} \hfill \\ { - c_{h} + \frac{1}{2}\rho WKB\left( {\phi _{{b1}} ^{2} H_{1}^{*} - \phi _{{t1}} ^{2} A_{1}^{*} Bm/S_{x} } \right)} \hfill \\ \end{array} } \right. \hfill \\ \left. {\begin{array}{*{20}l} { - c_{\alpha } m/J_{\alpha } - \frac{1}{2}\rho WKB^{2} \left( {\phi _{{b1}} ^{2} H_{2}^{*} - \phi _{{t1}} ^{2} A_{2}^{*} BS_{x} /J_{\alpha } } \right)m/S_{x} } \hfill \\ {c_{\alpha } \left( {m/S_{x} } \right)^{2} + \frac{1}{2}\rho WKB^{2} \left( {\phi _{{b1}} ^{2} H_{2}^{*} - \phi _{{t1}} ^{2} A_{2}^{*} Bm/S_{x} } \right)m/S_{x} } \hfill \\ \end{array} } \right] \hfill \\ \end{gathered} $$

$$ \begin{gathered} {\mathbf{K}} = \left[ {\begin{array}{*{20}c} {k_{{11}} } & {k_{{12}} } \\ {k_{{21}} } & {k_{{22}} } \\ \end{array} } \right] = \hfill \\ \left[ {\begin{array}{*{20}l} {k_{h} - \frac{1}{2}\rho W^{2} K^{2} \left( {\phi _{{b1}} ^{2} H_{4}^{*} - \phi _{{t1}} ^{2} A_{4}^{*} BS_{x} /J_{\alpha } } \right)} \hfill & { - k_{\alpha } m/J_{\alpha } - \frac{1}{2}\rho W^{2} K^{2} B\left( {\phi _{{b1}} ^{2} H_{3}^{*} - \phi _{{t1}} ^{2} A_{3}^{*} BS_{x} /J_{\alpha } } \right)m/S_{x} } \hfill \\ { - k_{h} + \frac{1}{2}\rho W^{2} K^{2} \left( {\phi _{{b1}} ^{2} H_{4}^{*} - \phi _{{t1}} ^{2} A_{4}^{*} Bm/S_{x} } \right)} \hfill & {k_{\alpha } \left( {m/S_{x} } \right)^{2} + \frac{1}{2}\rho W^{2} K^{2} B\left( {\phi _{{b1}} ^{2} H_{3}^{*} - \phi _{{t1}} ^{2} A_{3}^{*} Bm/S_{x} } \right)m/S_{x} } \hfill \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(15)

here, ${m}_{h}$ and ${m}_{\alpha }$ are decoupled masses at the centre of mass and can include aerodynamic inertia and mass terms, ${J}_{ae}$ and ${m}_{ae}$. Note the blade section position affects the local wind velocity W, the chord B and the modal aerodynamic force and moment through the mode shapes, ${\upphi }_{b1}$ and ${\upphi }_{t1}$. The fluid structure coupling effects may be identified directly in the components of the mass decoupled mass, damping and stiffness matrices M, C and K. Flutter onset may be inferred more easily due to the mass decoupling by inspection of the sign of the components in matrices, C and K in (15). In particular, the mode coupling flutter mechanism occurs when the aerodynamic lift overcomes the reaction force due to the coupled structural torsional stiffness causing k₁₂ to change sign compared to k₂₁. This mechanism driving binary flutter was identified as dynamic divergence in [42] but also requires the effective system modal damping to be negative as determined by fully decoupling the equations of motion (14) and (15) into modal form as,

$$ {\mathbf{p}}_{{\mathbf{L}}} ^{{\mathbf{T}}} {\mathbf{Mp}}{\ddot{{\bf Y}}} + {\mathbf{p}}_{{\mathbf{L}}} ^{{\mathbf{T}}} {\mathbf{Cp}}{\dot{{\bf Y}}} + {\mathbf{p}}_{{\mathbf{L}}} ^{{\mathbf{T}}} {\mathbf{KpY}} = 0,\quad \mathbf{Y} = {\mathbf{p}}^{{ - 1}} \left[ {\begin{array}{*{20}c} {x_{{h~}} } & {x_{{\alpha}} } \\ \end{array} } \right]^{T} $$

(16)

where x_h and x_α define the modal displacement vector, Y, based on the undamped eigenvectors p_L (left) and p (right),

$$ {\mathbf{p}}_{{\mathbf{L}}} = \left[ {\begin{array}{*{20}c} 1 & {p_{L2} } \\ {p_{L1} } & 1 \\ \end{array} } \right],where\;{\mathbf{p}}_{{\mathbf{L}}}^{{\mathbf{T}}} {\mathbf{K}} = \lambda^{2} {\mathbf{p}}_{{\mathbf{L}}}^{{\mathbf{T}}} {\mathbf{M}},\;{\mathbf{p}} = \left[ {\begin{array}{*{20}c} 1 & {p_{2} } \\ {p_{1} } & 1 \\ \end{array} } \right],where\;{\mathbf{Kp}} = \lambda^{2} {\mathbf{Mp}} $$

(17)

A closed-form solution for these eigenvectors has been obtained assuming non-proportional damping is small, as [23],

$$ p_{1} = \left[ {\omega _{h}^{2} - \omega _{\alpha }^{2} + \sqrt \Delta } \right]/\left[ { - 2k_{{12}} /m_{h} } \right],p_{2} = 1/\bar{p}_{1} ,\;p_{{L1}} = - m_{h} /\bar{p}_{1} m_{\alpha } ,\;p_{{L2}} = - m_{\alpha } /\bar{p}_{2} m_{h} $$

therefore $p_{L} p_{i} = 4\left( {k_{12} k_{21} /m_{j}^{2} } \right)/\left[ {\omega_{h}^{2} - \omega_{\alpha }^{2} - \sqrt {\Delta } } \right]^{2}$.

where

$$ \omega_{h}^{2} = k_{11} /m_{h} ,\; \omega_{\alpha }^{2} = k_{22} /m_{\alpha } ,\; {\Delta } = \left( {\omega_{h}^{2} - \omega_{\alpha }^{2} } \right)^{2} + 4k_{12} k_{21} /\left( {m_{h} m_{\alpha } } \right) $$

(18)

where ⁻ is the conjugate, i is the mode number and j = $\alpha$, h. The type of mode coupling is determined by the discriminant ∆, which is a measure of how close the uncoupled modes, ${\omega }_{h}, {\omega }_{\alpha },$ are. In particular, if it is positive then real eigenmodes occur associated with viscous mode coupling. Alternatively, if negative, complex eigenmodes occur associated with stiffness mode coupling see [23, 42] and Sect. 2.3. Equation (18) allows closed-form solutions for the effective system damping for each mode, ${c}_{effi}$, expressed as,

$$ m_{i} \ddot{y}_{i} \left( t \right) + c_{{effi}} \dot{y}_{i} \left( t \right) + k_{i} y_{i} \left( t \right) = 0, \,\,\,{\text {where}}\;c_{{effi}} \left( {H_{3}^{*} |_{{\alpha _{o} , > \alpha _{c} }}^{\alpha } } \right), $$

(19)

where ${c}_{effi}$ can be evaluated under pre-stall or post-stall conditions according to the bilinear flutter derivative ${H}_{3}^{*}$ at $\alpha ={\alpha }_{o}$ or at $\alpha >{\alpha }_{c}$. The modal parameters can be calculated in closed form,

$$ m_{i} = {\mathbf{p}}_{{\mathbf{L}}}^{{\mathbf{T}}} {\mathbf{Mp}}_{i,i} ,\;k_{i} = {\mathbf{p}}_{{\mathbf{L}}}^{{\mathbf{T}}} {\mathbf{Kp}}_{i,i} ,\;\;c_{i} = {\mathbf{p}}_{{\mathbf{L}}}^{{\mathbf{T}}} {\mathbf{Cp}}_{i,i} $$

(20)

Hence according to (19 and (20), the effective system damping is dependent on the complexity of the stability solution as,

$$ \begin{gathered} c_{{effi}} = \hfill \\ \left\{ {\begin{array}{*{20}c} {c_{i} {\text{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~if~~}}p_{i} ,p_{{Li}} = \text{Re} (p_{i} ),\text{Re} (p_{{Li}} )} \\ {\text{Re} \left( {c_{i} /\left( {2m_{i} } \right) \pm \sqrt {c_{i} ^{2} /(2m_{i} )^{2} - k_{i} /m_{i} } } \right)\;2m_{i} {\text{~~if~~}}p_{i} ,p_{{Li}} \ne \text{Re} (p_{i} ),\text{Re} (p_{{Li}} )} \\ \end{array} } \right\} \hfill \\ \end{gathered} $$

(21)

Equations (18)–(21) are closed-form solutions for localised flutter vibrations and its type (viscous or stiffness) for an airfoil section of a wind turbine blade. Note flutter will initially grow exponentially until the angle of attack oscillations encroach on the negative stall slope (stabilising effective positive stiffness) above ${\alpha }_{c}$. This periodic limit cycle amplitude can be approximated using an energy balance over one flutter oscillation, as described in [42]. Presently, it is noted that Eqs. (18)–(21) are closed-form analytical solutions to flutter onset and initial growth for a wind turbine blade section under unsteady aerodynamics.

In the following, a summary of the conditions for flutter onset are provided, which have been adapted from [42], which confirms a supercritical Hopf bifurcation to flutter, i.e. transition to a stable limit cycle from a stable equilibrium point. These results are then partly used as one of the necessary criteria for chaos following flutter as described subsequently in Sect. 2.3. Following the previous results in this section, the onset of flutter is governed by the effective system modal damping c_effi and stiffness matrix according to the necessary conditions [42]:

$$ {\text{flutter if}}\;c_{effi} < 0\;when\;k_{12} k_{21} \le 0 $$

(22)

where the second criterion of (22) represents dynamic divergence conditions more explicitly as,

$$ k_{{12}} k_{{21}} \le 0 \Rightarrow k_{\alpha } {\text{ }}\quad + \frac{1}{2}\rho W^{2} K^{2} B\left( {\phi _{{b1}}^{2} H_{3}^{*} J_{\alpha } /S_{x} - \phi _{{t1}}^{2} A_{3}^{*} B} \right){\text{ }}\quad \le 0~{\text{xor}}\;\;k_{h} {\text{ }}\quad - \frac{1}{2}\rho W^{2} K^{2} \left( {\phi _{{b1}}^{2} H_{4}^{*} - \phi _{{t1}}^{2} A_{4}^{*} Bm/S_{x} } \right)~ \le 0 $$

(23)

The first criterion of k₁₂ in (23) typically causes dynamic divergence for an airfoil because the aerodynamic component increases with the speed squared and ${H}_{3}^{*}$ is relatively, large and negative. Hence, aerodynamic energy input, via this mechanism, drives flutter (if it causes negative system damping, i.e. c_effi < 0). The complexity of the eigenvectors (real or complex) [23] determines the mode coupling type as described subsequently.

Viscous mode coupled flutter

When the discriminant is positive, ∆ > 0, (18) the eigenvector solutions are real and therefore the effective system modal damping reduces to c_effi = c_i (first line of (21)). This is known as viscous mode coupling and will cause flutter amplification (or decay) when the modal damping ratio, c_i, is less (or more) than the diagonal damping components, c_ii, which is dependent upon the dynamic divergence criterion, as

$$ \text{Viscous} \text{mode} \text{coupling} \text{amplification} \, \, c_{i} < c_{ii} \,\, {\text{when}} \,\, k_{12} k_{21} \le 0,\quad \Delta \ge 0, \text{Viscous} \text{mode} \text{coupling} \text{decay} \, \, c_{i} \ge c_{ii} \,\, {\text{when}} \,\, k_{12} k_{21} > 0,\quad \Delta \ge 0.$$

(24)

Hence (24), predicts viscous mode flutter amplification due to energy input via dynamic divergence conditions and sufficiently separated uncoupled modal frequencies, ${\omega }_{h}, {\omega }_{\alpha },$ such that Δ ≥ 0. Under viscous mode coupling, the phasing of the aerodynamic forces compared to velocity cause system power input due to dynamic divergence meaning increasing damping may surprisingly cause flutter under some conditions. In previous research [42], it was found that viscous mode coupling can occur at lower speeds than classical stiffness mode coupled flutter, described subsequently.

Stiffness mode coupled flutter

When the discriminant ∆ < 0 (18) under dynamic divergent conditions then stiffness mode coupling occurs causing complex undamped eigenmodes and complex stiffness, leading to negative system damping. This is the classical binary flutter mechanism [1, 4] that occurs due to mode coupling when the coupled modal frequencies become close, according to:

$$ {\text{Stiffness mode coupling amplification }} \,\,{\text{when}}\,\,\,k_{{12}} k_{{21}} \le 0, \quad \Delta \;{\text{ < }}\;0$$

(25)

Hence (25) predicts stiffness mode flutter amplification due to energy input via dynamic divergence conditions and close uncoupled modal frequencies, ${\omega }_{h}, {\omega }_{\alpha },$ such that Δ < 0. In this case, the system negative damping is determined primarily by the modal stiffness ${k}_{i}$ and will likely cause larger phase space expansion than viscous mode coupling, assuming the modes are not over critically damped. Also flutter growth tends to increase with speed as there is a W² effect. It is possible to solve for the critical speed for the onset of classical (stiffness mode coupled) flutter onset, ${W}_{f}$, assuming no damping and dominant angle of attack flutter derivatives as [42],

$$ W_{f}^{2} = \frac{{m_{\alpha } }}{{\frac{1}{2}\rho K^{2} B\left( { - \phi _{{b1}}^{2} H_{3}^{*} + \phi _{{t1}}^{2} A_{3}^{*} Bm/S_{x} } \right)m/S_{x} }}{\text{ }}\left[ {\left( {\sqrt {\frac{{k_{h} \left( {1 - \Delta p} \right)}}{{m_{h} }}} \mp \sqrt {\frac{{k_{\alpha } \left( {m/S_{x} } \right)^{2} }}{{m_{\alpha } }}} } \right)^{2} \mp 2\sqrt {\frac{{k_{h} k_{\alpha } \left( {m/S_{x} } \right)^{2} }}{{m_{h} m_{\alpha } }}} \left( {\sqrt {1 - \frac{{S_{x}^{2} }}{{mJ_{\alpha } }} - \Delta U} - \sqrt {1 - \Delta p} } \right)} \right]{\text{ }} $$

$$ \begin{gathered} {\text{where}}~\Delta p = \frac{{1 - S_{x} ^{2} /\left( {mJ_{\alpha } } \right)}}{{1 - \left( {\phi _{{b1}} ^{2} H_{3}^{*} /(\phi _{{t1}} ^{2} A_{3}^{*} } \right))\left( {S_{x} /Bm} \right)}},~~ \hfill \\ \Delta U = \frac{{\Delta p}}{2}\left[ {1 + \left( {1 - \frac{{\Delta p}}{2}} \right)\frac{{k_{h} m_{\alpha } }}{{k_{\alpha } \left( {m/S_{x} } \right)^{2} m_{h} }}} \right] \hfill \\ \end{gathered} $$

(26)

and $\Delta p$ and $\Delta U$ are normalised factors, i.e. 0 $\le \Delta p \le 1$ assuming the elastic centre and centre of pressure are aft of the centre of gravity and elastic centre, respectively. The closed-form solution (26) predicts that the classical critical flutter speed increases with increases in rotational inertia, spacing between uncoupled plunging (bending) and pitching (torsional) natural frequencies and decreases in air density. Added damping will tend to increase the critical flutter speed as well. Finally, it is noted that stiffness mode coupling instability realistically has a higher instability growth rate than viscous mode coupling, in accordance with the system damping predictions of (19) and (21), as the damping ratio is below unity for a wind turbine blade (and other vibrating structures [42]). This is important when considering criteria for chaos following flutter that requires high local phase space expansion as described subsequently.

2.3 Predicting chaos following flutter in a wind turbine

As shown in Sect. 2.2, flutter is a local instability that can reach a stable limit cycle, which is caused by the balance of energy between pre- and post-stall bilinear conditions, as detailed further in [42]. When this instability is combined with significant nonlinearities, it can lead to chaos following flutter, characterized by bounded motion that has local phase space expansion. This section is focussed on predicting the onset of chaos following flutter in wind turbines, which are based on a local phase space expansion and new sufficient nonlinearity criteria. Specifically, in [42] a well-known expansion test for chaos was used; the Lyapunov exponent, denoted by λ, as described in [35],

$$ {\text{Chaos possible if}}\;\lambda {\text{ > }}0.\quad where\;d = d_{{\text{o}}} 2^{{\lambda \left( {t - t_{o} } \right)}} $$

(27)

where d_o and d represent the initial and final spherical diameters at times, t_o, and t_. It is important to note that $\lambda$ only measures sensitivity to initial conditions so is measured locally using partial derivatives or using small time increments $t-{t}_{o}$ and averaged over a longer period. In [36], it was shown that the maximal Lyapunov exponent is an average of the real part of the maximum dynamic eigenvalue integrated over a sufficiently long period of time. Therefore, chaos is most likely to occur under stiffness mode coupled flutter conditions due to a larger maximum dynamic eigenvalue from the complex stiffness negative damping compared to damping under viscous mode coupling (assuming realistic damping values less than critical). This leads to the first necessary condition for wind turbine chaos following blade flutter as [35]:

$$ {\text{Chaos possible if}}\;W > W_{f} , \Delta \left( {W_{f} } \right) = 0 $$

(28)

where ${W}_{f}$ is the critical flutter speed obtained in closed form as (26) under no damping. Equation (28) is a conservative criterion as it has accounted for continuous averaging of the local trajectory expansion in phase space, and it is only necessary as it only measures sensitivity to initial conditions. In the flutter case, nonlinearity arises due to the bilinear lift curve. In particular, it was proposed and tested [42] that an offset in the angle of attack causes non-symmetry in the bilinear lift curve behavior and hence necessary nonlinearity, according to,

$$ \alpha_{o} \ne 0 $$

(29)

Again the necessary criterion (29) is rather conservative as it only provides a discrete measure of the nonlinear conditions. To address this, presently it is noted that this non-symmetrical bilinear lift curve behaviour (see Fig. 3) acts as a parametric bilinear stiffness excitation. It is well known that this causes subharmonic and higher harmonic excitation instabilities that grow into interacting limit cycles on the phase plane if damping is insufficient. In particular, the instability zones of the resonances may overlap if the excitation level is sufficiently high and this can result in bifurcations and chaotic behaviour of the system [47]. This behaviour is primarily determined by the magnitude of the change in stiffness and the damping. Therefore, less conservative conditions for chaos following flutter are additionally proposed presently, according to the criteria for all the parametric harmonic instability regions to exist, [49] as,

$$ \zeta _{{ti}} < \zeta _{{tic1}} = \zeta _{{crit}} 2~\sqrt {K_{f} /M_{f} } /\left( {1 + 1/\sqrt {k_{{stall}} } } \right) $$

(30)

where

$$ \log \left( {k_{{stall}} } \right) = 4\zeta _{{crit}} U^{{ - 1}} \left[ {{\text{atan}}\left( { - U/\left( {2\zeta _{{crit}} } \right)} \right) + \pi } \right] + 4\zeta _{{crit}} V^{{ - 1}} {\text{atan}}\left( { - V/\left( {2\zeta _{{crit}} } \right)} \right) $$

$$ U^{2} = \left( {1 + \sqrt {k_{{stall}} } } \right)^{2} - 4\zeta _{{crit}} ^{2} ,\;V^{2} = \left( {1 + 1/\sqrt {k_{{stall}} ~} } \right)^{2} - 4\zeta _{{crit}} ^{2} $$

$$ K_{f} = 1 - \left( {k_{{22}} \left( {S_{x} /m} \right)^{2} /k_{\alpha } } \right),\;M_{f} = m_{\alpha } \left( {S_{x} /m} \right)^{2} /(J_{\alpha} + J_{{ae}} ) $$

(31)

and $\zeta _{{tic1}}$ is the critical damping (with respect to the torsional degree of freedom) above which the first subharmonic instability region disappears and U and V are nondimensional intermediate parameters. The derivation of Eqs. (30) and (31) based on [49] involves modification from the critical damping ${\zeta }_{crit}$ using factors M_f and K_f of the mass moment of inertia and stiffness terms, to represent the mass decoupled flutter Eq. (13) and (14) for angle of attack (parametrically excited by the bilinear lift law) neglecting the cross-coupling terms with vertical displacement. The additional constraint that,

$$ 0 < \zeta _{{crit}} < \left( {1 + 1/\sqrt {k_{{stall}} ~} } \right)/ 2 $$

(32)

is always satisfied if $k_{stall}$ > 1. Finally, we can then propose the least conservative condition that there needs to be at least the first two instability regions for overlap and bifurcational chaos to occur. According to [48], the damping criteria is 1/3 smaller for the second instability region to exist so the least conservative criterion for chaos becomes,

$$ \zeta _{{ti}} < \zeta _{{tic1}} / 3 $$

(33)

Equations (28), (29) and ((30) or (33)), are conservative and necessary for wind turbine chaos following flutter from large local sensitivity to initial conditions and sufficient bounding nonlinearities causing overlap of parametric instability regions. If damping and non-angle of attack flutter derivatives are small, they can be evaluated in closed form using the critical flutter speed solution (26). Alternatively, the analytical solutions for ${c}_{effi}$ in (18)–(21) can be used. The criteria highlight that chaos following flutter is driven by local expansion due to: 1) High dynamic divergence caused by flutter instability from stiffness mode coupling following a Hopf bifurcation (28) and 2) nonlinear parametric excitation due to the bilinear lift aerodynamics causing interacting limit cycles if damping is insufficient according to (29), (30) or (33). It should be noted that the generality of the flutter model and analysis of (22) to (33) suggest that the criteria for chaos following flutter, in a wind turbine blade section, could also be applied to other structures. Subsequently, the chaos following flutter criteria ((28), (29) and ((30) or (33) of an optimised wind turbine blade are compared with full numerical solutions of the nonlinear equations of motion (1)–(13).

3 Results

Section 3 describes the utilization of the nonlinear numerical and analytical models to investigate the onset and chaotic behaviour of flutter in an optimised wind turbine blade. The numerical time domain solutions were obtained through the use of the fourth and fifth order Runge–Kutta routine in DYNAMICS by Nusse and Yorke and the Radua method in MathCad 15.0, with a minimum sampling rate of 20 times the nominal vibration frequency. The frequency of vibration was approximately adjusted to the simulated modal response frequency to minimize errors in the frequency-dependent aerodynamic loading. Appropriate dynamical system tools were used to characterize the chaotic state including phase space, Poincare Map and bifurcation diagrams and the Lyapunov spectrum of exponents [37] and pre-iterated at least 1000 flutter oscillation periods. Due to the continuous nature of the bilinear lift aerodynamics (13), there were no issues with exponent convergence for the parameters examined, in contrast to discontinuous systems [38]. The accuracy of the analytical predictions was verified through an optimal wind turbine case study, using full nonlinear numerical solutions and experimental measurements of the aerodynamics from the literature. For clarity, realistic system parameters were chosen in dimensional form, based on optimal conditions for a large 3 composite blade wind turbine, based on NACA4412 airfoil blade sections with optimal lift coefficient and offset angle of attack held constant at 3° and operating at a constant tip speed ratio of 6, as described in [44] and Table 1. The effect of varying these parameters is investigated in Sect. 3.4.

Table 1 Parameters used for wind turbine blade flutter simulations

Experimental measurements in a wind tunnel were used to first tune the approximate bilinear lift model (13) for the wind turbine blade section of a NACA 4412 nonsymmetric airfoil [30] as shown in Fig. 3. The critical angle of attack was first tuned to, α_c = 16° and then the stall slope to k_stall = 0.81 along with smoothing factor β = 9 between the bilinear slopes.

In Fig. 3, the approximate bilinear lift (nonlinear) coefficient curve displays a region of increasing lift coefficient of negative stiffness, prior to the critical angle of attack, followed by a declining slope of positive stiffness. The nonlinear estimate falls within a 5% range of the experimental measurements for the range of flow conditions (Reynolds numbers) [2, 30]. The small aerodynamic nonlinearities in the experimental measurement compared with the exact bilinear curve are also well represented by the simulated continuous curve of (13). The two Reynold’s numbers were selected as they are typical values representing the realistic wind turbine conditions investigated. At other Reynold’s numbers, the approximate bilinear lift curve may also be tuned using the parameters of (13). Note that the rising part of the lift coefficient curve, for low positive angles of attack, represents a negative stiffness contribution to the system stiffness (15) because increases in angle of attack are increasing the upwards aerodynamic lift, rather than retarding it like the structural torsional stiffness. Aerodynamic stall occurs for larger angles of attacks past a critical stall angle where upwards lift decreases. Hence, the opposite behaviour occurs (positive stiffness contribution) for angle of attacks greater than the stall angle of 16 degrees, causing an approximate bilinear nature. The wind turbine blade section aerodynamic properties of Fig. 3 can now be used with the other parameters of Table 1 to determine the optimum wind turbine blade design before investigating both classical flutter and chaos phenomena following flutter and potential methods of control.

3.1 Optimal wind turbine blade design

Based on the general parameters shown in Table 1, the optimal blade for a large variable speed wind turbine (to maintain a constant blade tip velocity ratio) can be designed according to Eqs. (1) - (9) In particular, the optimal local wind velocity, blade chord (width) and twist along its length to provide the maximum turbine output are plotted in Fig. 4.

Fig. 4

The optimal wind turbine blade geometry using a NACA 4412 airfoil; local angle of attack/lift coefficient = 3 deg/0.7, blade tip speed ratio = 6, number of blades = 3, blade length R = 86.4 m, aeroelastic axis position a = -0.4, centre of gravity position S_x/mb = 0.25, fundamental natural frequencies: pitching = 0.55 Hz, plunging 0.18 Hz, damping ratios = 1%

Figure 4 shows that the optimum blade geometry has a chord (or width), which tapers and twists towards its tip due to the local wind velocity increasing for larger radius due to the blade (and turbine) rotation. This ensures each section of the blade (past the root below 10% of its length) is operating at the ideal lift conditions at the same optimal angle of attack for the airfoil. Based on the blade geometry of Fig. 4 and the material properties in Table 1, the fundamental flapwise bending and torsional natural frequencies may be analytically approximated according to Eqs. (6) and (8) as 0.18 Hz and 0.55 Hz, respectively. For the bending fundamental frequency calculation, ${\uplambda }_{b1}$=2.5 based on the effect of the taper past 10% of the blade length and the tip section moment and cross-sectional areas were approximated to ${I}_{xc}=$ 0.075 m⁴ $\propto B$ ⁴, ${I}_{pc}=$ 26.4 m⁴ $\propto B$ ⁴ and $A$= 8 m² $\propto B$ ² based on a hollow NACA4412 airfoil [45] with additional internal structural support. Note, these tip properties can be extrapolated to any blade section radial position using the proportionalities ($\propto$) with chord size B stated. Similarly for the fundamental torsional frequency, the frequency constant was approximated as ${\uplambda }_{t1}$=1.1 π/2 based on the effects of the taper and twist and boundary conditions [45, 50, 51] and the tip torsional constant, approximated for an airfoil [45], to be $C=$ 0.3 m⁴ $\propto B$ ⁴. These blade geometric and dynamic parameters can now be used to determine the occurrence of flutter.

3.2 Flutter occurrence investigation.

Complex eigenvalue analysis of the equations of motion was performed for a range of wind velocities using the closed-form solutions (18)–(21) and numerical solution of the full system model matrices (15) based on the optimised system parameters and Table. 1. The real and imaginary parts versus local wind speed are shown in Fig. 5, for the case of the blade tip section.

Fig. 5

Local stability solutions of the optimised wind turbine blade, numerical (-),(_{Blue hypen}) and analytical (18)-(21), (_{Blue round}) (Black sqaure), as a function of local tip wind speed, W; a frequency Im(λ) and b negative damping Re(λ) in Hz. The thin black lines (-) show the numerical solution under undamped and angle of attack flutter derivatives only and the vertical marking (_{Ref double hypen}) shows the critical flutter speed (116.5 m/s) using (26) and [3] under the same conditions. Assumed constant nominal vibration frequency as wind speed changes

Figure 5a) shows the modal frequencies approach each other as local wind speed increases towards the critical flutter speed shown in Fig. 5 b) when the system damping is zero. Above this critical speed, stiffness mode coupled flutter occurs as Δ < 0 according to the criterion (25) and the modal frequencies come close (Fig. 5a) with approximately opposite damping levels (Fig. 5b) that are increased and offset by the structural and aerodynamic damping. The numerical flutter critical speed (that accounts for the effects of damping) occurs at 115.5 m/s when the real part of the eigenvalue first becomes greater than or equal to zero and is slightly less than the undamped analytical prediction of (26) and [3] at 116.5 m/s. This error is small for this case, as the effect of structural damping is counterbalanced by that of the other flutter derivatives. Figure 5 confirms that the closed-form analytical solution is an effective approximation to the complex eigenvalue analysis for the wind turbine blade flutter model of Fig. 2.

The critical flutter speed was investigated further by determining how it varies along the wind turbine blade (26) in Fig. 6 along with the local wind speed. In particular, Fig. 6 predicts flutter will occur when the local wind speed exceeds the critical flutter speed in the shaded region. This is shown to occur in the last 7.5% of the blade length at the tip end. The numerical result by direct integration of the equations of motion for the tip is also shown confirming the flutter predictions. Note the model flutter predictions for a fundamental airfoil section have already been experimentally verified in [42] using [2].

Fig. 6

Local Wind (_{Blue round shade}) and critical flutter speed (_{Red hypen}) along the blade length for a large wind turbine from analytical predictions and direct numerical integration of equations of motion (o). The shaded region predicts where flutter occurs

In Fig. 6, the trend of the critical flutter speed of the wind turbine blade, decreasing with blade radius position, may be directly predicted from the analytical expression of (26). In particular, the optimal blade chord decreases towards the tip as shown in Fig. 4, causing the decoupled rotational inertia ${m}_{\alpha }$ to decrease in a similar manner, while the natural frequencies and elastic centre position relative to the centre of gravity S_x/(mb), remain constant. Therefore Eq. (26) predicts the critical flutter speed reduces towards the blade tip, due to decreased rotational inertia of smaller airfoil sections to achieve optimal performance. In addition, the fundamental mode shapes cause higher aerodynamic excitation towards the tip antinodes and therefore also lower the critical flutter speed. Note the mode shapes will be different for higher modes (although they will still have antinodes at the tip) causing this effect to be more complicated if they are instead causing the mode coupled flutter. In any case, as shown in Fig. 6, it is predicted that the optimal design of the wind turbine blades, along with the higher local wind velocity due to rotation, will most likely cause flutter to first occur towards the wind turbine blade tip. These predictions, along with the occurrence of nonlinear behaviour, are investigated further, subsequently.

3.3 Investigation of the occurrence of chaos following flutter

The time history of the full nonlinear equations of motion showing the angle of attack oscillations of the blade tip section are shown in Fig. 7a) and b), using nominal conditions of Table 1 with a freestream wind speed of ${U}_{\infty }$=19.3 m/s (local tip wind speed 117.2 m/s) and those modified with a sharper stall slope. The corresponding lift curve oscillations were plotted below in Fig. 7c) and d). Note that this variation in stall slope is still consistent with measured experimental variations at high angles of attack near or in the stall region [56].

Fig. 7

Simulated time histories of flutter at wind speed 19.3 m/s (local tip wind speed 117.2 m/s) for blade tip section with: a nominal lift curve (Fig. 3) and for b sharper stall slope (smoothing factor β = 20, k_stall = 1.5)

Figure 7a) shows a periodic stable limit cycle at a speed, higher than the stable equilibrium point at the critical flutter speed, i.e. after a supercritical Hopf bifurcation transition [42]. Comparing Fig. 7a) and b), it is seen that the limit cycle oscillation amplitudes become irregular with the sharper stall slope of the lift curve in b), indicating non-periodic motion. Figure 7c) and d) supports the occurrence of this possible chaotic behavior under a steeper slope as consistent with the analytical predictions in Sect. 2. In addition, they show the irregular behavior range is restricted to a bilinear lift curve due to the angle of attack offset and wind speed. The effect of wind speed on the nonlinear behavior was investigated further using a bifurcation and phase space analysis, as shown in Fig. 8. Note the solutions were determined after initial transients had decayed and the Poincare plane of α = 0.0 was chosen for convenience.

Fig. 8

Bifurcation diagram a and phase spaces of flutter oscillations under increasing local wind speed; b W = 116.2 m/s c W = 116.4 m/s and d W = 116.5 m/s

Figure 8a) shows a bifurcation diagram with a well-recognised period doubling route to chaos as local tip wind speed increases passed the critical flutter speed and then decreases after a region of chaos between approximately 116.6 and 118.8 m/s, similar to what was found for a fundamental airfoil [42]. Figure 8b)-d) confirms this behaviour, depicting a two-loop limit cycle at 116.2 m/s in Fig. 8b), i.e. a closed set of 4 points in the bifurcation diagram due to crossing of the Poincare plane of α = 0.0 twice per loop. This bifurcates to more complex nonlinear behaviour as the local tip wind speed is increased. In particular, Fig. 8c) shows as the wind speed is increased to W = 116.4 m/s the limit cycle bifurcates into four-loop motion that bifurcates again as the local wind speed reaches W = 116.5 m/s (Fig. 8d). Further increases in wind speed results in increasingly compressed bifurcations to a strange attractor depicted in Fig. 9 at W = 117.2 m/s. The phase space of Fig. 9a) shows a wandering orbit that remains unclosed that is confirmed by the fractal arrangement of non-repeating points in the Poincare map of Fig. 9b).

Fig. 9

Phase space a and Poincare map b of wind turbine flutter oscillations for flow speed 117.2 m/s

In particular, the chaotic state is confirmed in Fig. 9b) as it shows a strange attractor fractal quantified by a non-integer Lyapunov dimension of 2.16 and a Lyapunov spectrum of [0.084 0.000 -0.392 -0.710]. Here, the first (maximum) Lyapunov exponent is greater than zero meaning; there is exponential sensitivity to initial conditions. The lowest local tip wind speed that chaos occurs in the time domain numerical simulations is W = 116.6 m/s (see Fig. 8a), which compares very closely to W_f = 116.5 m/s from (26) as part of the analytical criteria for chaos following flutter of (22) to (33). In agreement with the bilinear nonsymmetric criterion (29), bifurcation chaos were also found for offset angles of attack of 1°,4° and 6°. A deeper parametric investigation and comparison of the numerical and analytical predictions of the onset of chaos, was also performed for two wind turbine cases as shown in Fig. 10

Fig. 10

Critical torsional damping vs stall slope factor for chaos onset; conservative analytical criteria; no parametric excitation (_{Blue single hypen}) (30) less conservative analytical criteria; no overlapping harmonics (_{Blue double hyprn}) (33) and numerically simulated results for; nominal case (red round shade), thinner wall blade section case (_{Red round})

The numerical simulation results were obtained in a similar manner to Fig. 8 whereby the bifurcation diagram was used to identify the onset of bifurcation chaos several times for each stall slope factor to determine the critical onset values of chaos. The computational time for numerical simulations was approximately 4 h for 9 points compared to 50 ms for 400 points using the analytical predictions, giving a computational acceleration of approximately 10⁷ times. The nominal case of Table 1 was used as well as a significantly lighter blade case with wall thickness in the blade section reduced to 20% of the nominal value (i.e. m = 2.92 tonne/m_, J_α = 9.62 tonne m, k_h, = 3.71 kN/m², k_α = 114.9 kN, S_x = 2.30 tonne) to lower the local critical flutter speed (by 1/√5 according to modal mass reduction in (26)) to 52.1 m/s. Figure 10 shows a very good comparison between the (conservative) analytically predicted onset of chaos and the numerical bifurcation diagram simulations for both cases for critical torsional damping levels over a range of stall slope factors, k_stall. In particular, the critical torsional damping at chaos onset is predicted by the no overlapping harmonics criterion to within 1% damping error for both wind turbine blade cases (note mostly overlapping case results). The more conservative criterion of no parametric excitation has much larger errors for this case but shows a similar trend. This trend shows that chaos following flutter is more likely to occur for low damping and high stall slope conditions. In any case, the criteria based on stiffness mode coupling flutter provide a useful conservative analytical prediction of chaos following blade flutter onset as found in [42] but the added contribution based on overlapping parametric resonances contributes additional refinement to quantify the effects of damping and stall on the onset of chaos following flutter. Hence, the results confirm that chaos following flutter is characterized by conventional (stiffness mode coupled) flutter combined with parametric excitation nonlinearities associated with lower damping and sharper stall slope. These results also highlight that the analytical predictions can remarkably be generalized to any parameter set and provide almost instantaneous calculations representing many thousands of numerical simulations from many bifurcation diagrams almost instantaneously (computational acceleration factor of 10⁷ times). These verified predictive analytical criteria can subsequently be used to provide quantified insight into suppression of the chaotic instability in a wind turbine blade.

3.4 Chaos suppression

Methods to avoid or suppress the chaos following blade flutter onset, in a wind turbine, were investigated quantitatively in Table 2 with the nominal conditions of Table 1 modified to the chaos following flutter conditions of Fig. 7, i.e. sharper stall slope (smoothing factor β = 20, k_stall = 1.5). Specifically, the % change in nominal parameter value required to eliminate or suppress chaos following flutter to wind speeds above the very unlikely value of 30 m/s was calculated using the verified analytical criterion for no overlapping parametric resonances (33). Note, in this suppression investigation, the damping ratio is assumed to be constant (unless directly changed) irrespective of natural frequency changes. For Table 2, the dimensional parameters have been non-dimensionalised by their nominal values of Table 1.

Table 2 Parameter change required to suppress chaos following flutter of a wind turbine blade to excessive wind speeds, U_∞ > 30 m/s

Table 2 illuminates various ways of controlling wind turbine parameters to eliminate chaotic instability in blade flutter. Overall, the findings suggest that the occurrence of chaotic instability is influenced mainly by stiffness mode coupling or classical flutter, which in turn depends on the proximity of the uncoupled mode frequencies. However, the avoidance of overlapping parametric resonances is more important for control using damping and stall conditions. The following discussion of the Table 2 results, for elimination or suppression of chaos following blade flutter, are provided:

• The tip speed ratio has a strong effect on chaos following flutter via its effect on the onset of stiffness mode coupled flutter. In particular, lowering the tip speed ratio, directly lowers the local wind speed at the tip to below the onset of flutter. Lowering the tip speed ratio also increases the tip chord via optimal design which in turn increases the critical flutter speed.

• The blade length has no effect on the critical flutter speed under optimal design conditions. This is because increases in blade length causes increases in tip modal masses and corresponding decreases in the fundamental natural frequencies while the modal stiffnesses remain constant. These effects on the critical flutter speed cancel each other resulting in the surprising prediction that under optimal wind turbine design, the blade length has no effect on the critical flutter speed and hence the onset of chaos following flutter (if the damping ratios remain unaffected). Note, alternatively chaos following flutter is more likely to occur if the damping is held constant as blade length increases, since the damping ratio will be lowered.

• Wind turbine blade flutter and chaos can be suppressed by changes in modal mass or stiffness by separating (detuning) the plunging and pitching natural frequencies or lowering the modal mass according to (26) to increase the critical flutter speed due to stiffness mode coupling.

• A reasonable increase in the pitch modal damping (> + 1x) damps out any chaotic overlapping harmonic resonances from parametric excitation, caused by the bilinear lift curve. Note unrealistically large increases in damping would be needed to eliminate wind turbine flutter due to stiffness mode coupling.

• Changes in the coupled inertia term dictates the position of the centre of gravity with respect to the elastic centre. This in turn directly effects the dynamic divergence, which is a necessary driving mechanism for wind turbine flutter [42].

• Increases in chord length changes the airfoil section size, which changes several dynamic parameters. If the natural frequencies are held constant, this will mainly cause the modal mass to increase which in turn will increase the critical stiffness mode coupled flutter speed and hence suppress chaos following flutter.

• The bending mode shape amplitude determines how much unstable aerodynamic force is transmitted to the mode. Hence decreases in this amplitude via the coupling of a higher mode may be possible to increase the flutter critical velocity.

Wind turbine chaos suppression via aerodynamic parameter control is generally easier to achieve if the blade airfoil section can be redesigned according to:

• The position of the elastic centre is another critical parameter associated with dynamic divergence mechanism of airfoil flutter [42]. Moving the elastic centre further away from the midchord reduces the dynamic divergence criteria via the flutter derivatives, which will increase the critical stiffness mode coupled flutter speed.

• Only small decreases (-17%) in the stall slope factor are required to eliminate harmonics overlapping due to parametric excitation via the criterion for chaos following flutter. This is well within measured experimental variations at high angles of attack near or in the stall region [56] so larger decreases may be required to reduce the experimental uncertainty.

These results show the conservative analytical criteria can very efficiently investigate and evaluate several suppression techniques for chaos following flutter, without the need for lengthy and extensive multiple numerical integrations of the nonlinear equations of motion. Note that Table 2 summarises results for directly eliminating chaotic instability, not necessarily wind turbine flutter. By inspection of Fig. 8, it may be deduced that suppressing chaos following flutter to limit cycles can substantially reduce vibration velocity amplitudes by approximately 20%. Therefore, although the * cases of increasing damping and decreasing stall slope required generally smaller changes, it may be more desirable to eliminate flutter and chaos using the other means in Table 2. The frequency content of the flutter limit cycle will be necessarily more tonal than the chaos following flutter (as found in [25]).

The results highlight that the analytical closed-form solutions can be used to very efficiently predict and investigate the occurrence of conventional flutter and chaos following flutter in the blade of an optimally tuned wind turbine under aerodynamic, incompressible, unsteady flow conditions.

4 Conclusions

A pitching and plunging (binary) mathematical model for flutter of an optimally designed wind turbine blade, is used to predict the occurrence of classical and chaotic blade flutter in closed form. An optimal analysis of the wind turbine is first performed analytically to determine the blade section parameters to maximise energy generation. Numerical simulations of the nonlinear equations of motion including an approximate bilinear lift law, show wind turbine blade chaotic instability occurs under an increased (sharper) stall slope (consistent with measured experimental variations [56]), via a period doubling route as the wind speed was changed. Stiffness mode coupling, dynamic divergence and parametric excitation are shown to provide the necessary (phase space) expansion (or positive Lyapunov exponent) and nonlinearity for chaos via aerodynamics. Hence, wind turbine blade flutter is characterized by limit cycle behaviour via a supercritical Hopf bifurcation that can then bifurcate into chaotic motion. For the first time, conservative analytical criteria for wind turbine chaos following blade flutter are derived and numerically verified over a range of optimal wind turbine structural, dynamic and aerodynamic parameters. The predictive criteria are based on high local phase space expansion due to the occurrence of stiffness mode coupling and asymmetric bilinear aerodynamic stiffness causing parametric excitation and overlapping harmonics. They are found to efficiently (almost instantaneously) and conservatively predict the critical torsional damping levels at onset of chaos over a range of stall slope ratios to within 1% wind speed and critical damping error. The results provide important predictive insight into conditions under which wind turbine blade chaos following flutter occurs and its suppression. In particular, the efficient criteria are subsequently used to perform a parametric control investigation to eliminate chaos following flutter or suppress it to unrealistic wind speeds greater than 30 m/s. The results show small changes in tip speed ratio (−15%) and stall slope factor (−17%) can eliminate or suppress chaos following flutter while, in general, larger changes in dynamic parameters (i.e. mass, stiffness, damping) are required to achieve the same by detuning the coupled plunge and pitch natural frequencies or damping out overlapping parametric resonances. The positions of the elastic centre and centre of mass are found to effect and suppress chaos following flutter as found for conventional flutter. Interestingly, it is shown that the occurrences of conventional flutter and chaos following flutter is unaffected by the blade length when the wind turbine is optimally tuned, i.e. to a given tip speed ratio. This suggests that chaos following blade flutter could occur in any sized wind turbine if the local tip wind speed exceeds the relatively constant critical flutter speed (under the same optimal design conditions).

The results provide predictive insight into wind turbine blade classical flutter and chaos following flutter under optimal design conditions and its suppression. In particular, the main contributions of the analytical approach are that it provides a necessary condition for chaos following flutter to be very efficiently predicted (computational acceleration factor of 10⁷ times) and used to avoid its occurrence in optimal design to maximise power generation. It may also be used to verify more complex geometrical and numerical analyses using CFD and/or FEA modelling. The present closed-form results are necessarily limited to two dimensional aerodynamic incompressible flow on airfoil sections and approximations of the 3D blade geometry. In addition, the present analysis neglected dynamic interactions between multiple blades and turbine dynamics [69], which may affect some of the modes through coupling, but may complicate the closed solutions and insight gained from the present analysis. Hence, further research beyond the scope of the present paper is recommended to compare predictions with integrated 3D computation fluid dynamics and finite element analysis and/or wind tunnel test results if possible. Due to the generalised nature of the model, these results may provide insight into other types of mode coupled chaos.

Appendix A – Wind turbine blade airfoil flutter derivatives.

The flutter derivatives for a wind turbine blade section are the same as for a flat plate airfoil as derived in [1, 27]. For aerodynamic lift L they can be expressed as, $H_{1}^{*} = - 2\pi F/K$, $H_{2}^{*} = - \pi \left( {1 + 4G/K + 2F\left( {1/2 - a} \right)} \right)/\left( {2K} \right)$,

$$ H_{3}^{*} = - \pi \left( {2F - GK\left( {1/2 - a} \right) + aK^{2} /4} \right)/K^{2} ,\; H_{4}^{*} = \pi \left( {1 + 4G/K} \right)/ 2 $$

(A.1)

and for the aerodynamic moment, M, as,

$$ \begin{gathered} A_{1}^{*} = \pi F\left( {1/2 + a} \right)/K,\;~~A_{2}^{*} = - \pi \left( {K\left( {1/2 - a} \right)/2 - 2G\left( {1/2 + a} \right) + KF\left( {a^{2} - 1/4} \right)} \right)/\left( {2K^{2} } \right) \hfill \\ ~A_{3}^{*} = \pi \left( {K^{2} \left( {a^{2} + 1/8} \right)/4 + 2F\left( {1/2 + a} \right) + KG\left( {a^{2} - 1/4} \right)} \right)/\left( {2K^{2} } \right) \hfill \\ ~A_{4}^{*} = - \pi \left( {aK^{2} /2 + 2KG\left( {1/2 + a} \right)} \right)/\left( {2K^{2} } \right) \hfill \\ \end{gathered} $$

(A.2)

here F and G are the real and imaginary components of Theodorsen’s circulation function, efficiently approximated as,

$$ F\left( k \right) = 1 - 0.165/\left( {1 + \left( {0.0455/k} \right)^{2} } \right) - 0.335/\left( {1 + \left( {0.3/k} \right)^{2} } \right), $$

$$ G\left( k \right) = - 0.165*0.0455/k/\left( {1 + \left( {0.0455/k} \right)^{2} } \right) - 0.335*0.3/k/\left( {1 + \left( {0.3/k} \right)^{2} } \right), $$

(A.3)

where k = K/2. A comparison of (A.3) with those of a fourth order over fourth-order approximation of the Theodorsen circulation function [39, 40] show errors of complex modulus and phase angle of C(k) to within 0.3 percent and 0.25 degrees, respectively [42].