Stochastic analysis of a bistable piezoelectric energy harvester with a matched electrical load

Abstract

We present the analysis of a bistable piezoelectric energy harvester with matched electrical load, subject to random mechanical vibrations. The matching network optimizes the average energy transfer to the electrical load. The system is described by a set of nonlinear stochastic differential equations. A perturbation method is used to find an approximate solution of the stochastic system in the weak noise limit, and this solution is used to optimize the circuit parameters of the matching network. In the strong noise limit, the state equations are integrated numerically to determine the average power absorbed by the load and the power efficiency. Our analysis shows that the application of a properly designed matching network improves the performances by a significant amount, as the power delivered to the load improves of a factor about 17 with respect to a direct connection.

1 Introduction

Energy harvesting is a promising solution to enable the self-powering of a wide range of Internet of Things applications, of course with reference to systems requiring a small enough amount of electrical energy for their operation [1]. Many ambient energy sources are currently under consideration, from mechanical, to electromagnetic and to thermal gradients [2,3,4,5,6]. Ambient mechanical vibrations are considered promising [2] because of their ubiquity, relatively high power density, and easy conversion into electrical power exploiting different physical transduction principles [7].

One of the main performance limitations for a piezoelectric energy harvester is the sub-optimal energy transfer from the mechanical source to the electrical load, a condition that can be conveniently represented as an impedance mismatch between the electrical equivalent of the entire electro-mechanical system, and the load. This suggests to interpose a proper matching network between the harvester and the load to eliminate such mismatch [8,9,10].

In the simplest case of purely sinusoidal vibrations, i.e. when their energy is concentrated at a single frequency, a relatively straightforward analysis of the harvester is possible [8]. However, a more physically sound description considers the vibration energy spreading on a relatively wide frequency spectrum, thus requiring the use of a stochastic process description that, for a negligible noise correlation time, can be conveniently modeled through a white Gaussian noise forcing term [11].

In this contribution, we model a bistable piezoelectric energy harvester subject to random mechanical vibrations, and present novel results through analytical and numerical analysis. Bi-stability is introduced by means of magnetic repulsion and, as a consequence, nonlinearities are included in the mechanical elastic potential [12, 13]. The mathematical model is derived from the properties of the mechanical part, from the constitutive equations of linear piezoelectric materials, and from the circuit description of the electrical load.

Inspired by our recent work on the application of circuit theory to improve the efficiency of energy harvesting systems, we apply a low-pass L matching network to the load [8, 10, 14]. As the main contribution of the work, we assess the advantage offered by the modified load in terms of output average voltage, output average power and power conversion efficiency. In particular, we show that the application of the matching network increases the output average power by a factor 17 with respect to the simple resistive load, with a further more than 21% improvement with respect to other, previously proposed, solutions.

The equations of motion for the energy harvester are nonlinear stochastic differential equations (SDEs). The determination of the matching network’s parameters that maximize the output average voltage and power conversion efficiency, requires to solve the equations of motion for all values of the parameters, a computationally heavy and time consuming task. As a second main contribution, we develop a technique for the matching network optimization, based on an analytical, albeit approximate, calculation of the output average voltage, output average power and power efficiency. The technique is based on the determination of the SDEs solution in the weak noise limit, through a power series expansion, that can be used for an easy calculation of the quantities of interest for all values of the parameters. In the large noise limit, we solve numerically the SDEs for the set of parameters’ values found in the previous step, showing that the matching network still offers significantly better performances with respect to other setups.

The paper is organized as follows: In Sect. 2 we present the harvester model and we derive the equations of motion for three different loads: a simple resistive load, a power factor corrected load, and the matched load. Section 3 presents a systematic procedure to derive dimensionless SDEs, from a given SDEs system. This permits to obtain equations that are simpler to handle, and to reduce numerical issues during numerical simulations. Section 4 is devoted to the preliminary analysis of the equations of motion. In particular, in Theorem 1 we determine the equilibrium points and their stability for the energy harvester models in the absence of external perturbations. This result provides the foundation for the following analysis. Theorem 2 defines the relationship between average output power, power efficiency and second order moments of the SDE solution. In Sect. 5 we discuss the power series expansion method for the analysis and design of the harvester models, and for the matching network in the weak noise limit. The method allows to determine an analytical, albeit approximate, solution of the SDE system. Using the results of Sects. 3 and 4, in Theorem 3 we give a set of formulae to calculate all terms of the power series expansion representing the approximate solution. These terms permit to evaluate the average output power and the power efficiency, further used to optimize the matching network. Section 6 presents the application of the methodology to the optimization of the energy harvesting system. We use numerical simulations to solve the SDE system for relatively large values of the noise intensity, as a validation of the power series approximation and showing that the optimized matching network gives higher average output power and better power efficiency also in this noise range. Finally Sect. 7 is devoted to conclusions.

2 System description and modeling

Irrespective of the working principle, energy harvesters for ambient mechanical vibrations are composed by an oscillating structure, that is responsible for capturing the kinetic energy made available by ambient vibrations, by a transducer, that converts kinetic energy into usable electrical power, and by an electrical load, that uses the electrical power, or stores it for later use (namely, a battery).

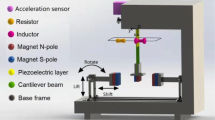
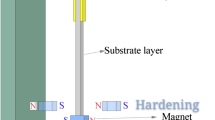
Energy harvesting systems that exploit nonlinear phenomena such as stochastic resonance and multi-stability, have been extensively studied in recent years [15,16,17,18,19]. A schematic representation of a single degree of freedom, bistable piezoelectric energy harvester is shown in Fig. 1. The oscillating structure is represented by a cantilever beam, fixed at one end to a vibrating support, and with a magnet of mass m at the opposite end to amplify oscillations. A layer of piezoelectric material covering the beam represents the transducer. Vibrations of the support induce oscillations of the beam, producing mechanical stress and strain in the piezoelectric layer that, in turn, are converted into electrical power.

Nonlinearity is introduced in the design by the tip magnet, that is fixed to a support in front of the inertial magnet with opposed polarities, so as to create a biased inverted pendulum with magnetic repulsive force. If the distance between the magnets is large enough, the magnetic repulsion becomes negligible with respect to the extermal force due to mechanical vibrations and to the elastic force of the beam. If nonlinear effects in the beam stiffness are neglected, the system is subject to a quadratic elastic potential and the cantilever beam behaves as a linear oscillator. In the absence of external forcing, the harvester exhibits a single stable equilibrium point, corresponding to the vertical rest position. Conversely, if the distance between the two magnets is so small that the magnetic repulsion cannot be neglected, the system is subject to a nonlinear elastic force. Magnetic repulsion forces the beam to the left or to the right of the vertical position. The two vertically tilted positions of the beam correspond to two stable equilibrium points, that are separated by an unstable saddle point, corresponding to the vertical position. Each stable equilibrium point has its own basin of attraction. For external forcing of small magnitude, the beam is expected to oscillate either around the left or the right equilibrium point, depending on the initial condition. The system can still be described in terms of a linear oscillator, with a resonant frequency higher than in the previous case [13], and the stationary distribution shows two marked peaks located around the stable equilibrium points. When the magnitude of the external forcing exceeds a critical threshold, oscillations around each of the two equilibrium points are expected to alternate with large excursions from one basin of attraction to the other. Correspondingly, the two peaks in the stationary distribution are expected to merge together and partially overlap. The irregular large excursions correspond to oscillations with larger amplitudes, that induce higher deformation of the beam producing more energy. For high noise intensity, the system is expected to exhibit more and more frequent excursions from the basin of attraction of one equilibrium to the other, with a motion that resembles a random wandering around the unstable saddle.

Fig. 1

Schematic representation of a piezoelectric cantilever beam energy harvester

The governing equations for the piezoelectric cantilever beam energy harvester can be derived from classical mechanics, from the characterization of piezoelectric materials, and from the circuit description of the electrical load [8, 10]. For the mechanical part, the equation of motion is

$$\begin{aligned} m \ddot{x} + \gamma \dot{x} + U^{\prime }(x) + f_{\text {tr}}(e,I) = f_{\text {ext}}(t) \end{aligned}$$

(1)

where x(t) represents the displacement of the inertial mass m from the vertical rest position, $\gamma$ is the internal friction constant, U(x) is the elastic potential of the beam, $f_{\text {tr}}(e,I)$ is the force exerted by the transducer on the mechanical part due to the electrical variables e(t), I(t), and $f_{\text {ext}}(t)$ is the external force due to the vibrating support. In (1), dots denote derivation with respect to time, while symbol $^{\prime }$ denotes derivation with respect to the argument. We shall assume that mechanical vibrations can be modelled as white Gaussian noise. White noise is characterized by a flat power spectrum, that cannot exist in the real world, because it would imply an infinite power content. However white noise is a reasonable approximation whenever the energy of the stochastic process is distributed over a wide enough frequency interval. For the elastic potential, we shall assume $U(x) = - k_1 \, x^2 /2+ k_3 \, x^4/4$, where $k_1$ and $k_3$ are the linear and the nonlinear elastic stiffness, respectively, to account for the bi-stability.

Fig. 2

Two-port network representation of a transducer

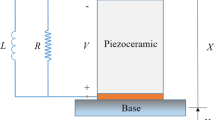
A transducer is responsible for converting mechanical quantities, like force and velocity, into electrical quantities, e.g. voltage and current. It can be represented as the electro-mechanical two-port shown in Fig. 2, with the mechanical variables at the input (left port) and the electrical variables at the output (right port). For a linear piezoelectric transducer, the governing equations can be derived from the characterization of piezoelectric materials [20,21,22], given by

$$\begin{aligned}&f_{\text {tr}}(e,I) = \alpha \, e(t) \end{aligned}$$

(2a)

$$\begin{aligned}&q(t) = \alpha \,x(t) - C_{\text {pz}} \, e(t) \end{aligned}$$

(2b)

where $\alpha$ is the electro-mechanical coupling constant (in N/V or As/m), $C_{\text {pz}}$ is the electrical capacitance of the piezoelectric layer, q(t) is the electrical charge, and $I(t) = \dot{q}(t)$, e(t) are the output current and voltage of the piezoelectric transducer, see Fig. 2.

Fig. 3

a Resistive load. b Power factor corrected load for a piezoelectric energy harvester. c An example of matched load: load with low-pass L-shaped matching network

Finally we consider the electrical load. Loads are electrical elements that absorb power from the rest of the circuit, therefore they are typically modeled as resistors, as shown in Fig. 3a. For the resistive load, application of Ohm’s law gives $I = G_L \, e$, where $G_L = R_L^{-1}$ is the load conductance. Combining Eqs. (1), (2) and the Ohm’s law, and rewriting as a system of first order SDEs (see Sect. 3), yields:

$$\begin{aligned} dx&= y \, dt \end{aligned}$$

(3a)

$$\begin{aligned} dy&= \left( -\dfrac{1}{m} U^{\prime }(x) - \dfrac{\gamma }{m} y - \dfrac{\alpha }{m} e \right) dt + \dfrac{\varepsilon }{m} dW_t\end{aligned}$$

(3b)

$$\begin{aligned} d e&= \dfrac{1}{C_{\text {pz}}} \left( \alpha y - G_L\, e \right) dt \end{aligned}$$

(3c)

where $dW_t$ is a scalar white Gaussian noise and $\varepsilon \in {\mathbb {R}}^+$ is a parameter that measures the noise intensity. Such a model, with white Gaussian noise, possibly replaced by a periodic forcing, has been extensively studied in the past, see for instance [9, 23,24,25,26,27,28], and it has been validated by numerous experiments [26, 29,30,31,32]. Further details about the structure and materials used for the harvester can be found in the aforementioned papers.

One of the most important limiting factors of energy harvesting systems, is the impedance mismatch between the electro-mechanical harvester and the electrical load. To illustrate the problem, consider a linear harvester subject to a periodic mechanical excitation. The maximum power transfer theorem states that the load absorbs maximum average power if its impedance is the complex conjugate of the harvester’s impedance. For the resistive load case, this requires the harvester to work at the resonant frequency, and the load’s resistance must be equal to the harvester’s resistance. In general, neither condition can be satisfied in real world applications because, for example, the frequency of ambient vibrations may change in time. This problem can be partially solved designing systems capable to self adapt, i.e. adjust their resonant frequency to that of the external stimulus [33,34,35,36]. However, in the vast majority of practical applications the load resistance is fixed a priori, and cannot be adjusted to match the harvester resistance.

A possible solution is based on the power factor correction, i.e. in connecting a reactive element (an inductor or a capacitor) in parallel with the resistive load, to compensate the time lag between the load current and voltage [8, 9, 25, 28], as shown in Fig. 3b. For the power factor corrected setup, application of Kirchhoff current law gives $I = I_L + G_L \, e$, while the characteristic relationship of the inductor is $\dot{I}_L = e/L$. Combining these equations with (1), (2), and rewriting as a system of first order SDEs yields:

$$\begin{aligned} d x&= y \, dt \end{aligned}$$

(4a)

$$\begin{aligned} d y&= \left( -\dfrac{1}{m} U'(x) - \dfrac{\gamma }{m} y - \dfrac{\alpha }{m} e \right) dt + \dfrac{\varepsilon }{m} dW_t \end{aligned}$$

(4b)

$$\begin{aligned} d e&= \dfrac{1}{C_\text {pz}} \left( \alpha y - I_L - G_L \,e \right) dt \end{aligned}$$

(4c)

$$\begin{aligned} d I_L&= \dfrac{1}{L} \, e \, dt \end{aligned}$$

(4d)

An alternative, more advanced solution amounts to interpose a matching network between the energy harvester and the resistive load [10, 14]. A matching network is composed of reactive elements, that do not absorb average power and therefore do not impair the efficiency of the harvester. Conversely, they reduce the impedance mismatch between the harvester and the load, thus improving the power absorbed by the latter. Perfect matching can be obtained only at a single frequency. Nevertheless, broadband matching networks can be designed that achieve partial load matching over a relatively large frequency interval, maximizing the power transfer also for power sources with distributed energy spectra. An example of matching network is shown in Fig. 3c. It is composed by an inductor and a capacitor connected to form an L-shaped structure. Because at very low frequencies the inductor is equivalent to a short circuit, the network is called low-pass. This is a convenient feature for harvesting ambient mechanical vibrations since, in general, most of the energy is concentrated at low frequencies.

For the matching network shown in Fig. 3c, combining Kirchhoff current and voltage laws with the characteristic relationships of inductors and capacitors gives

$$\begin{aligned} - I_L + C_P \dot{v}_o + G_L v_o&= 0\\ L_S \dot{I}_L + v_o - e&= 0 \end{aligned}$$

Combining these equations with (1) and (2) yields the following SDE system

$$\begin{aligned} d x&= y \, dt \end{aligned}$$

(5a)

$$\begin{aligned} d y&= \left( -\dfrac{1}{m} U'(x) - \dfrac{\gamma }{m} y - \dfrac{\alpha }{m} e \right) dt + \dfrac{\varepsilon }{m} dW_t \end{aligned}$$

(5b)

$$\begin{aligned} d e&= \dfrac{1}{C_\text {pz}} \left( \alpha y - I_L\right) dt \end{aligned}$$

(5c)

$$\begin{aligned} d I_L&= \dfrac{1}{L_S} \left( e - v_o \right) dt \end{aligned}$$

(5d)

$$\begin{aligned} d v_o&= \dfrac{1}{C_P} \left( I_L - G_L \, v_o \right) dt \end{aligned}$$

(5e)

3 Dimensionless equation system derivation

Ambient dispersed vibrations can be of a very different nature, from shock/impact force [37,38,39,40,41], to periodic forcing [29, 30, 42, 43]. In a complex environment, ambient vibrations are the result of the superposition of different sources and mechanisms, resembling a random signal [10, 13, 15, 16, 18, 23, 28, 44, 45]. The random nature of ambient vibrations in complex environments, therefore, implies that they are best described as stochastic processes.

The theory of stochastic processes and stochastic differential equations is well developed in the literature [46, 47]. Let $(\Omega ,\mathcal {F},P)$ be a probability space, where $\Omega$ is the sample space, ${\mathcal {F}} = ({\mathcal {F}}_t)_{t\ge 0}$ is a filtration, e.g. the $\sigma$-algebra of all the events, and P is a probability measure. A vector valued stochastic process ${\varvec{X}}_t$ is a vector of random variables, sampled from $\Omega$, and parameterized by $t \in T$. The parameter space T is usually the half-line $[0,+\infty [$. Alternatively, the stochastic process can be thought of as the function ${\varvec{X}}_t: \Omega \times T \mapsto {\mathbb {R}}^d$. We adopt the standard notation used in probability: Capital letters denote random variables, while lower case letters denote their possible values.

Let $W_t=W(t)$ be a one dimensional Wiener process, characterized by ${\textrm{E}}[W_t ] = 0$ (symbol ${\textrm{E}}[X_t]$ denotes expectation of the stochastic process $X_t$ with respect to the measure P), covariance ${\text {cov}}(W_t,W_s) = {\textrm{E}} [W_t \, W_s] = \min (t,s)$ and $W_t \sim \mathcal {N}(0,t)$, where symbol $\sim$ means “distributed as”, and ${\mathcal {N}}(0,t)$ denotes the normal distribution, centered at zero. A d-dimensional system of SDEs driven by the one-dimensional Wiener process $W_t$ reads

$$\begin{aligned} d {\varvec{X}}_t = {\varvec{a}}({\varvec{X}}_t) dt + {\varvec{B}}({\varvec{X}}_t) dW_t \end{aligned}$$

(6)

where ${\varvec{X}}_t: \Omega \times T \mapsto {\mathbb {R}}^d$ is a vector valued stochastic process. The vector valued functions ${\varvec{a}}: {\mathbb {R}}^d \mapsto {\mathbb {R}}^d$, ${\varvec{B}}: {\mathbb {R}}^d \mapsto {\mathbb {R}}^d$, are called drift and diffusion, respectively. They are measurable functions satisfying a global Lipschitz condition, to ensure the existence and uniqueness solution theorem [47]. If the function ${\varvec{B}}({\varvec{X}}_t)$ is constant, noise is called un-modulated or additive, otherwise it is modulated or multiplicative.

SDEs can be interpreted following two main interpretations: Statonovich and Itô [46, 47]. In this work we shall adopt Itô interpretation, because it simplifies some calculations, in particular for expected quantities. However, we stress that because (3)–(5) are characterized by an un-modulated noise, all the results are independent on the interpretation adopted.

It is sometimes convenient to work with a scaled version of the original equations, for example introducing dimensionless variables through a linear transformation. In the following, we give a systematic procedure to derive scaled and/or dimensioneless version of a given SDE system.

The SDEs (3)–(5) can be written in the form

$$\begin{aligned} d {\varvec{Z}}_t = \left( {\hat{{\varvec{A}}}} \, {\varvec{Z}}_t + {\hat{{\varvec{n}}}}({\varvec{Z}}_t) \right) dt + {\hat{{\varvec{B}}}} \, dW_t \end{aligned}$$

(7)

where ${\hat{{\varvec{A}}}} \in {\mathbb {R}}^{d,d}$, ${\hat{{\varvec{n}}}}: {\mathbb {R}}^d \mapsto {\mathbb {R}}^d$ collect the linear and nonlinear terms of the drift, respectively, and ${\hat{{\varvec{B}}}} \in {\mathbb {R}}^d$ is the constant diffusion vector. Consider a linear transformation ${\varvec{y}}= {\varvec{P}}{\varvec{z}}$, where ${\varvec{P}}\in {\mathbb {R}}^{d,d}$ is a constant regular matrix. For dimensionless variables, matrix ${\varvec{P}}$ is diagonal with entries represented by normalizing parameters. Using Itô rule [46, 47], the following SDE system for the stochastic processes ${\varvec{y}}$ is obtained:

$$\begin{aligned} d {\varvec{Y}}_t = \left( {\varvec{P}}{\hat{{\varvec{A}}}} {\varvec{P}}^{-1} {\varvec{Y}}_t \!+\! {\varvec{P}}\hat{\varvec{n}}({\varvec{P}}^{-1} {\varvec{Y}}_t) \right) dt \!+\! {\varvec{P}}\, {\hat{{\varvec{B}}}}\, dW_t\nonumber \\ \end{aligned}$$

(8)

A linear change of time in SDEs, and in particular a time scaling, is obtained introducing a new time variable $\tau (t) = \omega \, t$, with $\omega >0$. If ${\varvec{Y}}_t$ solves (8), then ${\varvec{Y}}_{\tau }$ solves the SDE system

$$\begin{aligned} d {\varvec{Y}}_{\tau }&= \dfrac{1}{\omega } \left( {\varvec{P}}{\hat{{\varvec{A}}}} {\varvec{P}}^{-1} {\varvec{Y}}_{\tau } + {\varvec{P}}{\hat{{\varvec{n}}}}({\varvec{P}}^{-1} {\varvec{Y}}_{\tau }) \right) d\tau \nonumber \\&\quad + {\varvec{P}}\, {\hat{{\varvec{B}}}} \, dW_{t} \end{aligned}$$

(9)

The change of time theorem for Itô integrals (see [47], page 156) implies that

$$\begin{aligned} W_{\tau (t)} \sim \sqrt{\tau '(t)} \, W_t = \sqrt{\omega } \, W_t \end{aligned}$$

(10)

where symbol $\sim$ means, again, “distributed as”. Denoting by ${\varvec{X}}_{\tau }$ the solution to the SDEs system

$$\begin{aligned} d {\varvec{X}}_{\tau } = \dfrac{1}{\omega } \left( {\varvec{A}}{\varvec{X}}_{\tau } + {\varvec{n}}({\varvec{X}}_{\tau }) \right) d {\tau } + \dfrac{1}{\sqrt{\omega }} {\varvec{B}}\, dW_{\tau } \end{aligned}$$

(11)

where ${\varvec{A}}= {\varvec{P}}{\hat{{\varvec{A}}}} {\varvec{P}}^{-1}$, ${\varvec{n}}({\varvec{x}}) = {\varvec{P}}{\hat{{\varvec{n}}}}({\varvec{P}}^{-1} {\varvec{x}})$, and ${\varvec{B}}= {\varvec{P}}{\hat{{\varvec{B}}}}$, it follows that ${\varvec{X}}_{\tau } \sim {\varvec{Y}}_{\tau }$, because they are solutions for the same SDEs system, but for two different realizations of the Wiener process.

In most practical applications, the knowledge of the probability distribution, and/or of the first few moments of such distribution, is more important than finding the explicit solution of the SDEs for a specific realization of the Wiener process.

Hereafter, we shall consider the SDEs (5) only. The method described can also be applied, mutatis mutandis, to the SDEs (3) and (4), that will be used as a reference to assess the advantage provided by the matching network.

We shall assume that the inertial and the tip magnets are so close that the magnetic repulsion cannot be neglected. The nonlinearity and the bistability due to the magnetic force will be accounted for by the nonlinear elastic potential. The dimensionless version of the SDE system is obtained introducing the diagonal matrix:

$$\begin{aligned} {\varvec{P}}= {\text {diag}}[l_0^{-1}, T l_0^{-1}, C_{\text {pz}} Q_0^{-1}, TQ_0^{-1}, C_{\text {pz}} Q_0^{-1}] \end{aligned}$$

(12)

where $l_0$, $Q_0$ are normalizing constants equal to one, with dimensions of a length and a charge, respectively, and $T = {1}/{\omega } = \sqrt{{m}/{k_1}}$ is a normalization time. The following SDE system for the dimensionless variables is obtained

$$\begin{aligned} d {\varvec{X}}_t = \left( {\varvec{A}}{\varvec{X}}_t + {\varvec{n}}({\varvec{X}}_t) \right) + {\varvec{B}}dW_t \end{aligned}$$

(13)

where ${\varvec{X}}= [X_1,X_2,X_3,X_4,X_5]^T$ is a vector of stochastic processes, and

$$\begin{aligned} {\varvec{A}}= & {} \left[ \begin{array}{ccccc} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} -\rho &{} -\beta &{} 0 &{} 0 \\ 0 &{} \alpha &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} \mu &{} 0 &{} -\mu \\ 0 &{} 0&{} 0&{} \eta &{} -\delta \end{array} \right] \end{aligned}$$

(14)

$$\begin{aligned} {\varvec{n}}({\varvec{x}})= & {} [0,-\kappa x^3, 0,0,0]^T \end{aligned}$$

(15)

$$\begin{aligned} {\varvec{B}}= & {} [0,\sigma ,0,0,0]^T \end{aligned}$$

(16)

with parameters

$$\begin{aligned} \kappa&= \dfrac{k_3}{k_1}, \quad \rho = \dfrac{\gamma }{\sqrt{m k_1}}, \quad \beta = \dfrac{\alpha }{C_\text {pz} k_1}, \quad \mu = \dfrac{m}{k_1 \, C_\text {pz} \, L_S} \nonumber \\ \eta&= \dfrac{C_\text {pz}}{C_P}, \quad \delta = \dfrac{G_L}{C_P} \sqrt{\dfrac{m}{k_1}}, \quad \sigma = \dfrac{\varepsilon }{m} \left( \dfrac{m}{k_1} \right) ^{\frac{3}{4}} \end{aligned}$$

(17)

Note that, by definition, all parameters are positive.

4 Preliminary system analysis

We begin the analysis considering the underlying deterministic system, i.e. the system obtained setting $\varepsilon = 0$ in the SDE system (5) or, equivalently, setting $\sigma = 0$ in the dimensionless SDE system (13). In particular, we shall consider the dimensionless version.

The following theorem establishes the existence, position and stability of the equilibrium points for the energy harvester with matching network. This result is instrumental for further analysis, and in particular for the application of the power series expansion method and the calculation of expected quantities provided in Theorem 3.

Theorem 1

The ODE system

$$\begin{aligned} {\dot{{\varvec{x}}}} = {\varvec{A}}{\varvec{x}}+ {\varvec{n}}({\varvec{x}}) \end{aligned}$$

(18)

where ${\varvec{A}}$ and ${\varvec{n}}({\varvec{x}})$ are given by (14) and (15), respectively, has an unstable equilibrium point at the origin, and two asymptotically stable equilibrium points at

$$\begin{aligned} {\varvec{x}}_{\pm }^* =\left[ \pm \sqrt{\frac{1}{\kappa }}, 0,0,0,0\right] ^T. \end{aligned}$$

Proof

It is straightforward to verify that ${\varvec{x}}= {\varvec{x}}_0^*= 0$ and ${\varvec{x}}= {\varvec{x}}_{\pm }^*$ are equilibrium points of (18). To verify that the origin is unstable, consider the Jacobian matrix ${\varvec{J}}= {\varvec{A}}+ \partial {\varvec{n}}({\varvec{x}})/\partial {\varvec{x}}$, evaluated at ${\varvec{x}}={\varvec{x}}_0^*$. The characteristic polynomial for this Jacobian matrix is

$$\begin{aligned} P(s)&= s^5 + (\delta + \rho ) s^4 + (\mu + \alpha \beta + \eta \mu + \delta \rho ) s^3\nonumber \\&\quad + (\delta \mu - \delta + \mu \rho + \alpha \beta \delta + \eta \mu \rho ) s^2\nonumber \\&\quad + (\delta \mu \rho - \eta \mu - \mu + \alpha \beta \eta \mu ) s - \delta \mu \end{aligned}$$

(19)

Given that all parameters in (17) are positive, it follows from the necessary condition of Routh–Hurwitz stability criterion that the origin is unstable.

Next we prove that ${\varvec{x}}_{+}^*$ is asymptotically stable. Stability of ${\varvec{x}}_{-}^*$ is proved analogously, considering that the system is invariant under the transformation ${\varvec{x}}\rightarrow -{\varvec{x}}$.

First we move the equilibrium point to the origin with the change of variables ${\overline{{\varvec{x}}}} = {\varvec{x}}- {\varvec{x}}_+^*$. The new variables satisfy the ODE system (written in components)

$$\begin{aligned} \dot{{\overline{x}}}_1&= {\overline{x}}_2 \end{aligned}$$

(20a)

$$\begin{aligned} \dot{{\overline{x}}}_2&= -U'({\overline{x}}_1) - \rho {\overline{x}}_2 - \beta {\overline{x}}_3 \end{aligned}$$

(20b)

$$\begin{aligned} \dot{{\overline{x}}}_3&= \alpha {\overline{x}}_2 - {\overline{x}}_4 \end{aligned}$$

(20c)

$$\begin{aligned} \dot{{\overline{x}}}_4&= \mu \left( {\overline{x}}_3 - {\overline{x}}_4 \right) \end{aligned}$$

(20d)

$$\begin{aligned} \dot{{\overline{x}}}_5&= \eta {\overline{x}}_4 - \delta {\overline{x}}_5 \end{aligned}$$

(20e)

where

$$\begin{aligned} U({\overline{x}}_1) = -\frac{1}{2} \left( {\overline{x}}_1 + \sqrt{\frac{1}{\kappa }}\right) ^2 + \frac{1}{4} \kappa \left( {\overline{x}}_1 + \sqrt{\frac{1}{\kappa }}\right) ^4 \end{aligned}$$

(21)

Consider function $V({\varvec{x}}) \in \mathcal {C}^{1}$

$$\begin{aligned} V({\overline{{\varvec{x}}}})&= \frac{1}{4\kappa } + U({\overline{x}}_1) + \frac{1}{2} {\overline{x}}_2^2\nonumber \\&\quad + \frac{1}{2} \frac{\beta }{\alpha } \left( {\overline{x}}_3^2 + \frac{1}{\mu } {\overline{x}}_4^2 + \frac{1}{\eta } {\overline{x}}_5^2 \right) \end{aligned}$$

(22)

Clearly, $V(0) = 0$ and $V({\overline{{\varvec{x}}}}) > 0$ for ${\varvec{x}}\ne 0$. Moreover

$$\begin{aligned} \dot{V}({\varvec{x}}) = - \rho \, {\overline{x}}_2^2 - \dfrac{\delta \beta }{\alpha \eta } \, {\overline{x}}_5^2 <0 \end{aligned}$$

(23)

Therefore $V({\overline{{\varvec{x}}}})$ is a strict weak Liapunov function [48], and the origin is an asymptotically stable equilibrium point. $\square$

To determine the power performance of the energy harvester, relations are needed for the output average power and the power efficiency. For this derivation, it is easier to consider the original system (5).

Theorem 2

(Power balance equation) Consider the SDE system (5). The average power exchanged is

$$\begin{aligned} \textrm{E}\left[ \dfrac{d E(t)}{dt} \right] = - \gamma \, {\textrm{E}}\left[ y^2(t) \right] - G_L \, {\textrm{E}}\left[ v_o^2(t) \right] + \dfrac{\varepsilon ^2}{ 2 m} \end{aligned}$$

(24)

where E(t) is the total energy stored in the system.

Proof

The total energy stored in the system is the sum of the mechanical energy, of the energy stored in the piezoelectric transducer, and of the energy stored in the reactive components of the electrical part. The mechanical energy is the kinetic energy of the mass, plus the elastic potential energy of the beam: $E_{\text {mec}}(t) = m y^2/2 + U(x)$. For the energy stored in the transducer, with reference to Fig. 2, the instantaneous power absorbed by the two port network, using the passive sign convention, reads $p_\text {tr}(t) = f_\text {tr} \, \dot{x} - e \, \dot{q}$. Using (2) we obtain $p_\text {tr}(t) = C_\text {pz} \, e \, \dot{e}$, and the stored energy is

$$\begin{aligned} E_\text {tr}(t) = \int p_\text {tr}(t) \, dt = \dfrac{1}{2} C_\text {pz} e^2 + K \end{aligned}$$

(25)

where K is an arbitrary constant. Finally, the energy stored in the reactive components of the load, including the matching network, is $E_\text {el}(t) = L_S I_L^2/2 + C_P v_0^2/2$.

Taking the differential of the total energy, using (5) and Itô lemma yields:

$$\begin{aligned} dE&= m y \, dy + U'(x) dx + C_\text {pz} e \, de + L_S \, I_L \, d I_L \nonumber \\&\quad + C_P \, v_{\text {o}} \, dv_{\text {o}} + \frac{1}{2} m (dy)^2 \nonumber \\&= \left( - \gamma y^2 - G_L v_{\text {o}}^2 + \frac{\varepsilon ^2}{2m} \right) dt + \varepsilon \, y \, dW_t \end{aligned}$$

(26)

Taking expectations on both sides and using the martingale property of Itô integrals, the thesis follows. $\square$

It is worth noticing that the same Power Balance Equation is obtained for both the harvester with resistive load and with the power factor corrected load. In fact, it is well known in circuit theory that reactive elements like capacitors and inductors do not absorb average power, but only reactive power.

The power balance equation implies that the system eventually reaches a steady state, where the power injected by the noise is partially dissipated by the internal friction, and partially absorbed by the load.

Corollary 1

At steady state, the power absorbed by the load and the power efficiency are given by

$$\begin{aligned} P_L&= G_L \textrm{E}[v_{\text {o}}^2] \end{aligned}$$

(27)

$$\begin{aligned} \eta _E&= \frac{2\, m \, G_L}{\varepsilon ^2} \textrm{E}[v_{\text {o}}^2] \end{aligned}$$

(28)

Proof

It follows directly from the power balance equation, and the definition of power efficiency as the ratio between input and output average powers. $\square$

5 Power series analysis and moment calculation

Corollary 1 shows that, in order to maximize the average power absorbed by the load and the power efficiency, the matching network must be designed to maximize $\textrm{E}[v_{\text {o}}^2]$. The value of $\textrm{E}[v_{\text {o}}^2]$, can be found from the stationary distributions for the stochastic processes that, in turn, require to either solve analytically the SDE system (5) (or the equivalent dimensionless version (13)), or the associated Fokker–Planck equation [46, 47]. Both problems are very challenging and, in practice, neither can be solved for nonlinear systems of high order. Alternatively, expected quantities can be calculated solving numerically the SDE systems, and averaging over long simulated times. This approach rapidly becomes extremely expensive, especially when the numerical simulations have to be repeated for many different parameter values.

In this work we propose a different approach. We use a power series expansion to find an approximate solution of the SDE system. The approximate solution is then used to calculate the desired expected quantities for any value of the parameters, thus making possible to find the parameter values that maximize the harvested power and the power efficiency.

5.1 Power series expansion

Consider a d-dimensional system of SDEs driven by the one-dimensional Wiener process $W_t$

$$\begin{aligned} d {\varvec{X}}_t = {\varvec{a}}({\varvec{X}}_t) dt + \varepsilon {\varvec{B}}({\varvec{X}}_t)\, dW_t \end{aligned}$$

(29)

For small values of $\varepsilon$, the solution can be expanded in power series of the same small parameter

$$\begin{aligned} {\varvec{X}}_t = {\varvec{X}}_0 + \varepsilon {\varvec{X}}_1 + \varepsilon ^2 {\varvec{X}}_2 + \cdots \end{aligned}$$

(30)

Similarly, the drift vector is expanded in Taylor series as (the t dependence is dropped in ${\varvec{X}}_k$, $k=0,1,2$, for the sake of notation simplicity)

$$\begin{aligned} {\varvec{a}}({\varvec{X}})&= {\varvec{a}}({\varvec{X}}_0) + {\varvec{A}}_1({\varvec{X}}_0) (\varepsilon {\varvec{X}}_1 + \varepsilon ^2 {\varvec{X}}_2) \nonumber \\&\quad + \varepsilon ^2 {\varvec{A}}_2({\varvec{X}}_0,{\varvec{X}}_1) + \mathcal {O}(\varepsilon ^3) \end{aligned}$$

(31)

where ${\varvec{A}}_1({\varvec{X}}_0) = \partial {\varvec{a}}/\partial {\varvec{x}}\big |_{{\varvec{X}}_0}$ is the Jacobian matrix of ${\varvec{a}}({\varvec{x}})$ evaluated at ${\varvec{X}}_0$, and ${\varvec{A}}_2({\varvec{X}}_0,{\varvec{X}}_1)$ is the vector made of the components

$$\begin{aligned} A_{2,i}({\varvec{X}}_0,{\varvec{X}}_1) = \dfrac{1}{2} \, {\varvec{X}}_1^T {\varvec{H}}_i({\varvec{X}}_0) {\varvec{X}}_1 \end{aligned}$$

(32)

being ${\varvec{H}}_i$ the Hessian matrix ${\varvec{H}}_i({\varvec{X}}_0) = \partial ^2 a_i/\partial {\varvec{x}}^2\big |_{{\varvec{X}}_0}$ evaluated at ${\varvec{X}}_0$.

Similarly, Taylor expanding the diffusion vector yields

$$\begin{aligned} {\varvec{B}}({\varvec{X}}) = {\varvec{B}}({\varvec{X}}_0) + {\varvec{B}}_1({\varvec{X}}_0) (\varepsilon {\varvec{X}}_1 + \varepsilon ^2 {\varvec{X}}_2) + \mathcal {O}(\varepsilon ^2) \end{aligned}$$

(33)

where ${\varvec{B}}_1({\varvec{X}}_0) = \partial {\varvec{B}}/\partial {\varvec{x}}\big |_{{\varvec{X}}_0}$.

Substituting (30), (31) and (33) into (29), and equating the coefficients of the same powers of $\varepsilon$, yields the hierarchy of equations

$$\begin{aligned} \varepsilon ^0: d {\varvec{X}}_0&= {\varvec{a}}({\varvec{X}}_0) dt \end{aligned}$$

(34a)

$$\begin{aligned} \varepsilon ^1: d {\varvec{X}}_1&= {\varvec{A}}_1({\varvec{X}}_0) {\varvec{X}}_1 dt + {\varvec{B}}({\varvec{X}}_0) dW_t \end{aligned}$$

(34b)

$$\begin{aligned} \varepsilon ^2: d {\varvec{X}}_2&= \left( {\varvec{A}}_1({\varvec{X}}_0) {\varvec{X}}_2 + {\varvec{A}}_2({\varvec{X}}_0, {\varvec{X}}_1) \right) dt \nonumber \\&\quad + {\varvec{B}}_1({\varvec{X}}_0) \, {\varvec{X}}_1 dW_t \end{aligned}$$

(34c)

These differential equations are completed by a set of appropriate initial conditions: ${\varvec{X}}_0(0) = {\varvec{x}}_0$, ${\varvec{X}}_1(0) = {\varvec{X}}_2(0) = 0$, so that the solutions ${\varvec{X}}_0(t)$, ${\varvec{X}}_1(t)$, and ${\varvec{X}}_2(t)$ become unique.

The zeroth order equation (34a) is a system of ordinary differential equation (ODEs) describing the “underlying” deterministic problem. Without loss of generality, the initial condition can be chosen such that ${\varvec{x}}_0$ corresponds to an asymptotically stable equilibrium point, therefore ${\varvec{X}}_0(t) = {\varvec{x}}_0$ for all t. The first order SDE system (34b) describes ${\varvec{X}}_1(t)$ as an Ornstein–Uhlenbeck process [46, 47], whose expression can be found analytically. Finally, the second order SDE system (34c) describes a linear system of non-homogeneous SDEs.

5.2 Moment calculation

First order moments are found taking expectations in (30), yielding:

$$\begin{aligned} \textrm{E}[{\varvec{X}}_t ] = {\varvec{X}}_0 + \varepsilon \textrm{E}[{\varvec{X}}_1] + \varepsilon ^2 \textrm{E}[{\varvec{X}}_2 ] + \mathcal {O}(\varepsilon ^3) \end{aligned}$$

(35)

Concerning second order moments, using again (30) we find

$$\begin{aligned} {\varvec{X}}_t {\varvec{X}}_t^T&= {\varvec{X}}_0 {\varvec{X}}_0^T + \varepsilon \left( {\varvec{X}}_0 {\varvec{X}}_1^T + {\varvec{X}}_1 {\varvec{X}}_0^T \right) \nonumber \\&\quad + \varepsilon ^2 \left( {\varvec{X}}_0 {\varvec{X}}_2^T + {\varvec{X}}_1 {\varvec{X}}_1^T + {\varvec{X}}_2 {\varvec{X}}_0^T \right) + \mathcal {O}(\varepsilon ^3) \end{aligned}$$

(36)

Taking expectations

$$\begin{aligned} \textrm{E}[{\varvec{X}}_t {\varvec{X}}_t^T ]&= {\varvec{X}}_0 {\varvec{X}}_0^T + \varepsilon \left( {\varvec{X}}_0 \, \textrm{E}[{\varvec{X}}_1^T ] + \textrm{E}[{\varvec{X}}_1 ] {\varvec{X}}_0^T \right) \nonumber \\&\quad + \varepsilon ^2 \left( {\varvec{X}}_0 \, \textrm{E}[{\varvec{X}}_2^T ] + \textrm{E}[ {\varvec{X}}_1 {\varvec{X}}_1^T ] + \textrm{E}[ {\varvec{X}}_2 ] {\varvec{X}}_0^T \right) \nonumber \\&\quad + \mathcal {O}(\varepsilon ^3) \end{aligned}$$

(37)

Therefore, the first and all the second order moments are approximated as linear combinations of the first order moments $\textrm{E}[ {\varvec{X}}_1 ]$, $\textrm{E}[ {\varvec{X}}_2 ]$, and of the second order moment $\textrm{E}[{\varvec{X}}_1 {\varvec{X}}_1^T ]$.

In the following theorem, we give analytical formulae to calculate all the required expectations.

Theorem 3

Consider the Itô SDE system (29), and let ${\varvec{x}}_0$ be an asymptotically stable equilibrium point for the ODE system $\dot{\varvec{x}}= {\varvec{a}}({\varvec{x}})$. Then the hierarchy equation system (34) gives asymptotically for $t\rightarrow +\infty$:

• (a) $\textrm{E}[{\varvec{X}}_1] = 0.$

• (b) $\textrm{E}[{\varvec{X}}_2] = - {\varvec{A}}_1^{-1}({\varvec{X}}_0) {\varvec{h}}({\varvec{X}}_0,{\varvec{X}}_1)$, where vector ${\varvec{h}}({\varvec{X}}_0,{\varvec{X}}_1)$ has components $h_i({\varvec{X}}_0,{\varvec{X}}_1) = \textrm{tr} \left( {\varvec{H}}_i({\varvec{X}}_0) \sigma _{{\varvec{X}}_1 {\varvec{X}}_1} \right)$, and $\sigma _{{\varvec{X}}_1 {\varvec{X}}_1} = \textrm{E}[{\varvec{X}}_1^T \, {\varvec{X}}_1]$.

• (c) The covariance matrix $\sigma _{{\varvec{X}}_1 {\varvec{X}}_1}$ is the unique solution of the stationary Liapunov equation

  $$\begin{aligned} {\varvec{A}}_1({\varvec{X}}_0) \sigma _{{\varvec{X}}_1 {\varvec{X}}_1} + \sigma _{{\varvec{X}}_1 {\varvec{X}}_1} {\varvec{A}}_1^T({\varvec{X}}_0) + {\varvec{B}}_0 {\varvec{B}}_0^T = 0 \end{aligned}$$

Proof

Taking stochastic expectations on both sides of (34), and using the martingale property of Itô integrals gives

$$\begin{aligned} \dfrac{d}{dt} \textrm{E}[ {\varvec{X}}_1 ]&= {\varvec{A}}_1({\varvec{X}}_0) \, \textrm{E}[ {\varvec{X}}_1 ] \end{aligned}$$

(38a)

$$\begin{aligned} \dfrac{d}{dt} \textrm{E}[ {\varvec{X}}_2 ]&= {\varvec{A}}_1({\varvec{X}}_0) \, \textrm{E}[ {\varvec{X}}_2 ] + \textrm{E}[ {\varvec{A}}_2({\varvec{X}}_0,{\varvec{X}}_1)] \end{aligned}$$

(38b)

Because ${\varvec{x}}_0$ is asymptotically stable, choosing ${\varvec{X}}_0(0) = {\varvec{x}}_0$ implies that the Jacobian ${\varvec{A}}_1({\varvec{X}}_0)$ has negative real part eigenvalues. Therefore (38a) implies $\textrm{E}[ {\varvec{X}}_1 ] \rightarrow 0$ for $t \rightarrow +\infty$, i.e. point (a).

For $\textrm{E}[ {\varvec{X}}_2 ]$, we have at steady state

$$\begin{aligned} \textrm{E}[ {\varvec{X}}_2 ] = - {\varvec{A}}_1^{-1}({\varvec{X}}_0) \, \textrm{E}[ {\varvec{A}}_2({\varvec{X}}_0,{\varvec{X}}_1) ] \end{aligned}$$

(39)

where $\textrm{E} [{\varvec{A}}_2({\varvec{X}}_0,{\varvec{X}}_1) ]$ is calculated as follows. Taking into account that ${\varvec{X}}_1^T {\varvec{H}}_i({\varvec{X}}_0) {\varvec{X}}_1$ is a scalar, we have

$$\begin{aligned} \textrm{E}[{\varvec{X}}_1^T {\varvec{H}}_i({\varvec{X}}_0) {\varvec{X}}_1 ]&= \textrm{tr} \left( \textrm{E}[{\varvec{X}}_1^T {\varvec{H}}_i({\varvec{X}}_0) {\varvec{X}}_1 ] \right) \nonumber \\&= \textrm{tr} \left( {\varvec{H}}_i({\varvec{X}}_0) \, \textrm{E} \left[ {\varvec{X}}_1 {\varvec{X}}_1^T \right] \right) \end{aligned}$$

(40)

where we used to cyclic property of the trace, and the fact that ${\varvec{H}}_i$ is symmetric. Taking into account that asymptotically $\textrm{E}[{\varvec{X}}_1] = 0$, it follows that $\textrm{E}[{\varvec{X}}_1 \, {\varvec{X}}_1^T ] = \sigma _{{\varvec{X}}_1 {\varvec{X}}_1}$ that proves (b).

To prove (c), we use (34b) to obtain

$$\begin{aligned} d ({\varvec{X}}_1^T \, {\varvec{X}}_1)&= ({\varvec{A}}_1 {\varvec{X}}_1 {\varvec{X}}_1^T + {\varvec{X}}_1 {\varvec{X}}_1^T {\varvec{A}}_1^T + {\varvec{B}}_0 {\varvec{B}}_0^T ) dt \nonumber \\&\quad + ({\varvec{B}}_0 \, {\varvec{X}}_1^T + {\varvec{X}}_1 \, {\varvec{B}}_0^T) dW_t \end{aligned}$$

(41)

Taking expectation on both sides yields the Liapunov equation

$$\begin{aligned} \dfrac{d \sigma _{{\varvec{X}}_1 {\varvec{X}}_1}}{dt} = {\varvec{A}}_1 \, \sigma _{{\varvec{X}}_1 {\varvec{X}}_1} + \sigma _{{\varvec{X}}_1 {\varvec{X}}_1} \, {\varvec{A}}_1^T + {\varvec{B}}_0 {\varvec{B}}_0^T \end{aligned}$$

(42)

Considering that ${\varvec{A}}_1$ is stable and that ${\varvec{B}}_0 \, {\varvec{B}}_0^T$ is symmetric, the steady state solution

$$\begin{aligned} \lim _{t\rightarrow + \infty } \sigma _{{\varvec{X}}_1 {\varvec{X}}_1} \end{aligned}$$

is unique, and it satisfies the Liapunov equation in point (c). $\square$

Using the results of theorem 3, it is possible to calculate each term of (35) and (37), finding the approximate first and second order moments for the stochastic process ${\varvec{X}}_t$.

6 Results and discussion

We have applied the method derived in Sect. 5 to the analysis and design of the piezoelectric energy harvesters described in Sect. 2. We have used Theorem 3 to calculate the approximate second order moments given by (37), that in turns permits to determine the average harvested power and power efficiency thanks to Corollary 1.

To assess the advantage provided by the matching network, we have applied the method also to the energy harvester with the simple resistive load, and to the power factor corrected load. For the harvester with matching network and with power factor corrected load, we have calculated the harvested power and power efficiency for all values of the circuit parameters in the electrical part ($L_S$ and $C_P$ for the former, L for the latter) in a given range, in order to find the values that correspond to the maximum output average power.

The values of the other parameters used in our analysis are summarized in Table 1. With these values, the Jacobian matrix evaluated at ${\varvec{x}}_{\pm }^*$ has one real negative eigenvalue, and two pairs of complex conjugate eigenvalues, all with negative real parts, confirming that the two equilibrium points are both stable, of focus type. Conversely, the Jacobian matrix evaluated at ${\varvec{x}}_0^*$ has one real positive eigenvalue, two real negative eigenvalues, and one pair of complex conjugate eigenvalues with negative real parts, confirming that that the origin is an unstable equilibrium point, of saddle–focus type.

Table 1 Values of the energy harvester parameters

Figure 4 shows the root mean square of the output voltage $v_{\text {o(rms)}} = \sqrt{\textrm{E}[v_{\text {o}}^2(t)]}$, versus the parameters of the matching network $L_S$ and $C_P$. The strength of mechanical vibrations is set to $\varepsilon = 20$ mN. The output voltage is maximum for $L_S=162.4545$ H, and $C_P = 22.273$ nF. It is worth noticing that the relatively high value of the inductance (and of the root mean square output voltage) is a consequence of the normalization imposed on the harvester mechanical mass, as discussed in [10, 14].

Fig. 4

Root mean square value of the output voltage $v_{\text {o(rms)}} = \sqrt{\textrm{E}[v_0^2(t)]}$ vs. parameters of the matching network $L_S$ and $C_P$

For comparison, Fig. 5 shows the root mean square of the output voltage for the energy harvester with power factor corrected load (4), versus the inductance L. Again, the output voltage shows a maximum at $L=36.69$ H.

A comparison between the power performance for the three load setups is summarized in Table 2. Our analysis shows that for the energy harvester with the resistive load, the load absorbs a very limited average power and thus the system offers a very limited power efficiency. Application of a power factor correction improves significantly both the output average power and the power efficiency. However, the matched load setup provides a better average harvested power and a higher efficiency, even with respect to the power factor corrected load.

Fig. 5

Root mean square value of the output voltage $v_{\text {o(rms)}} = \sqrt{\textrm{E}[v_{\text {o}}^2(t)]}$ vs. inductance L for the power factor corrected load

Table 2 Average harvested power and power efficiency for the energy harvester with the three different load setups

In general, it is impossible to prove that the approximate solution obtained through the power series expansion converges to the true solution, but there is a large amount of evidence that the error becomes negligible for $\varepsilon \rightarrow 0$. To validate the accuracy of the the power series expansion method, we compare theoretical predictions with results from numerical simulations. We have performed Monte Carlo simulations, integrating numerically the SDE systems (3)–(5) for different values of $\varepsilon$, and we calculated the corresponding output voltage, average output power and power efficiency. The numerical integration has been performed using as integration schemes both Euler–Maruyama and stochastic Runge–Kutta with strong order of convergence equal to one. For both methods, the integration length was set to $\Delta t = 10^4$ s, with an integration step $\delta t \sim 30\,\upmu$s. Given the small value of $\delta t$, no significant differences between the two numerical schemes were observed. To obtain more accurate results, for each set of parameter values, we did run 20 simulations, with 20 different realizations of the Wiener process, and we averaged the results after eliminating the transient portion of the solution.

Figure 6 shows the relative error between theoretical predictions and numerical simulations, as a function of the noise intensity, for the energy harvester with matched load. The relative error for both the root mean square output voltage (red diamonds), and the power efficiency (black circles) are shown. The relative error is evaluated as the difference between theoretical predictions and numerical simulations, normalized to the latter:

$$\begin{aligned} \Delta x_{\text {rel}} = \dfrac{\left| x_{\text {th}} - x_{\text {sim}}\right| }{x_{\text {sim}}} \end{aligned}$$

(43)

As expected, the relative error is negligible for $\varepsilon \rightarrow 0$, and it increases along with the noise intensity. The error becomes rapidly significant when the beam begins to jump between the two potential wells.

Fig. 6

Relative error between theoretical predictions power series expansion method and Monte-Carlo simulations versus the noise intensity, for the root mean square output voltage (red diamonds), and the power efficiency (black circles). (Color figure online)

Fig. 7

Displacement x(t) versus time for the harvester with resistive load. Top: Noise intensity $\varepsilon = 200$ mN. Bottom: Noise intensity $\varepsilon = 500$ mN

Fig. 8

Displacement x(t) versus time for the harvester with matched load. Top: Noise intensity $\varepsilon = 200$ mN. Bottom: noise intensity $\varepsilon = 500$ mN

Figures 7 and 8 show one realization of the displacement x(t) as a function of time, obtained through numerical simulations, for the resistive and for the matched load case, respectively. We show results for two values of the vibration intensity: $\varepsilon = 200$ mN (above), and $\varepsilon = 500$ mN (below). In the first case the cantilever beam vibrates around one of the stable equilibrium points (which one, depends on the initial condition), while in the second case excursions from the basin of attraction of one equilibrium point to the other occur.

Figure 9 offers an alternative visualization of the same process. It shows the asymptotic probability distribution for the position x(t), for the two different noise intensities above. The probability to find the system in the state $x + dx$ has been evaluated as the number of samples in that interval, normalized to the total number of samples. For noise intensity $\varepsilon = 200$ mN, the system is trapped in the basin of attraction of one equilibrium point, that corresponds to one potential well of $U(x) = - k_1 x^2 + k_3 x^4/4$ (top). For a noise intensity $\varepsilon = 800$ mN, the system wanders from one well to the other, because the two wells are equally deep, the probability distribution also tends to be symmetric. If the noise intensity is large enough, the two peaks of the probability distribution merge together partially overlapping.

Fig. 9

Asymptotic probability distribution for the position x(t). Top: noise intensity $\varepsilon = 200$ mN. Bottom: Noise intensity $\varepsilon =800$ mN

Fig. 10

Root mean square of the output voltage versus vibration intensity for the harvester with simple resistive load (black circles), power factor corrected load (blue squares), and with matched load (red diamonds). (Color figure online)

Finally, Fig. 10 shows a comparison of the root mean square output voltage versus the vibration intensity for the energy harvester with the simple resistive load, the power factor corrected load, and the matched load. The power factor corrected load offers higher output average voltage, and therefore higher power efficiency with respect to the simple resistive load. In particular, the power factor corrected load offers more than 14 times the power harvested by the simple resistive load, increasing the efficiency from less than 5% to almost 64%. Application of the matching network increases the output voltage by almost 17 times with respect to the resistive load, boosting the efficiency to more than 74%.

7 Conclusions

In this contribution we have presented a comprehensive modeling approach for a bistable piezoelectric energy harvester subject to random mechanical vibrations. The model combines the description of the mechanical oscillator, of the linear description of the piezoelectric transducer, and of the possible inclusion of a reactive matching stage interposed between the piezoelectric transducer and the electrical load. Nonlinearity is included in the mechanical elastic potential. The resulting equations of motion form a system of nonlinear SDEs.

As the main contribution, we have shown that interposing a matching network between the transducer and the load significantly increases the output average power and the power efficiency. In fact, a properly designed matching network reduces the impedance mismatch between the harvester and the electrical load, increasing the average power absorbed by the latter. Although perfect matching is possible only for a linear harvester and at a single frequency, a broadband matching network can be designed that achieves partial matching over a wide frequency interval.

To design the optimal matching network, one should solve the SDE system for all values of the circuit parameters, a computationally heavy and time consuming task. As a second contribution, we have developed a methodology to determine the ideal matching network parameters. The technique is based on finding an approximate solution to the SDE system in the weak noise limit, using a power series expansion method. The approximate solution is then used to calculate the first moments for the stochastic processes, in particular the average output voltage.

Monte Carlo numerical simulations confirm that application of the matching network offers higher average output voltage and power efficiency also for moderately high noise intensity, even with respect to other, previously proposed, load setups.