1 Introduction

Real-world engineering systems typically consist of many components accompanied by a large number of parameters and degrees of freedom, which give rise to complex emergent dynamical behavior. The analysis of structural vibrations remains challenging in many fields of engineering today, not only because large-scale numerical methods exhaust the computational resources but also because nonlinear and damping phenomena [1] pose difficulties to our modeling and prediction capabilities [2, 3]. The dynamics of these machines often depend on a large number of parameters [4, 5], such as loading conditions or uncertain components [6], whose change during the operation or the lifetime of the system can cause bifurcations or critical regime shifts [3, 7]. It is crucial for the safe operation of complex machines to analyze and understand the mechanisms behind parametrically driven regime changes to prevent critical transitions into unwanted or even dangerous points of operation. In the following, we refer to parameters when reasoning about different external loads imposed by the operation and secondary changes to system component properties, such as reduced stiffness values resulting from higher temperatures caused by heavy loading conditions. Our approach is generically applicable to many high-dimensional nonlinear dynamical systems. In this paper, automotive disk brake systems and their rich friction-induced vibrations are taken as illustrative exemplary application case.

Today, the main approaches to understanding the rich nonlinear dynamics of machines are either of experimental nature or rooted in simulations based on first principles of physics [5]. Some engineering domains rely primarily on experimental tests for research and design purposes [3], which are often costly and time-consuming [8]. Since only a limited number of tests can be performed for some characteristic points of operation, the information on the state of the dynamical system in the high-dimensional parameter space is only available at specific points. This sparse experimental sampling of the parameter space could lead to unobserved phenomena in the system dynamics for unseen parameters. An example of this aspect is depicted in Fig. 1: The dynamical system under consideration exhibits unstable behavior for a given set of parameters that is not covered by experimental data. The second common approach to analyzing the dynamics of a sizable dynamical system is rooted in numerical simulation. High-dimensional numerical models and complex multi-scale, multi-physics simulations are often necessary to represent the dynamics. Large-scale multi-physics simulations of a system are computationally expensive and have a significant climate footprint. Because experimental tests are time-consuming and expensive, and numerical models are often computationally very costly, obtaining a finely-grained state map for a dynamical system is complex with current methods. Our research aims at providing a time- and cost-efficient way of generating a high-resolution state map as a post-processing technique for either experimental or numerical results. On the example of automotive disk brake systems, a detailed description of state-of-the-art methods, and our contribution, is given in the following.

Friction-induced vibrations (FIV) of vehicles, for example, automotive or aircraft braking systems, represent a family of complex dynamical systems [6, 9, 10] whose dynamics depend on many parameters and parameter inter-dependencies [9, 11, 12], as well as being sensitive to parameter variations [10, 13]. Several mechanisms for explaining FIV have been proposed in [9, 11, 14, 15], as friction brake systems have seen a rich research history in the last decades [9,10,11,12, 15,16,17]. A detailed review of these can be found in [9] and [18]. However, FIV are notoriously difficult to grasp experimentally, because of the limited repeatability of results [9, 13], which is likely due to the sensitive dependence of the system on small-scale parameter variations [7]. Still, expensive experiments [9, 12] remain a crucial pillar in the analysis of brake systems and validation of simulation models. Because simplified models that neglect the effects of time-varying, uncertain parameters are often not accurate enough in their predictions [7, 13, 16, 19], the brake system models often involve large-scale finite element models and elaborate computational schemes such as complex eigenvalue analysis [9, 10, 12, 17] and transient analysis [10, 11, 14, 17, 20]. As complex eigenvalue analysis misses the effects of nonlinearities [9, 10], a nonlinear transient analysis is often required to study the impact of parameter variations on the stability of the system [9, 11, 14, 17, 20]. In all these methods, considerable computational times remain an issue [9, 11, 14, 16, 17, 20, 21], which poses a challenge to performing extensive parameter studies [16] for realistic loading conditions seen during customer driving. Therefore, current research efforts focus on advancing methods to deal with uncertainties and nonlinear effects, increasing model accuracy and decreasing computation time, see [9,10,11, 16, 17, 20].

Fig. 1
figure 1

Illustration of a data-based state map. A data-based state map for a complex dynamical system illustrates the system states within a space spanned by two predefined parameters. Each point on the map represents one data sample and is color-coded to the state of the system for a given sample. Darker colored dots mark the sparse information available from experiments; lighter colors represent a possible fill-in of the white spaces that will be obtained with the method proposed in this work. It is possible that “islands of instability” exist, which are not captured by the data gained from experiments

Full size image

As both experimental analysis and modeling of brake system remain challenging, obtaining a detailed state map for a brake system with state-of-the-art methods, for example, from measured data or numerical simulation alone, is currently very expensive. Therefore, the system state, in the simplest form given by the binary indication of the occurrence of high-amplitude vibrations, is only known for a few points of operation and unknown in most of the high-dimensional (loading) parameter space. In this work, we propose a purely data-based approach to obtaining a fine-grained map, which is computationally less expensive and requires only a limited number of experimental results. Data-driven methods have recently evolved to complement conventional modeling methods [22]. Neural network models trained on large data sets do not rely on suitable reduced order modeling [23] or quasi-static dynamic observations and can interpolate within the input value range they have been trained in, making these models ideal candidates for the computation of state maps from sparse measurements.

In this work, we propose a new, data-driven approach for approximating the functional behavior of real-world machines using input–response relationships from experimental observations to generate a machine learning-based state map. First, a neural network model is trained with real-world measurement data to predict the system state in a specific loading and parameter configuration. If this data-driven modeling is successful, the neural network model has picked up complex parametric relations and hidden mechanisms that were activated during testing, but are not necessarily discernible to a human or accessible via classical system identification. The trained model can then be queried for the system state for new conditions and parameters beyond those tested experimentally. A set of synthetic input data is generated to fill the white spots in the parameter space and fed into the neural network model. The predictions of the model for these new points can be used to build a data-based state map over the “complete parameter space” in a very cost- and time-efficient manner, even if the parameter space was originally only sparsely sampled through measurement data, as illustrated in Fig. 1. The method is demonstrated with real-world experimental data from a friction brake obtained at Hitachi Astemo in Drancy, France. This complex system contains rich dynamical behavior that has not been fully understood until today [7, 10, 11, 13, 24], making it an interesting case study for the proposed method.

2 Methods

A novel and universal way of obtaining a state map illustrating the state of a dynamical system over a space spanned by a chosen set of parameters in a purely data-based fashion is proposed in this work. This section gives a schematic overview of the process, followed by more detailed presentations of the underlying real-world measurement data, the involved machine learning process, necessary data preparation, and the data augmentation procedure.

2.1 Schematic overview

The method proposed in this work can be split into two stages, namely a machine learning model training phase and a state map computation phase, as illustrated in Fig. 2. In the first phase, a neural network model is trained and validated using real-world experimental data from brake testing to predict the system state for a given set of input data. In the second phase, the model is queried for the system state using synthetically generated data to fill up the parameter space that is only sparsely sampled through the experimental data. Physics-consistent augmentation of the measurement data is the essential piece to this undertaking. This way, the model can be used to predict the state of the system over the entire range of parameter combinations, ultimately yielding a state map of the complete parameter space.

Fig. 2
figure 2

Generation of a machine learning-based state map. A schematic overview of the method proposed in this paper, in which a two-dimensional state map representing the state of a dynamical system over a chosen set of features is computed in a purely data-driven way. The process can be split into two phases, a neural network model training phase, and a state map computation phase

Full size image

During the first phase, a neural network model is trained with experimental data obtained from a test rig at Hitachi Astemo France to represent complex input–output relationships between a set of measured quantities and a system state, here encoded in form of a binary squeal/no-squeal label. In preparation for the machine learning application, the raw data is processed using a sliding window method and split into a training and validation set for neural network model training and validation, as described in Sect. 2.2. During the data processing, binary squeal/no-squeal labels are assigned to each data sample from machine learning input/output data. A neural network model is then trained and validated with the processed real-world data, see Sect. 2.3. When the training is successful, the neural network model has learned complex parametric relations in terms of a mapping from input to output data that is based on features of the high-dimensional input data. These features can be any property of the input data or a combination thereof, and as these are not directly discernible to the user, they are referred to as “hidden.” The model can predict whether or not a section of a braking is noisy for a given set of input parameters. Then, the obtained model can be deployed to predict the system state for parameter sets it has not seen before.

In the second phase, the trained model is exploited to compute state maps based on physics-consistent variations of the experimental data. The two-dimensional state map requires a featurization of the input samples with two basis parameters that form the two axes of the state map. As the parameter space spanned by the two chosen parameters is sampled only sparsely through the available measurement data, additional data has to be generated. The sparse measurement data is augmented in a physics-consistent manner to fill the parameter space, as described in Sect. 2.4. This synthetic data is fed into the machine learning model that outputs the system state in a binary label form, namely silent or noisy, for each new, synthetically generated data sample. These predicted labels are recorded in the two-dimensional parameter space, forming a purely data-based state map. The following sections are dedicated to describing the process in more detail.

2.2 Data acquisition

The data used in this work is real-world measurement data obtained from a dynamometer test rig at Hitachi Astemo. A standard disk brake system with prototype-material brake pads is tested. The test setup is depicted in Fig. 3, including the microphone location for recording the brake noise 50 cm away from the axle. The measurements are taken in a temperature- and humidity-controlled environment. The load on the brake system originating from the vehicle chassis is simulated by the surrounding structure.

Fig. 3
figure 3

Test rig. The dynamometer test rig at Hitachi Astemo France, which was used to record the data used in this work. A disk brake system consisting of disk, caliper, bracket, and brake pads is tested in a controlled environment, where the impact of the vehicle chassis is simulated by the surrounding structure. A microphone is located close to the disk for recording the brake noise. Additional verification of the noise is given by accelerometers located on the caliper

Full size image

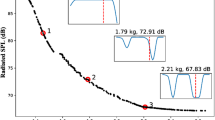
The brake testing is performed according to the industry standard noise, vibration, and harshness (NVH) test procedure SAE-J2521 [25], which consists of a set of initial break-in and burnishing tests, after which several drag and stop brakings are carried out. The brake system is subjected to a series of temperature and velocity ramps to cover a wide range of braking scenarios. Figure 4 shows an overview of the SAE-J2521 data channels used in this work, namely brake pressure p, rotational velocity \(v_{\text {rot}}\), brake torque M, friction coefficient \(\mu \), rotor temperature \(T_{\text {rot}}\), ambient temperature \(T_{\text {amb}}\), relative ambient humidity \(H_{\text {rel}}\), and noise level. The friction coefficient \(\mu \) is a derived quantity that is computed by the test bench directly using a Coulomb-type friction model assumption, i.e., the linear relationship between normal force and resulting friction force via the friction value. A total of 2498 brakings with 36 % noise occurrence are available. An overview of the measurement channels and value ranges is given in Table 1. The first seven measurement channels are recorded with a frequency of 100 Hz, while the sound pressure for the brake noise detection is recorded with a microphone and accelerometer at 51.2 kHz.

Fig. 4
figure 4

Available data. Overview of the measurement data from 2498 brakings recorded with the industry standard SAE-J2521 [25] test procedure. The test protocol consists of a series of temperature ramps combined with different load cases, i.e., various velocity and brake pressure conditions. The recorded noise levels are also indicated. For clarity, maximum values are reported for the first five channels, and mean values for ambient temperature and relative humidity, while the noise-level information is limited to the number of available frequencies

Full size image
Table 1 Summary of experimental data channels and value ranges
Full size table

During the brake tests, noise detection is carried out with the microphone signal using a dBA threshold on the peak value of the sound pressure level (SPL) and the average spectrum. Tonal noises in the frequency range of 1 to 12 kHz and more than 70 dBA are labeled brake noises. The detected noise is validated using an additional accelerometer which measures the vibrations on the brake directly. Only if a noise is found in both signals, it is considered valid. For the purpose of this work, the noise start time and duration were recorded additionally to the standard time of maximum SPL for each braking. This procedure allows for more precise localization of the noise occurrence within a given braking and facilitates a straightforward label generation.

Fig. 5
figure 5

Data processing. The data-processing procedure consists of generating a binary label classifying the system state as either “0” or “1” for silent or squealing, respectively, and a sliding window approach for generating equal-sized samples. The process is illustrated for one exemplary braking. The final input–output data for our machine learning models consists of 9896 samples, each of which is 4 s long and has a binary label denoting the system state as either squealing or non-squealing

Full size image

The recorded raw data is submitted to some preprocessing for the machine learning application, as illustrated in Fig. 5, for one exemplary braking with eight measurement channels. For each time instance, the system state is labeled either squealing or non-squealing, generating a time series of binary labels encoding the system state as 0—silent, or 1—noisy, which replaces the sound pressure level of the raw data. Additionally, the data is split into equally-sized windows using a sliding window approach with a window length of 400 time steps, or 4 s and an overlap of 50 %. To determine an optimal sliding window size, different variants in the range of 2 to 10 s were tested. The chosen option of 4-s samples was found to yield the best predictions results, balancing the number of generated samples, which here increases with a smaller sample size, with the time history included in each sample, which increases with a larger sample size. To avoid data leakage between the training and test set and a clean training procedure, the original set is split into five folds of training and test (validation) data at an 80–20 split before the sliding window is performed. A stratified split is implemented to ensure an equal class distribution between training and test data. The entire processed data consists of 9896 samples in total. In the final preparation step, the channel containing the time-distributed labels is condensed from 400 time steps down to one value. A sample is given the label “1” for noisy if a squeal is indicated within a given sample, that is, if there is a noisy section within the 4-s interval, or “0” otherwise. The final input/output data consist thus of sets of 4-s samples, seven channel samples input with a binary label output. The noise occurrence of 20 % in the processed data set of smaller samples differs from the original noise occurrence due to the sliding window processing.

An overview of the experimental data before and after the processing is given in Table 2, indicating the value range for each data channel. The fivefold 80:20 data split for the neural network modeling results in five training–test data pairs, where each training split contains 7975 samples and each test split consists of 1921 samples, each with a noise ratio of 20 % ± 1 %, respectively.

Table 2 Summary of processed data characteristics. The ratio of noisy samples varies from raw data to processed samples due to the slicing during the sliding window processing routine
Full size table

2.3 Neural network modeling

The neural network modeling task at hand is a binary classification task, where the neural network model classifies the system state in terms of a binary label of “0” or “1” for silent or noisy for a given input sample. One input sample consists of 4 s or 400 time steps of a multi-variate time series with seven channels given by the recorded measurement channels brake pressure p, rotational velocity \(v_{\text {rot}}\), brake torque M, friction coefficient \(\mu \), rotor temperature \(T_{\text {rot}}\), ambient temperature \(T_{\text {amb}}\), and relative ambient humidity \(H_{\text {rel}}\). A convolutional neural network (CNN) is trained with the experimental data using a binary cross-entropy loss function. The neural network modeling is implemented in Python using the machine learning framework TensorFlow. Several hyperparameter studies are performed to obtain a suitable model for the given prediction task, for example, testing different numbers of hidden layers. Additionally, k-fold cross-validation with five folds is carried out for each set of hyperparameters to ensure model performance does not depend on a lucky training–test data split. It is also possible to retain a certain amount of data from the training for independent model evaluation, but since the experimental data set is already relatively small, k-fold cross-validation is deemed a more suitable method in this case. A 1D CNN with two hidden layers, 64 filters per layer, and a kernel size of 3 is found to attain the highest classification scores.

After the training is completed, the model is evaluated using the Matthews correlation coefficient (MCC) [26] to obtain a more tangible measure of model performance. The MCC is defined as

$$\begin{aligned} MCC \!=&\!\frac{TP \cdot TN \!-\! FP \cdot FN}{\sqrt{(TP\!+\!FP)(TP\!+\!FN)(TN\!+\!FP)(TN\!+\!FN)}} \nonumber \\&\in [-1,1], \end{aligned}$$
(1)

where TP, TN, FP, and FN denote true positives, true negatives, false positives, and false negatives, respectively. This performance measure accounts for the class imbalance between silent and noisy samples and ranges from \(-1\) to 1, indicating a perfect negative and perfect positive correlation between the true and the predicted labels, respectively. Due to its value range, the MCC is not usable directly as a loss function.

The neural network model deployed for computation of the state map in the following achieves an MCC = 0.73 ± 0.02 (accuracy of 90.6 % ± 0.01) on the test data set. The confusion matrix obtained with the said model on the test data set is shown in Fig. 6, where the labels predicted by the CNN are plotted against the true labels. For better readability, the values are given in percent of the total number of samples in the test set.

Fig. 6
figure 6

Model training performance. The performance of the trained CNN, which is used for further computations, is illustrated by the confusion matrix on the test data set. The labels predicted by the CNN are shown against the ground-truth labels; values are given in % of the total number of samples in the test set. The model achieves a MCC = 0.73 ± 0.02 (accuracy of 90.6 % ± 0.01) for the test data set

Full size image

2.4 Physics-consistent data augmentation

This work aims at generating a complete 2D state map that represents the system state over a space spanned by two chosen parameters to obtain a high measure of abstraction. The first step in the data augmentation process is thus the choice of an appropriate featurization of the data samples from a seven-dimensional time series into two parameters. This step is necessary to visualize the high-dimensional data set in a two-dimensional space. Here, the maximum rotational velocity \(v_{\text {rot,max}}\) and maximum brake pressure \(p_{\text {max}}\) per 4-s sample time series are chosen, which represent two characteristics of the macroscopic load conditions on the brake system. Any other measure of the samples, such as mean values, derivatives of the measurement time series, or values from the remaining measurement channels, for example, the temperatures, would be conceivable, as well as an extension to more than three dimensions. A purely measurement data-based state map results from this featurization. Figure 7 shows the result of the featurization of the test data set, illustrating that the parameter space spanned by \(v_{\text {rot,max}}\) and \(p_{\text {max}}\) is only sparsely sampled by experimental data. Blue squares denote non-squealing samples, and red dots mark noisy samples.

To fill in the white spaces in this initial, very sparsely populated state map obtained from the measurement data, synthetic data samples are generated that fill up the 2D parameter space. The new data is fed into the machine learning model for state prediction. The additional data is generated from a base sample taken from experimental data, which is subjected to a physics-consistent data augmentation, as depicted in Fig. 7. To begin with, a base sample is chosen from the test data set of the processed experimental data, ensuring the neural network model predicted the system state for the base sample correctly during the model testing phase. The time-series values of this base sample are varied systematically by adding and subtracting constant values to the time series in the two featurized dimensions \(v_{\text {rot}}\) and p until the parameter space is filled up in a grid-like fashion. To remain consistent with the physics of the system, the brake torque M is varied along with the brake pressure p. All other parameters such as the friction coefficient \(\mu \), rotor temperature \(T_{\text {rot}}\), ambient temperature \(T_{\text {amb}}\), and relative ambient humidity \(H_{\text {rel}}\) are kept as in the original sample to ensure the state map represents the system stability over a variation of the chosen parameterization instead of other hidden variables.

Fig. 7
figure 7

Data augmentation. The physics-consistent data augmentation process forms the basis for the state map computation. First, a featurization of the full-scale data samples with two parameters is chosen. In this case, the maximum rotational velocity \(v_{\text {rot,max}}\) and maximum brake pressure \(p_{\text {max}}\) for a given 4-s sample. Plotting the system state in form of blue dots for non-squealing measurement samples and red squares for squealing samples over these two parameters yields a sparely sampled state map. To fill in the blank spaces, a systematic variation of the two parameters \(v_{\text {rot,max}}\) and \(p_{\text {max}}\) is performed from one base sample by adding constant values to the respective time series \(v_{rot}\) and p of the base sample. The other measurement channels are kept at their initial time series to separate out the two chosen parameters. However, to remain consistent with the physics of the system, the brake torque M is varied along with the brake pressure p. The result of the data augmentation process is a new, synthetic set of input data for which the system state is not yet known and thus illustrated by black dots in the right image

Full size image

The data augmentation process is performed carefully, with the laws of physics and information from the experimental data in mind. Nonetheless, there can be no guarantee that our newly generated data is physically meaningful, especially for points of the state map far away from the base sample. However, there are several points in favor of our data augmentation method being consistent, which we will be elaborated on in the following. First, the SAE-J2521 procedure is parameterized to contain repeating brakings with the same brake pressure and rotational velocity profiles, while systematically varying the overall pressure and velocity levels and the (initial) rotor temperature. The imposed temperature ramps are shown in Fig. 4. As a result, brakings with similar profiles but different value levels for each channel exist. Second, basic physical principles are accounted for in our data augmentation method since the brake torque is varied along with the brake pressure. The range of brake pressure and torque pressure is computed over the data set, and the torque is varied by the same relative amount as the pressure. The main physical effect underlying our data is therefore accounted for. Any secondary effects such as a greater rise in rotor temperature with a greater energy input due to a greater brake torque are negligible locally because the induced changes are small. There are data samples in our experimental data set that support this hypothesis, as shown in Fig. 8. Each subfigure shows two samples taken from our experimental data set. Figure 8a shows two samples with different rotational velocities, where all other measurement channels are very similar. Figure 8b shows two samples with different brake pressure, and, respectively, different brake torque, where all other channels remain similar. Figure 8c shows two samples for which both quantities are varied, but the remaining channels are similar. These three data samples illustrate that variations like the ones we are performing in our data augmentation process do in fact exist in our data set and that it is reasonable to believe that our approach is physically meaningful.

Fig. 8
figure 8

Validation of the data augmentation procedure. Samples taken from the experimental data set underline the validity of the data augmentation method. In each subfigure, two experimental data samples are shown that differ only in 8a maximum rotational velocity \(v_{\text {rot,max}}\), 8b maximum brake pressure \(p_{\text {max}}\) and torque \(M_{\text {max}}\), and 8c all of these dimensions, while the remaining variables are very similar

Full size image

Nevertheless, it can be assumed that the augmented data is more meaningful closer to the base sample and that the resulting state map is more reliable the smaller the extent of the data augmentation. Improving the data augmentation process and including some measure of confidence in the final state maps are interesting and important points for further research.

A matrix of 100 by 100 augmented samples is generated using our data augmentation procedure, which densely fills up the parameter space spanned by the two chosen features maximum rotational velocity \(v_{\text {rot,max}}\) and maximum brake pressure \(p_{\text {max}}\), as shown in Fig. 7. As the system state for these newly generated data samples is not known a priori, these are marked by gray dots. In theory, it is possible to choose an arbitrarily high number of samples to fill up the space arbitrarily densely; however, the computational cost involved has to be taken into consideration.

Finally, the trained CNN obtained in Sect. 2.3 is queried for the system state for each sample in the augmented data set. If the model has picked up the hidden underlying dynamic mechanisms correctly, it can predict the system state for these synthetically generated data samples, filling up the white spaces in the state map given by the experimental data alone. This way, a state map over the entire parameter space is generated, as illustrated in Fig. 2. The state map divides the parameter space into squealing and non-squealing sections according to the binary label defined in the initial preprocessing routine. Theoretically, it would be possible to validate the obtained results by comparing the predictions of the ML model for specific \(v_{\text {rot,max}}\) and \(p_{\text {max}}\) to the known system state for the same value range from the experimental data set. However, the results presented in the next section indicate that a proper validation requires the samples to match not only in terms of \(v_{\text {rot,max}}\) and \(p_{\text {max}}\), but also in terms of hidden variables, which makes finding appropriate samples hard if they even exist in the experimental database. Developing a sophisticated validation scheme is therefore left for future work. Exemplary results are shown in the following section.

The entire process from generating the augmented data set to obtaining the state map can be repeated for different base samples, generating as many state maps as there are samples in the measurement data. By averaging the binary system state overall computed state maps, a probability state map can be computed, which contains not only binary 0/1 labels but probability values between 0 and 1, which approximate the probability of the system state to be squealing for a given set of parameters, here \(p_{\text {max}}\) and \(v_{\text {rot,max}}\). This probability state map is also presented in the next section.

Fig. 9
figure 9

State maps from base samples with similar \(p_{\text {max}}\) and \(v_{\text {rot,max}}\). Exemplary state maps (a) and b computed using two different base samples c in the data augmentation process. The location of the base sample in each state map is marked by a black star. Red areas indicate the system state as “squealing,” while blue areas indicate a non-squealing state. The two state maps appear quite different, even though the base samples are located closely together in the \(p_{\text {max}}\) and \(v_{\text {rot,max}}\) parameter space. A closer look at the qualitatively very different dynamics between sample 1 (dark blue line) and sample 2 (light blue, dashed line) in (c) suggests that the neural network model has indeed picked up hidden mechanisms and predicts the system state based on a complex system understanding beyond a mere pressure and velocity threshold

Full size image
Fig. 10
figure 10

State maps from base samples with similar \(p_{\text {max}}\) and \(v_{\text {rot,max}}\), and similar dynamics. For two base samples that not only match in terms of maximum values but also in terms of qualitative dynamic behavior (see (c)), the resulting state maps a and b appear very similar, illustrating the consistency of the method. State map 1 in a is generated based on sample one, shown by the dark blue line in (c), while state map 2 b is generated from sample 2, represented by the light blue dashed line in (c)

Full size image

3 Results

As explained in the previous section, the content of the synthetically generated data set depends on the chosen base sample. From a given data set, it is thus possible to obtain as many state maps for a given system as there are different base samples available within this framework. It is found that the shape of the squealing/non-squealing areas within a binary state map depends heavily on the underlying base sample, as will be elaborated on in the following.

Figure 9 shows two state maps, 9a and 9b, which are generated from two base samples as indicated by black stars in each subfigure. At a first glance, the two base samples appear to be similar since they are located closely together on the state map with \(p_{\text {max},1} = 22.5\) bar, \(p_{\text {max},2} = 22.5\) bar, and \(v_{\text {rot,max},1} = 78.5\) 1/min, \(v_{\text {rot,max},2} = 78.8\) 1/min, and the system state for both given samples is non-squealing. However, the resulting state maps look different. While the first state map 9a shows only a small squealing area for high brake pressures and low rotational velocity, accompanied by another small squealing area around \(p_{\text {max}}\) = 15 bar and low rotational speed, the second one 9b not only connects these two areas but expands them to higher rotational velocities and a small, disconnected island of the squealing state appears at about \(p_{\text {max}}\) = 5 bar and \(v_{\text {rot,max}}\) = 100 1/min. A closer look at the two base samples, see 9c, reveals that the qualitative dynamics of the system within the given 4-s intervals are different. While the brake pressure and brake torque decrease overall in sample one (illustrated by the dark blue line), these two parameters increase in total in the second sample (shown by the dashed light blue line), and the peaks of the respective channels, though reaching a similar maximum, are located at different times in each sample. Additionally, the gradients of both the friction coefficient and the disk temperature differ from one sample to the other. Considering the differences in the underlying hidden parameters in the two base samples, it is not surprising that the resulting state maps appear unalike. On the contrary, this observation indicates that the machine learning model has picked up some hidden variables and features in the training process and predicts the system state for a given sample based on a system understanding beyond a simple threshold on brake pressure and rotational velocity. Otherwise, the state maps would be the same for the same value range of \(p_{\text {max}}\) and \(v_{\text {rot,max}}\), independently of the remaining dynamics that may be prominent in the sample.

Following this reasoning, state maps generated with two similar base samples, namely samples that exhibit matching dynamics over time, should generate resembling state maps for our method to be consistent. Figure 10 shows that this is the case: The two base samples in 10c not only share almost identical maximum parameter values but also exhibit qualitatively very similar dynamics over all measurement channels, and the corresponding state maps in 10a and 10b match well. It can be concluded that our method yields congruent results, consistently exploiting hidden features from the input time series that are not directly accessible from the outside.

The results displayed in Figs. 9 and 10 illustrate that the state maps generated from different base samples with qualitatively different dynamics can be quite different. This distinctness is to be expected since it is well known that the appearance of brake squeal does not solely depend on a velocity or pressure threshold, but originates from a more intricate mechanism. It is reasonable to extend the concept of a binary state map to a probability state map, where the probability of the system operating in one state or the other for a given set of features is approximated within a value range from 0 to 1. As introduced in Sect. 2.4, such a probability state map can be obtained by computing a large set of binary state maps and averaging across the results. To obtain the probability state map shown in Fig. 11, \(N = 1223\) binary state maps were calculated and combined. The resulting probability state map represents how likely it is that the dynamical system, here the friction brake, assumes one of the two states, non-squealing or squealing, for a given maximum brake pressure and maximum rotational velocity over a given time span. Since many different base samples with different hidden variables, such as other channels or derivative measures, underlie each binary state map, the individual state maps used to compute the probability state map may differ. In averaging over a large number of samples, the influence of the hidden parameters is smoothed out, and the probability of different phenomena can be estimated. For example, it can be concluded from the probability state map in Fig. 11 that the island of the noisy state at low pressure and velocity visible in Fig. 9b rarely occurs for the given \(p_{\text {max}}\) and \(v_\text {rot,max}\) and its appearance is therefore highly dependent on the hidden variables.

Fig. 11
figure 11

Probability state map. A probability state map is obtained by computing binary stability maps for \(N = 1223\) different basis samples and averaging over the results. The map thus encodes the probability of the brake system to operate in the squealing or non-squealing state, where 1 indicates a 100 % chance of operation in the squealing regime and 0 represents a 100 % chance of arriving in the non-squealing regime

Full size image

4 Conclusion

A method for obtaining fine-grained maps representing the state of a dynamical system within a space spanned by operational conditions and high-dimensional parameters has been proposed in this work. Such a state map is difficult to obtain from numerical analysis or experimental data alone due to reasons including parameter uncertainties, numerical costs, and time consumption of experiments. Especially in the case of brake systems, where the system likely depends on small-scale parameter variations, existing measurements represent only sparse support in the parameter space. The presented method uses machine learning and physics-consistent data augmentation to generate state maps for the input samples in a time- and cost-efficient manner. By calculating many binary state maps using different base samples and averaging over them, probability state maps can be obtained that encode the probability of the dynamical system operating in one of two states. This way, only a limited number of real-world experiments are necessary to generate a full-scale and highly resolved state map. The method is shown to yield consistent results, exploiting the complex system representation picked up by a neural network during the training phase. The resulting state maps indicate the influence of the chosen parameters on the system state, while clearly illustrating that these are not the only relevant factors driving the system state. On the contrary, our results indicate that the chosen parameters, while providing an intuitive featurization for visualizing the data, cannot be taken as a single measure for reproducing the exact data labels. Testing different featurization or higher-dimensional state maps could yield additional insight into the driving mechanisms, which constitutes a starting point for future work.

Even nonlinear phenomena, such as multi-stability, become manageable through an appropriate choice of input data, i.e., by including the relevant initial conditions into the input data set. Choosing suitable parameters for the axes of the state map would make it possible to unfold even the hidden mechanisms driving the system through more than two states. The many interesting conceivable extensions to the proposed concept constitute additional possibilities for future work, including integrating a confidence interval into the computation of a probability state map such that the impact of each sample decreases radially around the initial feature values. An expansion of the method to higher-dimensional state maps by adding more parameters in the featurization is straightforward and might yield detailed insight into the mechanisms underlying dynamical regime changes.

This work hopes to contribute to a machine learning-driven system understanding beyond simple system representation and black-box modeling. As more and more real-world measurement data is available, data-based methods become increasingly valuable when it comes to analyzing dynamical systems. With a growing demand for sophisticated machines that can operate even under severe and changing environmental conditions, the need for a more detailed understanding of the underlying dynamics of a given system rises as well. The proposed method for data-driven state maps constitutes a significant step toward machine learning-based system understanding.