H_∞ optimization of cubic stiffness nonlinear energy sink attached to a linear system

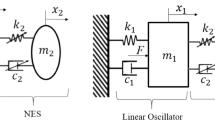
Abstract

Nonlinear energy sinks (NESs) have become a research hotspot due to their frequency robustness, but the optimization problem under harmonic excitation has not been adequately addressed. In this paper, the response of a single-degree-of-freedom system with a cubic stiffness NES attached under harmonic excitation is simplified to 1:1 internal resonance through the harmonic balance method, and H_∞ optimization is carried out on this basis. By comparing the frequency response curves (FRCs) of the system and the response of the system under the chirp excitation, the reliability of this approximation method is verified. Through the analysis of the fold bifurcations, the variation trend of the FRCs changing with the external excitation and the conditions for detached resonance curves to appear are obtained. The performance in three special cases is analyzed analytically, while the optimal parameters in general cases are analyzed numerically and fitted to obtain empirical formulas. The results show that the NES will fail applied on the undamped system due to a fixed point tending to infinity. When the external excitation is too large, the NES will amplify vibration of the linear system, and the damping of the NES has a very important influence on the vibration control if the damping of the system is relatively high. Finally, the performance of the NES is compared with the traditional linear vibration absorber (LVA). Although the best performance of the NES is not as good as the LVA, it can achieve multi-mode control under certain conditions.

Appendices

Appendix A

Stability analysis

Superimpose a small perturbation on the solution of periodic response

$$ u\left( \tau \right) = u_{0} \left( \tau \right) + u_{1} \left( \tau \right),\;w\left( \tau \right) = w_{0} \left( \tau \right) + w_{1} \left( \tau \right) $$

(A.1)

Substitute Eq. (A.1) into Eq. (2), and ignoring the infinitesimals obtains

$$ u^{\prime\prime}_{1} + \delta_{1} u^{\prime}_{1} - \delta_{2} w^{\prime}_{1} + u_{1} - 3\beta_{1} w_{0}^{2} w_{1} = 0 $$

(A.2a)

$$ \left( {1 + \varepsilon } \right)u^{\prime\prime}_{1} + \varepsilon w^{\prime\prime}_{1} + \delta_{1} u^{\prime}_{1} + u_{1} = 0 $$

(A.2b)

The perturbation is assumed to be

$$ u_{1} \left( \tau \right) = e^{\lambda \tau } \phi_{u} \left( \tau \right), $$

(A.3a)

$$ w_{1} \left( \tau \right) = e^{\lambda \tau } \phi_{w} \left( \tau \right) $$

(A.3b)

where $\phi_{u} \left( \tau \right) = C_{u} \cos \left( {\Omega \tau } \right) + S_{u} \sin \left( {\Omega \tau } \right),\;\phi_{w} \left( \tau \right) = C_{w} \cos \left( {\Omega \tau } \right) + S_{w} \sin \left( {\Omega \tau } \right)$

Substituting Eq. (A.3) into Eq. (A.2) yields

$$ \phi^{\prime\prime}_{u} \left( \tau \right) + \left( {2\lambda + \delta_{1} } \right)\phi^{\prime}_{u} \left( \tau \right) + \left( {\lambda^{2} + \delta_{1} \lambda + 1} \right)\phi_{u} \left( \tau \right) - \delta_{2} \phi^{\prime}_{w} \left( \tau \right) - \left( {\delta_{2} \lambda + 3\beta_{1} w_{0}^{2} } \right)\phi_{w} \left( \tau \right) = 0 $$

(A.4a)

$$ \left( {1 + \varepsilon } \right)\phi^{\prime\prime}_{u} \left( \tau \right) + \left[ {2\left( {1 + \varepsilon } \right)\lambda + \delta_{1} } \right]\phi^{\prime}_{u} \left( \tau \right) + \left[ {\left( {1 + \varepsilon } \right)\lambda^{2} + \delta_{1} \lambda + 1} \right]\phi_{u} \left( \tau \right) + \varepsilon \phi^{\prime\prime}_{w} \left( \tau \right) + 2\varepsilon \lambda \phi^{\prime}_{w} \left( \tau \right) + \varepsilon \lambda^{2} \phi_{w} \left( \tau \right) = 0 $$

(A.4b)

Using the Galerkin method to process Eq. (A.4) obtains a set of linear algebraic equations

$$ \left[ {\begin{array}{*{20}c} {\lambda^{2} + \delta_{1} \lambda + 1 - \Omega^{2} } & {2\lambda \Omega + \delta_{1} \Omega } & { - \delta_{2} \lambda - \mu_{1} } & {\mu_{2} - \delta_{2} \Omega } \\ { - 2\lambda \Omega - \delta_{1} \Omega } & {\lambda^{2} + \delta_{1} \lambda + 1 - \Omega^{2} } & {\mu_{2} + \delta_{2} \Omega } & { - \delta_{2} \lambda - \mu_{3} } \\ {\left( {1 + \varepsilon } \right)\left( {\lambda^{2} - \Omega^{2} } \right) + \delta_{1} \lambda + 1} & {2\left( {1 + \varepsilon } \right)\lambda \Omega + \delta_{1} \Omega } & {\varepsilon \lambda^{2} - \varepsilon \Omega^{2} } & {2\varepsilon \lambda \Omega } \\ { - 2\left( {1 + \varepsilon } \right)\lambda \Omega - \delta_{1} \Omega } & {\left( {1 + \varepsilon } \right)\left( {\lambda^{2} - \Omega^{2} } \right) + \delta_{1} \lambda + 1} & { - 2\varepsilon \lambda \Omega } & {\varepsilon \lambda^{2} - \varepsilon \Omega^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{u} } \\ {S_{u} } \\ {C_{w} } \\ {S_{w} } \\ \end{array} } \right] = 0 $$

(A.5)

where $\mu_{1} = \frac{{3\beta_{1} \left[ {3\Re \left( W \right)^{2} + \Im \left( W \right)^{2} } \right]}}{4},\;\mu_{2} = \frac{{3\beta_{1} \Re \left( W \right)\Im \left( W \right)}}{2},\;\mu_{3} = \frac{{3\beta_{1} \left[ {3\Im \left( W \right)^{2} + \Re \left( W \right)^{2} } \right]}}{4}.$

In order to ensure that there are nonzero solutions to Eq. (A.5), the determinant of the matrix on the left must be 0. From this, the Floquet exponents λ can be solved, which can be used to judge the stability of the periodic solution. If $\Re \left( \lambda \right) < 0$, the solution is stable. If $\Re \left( \lambda \right) = 0$ and $\Im \left( \lambda \right) = 0$, this solution is a point of fold bifurcations. If $\Re \left( \lambda \right) = 0,$ $2\pi \Im \left( \lambda \right)/\Omega$ is not equal to 0 or π, indicating that Hopf bifurcations occur.