Design and validation of a nonlinear vibration absorber to attenuate torsional oscillations of propulsion systems

Abstract

Recent developments in propulsion systems to improve energy efficiency and reduce hazardous emissions often lead to severe torsional oscillations and aggravated noise. Vibration absorbers are typically employed to palliate the untoward effects of powertrain oscillations, with nonetheless an adverse impact on cost and constrained efficacy over a limited frequency range. Recently, the authors proposed the use of nonlinear vibration absorbers to achieve more broadband drivetrain vibration attenuation with low complexity and cost. These lightweight attachments follow the concept of targeted energy transfer, whereby vibration energy is taken off from a primary system without tuning requirements. In this paper, the design and experimental investigation of a prototype absorber is presented. The absorber is installed on a drivetrain experimental rig driven by an electric motor through a universal joint connection placed at an angle, thus inducing the second-order torsional oscillations. Vibration time histories with and without the absorber acting are recorded and compared. Frequency–energy plots are superimposed to the system nonlinear normal modes to verify the previously developed design methodology, whereas the achieved vibration reduction is quantified by comparing the acceleration amplitudes of the primary system and monitoring the distribution of energy damped in the primary system and the absorber. The absorber prototype was found to lead to significant vibration reduction away from resonance and near resonance with the additional feature of activation over a relatively broad frequency range.

1 Introduction

Global legislations require the development of propulsion systems that produce lower levels of hazardous emissions, with particular emphasis on diesel engines. Lower emissions and improved energy economy are achieved through recent technological advancements, such as downsized engines [1]. However, there is an increased propensity for severe torsional oscillations due to reduced system weight. To mitigate these, manufacturers are employing various palliative measures. These include tuned vibration absorbers, such as clutch pre-dampers, the dual mass flywheel (DMF) [2] and DMF with centrifugal pendulum vibration absorbers (CPVA) [3, 4]. These palliatives are tuned to specific frequency range, and consequently, they are not acting in a broadband manner over the powertrain response. Thus, there is a requirement for vibration absorbers that would respond effectively over a broad frequency range without precise prior tuning. Nonlinear energy sinks (NESs) can play this role. The NES is a passive absorber, which follows the concept of targeted energy transfer (TET). The energy of mechanical oscillations is shifted in an almost irreversible manner from the donor (linear primary system) to a recipient (NES), where it may be absorbed, redistributed or dissipated [5].

Numerous publications in the available literature are dedicated to the understanding of TET and its potential applications in systems undergoing translational motion. Vakakis et al. [6] and Gendelman et al. [7] have studied TET in engineering systems that were excited by impulses. 1:1 stable sub-harmonic orbits (i.e. p:1 periodic orbits with period equal to p-times the period of the forcing term) were noted to act effectively on transferring energy from the primary system donor to the nonlinear vibration absorber. Vakakis et al. [8] studied the nonlinear normal modes (NNMs) activated in order to describe how the nonlinear absorbers interact with energy donors (linear primary systems). Kerschen et al. [9] studied linear systems attached to grounded and ungrounded NES to understand their nonlinear dynamics and the absorbers’ effectiveness. Luo et al. [10] designed a passive nonlinear vibration absorber to mitigate vibrations of a large-scale nine-floor structure. The design of NES nonlinear springs was realised through the use of pyramid-shaped elastomers, providing effective control on achieving the desired nonlinear force profile.

Limited number of studies exists on applications that include rotational NES, which are more suitable for attenuating torsional oscillations. In this regard, the application of a torsional NES to stabilise a drill-string system was examined in [11]. Gendelman et al. [12] studied the dynamics of a rotational NES mounted within a linear oscillator. Hubbard et al. [13, 14] studied experimentally the suppression of aeroelastic instabilities on a flexible wing using a rotational nonlinear vibration absorber. The NES was housed on the tip of the wing with piano steel wires as a mechanism for generating the cubic force nonlinearity. Recently, Haris et al. [15,16,17] showed numerically that nonlinear vibration absorbers with significantly low inertia can be effective in attenuating torsional vibrations of drivelines over a broader frequency range.

This paper presents the design and experimental analysis of an NES for suppressing torsional oscillations in a propulsion system. To the best knowledge of the authors, this is the first numerical and experimental demonstration of oscillation reduction for propulsion systems using NES hardware. In the next section, numerical analysis of the subsystem model with NES is presented, highlighting vibration attenuation over a broad frequency range. The design and experimental testing of the NES is then presented, correlating well with the model results for operation away and near resonance.

Fig. 1

a Subsystem rig schematic, b Inertia 2 acceleration amplitudes of the 1.5 Engine Order contribution with NES parameters $\hbox {J}_\mathrm{{NES}} = 10.7{\%}$ of Inertia 2, $\hbox {k}_{n} =2.2\times 10^{3}\hbox { Nm/rad}^{3}$ and $\hbox {c}_{n} = 0.001$ Nms/rad

Fig. 2

Angular velocity time history of Inertia 2 with Active and Locked NES ($\hbox {J}_\mathrm{{NES}} = 10.7{\%}$ of Inertia 2, $\hbox {k}_\mathrm{{N}} = 2.2\times 10^{3}\hbox { Nm/rad}^{3}$, $\hbox {c}_\mathrm{{N}} = 0.001$ Nms/rad)

2 Subsystem model equipped with NES

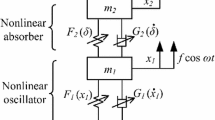
In recent publications, the authors demonstrated numerically that a single NES with cubic stiffness nonlinearity can attenuate the torsional oscillations of a driveline [15, 16]. In comparison with current state-of-the-art palliatives, the NES has the potential of being significantly lightweight, nevertheless capable of achieving more broadband vibration attenuation. Other types of stiffness nonlinearity were analysed, whereby it was conjectured that the lack of impacts in the driveline leads to ineffectiveness of vibro-impact NES. The authors have also demonstrated that the NES functions either by absorbing energy from the primary system while dissipating a fraction of energy locally or through redistribution of energy to the higher modes where it is dissipated easier due to their higher structural damping content [17]. These criteria were used in [15] to study the effect of different types of nonlinearity on reducing the amplitude of torsional vibrations, including cubic, quintic and vibro-impact. A large number of numerical simulations led to the conclusion that an NES with cubic stiffness can efficiently reduce the amplitude of torsional vibrations of automotive drivetrains within a higher frequency range. NES absorbers with vibro-impacts and fifth-order nonlinearity did not demonstrate better performance. For practical reasons related to the realisation of the nonlinearity, the cubic NES has been prioritised for experimental validation in this paper. Owing to the effective numerical performance of the NES, a prototype was designed and built for testing in a small-scale propulsion system rig, similarly to the model layout depicted in Fig. 1a. The two main inertias of the propulsion system are excited by the cyclic irregularities originating from an engine or motor. Brief description of the numerical model (originally presented in reference [16]) comprising the equations of motion, key parameter values and methods employed to generate the results presented in Figs. 1, 2 and 3 is provided in “Appendix A”.

Fig. 3

NES torque–deflection curve

Fig. 4

Schematic of the NES prototype a front view and b side view

Considering that low vibration absorber inertia is desirable in propulsion systems, the following set of NES characteristics has been selected: $J_\mathrm{{NES}} = 10.7{\%}$ of Inertia 2, $k_\mathrm{{N}} = 2.2\times 10^{{3}}\hbox { Nm/rad}^{{3}}$ and $c_\mathrm{{N}} = 0.001$ Nms/rad. A vehicle manoeuvre in first gear at 100% throttle is used to analyse the performance of the NES through the entire engine speed range. The 1.5 Engine Order (EO) acceleration amplitudes observed on Inertia 2 with (Active) and without (Locked) the NES acting are depicted in Fig. 1b, clearly indicating significant vibration attenuation in the frequency range 55–70 Hz. The time history of Inertia 2 angular velocity is shown in Fig. 2 for the aforementioned vehicle manoeuvre. The input speed range where the NES suppresses the 1.5 EO torsional oscillations is ranging approximately between 2200 and 3000 rpm (55–70 Hz). In the inset of Fig. 2 (starting around 1.8 s), the angular velocity fluctuations for the system with Active NES are noticeably reduced when compared to the system with Locked NES. The torque–deflection curve (generated by the numerical model) resulting in this effective NES performance is shown in Fig. 3. During peak performance, the NES would be producing approximately 15 Nm torque with a corresponding deflection of about $11^{\circ }$.

3 NES identification (quasi-statically)

Based on the numerical analysis and the identified nonlinear stiffness and inertia properties, a concept NES prototype was manufactured. The NES comprises two discs representing the inertia of the NES with two conical springs (Fig. 4) housed $180^{\circ }$ apart for targeting both the positive and negative regions of the torque–deflection characteristic curve (Fig. 3).

Fig. 5

a Comparison of the NES torque–deflection curves (model vs. experiment), b testing machine hysteretic curve

Fig. 6

a CAD drawing of the experimental rig and b rig photograph showing the NES, jaw coupling and universal joint

In order to ascertain that the designed NES conforms to the required parameters, quasi-static torque–deflection tests were performed. The NES was loaded and increasing torque was applied. The recorded torque–deflection curve is shown in Fig. 5a. It can be observed that the experimental curve follows the theoretical design characteristics closely. Nevertheless, the experimental torque–deflection curve shows a linear component at small deflections, which is expected to influence the NNMs of the system. Moreover, it is seen that a quintic function is more accurate than the cubic one. Therefore, the NES torque function selected for the computations to follow reads $T_\mathrm{{NES}}=k_{n}\, \theta +k_\mathrm{{nl}}\, \theta ^{5}$. The experimental curve has a small amount of hysteretic damping, which can be computed by evaluating the area enclosed by the hysteretic loop. The energy loss in the NES (Fig. 5a) during quasi-static testing was 0.3934 Nm. The energy loss of the testing machine itself was evaluated to be 0.3933 Nm (Fig. 5b) for the same test. This signifies that the NES has indeed low damping content.

Following the successful identification of the NES torque–deflection characteristics, it is essential to evaluate the designed prototype inertia. The NES device was loaded on a pendulum machine, where the pendulum plate was initially displaced and then released to perform 100 oscillations for which the total time was noted down. The process was repeated a few times, and an average inertia value was found to be within 2% of the designed value. This difference is not expected to significantly affect the NES performance.

4 Experimental set-up

The identification tests validated the designed NES stiffness and inertia to match the performance exhibited in the numerical simulations presented in Sect. 2. An experimental rig was built capable of producing speed harmonics of a rotating assembly driven by an electric motor. The set-up, shown in Fig. 6, includes an electric motor with a universal joint (UJ) connected to the motor’s output shaft. This type of connection introduces the second-order harmonics of the input speed, and it is therefore consistent with engine or motor-order vibrations typically observed in propulsion systems. The UJ output shaft is connected to a jaw coupling, which is used to induce an independent degree of freedom at the end of the set-up. This is required to assess the NES effectiveness in reducing the vibrations of a component that is not directly driven by the motor. The end connection of the jaw coupling is attached to a solid steel shaft, which will be hereafter referred to as the coupling shaft. The latter accommodates a hub to mount the NES onto the rotating component. The coupling shaft is connected to a weight disc representing the END inertia (see Fig. 6a) via a bellow coupling with high torsional stiffness. The whole rotating assembly was supported by self-aligning pillow block bearings.

The purpose of the experiments is to assess the torsional vibration reduction experienced by the coupling shaft due to the NES action. This is accomplished by running speed (frequency) ramps between 0-2000 rpm motor speed under two scenarios (namely, Active NES and Locked NES). In the first case of the Active NES scenario, the END inertia disc is removed and the system is excited at a range away from any resonant frequency. In the second of the same scenario, the END inertia is attached and resonance can be observed in the primary system. In both cases, the NES is attached to the coupling shaft and measurements are recorded using non-contact, rotational laser Doppler vibrometers at three of the following locations depending on the scenario: (i) the UJ output; (ii) the coupling shaft; (iii) the NES inertia disc and iv) the END inertia disc. In the Locked NES scenario, the NES is replaced by a mock solid disc (with a centred mounting hole) that matches the NES inertia. In this way, any change in the coupling shaft oscillations is due to the NES action, rather than to any additional inertia on the system. During the Locked NES scenario, the vibrations of the UJ output, coupling shaft and END inertia disc (in the second resonant case) are recorded and then used as baseline data to assess the NES performance.

4.1 Universal joint harmonics

The kinematics of the universal joint running at an angle $\beta$ is governed by the relationship : $\tan \theta _\mathrm{{in}}=\cos \beta \tan \theta _\mathrm{{out}}$ [18], with respect to the angles of rotation of the input shaft, $\theta _\mathrm{{in}}$, and the output shaft, $\theta _\mathrm{{out}}$. Differentiating this equation leads to a formula for the angular velocities:

$$\begin{aligned} \omega _\mathrm{{in}}=\frac{\omega _\mathrm{{out}}\, \cos \beta }{1-\sin ^{2}\beta \sin ^{2}\theta _\mathrm{{out}}}. \end{aligned}$$

(1)

A Taylor expansion of Eq. (1) leads to:

$$\begin{aligned} \omega _\mathrm{{in}}=\omega _\mathrm{{out}}\cos \beta \sum \limits _{n=0}^\infty {\sin ^{2\mathrm{n}}\beta \sin ^{2\mathrm{n}}\theta _\mathrm{{out}}} . \end{aligned}$$

(2)

Then, recall the following trigonometric identity [19]:

$$\begin{aligned} \sin ^{2\mathrm{n}}x= & {} \frac{1}{2^{2\mathrm{n}}}\left( {\begin{array}{*{20}c} 2n\\ n\\ \end{array} } \right) +\frac{\left( -1 \right) ^{n}}{2^{2n-1}}\sum \limits _{k=0}^{n-1} \left( -1 \right) ^{k}\nonumber \\&\left( {\begin{array}{*{20}c} 2n\\ k\\ \end{array} } \right) \cos {2\left( n-k \right) x} , \end{aligned}$$

(3)

where $\left( {\begin{array}{*{20}c} a\\ b\\ \end{array} } \right)$ is the binomial coefficient. Constraining the expansion to terms of the second harmonic, i.e. $n-k=1$, we get:

$$\begin{aligned} \omega _\mathrm{{in}}= & {} \omega _\mathrm{{out}}+\omega _\mathrm{{out}}\cos \beta \sum \limits _{n=1}^\infty \sin ^{2\mathrm{n}}\beta \frac{\left( -1 \right) ^{n}}{2^{2n-1}}\left( -1 \right) ^{n-1}\nonumber \\&\left( {\begin{array}{*{20}c} 2n\\ n-1\\ \end{array} } \right) \cos {2\theta _\mathrm{{out}}}, \end{aligned}$$

(4)

which is a converging series, yielding:

$$\begin{aligned} \omega _\mathrm{{in}}= & {} \omega _\mathrm{{out}}\left[ 1-\frac{2\sin ^{2}\beta }{\left( 1+\cos \beta \right) ^{2}}\cos {2\theta _\mathrm{{out}}} \right] \nonumber \\= & {} \omega _\mathrm{{out}}\left[ 1-A\cos {2\theta _\mathrm{{out}}} \right] , \end{aligned}$$

(5)

where A is a constant depending on angle $\beta$.

Fig. 7

Sketch of the experimental rig model

4.2 Numerical model of the experimental layout

A model has been built in $\hbox {MATLAB}^{{\textregistered }}$ environment to simulate the torsional response of the system (with and without the NES), as shown in Fig. 7. The UJ input shaft is connected to a motor with large inertia, which is considered as ideal excitation for modelling purposes. Three inertias constitute the independent degrees of freedom: $J_{1}, J_{2}$ and $J_{n}$. The equations of motions are then expressed as follows:

$$\begin{aligned}&J_{1}\ddot{\theta }_{1}+c_{1}\left( \dot{\theta }_{1}-\dot{\theta }_\mathrm{{out}} \right) +k_{1}\left( \theta _{1}-\theta _\mathrm{{out}} \right) -c_{2}\left( \dot{\theta }_{2}-\dot{\theta }_{1} \right) \nonumber \\&\quad -\, k_{2}\left( \theta _{2}-\theta _{1} \right) -c_{n}\left( \dot{\theta }_{n}-\dot{\theta }_{1} \right) -k_{n}\left( \theta _{n}-\theta _{1} \right) \nonumber \\&\quad -\, k_\mathrm{{nl}}\left( \theta _{n}-\theta _{1} \right) ^{5}=0, \nonumber \\&J_{n}\ddot{\theta }_{n}+c_{n}\left( \dot{\theta }_{n}-\dot{\theta }_{1} \right) +k_{n}\left( \theta _{n}-\theta _{1} \right) +k_\mathrm{{nl}}\left( \theta _{n}-\theta _{1} \right) ^{5}=0,\nonumber \\&J_{2}\ddot{\theta }_{2}+c_{2}\left( \dot{\theta }_{2}-\dot{\theta }_{1} \right) +k_{2}\left( \theta _{2}-\theta _{1} \right) =0, \end{aligned}$$

(6)

where $J_{1}$ is the coupling shaft inertia; $J_{2}$ is the End inertia; $J_{n}$ is the NES inertia; $\theta _{i}\, (i=1,\, 2,\, n)$ are angular displacements; $k_{1}$ and $k_{2}$ are linear stiffness coefficients of the corresponding shaft and coupling combinations; $k_{n}$ and $k_\mathrm{{nl}}$ are the NES linear and nonlinear stiffness coefficients, respectively; $c_{i}\, (i=1,\, 2,\, n)$ are damping coefficients. Table 1 shows the values used for the system parameters. The driving angle $\theta _\mathrm{{out}}$ is acting as base excitation of the torsional system and is taken from Eq. (5). Equation (6) describes the dynamics when the END inertia is attached (case near resonance). In the non-resonance case, the third equation in Eq. (6) is mute. Thus, the stiffness and damping forces (proportional to $c_{2}$ and $k_{2})$ entering the first equation are also omitted.

Table 1 Model parameters in the two experimental set-ups

5 Results and discussion

This section presents the experimental results obtained with the rig shown in Fig. 6 away and near resonance. The latter is practically induced by the presence of the END inertia disc. In what follows, time histories of the NES and the corresponding primary system are presented, the acceleration amplitudes are processed and compared between the Locked and Active NES cases, whereas the system energy is calculated and plotted along with the system’s NNMs.

5.1 Away from resonance

Figure 8 exhibits the rotational velocity time histories during a forward speed sweep between 0 and 2000 rpm, with an additional backward sweep in Fig. 8e showing the NES nonlinearity. Equation (5) signifies that the torsional excitation depends on motor’s speed not only regarding the frequency content but for the amplitude as well. The system is therefore subjected to an excitation of increasing amplitude as the sweep progresses. The results correspond to a UJ angle of $\beta ={20}^{\mathrm{{o}}}$. Comparing the Active NES results with the time history of the Locked NES case, a vibration reduction of the primary system is observed, located around 20–35 s in the time domain. The magnitude of the reduction is more clearly shown in the zoom-in extracts of Fig. 8c, d. It can also be noted that multiple co-existing solutions for the NES are realised in this region (see Fig. 8e, f).

Fig. 8

Rotational velocity time histories without the End inertia: a Locked NES, b Active NES, c zoom-in plot from a, d zoom-in plot from b, e NES in forward and backward sweeps, f zoom-in plot from e

The achieved reduction is more apparent when the acceleration amplitudes are compared. In Fig. 9, the acceleration amplitudes are plotted against the instantaneous excitation frequency, as this was computed from the spectrograms of the time histories. The observed reduction is consistent with the remarks made for the time histories. As the NES vibration grows, energy is extracted from the primary system which results in the corresponding vibration amplitude reduction. As soon as the NES motion “jumps down” (detaching from the high amplitude response), the primary system oscillations in the Active NES case are almost identical to these of the Locked NES cases. This indicates that the achieved reduction is due to the NES action, and further investigation using the frequency–energy plots becomes pertinent. The system’s vibratory energy (excluding the rigid body motion) reads:

$$\begin{aligned} E_\mathrm{{V}}= & {} K_\mathrm{{V}}+U_\mathrm{{V}}=\, \frac{1}{2}\, J_{1}\, \left( \dot{\theta }_{1}-\dot{\theta }_\mathrm{{RB}} \right) ^{2}\nonumber \\&+\frac{1}{2}\, J_{n}\, \left( \dot{\theta }_{n}-\dot{\theta }_\mathrm{{RB}} \right) ^{2}+\frac{1}{2}k_{1}\left( \theta _{1}-\theta _\mathrm{{out}} \right) ^{2}\, \nonumber \\&+ \frac{1}{2}k_{n}\left( \theta _{n}-\theta _{1} \right) ^{2}+\frac{1}{6}k_\mathrm{{nl}}\left( \theta _{n}-\theta _{1} \right) ^{6}, \end{aligned}$$

(7)

Fig. 9

End shaft acceleration amplitude for the Active NES case versus the Locked NES case

Fig. 10

Frequency–energy plot of the Active NES case computed using Eq. (7), superimposed to the NNMs branch

where $\dot{\theta }_\mathrm{{RB}}$ is the rigid body motion velocity of the system. Figure 10 shows the frequency–energy plot of the system with the branch of NNMs superimposed. The latter describes the locus of the conservative solutions of the system in the frequency–energy space. The distribution of energy in the NNMs has been shown to influence TET in impulsive and forced systems with light damping and is therefore essential to design an NES. Figure 11 shows examples of these NNMs for selected cases. Note that this is not the only branch that exists for this system. A second branch exists in a higher frequency range due to the relatively high stiffness of the primary system; however, this section explores TET away from resonance, and therefore, the higher frequency NNM branch is only relevant for Sect. 5b, where TET in a resonant region is discussed. NNMs were computed using the NNMcont®computational package [20]. It is noticed that the NES amplitude grows (see Fig. 8e) when the excitation frequency drives the system energy close to overlapping with the NNMs. The region where the NNM crosses through the system energy is the range of the observed vibration reduction. This confirms previous observations in the development of a graphical method to design an NES vibration absorber [15, 16], where an overlap of the system energy with the NNMs has been identified as key to the design of effective absorbers. Moreover, Fig. 10 also suggests that vibration reduction is most effective when the forced response of the system is closely related to the conservative system’s NNMs. When the NES detaches from the high amplitude response and thus, its vibration mitigation capability diminishes, the system energy also recedes from the NNMs in the frequency–energy plot, indicating a direct correlation of the system’s NNMs with the NES capability to absorb energy.

Fig. 11

a–c–e NES and End shaft velocity time histories, b–d–f corresponding dominant NNMs

The above described correlation is more evident at the system’s time histories and the corresponding NNMs, shown in Fig. 11. Time histories from three time snapshots corresponding to qualitatively different responses are shown in the left-hand side column, with the NNMs acting at that time in the right-hand side column. The top set of figures is taken before the NES reaches the high amplitude response at about 15.5 s. The system energy is not broadly affected by the NNM due to the frequency mismatch: energy is supplied at a frequency of about 21 Hz, whereas the frequency of the NNM is monochromatic and close to 35 Hz. As the sweep progresses, the NES gains energy and reaches higher oscillating amplitudes. The middle set of figures corresponds to the region of effective vibration reduction at about 34 s. The NES NNM amplitude is more than an order of magnitude larger than primary system’s NNM and out of phase. Due to the overlap of the system energy with the NNM locus, this is manifested as strong vibration reduction in the forced response. When the system detaches from the NNM branch (bottom set of figures), the influence of the conservative dynamics diminishes, leading to the primary system vibrating at amplitudes similar to the locked case.

Another important metric worth considering is the energy that the NES damping consumes, given by the integral over time of the NES damping power, $c_{n}\left( \dot{\theta }_{n}{-}\dot{\theta }_{{1}} \right) ^{{2}}$. Figure 12 shows the ratio of the total energy damped by the NES over the total input (oscillatory) energy, as described by Eq. (8), where $E_\mathrm{{in}}(t)$ is the instantaneous input energy.

$$\begin{aligned} E_{\mathrm{{r}}}=\frac{\int _0^{t_\mathrm{{end}}} {c_{n}\left( \dot{\theta }_{n}{-}\dot{\theta }_{{1}} \right) ^{{2}}} \mathrm{{d}}t}{\int _0^{t_\mathrm{{end}}} {E_\mathrm{{in}}(t)} \mathrm{{d}}t}\, . \end{aligned}$$

(8)

A steep increase in the plotted ratio occurs between 20 and 35 s, which is the region identified from previous graphs as the vibration reduction area. This plot shows a remarkable ability of the NES to absorb energy from the primary system when it is operating within its effective, overlapping frequency range. Up until 35 s, the NES has damped more than 70% of the total energy input between 0 and 35 s. After 35 s, the primary system has much higher instantaneous damped energy, which leads to the ratio slightly declining.

Fig. 12

Percentage of total energy damped by the NES over total input energy

A comparison is also carried out between the experimentally obtained data versus model predictions to verify the predictive capabilities of the model and the validity of the design method. Figure 13 depicts this comparison, starting with NES and primary system time histories in Fig. 13a, b. The region of strong NES performance is well captured by the model for both the NES and primary system, whereas a minor deviation in the NES response is observed at higher running speeds. Recalling that NES damping is dominated by metallic interactions in the conical springs, it is anticipated that a viscous damping model would not accurately describe all forcing conditions. However, this is not concerning since the NES vibrates at low amplitudes away from the region of interest. Moreover, the acceleration amplitudes predicted by the model match well the experimental data (Fig. 13c), whereas the relation of the predicted amplitudes of the Active NES case to the Locked NES case is similar to what is experimentally obtained (Fig. 13d).

This section has revealed that the NES is capable of extracting energy from the primary system, even away from the main resonance. The methods employed have been verified, and the model’s predictive power has been reaffirmed. The next section will consider the system response near resonance.

5.2 Near resonance

This section examines the NES capability to mitigate the primary system resonance. In order to induce resonant conditions (within the frequency limitations of the experimental apparatus), two modifications are made in the experimental set-up. First an inertia disc is attached at the end of the coupling shaft using a bellow coupling with torsional stiffness coefficient of 20,000 Nm/rad. Combining this with the additional shaft’s torsional stiffness yields a value of equivalent stiffness coefficient $k_{2}=8,500$ Nm/rad. A second identical jaw coupling is added in series to the existing one, reducing the torsional stiffness coefficient to $k_{1}=270\, \hbox {Nm/rad}$, whereas the END inertia disc further reduces the modal frequencies of the primary system. The rig layout corresponds to the set of Eq. (7)

Fig. 13

Experiment versus numerical model response comparisons a, b NES and End shaft velocity time histories, c End shaft acceleration amplitude, d ratio of End shaft acceleration amplitude for Active over Locked NES

Figure 14 shows the recorded time histories during a forward motor speed sweep from 0 to 2000 rpm. Even though the excitation amplitude is increasing during the sweep, there is a clear resonant region in the vibrations of the END inertia at around 1400 rpm, as shown in the Locked NES case time history of Fig. 14a. The aim is to evaluate the NES effectiveness on mitigating the primary system resonance oscillations by performing an identical sweep with the NES attached to the mounting hub (instead of the mock disc). Figure 14b, c includes the time histories of the END inertia and NES, respectively. It is readily observed that the NES vibrates with relatively large amplitudes for a wide range of input frequencies. Moreover, it appears that the NES engages with—qualitatively—two different response regimes. Up until 1400 rpm, the response builds up in the same way as in the non-resonance case. After that, instead of jumping down, the NES continues to vibrate with almost constant amplitude for about 200 rpm, before starting a beating-like motion. Eventually, just before 1800 rpm, its response reduces to low amplitude vibrations. Cross-checking with Fig 14b, the effect of the NES on the END inertia time history can be concurred. Interestingly, the initial NES activation leads to increasing amplitude of the END inertia vibrations. In order though to evaluate the magnitude of this increase, a closer look is taken on the acceleration amplitudes in Fig. 15a. In fact, the vibration amplitudes of the END inertia are almost identical to the locked case, leading to the conclusion that the NES is not affecting the primary system to this point ($\sim 1350$ rpm). As soon as the NES reaches its peak amplitude (and for the second region), a simultaneous significant reduction in the End inertia vibrations is observed, which lasts until the third region of the beating and can be distinguished even in the time history of the response. This effect is more evident if the primary system’s kinetic energy is considered. In Fig. 15b, the energy transferred away from the primary system is more prominent, reaching a peak mitigation of 79.76%, calculated based on the maximum instantaneous difference between the active and locked curves: $\left( K_\mathrm{{P,Locked}}-K_\mathrm{{P,Active}} \right) /K_\mathrm{{P,Locked}}\vert _{t=t_{0}}$, where $K_\mathrm{{P}}$ is the primary kinetic energy and $t_{0}$ is the time instance when the maximum difference occurs.

Fig. 14

Velocity time histories near resonance a, b End inertia for the Locked and Active NES cases, c NES

Fig. 15

a Primary system acceleration amplitude and b kinetic energy ratio for the Active and Locked NES cases

Fig. 16

a Frequency–energy plot of the system energy with NNMs, b damped energy ratios of the NES and End inertia with the NNMs, c damped energy ratios for the NES and End inertia, superimposed to their time histories

The energy interactions between the NES and the primary system can be better elucidated via juxtaposing the system’s response energy with the NNM branches. It is worth mentioning that in this case, two NNM branches are falling within the speed range of interest (Fig. 16a). The system energy in the case near resonance is computed from the experimental data by adding to Eq. (8) the End inertia kinetic and potential energies: $0.5\, J_{2}\left( \dot{\theta }_{2}-\dot{\theta }_\mathrm{{RB}} \right) ^{2}+0.5\, k_{2}\left( \theta _{2}-\theta _{1} \right) ^{2}$. The damped energy ratios for the NES and the END inertia are computed in an analogous way to the previous section. Figure 16a exhibits the system energy superimposed to the system NNMs. The first region of NES activation is dominated by the lower frequency NNM branch. The system is drawn to follow this branch until about 1400 rpm (or 46.67 Hz in excitation frequency terms), leading to the response observed in the time histories of Fig. 14. Even though the vibration amplitudes are not mitigated in this region, it is interesting to see how damping is distributed in the system (recall that in a forced system, the energy input depends on system dynamics, in contrast with impulsively excited system where the energy input is given). Indeed, as Fig. 16b shows, there is a lively interaction between the NES and the primary system (note that the bottom horizontal axis of this plot refers to the NNMs, whereas the top horizontal axis refers to the damping ratios).

Fig. 17

a Zoom-in plot of the NES time history modulated response, b steady-state NES response at 1555 rpm

At the beginning of the sweep test, the NES follows a nearly rigid body motion and most of the input energy is damped by the END inertia damper, indicating that this energy is maintained within the primary system. Moving to higher frequencies and as soon as the system energy reaches the first NNM branch (at about 25 Hz in Fig. 16b), there is a steep change in the damped energy distribution. This is a rapid energy shift from the primary damper to the NES, leading the NES damping ratio to surpass the END inertia ratio, reaching a peak shortly above 30 Hz. After that, and for as long as the response is dominated from the first NNM, there is a reversal of the damped energy distribution to the previous state of the END inertia damper prevalence. This is consistent with previous observation of targeted energy transfer via the 1:1 resonance, due to the magnitude of the NNMs along the first branch. After the system is detached from the first NNM, there is a second region of strong energy transfer from the primary system to the NES, evidenced by the rapid recurrence of the NES damped energy ratio located in the region of the second NNM (corresponding to the second response tier based on the time histories of Fig. 14). The correlation of the damped energy ratios with the time histories is shown in Fig. 16c, where it is even clearer that the NES absorbs energy from the primary system while vibrating in the second response region. In fact, this is the region of the most effective vibration mitigation where the primary system has been seen to vibrate with as low as 79.76% reduced amplitudes.

The relatively high damped energy ratio persists in the region of beating response as well, even though the NES damping ratio attains significantly lower values. The attachment of an NES to a forced primary system is known to induce modulated response, either in a strong modulation regime (SMR) or in a weak modulation regime (WMR) [21, 22]. Herein, the main aim was to establish the effectiveness of the NES to mitigate vibrations based on the previously developed design techniques targeting the 1:1 resonance and the action of the relevant superharmonics. It is observed that the NES engages with a modulated response, shown in the zoom-in plot of Fig. 17a. This is an important observation that corroborates the activation of nonlinear energy transfer, utilised in this work for achieving mitigation of torsional oscillations. To further validate the manifestation of modulated response, steady-state tests were recorded with the motor running at 1555 rpm. The NES modulated response shown in Fig. 17b confirms the nonlinear energy transfers. However, a detailed analysis of the slow invariant manifold that would be required to predict the forcing conditions and the design parameters leading to this modulation is out of the scope of this paper.

6 Conclusions

A combined numerical and experimental study was presented on the design and validation of an NES for torsional vibration mitigation purposes of a propulsion system. The set-up comprised an electric motor driving a primary (propulsion) system of shafts and inertia discs through a universal joint, which induces the second-order torsional oscillations. The NES was designed following previously developed techniques, for the purpose of experimentally validating the methodology followed and the predicted vibration reduction of the primary system. The NES prototype included two conical springs as the elements providing essential stiffness nonlinearity. The prototype stiffness and damping were identified to feed inputs to a model, used for validation purposes. Two different forcing scenarios were considered, away from resonance and near resonance by modifying the set-up of the primary system accordingly. In both cases, the NES was found to lead to significant vibration reduction with the additional feature of activation over a relatively broad frequency range, particularly for mitigating resonant oscillations. This capacity of the NES to suppress vibrations over broad frequency ranges is advantageous, especially when compared with typical tuned mass dampers. Post-processing analysis was used to derive frequency–energy plots that signified the importance of the NNM branches in the forced response of the nonlinear system. Different regions were identified where the conservative dynamics drive the system to increasing energy transfer to the NES, evidenced not only by the reduction of the primary system’s kinetic energy, but also via the increase in the energy damped by the NES. Noteworthily, rapid energy exchanges between the NES damper and the primary damper were observed that could lead to efficient vibration mitigation. The nonlinear energy interactions were confirmed through the manifestation of modulated response—characteristic of the essentially nonlinear dynamics—both in speed sweeps (transient) and steady-state (constant speed) tests. These results establish an encouraging background for further development and optimisation of the nonlinear vibration absorber for real-world applications.

Appendix A

The drivetrain dynamic model of Fig. 1a equipped with an NES has been presented in detail in reference [16] and is described by the following matrix set of equations of motion:

$$\begin{aligned}&\left[ {\begin{array}{*{20}c} J_{1} &{} 0 &{} 0\\ 0 &{} J_{2} &{} 0\\ 0 &{} 0 &{} J_{n}\\ \end{array} } \right] \left[ {\begin{array}{*{20}c} \ddot{\theta }_{1}\\ \ddot{\theta }_{2}\\ \ddot{\theta }_{n}\\ \end{array} } \right] +\, \left[ {{\varvec{C}}}_{\mathbf{N }} \right] \left[ {\begin{array}{*{20}c} \dot{\theta }_{1}\\ \dot{\theta }_{2}\\ \dot{\theta }_{n}\\ \end{array} } \right] \\&\qquad +\, \left[ {\begin{array}{*{20}c} k_{2}+k_{1} &{} {-k}_{2} &{} 0\\ {-k}_{2} &{} k_{2} &{} 0\\ 0 &{} 0 &{} 0\\ \end{array} } \right] \left[ {\begin{array}{*{20}c} \theta _{1}\\ \theta _{2}\\ \theta _{n}\\ \end{array} } \right] \\&\quad = \left[ {\begin{array}{*{20}c} k_{1}\theta _{F}+c_{1}\dot{\theta }_{F}-\, k_\mathrm{{N}}{(\theta _{1}-\theta _{n})}^{3}\\ -T_\mathrm{{Res}}\\ k_{n}{(\theta _{1}-\theta _{n})}^{3}\\ \end{array} } \right] \end{aligned}$$

$T_\mathrm{{Res}}$ is the resisting torque on the transmission input shaft. More details about the derivation of the damping matrix $\left[ C_\mathrm{{N}} \right]$ and $T_\mathrm{{Res}}$ can be found in reference [16].

The typical range of the drivetrain model parameters and the NES data are as follows [16]:

Inertia ($\hbox {kgm}^{{2}}$)	Stiffness (Nm/rad)
$J_{1} = 0.0005 - 0.005$	$k_{1} = 500 - 5000$
$J_{2} = 0.001 - 0.006$	$k_{2} = 5000 - 30000$

$J_{n} = 10.7{\%}$ of transmission input shaft inertia $(J_{2})$ and $K_{n} = 2,200\hbox { Nm/rad}^{{3}}$.

The NES performance is evaluated for the three-cylinder engine case study by comparing the acceleration amplitude of the transmission input shaft at 1.5 Engine Order (EO) for systems with (Active) and without (Locked) NES. This metric was selected as the main performance index because the 1.5 EO is the fundamental firing order of a three-cylinder engine.

The Matlab command Pwelch is used to obtain the acceleration amplitudes corresponding to the 1.5 EO harmonics by calculating the power spectral density (PSD) of the transmission input shaft acceleration signal using Welch’s overlapped segment-averaging estimator. The resultant PSD output (units $\mathrm{{rad}}^{2}/\mathrm{{s}}^{4}{/\mathrm{{Hz}}}$) is processed as $\sqrt{\mathrm{{PSD}}\, \times 1.5\, \mathrm{{Engine\, Order\, Frequency}}}$, where the nominated frequency is the 1.5 EO harmonic.