Dynamic analysis of magnetic spring-based nonlinear oscillator system

Abstract

This paper aims to study the dynamics of the single-degree-of-freedom magnetic spring-based oscillator system. The proposed oscillator system contains a nonmagnetic shaft, a floating permanent magnet (PM), and two fixed permanent magnets (PMs). All PMs are placed in such a way that they can repel each other. At first, the proposed system's magnetic properties and magnetic restoring force are studied. Experimental and numerical analyses have been carried out to validate the analytical investigation of the magnetic restoring force. The linear and nonlinear coefficients of the oscillator system are analysed from the magnetic restoring force. Moreover, how the gravitational force affects the equilibrium position is studied by varying the height of the oscillator. The magnetic restoring forces for different oscillator heights are also analysed. In addition, the system dynamics, such as damping ratio, eigenvalues and natural frequencies of the oscillator system, are investigated with and without electromechanical coupling. Finally, the proposed system's energy generation capacity is examined using electromechanical coupling.

1 Introduction

Compared to other power take-offs (PTO) systems, the linear generator-based PTO system contains fewer moving parts resulting in less mechanical complexity and less installation and maintenance costs. Different design concepts have been proposed, developed, and tested to overcome the disadvantages of linear generators and increase their efficiency [1,2,3,4]. In most cases for wave energy conversion, linear generator systems have been designed based on linear oscillators and traditional design concepts. Conventionally, permanent magnets are usually mounted in the translators with opposite poles facing each other. An iron core is sandwiched between two permanent magnets. Translators move inside stators, causing the magnetic flux to change inside winding coils, which generates electrical energy. A linear oscillator-based energy generator generally produces the maximum power output, while a nonlinear oscillator harvester has a broader frequency bandwidth. Therefore, nonlinear oscillators can harvest more energy from random vibrations [5]. Owens et al. found that nonlinear oscillators are more efficient at expanding frequency response bandwidth than linear oscillators [6].

A magnetic levitation (magnetic spring) system can be used in the translator design to make the oscillator nonlinear. Magnetic springs work like physical springs and are formed when two magnets face each other in the same poles (N–N or S–S). A study showed that a magnetic spring-based linear generator would harness energy more efficiently from low-frequency vibration sources [7]. The design of the magnetic spring-based linear generator is relatively straightforward; however, several important aspects still need to be thoroughly investigated or analysed, such as the dynamics, the optimal design of the multi-pole magnet arrangements, the accurate modelling of the magnetic restoring force, and the nonlinear response.

So far, many magnetic spring-based energy harvesters have been proposed and developed to generate energy from vibrations such as handshaking, human motion and the environment. Zhu and Zu developed and simulated a linear generator based on a magnet spring system [7]. A cubic polynomial curve fit was used to model the magnetic levitation or restoring force. Moreover, an analytical formula was employed to compute the average axial magnetic flux. However, the nonlinear behaviour of the magnetic spring-based oscillator system was not studied. Mann and Sims studied a novel linear generator based on a magnetic levitation system [8]. The magnetic levitation system was used to create an oscillator with a tuneable resonance, and a cubic polynomial function was proposed to measure the magnetic restoring force. The stiffness coefficients of the cubic polynomial law were determined experimentally. However, the effects of the gravitational force and the position of a fixed magnet have not been discussed. Lee et al. used cubic and quintic polynomials to study the linear and nonlinear coefficients of the magnetic restoring force [9]. The polynomial coefficients and electromechanical coupling were determined experimentally. The floating magnet's static displacement was directly measured under gravitational force to determine the magnetic restoring force, but its equilibrium position was not examined under gravitational force. A variety of magnetic spring-based generator structural designs were studied by Munaz et al. [10]. Multipole magnets were studied using the superposition principle, and magnetic flux density was modelled using analytical functions. Finite element analysis (FEA) was performed to determine the optimal flux distribution of the moving magnet and the number of poles. Although the system's dynamics were considered, the effect of the changing position of the fixed magnet was not considered. Priya and Apo explored the impact of magnet multipole arrangements and used the cubic polynomial to estimate the stiffness terms [11]. To find the optimal magnetic configuration, a finite element analysis was presented. However, no information about how to solve the equation of motion was provided. Avila Bernal and Garca proposed an analytical model for the magnetic field distribution and magnetic force, as well as a mathematical derivation to represent the dynamics of the monopole linear generator [12]. The analytical analyses were compared with FEM. The dynamic behaviour of the oscillator system was not studied. Masoud Masoumi and Ya Wang proposed a nonlinear oscillator system called the repulsive magnetic scavenger [13]. Magnetic properties were estimated numerically for different magnet arrays and arrangements using FEM. The restoring force coefficients were identified from numerical simulation using the cubic polynomial law, and the numerical procedures were evaluated experimentally. However, the gravitational force was not considered during the measurement of the magnetic restoring force. In addition, Pedro Carneiro et al. reviewed the architectures of electromagnetic energy generators based on magnetic levitation systems [14]. Twenty-one design arrangements were compared in terms of geometric parameters, constructive parameters, optimisation approaches, and energy-generating performances. In addition, this review introduces the essential advanced models used to describe the physical phenomena of transduction mechanisms.

The literature shows that the magnetic restoring force is a function of the floating magnet's position, which is estimated in most research investigations by seeking the polynomial power series coefficients by curve fitting [14]. The magnetic restoring force must be measured correctly to determine a system's linear and nonlinear coefficients. The magnetic restoring force has been measured using numerical [15, 16], analytical [17, 18], and experimental models [8, 13, 19, 20]. To date, no paper has been published that simultaneously validates experimental measurements of magnetic restoring force with numerical and theoretical measurements. Because of the gravitational force, the equilibrium position of the magnetic spring-based system (vertical arrangement) is affected, but very few researchers considered this fact without studying how the gravitational force effect changes the equilibrium position. Furthermore, not a single researcher in the literature studied the changing position of the top fixed magnet, which determines the total height of the oscillator, and how it affects the oscillator design. The dynamics of the magnetic spring-based system are fundamental for understanding and developing the system deeply, but unfortunately, none of the articles that appear in the literature has studied the dynamics intensely. Therefore, this paper aims to investigate the magnetic restoring forces with validation, the effect of the changing height of the oscillator, and how the gravitational effect changes the system's equilibrium position for different positions of the top fixed magnet and the dynamics of the nonlinear oscillator system.

The paper introduces the advantages of using the nonlinear over linear oscillator system, previous research works, and research gaps. Following this, the design configuration and investigation of the magnetic properties are presented. The following section presents the magnetic restoring force and coefficient analysis of the magnetic spring-based oscillator system. The design is analysed for various lengths of the oscillator in the following section. Moreover, the nonlinear oscillator model is analysed with and without electromechanical coupling in Sect. 5. Section 6 presents the oscillator system’s dynamics, including the dynamics for different heights of the oscillator, with and without electromechanical coupling and the model of the energy generator for different oscillator lengths. Finally, the paper discusses where the proposed model is compared with the existing models.

2 Design configuration and investigation of the magnetic properties

As shown in Fig. 1, the proposed nonlinear oscillator consists of three permanent ring magnets and a circular aluminium shaft. All magnets are axially magnetised (N42) through the height (13 mm), and each magnet's outer and inner diameters are 72 mm and 32.5 mm, respectively. Two fixed ring magnets are attached to the shaft, whose polarities are switched to create a repulsive force between the levitating magnet and the fixed magnets. SN-NS-SN is the orientation of the magnetic poles in order to repel each other. This test rig is 300 mm high and 300 mm wide. The shaft has a diameter of 12 mm and a height of 550 mm. The middle and bottom magnets are separated by 79 mm, and the top and middle magnets by 104 mm.

Fig. 1

Test rig

A fishing line connects the floating magnet with the servo motor pulley to create a sine wave. The displacement sensor measures the displacement of the middle floating magnet. Initially, the magnetic properties of the oscillator are studied without a winding coil. Figure 2 shows the magnetisation direction and the magnetic flux density on the magnet surface. The magnitude of the magnetic flux density is shown in Fig. 3.

Fig. 2

a Magnet surface flux density and b magnetisation direction and c Magnetic flux density (B_Vector) in XZ plane

Fig. 3

Magnetic flux density B_Vector a axial direction and b radial direction

Figure 2c displays how the distributed magnetic field moves through the air gap. Line d, 37 mm from the magnet stack chosen as the coil location, is used to calculate the magnetic flux density radially for the system. When selecting the winding coil position, it is essential to consider the magnetic flux density in the air gap. The vertical arrows move in equivalent ways due to the symmetry in Fig. 2c. Figure 3 displays the numerically measured (ANSYS Maxwell) axial and radial magnetic flux densities.

Magnetic flux density is affected much more by external forces or vertical movement of the middle magnet than by keeping them stationary, as shown in Fig. 3a, b. During magnet vibrations, magnetic flux density changes, which is an essential factor for maximising power harvesting.

3 Magnetic restoring force and coefficient analysis of the magnetic spring-based oscillator system

The pole orientation of magnets determines whether it will attract or repel another magnet when moved near it. When opposite poles are aligned (SN-SN or NS-NS), attraction occurs, while repulsion occurs when the same poles are oriented together (NS-SN or SN-NS). The forces will vary depending on the magnets' shape, orientation, magnetisation direction, and separation. The numerical, theoretical and experimental methods can be used to calculate attractive and repulsive forces. There are three magnets in Fig. 4; the central floating ring magnet is free to move, while the upper and underneath ring magnets are fixed.

Fig. 4

Magnetic spring-based oscillator system

The magnetic force between two magnets can be written as [17],

$${F}_{t}=\frac{{\mu }_{0}{Q}_{t}{Q}_{m}}{4\pi {{r}_{t}}^{2}}$$

(1)

$${F}_{b}=\frac{{\mu }_{0}{Q}_{b}{Q}_{m}}{4\pi {{r}_{b}}^{2}}$$

(2)

The top and middle magnets are separated by ${r}_{t}$, and the bottom and middle magnets are separated by ${r}_{b}$. The magnetic field intensities of the top, bottom, and middle magnets are ${Q}_{t}$, ${Q}_{b}$ and ${Q}_{m}$, respectively. The magnetic restoring force of the moving magnet (${F}_{res}$) can be calculated using the distance x, representing the displacement of the middle moving magnet in Fig. 4.

$${F}_{res}={F}_{t}-{F}_{b}=\frac{{\mu }_{0}{Q}_{m}}{4\pi }\left(\frac{{Q}_{t}}{{\left({r}_{t}-x(t)\right)}^{2}}-\frac{{Q}_{b}}{{\left({r}_{b}+x(t)\right)}^{2}}\right)$$

(3)

According to Fig. 1, all ring magnets are placed vertically. Magnetic restoring force curves changed due to gravitational force shifting the equilibrium point away from the centre point. The Taylor series can be used to express Eq. 3 for the test rig setup as follows:

$${F}_{res}={k}_{1}x+{k}_{2}{x}^{2}+{k}_{3}{x}^{3}+{k}_{4}{x}^{4}+{k}_{5}{x}^{5}+a$$

(4)

where a is the constant, ${k}_{1}$ is the linear spring coefficient and ${k}_{2}, {k}_{3}, {k}_{4}$ and ${k}_{5}$ are the nonlinear coefficients of the system. Figure 5 shows the calculated magnetic restoring forces derived analytically (using Eq. 3), numerically (Using Ansys Maxwell) and experimentally.

Fig. 5

a Validation of magnetic restoring force and b Residual error

Due to the gravitational effect, the magnetic restoring force between the bottom and middle magnets is higher than that between the top and middle magnets in Fig. 5. There is a striking similarity between the experimentally measured and numerically and theoretically calculated magnetic restoring forces. Figure 5b displays the residual error analysis for the experimental, numerical and theoretical measurements. The standard error for experimental, numerical and analytical analysis are 0.117, 0.117 and 0.042, respectively. Moreover, the experimental measurement's standard deviation and sample variance are 0.694 and 0.481, respectively. The standard deviation values for numerical (0.838) and analytical (1.359) measurements are higher than those for the experimental measurement. Even though some articles have been published on magnetic levitation-based nonlinear oscillators, their dynamics have yet to be clarified. In some studies, researchers used the linear equation for small excitations of the floating magnet. In other studies, the magnetic restoring force was measured using cubic (3rd order) and quintic (5th order) polynomials curve fitting. The magnetic restoring force curves in Fig. 6 can be used to calculate the linear and nonlinear stiffness. Least-squares curve fitting of the graph can be used to measure of ${k}_{1}$, ${k}_{2}, {k}_{3}, {k}_{4}$ and ${k}_{5}$. A polynomial of cubic and fifth order in Fig. 6 represents the magnetic restoring force.

Fig. 6

Magnetic restoring force (3rd order and 5th order polynomial model (50 mm excitation ranges)) a Experimental measurement and b Residual error

Fig. 7

Natural frequency analysis for 3rd and 5th-order polynomial curve fittings

It can be seen from Fig. 6 that the 5th-order (quintic) polynomial fits the data more accurately than the 3rd-order (cubic) polynomial. The distance between permanent magnets strongly influences the coefficient of the proposed system. The characteristic changes substantially when the distance changes. Figure 7 presents the natural frequencies of the experimental, theoretical and numerical measurements for fitting 3rd-order and 5th-order polynomial models. Figure 7 shows the floating magnet's theoretical natural frequencies for different excitation ranges are almost identical. In addition, for small excitation ranges, as shown in Fig. 7, the measured natural frequencies for 3rd-order polynomial curve fitting are almost the same as those for 5th-order polynomial curve fitting. Measured natural frequencies for fitting the 3rd and 5th-order polynomial curves are around 4.85 Hz and 5 Hz, respectively.

For the curve fitting of experimental measurements, Fig. 8 shows the Root Mean Squared Error (RMSE) and R-square values. Based on Fig. 8, it can be seen that higher-order polynomials are more accurate than lower-order polynomials. Based on the RMSE values, Fig. 8 shows that higher-order polynomials deliver a good match for both high and small excitation ranges.

Fig. 8

Goodness of fit for the experimental measurement

Based on the measurements of the RMSE for all curve-fitting analyses for various ranges of the floating magnet's position, the polynomial model of the 5th order provided the lowest RMSE. The 3rd-order polynomial models produced the minimum RMSE values for smaller excitation ranges, such as 5 mm and 10 mm. Thus, the lower-order polynomial model for small excitation ranges is generally more appropriate, but a higher-order polynomial model is more suitable for long excitation ranges.

4 Design analysis for various lengths of the oscillator

The system has a total length of 222 mm for the normal equilibrium position. Because of the different lengths of the oscillator, the middle and bottom magnets and the middle and top magnets have different distances between them, as shown in Fig. 9. By changing the total length of the oscillator, the equilibrium position changes.

Fig. 9

Change of damping ratio and natural frequency for different positions of the top magnet

The floating magnet's position changed as expected because of gravitational force effects when the top magnet moved or varied the total length of the oscillator, as seen in Fig. 9. During the equilibrium position of the oscillator, the middle magnet moved by 13 mm toward the bottom magnet from the projected position (equilibrium position for floating magnet) due to gravitational force effects. This length, due to gravitational force effects, decreased when reduced the oscillator length but it increased when increased the oscillator length as seen in Fig. 9. Figure 9 shows that the distance between the middle and bottom magnets and between the middle and top magnets changed with varying the oscillator length. The distance between the middle and bottom magnets changes slightly compared to the distance between the top and middle magnets.

Moreover, the damping ratio and natural frequency of the oscillator changed with changing the total length of the oscillator. Figure 9 presents the change in damping ratio and natural frequency of the oscillator for different top fixed magnet positions. It is clear from Fig. 9 that when the length of the oscillator is reduced, the damping ratio and natural frequency increase. Alternatively, the damping ratio and the natural frequency decreased when the oscillator length increased. The magnetic restoring forces for different lengths of the oscillator have been measured experimentally, as shown in Fig. 10.

Fig. 10

Magnetic restoring force for different oscillator lengths (experimental measurement)

It can be said from Fig. 10 that the magnetic restoring force changes with changing the total length of the oscillator. Increasing oscillator length leads to decreases magnetic restoring force, and decreasing oscillator length leads to increases magnetic restoring force.

The cubic (3rd order) polynomial curve fit has been used to measure the magnetic restoring force for various lengths of the oscillator. The magnetic restoring force curve is displayed in Fig. 10, and from this curve, the linear and nonlinear stiffness have been calculated. The experimental measurement for the restoring force has been used to measure the system's linear and nonlinear stiffness by changing the top magnet's fixed position. The polynomial of the cubic model for this new position is selected to represent the magnetic restoring force, as shown in Table 1. The values of ${k}_{1}, \;{k}_{2} \; \text{and} \; {k}_{3}$ have been measured from the least-squares curve fitting of the above graph. By changing the position of the top magnet, the linear and nonlinear coefficients for 50 mm excitation ranges are investigated, as presented in the following Table 1.

Table 1 Linear and nonlinear stiffnesses of the oscillator system for various lengths (Theoretical measurement)

It can be seen from Table 1 that the coefficients of the system changed with changing the length of the oscillator. The linear stiffness increased with reducing the oscillator length, and it declined with increasing the oscillator length, which can be seen in Table 1.

5 Model analysis with and without electromechanical coupling

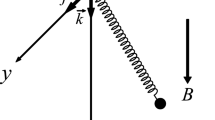
In the equilibrium position, the separation distance between the bottom and the floating magnet is 79 mm, and between the floating and top magnets is 104 mm. The middle magnet creates elastic restoring forces (${F}_{r}={k}_{1}y+{k}_{2}{y}^{2}+{k}_{3}{y}^{3}$) when an external force is applied to it or when it moves up and down. The free-body diagram in Fig. 11 illustrates the oscillator system with electromechanical coupling. ${F}_{\beta }$ (${F}_{\beta }=\beta \dot{y}$) is the damping force of the oscillator system. y represents the relative displacement, $\dot{y}$ represents the relative velocity and $\ddot{y}$ represents the relative acceleration of the magnet. The coil has a length of l, and the magnet’s flux density is B(y). The electromagnetic coupling coefficient is $\alpha$($\alpha ={B}_{(y)}l$) and ${F}_{e}$ (${F}_{e}=\alpha I$) is the electromagnetic force. The oscillator system's dynamic equation can be expressed as follows,

$$ M\frac{{d^{2} y}}{{dt^{2} }} + F_{\beta } + F_{r} = F_{b} Sin\left( {\omega t} \right) $$

(5)

where ${k}_{1}$ is the linear spring constant and ${k}_{2} \; \text{and} \; {k}_{3}$ are the nonlinear coefficients of the system. In the presence of electromechanical coupling, the oscillator system's dynamic equation can be written as,

$$ M\frac{{d^{2} y}}{{dt^{2} }} + F_{\beta } + F_{r} + F_{e} = F_{b} {\text{Sin}} \left( {\omega t} \right) $$

(6)

$$ R_{in} I + L\frac{dI}{{dt}} = \alpha \frac{dy}{{dt}} $$

(7)

Fig. 11

Free body diagram of the nonlinear oscillator system with electromechanical coupling

Equations 6 and 7 can be expressed as

$$M\frac{{d}^{2}y}{{dt}^{2}}+\beta \frac{dy}{dt}+{k}_{1}y+{k}_{2}{y}^{2}+{k}_{3}{y}^{3}+\alpha I = {F}_{b}Sin(\omega t)$$

(8)

$$M\ddot{y}+\beta \dot{y}+{k}_{1}y+{k}_{2}{y}^{2}+{k}_{3}{y}^{3}+\alpha I = {F}_{b}Sin(\omega t)$$

(9)

$$ R_{in} I + L\dot{I} = \alpha \dot{y} $$

(10)

$$V+L\frac{dI}{dt}=\alpha \frac{dy}{dt}$$

(11)

where ${R}_{in}$ is the coil's resistance, $L$ is the winding coil’s inductance, and $I$ is the induced current ($I=\frac{V}{R}$) and $V$ is the induced voltage.

5.1 State space analysis of the nonlinear oscillator system

A state space model is a linear representation of a dynamic system's discrete or continuous time. The continuous time form of a model in state space form can be written by

$$\dot{x}=Ax+Bu$$

(12)

$$z=Cx+Du$$

(13)

where A, B and C are the system matrix, input matrix and output matrix, respectively. The remaining matrix is D which is typically zero because the input directly does not normally affect the output.

$$M\frac{{d}^{2}y}{{dt}^{2}}+\beta \frac{dy}{dt}+ky+{k}_{2}{y}^{2}+{k}_{3}{y}^{3}={F}_{b}Sin(\omega t)$$

(14)

$$ \ddot{y} = \frac{1}{M}\left( {F_{b} Sin\left( {\omega t} \right) - \beta \dot{y} - k_{1} y - k_{2} y^{2} - k_{3} y^{3} } \right) $$

(15)

By considering the state variables ${Z}_{1}$ and ${Z}_{2}$, the system Eq. 15 can be written in state space form by the following:

$${Z}_{1}=y$$

(16)

$${Z}_{2}=\dot{y}={\dot{Z}}_{1}=\frac{d{Z}_{1}}{dt}$$

(17)

$$\frac{d{Z}_{2}}{dt}=\ddot{y}$$

(18)

$$u={F}_{b}Sin(\omega t)$$

(19)

The differential equation is expressed as a state space matrix as follows,

$$ \dot{Z}_{2} = \frac{{dZ_{2} }}{dt} = \frac{1}{M}\left( {U_{1} - \beta Z_{2} - k_{1} Z_{1} - k_{2} Z_{1}^{2} - k_{3} Z_{1}^{3} } \right) $$

(20)

The resulting state space matrix for 3rd order polynomial model form of the differential equation gives:

$$ \left[ {\begin{array}{*{20}c} {\frac{{dZ_{1} }}{dt}} \\ {\frac{{dZ_{2} }}{dt}} \\ \end{array} } \right] = \underbrace {{\left[ {\begin{array}{*{20}c} 0 & 1 \\ {\frac{{ - k_{1} - k_{2} Z_{1} - k_{3} Z_{1}^{2} }}{M}} & {\frac{ - \beta }{M}} \\ \end{array} } \right]}}_{A}\left[ {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ \end{array} } \right] + \underbrace {{\left[ {\begin{array}{*{20}c} 0 \\ \frac{1}{M} \\ \end{array} } \right]}}_{B}\left[ {U_{1} } \right] $$

(21)

$$ \left[ y \right] = \underbrace {{\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]}}_{C}\left[ {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ \end{array} } \right] + \underbrace {\left[ 0 \right]}_{D}\left[ u \right] $$

(22)

The matrix form of the state-space model of the oscillator system with electromechanical coupling can be expressed as

$$ \left[ {\begin{array}{*{20}c} {\dot{Z}_{1} } \\ {\dot{Z}_{2} } \\ {\dot{Z}_{3} } \\ \end{array} } \right] = \left[ {\underbrace {{\begin{array}{*{20}c} 0 & 1 & 0 \\ {\frac{{ - k_{1} - k_{2} Z_{1} - k_{3} Z_{1}^{2} }}{M}} & {\frac{ - \beta }{M}} & {\frac{ - \alpha }{M}} \\ 0 & {\frac{\alpha }{L}} & {\frac{{ - R_{in} }}{L}} \\ \end{array} }}_{A}} \right]\left[ {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ \end{array} } \right] + \left[ {\underbrace {{\begin{array}{*{20}c} 0 \\ \frac{1}{M} \\ 0 \\ \end{array} }}_{B}} \right]\left[ {U_{1} } \right] $$

(23)

$$ \left[ {\dot{y}} \right] = \underbrace {{\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]}}_{C}\left[ {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ \end{array} } \right] + \underbrace {\left[ 0 \right]}_{D}\left[ u \right] $$

(24)

6 Dynamics analysis of the nonlinear oscillator system

The dynamics of the 3rd-order polynomial model have been analysed. The linear and nonlinear coefficients of the oscillator system for various excitation have been presented in Table 2.

Table 2 Coefficients of the oscillator system (3rd order polynomial model)

The log decrement method has been used to measure the oscillator's damping ratio, constant, and natural frequency (total length 222 mm). The measured damping ratio, damping constant, and natural frequency are 0.031, 0.74 $Ns/m$ and 32.35 $rad/s$, respectively. The theoretical simulation of the system has been run by MATLAB code using the values of M (mass including plastic bush), $\beta$, ${k}_{1}$, ${k}_{2}$ and ${k}_{3}$ are 0.37 kg, 0.74 $Ns/m$, 269.31 $N/m$, 5680.4 $N/{m}^{2}$ and 163,159 N/m³, respectively. The simulation results of the system are displayed in Fig. 12. The colour bar in Fig. 12 shows the floating magnet's various positions. When the magnet is in the expected equilibrium position (0 mm), the resulting eigenvalues are ${\lambda }_{i=1 to 4}=$ − 1.0000+26.9604i, 0, 0 and − 1.0000+26.9604i, and the corresponding frequency is 26.9790 rad/s or 4.296 Hz. It has been seen from the analysis that the real parts of the eigenvalues remained constant for all various positions of the middle magnet when it moved toward the top and bottom magnets. However, the imaginary parts of the eigenvalues, and thus the frequencies, changed with the changing position of the floating magnet. There is a considerable decrease in the imaginary part of the eigenvalues, and thus frequencies, until 17 mm is reached before increasing when the floating magnet moves toward the top magnet from the equilibrium position.

Fig. 12

Eigenvalues and frequency responses for various positions of the floating magnet (50 mm excitation ranges, 3rd order polynomial model)

The minimum resulting eigenvalues and frequency were − 1.0000+24.3580i, 0, 0 and − 1.0000 − 24.3580i and 3.88 Hz (24.37 rad/s), respectively, found at 17 mm up towards the top magnet. After 17 mm towards the top magnets, the imaginary parts of the eigenvalues and natural frequencies rose steadily. On the other hand, the imaginary parts of the eigenvalues and frequencies increased steadily with the increasing distance of the floating magnet from the equilibrium position towards the bottom magnet. The minimum values for the imaginary part of the eigenvalues and natural frequency should be found in the equilibrium position. However, it did not occur due to the gravitational force's effect on the equilibrium position. Because of the gravitational effects, the equilibrium position moved 17 mm away toward the bottom magnet where it should be. When the position of the floating magnet is 50 mm towards the top magnet (− 50 mm), the resulting eigenvalues are ${\lambda }_{i=1 to 4}=$ − 1.0000 + 32.5833i, 0, 0 and − 1.0000+32.5833i. Moreover, when the position of the floating magnet is 50 mm towards the bottom magnet (+50 mm), the resulting eigenvalues found are ${\lambda }_{i=1 to 4}=$ − 1.0000+50.9599i, 0, 0 and − 1.0000–50.9599i as displayed in Fig. 12.

The eigenvalues can be calculated by using the following equations.

$${\lambda }_{i}=-\frac{\beta }{2M},-\frac{1}{2M}\sqrt{4Mk-{\beta }^{2}i}$$

(25)

$${\lambda }_{i}=-\frac{\beta }{2M},\frac{1}{2M}\sqrt{4Mk-{\beta }^{2}i.} $$

(26)

The calculated eigenvalues were − 1.000+26.9604i and − 1.000 − 26.9604i when the position of the floating magnet is 0 mm (expected equilibrium position). These equations work when the system is linear and the displacement of the floating magnet is very small (near equilibrium position). For the other displacement (high displacement), this system works as a nonlinear system, and these equations will not work. Moreover, with the changing of the floating magnet's position, the oscillator's frequency changes, as shown in Fig. 12. The corresponding natural frequencies could be measured by using the following formula:

$${\omega }_{i}=\sqrt{Re{({\lambda }_{i})}^{2}+Im{({\lambda }_{i})}^{2}}$$

(27)

The calculated natural frequencies for -50 mm, 0 mm and + 50 mm positions of the floating magnet are $32.5986$ rad/s (5.20 Hz), $26.9790$ rad/s (4.30 Hz) and $50.9697$ rad/s (8.11 Hz), respectively which are close to the measured frequency, as shown in Fig. 13. Figure 13b, c show the asymptotic analysis for the floating magnet when it is equilibrium position and a different position, respectively. The legend y in Fig. 13 is the position of the floating magnet from the equilibrium position. In the legend, y = 0 means the floating magnet is in equilibrium. In legend, y = − 0.05 means the position of the floating magnet is 50 mm away from the equilibrium position toward the top magnet. The position of the floating magnet 50 mm away from the equilibrium position toward the bottom magnet is presented in legend as y = 0.05. The analytically calculated average natural frequency for this test rig setup (total length of the oscillator is 222 mm) is 32.66 rad/s (5.20 Hz) which is almost similar to the experimentally measured (log-decrement) natural frequency of 32.35 rad/s (5.15 Hz).

Fig. 13

Frequency response of the system when the floating magnet moved 50 mm toward the top magnet and 50 mm toward the bottom magnet from the equilibrium position (3rd order polynomial model) a Bode diagram b Asymptotics analysis for the equilibrium position of the floating magnet and c Asymptotics analysis for different positions of the floating magnet

Moreover, both eigenvalues’ real numbers are negative; therefore, the model is stable. The damping ratio can be found using the formula

$${\zeta }_{i}=Re({\lambda }_{i})/\sqrt{Re{({\lambda }_{i})}^{2}+Im{({\lambda }_{i})}^{2}}$$

(28)

The calculated average damping ratio is 0.032 when the oscillator length is 222 mm, which is almost similar to the experimentally measured damping ratio of 0.031. With changing excitation positions of the floating magnet, the coefficients of the magnetic spring system change. Figure 14 presents the resulting eigenvalues and frequencies for different ranges of excitation of the floating magnet.

Fig. 14

Eigenvalues and frequency response for floating magnet’s different excitation ranges (3rd order polynomial model)

The legends in Fig. 14 present the floating magnet’s excitation ranges. The variable − 0.005 to 0.005 in the legend is indicated that the floating magnet moved 5 mm toward the top magnet and 5 mm toward the bottom magnet from the equilibrium position. From Fig. 14, it can be seen that the real parts of the eigenvalues stayed constant for all excitation ranges of the floating magnet, but the imaginary parts of the eigenvalues changed with the changing of the excitation ranges of the floating magnet. Moreover, the resulting frequency responses for all excitation ranges are closer to each other. If an external force is applied to the floating magnet, then the displacement and velocity of the magnet are shown in Fig. 15. The applied external harmonic force (Fb) amplitude is 10N, and the frequency (f) is 0.1 Hz. Moreover, the values of M, $\beta$, ${k}_{1}$, ${k}_{2}$ and ${k}_{3}$ are 0.37 kg, 0.74 Ns/m, 269.31 N/m, 5680.4 N/m² and 163,159 N/m³, respectively. The ode23t solver has been used in MATLAB to find the displacement and velocity of the floating magnet.

Fig. 15

Displacement and velocity of the floating magnet under harmonic force

The excitation of the floating magnet was assumed to have the initial displacement y = 0 and its corresponding velocity $\dot{y}=0$. The frequency of the harmonic force was 0.1 Hz. As expected, the displacement and the velocity were sinusoidal and were 90° out of phase with one another. The displacement amplitude was around 20 mm toward the bottom magnet and about 30 mm toward the top magnet. This confirms the amplitude of the displacement signal, as shown in Fig. 15. Moreover, the velocity versus displacement graph of the floating magnet under this harmonic force has been presented in Fig. 16b as well. Figures 15 and 16 show that at the beginning of the middle magnet’s movement under the harmonic force, it creates some noises and becomes smooth afterwards.

Fig. 16

a Displacement and velocity of the floating magnet under harmonic force b Displacement versus velocity

Furthermore, the nonlinear and linear models of the oscillator (total length 222 mm) system have been compared, as shown in Figs. 17, 18 and 19, respectively. The applied external harmonic force (Fb) amplitude is 10 N, and the frequency (f) is 0.1 Hz. Moreover, the values of M, $\beta$, ${k}_{1}$, ${k}_{2}$ and ${k}_{3}$ are 0.37 kg, 0.74 Ns/m, 269.31 N/m, 5680.4 N/m² and 163,159 N/m³, respectively.

Fig. 17

Displacement of the floating magnet for linear and nonlinear model analysis

Fig. 18

Velocity of the floating magnet for linear and nonlinear model analysis

Fig. 19

Velocity versus displacement

It can be seen from the above Figures that the floating magnet creates higher displacement in the linearised model than in the nonlinear model, but it achieves higher velocity in the nonlinear model than the linear model under the same external applied harmonic forces. Consequently, the nonlinear model is more effective in generating a higher velocity of the floating magnet.

6.1 Dynamics analysis of the nonlinear oscillator system for different heights

The eigenvalues and frequencies have been analysed for different lengths of the oscillator. All linear and nonlinear values have been used here for -50 mm to 50 mm excitation ranges. The eigenvalues and frequency responses have been measured by using the theoretical 3rd-order polynomial curve fitting’s data. It has been seen from Fig. 9 that the damping ratio increases means the damping constant increases when the oscillator length decreases and the damping constant declines when the oscillator length rises. Therefore, it can be said that the system becomes more unstable when the oscillator length increases. The system's eigenvalues have been measured to check these findings, as shown in Fig. 20.

Fig. 20

Eigenvalues for various positions of the top fixed magnet

The real parts of the eigenvalues are always − 1 for various positions of the floating magnet when the oscillator’s total length is 222 mm (considered equilibrium position means 0 mm position of the top mixed magnet). The real parts of the eigenvalues increase on the negative side when the top fixed magnet travels toward the central magnet (decreases the total length of the oscillator) from 0 mm position (222 mm, equilibrium position for this particular magnet setup), as seen in Fig. 20. Alternatively, when the top fixed magnet moves away from the 0 mm position, then the eigenvalues' real parts decrease and come close to zero in the scale. The system becomes more stable when the top fixed magnet travels toward the central magnet (decreases the total length of the oscillator), and it becomes more unstable when the top fixed magnet moves away continuously from the equilibrium position. Figure 21 displays the frequency responses of the system for different oscillator lengths. Figure 21 shows that the natural frequency increases when the top fixed magnet travels toward the central magnet and decreases when it moves away from the central magnet.

Fig. 21

Frequency response for various positions of the top magnet

6.2 Dynamics analysis of the nonlinear oscillator with electromechanical coupling

The dynamics of the proposed energy harvester have been analysed using the system’s state-space model. The used parameters of the system are presented in Table 3. Initially, the eigenvalues and frequency of the system were analysed. During the experimental excitation of the middle magnet by an applied external force, the floating magnet moved a maximum of 20 mm toward the bottom magnet and 50 mm toward the top magnet from the equilibrium position. Therefore, the excitation range has been considered 20 mm toward the bottom magnet and 50 mm toward the top magnet from the equilibrium position. The magnetic restoring force has been determined for this excitation range, and the linear and nonlinear coefficients have been measured from this magnetic restoring force. The system's eigenvalues for various positions of the middle/floating magnet have been shown in Table 4.

Table 3 Required parameters for the system

Table 4 Eigenvalues of the system

The real parts of the eigenvalues (Mechanical part) remained almost similar for the floating magnet’s various positions. However, the eigenvalues' imaginary part changed with changing the floating magnet's position. On the other hand, the real part of the eigenvalues of the electrical part is almost similar for various floating magnet’s positions. Still, the imaginary parts remained zero for all floating magnet’s different positions. The system’s eigenvalues when the floating magnet was in the equilibrium position have been presented in Table 4. The natural frequency of the mechanical part changed with the floating magnet’s different positions. However, the natural frequency of the electrical part remained constant at around 151.79 Hz for all positions of the floating magnet. The natural frequencies of the mechanical part increased when the floating magnet travelled toward the bottom or top magnets. The system’s resonance frequency has been analysed with and without electrical–mechanical coupling. The system’s resonance frequency without electrical–mechanical is shown in Fig. 22a (with asymptotics analysis), and the system’s resonance frequency with electrical–mechanical coupling is presented in Fig. 22b (with asymptotics analysis). The asymptotic analysis indicated the resonance frequency of the mechanical and electrical systems, as shown in Fig. 22b, c. To determine the system's resonance frequency, the selected coil's average magnetic flux density, length, resistance and inductance were 0.35 T, 23.5 m, 5.48 Ω and 0.005546 H, respectively. Figure 22c shows the resonance frequencies for various positions of the floating magnet.

Fig. 22

Resonance frequency of the system a in the absence of electrical–mechanical coupling, b in the presence of electrical–mechanical coupling and c for various positions of the floating magnet

The generator system's frequency response showed no maximum (or peak) amplitude due to electrical–mechanical coupling effects, as shown in Fig. 22c. It has been known from the literature that the stiffness, mass and damping constant affect the resonance frequency of any system.

The movement of the middle floating magnet generates an electric field inside the winding coil. When a constant velocity of 0.5 m/s moves the floating magnet from the equilibrium position, it generates induced voltage and flux linkage, as presented in Fig. 23. As shown in Fig. 23, the maximum flux linkage occurred inside the winding coil only when the moving magnet and coil were parallel (both the floating magnet and the coil were in the same position). The induced voltage was zero when the flux linkage was at its maximum. Figure 24a shows an electromechanical coupling for a single coil, whereas Fig. 24b displays electromagnetic force and damping. In the absence of a magnet, the magnetic flux changes in each loop cancel out, resulting in a zero value.

Fig. 23

Induced voltage and flux Linkage in the winding coil

Fig. 24

a Electromechanical coupling coefficient and b Electromagnetic force and damping

Moreover, the theoretical generator model dynamics have been analysed using the state-space model (ode23t). The generator system’s displacement, velocity, and induced voltage for different simulation times have been determined under harmonic force. The harmonic force’s amplitude and frequency were 25 N and 0.1 Hz, respectively. The initial displacement, velocity and induced voltage were considered zero, and the simulation was run for 20 s. Figure 25 displays the system’s displacement, velocity, and induced voltage. The bifurcation analysis has been performed to know the behavior of the generator's displacement, velocity, and output for different time periods. The bifurcation analysis have been presented in Fig. 26.

Fig. 25

Displacement, velocity and induced voltage of the system

Fig. 26

Bifurcation analysis a Displacement versus time period, b Velocity versus time period and c voltage versus time period

Figure 26 shows the maxima and minima of the displacement, velocity, and output voltage of the generator for different periods. The generator shows high voltage output and high velocity during a small period means it is in the high-frequency range. The displacement of the oscillator decreased with increasing the frequency of the floating magnet. On the other hand, the velocity and output voltage increased with the increasing frequency of the oscillator. Figure 27 presents the power of the system for 0.1 Hz.

Fig. 27

Power output of the system

For the 25sin(2phi*0.1*t) applied harmonic force, the floating magnet moved around 31 mm towards the bottom and about 43 mm towards the top. Between that time, the maximum velocity of the floating magnet was 0.026 m/s. The measured maximum induced voltage was around 0.23 V for this displacement of the floating magnet. Moreover, the determined maximum power was 0.01 W, as shown in Fig. 27. The harmonic force frequency was 0.1 Hz, so the displacement line should touch the 0 points after a complete cycle. Figure 25 shows that the displacement curve did not touch the 0 points after an entire cycle (when the simulation was run for 10 s) due to the electromechanical coupling effect.

6.3 Analyses of the energy generator model for different oscillator lengths

The linear and nonlinear stiffnesses, damping constants and natural frequencies of the oscillator system changed with the oscillator length. In this section, the generator system has been analysed by changing the oscillator’s length. The displacements and velocities of the floating magnet have been determined. The induced voltages have been measured for various oscillator lengths. During that analysis, the amplitude and frequency of the applied harmonic force were considered 25 N and 0.1 Hz, respectively. A winding coil (100 turns) which consists of 5.48-Ω internal resistance and 0.005546 H inductance, was considered to determine the induced voltage. The length of the oscillator varies from 212 to 272 mm. Figure 28 displays the displacement and velocity of the generator system for various lengths of the oscillator.

Fig. 28

a Displacement and b Velocity of the SDOF generator system for different oscillator lengths

Increasing oscillator length increased the floating magnet's displacement and velocity, as shown in Fig. 28. The generated induced voltage increased with expanding the oscillator length, as presented in Fig. 29. Therefore, it can be said that increasing the oscillator length can improve the generator's efficiency.

Fig. 29

Generated voltage of the SDOF generator system for different lengths of the oscillator

7 Discussion

The mass and size of the magnets are comparably higher than those of the magnets used to build magnetic levitation-based oscillator systems in literature, as presented in Table 5. The equation used in the literature is applied to measure the magnetic flux density of ring types of permanent magnets to measure the axial magnet flux density but not for radial magnetic flux density. Measuring radial magnetic flux density is essential as the winding coils are placed outside the floating magnet's surface. Thus, the axial magnetic flux density was measured using the analytical method, whereas the radial magnetic flux density was measured using the experimental method [21]. The findings (analytical) were validated with numerical measurement to justify the analytical analysis of axial magnetic flux density. The measurements (experimental) were validated with the numerical results to justify the experimental measurement of radial magnetic flux density. It was found that the numerical methods showed very similar findings to analytical and experimental methods. The magnetic properties of the proposed magnetic spring-based oscillator system were studied using numerical methods. In the literature, it was seen that the magnetic restoring forces were measured using either numerical, analytical, or experimental methods, as shown in Table 5. However, the novelty of this present work is that the magnetic restoring force of the proposed oscillator system is measured using analytical, numerical and experimental methods, and the measurements are validated by comparing each other.

Table 5 Comparison of the parameters of the oscillator system from the literature

Compared with other oscillator systems, the proposed single-degree-of-freedom system has a higher magnetic restoring force [6, 8, 25]. It was also found that gravitational force impacts the system's equilibrium position and magnetic restoring force. The centre floating magnet moved toward the bottom fixed magnet by 12.5 mm from the expected equilibrium position. Maximum researchers in the literature did not consider or ignore the gravitational force effects presented in Table 6. Therefore, analysing the gravitational force effects on equilibrium position is the originality of this current study. The coefficients of the proposed SDOF oscillator system were determined from the magnetic restoring force curve using the polynomial curve fitting method. The stiffnesses of the system were determined for various excitation ranges of the centre floating magnet. It was found that the higher-order polynomial curve fitting provided a good fit for high excitation ranges; however, lower-order polynomial curve fitting provided a good fit for the low excitation range.

Table 6 Comparison of the parameters of the oscillator system from the literature

The linear and nonlinear stiffnesses were used to study the dynamics of the SDOF nonlinear oscillator system. As the maximum researchers did not consider the gravitational force effects, one of the nonlinear spring constants (k2) (N/m2) was ignored, as shown in Table 7.

Table 7 Coefficients and dynamics of the system compared with other existing systems

The eigenvalues and frequency responses were analysed by changing the floating magnet’s position. It was found from this study that the eigenvalue and resonance frequency of the oscillator system changed with changing the floating magnet’s position. The oscillator system has shown an average 5.19 Hz (analytical measurement) natural frequency in the system's equilibrium position, which changed with changing the position of the floating magnet. The experimental measured natural frequency was 5.14 Hz, and the findings' error percentage was 0.962%. Moreover, the damping ratio of the system was determined analytically (0.032) and experimentally (0.031) with a percentage of error of 3.22%. The measured natural frequency of the system is lower than the other system's natural frequency, as presented in Table 7. Moreover, the system was analysed by changing the oscillator length. The damping ratio varied from 0.0153 to 0.0463, and the natural frequency varied from 3.76 to 5.47 Hz. The magnetic restoring force of oscillators increased with decreasing lengths and declined with increasing lengths. However, the dynamics study of the oscillator system for various positions of the floating magnet and different oscillator length are one of the main novelties of this present work.

8 Conclusion

This paper studied an SDOF magnetic spring-based oscillator mechanism, dynamics, and magnetic repulsive force. The benefits of the magnetic spring-based linear generator design are that it has few moving mechanical parts and a stronger magnetic field, leading to a high voltage output. The coefficients of the proposed oscillator system have been studied numerically, theoretically and experimentally. The coefficients of the system were determined using cubic and quintic polynomial curve fitting models. The characteristics and dynamics of the proposed oscillator have been studied using analytical, numerical and experimental methods. The eigenvalues and resonance frequency of the oscillator system have been analysed with and without electromechanical coupling. The magnetic properties of the proposed oscillator system have been analysed to evaluate the magnetic flux density and magnetic field strength for different arrays and configurations. According to the study, the separation distance between magnets influences the system's dynamics, leading to behavioural changes from hardening to softening based on its linear and nonlinear characteristics. The height of the oscillator system greatly impacts the oscillator system, which has also been analysed by changing the height of the oscillator. Moreover, the present study was compared with the other existing studies presented in the literature. The comparison study shows that the proposed system has a higher magnetic restoring force. With all these investigations, the researchers will gain a deeper understanding of magnetic restoring forces, coefficients and dynamics of the SDOF oscillator system.