1 Introduction

The most fundamental phenomena in oscillations of complex systems are connected with different types of collective behavior. Patterns existing in dynamics of such systems, such as different types of synchronization or chimera states, have attracted scientists for decades.

Advantages of the most common synchronization state have benefited various man-made inventions, such as pendulum clocks, musical instruments, radio waves, electric power systems, lasers, and electronic generators, and have featured in other applications in electrical and mechanical engineering. It has also been fundamental to our understanding of a wide range of natural phenomena, ranging from cosmology [1], natural rhythms of, for instance, heart beat [2] to engineering [3]. The synchronization can have both beneficial and undesirable effects. It can lead to species extinction [4] or survival [5]. Synchronization of neural impulses causes pathologies of the brain such as Parkinson’s disease [6], or epilepsy [7], on the other hand synchronizing human brain hemispheres is a key mechanism underlying perceptual integration [8] and constitutes basis of faster and more effective learning methods [9].

In 2002, Yoshiki Kuramoto found more complex, unexplained phenomena [10]. He discovered that in a set of identically coupled oscillators, some of them could synchronize, while others remained incoherent (chimera states). Chimeric behavior can be found in a variety of models: Kuramoto networks [11], chemical oscillators [12], neural networks [13] or mechanical and electrical systems [14, 15], among others. However, many problems remain unsolved. For instance, a traveling chimera has been observed recently, in which its synchronized part can migrate in a stable form, or the so-called state or pulse (breathing chimera) [16].

Dynamics of complex systems can be investigated with emphasis on different aspects, features and systems’ properties. One of the most universal tools allowing investigations of many aspects of systems’ dynamics are Lyapunov exponents [17] analysis. Universality of this approach is the reason why it is so frequently applied in investigations of many different types of nonlinear systems [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. However, when studying topological properties, the most applicable invariant is fractal dimension [39, 40]. On the other hand, when analyzing dynamics in regard to the amount of information, entropy is the superior invariant to be applied [41]. Other important aspects of complex systems dynamics give FFT spectrum frequencies analysis [42], Lyapunov dimension [18, 43], fractional-order [44,45,46], recurrence quantification [12, 25], energy flow control [47,48,49], harmonic balance [50], master stability method [51, 52], statistical analyses [53], or other, combined methods [54]. Effectiveness of these approaches has been also verified during experiments [55,56,57,58].

All these methods require stabilization of the system on a attractor, while our approach allows for concluding about final relative behavior of the oscillators from early tendency of analyzed state. It is especially important in case of investigations of complex systems, which are connected with high computational costs, thus there is continuous need to improve effectiveness of these approaches as well as introduce new effective numerical algorithms of control methods. We propose a combined approach of our effective method of Lyapunov exponents estimation [59, 60] along with reduction of applied information thanks to providing analyses in two-dimensional subspaces.

The article is organized as follows:

  • In the first part of the article we introduce approach, which stands for the basis of our proposed method. In this section we prove that it is possible to reduce amount of information while obtaining different types of indicators, allowing to control system’s dynamics. We also prove effectiveness of our approach, its accuracy and simplicity and thus we justify its implementation to our further investigations. The method can be applied both in analyses of presented in the first part two-dimensional systems, as well as in presented in the second section analyses of complex systems.

  • In the second part we introduce new indicator, Directional, Lyapunov Exponent (DLE), which is based on the method from the first section. Firstly we introduce we apply this approach to analysis of complex system dynamics and perform our studies in two-dimensional subspaces with use of DLEs. We show results proving our assumptions connected with possibility of analyzing of relative behavior of the node oscillators using DLEs. As commonly applied methods of searching different types collective behavior demand stabilization of the system, our method showing early tendency of oscillators synchronization or desynchronization has a big potential in fast recognition of complex behavior o coupled systems.

We prove that our method is simpler, more effective and more accurate than the commonly applied methods.

2 The method

Assume that a dynamical system is described by a set of differential equations in the form of:

$$ \frac{{{\text{d}}{\varvec{x}}}}{{{\text{d}}t}} = {\varvec{f}}\left( {{\varvec{x}}, \;t} \right) $$
(1)

where \({\varvec{x}}\) is a state vector, \(t\) is time and \({\varvec{f}}\) is a vector field that (in general) depends on \({\varvec{x}}\) and \(t\). Consider a situation in which the state vector \({\varvec{x}}\) is disturbed by an infinitesimal perturbation \({\varvec{z}}\). The evolution of the perturbation \({\varvec{z}}\) can be determined by linearization of Eq. (1):

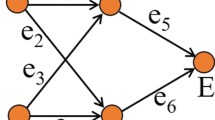
$$ \frac{{{\text{d}}{\varvec{z}}}}{{{\text{d}}t}} = {\varvec{f}}\left( {{\varvec{x}} + {\varvec{z}}, \;t} \right) - {\varvec{f}}\left( {{\varvec{x}}, \;t} \right) = \frac{{\partial {\varvec{f}}}}{{\partial {\varvec{x}}}}\left( {{\varvec{x}},\;\user2{ }t} \right){\varvec{z}} = {\varvec{U}}\left( {{\varvec{x}},\;\user2{ }t} \right){\varvec{z}} $$
(2)

where \({\varvec{U}}\left({\varvec{x}},\boldsymbol{ }t\right)=\frac{\partial {\varvec{f}}}{\partial {\varvec{x}}}\left({\varvec{x}},\boldsymbol{ }t\right)\) is the Jacobi matrix obtained by differentiation of \({\varvec{f}}\) with respect to \({\varvec{x}}\). If the Jacobi matrix were constant, then the evolution of the perturbation \({\varvec{z}}\) in directions of subsequent eigenvectors would be specified by corresponding eigenvalues of that matrix. However, as long as the system (1) is non-linear, the Jacobi matrix varies along the trajectory meaning that the evolution of the perturbation \({\varvec{z}}\) cannot be directly predicted from the properties of the Jacobi matrix. In such a case, Lyapunov exponents are applied to describe an average rate of expansion or contraction of a perturbation. Consequently, Lyapunov exponents can be treated as a generalization of eigenvalues [61] of the Jacobi matrix. Moreover, according to [61], during an evolution of the system, eigenvector connected with the largest eigenvalue tends to align with the direction of the perturbation z(t). Thus, the direction of the vector z determines the direction of the first linearly independent subspace ϕ1 connected with the eigenvector corresponding to the biggest eigenvalue (Fig. 1).

Fig. 1
figure 1

Scheme of perturbation vector and its derivative

Full size image

Let us analyze the evolution of the initial perturbation z in the subspace ϕ1. The perturbation change in the direction dz1 is equal to the projection of dz on ϕ1. Thus, Eq. (2) in this direction can be presented in the following scalar form:

$$ \frac{{{\text{d}}z_{1} }}{{{\text{d}}t}} = \lambda_{1} z $$
(3)

where λ1 is the biggest eigenvalue of \({\varvec{U}}\left({\varvec{x}},\boldsymbol{ }t\right)\) with the corresponding eigenvector aligning to ϕ1.

Equation (3) can be expressed in the form of:

$$ \frac{{{\text{d}}z_{1} }}{z} = \lambda_{1} {\text{d}}t $$
(4)

Numerical integration of Eq. (4) during the time evolution of the perturbation z allows obtaining the value of λ1 averaged in time, equal to the first and the biggest Lyapunov exponent LE1.

$$ \mathop \int \limits_{0}^{t} \frac{{{\text{d}}z_{1} }}{z} = \mathop \int \limits_{0}^{t} \lambda_{1} {\text{d}}t $$
(5)
$$ \frac{{\mathop \int \nolimits_{0}^{t} \frac{{{\text{d}}z_{1} }}{z}}}{t} = \widetilde{{\lambda_{1} }} = {\text{LE}}_{1} $$
(6)

In the methods commonly applied to obtain the second Lyapunov exponent LE2, one has to analyze the evolution of the second perturbation \({{\varvec{z}}}_{\perp }\) (Fig. 1), which is orthogonal to the perturbation z. and determines the subspace ϕ2 linearly independent on ϕ1. In the new method presented here, LE2 in the two-dimensional system can be obtained much easier. As the subspace ϕ2 is linearly independent on ϕ1, the evolution of the perturbation in this direction is influenced only by the second eigenvector of \({\varvec{U}}\left({\varvec{x}},\boldsymbol{ }t\right)\) with the corresponding eigenvalue λ2. Analogous to λ1 and Eq. (3), λ2 can be obtained from Eq. (7), (Fig. 1).

$$ \frac{{{\text{d}}z_{2} }}{{{\text{d}}t}} = \lambda_{2} z_{ \bot } $$
(7)

As the direction of the vector z is defined for each time of the system evolution, direction of \({{\varvec{z}}}_{\perp }\) (Fig. 1) is also known through the whole evolution of the system. Assuming coordinates of \({{\varvec{z}}}_{\perp }\) satisfying the condition of orthogonality to vector z from Eq. (2), one can obtain vector \({d{\varvec{z}}}_{\perp }\) and its projection \({d{\varvec{z}}}_{2}\). (Fig. 1). Basing on the linear properties of \({\varvec{U}}\left({\varvec{x}},\boldsymbol{ }t\right)\), the value of λ2 in Eq. (7) does not depend on the length of the vector \({d{\varvec{z}}}_{2}\). Thus, provided that any vector \({{\varvec{z}}}_{\perp }\) is the element of ϕ2, the corresponding value of λ2 is explicitly known from Eq. (2), without the need of numerical integration of the perturbation in the direction orthogonal to vector z.

Following the reasoning given for λ1, from Eqs. (8, 9), after numerical integration of the system, the value of second Lyapunov exponent LE2 can be yielded.

$$ \int \frac{{{\text{d}}z_{2} }}{z} = \int \lambda_{2} {\text{d}}t $$
(8)
$$ \frac{{\int {\frac{{{\text{d}}z_{2} }}{z}} }}{t} = \widetilde{{\lambda_{2} }} = {\text{LE}}_{2} $$
(9)

The reasoning presented above constitutes a basis for a new method (M3), which will be compared with two other algorithms, commonly applied M1 presented in [61], which differs in need of orthonormalization, and M2 and presented in [60], which is the basis of the method M3 and differs in extracting LEs values straightly from the vector field.

It also proves, that the method has to be simpler, more effective and accurate, than commonly applied methods.

It is simpler as it is based on analysis of only one initial perturbation without need of analysis of the second one and application of the Gram-Schmidt orthonormalization.

It is more effective as instead of application of logarithm functions, our algorithm is based on simple computations based on summations, multiplications and divisions which are characterized by much lower computations costs.

It is also more accurate as it is based on the vector field properties, and invariants are calculated before the integration step, and thus it avoids the integration errors.

3 Numerical simulations

3.1 Methodology

All the programs for conducting numerical simulations have been written in C +  + by means of the Code: Blocks and Visual Studio Code environments. The Runge Kutta method of the fourth order (RK4) has been used to solve ordinary differential equations. The integration step has been adjusted for each analyzed system individually, taking into account its own time scale.

All the considered algorithms of the LE estimation require integration of the system (1) along with Eq. (2) in order to obtain the state vector \({\varvec{x}}(t)\) and the perturbation \({\varvec{z}}(t)\) in subsequent moments of time. All the programs for the estimation of the LE share the same code for integration of the systems (1), (2). The only difference between these programs are methods of the LE calculation.

In the case of M1 and M2, the evolution of the vector \({{\varvec{z}}}_{\perp }\) was obtained by numerical integration of the orthogonalized vector z, together with numerical integration of the vector z. Note that it means that in these cases, two perturbation vectors have to be integrated.

In the case of the algorithm M3, formula Eq. (7) was applied before each integration step in order to obtain the value of λ2. The procedure begins with determining the vector \({{\varvec{z}}}_{\perp }\) as the orthogonal vector to the vector z. Then, vector \({\mathrm{d}{\varvec{z}}}_{\perp }\) is obtained from Jacobi matrix (Eq. (2)). Subsequently, \({\mathrm{d}{\varvec{z}}}_{2}\) has been obtained from the projection of the vector \({\mathrm{d}{\varvec{z}}}_{\perp }\) onto the direction of \({{\varvec{z}}}_{\perp }\). Then, formula Eq. (7) has been applied to obtain the value of λ2 and all these values were averaged using Eq. (9), to arrive at the actual value of LE. Finally, vector z has been integrated and the procedure has been repeated. Note that contrary to the methods M and M2, in algorithm M3 only one perturbation vector has to be integrated. It constitutes the novelty of the proposed method.

In simulations algorithms, conditions for termination of calculations have to be selected. It seems reasonable to finish the estimation procedure if the obtained value of the LE stabilizes at some fixed value and does not display any relevant fluctuations. In order to measure stabilization of the LE value, the authors propose to define a buffer of a selected fixed size. In this research, the buffer capacity equal to 100 was selected as a good compromise between the accuracy of LE estimation and the time of simulations. After each calculation step, the current value of the LE was saved to the buffer. When the buffer was full, the standard deviation of all the LE values in the buffer was calculated. If the standard deviation related to the actual average LE was below a specified threshold, the value of the LE was considered as stable and the calculations could be terminated. Failing that, the buffer was cleared and the procedure repeated. The value of the selected threshold corresponded to the desired accuracy of estimation. Lowering the threshold meant higher accuracy but, consequently, a longer estimation time. Considering standard deviation threshold, two methods, with relative and not relative deviation value can be applied. They differ in the accuracy of LE estimation depending on the dynamical state of the system. In the regions of higher absolute LE values for high accuracy it is better to use nonrelative deviation, in the case of quasiperiodic regions, a relative value will produce a more accurate result. Since minor differences in values in the periodic and chaotic regions are not significant and, conversely, detection of the exact bifurcation point is one of the most important issues in nonlinear systems investigations, relative deviation was applied in our simulations.

Robustness of our approach can be seen in the bifurcational analyses, and stable values of presented indicators, while changing system parameter values.

3.2 Results of numerical simulations

In order to verify the presented methods of the LE estimation, two typical nonlinear systems have been analyzed. What follows are the results obtained for Duffing and Van der Pol systems with external forcing.

The following graphs provide the obtained values of the LE, along with relative computation time, Kolmogorov entropy (KE), Lyapunov Fractal dimension (LFD), and divergence of the system (div), presented as the comparison between method M3 and algorithms M1, M2. In order to ensure proper comparability of results, programs exploiting methods M1, M2 and M3 differ only in the way of calculating actual values respective indicators values.

Since the details that follow are organized in the similar manner, in order to avoid repeating the same description, specification of the graphs is provided only once, below.

Each figure presenting the values of the LEs show a comparison of the results obtained for all three methods (M1…M3) as introduced above. Throughout the article the same colors and types of curves have been associated with respective methods.

In the cases where the dependence of LE on bifurcation parameter is presented, these charts are associated with the analyses of LE estimation accuracy in three types of dynamical states: periodic, quasiperiodic and chaotic.

Subsequently, the ratios of the program execution times t1…t3 for all the five methods, depending on the selected system’s bifurcation parameter are presented. Times t1…t3 present the execution time of LE estimation for the specified bifurcation parameter and method, respectively.

Then, the efficiency analysis is presented. Special efficiency indicators were introduced. Let T1…T3 be sums of ti values, presenting the time from the commencement of simulations until a specified bifurcation parameter is reached for each three methods. Let us use these values to introduce efficiency indicators:

\({\varvec{\eta}}_{{\varvec{i}}} = \frac{{{\varvec{T}}_{{\varvec{i}}} }}{{{\varvec{T}}_{1} }}\)

Relations of ηi, with respect to bifurcation parameter of the investigated algorithms M2, M3, as compared to the classical method M1 are presented on the next type of charts. What can be appreciated are efficiencies of the methods M2 and M3 with respect to the commonly applied method M1. Subsequent charts compare, respectively:

  • Divergences of the systems (div) as the sum of the Lyapunov exponents [20]

  • Lyapunov fractal dimensions (LFD) obtained from Kaplan-Yorke formula [62]

  • And Kolmogorov–Sinai entropies (KE) obtained using Pesin's theorem [19].

3.2.1 Duffing oscillator

The Duffing oscillator can be described by the following set of differential equations:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} } \\ {\dot{x}_{1} = - \beta x_{2} - \alpha x_{1}^{3} + q\cos \left( {\omega t} \right)} \\ \end{array} } \right. $$
(10)

According to Eq. (2), Jacobi matrix is necessary to observe the evolution of a perturbation. For the Duffing oscillator, the Jacobi matrix is defined as follows:

$$ {\varvec{U}} = \left( {\begin{array}{*{20}c} 0 & 1 \\ { - 3\alpha x_{1}^{2} } & { - \beta } \\ \end{array} } \right) $$
(11)

The plot of the LE for different values of the parameter \(q\) and graphs depicting accuracy of LE estimation in three different dynamical states are presented in Fig. 2. The range of parameters used in the simulation was selected to present all the types of the dynamical behavior of the system.

Fig. 2
figure 2

Diagram of the Lyapunov exponents of the Duffing system α = 1, β = 0.05, ω = 0.47

Full size image

In the lower part, one can see that the results of LE estimation obtained using all the three methods overlap.

Higher scale results for the three different dynamical states of the system are presented in the upper part of Fig. 2. It is evident that there is a good agreement for M2 and M3 methods and few differences for the M1 method. Particularly important is the analysis of the quasiperiodic region. One can see that the results of M2 and M3 have very high accuracy of predicting bifurcation point, while M1 shows two bifurcation points in this region.

The same relationship was observed for other bifurcation points and it suggests that M1 and M2 characterize higher accuracy of LE Estimation. It may be related to the fact that the results of λ1 and λ2 in Eq. (7) are obtained from the vector field before the integration step. Therefore, in the case of M2 and M3 numerical integration errors do not influence the values of LE. Such an accuracy analysis was continued in the case of the other indicators in the subsequent part of the article. In these cases the same conclusions emerged.

The efficiency analysis comparison is presented in Fig. 3. The times of simulations for the algorithms M2 and M3 were compared with M3. From the method of construction of the ηi indicators one can deduce that these values characterizing the specified bifurcation parameter q represent the average efficiencies of computations of each method from the commencement of calculations until the parameter q has been reached. Therefore, the values ηi corresponding to the last values of bifurcation parameter, present the entire average efficiencies of each of the methods. From Fig. 3 one can see that both the methods, M2 and M3, have similar efficiencies. The final values of η2 and η3, presenting the average efficiencies, are equal to 0.838 and 0.833, respectively. Therefore, on average, M2 and M3 save approximately 17% of the computation time in comparison to the commonly applied method M1. Algorithm M3 is marginally faster than M2, the difference between these methods is in the range of 0.5%.

Fig. 3
figure 3

Diagram of efficiencies η2, η3 of LE computations of the Duffing system. α  = 1, β = 0.05, ω = 0.47

Full size image

The comparison of the divergence obtained from the sum of Lyapunov exponents, as estimated using algorithms M1…M3, is presented in Fig. 4. As the Duffing system has a constant value of divergence, one can easily predict its theoretical value from the vector field parameters. In the presented case it is equal to 0.1. In Fig. 4 one can see that the accuracy of the divergence estimation using methods M2 and M3 is far superior to M1. It confirms the conclusions reached in the estimation accuracy analysis of Lyapunov exponents presented above.

Fig. 4
figure 4

Diagram of divergence of the Duffing system. α = 1, β = 0.05, ω = 0.47

Full size image

In Fig. 5 we present the diagram of the Lyapunov fractal dimension (LFD) of the Duffing system, obtained using Kaplan-Yorke formula [62]. One can see LFD = 1 for the periodic regions with one-dimensional limit cycle attractor. The two-dimensional torus is confirmed for bifurcation points, and the fractional values of LFD confirm chaotic dynamics with the strange attractor. In the focused upper part it can be seen that methods M2 and M3 are more accurate in the prediction of bifurcation points with quasiperiodic trajectory on two-dimensional torus surface.

Fig. 5
figure 5

Diagram of Lyapunov fractal dimension of the Duffing system. α = 1, β = 0.05, ω = 0.47

Full size image

Diagram of Kolmogorov entropy of the Duffing system, obtained from sum of positive LE [19], is presented in Fig. 6. One can see that for the quasiperiodic regime, method M1, contrary to M2, M3, predicts the lost information about the dynamical state of the system. Similarly to all of the earlier analyses conducted for the Duffing system, Kolmogorov entropy investigations also confirm higher accuracy of the methods M2 and M3 as compared to M1.

Fig. 6
figure 6

Diagram of Kolmogorov entropy of the Duffing system. α = 1, β = 0.05, ω = 0.47

Full size image

3.2.2 The Van der Pol oscillator

The Van der Pol oscillator can be described by the following set of differential equations:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} } \\ {\dot{x}_{2} = \mu \left( { - x_{1}^{2} + 1} \right)x_{2} - x_{1} + q\cos \left( {\omega t} \right)} \\ \end{array} } \right. $$
(12)

Jacobi matrix was used to simulate the evolution of a perturbation according to Eq. (2). For the Van der Pol oscillator, the Jacobi matrix is defined as follows:

$$ {\varvec{U}} = \left( {\begin{array}{*{20}c} 0 & 1 \\ { - 2\mu x_{1} x_{2} - 1} & {\mu \left( { - x_{1}^{2} + 1} \right)} \\ \end{array} } \right) $$
(13)

The plot of the LE for different values of the parameter \(q\) and graphs depicting accuracy of LE estimation in three different dynamical states are presented in Fig. 7. As the values of the first and second LEs differ vastly, the middle, empty part of the chart was cut out.

Fig. 7
figure 7

Diagram of the Lyapunov exponents of the Van der Pol system q = 12.95, ω = 4.64

Full size image

In the lowscale, lower part, one can see that the results of LE estimation obtained using all the three methods overlap.

Higher scale results for the three different dynamical states of the system are presented in the upper part of Fig. 7. Similarly to the case of Duffing system, there exists a good agreement for M2 and M3 methods and few differences for the M1 method. In the quasiperiodic region, one can see that none of the methods predicts an accurate value of LE for bifurcation point. However, the results of M2 and M3 have negative values of LE confirming the instability of the system. On the other hand, M1 predicts qualitative change of the system dynamics and chaotic behavior of the system.

The efficiency analysis of the four methods M1, M2, with respect to M1 is presented in Fig. 8. Similarly as in the case of Duffing system, both of the methods, M1 and M2, have a better efficiency than M3. Finally, the values of η2 and η3, presenting the average efficiencies, are equal to 0.727 and 0.724, respectively. Therefore, on average, M2 and M3 save approximately 27% of the computation time when compared to the commonly applied method M1. Algorithm M3 is slightly faster than M2. Similarly to Dufing system, the difference between these methods is in the range of 0.5%.

Fig. 8
figure 8

Diagram of efficiencies η2, η3 of LE computations of the Van der Pol system. q = 12.95, ω = 4.64

Full size image

Figure 9 presents a diagram of the divergence of the Van der Pol system. Contrary to the Duffing system, here, the divergence is not constant. It consists of two components having opposite influence on the system. The first one, − µx12, is connected with the nonlinear damping which depends on the state variable x1. The second component, + µ, is linear and is responsible for supplying the energy to the system. Naturally, the variable bifurcation parameter influences the slope of the chart as µ appears in both components of the system’s divergence. However, the linear change of this parameter is not responsible for divergence nonlinearity. Each change of the slope of the chart is connected with the corresponding bifurcation point and a qualitative change of the system’s dynamics. The results obtained using all the algorithms are similar and there is no point in presenting differences in a higher scale.

Fig. 9
figure 9

Diagram of divergence of the Van der Pol system. q = 12.95, ω = 4.64

Full size image

In Fig. 10, we present the diagram of Lyapunov fractal dimension of the Van der Pol system. As the values of the upper and lower ranges of the LFD are very narrow-filled, the middle, empty part of the chart was cut out. Comparing the values of LFD in chaotic ranges for Duffing—Fig. 5, and Van der Pol systems one can conclude that the structures of the attractors differ much. In the case of Duffing system, the range of the upper part is approximately 0.3, while in the case of Van der Pol it is only 0.016 and the values of LFD are very close to 2. On the other hand, analyzing positive values of maximal LEs, one can see that in the case of the Van der Pol system LEs are twice bigger than for Duffing system—Fig. 2, even though Van der Pol system is “less chaotic”, and the solution is almost quasiperiodic.

Fig. 10
figure 10

Diagram of Lyapunov fractal dimension of the Van der Pol system. q = 12.95, ω = 4.64

Full size image

Similar aspects of this feature shows the analysis the entropy of the system, as presented in Fig. 11. Comparing its values with the entropy of Duffing system—Fig. 5, one can see that although the Van der Pol system behaves in an almost quasiperiodic manner, the information lost is twice bigger than in the case of evident chaotic behavior of the Duffing system.

Fig. 11
figure 11

Diagram of entropy of the Van der Pol system. q = 12.95, ω = 4.64

Full size image

3.3 Extension of the method into investigations of a complex systems—directional Lyapunov exponents (DLEs)

In this section we present, how our approach can be extended to the analysis of complex systems. As collective behavior of such systems results from relative behavior of the node oscillators, we introduce such a relative two-dimensional perturbation subspaces in which we calculate DLEs using method presented in the first section. We show results proving our assumptions connected with possibility of analyzing of relative behavior of the node oscillators using DLEs. As commonly applied methods of searching different types collective behavior demand stabilization of the system, our method showing early tendency of oscillators synchronization or desynchronization has a big potential in fast recognition of complex behavior o coupled systems.

We show the results of our studies on dynamics of the set of four Duffing oscillators that have been coupled in the ring scheme—Fig. 12.

Fig. 12
figure 12

Scheme of the coupling

Full size image

The system is governed by the following set of differential equations.

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} } \\ {\dot{x}_{2} = - \beta x_{2} - x_{1}^{3} + q\sin \left( {\omega t} \right) - 2\alpha x_{1} + \alpha \left( {x_{3} + x_{7} } \right)} \\ {\dot{x}_{3} = x_{4} } \\ {\dot{x}_{4} = - \beta x_{4} - x_{3}^{3} + q\sin \left( {\omega t} \right) - 2\alpha x_{3} + \alpha \left( {x_{1} + x_{5} } \right)} \\ {\dot{x}_{5} = x_{6} } \\ {\dot{x}_{6} = - \beta x_{6} - x_{5}^{3} + q\sin \left( {\omega t} \right) - 2\alpha x_{5} + \alpha \left( {x_{3} + x_{7} } \right)} \\ {\dot{x}_{7} = x_{8} } \\ {\dot{x}_{8} = - \beta x_{8} - x_{7}^{3} + q\sin \left( {\omega t} \right) - 2\alpha x_{7} + \alpha \left( {x_{1} + x_{5} } \right)} \\ \end{array} } \right. $$
(14)

In the investigations, the values of the constant system parameters were assumed as follows:β = 0.1, q = 7, ω = 1, parameter α was either given a constant value, or was a variable bifurcation parameter.

In our approach, we introduce a new type of perturbation space which spans on relative displacements and velocities of the node oscillators. For the proper analysis of the proposed method we present the results of the analysis prepared in the perturbation space (z1…z12) spanned on all the relative displacements and velocities (x1…x8)

$$ \left\{ {\begin{array}{*{20}c} {z_{1} = x_{1} - x_{3} \;\;z_{2} = x_{2} - x_{4} \;\;{\text{Subspace}} S_{1} - {\text{LDLE}}_{1} - {\text{NODE}}1,\;{\text{NODE}}2 - {\text{adjacent}}} \\ {z_{3} = x_{1} - x_{5} \;\;z_{4} = x_{2} - x_{6} \;\;{\text{Subspace}} S_{2} - {\text{LDLE}}_{2} - {\text{NODE}}1,\;{\text{NODE}}3 - {\text{adjacent}}} \\ {z_{5} = x_{1} - x_{7} \;\;z_{6} = x_{2} - x_{8} \;\;{\text{Subspace}} S_{3} - {\text{LDLE}}_{3} - {\text{NODE}}1,\;{\text{NODE}}4 - {\text{adjacent}}} \\ {z_{7} = x_{3} - x_{5} \;\;z_{8} = x_{4} - x_{6} \;\;{\text{Subspace}} S_{4} - {\text{LDLE}}_{4} - {\text{NODE}}2,\;{\text{NODE}}3 - {\text{ adjacent}}} \\ {z_{9} = x_{3} - x_{7} \;\;z_{10} = x_{4} - x_{8} \;\;{\text{Subspace}} S_{5} - {\text{LDLE}}_{5} - {\text{NODE}}2,\;{\text{NODE}}4 - {\text{adjacent}}} \\ {z_{11} = x_{5} - x_{7} \;\;z_{12} = x_{6} - x_{8} \;\;{\text{Subspace}} S_{6} - {\text{LDLE}}_{6} - {\text{NODE}}3,\;{\text{NODE}}4 - {\text{ adjacent}}} \\ \end{array} } \right. $$
(15)

A space constructed in this manner was divided onto two-dimensional subspaces S1…S6, in which relative behavior of the node oscillators can be studied both qualitatively and quantitatively.

To simplify our approach let us focus on the behavior of perturbation (z1, z2) in the subspace S1. The decay of this perturbation is equivalent to the synchronization of nodes 1 and 2, whereas its growth means desynchronization. Our idea was to quantitatively express the decay/growth perturbation, basing on the concept of Lyapunov exponents. We introduced new indicators, Directional Lyapunov Exponents (DLE), which can be calculated in the presented two-dimensional subspace, using the method discussed in the first section of the article. The term ‘directional’ refers to the properties of these indicators, as they measure exponential growth or decay of a perturbation in arbitrarily assumed, constant directions. Note that it is unlike the case of commonly used Lyapunov exponents, where directions of measured decay/growth depend on the direction of the vector of perturbation and vary in space and time. Hence, there is need for vector orthonormalization in order to divide the space into linearly independent subspaces, in which growth/decay is expressed using idea of Lyapunov exponents. While using the proposed Directional Lyapunov Exponents there is no need for such orthonormalization.

In our introductory studies, for each of the subspaces, we have analyzed only the Largest values Directional Lyapunov Exponents (LDLE), as these values are sufficient for reasoning about relative behavior of the node oscillators. As an example, let us to analyze the above mentioned perturbation (z1, z2), spanning the subspace S1. From the values of LDLE1 one can conclude about synchronization/desynchronization of the Nodes 1 and 2. A negative value of this indicator means the decay of the whole perturbation in the subspace S1. Thus, it is the sufficient condition for the Nodes 1 and 2 synchronization, contrary to the positive value of the indicator meaning their desynchronization.

Note that application of the method presented in the first section of the article, allows also for a simple estimation of the values of the second Lyapunov exponents for each of the subspaces. All the aspects of reasoning about the systems’ dynamics based on the full spectrum of Directional Lyapunov Exponents is still studied and the results will be presented in the subsequent article.

As topology of the system (Eq. 14) is symmetrical, a symmetry in the solutions was also expected and observed. However, our studies also showed different scenarios of symmetry breaking and switching between 3 coexisting types of symmetrical solutions:

  1. 1.

    Full synchronization SYNC—Fig. 13:

    $$ {\text{Node }}1 \equiv {\text{Node }}2 \equiv {\text{Node }}3 \equiv {\text{Node }}4 \Leftrightarrow {\text{LDLE}}1 \approx {\text{LDLE}}2 \approx \ldots \approx {\text{LDLE}}6 < 0 $$
  2. 2.

    Chimera state CH1—Fig. 14a:

    $$ \begin{array}{*{20}c} {{\text{Synchronization of the left}} - {\text{side Nodes 1 and 4}}} & \Leftrightarrow & {{\text{LDLE}}4 < 0} \\ {\text{Desynchronization of the upper Nodes 1 and 2}} & \Leftrightarrow & {{\text{LDLE}}1 > 0} \\ {\text{Desynchronization of the bottom Nodes 3 and 4}} & \Leftrightarrow & {{\text{LDLE}}6 > 0} \\ \end{array} $$
  3. 3.

    Chimera state CH2—Fig. 14b:

    $$ \begin{array}{*{20}c} {\text{Synchronization of the upper Nodes 1 and 2}} & \Leftrightarrow & {{\text{LDLE}}1 < 0} \\ {\text{Synchronization of the bottom Nodes 3 and 4}} & \Leftrightarrow & {{\text{LDLE}}6 < 0} \\ {{\text{Desynchronization of the left}} - {\text{side Nodes 1 and 4}}} & \Leftrightarrow & {{\text{LDLE}}3 > 0} \\ {{\text{Desynchronization of the right}} - {\text{side Nodes 2 and 3}}} & \Leftrightarrow & {{\text{LDLE}}4 > 0} \\ \end{array} $$
Fig. 13
figure 13

Largest Directional Lyapunov Exponents LDLE 1 … LDLE 6. Full synchronization state α = 0.9

Full size image
Fig. 14
figure 14

LDLE 1 … LDLE 6, a chimera state CH1 α = 0.98, b chimera state CH2 α = 0.96

Full size image

Note that two cases of diagonal nodes synchronization, first between Nodes 1 and 3 \((\mathrm{LDLE}2<0)\), second between Nodes 2 and 4 \((\mathrm{LDLE}2<0)\), fulfill the above symmetry conditions only in the case of full synchronization. It was also observed in our investigations.

Besides the negative values of all the LDLEs in Fig. 13, confirming the full synchronization state, it can also be noticed that there is a slight difference in the final values. The diagonal nodes synchronize faster than the adjacent nodes. No conclusions have been drawn from this fact at this juncture, as it will be further analyzed in our extended studies of the method, and algorithms of LDLEs estimation are still being improved.

In Fig. 14, there can be noticed patterns of the relative behavior of the nodes for the chimera states CH1 and CH2. CH1 is the state of side nodes synchronization together with the upper and bottom nodes desynchronization, while CH2 is the opposite state.

It can also be seen that the synchronization in the case of CH2 is faster, and should be more stable than is the case with CH1. This is evident in Fig. 15 together with the time series perturbations. Since symmetry conditions seem to be violated here, similarly to the earlier comment, we just outline this fact but not draw any conclusions.

Fig. 15
figure 15

Partial synchronization a LDLE 3, z3, chimera state CH1 α = 0.98, b LDLE 1, z1, chimera state CH2 α = 0.96

Full size image

Figures 15 and 16 confirm a correlation between the changes of perturbation and LDLEs. The negative values for perturbations decay—Fig. 15 are followed by negative LDLEs, contrary to the positive values for desynchronization states—Fig. 16.

Fig. 16
figure 16

Partial desynchronization a LDLE 1, z1, chimera state CH1 α = 0.98, b) LDLE 3, z3, chimera state CH2 α = 0.96

Full size image

In Figs. 14, 15 there can also be seen the influence of the limitations of perturbation growth in desynchronization states onto the limitations of the average exponential change shown by LDLEs. As the perturbations are limited by the values of the system state variables, LDLEs for desynchronization states are not much higher than zero. Thus, it seems rather impossible to differentiate the borderline state of LDLEs = 0.

A symmetry of the system can be also seen when grouping LDEs values into pairs. In Fig. 17 there is presented a bifurcation diagram demonstrating a switch of pairs between chimeras CH1 and CH2. To simplify the analysis, one chart for each of the pairs is presented together in Fig. 18. It can be seen that half the parts of the system are switching oppositely between chimera states CH1 and CH2. However, there also exists one point where both LDLEs are negative. It is the case of full synchronization, and consistent with a comment from above it can be seen in Fig. 19 that in that case, the diagonal LDEs are negative as well.

Fig. 17
figure 17

Pairs of bifurcation diagrams a Upper and lower sides LDEs, b Left and right side LDEs

Full size image
Fig. 18
figure 18

Bifurcation diagram of directional Lyapunov exponents LDLE 3 and LDLE 4

Full size image
Fig. 19
figure 19

Full Synchronization a Diagonal LDLEs, b Full spectrum of LDLEs

Full size image

To confirm the differences between dynamical states of the node oscillators, and to prove chimera states existence, we have also analyzed average values of the nodes velocities. We decided to focus on investigating the average absolute values of the relative velocities of the nodes—Eq. (16). Consistent with the earlier analysis, we introduced following values of the average velocities.

$$ \begin{array}{*{20}c} { v_{1} = {\text{average}}(|x_{2} | - \left| {x_{6} } \right|)} & {{\text{Subspace}} S_{1} } & {{\text{NODE}}1,\;{\text{NODE}}2} & {{\text{adjacent}}} \\ { v_{2} = {\text{average}}(|x_{2} \left| - \right|x_{6} |)} & {{\text{Subspace}} S_{2} } & {{\text{NODE}}1,\;{\text{NODE}}3} & {{\text{adjacent}}} \\ { v_{3} = {\text{average}}\left( {|x_{2} \left| { - |x_{8} } \right|} \right)} & {{\text{Subspace}} S_{3} } & {{\text{NODE}}1,\;{\text{NODE}}4} & {{\text{adjacent}}} \\ { v_{4} = {\text{average}}(\left| {x_{4} } \right| - |x_{6} |)} & {{\text{Subspace}} S_{4} } & {{\text{NODE}}2,\;{\text{NODE}}3} & {{\text{adjacent}}} \\ { v_{5} = {\text{average}}\left( {|x_{4} \left| { - |x_{8} } \right|} \right)} & {{\text{Subspace}} S_{5} } & {{\text{NODE}}2,\;{\text{NODE}}4} & {{\text{adjacent}}} \\ { v_{6} = {\text{average}}\left( {|x_{6} \left| { - |x_{8} } \right|} \right)} & {{\text{Subspace}} S_{6} } & {{\text{NODE}}3,\;{\text{NODE}}4} & {{\text{adjacent}}} \\ \end{array} ` $$
(16)

Additionally, as the bifurcation analysis showed high sensitivity to parameter α changes, we decided to combine the velocities analysis with a possibility of the attractors coexistence if the sensitivity to initial conditions was identified. The subsequent figures prove that, indeed, depending on the initial conditions, the system switches between chimera states CH1 and CH2. We did not detect switching to complete synchronization for the introduced initial conditions and the assumed value of α = 0.96.

The initial conditions were as follows: the first node had random initial conditions. Subsequent nodes were dependent on the perturbation 1 and perturbation 2 such that for perturbation 1 = perturbation 2 = 0 all the nodes had the same initial conditions.

The first general approach Fig. 20a proves that depending on the initial conditions of the system, velocities of the nodes have two different values. It confirms a possibility of the chimera dynamics existence. There can also be seen switching between these values, as both the planes consist of all the four velocities—colors.

Fig. 20
figure 20

3-D basins of attraction based on a velocities of the nodes, b relative velocities of the nodes

Full size image

The relative velocities analysis in Fig. 20b confirms such switching. However, thanks to analyzing relative velocities, in the middle part it also includes the synchronization plane where relative velocities approach zero. According to bifurcation analysis, the velocities in this chart were grouped in two colors, which allows distinguishing chimera states, and showing switching between these states depending on the initial conditions. What follows is a detailed analysis of the switching, which confirms chimeras coexistence.

Respective to Fig. 20b, in Fig. 21a there can be seen three different regions, upper and lower values in desynchronization states, as well as synchronous in the middle. It can be also seen that system switches not only between chimera states CH1 and CH2, but also between CH1 upper and lower states of desynchronization. It is connected with the presented in Fig. 20a switching between upper and lower planes, which causes a change of the sign of the relative velocities.

Fig. 21
figure 21

Basins of attraction based on relative velocities—upper and bottom nodes; a one-dimensional for perturbation 2 = 0, b two-dimensional

Full size image

Similar conclusions can be drawn for the side nodes presented in Fig. 22.

Fig. 22
figure 22

Basins of attraction based on relative velocities—side nodes; a one-dimensional for perturbation 2 = 0, b two-dimensional

Full size image

4 Conclusions

We presented a new simple method of investigations of complex systems based on vector field properties and reducing the amount of applied information.

Firstly, we presented the basis of our approach to extraction of nonlinear indicators of two-dimensional systems. We demonstrated that basing on simplified analyses and exploiting half of commonly applied information we can precisely estimate indicators widely applied in investigations of nonlinear systems. We proved that our method is simpler, more efficient and more accurate than commonly applied algorithms.

Then we extended our studies and applied the presented method in investigations of complex systems. Initially, we have constructed a new type of phase space and in combination with the approach that we discussed in the first section of the article we continued our studies, basing on LDLEs indicators introduced into two-dimensional subspaces. We applied these indicators in investigations of dynamics of the set of Duffing oscillators, coupled in the ring scheme. We analyzed synchronization and chimera phenomena, switching between these states, sensitivity of the system to initial conditions, coexistence of the attractors and their basins of attraction. Thanks to the application of the reduced amount of information, estimation of indicators directly from the vector field properties, analysis being held in two-dimensional subspaces with no need for orthonormalization, we constructed a very effective tool for investigations of complex systems. We proved simplicity and effectiveness of our approach and showed how it simplifies investigations of complex dynamical phenomena. One of the most important achievements of this research is that it allows reducing costs of computations, which would be very important in the case of investigations of more complex systems with much more complicated dynamics [63].

The presented studies constitute only a preliminary stage of our method development. Extended investigations, with estimation of the values of the second Directional Lyapunov Exponents, for each of the subspaces, as well as a discussion of the systems’ dynamics based on the full spectrum of Directional Lyapunov Exponents will be conducted and the results will be presented in a subsequent article.