1 Introduction

Owing to their low bulk modulus and outstanding in-plane stiffness, sensors made of ultra-thin membranes and two-dimensional (2D) materials have recently gained interest for gas [1, 2], pressure [3,4,5], and biosensing [6] applications. Despite numerous experimental and theoretical studies [7, 8], probing the elasticity of these membranes has remained challenging [9, 10], making the development of new methods for their mechanical characterization of great importance [11,12,13].

Atomic force microscopy (AFM) is the most widely used technique for extracting Young’s modulus of 2D membranes, which is achieved by fitting their nonlinear force–deflection response [14, 15]. Pressurized blister test [16, 17], electrostatic deflection method [18,19,20], and Duffing-type nonlinear response at large amplitude vibrations [11, 13] are other methods used to characterize thin membranes.

Recently, it was also shown that the tension-induced shift in the resonance frequency of 2D membranes as a function of applied pressure could be used to characterize elastic properties [21]. In contrast to AFM which requires large indentations to enter the nonlinear regime for estimating Young’s modulus [22], it was demonstrated that the geometrically nonlinear regime may be easily reached using this approach by sweeping the pressure across the membrane. However, it was found that the fit of the pressure-frequency response, results in estimations of Young’s modulus that are an order of magnitude lower than the well-accepted values in the literature [21, 23]. Therefore, in order to use this method to characterize suspended ultra-thin materials that undergo large deflections, a more comprehensive model is required to describe the underlying physics.

Unlike models commonly used for characterizing pressurized nanodrums [24, 25], here, we develop a model that accounts for a change in the static equilibrium shape of the vibrating membrane, mid-plane stretching, and in-plane and out-of-plane mode coupling. By comparing the model to the finite element method (FEM) simulations of nanodrums subjected to large deflections, we validate the analytic formulation. Finally, we acquire the nonlinear pressure-frequency response of polysilicon nanodrums experimentally and demonstrate that the suggested multi-mode model can be utilized to characterize (extract Young’s modulus) from the high-frequency dynamic response of pressurized ultra-thin membranes.

2 Theory

2.1 Governing equations

Fig. 1
figure 1

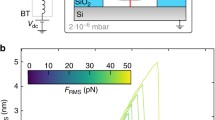
a Schematic of the membrane and its cross-sections. b Side-view of the undeformed membrane, and c deformed configuration under transverse loading due to pressure difference alongside the membrane. g is the cavity depth, and \(P_{ext}\) and \(P_{cav}\) are pressure above the membrane and inside the cavity, respectively

Full size image

We consider a thin circular drum with a diameter of 2R and thickness \(h \ll R\) clamped at the outer edge, as shown in Fig. 1a. The drum is assumed to be made of a homogeneous and isotropic material of density \(\rho \), Young’s modulus E, and Poisson’s ratio \(\nu \). The drum is also assumed to be subjected to an axisymmetric tension \({n_0}\), and the pressure difference alongside it is \(\Delta p\) (see Fig. 1b, c). We only account for axisymmetric vibrations and suppose that the aspect ratio is very small (i.e., \(h/R < 0.001\) [26]) such that the effect of bending rigidity can be discarded, and the motion can be modeled using membrane theory [27]. The equations of motion for a membrane subjected to large transverse displacement w, moderate rotations, are the dynamic equivalents of the von Kármán equations. In this context, the governing equations of a pre-stressed membrane with negligible bending rigidity are [27]:

$$\begin{aligned}&\rho h \ddot{w} -n_0 \nabla ^2 w - {{\text {div}}}\,({\varvec{N}}\varvec{\nabla }w) = {\Delta p}, \end{aligned}$$
(1a)
$$\begin{aligned}&\rho h \ddot{{\varvec{u}}} - {\text {\textbf{div}}}\,{\varvec{N}} = 0. \end{aligned}$$
(1b)

where:

$$\begin{aligned} \begin{array}{r} {\varvec{N}}=[Eh/(1- \nu ^2)]\left[ (1-\nu ){\varvec{\epsilon }}+\nu {\text {tr}}{\varvec{\epsilon }}{\varvec{1}}\right] , \\ {\varvec{\epsilon }}=\frac{1}{2}\left( \varvec{\nabla }{\varvec{u}}+\varvec{\nabla }^{{\text {T}}}{\varvec{u}} + \varvec{\nabla }w\otimes \varvec{\nabla }w\right) . \end{array} \end{aligned}$$
(2)

Here, \({\varvec{u}}=[ u; v ]\) is the axial displacements; moreover, \(\nabla ^2 w\), \(\varvec{\nabla }w\) and \(\varvec{\nabla }{\varvec{u}}\) denote the Laplacian of scalar field w, the vector gradient of scalar field w and the tensor gradient of the vector field \({\varvec{u}}\), respectively. \(\text {div} {\varvec{u}}\) and \({\text {\textbf{div}}}\,{\varvec{N}}\) are the scalar and vector divergences of vector field \({\varvec{u}}\) and tensor field \({\varvec{N}}\). Finally, \(\varvec{\nabla }w\otimes \varvec{\nabla }w\) corresponds to the tensor product between vectors \(\varvec{\nabla }w\) and \(\varvec{\nabla }w\). Overdot indicates derivation with respect to time. Considering only axisymmetric vibrations the following set of equations can be obtained in cylindrical coordinates and in terms of radial (u) and transverse (w) displacements:

$$\begin{aligned} \begin{array}{l} \rho h\ddot{w} - n_0 \Delta w - \left( {{{Eh}/{\left( {1 - {\nu ^2}} \right) }}} \right) [{u_{,rr}}{w_{,r}} + {u_{,r}}{w_{,rr}} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+ (1 + \nu )\frac{{{u_{,r}}}}{r}{w_{,r}} + \nu \frac{u}{r}{w_{,rr}} + \frac{{{{({w_{,r}})}^3}}}{{2r}} + \frac{3}{2}{({w_{,r}})^2}{w_{,rr}}] = {{\Delta p}},\\ \end{array} \end{aligned}$$
(3a)
$$\begin{aligned} \left( {{{Eh}/{\left( {1 - {\nu ^2}} \right) }}} \right) [{u_{,rr}} + \frac{{{u_{,r}}}}{r} - \frac{u}{{{r^2}}} + \frac{{1 - \nu }}{2}\frac{{{{({w_{,r}})}^2}}}{r} + {w_{,r}}{w_{,rr}}] = 0, \nonumber \\ \end{aligned}$$
(3b)

where \(_{,r}\) and \(_{,rr}\) denote the first and second derivatives with respect to r.

To write Eqs. (3a, b) in dimensionless form, we introduce the following set of dimensionless variables:

$$\begin{aligned} \begin{array}{l} \bar{w} = \frac{w}{h},\quad \bar{u} = \frac{R}{{{h^2}}}u,\quad \bar{r} = \frac{r}{R},\\ \bar{t} = \frac{1}{R}\sqrt{\frac{{{n_0}}}{{\rho h}}} t, \quad \overline{\Delta p} = \frac{{{R^2}}}{{{n_0}h}}{{\Delta p}},\quad \varepsilon = \frac{1}{{1 - {\nu ^2}}}\frac{{Y{h^3}}}{{{n_0}{R^2}}}, \end{array} \end{aligned}$$
(4)

This would yield the following non-dimensional form of Eq. (3):

$$\begin{aligned} \begin{array}{l} \ddot{\bar{w}} - \Delta \bar{w} - \varepsilon \left[ {{{\bar{u}}_{,rr}}{{\bar{w}}_{,r}} + \left( {1 + \nu } \right) \frac{{{{\bar{u}}_{,r}}}}{r}{{\bar{w}}_{,r}} + \nu \frac{{\bar{u}}}{r}{{\bar{w}}_{,rr}}} \right. \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{{{\left( {{{\bar{w}}_{,r}}} \right) }^3}}}{{2r}} + \frac{3}{2}{{\left( {{{\bar{w}}_{,r}}} \right) }^2}{{\bar{w}}_{,rr}}} \right] = \overline{\Delta p} \end{array} \nonumber \\ \end{aligned}$$
(5a)
$$\begin{aligned} {\bar{u}_{,rr}} + \frac{{{{\bar{u}}_{,r}}}}{r} - \frac{{\bar{u}}}{{{r^2}}} + \frac{{1 - \nu }}{2}\frac{{{{\left( {{{\bar{w}}_{,r}}} \right) }^2}}}{r} + {\bar{w}_{,r}}{\bar{w}_{,rr}} = 0. \nonumber \\ \end{aligned}$$
(5b)

In order to solve Eqs. (5a, b), we first expand the transverse displacement w and radial displacement u as follows:

$$\begin{aligned}&\bar{w}(r,t) = \sum \limits _{k = 1}^{{N_w}} {{\Phi _k}\left( r \right) {q_k}(t){\hspace{0.55542pt}} {\hspace{0.55542pt}} }, \end{aligned}$$
(6a)
$$\begin{aligned}&\bar{u}(r,t) = \sum \limits _{p = 1}^{{N_u}} {{\Psi _p}\left( r \right) {\eta _p}(t)} , \end{aligned}$$
(6b)

where \(q_k\) and \( \eta _p\) denote the unknown modal coordinates, and \(N_w\) and \(N_u\) are the number of generalized coordinates that will be retained in the analysis. Moreover, \(\Phi _k\) and \(\Psi _p\) are mode shapes associated with the transverse and radial displacements, respectively. These modes are chosen such that they satisfy the following eigenvalue problems that originate from the linear counterpart of Eqs. (5):

$$\begin{aligned} \Delta \Phi _k {+} \omega _k^2 \Phi _k{=} 0, \quad \Psi _{,rr} {+} \frac{\Psi _{,r}}{r} {-} \frac{\Psi }{r^2} {+} \gamma _p^2 \Psi _p {=} 0 \end{aligned}$$
(7)

with \(\omega _k\) and \(\gamma _p\) being the transverse and in-plane dimensionless eigenfrequencies, respectively. We note that Eqs. (7) are Bessel equations, and their solution can be expressed as:

$$\begin{aligned} \Phi _k(r) = \kappa _k J_0 (\omega _k r), \qquad \Psi _p(r) = \lambda _p J_1 (\gamma _p r). \end{aligned}$$
(8)

These modes have orthogonality properties and are normalized with respect to the modal mass, by fixing the values of \(\kappa _k\), \(\lambda _p\) introduced in Eqs.  (8) and (7). They are chosen such that:

$$\begin{aligned} \iint _S \Phi _{i} \Phi _{j} \text {d} S \!=\! \delta _{ij} \quad \text {and} \quad \iint _S \Psi _{p}\Psi _{l} \text {d} S \!=\! \delta _{pl}. \end{aligned}$$
(9)

where S is the domain of integration. By applying Galerkin technique, namely inserting Eqs. (8), and Eqs. (6) in Eqs. (5), multiplying Eq. (5a) by \(\Phi _k\) and Eq. (5b) by \(\Psi _p\), and then integrating over the entire domain, the nonlinear partial differential Eqs. (5a) and (5b) reduce to:

$$\begin{aligned}{} & {} \ddot{q}_k + \omega _k^2 q_k + \varepsilon \sum _{p=1}^{N_u} \sum _{i=1}^{N_w} a_{pi}^k \eta _p q_i \nonumber \\{} & {} + \varepsilon \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} \sum _{l=1}^{N_w} c_{ijl}^k q_i q_j q_l = Q_k \end{aligned}$$
(10a)
$$\begin{aligned}{} & {} \gamma _p^2 \eta _p - \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} b_{ij}^p q_i q_j = 0 \end{aligned}$$
(10b)

where \({Q_k} = \overline{\Delta p} {\left[ {\int _0^1 {\Phi _k^2r\mathrm{{d}}r} } \right] ^{ - 1}}\left[ {\int _0^1 {{\Phi _k}r\mathrm{{d}}r} } \right] \) is the projection of \({\overline{\Delta p}}\) on the k-th mode of vibration, and the nonlinear modal coefficients \(a_{pi}^k,b_{ij}^p\), and \(c_{ijl}^k\) are:

$$\begin{aligned}{} & {} \begin{array}{l} a_{pi}^k = - {[\int _0^1 {\Phi _k^2r\mathrm{{d}}r} ]^{ - 1}}\int _0^1 {{\Phi _k}} ({\Psi _{p,rr}}{\Phi _{i,r}}\\ + {\Psi _{p,r}}{\Phi _{i,rr}} + (1 + \nu )\frac{{{\Psi _{p,r}}{\Phi _{i,r}}}}{r}\\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \nu \frac{{{\Psi _p}{\Phi _{i,rr}}}}{r})r\mathrm{{d}}r, \end{array} \end{aligned}$$
(11a)
$$\begin{aligned}{} & {} b_{ij}^p = + \frac{1}{2}{[\int _0^1 {\Psi _p^2r\mathrm{{d}}r} ]^{ - 1}}\int _0^1 {{\Psi _p}} (\frac{{1 - \nu }}{r}{\Phi _{i,r}}{\Phi _{j,r}} \nonumber \\{} & {} \quad \qquad + {({\Phi _{i,r}}{\Phi _{j,r}})_{,r}})r\mathrm{{d}}r, \end{aligned}$$
(11b)
$$\begin{aligned}{} & {} c_{ijl}^k = - \frac{1}{2}{[\int _0^1 {\Phi _k^2r\mathrm{{d}}r} ]^{ - 1}}\int _0^1 {{\Phi _k}} ({\Phi _{i,r}}{\Phi _{j,r}}{\Phi _{l,r}} \nonumber \\{} & {} \quad \qquad +\frac{{{{({\Phi _{i,r}}{\Phi _{j,r}}{\Phi _{l,r}})}_{,r}}}}{r})r\mathrm{{d}}r. \end{aligned}$$
(11c)

In order to find \(\eta _p\) in terms of \(q_k\), we rewrite Eq. (10b) as:

$$\begin{aligned} {\eta _p} = \frac{1}{\gamma _p^2} \sum \limits _{i = 1}^{{N_w}} {\sum \limits _{j = 1}^{{N_w}} {b_{ij}^p{q_i}{q_j}}}. \end{aligned}$$
(12)

Inserting Eq. (12) in Eq. (10a) [28] leads to:

$$\begin{aligned}{} & {} \ddot{q}_k + \omega _k^2 q_k + \varepsilon \sum _{i=1}^{N_w} \sum _{j=1}^{N_w} \sum _{l=1}^{N_w} \Gamma _{ijl}^k q_i q_j q_l = Q_k, \end{aligned}$$
(13)

with

$$\begin{aligned}{} & {} \Gamma _{ijl}^k = c_{ijl}^k + \sum _{p=1}^{N_u} \frac{b_{jl}^p a_{pi}^k}{\gamma _p^2}. \end{aligned}$$
(14)

Eq. (13) is a reduced-order model, which accounts for mid-plane stretching and higher-mode interactions and can be used for investigating nonlinear pressure-frequency response of nanodrums.

2.2 Solution procedure

Generally, the force vector applied on a membrane can be split into a constant, and a time-varying part. The constant force leads to a static deflection, and the time-varying force vibrates the structure around the new configuration. Considering small-amplitude oscillations around large pressure-induced deflections, it is a decent approximation to separate the contribution into static (\({q_k^s}\)) and dynamic (\({ q_k^d}\)) components as follows [12]:

$$\begin{aligned} {q_k}= & {} {q_k^s} + { q_k^d}. \end{aligned}$$
(15)

This separation allows us to separate Eq. (13) to a static and dynamic part as well. We can obtain the static deflection due to \(Q_k\), and obtain the dynamic equations around the statically deflected configuration which we will then use for obtaining the natural frequencies of the nanodrum in the deformed state and as a function of the applied pressure, as follows:

$$\begin{aligned}&\omega _k^2q_k^s + \varepsilon \sum \limits _{i = 1}^{{N_w}} {\sum \limits _{j = 1}^{{N_w}} {\sum \limits _{l = 1}^{{N_w}} {\Gamma _{ijl}^kq_i^s} } } q_j^sq_l^s = {Q_k}, \end{aligned}$$
(16a)
$$\begin{aligned}&\ddot{q}_k^d + \omega _k^2q_k^d + \varepsilon \sum \limits _{i = 1}^{{N_w}} {\alpha _i^kq_i^d} = 0, \end{aligned}$$
(16b)

where

$$\begin{aligned}{} & {} {\alpha _i^k = \sum \limits _{j = 1}^{{N_w}} {\sum \limits _{l = 1}^{{N_w}} {(2\Gamma _{jil}^k + \Gamma _{ijl}^k)q_j^sq_l^s} }.} \end{aligned}$$
(17)

In order to solve Eq. (16a) for \(q_k^s\), we use the software package MANLAB. The software uses the Asymptotic Numerical Method (ANM) [29], a continuation algorithm based on high-order Taylor series expansions, to solve nonlinear systems of equations. The ANM continuation method allows for solving nonlinear algebraic equations written in the form:

$$\begin{aligned}{} & {} {\varvec{F}} ({\varvec{U}},\lambda ) = {\varvec{0}}, \end{aligned}$$
(18)

where \({\varvec{F}}\) denotes a set of nonlinear algebraic equations, \({\varvec{U}}=[q_1^s,q_2^s, \ldots ,q_{{N_w}}^s]\) is a vector of unknown coefficients, and \(\lambda \) is the continuation parameter. The method also requires the system of equations to be written with quadratic nonlinearities [29]. To perform continuation, we thus recast the static part of Eq. (16a) to:

$$\begin{aligned}&\omega _k^2q_k^s + \varepsilon \sum \limits _{i = 1}^{{N_w}} {\sum \limits _{j = 1}^{{N_w}} {\sum \limits _{l = 1}^{{N_w}} {\Gamma _{ijl}^k} } } {S_{jl}}q_i^s - \lambda {Q_k} = 0, \end{aligned}$$
(19a)
$$\begin{aligned}&{S_{jl}} - q_j^sq_l^s = 0. \end{aligned}$$
(19b)

By solving Eq. (19) for \(q_k^s\), one can find the shift in resonance frequencies due to pressure. We note that the fundamental frequency of the pressurized nanodrum \({\Omega _u}\) can be obtained by considering the pre-factors of \(q_k^d\) in Eq. (16b) which is denoted with the matrix \({\varvec{A}}\), defined as:

$$\begin{aligned}{} & {} {A_{uv}} = \omega _u^2{\delta _{uv}} + \varepsilon \alpha _u^v. \end{aligned}$$
(20)

where \(\delta _{uv}\) is the kronecker delta. Diagonalizing the matrix \({\varvec{A}}\) leads to the modified frequencies and mode shapes of the bulged nanodrum with an initial bulged shape:

$$\begin{aligned}{} & {} {\left[ {\Omega _u^2{\delta _{uv}}} \right] _{u,v \in \left[ {1,{N_w}} \right] }} = {{\varvec{P}}^{ - 1}}{\varvec{A}}{\varvec{P}}, \end{aligned}$$
(21)

where \({\varvec{P}}\) are the eigenvectors associated with the frequencies \({\Omega _u}\) for the pressurized membrane.

3 Results

3.1 Numerical simulations

3.1.1 Convergence study

Fig. 2
figure 2

Variation of the static and dynamic displacement fields with pressure. a Normalized static transverse displacement varying from a flat to a nearly parabolic configuration; b normalized in-plane displacement showing deviation from linear variation in the radial direction with increasing pressure; c normalized mode shape as a function of external pressure obtained from the multi-mode model (\(w_0^d\) denotes the dynamic transverse deflection at the center of the membrane). One must bear in mind that the membrane is flat at \(\Delta p = 0\,\,\,\mathrm{{mbar}}\)

Full size image
Fig. 3
figure 3

Comparison of the proposed model to the FEM result by a linearizing the dynamic governing equation about the deformed static configuration rather than flat position; b increasing the number of in-plane modes; c addition of out-of-plane modes

Full size image

As mentioned in Sect. 2, in order to better capture small-amplitude oscillations of a pressurized membrane, one must (i) linearize the dynamic response around the new static configuration, (ii) account for mid-plane stretching effect, and (iii) include contributions from out-of-plane modes. Thus, to emphasize the significance of these assumptions and to facilitate a more accurate comparison of these parameters in a pressurized configuration versus a flat configuration, in Fig. 2, we simulate the effect of pressure on the static and dynamic in-plane and out-of-plane displacements of a nanodrum with \(R=5~\mu \hbox {m}\), \(h=20~\hbox {nm}\), \(\rho =2300~\hbox {kg}.\hbox {m}^{-3}\), \(E=160\,\hbox {GPa}\), \(\nu =0.22\), \(n_0=0.3~ \hbox {N/m}\).

Figure 2a shows that the original flat configuration changes significantly with increasing pressure. This result suggests that when estimating frequency shifts due to pressure, the dynamic governing equation must be obtained around the new bulged shape (\(q_k^s\ne 0\)) rather than the flat configuration (\(q_k^s=0\)). The application of pressure causes a nonlinear in-plane displacement field at high pressures, as depicted in Fig. 2b. In addition, Fig. 2c illustrates the slight differences in the first mode shape that emerge due to statically deformed configurations. As we will discuss next, neglecting these effects could yield wrong estimation of the resonance frequencies of pressurized ultra-thin membranes.

We also note that the model is obtained in modal coordinates. Nonetheless, the governing partial differential equations (Eq. (3)) were formulated with in-plane (u) and out-of-plane (w) displacement fields. Moreover, Fig. 2 depicts the results for u, \(w^s\), and \(w^d\), rather than \(q^s\), and \(q^d\). Thus, to retrieve u from the modal equations, one must use Eqs. (4), (6b), and (12) and obtain u(r, t) as follows:

$$\begin{aligned}{} & {} u(r,t) = \frac{{{h^2}}}{R}\sum \limits _{p = 1}^{{N_u}} {\sum \limits _{i = 1}^{{N_w}} {\sum \limits _{j = 1}^{{N_w}} {{\Psi _p}\left( r \right) \frac{{b_{ij}^p}}{{\gamma _p^2}}q_i^sq_j^s} } }. \end{aligned}$$
(22)

However, for the out-of-plane deflection, one should note that separation of static and dynamic modal coordinates results in the separation of static and dynamic transverse displacements. Using Eqs. (15), (6a) and (4), the transverse displacement can be then obtained as follows:

$$\begin{aligned} w= & {} {w^s} + {w^d}, \end{aligned}$$
(23)

where:

$$\begin{aligned} {w^s} = h \sum \limits _{k = 1}^{{N_w}} {{\Phi _k}\left( r \right) q_k^s}&, \end{aligned}$$
(24a)
$$\begin{aligned} {w^d} = h \sum \limits _{k = 1}^{{N_w}} {{\Phi _k}\left( r \right) q_k^d}&. \end{aligned}$$
(24b)

In order to highlight the influence of the effects depicted in Fig. 2 on the estimation of the resonance frequencies, we benchmark in Fig. 3a–c the fundamental frequency derived from our model against FEM results. The simulations are performed for the same drum specifications as Fig. 2. In Fig. 3a, we simulate the frequency shift where only one single out-of-plane mode is retained in the analysis (\(N_u=0, N_w=1\)). Frequency shifts are found, by using Eq. (16b) for the undeformed (flat) as well as deformed configurations. The figure confirms our earlier prediction in Fig. 2a that using the equations around the deformed configuration substantially increases accuracy. When compared to FEM results, the model still has a maximum error of \(9\%\) at 1 bar.

To illustrate the effect of in-plane displacements on the predicted frequencies, we increase \(N_u\) from 0 to 4 in Fig. 3b while retaining only one out-of-plane generalized coordinate (\(N_w=1\)) in the analysis. It can be seen that including more in-plane modes in the model results in a more accurate result (the error relative to FEM simulations decreases to \(4\%\) at 1 bar). This confirms the important role of mid-plane stretching when tracing the fundamental resonance frequency of nanodrums as a function of pressure.

Although the response from this model is already close to the FEM simulations, Fig. 3c shows that the accuracy can be even further improved by including more transverse degrees-of-freedom in the basis functions by increasing \(N_w\) in Eqs. (16). This finally leads to a negligible difference between simulations based on the present multi-mode model and FEM results, which highlights the slight contribution of higher order out-of-plane modes to the estimated resonance frequency [30]. Notably, each of these three criteria contributes to model convergence, and neglecting them would reduce the accuracy the model. It should be also noted that, considering more out-of-plane displacements while ignoring in-plane displacements would not produce accurate results, as in-plane displacements are always required to account for the mid-plane stretching effect.

3.1.2 Single-transverse-mode approximation

Although increasing the number of transverse modes improves model accuracy, it also increases the complexity of the governing equations, necessitating the employment of numerical techniques to solve them. However, the model can be analytically solved using just one transverse mode. Figure 3 demonstrates that the single-transverse-mode approximation is precise enough for tracing the pressure induced resonance frequency shifts up to 1 bar. Considering only \(N_w=1\) and \({N_u}=4\), and converting equations back to dimensional form using Eq. (4) one can find the following equations as a simplified version of Eq. (16):

$$\begin{aligned}&\frac{{5.7831{n_0}}}{{\rho h{R^2}}}\tilde{q}_1^s + 1.181\frac{{E\varpi \left( \nu \right) }}{{\rho {R^4}}}{\left( {\tilde{q}_1^s} \right) ^3} = \frac{{1.6019}}{{\rho h}}\Delta p, \end{aligned}$$
(25a)
$$\begin{aligned}&\ddot{\tilde{q}}_1^d + \frac{{5.7831{n_0}}}{{\rho h{R^2}}}\tilde{q}_1^d + 3.543\frac{{E\varpi \left( \nu \right) }}{{\rho {R^4}}}{\left( {\tilde{q}_1^s} \right) ^2}\tilde{q}_1^d = 0, \end{aligned}$$
(25b)

where \(\varpi (\nu )\) is plotted in Fig. 4. Moreover, \(\tilde{q}_1^s = hq_1^s\) denotes dimensional static deflection at the center of the nanodrum and \(\tilde{q}_1^d = hq_1^d\) is the dimensional dynamic deflection at the center of the membrane. For this simplified scenario, the nonlinear pressure-deflection and pressure-frequency relationships are derived analytically as follows:

$$\begin{aligned}&\Delta p = A\frac{{{n_0}}}{{{R^2}}}\tilde{q}_1^s + B\frac{{Eh}}{{{R^4}}}{\left( {\tilde{q}_1^s} \right) ^3}, \end{aligned}$$
(26a)
$$\begin{aligned}&f = \frac{{2.4048}}{{2\pi R}}\sqrt{\frac{{{n_0}}}{{\rho h}} + C\frac{E}{{\rho {R^2}}}{{\left( {\tilde{q}_1^s} \right) }^2}}, \end{aligned}$$
(26b)

where A, B, and C are defined for the current study in Table (1). It is worth noting that Eq. (26a) only retains the cubic term in the high pressure regime, hence \(\Delta p \propto {\left( {\tilde{q}_1^s} \right) ^3}\). By applying the same reasoning, it is possible to demonstrate that Eq. (26b) results in \(f \propto \left( {\tilde{q}_1^s} \right) \) and thus \(f \propto \Delta {p^{{1/3}}}\).

Table 1 Benchmarking the present model against the analytic formulations available in the literature
Full size table

We finally compare the result of our reduced-order model (Eq. (26)) with analytic models available in the literature, which are often used for the dynamic characterization of pressurized nanodrums [24, 25] (see Fig. 5).

In Table (1) we benchmark this new formulation against the analytic solutions available in the literature for pressurized nanodrums [24, 25]. Significant discrepancies between our model and those of Refs. [24, 25] can be attributed to the simplifying assumptions lifted in our study, including linearization about flat configuration, absence of mid-plane stretching, and out-of-plane modal interactions. As demonstrated in Fig. 3, the first two assumptions have a greater impact on the model’s accuracy than the third one.

Fig. 4
figure 4

Function \(\varpi (\nu )\) used in single-transverse-mode analysis (see Eqs. (26)). The function is evaluated for finite numbers of Poisson ratios and interpolated with the cubic spline method

Full size image
Fig. 5
figure 5

Comparison of models available in the literature and single-mode approximation proposed in Eqs. (26)

Full size image

3.2 Experimental validation

Fig. 6
figure 6

The laser interferometry setup and obtained frequency spectra of polysilicon drums. a After passing through the polarized beam splitter (PBS) and the quarter-wave plate (\(\lambda /4\)), the red laser is combined with the blue laser and focused on the drum using a dichroic mirror (DM). The readout is performed by a high-frequency photodiode (PD), and the output is fed into the Vector Network Analyzer (VNA). The VNA modulates the blue laser that actuates the drum. A PID controller is used to regulate gas pressure inside the vacuum chamber. b Frequency spectra (light green) are obtained from the VNA at different pressures. To determine the fundamental mode’s resonance frequency, a damped harmonic oscillator model is fitted (dark green). (Color figure online)

Full size image

To verify the applicability of the proposed formulation for the dynamic characterization of ultra-thin drums, we measure 33 nm thick polysilicon membranes measured by Atomic Force Microscopy (AFM), which we transfer over SiO2 substrate cavities, that are created using reactive ion etching with a depth of 350 nm. The 10 µm-diameter drums are placed in a vacuum chamber with variable pressure ranging from 50 to 1000 mbar. We employ a modulated blue laser diode (\(\lambda = 405\) nm) to push the polysilicon nanodrums into resonance (Fig. 6a). The suspended nanodrum modulates the intensity of the reflected red laser (\(\lambda = 633\) nm), which is collected at a photodiode and analyzed by a Vector Network Analyser (VNA). Our setup includes a PID controller that monitors chamber pressure using a vacuum pump and gas supply (nitrogen). Figure 6b depicts the frequency spectra of a polysilicon drum at different pressures \(\Delta P = {P_{\mathrm{{ext}}}} - {P_{\mathrm{{cav}}}}\), where \(P_{\mathrm{{cav}}}\) and \(P_{\mathrm{{ext}}}\) are the pressure outside and inside the cavity, respectively (see Fig. 1). As a result of increased pressure, we observe an apparent tension-induced increase in the nanodrum’s resonance frequency. To obtain the pressure-frequency response, we sweep the pressure from 50 to 1000 mbar and fit the resonance peaks with the damped linear harmonic oscillator model to obtain resonance frequencies at each pressure values (See Fig. 6b). In Fig. 7a we show typical pressure-frequency measurement data which we fit using our model (E = 155 GPa, \(n_0=1.6\, \hbox {N/m}\)). In contrast to Fig. 3, we see a minimum in the pressure-frequency response at \(P_{\mathrm{{cav}}}= 248\) mbar, which corresponds to a flat configuration. In this configuration, the drum’s fundamental frequency is determined solely by pre-tension. By increasing pressure, the nanodrum deforms statically, and the resonance frequency varies nonlinearly as \(f \propto \root 6 \of {E}\Delta {p^{1/3}}\). Knowing this relation, such pressure-frequency measurements can also be used to determine the nanodrum’s Young’s modulus.

Fig. 7
figure 7

Experimental result obtained for polysilicon drums. a Pressure-frequency of a drum in both sweeping up and down of pressure, fitted with our model with \(E = 155\) GPa. b Histogram of the Young’s moduli obtained through fitting the experimental data with the average value of 148 GPa, and standard deviation of 7 GPa

Full size image

To demonstrate the versatility of the method for characterizing Young’s modulus of ultra-thin membranes, we repeated the same measurements on 13 nanodrums that were adequately sealed (or the leak rate was low enough relative to the experiment’s data collection speed) and did not exhibit hysteresis in the pressure-frequency response when the pressure was swept up and down. From these measurements, we determined \(n_0 = 1.1 \pm 0.5\,\hbox {N/m}\) for the nanodrums. Figure 7b depicts the retrieved Young’s moduli histogram. We see that the obtained average value \(E = 148 \pm 7\) GPa from our technique is comparable to the literature-reported uni-axial stretching test findings for thin polysilicon beams [31, 32], further validating the accuracy of our model. We note that in our experiments, owing to the low aspect ratio of the fabricated devices, the bending rigidity is very small and the linear stiffness mediated by bending rigidity is proportional to \({k_\textrm{bending}} = {{E{h^3}}/({12R^2(1 - {\nu ^2})) = 0.02}}\) N/m which compared to the linear stiffness due to the pre-tension of the nanodrum (\({k_\textrm{stretching}} = {n_0} = 1.1\) N/m) in the flat configuration is negligible. Therefore, consistent with our modelling approach, the motion of the nanodrum is dominated by its tension.

At high pressures, the damping also rises, which may make it difficult to observe resonance peaks. Yet, our experiments demonstrate that even at ambient pressure the oscillation is under-damped and the resonance peak is apparent. In addition, as depicted in Fig. 7a, the membranes reach the nonlinear regime at \(\Delta p \approx 400\,\,\,\mathrm{{mbar}}\), which is sufficient for characterization purposes.

4 Discussion

Employing the pressure-frequency response as a material characterization method has several advantages over commonly used techniques. Compared to AFM that requires considerable deflections to estimate Young’s modulus, i.e., the force–deflection curve should reach a cubic regime [22] (\(F \propto \delta ^3\); F: tip force, \(\delta \): membrane’s center deflection), pressurization using the surrounding gas requires a lower force for determining Young’s modulus and distributes the load over the membrane, minimizing the chance of membrane failure. The method also reaches the nonlinear regime suitable for estimating Young’s modulus with substantially less deflections and stresses, thus making it a more practical method for characterizing brittle nanomaterials such as polysilicon (see supplementary information S1). Furthermore, unlike nonlinear dynamic characterization, which uses large driving signals to push the membrane into a nonlinear Duffing regime and requires proper calibration of the vibration amplitude [11], this method is independent of the vibration amplitude and only measures the resonance frequency as a function of the applied pressure.

It is worth noting that the low aspect ratio of ultra-thin membranes is an inherent feature of nanomechanical systems, which accounts for their display of nonlinear dynamics even at small amplitudes. In cases where a higher aspect ratio is present, plate models can be utilized instead of the membrane model proposed in this study. Yet, it is important to note that the bending rigidity essentially re-scales the linear stiffness of these systems, and in high-pressure regimes, the nonlinear stretching factors caused by pressure continue to dominate the Young’s modulus characterization.

Several points should be kept in mind when employing the proposed method for characterization. First, in an optical detection scheme, the cavity depth has to be optimized so that the photodiode voltage is still linearly related to the motion at high amplitudes [33]. Moreover, gas leakage through the clamped boundaries and poor adhesion forces between the nanodrum and substrate should be avoided to ensure negligible leakage rates and to prevent significant variations of the internal cavity pressure during the measurement [21, 34, 35]. We note that the present model does not account for morphological imperfections such as wrinkles [36] and boundary slippage [37], that are proven to affect the stiffness of 2D material membranes.

Furthermore, when \({{{P}}_\textrm{cav}} > 0\), the cavity pressure change with the membrane’s static deflection, and the squeeze film effect [38] may influence the dynamics of pressurized ultra-thin drums. Although both effects contribute significantly to the tension induced in the membrane, their cumulative effect on the drum’s frequency shift near 1 bar and in the high-pressure regime is negligible for our polysilicon nanodrums, keeping the extracted value of Young’s modulus unchanged. We also note that neglecting the squeeze-film effect and the bending rigidity of a relatively thick membrane may result in an overestimation of pre-tension; therefore, accounting for these two effects can enhance the accuracy of the anticipated pre-tension value which was estimated to be high in our analysis due to neglecting these effects. As discussed in the supplementary information S2, by accounting for these two effects, the pre-tension value drops from 1.6 to \(1.1~\hbox {N/m}\).

Other than material characterization, the model developed in this work can be used for estimating the deflection and resonance frequency shifts of pressurized membranes. These include 2D material resonant pressure sensors [4], microphones [39], and biosensors [6], where correct estimation of deflection due to surrounding fluid is important for probing the stiffness of the membrane. Furthermore, the analytical models provided here are also useful for accurate estimation of the mass-density of 2D membranes [40], which is often achieved by fitting the resonance frequency curves of the membrane as a function of pressure with tension and mass-density as the fit parameters.

5 Conclusion

In summary, attempts to use frequency shifts of pressurized nanodrums for characterization purposes were inaccurate previously due to lack of appropriate mathematical models. To resolve this, a multi-mode continuum model for predicting the dynamics of ultra-thin pre-tensioned drums subjected to high pressures is presented here. By maintaining in-plane and out-of-plane membrane deformations, we investigate the pressure-dependent resonance frequency and mode shapes and illustrate the crucial importance of mid-plane stretching in the high-pressure regime. We highlight the discrepancies by comparing the model’s accuracy to previously reported analytical models and FEM simulations. By fitting the resonance frequency measurements of a series of polysilicon drums as a function of the applied pressure as determined by laser interferometry, we demonstrate the model’s validity and applicability for determining Young’s modulus of ultra-thin nanomaterial membranes using on-resonance high-frequency characterization. Since pressurization results in a distributed stress field compared to indentation, this method could be utilized as an effective toolset for determining the Young’s modulus of brittle nanomaterials.