Effect of pressure on nonlinear dynamics and instability of electrically actuated circular micro-plates

Abstract

Characterization of nonlinear behavior of micro-mechanical components in MEMS applications plays an important role in their design process. In this paper, nonlinear dynamics, stability and pull-in mechanisms of an electrically actuated circular micro-plate subjected to a differential pressure are studied. For this purpose, a reduced-order model based on an energy approach is formulated. It has been shown that nonlinear dynamics of an electrically actuated micro-plate, in the presence of differential pressure, significantly differs from those under purely electrostatic loads. The micro-plate may lose stability upon either saddle-node or period-doubling bifurcations. It has also been found that in the presence of a differential pressure, increasing the DC or AC voltages may surprisingly help to stabilize the motion of the micro-plate.

1 Introduction

Electrically actuated micro-electro-mechanical systems (i.e., MEMS) are increasingly being used in diverse engineering applications, such as sensors and actuators [1, 2]. Electrostatic instability is one of the main features of these devices, which for many applications is considered as a failure, and thus, avoided. Though, in electrostatic switches and sensors, for example, electrostatic instability is often employed as the main driving mechanism and therefore, it is intentionally triggered [3, 4]. In either way, in order to avoid or to exploit the electrostatic instability, a good understanding of this phenomena is essential to obtain a high-performance MEMS device.

Electrically actuated micro-devices typically employ a parallel-plate capacitor, in which at least one electrode is flexible. When an electric potential is applied to the capacitor, an attractive electrostatic load is induced between the two electrodes, leading to the deformation of the flexible one. When the potential fluctuates with time, a forced dynamic motion is induced in the system, which can be detected by capacitive changes of the system [5, 6].

The electrostatic load driving the motion of the flexible electrode is a function of the applied bias (DC) and alternating (AC) voltages, and the distance between the two electrodes. Consequently, it also depends nonlinearly on the electrode deflection. In case of finite defections of the electrode, geometrical nonlinearity also appears in the elastic potential of the structure. As a result, the system might exhibit nonlinear softening or hardening. Particularly, at a critical combination of DC and AC voltages and also the excitation frequency, the motion of the flexible electrode becomes unstable, and then, the micro-plate falls on to the stationary one. This phenomenon is known as pull-in [7, 8].

If the applied electric potential is a static DC voltage, the deformation of the electrode is static as well. In that case, the only load parameter in assessment of stability is the applied DC voltage, and the critical stability appears as a ‘fold’ or a ‘limit point’ in the response of the system. Many studies have addressed the static pull-in phenomenon, and proposed analytical or numerical methods to estimate the pull-in voltage [6, 8,9,10,11,12,13]. A literature survey on this topic has been carried out in Ref. [5]. It has been shown that the critical voltage and deflection of the flexible electrode depend on the material properties, geometry and dimensions of the flexible electrode, and the initial gap size between the two electrodes. Particularly, for circular plate-like electrodes, the critical deflection in static pull-in varies between 51 and 71% of the initial gap between the electrodes, depending only on the thickness of the structure [14, 15].

In electrostatic actuators, in which the applied electric potential includes a dynamic AC component, the deflection of the electrode will be dynamic as well. In studying the stability of such a system, in addition to the DC voltage, the frequency and the amplitude of the AC voltage play influential roles. Many studies have addressed the dynamic pull-in phenomenon, and proposed analytical or numerical methods to estimate the pull-in voltage [7, 8, 16]. It has been reported that for micro-resonators, the dynamic pull-in can be triggered by dynamic instabilities, and therefore, it might occur at much lower voltages compared to the static pull-in voltage [17, 18]. The dynamic pull-in can be triggered by different mechanisms [7, 19]: (i) a cyclic fold in the frequency response function due to nonlinearities of the system, (ii) a transient jump between two or more coexisting stable solution branches due to a disturbance in the AC voltage or, (iii) a period doubling bifurcations leading to chaos.

The dynamic pull-in threshold (i.e., the critical deflection, and the critical combination of DC and AC voltages) is shown to be highly influenced by any mechanical load applied to the micro-mechanical component. For example, the effects of van der Waals or Casimir forces between the electrodes on the dynamic behavior and stability of the micro/nano-plates have been reported [20,21,22,23]. Moreover, the effect of a uniform hydrostatic pressure on the linear resonance frequency of an electrically actuated circular micro-plate has been observed [24]. In practice, the additional mechanical loads, such as a differential pressure, are very common in MEMS applications, and insufficient attention for the effect of these factors on pull-in threshold can result in decreasing the reliability of the MEMS device. Therefore, in this paper, we investigate nonlinear vibrations and stability of an electrically actuated circular micro-plate when subjected to a differential pressure.

A Lagrangian approach is used to obtain a reduced-order model and to derive the approximate equations of motion. In the proposed model, nonlinear stretching, and non-uniformity and nonlinearity of the electrostatic load due to finite deflection of the flexible plate are considered. It shall be mentioned that reduced-order modeling of electrically actuated micro-plates has been performed in the literature following different approaches [9, 19, 25,26,27]. However, the distinguishing feature of the present model is its simplicity while maintaining the accuracy. In this study, as a consequence of using a proper set of polynomials as the basis functions, a simple and yet accurate equation of motion is obtained which is more versatile for performing bifurcation analysis as compared to the alternative available models.

In order to investigate the branches of periodic solutions and detect instabilities, a pseudo arc-length continuation and collocation technique are utilized. Based on the proposed solution, the effects of load parameters, namely DC and AC driving voltages, the excitation frequency, and particularly the differential pressure on the stability of the system are explored. The results of this study show that the applied load parameters can significantly affect the dynamic characteristics, resonance frequency, and the pull-in mechanisms of a micro-plate. The method presented in this paper is shown to be simple, easy to use, fast, and accurate enough to be used as a design tool for MEMS devices.

2 Problem formulation

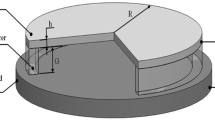
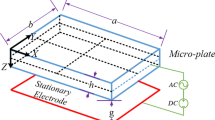
In this section we propose a model for the harmonic motion of a parallel-plate capacitor with a very thin, circular, fully clamped plate as the flexible electrode. The schematic model is shown in Fig. 1. The radius of the plate is R and its thickness is h. The plate is isotropic and homogeneous and its Young’s modulus, Poisson’s ratio and density are E, $\nu$ and $\mu$, respectively. The plate is suspended over a grounded electrode having the same radius, and the initial gap between the two electrodes is d. An electric potential V consisting of a DC bias voltage and an alternating AC voltage is applied to the electrodes. The flexible electrode is loaded with a differential pressure P, positive outward (in the opposing direction the electrostatic load).

Fig. 1

Schematic of a a capacitor with flexible, circular electrode subjected to a differential pressure, its cross section in b undeformed and c deformed configurations due to the electrostatic load and the differential pressure

Due to the alternating electrostatic field induced by the AC voltage, a forced dynamic motion is induced in the system. We use a reduced-order model and a Lagrangian approach to obtain the equations of motion for such a system. For this purpose, the following simplifying assumptions are considered: first, the plate is modeled by nonlinear von Kármán plate theory for thin plates, which accounts for finite deflections and moderate rotations [28]. Second, due to radial symmetry in the geometry and the loads, the problem is assumed axisymmetric [29]. In fact, we assume that the plate is excited around its fundamental frequency, and the first mode is not involved in an internal resonance with other modes of vibration. Hence, other modes (including the anti-symmetric modes), even if accidentally excited, will decay with time due to the presence of damping [30]. Therefore, the only existing displacement components are radial (u) and transverse (w) components, which are functions of the radial coordinate (r), only.

Considering that the plate is clamped around its circumference, the following approximate displacement field is used to present the radial (u) and the transverse (w) displacements:

$$\begin{aligned} w= & {} q(t)\mathrm{d}\Phi _0(\rho ), \end{aligned}$$

(1)

$$\begin{aligned} u= & {} \sum _{i=1}^{N} \xi _i(t) R \Phi _i(\rho ), \end{aligned}$$

(2)

where $\rho =r/R$ is the normalized radial coordinate, and, the functions $\Phi _0(\rho )$ and $\Phi _i(\rho )$ are the Admissible basis functions and are defined as follows:

$$\begin{aligned} \Phi _0(\rho )= & {} (1-\rho ^2 )^2, \end{aligned}$$

(3)

$$\begin{aligned} \Phi _i(\rho )= & {} \rho ^i(1 -\rho ),\quad \quad (i=1,\ldots ,N). \end{aligned}$$

(4)

The function $\Phi _0(\rho )$ is a 4th order polynomial representation of the first linear mode shape of the plate (see Fig. 2), and $\Phi _i(\rho )$ are capable of reflecting the associated in-plane displacement [31]. The functions q(t) and $\xi _i(t)$ are dimensionless, time-dependent generalized coordinates, and q(t) is physically restricted to $-1<q(t)$. The proposed displacements are admissible functions satisfying the geometric boundary conditions:

$$\begin{aligned} w=u=\frac{\partial w}{\partial \rho }=0\quad \quad \text {at} \quad \quad \rho =1, \end{aligned}$$

(5)

the continuity condition of $\Phi _i=0$ at $\rho =0$, and the finitude of the resulted Cauchy strain components at $\rho =0$. The validity and accuracy of the chosen mode shapes will be discussed in Sect. 4.

Fig. 2

The normalized proposed global mode in comparison with the first linear mode shape of a clamped circular plate calculated with classical plate theory $\left( J_0(\kappa \rho )-\left( \frac{J_0(\kappa )}{I_0(\kappa )}\right) I_0(\kappa \rho ), \kappa =3.19625\right)$

The total potential energy of the system consists of four terms: the potential associated with elastic deformation due to bending ($U_{\mathrm{b}}$) and stretching ($U_{\mathrm{s}}$) of the plate, the electrostatic potential ($U_{\mathrm{e}}$), and finally, the potential associated with the mechanical pressure (W);

$$\begin{aligned} U =U_{\mathrm{b}}+U_{\mathrm{s}}+U_{\mathrm{e}}-W. \end{aligned}$$

(6)

The potential associated with elastic deformation can be approximated by ($U_{\mathrm{b}}+U_{\mathrm{s}}$) [28]:

$$\begin{aligned} U_{\mathrm{b}}= & {} \frac{\pi D}{R^2}\int _0^1\Bigg ({\left( \frac{\partial ^2w}{\partial \rho ^2}\right) }^2+{\left( \frac{1}{\rho }\frac{\partial w}{\partial \rho }\right) }^2 \nonumber \\&+\,\left( \frac{2\nu }{\rho }\frac{\partial w}{\partial \rho }\frac{\partial ^2w}{\partial \rho ^2}\right) \Bigg )\rho \mathrm{d}\rho , \end{aligned}$$

(7)

$$\begin{aligned} U_{\mathrm{s}}= & {} \frac{\pi Eh}{(1-\nu ^2)}\int _0^1\Bigg ({\left( \frac{u}{\rho }\right) }^2\nonumber \\&+\,{\left( \frac{\partial u}{\partial \rho }+ \frac{1}{2R}{\left( \frac{\partial w}{\partial \rho }\right) }^2\right) }^2 \nonumber \\&+\,\frac{2\nu u}{\rho }\bigg (\frac{\partial u}{\partial \rho }+\frac{1}{2R}{\left( \frac{\partial w}{\partial \rho }\right) }^2\bigg )\Bigg )\rho \mathrm{d}\rho , \end{aligned}$$

(8)

where $D=\frac{Eh^3}{12(1-\nu ^2)}$ is the bending stiffness of the flexible plate.

Since the deflection of the plate due to mechanical and electrostatic loads is very small compared to its lateral dimensions, the loads on the plate are assumed to be always perpendicular to its undeformed surface [32]. This is, in fact, consistent with the moderate rotation assumption. Therefore, the parallel-plate capacitor theory can be employed and the electrostatic potential can be formulated as [5]:

$$\begin{aligned} U_{\mathrm{e}}=-\,\pi \epsilon V^2 R^2 \int _0^1\frac{\rho \mathrm{d}\rho }{d+w}, \end{aligned}$$

(9)

where $\epsilon$ is the electric permittivity of the dielectric between the electrodes. Notice that in formulating the electrostatic potential ($U_\mathrm{e}$), the local distance between the electrodes ($d+w$) is employed to calculate the electrostatic potential. Finally, the potential associated with the pressure can be calculated as follows:

$$\begin{aligned} W=2\pi PR^2\int _0^1w\rho \mathrm{d}\rho . \end{aligned}$$

(10)

In vibrations of a clamped microplate, the in-plane displacement and its time derivative are much smaller than the transverse displacement and velocity. Hence, in calculating the kinetic energy, the contribution of the in-plane velocity is in orders of magnitude lower than the transverse velocity ($\dot{\xi }_i(t)^2\ll \dot{q}(t)^2$) and thus, it can be neglected. Consequently, the kinetic energy of the system can be expressed as:

$$\begin{aligned} T=\pi \mu R^2 h \int _0^1 \dot{w}^2\rho \mathrm{d}\rho . \end{aligned}$$

(11)

By substituting Eqs. (1) and (2) into (7)–(11), the Lagrangian of the system can be obtained analytically and expressed in terms of the generalized coordinates $L(q,\xi _i,\dot{q},t)$.

$$\begin{aligned} L=T- \left( U_{\mathrm{e}}+U_{\mathrm{b}}+U_{\mathrm{s}}-W\right) \end{aligned}$$

(12)

Next, Lagrange equations can be employed:

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{q}}\right) -\frac{\partial L}{\partial q}=0, \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\partial L}{\partial \xi _i}=0 \quad \quad i=1,\ldots ,N. \end{aligned}$$

(14)

Equation (14) yields a set of N nonlinear algebraic equations in terms of $\xi _i$ ($i=1,\ldots ,N$) and q. By solving this set of equations for $\xi _i$, one can find all $\xi _i$ analytically as:

$$\begin{aligned} \xi _i(t)=\xi _i({q(t)}) \quad \quad i=1,\ldots ,N. \end{aligned}$$

(15)

In fact, Eq. (15) would describe the relation between the plate stretching and its transverse deflection, independent of the applied loads. Hence, the degrees of freedom can be reduced to q(t) only, while incorporating the in-plane displacement and its associated stiffness which is a major contributor to nonlinearity. This simple form appears as a result of neglecting the contribution of $\dot{\xi _i}(t)$ in the inertia. Next, the equation governing the transverse motion of the micro-plate can be obtained from Eq. (13):

$$\begin{aligned} \begin{aligned}&\ddot{q}(t)+2 \zeta \omega _0\dot{q}(t)+\omega _0^2q(t)= -\,\alpha _{1}D{q(t)}^3\\&\quad \quad \quad \quad +\,\alpha _{2}{V(t)}^2\left( \frac{1-(q+1)\digamma (q)}{2q(1+q)}\right) \\&\quad \quad \quad \quad -\,\alpha _{3} P, \end{aligned} \end{aligned}$$

(16)

The parameter $\zeta$ is the modal damping that has been added to the equation of motion to account for the dissipation. Furthermore,

$$\begin{aligned} \begin{aligned}&\digamma (q(t)) =\frac{a\text {tan}h \sqrt{-q(t)}}{\sqrt{-q(t)}}&\text {if }q(t)<0,\\&\digamma (q(t)) =1&\text {if }q(t)=0,\\&\digamma (q(t)) =\frac{a\text {tan} \sqrt{q(t)}}{\sqrt{q(t)}}&\text {if }q(t)>0. \end{aligned} \end{aligned}$$

(17)

Note that at $q(t)=0$, the function $\digamma (q(t))$ is described as unity to maintain the continuity and smoothness of this function at zero. The parameter $\alpha _{1}$ is the coefficient of geometric nonlinearity, and its convergence and accuracy is determined by in-plane degrees of freedom N in Eq. (2). The parameter $\alpha _{2}$ is the coefficient of the nonlinear electrostatic force, and parameter $\alpha _{3}$ is the projection of the pressure to the assumed mode shape in transverse direction:

$$\begin{aligned} \begin{aligned}&\alpha _{2}=2.50\frac{\epsilon }{\mu hd^3},\\&\alpha _{3}=1.67\frac{1}{\mu hd}. \end{aligned} \end{aligned}$$

(18)

The parameter $\omega _0$ is the natural frequency of the circular clamped plate and is equal to $\frac{10.32}{R^2}\sqrt{\frac{D}{\mu h }}$. The obtained fundamental frequency is less than 1% different from the natural frequency of the plate calculated with classical plate theory. It is worth noting that if $V_{\mathrm{DC}}$ is nonzero, it will influence the natural frequency of the system even if linearized around q(t).

The electric potential V(t) in Eq. (16) consists of a DC bias voltage $V_{\mathrm{DC}}$, and an alternating AC voltage $V_{\mathrm{AC}}$ with the excitation frequency $\Omega$:

$$\begin{aligned} V=V_{\mathrm{DC}}+V_{\mathrm{AC}}\sin {(\Omega t)}. \end{aligned}$$

(19)

Thus, Eq. (16) describes the nonlinear axisymmetric motion of a circular clamped plate, loaded with a uniform differential pressure and electrically actuated by its fundamental mode.

3 Solution methodology

In order to solve Eq. (16), first, the nonlinear term associated with the electrostatic field is approximated by a polynomial function:

$$\begin{aligned} \begin{aligned} G(q)&=\frac{1-(q+1)\digamma (q)}{2q(1+q)}&\\&\simeq \sum _{i=0}^{n} A_i q^{i}+\mathscr {O}(q^{n+1}),&\text {if }\quad q\ne 0,\\ G(q)&=-\frac{1}{3}&\text {if }\quad q=0,\\ \end{aligned} \end{aligned}$$

(20)

where coefficients $A_i$ are obtained by using the least squares technique (polynomial regression) for $-\,1<q<1$. Similar to $\digamma (q)$, G(q) is described at $q=0$ in a manner to maintain its continuity. Figure 3 shows the comparison between the exact function and approximate ones (for $n=4$ and $n=12$). It can be seen that with a polynomial of order 12 the exact function could be very well approximated.

Fig. 3

Approximation of the nonlinear electrostatic load (G(q)). A polynomial of order 12 has a good match with the exact function

Next, in order to investigate the periodic solutions and perform bifurcation analysis, a pseudo arc-length continuation and collocation scheme have been used [33, 34]. More details about the employed continuation algorithm are given in “Appendix A”. In this analysis in particular, a bifurcation analysis is carried out in two essential steps: (i) The continuation starts at a trivial steady-state solution, zero AC and DC voltages, and zero pressure. In turn, three out of the four parameters ($V_{\mathrm{AC}}$, $V_{\mathrm{DC}}$, $\Omega$ and P) are taken as the continuation parameters. The unstable solution branches are avoided in this step. (ii) Bifurcation analysis is performed by using the remaining parameter, whereas the other three parameters are fixed. In this step, the continuation is performed over the entire physical range. The stability of the solution branches is determined using Floquet theory. The obtained solution is stable only if all Floquet multipliers are inside the unit circle [28]. It is noteworthy that an alternative approach for analysis of bifurcations of periodic responses in nonlinear structures is proposed by Ref. [35].

4 Results and discussion

The procedure outlined in previous sections has been applied to a silicon micro-plate with the following properties: $E= 169 \, \hbox {GPa}$, $\nu =0.17$, $\mu = 2328 \, {\hbox {kg}\,\hbox {m}}^{-3}$, $h= 0.6 \, \upmu \hbox {m}$, $R= 100 \, \upmu \hbox {m}$ and $d= 2 \, \upmu \hbox {m}$. The electric permittivity of air $\epsilon = 8.854 \times 10^{12} \, \hbox {F}\,\hbox {m}^{-1}$ has been considered for the gap between the electrodes. Hence, the coefficients in Eq. (16) are obtained as: $\alpha _1=4.139\times 10^{21}$, $\alpha _2=1.981\times 10^{9}$, $\alpha _3=5.978\times 10^8$, $\omega _0=1.545\times 10^6$ rad/sec, $D=3.132\times 10^{-9}$ Nm. Moreover, a damping ratio of $\zeta =0.004$ is used. In the graphs provided in this section, the amplitudes of vibrations and the deflections are normalized with the initial gap between the electrodes (d).

Fig. 4

Normalized amplitude of vibrations of the system $\left( \frac{w_{\mathrm{max}}-w_{\mathrm{min}}}{2d}\right)$ with an electrostatic load equivalent to $V_{\mathrm{AC}}= 8 \, \hbox {V}$ as a function of excitation frequency, while $V_{\mathrm{DC}}=0$ and $P=0$. The graphs are obtained with one transverse degree of freedom and different numbers of in-plane degrees of freedom

A convergence analysis has been performed to find the minimum number of in-plane degrees of freedom able to capture the nonlinear motion of the plate accurately. Figure 4 shows the frequency response curves of the micro-plate while subjected to a relatively large load equivalent to $V_{\mathrm{AC}}= 8 \, \hbox {V}$, while $V_{\mathrm{DC}}=0$ and $P=0$, and by using different numbers of degrees of freedom for the in-plane displacement. It should be noticed that in Eq. (16), if $V_{\mathrm{DC}}=0$, the actuation load is proportional to $(V_{\mathrm{AC}} \sin (\omega t))^2$, which means the actual excitation frequency is equal to ($2\Omega$). Therefore, resonance is observed at $\Omega /\omega _0=0.5$. Figure 4 shows that convergence of the solution can be obtained by only three degrees of freedom (one transverse and two in-plane), and therefore, considering two in-plane degrees of freedom is sufficiently accurate to be used in the reduced-order model. Moreover, the parameter $\alpha _{1}$ (the coefficient of geometric nonlinearity in Eq. (16)) converges to $\alpha _1=52.04 \frac{d^2}{\mu h^3R^4}$ for two in-plane degrees of freedom.

Fig. 5

The normalized frequency at which the maximum amplitude in the nonlinear resonance peak is obtained as a function of the AC voltage using the propose mode shape and the first linear mode shape of a clamped circular plate calculated with classical plate theory $\left( J_0(\kappa \rho ) - \left( \frac{J_0(\kappa )}{I_0(\kappa )}\right) I_0(\kappa \rho ), \kappa =3.19625\right)$

It is worth to note that a convergence study is only reliable if the shape of the displacement field is representative of the motion. Therefore, in order to verify the accuracy of the proposed 4th order mode shape, we compare the hardening effects—as a result of the differential pressure and the high AC voltage—to two other methods. First, the frequency associated with the maximum amplitude in the nonlinear resonance peak is calculated using the proposed model and compared to those obtained using the exact linear mode shape of a circular plate (both previously shown in Fig. 2) as $\Phi _0$. Figure 5 shows the obtained frequency of the peak amplitude, normalized with respect to the natural frequency ($\omega _0$), as a function of the applied AC voltage. The graphs in this figure are both derived using two in-plane degrees of freedom ($N=2$). The proposed 4th order mode shape is capable of predicting the change in resonance frequency with less than 1.5% difference from the model with the exact linear mode shape of a circular plate.

Fig. 6

Normalized resonance frequency as a function of the differential pressure, while $V_{\mathrm{DC}}= 0\, \hbox {V}$

Finally, to verify the efficiency of the proposed model for capturing the geometrically nonlinear stiffness, an eigenfrequency analysis has been performed in a 3D finite element model built in COMSOL Multiphysics. More details about this eigenfrequency analysis is given in “Appendix B”. Figure 6 shows the linear resonance frequency (normalized with the natural frequency $\omega _0$), as a function of the applied differential pressure, obtained by the proposed 4th order mode shape, and the finite element model. As shown in Fig. 6, the proposed model is capable of predicting the change in resonance frequency and is in good agreement with the finite element solution (with less than 3.6% difference). This verifies the suitability of the basis functions, for expressing the inplane displacements of the plate, and for capturing the eigenfrequency of the deflected system linearized around its static equilibrium point.

Next, in order to perform a thorough bifurcation analysis, four different sequences of loading have been applied. In each case, three out of four load parameters ($V_{\mathrm{DC}}$, $V_{\mathrm{AC}}$, $\omega$ and P) are preserved and one is varied. The associated dynamic pull-in mechanisms of different sequences of loading are investigated.

4.1 Sweep over DC voltage

In this section, the solution branches over the full possible range of DC voltage are investigated while the differential pressure, AC voltage, and its frequency are kept constant. First, we consider the case when the AC component of the applied voltage is zero (see Fig. 7). In the absence of differential pressure ($P=0$), the deflection of the midpoint of the flexible electrode increases monotonically with the applied voltage until the system reaches a limit point or saddle-node bifurcation. At this critical point, the system becomes unstable, and if the voltage is increased, it leads to pull-in. However, when a differential pressure is applied, three saddle-node bifurcations ($P_1$, $P_2$, and $P_3$) appear in the solution of the system which we refer to as the primary, secondary, and the ultimate limit points. Therefore, the system becomes bi-stable, and sweeping the DC voltage over these limit points leads to a snap-through behavior between coexisting solution branches or failure of the system. This bi-stability can be of interest for actuation or binary sensing mechanisms (for differential pressure measurements for example [15]).

Fig. 7

The normalized static deflection $\left( \frac{w}{d}\right)$ of the micro-plate as a function of applied DC voltage for different differential pressures, while $V_{\mathrm{AC}}=0$. Straight line: stable solution, dotted line: unstable solution. $P_1$,$P_2$ and $P_3$ indicate primary, secondary and ultimate limit points

Fig. 8

The normalized deflection of the micro-plate averaged over time as a function of applied DC voltage, while $P= 3300 \, \hbox {Pa}$, $\Omega /\omega _0=1$. Straight line: stable solution, dotted line: unstable solution. $P_1$,$P_2$ and $P_3$ indicate primary, secondary and ultimate limit points, while PD demonstrates period-doubling bifurcation

The bi-stable behavior of the micro-plate is only observed in a limited pressure range, which in this case is $P=$ 3000–4100 Pa. This pressure range is a function of the thickness, radius, and material properties of the plate. In order to investigate the nonlinear dynamic behavior of the micro-plate in the bi-stable regime, we set the differential pressure to $P= 3300 \, \hbox {Pa}$. Moreover, the excitation frequency is set at the natural frequency of the non-pressurized plate ($\Omega /\omega _0=1$). Figure 8 shows the variation of the average deflection of the center of the plate (i.e., static deflection) as a function of the applied DC voltage. The graphs are obtained for different AC voltages. The static case (i.e., $V_{\mathrm{AC}}= 0 \, \hbox {V}$) and its associated limit points are also illustrated in this figure.

When the plate is dynamically actuated, it goes through a nonlinear resonance for a certain combinations of load parameters (see $V_{\mathrm{AC}}= 0.1 \, \hbox {V}$ in Fig. 8). Therefore, unstable branches emerge in the solution and at the points where the stable and unstable solution branches coincide, a saddle-node bifurcation is noticed (see points $P_4$ and $P_5$). Increasing the DC voltage around $P_4$ (or similarly decreasing the DC voltage around $P_5$) would result in jump from a stable solution to a second stable branch.

When a relatively large AC voltage is applied (see $V_{\mathrm{AC}}= 0.3 \, \hbox {V}$ in Fig. 8), the resonance occurs with a highly nonlinear behavior. In that case, in addition to critical saddle-node bifurcations, a period-doubling (PD) bifurcation appears in the solution. This type of bifurcation is a consequence of one of the Floquet multipliers leaving the unit circle through − 1. As a result, a new limit cycle with a period twice the period of the excitation frequency will be generated. This phenomenon usually leads to a transition to chaos and at ultimately, failure of the system [34, 36].

It is worth to note that although the period-doubling bifurcation is in the solution of the system, the prominent form of instability is still the saddle-node (i.e., the static pull-in). In fact, the period-doubling bifurcation can be only reached through several loadings and unloadings.

Fig. 9

The normalized amplitude of vibrations of the micro-plate $\left( \frac{w_{\mathrm{max}}-w_{\mathrm{min}}}{2d}\right)$ as a function of applied DC voltage, while $P= 3300 \, \hbox {Pa}$, $\Omega /\omega _0=1$. Straight line: stable solution, dotted line: unstable solution. $P_1$,$P_2$ and $P_3$ indicate primary, secondary and ultimate limit points, while PD demonstrates period-doubling bifurcation

Figure 9 shows the amplitude of vibration (i.e., around the static deflection) as a function of the applied DC voltage. The critical points marked in Fig. 8 are illustrated in this figure, as well. As it can be observed, the vibration has the highest amplitude just before the period-doubling bifurcation.

4.2 Sweep over excitation frequency

Next, we study the frequency response curves of the micro-plate, while maintaining other parameters. In this way, we can detect the frequencies at which the maximum amplitude in the nonlinear resonance peak is obtained, and hardening/softening responses for different cases.

Fig. 10

The frequency response function of the micro-plate; the normalized amplitude of vibrations $\left( \frac{w_{\mathrm{max}}-w_{\mathrm{min}}}{2d}\right)$ as a function of excitation frequency, while $P= 3300 \, \hbox {Pa}$, and $V_{\mathrm{AC}}= 0.01 \, \hbox {V}$. Straight line: stable solution, dotted line: unstable solution. PD indicates period-doubling bifurcation

Figure 10 shows the frequency response curves of the micro-plate subjected to a small AC voltage of $0.01 \, \hbox {V}$ and a differential pressure $P= 3300 \, \hbox {Pa}$. The graphs in this figure are determined for different values of DC voltage. The excitation frequency in this graph is normalized with respect to the natural frequency (undeformed configuration). The applied differential pressure (when $V_{\mathrm{DC}}$ is small) leads to a static deflection and therefore, a stretch in the micro-plate. This induces a geometrically nonlinear stiffness and as a result, a shift (static hardening) in resonance frequency of the system to $1.97 \omega _0$ (see $V_{\mathrm{DC}}= 2 \, \hbox {V}$ in Fig. 10a).

As Fig. 10 shows, when a DC voltage below the static pull-in is applied to the system (e.g., $50 \, \hbox {V}$), the vibration of the system is approximately linear. Therefore, no dynamic hardening or softening is observed in the resonance and the frequency response of the system. However, the applied DC voltage relaxes the static deflection and as a result, a shift (static softening) is observed. In higher DC voltages though, both static and dynamic softening appear in the frequency response of the system (see $V_{\mathrm{DC}}= 54 \, \hbox {V}$ and $54.6 \, \hbox {V}$ in Fig. 10a). As a result, an unstable solution branch emerges in the frequency response curve. At points where the stable and unstable solution branches coincide, a saddle point bifurcation is noticed. If the frequency is swept over the saddle points, the system will jump from one stable branch to the other one. However, it might also become unstable, leading to pull-in. Indeed in such cases, the transient dynamics of the system would determine whether the system settles at a stable orbit, or fails [7, 19]. Finally, when the voltage gets close to primary limit point (i.e., P1 in Fig. 8), the system loses stability and therefore, the resonance frequency of the system tends to zero (see $V_{\mathrm{DC}}= 54.7 \, \hbox {V}$ in Fig. 10a), passing a period-doubling bifurcation.

Figure 10b shows the frequency response curves of the system for higher DC voltages. These frequency response curves are equivalent to the lower stable branch (i.e., from P2 to P3) of Fig. 8. As it can be observed, increasing the DC voltage increases the resonance frequency (see $V_{\mathrm{DC}}= 55.5$ and $56.5 \, \hbox {V}$ in Fig. 10b). When the DC voltage approaches the ultimate limit point (i.e., P3 in Fig. 8), the frequency response function exhibits a dynamic softening and finally, loses stability through period doubling (see $V_{\mathrm{DC}}= 57 \, \hbox {V}$ in Fig. 10b).

Fig. 11

The normalized amplitude $\left( \frac{w_{\mathrm{max}}-w_{\mathrm{min}}}{2d}\right)$ as a function of excitation frequency observed in a sweeping up, b sweeping down the frequency, and c after the period doubling (zoom-in), while $P= 3300 \, \hbox {Pa}$, $V_{\mathrm{DC}}= 54.7 \, \hbox {V}$, and $V_{\mathrm{AC}}= 0.01 \, \hbox {V}$. Straight line: stable solution, dotted line: unstable solution. PD indicates period-doubling bifurcation

Figure 11 illustrates the feasible path taken by the system when sweeping up and down the frequency, when $V_{\mathrm{DC}}= 54.7 \, \hbox {V}$. As it can be observed when the frequency is increased, the system either jumps between the stable solution branches (Fig. 11a), or the transient behavior ends up in pull-in. In either case, the period-doubling instability would not be noticed. On the other hand, by decreasing the frequency, the system exhibits a first period-doubling bifurcation and as a result, the plate oscillates with a period twice the period of the excitation frequency (Fig. 11b). By slightly decreasing the frequency, a second period-doubling bifurcation is detected (Fig. 11c). In fact, this shows that the system could be susceptible to losing stability upon continuous period-doubling bifurcations. For the present load combination, sweeping down the frequency is a sufficient condition for observation of the dynamic pull-in.

Fig. 12

The phase portrait, the Poincaré section (the blue dot) and time response of the plate in a just before period doubling $\Omega /\omega _0=0.1765$ and b after period doubling with the new limit cycle $\Omega /\omega _0=0.17585$, while $P= 3300 \, \hbox {Pa}$, $V_{\mathrm{DC}}= 54.7 \, \hbox {V}$, and $V_{\mathrm{AC}}= 0.01 \, \hbox {V}$. (Color figure online)

The phase portrait, Poincaré section, and the time response of the system just before and after the period doubling (for $V_{\mathrm{DC}}= 54.7 \, \hbox {V}$) are illustrated in Fig. 12. Before the bifurcation (see Fig. 12a), a stable periodic solution with frequency $\Omega$, and a closed loop in the phase plane can be observed. After the bifurcation (see Fig. 12b), the only stable solution is a bifurcated branch with frequency $\Omega /2$, and a single closed curve with two loops in the phase plane.

Fig. 13

The frequency at which the maximum amplitude in the nonlinear resonance peak is obtained as a function of the applied DC voltage, while $V_{\mathrm{AC}}= 0.01 \, \hbox {V}$. Straight line: stable solution, dotted line: unstable solution

In Fig. 10 it was clearly observed that the frequency of the nonlinear resonance peak has a strong dependence on the applied DC voltage. This dependence is explicitly shown in Fig. 13, when the micro-plate is under the action of combined pressure and DC voltage. For comparison, the resonance frequency of a similar system without differential pressure is also shown in this figure. For $P= 3300 \, \hbox {Pa}$, the results indicate initially a static hardening (due to the presence of differential pressure), which changes to softening when increasing the DC voltage, down to zero resonance frequency at the primary critical DC voltage. Increasing the DC voltage above $54.7 \, \hbox {V}$ stabilizes the system, and finally at the ultimate limit point the system becomes unstable and fails.

Fig. 14

The frequency response function of the micro-plate; the normalized amplitude of vibrations $\left( \frac{w_{\mathrm{max}}-w_{\mathrm{min}}}{2d}\right)$ as a function of excitation frequency, while $P= 3300 \, \hbox {Pa}$, and $V_{\mathrm{DC}}= 30 \, \hbox {V}$. Straight line: stable solution, dotted line: unstable solution

Figure 14 shows the dynamic response of the micro-plate subjected to different AC voltages and relatively small DC voltage (i.e., $V_{\mathrm{DC}}= 30 \, \hbox {V}$). Exciting the system with a small AC voltage leads to an approximately linear periodic motion around the static configuration ($V_{\mathrm{AC}}= 0.01 \, \hbox {V}$ in Fig. 14a). When the AC voltage is increased, the vibration of the electrode allows for lower geometrically nonlinear stiffness and therefore, a local nonlinear softening is observed ($V_{\mathrm{AC}}= 0.20 \, \hbox {V}$). If the voltage is further increased, the softening behavior turns into hardening at $V_{\mathrm{AC}}= 0.60\, \hbox {V}$, and turns back to softening at $V_{\mathrm{AC}}= 0.65 \, \hbox {V}$ (in Fig. 14b) which would lead to dynamic pull-in through period-doubling bifurcation. A similar behavior was also reported in Ref. [7] for micro-beam resonators. However, this bifurcation will be observed only through several steps of sweeping up or down the frequency. In fact, when a relatively small DC is applied, the system is very robust to frequency sweep and therefore, not prone to dynamic pull-in.

4.3 Sweep over AC voltage

In this section, we study the stability of the micro-plate by varying $V_{\mathrm{AC}}$, and other parameters are preserved. Figure 15 shows the variation of amplitude of vibrations as a function of the applied AC voltage. The graphs in this figure are calculated for $P= 3300 \, \hbox {Pa}$, $V_{\mathrm{DC}}= 30 \, \hbox {V}$, and different driving frequencies. Due to the presence of the differential pressure and DC voltage, the plate has an initial upward static deflection of $\sim 0.37d$. This static deflection induces a geometrically nonlinear stiffness and therefore, the resonance frequency of the system (when the AC voltage is relatively small) has a shift with respect to its fundamental frequency ($\Omega /\omega _0=1.75$).

Fig. 15

The normalized amplitude of vibrations $\left( \frac{w_{\mathrm{max}}-w_{\mathrm{min}}}{2d}\right)$ as a function of the AC voltage, while $P= 3300 \, \hbox {Pa}$, and $V_{\mathrm{DC}}= 30 \, \hbox {V}$. Straight line: stable solution, dotted line: unstable solution

When the driving frequency is much lower than the resonance frequency of the pressurized system ($\Omega /\omega _0=1$ in Fig. 15), the AC voltage can be increased even to $24.7 \, \hbox {V}$ and the system would be stable. Finally, in a critical AC voltage the system loses stability upon a period-doubling bifurcation and fails. At this critical point, the maximum voltage $V=V_{\mathrm{DC}}+V_{\mathrm{AC}}$ is very close to the primary limit point for static loading (Fig. 8).

At a higher driving frequency $\Omega /\omega _0=1.4$, three saddle node bifurcations appear in the graph. When increasing (or decreasing) the AC voltage over Point P6 (or P7), the system will snap from one stable solution branch to another. However, increasing the voltage over the other critical point (i.e., P8) will always lead to failure of the system. When the driving frequency is close to the resonance of the pressurized system $\Omega /\omega _0=1.75$, a small AC voltage can cause a relatively high amplitude of vibrations. In this case, also, the pull-in occurs via a saddle-node bifurcation (i.e., Point P9).

Fig. 16

The static normalized deflection of the micro-plate $\left( \frac{w}{d}\right)$ as a function of pressure. Straight line: stable equilibrium, dotted line: unstable equilibrium

4.4 Sweep over pressure

Finally, we study the vibration of the micro-plate by varying the differential pressure as the bifurcation parameter, while keeping all other parameters constant. Figure 16 shows the static deflection of the micro-plate while loaded by pressure and DC voltage (i.e., $V_{\mathrm{AC}}=0$). As it can be observed, for voltages larger than zero, at least one limit point exists in the equilibrium path of the flexible electrode (i.e. Point P10 in $V_{\mathrm{DC}}= 30 \, \hbox {V}$). At this point, if the amplitude of the pressure increases in the negative direction (similar to electrostatic load), or any other perturbation is introduced to the system, pull-in occurs. For larger voltages, two other limit points appear in the equilibrium path. For example, in the curve corresponding to $V_{\mathrm{DC}}= 58 \, \hbox {V}$, if we sweep down the pressure around Point P11, the system snaps from a positive to a negative deflection.

Next, we preserve the DC voltage at $30 \, \hbox {V}$ and introduce a small AC voltage to the system. The driving frequency is fixed at $\Omega /\omega _0=1$. In Fig. 17a, a comparison is made between the maximum deflection in case of static (i.e., $V_{\mathrm{AC}}= 0 \, \hbox {V}$) and dynamic loading (i.e., $V_{\mathrm{AC}}= 0.05 \, \hbox {V}$). As it can be noticed, when a small AC voltage is applied to the system, the overall shape of the equilibrium path does not change. However, in certain combination of load parameters, the system goes through nonlinear resonance. In this case, the resonance occurs in two configurations, at which the system has very similar deformations though in opposite directions.

Fig. 17

The normalized deflection of the micro-plate (its minimum over time $\frac{w_{\mathrm{min}}}{d}$) as a function of pressure, while $V_{\mathrm{DC}}= 30 \, \hbox {V}$, for a whole pressure range and, b the pressure range with nonlinear resonance straight line: stable solution, dotted line: unstable solution

Figure 17b shows the deflection of the micro-plate while actuated with different AC voltages, in the pressure range which leads to the nonlinear resonance of the system. As it can be observed, by increasing the AC voltage, unstable solution branches might emerge in the response of the system (see $V_{\mathrm{AC}}= 0.10 \, \hbox {V}$). Therefore, sweeping the pressure over these points would result in resonance and finally, a jump to another stable solution branch. Increasing the AC voltage further leads to combination of nonlinear resonances into one stable region (e.g., $V_{\mathrm{AC}}= 0.30 \, \hbox {V}$). As a matter of fact, when sweeping over pressure, the stability of the micro-plate is increased when a higher AC voltage is applied to the system. Overall, when sweeping the pressure, the main mechanism of pull in remains similar to the static pull-in. However, due to the dynamic motion of the micro-plate, the pull-in occurs at a different voltage and deflection.

5 Conclusions

The nonlinear dynamics and stability of an electrically actuated micro-plate subjected to a differential pressure has been addressed. Using an energy approach, a reduced-order model was obtained, and then solved numerically. As a consequence of employing proper polynomials as the basis functions, we have been able to calculate the electrostatic load analytically and to obtain a reduced-order model for investigating the nonlinear dynamic behavior of circular micro-plates. The obtained equation incorporates dominant sources of complexities such as geometric and electrostatic nonlinearities and the non-uniform distribution of the electrostatic pressure and is versatile for performing bifurcation analysis. Bifurcation analysis was particularly performed considering pressure, DC and AC voltages and the excitation frequency.

The results of this study reveal the different possible failure mechanisms depending on the order of the loading applied to the micro-plate. Saddle-node and period-doubling bifurcations were repeatedly observed in the analysis and, therefore, are recognized as the dominant mechanisms of failure. Moreover, this study shows that in the presence of pressure, increasing the DC or AC voltages could surprisingly help to stabilize the motion of the micro-plate. This is while, in the absence of pressure, increasing the voltage always deteriorates the stability. In addition, in the presence of pressure, the motion of the micro-plate can be bi-stable or multistable.

The proposed description is potentially useful for designing sensing mechanisms relying on nonlinear dynamics (e.g., micro-mechanical mass sensors), as well as electrical actuators (such a inkjet printer head, RF switches, and vacuum resonators). The presented method in this paper provides a great insight into the nonlinear dynamics of clamped circular micro-plates. Such an insight is necessary for improving the performance of existing MEMS devices, as well as development of new applications.

Appendices

Appendix A: Numerical continuation of periodic solutions

This section is adopted from Refs. [28, 33, 34]. We use the software AUTO for continuation of the periodic solutions. The algorithm implemented in AUTO performs numerical continuation on a set of the first-order differential equations of the form:

$$\begin{aligned} \dot{\mathbf{x }}= F(\mathbf{x },\mu ). \end{aligned}$$

(A1)

A solution $x(T(s),\eta (s),\mu (s))$ of A1 with period T(s) is then sought such that

$$\begin{aligned} \mathbf{x }[T(s),\eta (s),\mu (s)] = \eta (s). \end{aligned}$$

(A2)

where $\mu$ is a system parameter. The system A1 together with the boundary conditions A2 constitute a set of n differential equations with $n+2$ unknowns, which are $\eta$, T and $\mu$. Therefore, in order to obtain the periodic solutions, two equations shall be added. The first equation gives a phase condition in the form of an integral equation. In particular, two consecutive points $\mathbf{x }_0 = \mathbf{x }(T_0,\eta _0,\mu _0)$ and ${\hat{\mathbf{x }}}$ are considered on the same branch of solution. Therefore, for any time shift $\sigma$, ${\hat{\mathbf{x }}} (t + \sigma )$ is also a solution. As a matter of fact, the phase condition can then be obtained by requiring that the distance $|{\hat{\mathbf{x }}} -\mathbf{x }_0|$ be minimized with respect to $\sigma$ as

$$\begin{aligned} D(\sigma ) =\int _0^T | {\hat{\mathbf{x }}} (t + \sigma )- \mathbf{x }_0 (t)|^2 \mathrm{d}t. \end{aligned}$$

(A3)

Setting $\mathrm{d}D/\mathrm{d}\sigma = 0$ and following few mathematical steps, it can be shown that the phase condition yields [28]:

$$\begin{aligned} \int _0^T \mathbf{x }^T F [\mathbf{x }(T_0,\eta _0,\mu _0),\mu _0] \mathrm{d}t = 0 . \end{aligned}$$

(A4)

The second equation is the pseudo arc-length constraint:

$$\begin{aligned} \int _0^T (\mathbf{x } - \mathbf{x }_0 )^T \mathbf{x }_0'\mathrm{d}t + (T - T_0 ) T_0'+ (\mu - \mu _0 ) \mu _0'-\Delta s = 0, \end{aligned}$$

(A5)

where the prime denotes a derivative with respect to s and $\Delta s$ is the continuation step. In the program AUTO, the integrals A4 and A5 are approximated by back-forward difference formulas and the ($n+2$)-dimensional system of equations given by A1, A4 and A5 with the boundary conditions A2 are discretized by using a collocation algorithm. AUTO discretizes this set of boundary value problems by the method of orthogonal collocation using piecewise polynomials with 2–7 collocation points per mesh interval.

Appendix B: Eigenfrequency analysis in COMSOL Multiphysics

To verify the obtained pressure-dependent natural frequency, a circular micro-plate has been modeled using the solid mechanics module of COMSOL multiphysics. The material properties and specifications that are used for the test case are: $E= 169\, \hbox {GPa}$, $\nu =0.17$, $h= 0.6 \, \upmu \hbox {m}$, $R= 100 \, \upmu \hbox {m}$, and $\mu = 2328 \, {\hbox {kg}}\,\hbox {m}^{-3}$. The outer edge of the micro-plate is fully clamped and a differential pressure is applied as a boundary load to the surface of the micro-plate. The micro-plate is then discretized with solid elements using free tetrahedral meshing, with at least two elements in transverse direction. The FE study consists of three step, (i) a parameter sweep which varies the differential pressure step by step, (ii) a stationary analysis in which the deflection and geometric nonlinearities induced by the pressure are calculated, and (iii) an eigenfrequency analysis to obtain the eigenfrequencies and eigenmodes of the system while incorporating the geometric stiffness linearized around the deformed configuration. As a result, the pressure-dependent resonance of the circular micro-plate is obtained. We remind that this eigenvalue analysis is in fact a linearization around the deformed configuration.