Vortex-induced rotational vibration of an eccentric circular cylinder at low Reynolds number of 100

Abstract

Vortex-induced rotational vibration (VIRV) of an eccentric circular cylinder in uniform flow is studied by fluid–structure interaction (FSI) simulation. Firstly, the mechanics model of VIRV of an eccentric circular cylinder in laminar flow is proposed, and the corresponding mathematical formulations are derived. Then, an FSI solver combining the modified characteristic-based split finite element method, dual-time stepping method and spring analogy method is developed for VIRV of a bluff body in laminar flow, and its stability and accuracy are validated by two benchmark FSI problems. Using FSI code validated, VIRVs of an eccentric circular cylinder at Re = 100, ζ (damping ratio) = 0, m^*(mass ratio) = 2, 5 and 10, l/D (l is the eccentricity and D is the cylinder diameter) = 0–5, and Ur (reduced velocity) = 1–30 are computed. The effects of m^*, l/D and Ur on the dynamic response, fluid load and vortex pattern of the eccentric cylinder are analyzed. Significant rotational response with maximum angle up to 36.3° is observed, and some VIRV features such as “lock-in” are analyzed. Finally, the underlying mechanisms of VIRV characteristics of the eccentric cylinder are discussed based on the governing equation of vibration. The model proposed could be taken as a benchmark for VIRV of the bluff body in laminar flow, and the results obtained are insightful to the design of VIRV-based energy harvesters.

Appendix

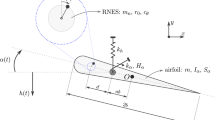
We describe the derivation process of the equation of motion (Eq. 3) employed in this paper. Following the Newton’s law, the governing equation of the rotational vibration of the eccentric circular cylinder (see Figs. 1 and

Fig. 16

Fluid loads on the eccentric circular cylinder

16) can be written as

$$ J\ddot{\theta } = - c_{\theta } \dot{\theta } - k_{\theta } \theta + M^{\prime} $$

(A1)

where $J = m\left( {l^{2} + R^{2} /2} \right)$ is the rotational mass moment of inertia with respect to the rotational center “o”, $c_{\theta }$ is the rotational damping coefficient from the structure, $k_{\theta }$ is the rotational stiffness from the structure, and $M^{\prime}$ is the resultant fluid moment with respect to the rotational center “o”, which can be expressed as

$$ \begin{aligned} M^{\prime} &= \int_{0}^{2\pi } \left\{ \left[l\cos \theta + R\cos (\theta + \alpha)\right]\sigma_{y} R{\text{d}}\alpha\right. \\&\left.\quad- \left[ l\sin \theta + R\sin ( \theta + \alpha)\right]\sigma_{x} R{\text{d}}\alpha \right\}\\& = \int_{0}^{2\pi }l\cos \theta \sigma_{y} {\text{d}}\alpha + \int_{0}^{2\pi } R\cos\left( {\theta + \alpha } \right)\sigma_{y} R{\text{d}}\alpha\\&\quad - \int_{0}^{2\pi } l\sin \theta \sigma_{x} R{\text{d}}\alpha- \int_{0}^{2\pi } {R\sin \left( {\theta + \alpha }\right)\sigma_{x} R{\text{d}}\alpha }\\ &= l\cos \theta\int_{0}^{2\pi } \sigma_{y} R{\text{d}}\alpha - l\sin \theta\int_{0}^{2\pi } {\sigma_{x} R{\text{d}}\alpha } \\&\qquad+\int_{0}^{2\pi } \left[ R\cos \left( {\theta + \alpha }\right)\sigma_{y} R{\text{d}}\alpha - R\sin \left( {\theta+\alpha}\right)\sigma_{x} R{\text{d}}\alpha \right]\\ \end{aligned} $$

(A2)

where R is the radius of the circular cylinder, α is the angular angle as shown in Fig. 16, $\sigma_{x}$ and $\sigma_{y}$ are components of fluid stress imposed on the cylinder surface, and Rdα = ds is a micro arc of the circular cylinder. Note that

$$ \begin{aligned} F_{x} & = \int_{0}^{2\pi } {\sigma_{y} R{\text{d}}\alpha ,\;F_{y} = \int_{0}^{2\pi } {\sigma_{x} R{\text{d}}\alpha } ,} \\ M & = \int_{0}^{2\pi } {[R\cos \left( {\theta + \alpha } \right)\sigma_{y} R{\text{d}}\alpha } \\ & \quad - R\sin \left( {\theta + \alpha } \right)\sigma_{x} R{\text{d}}\alpha ] \\ \end{aligned} $$

(A3)

where F_x and F_x are components of the resultant fluid load on the cylinder, and M is the resultant fluid moment with respect to the cylinder center “$o^{\prime}$”. Substituting Eq. (A3) into Eq. (A2), we have

$$ M^{\prime} = lF_{x} \cos \theta - lF_{y} \sin \theta + M $$

(A4)

Therefore, Eq. (A1) can be rewritten as

$$ m\left( {l^{2} + R^{2} /2} \right)\ddot{\theta } + c_{\theta } \dot{\theta } + k_{\theta } \theta = lF_{x} \cos \theta - lF_{y} \sin \theta + M $$

(A5)

Define non-dimensional parameters as follows

$$ \left\{ \begin{array}{l} m^{*} = \frac{m}{{\frac{1}{4}\pi D^{2} \rho_{{\text{F}}} }},\;l^{*} = \frac{l}{D},\;c_{\theta }^{*} = \frac{{c_{\theta } }}{{\rho_{{\text{F}}} D^{3} U}}, \hfill \\ t^{*} = \frac{tU}{D},\;k_{\theta }^{*} = \frac{k}{{\rho_{{\text{F}}} D^{2} U^{2} }}, \hfill \\ C_{{\text{L}}} = \frac{{F_{y} }}{{\frac{1}{2}\rho_{{\text{F}}} DU^{2} }},\;C_{{\text{D}}} = \frac{{F_{x} }}{{\frac{1}{2}\rho_{{\text{F}}} DU^{2} }}, \hfill \\ C_{{\text{M}}} = \frac{M}{{\frac{1}{2}\rho_{{\text{F}}} D^{2} U^{2} }}. \hfill \\ \end{array} \right. $$

(A6)

Substituting Eq. (A6) into Eq. (A5), we have

$$ \begin{aligned} & \frac{1}{4}\pi m^{*} \left( {l^{*2} + \frac{1}{8}} \right)\ddot{\theta } + c_{\theta }^{*} \dot{\theta } + k_{\theta }^{*} \theta \\ & \quad = \frac{1}{2}l^{*} C_{{\text{L}}} \cos \theta - \frac{1}{2}l^{*} C_{{\text{D}}} \sin \theta + C_{{\text{M}}} \\ \end{aligned} $$

(A7)

Defining $J_{\theta }^{*} = \frac{1}{4}\pi m^{*} \left( {l^{*2} + \frac{1}{8}} \right)$, $\omega_{{\text{N}}} = 2\pi f_{{\text{N}}} = \sqrt {\frac{{k_{\theta }^{*} }}{{J_{\theta }^{*} }}}$ and $\zeta = \frac{{c_{\theta }^{*} }}{{2\omega_{{\text{N}}} J_{\theta }^{*} }}$, Eq. (A7) can be rewritten as

$$ \begin{aligned} & \ddot{\theta } + 4\pi f_{{\text{N}}} \zeta \dot{\theta } + \left( {2\pi f_{{\text{N}}} } \right)^{2} \theta = \frac{{2\left( {l^{*} C_{{\text{L}}} \cos \theta - l^{*} C_{{\text{D}}} \sin \theta + C_{{\text{M}}} } \right)}}{{\pi m^{*} \left( {l^{*2} + } 1/8 \right)}} \\ \end{aligned} $$

(A8)

which is the non-dimensional governing equation of rotational vibration of the eccentric circular cylinder.