1 Introduction

Analysis and prediction of data play an important role in people’s production and life, such as weather prediction, environmental pollution control, earthquake prediction, financial data analysis, speech recognition, image processing, and aircraft control [1,2,3,4,5,6,7,8,9,10]. For the field of time series prediction, various methods have been proposed and obtained more satisfactory prediction results, such as system dynamics reconstruction and neural network prediction. However, in various applications, all the prediction methods are facing a central problem—noise, which brings great difficulties for prediction. For example, when extracting valuable signals from the collected data, the correlation between the noises affects the estimation performance of the signal parameters seriously [11]. In radar monitoring, the presence of noise can make the dynamic reconstruction results unstable [12]. In remote sensing, the effect of noise on the prediction of system dynamics can lead to biased detection of spatiotemporal concentration distribution information [13]. Therefore, the ability to accurately obtain system dynamics from noisy data becomes one of the essential indicators of prediction methods.

To overcome the effects caused by noise in the data, researchers have proposed a variety of dynamical reconstruction methods, such as smoothing method [14], polynomial fitting method [15], local dynamics global fitting method [16], and high-order correlation computation (HOCC) method [17]. The smoothing method takes multi-step averaging to attenuate the noise effect. The polynomial fitting method proposed by Lu et al. [15] directly uses polynomials to fit the time series with noise. The local dynamics global fitting method proposed by Wang and Lan et al. [16] uses globally invariant polynomials to fill all the local pieces of time series. The HOCC method proposed by Chen et al. uses the differential-time correlation of variables to filter out the noise and solves all the unknown coefficients in the system equation by calculating the high-order correlation between variables. In HOCC, the use of differential-time correlation to remove the effect of noise can adjust the time difference in a considerable range to adapt to different noise conditions.

In the last decades, lots of new methods have been proposed to learn, predict and reconstruct the dynamics from data, such as different network structures detection methods [18, 19], extra local driving for topology inference [20], and the compressive sensing technology [21, 22]. Among all these new methods, neural networks have also attracted much attention and applications in the field of prediction due to their good nonlinear mapping capability, self-learning adaptation ability, and parallel information processing capability [23,24,25,26,27]. At the beginning of this century, a novel recurrent neural network method, reservoir computing (RC), was proposed to bring a breakthrough to chaotic forecasting with its simple structure and training method [28,29,30,31,32,33,34]. Recently, the next-generation reservoir computing (NG-RC) method, proposed by Gauthier et al. [35] simplifies the RC computation system, significantly reducing its demand on computer resources and saving a lot of time. The new method creates linear and nonlinear feature vectors directly from discretely sampled input data without using a neural network. In NG-RC, the linear feature vector consists of constant terms and observations of the input vector at the current and certain previous time steps. The nonlinear feature vector consists of a two-by-two combination of linear components. The NG-RC method is 33–162 times faster than traditional RC calculations and requires only 28 neurons to achieve the accuracy that would have been achieved with 4000 neurons. Besides, the new method uses 400 data points to obtain the same results as the traditional RC using 5000 or even more data points for training (the exact number of data points depends on the required accuracy).

The high efficiency of the NG-RC methods attracts lots of attention. However, as one of the learning and prediction methods, the noise resistance of NG-RC is not discussed in detail yet, limiting its applications in practice where the available data is always contaminated with noise. Different from classical reservoir computing methods, the NG-RC method depends on the feature vectors, which is similar to the function bases of some reconstruction methods, such as HOCC. As one of the well-developed noise-resistant methods, the effectiveness, robustness, and adaptability of HOCC to different conditions have also been studied comprehensively in simulation validation [17, 36, 37]. Hence, to study the noise resistance of NG-RC comprehensively, we take the HOCC as a reference and compare the differences between these two methods and their noise resistance ability. Surprisingly, we find that even though the NG-RC method does not have special designs for noise resistance, it surpasses the HOCC method for systems with white noise and provides reasonable prediction ability for small colored noise.

In this paper, we compare the noise resistance ability and characteristics of NG-RC with reference to HOCC methods from theoretical analysis and numerical experiments. In terms of theory, we analyze the similarities between the two methods. Both methods have similar procedures in the respect of function bases and regression processes, especially when one considers the NG-RC method without time-delay function bases. We take the Lorenz system as an example and explore the difference in the coefficient reconstructed by the two methods. In terms of numerical experiments, four indicators are introduced to show the noise resistance of methods, such as the training error, prediction error, prediction time, and auto-correlation prediction error. Both the white and colored noise are considered in this paper. The effects of the noise intensity, training length, and sampling interval on the noise resistance ability of the two methods are explored comprehensively. Besides, the noise resistance to colored noise with the change of time delay in NG-RC and HOCC is also studied to study the potential variations of the method for colored noise.

This paper is organized as follows: Section 2 introduces NG-RC and HOCC methods and compares their difference theoretically. Sections 3 and 4 show the numerical experimental results of the NG-RC method without and with time-delay function bases on the white and colored noise-driven system. Section 5 concludes the paper.

2 Theoretical comparative analysis of NG-RC and HOCC

Considering the dynamics of an arbitrary noise-driven system as:

$$\begin{aligned} \begin{aligned} \varvec{{\dot{x}}}(t)&={\varvec{f}}({\varvec{x}}(t))+\varvec{\Gamma }(t),\\ {\varvec{x}}&=(x_1,x_2,\ldots ,x_M)^T,\\ {\varvec{f}}&=(f_1,f_2,\ldots ,f_M)^T,\\ \varvec{\Gamma }&=(\Gamma _1,\Gamma _2,\ldots ,\Gamma _M)^T, \end{aligned} \end{aligned}$$
(1)

where \({\varvec{x}}\) is the state variable, M the dimensionality of the state variable, t the time variable, and \({\varvec{f}}\) the function. The \(\Gamma _i(t),i=1,2,\ldots ,M\) is the noise term which is either Gaussian white with \(<\varvec{\Gamma }(t)>=0\) and \(<\varvec{\Gamma }(t)\varvec{\Gamma }(s)>=2D\delta (t-s)\) where D is the noise intensity, or Ornstein–Uhlenbeck colored noise with \(<\varvec{\Gamma }(t)\varvec{\Gamma }(s)>=\frac{1}{2\tau }\exp (-|t-s|/\tau )\) in this paper. From the dynamical system Eq. (1), one gets the measurable data as time series,

$$\begin{aligned}{} & {} {\varvec{x}}(t_1),{\varvec{x}}(t_2),\ldots ,{\varvec{x}}(t_k),\ldots ,{\varvec{x}}(t_N), \nonumber \\{} & {} \quad \Delta t=t_{k+1}-t_k\ll 1;k=1,2,\ldots ,N-1;N\gg 1, \end{aligned}$$
(2)

where N denotes the time series length, and \(\Delta t\) is the time sampling interval.

In this paper, we consider the inverse problem that given the time series in Eq. (2), how to obtain the original dynamical system Eq. (1). Here, we take the Lorenz system [5] as the example of an original noise-driven dynamic system. It is one of the most famous models in chaos studies, developed in 1963 as the first system discovered to produce chaotic attractors. The Lorenz system follows the dynamics of Eq. (1) with three coupled nonlinear differential equations:

$$\begin{aligned} \begin{aligned} {\varvec{f}}&=(f_1,f_2,f_3)^T\\&=(\sigma (y-x),x(\rho -z)-y,xy-\beta z)^T, \end{aligned} \end{aligned}$$
(3)

where x, y, z denote the state variables. In this paper, we take the parameters \(\sigma =10,\rho =28,\beta =8/3\) to for chaotic time series. In the following, we use NG-RC and HOCC methods for the inverse problems with noise to get the original Lorenz dynamical systems.

2.1 NG-RC method

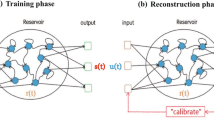
The NG-RC method is developed from the traditional RC. It is no longer requiring a linear combination of the input signals using a randomly generated neural network to obtain the output signal, but instead directly creates feature vectors with discretely sampled input data, where the feature vectors are called bases. For prediction, the bases consist of three parts: constant term, linear terms, and nonlinear terms. For the Lorenz system, the linear terms at the moment \(t_k\) are usually composed of \(x(t_k),y(t_k),z(t_k),x(t_{k-1}),y(t_{k-1}),z(t_{k-1})\) [35], where \(k=2,\ldots ,N-1\). The nonlinear terms component is composed of two combinations of constant and linear terms, totaling 21 terms. The whole basis function matrix \({\varvec{P}}\) is obtained from the observed data \({\varvec{x}}\), where the k-th column \(\varvec{P_k}\) for time \(t_k\) is:

$$\begin{aligned} \begin{aligned} \varvec{P_k}&=(1,x(t_k),y(t_k),z(t_k),x(t_{k-1}),y(t_{k-1}),\\&z(t_{k-1}),x^2(t_k),x(t_k)y(t_k),x(t_k)z(t_k),\\&x(t_k)x(t_{k-1}),x(t_k)y(t_{k-1}),x(t_k)z(t_{k-1}),\\&y(t_k)y(t_{k-1}),y(t_k)z(t_{k-1}),z^2(t_k),y^2(t_k),\\&y(t_k)z(t_k),y(t_k)x(t_{k-1}),z(t_k)x(t_{k-1}),\\&z(t_k)y(t_{k-1}),z(t_k)z(t_{k-1}),x^2(t_{k-1}),\\&x(t_{k-1})y(t_{k-1}),x(t_{k-1})z(t_{k-1}),\\&y^2(t_{k-1}),y(t_{k-1})z(t_{k-1}),z^2(t_{k-1})). \end{aligned} \end{aligned}$$
(4)

The basic assumption of NG-RC is that the function base is complete for the original dynamical systems, from which the dynamical function \({\varvec{f}}({\varvec{x}})\) in Eq. (1) could be expressed as a linear transformation of \({\varvec{P}}\) as

$$\begin{aligned} {\varvec{f}}({\varvec{x}})=\varvec{A}_1{\varvec{P}}, \end{aligned}$$
(5)

where \({\varvec{A}}_1\) is the coefficient matrix. The left hand side of Eq.(5) can be estimated through a simple difference method as:

$$\begin{aligned} {\varvec{f}}(\varvec{x_k}) \approx \varvec{X_k}=\frac{1}{\Delta t} \begin{pmatrix} x(t_{k+1})-x(t_k) \\ y(t_{k+1})-y(t_k) \\ z(t_{k+1})-z(t_k) \end{pmatrix}. \end{aligned}$$
(6)

Taking \(\varvec{X_k}\) as the k-th column, one gets the target matrix \({\varvec{X}}\) whose size is \(3\times L\), where \(L=N-2\) is the length of training data. Correspondingly, the size of coefficient the matrix \({\varvec{A}}_1\) and basis function matrix \({\varvec{P}}\) are \(3\times 28\) and \(28 \times L\) respectively.

In NG-RC method, the ridge regression method is used to solve \({\varvec{A}}_1\):

$$\begin{aligned} \varvec{A}_1=\varvec{X P^T (PP^T}+\alpha {\varvec{I}})^{-1}, \end{aligned}$$
(7)

where \(\varvec{P^T}\) is matrix transpose of \({\varvec{P}}\), \(\alpha \) ridge regression parameter, and \({\varvec{I}}\) the identity matrix. After solving the reserve problem and getting \({\varvec{A}}_1\), an Euler-like integration step can be used to obtain the prediction time series \({\varvec{y}}\):

$$\begin{aligned} \varvec{y}_{\mathrm {i+1}}=\varvec{y_i}+\varvec{A}_1 {P_i}\Delta t, \end{aligned}$$
(8)

with \({\varvec{i}}=1,2,\ldots ,\infty \). For learning and prediction of chaotic time series, the NG-RC method using bases with time delay is shown to have the same or even better prediction capacity compared to the traditional RC using randomly generated neural networks [35]. But here we focus on its noise resistance ability.

2.2 HOCC method

In this paper, we take the HOCC method as the reference, which uses the differential-time correlations of variables to remove noise and solves all unknown coefficients in the system equation by calculating the high-order correlations among the variables. When using the HOCC method for prediction, it is necessary to select an appropriate function basis in advance, denoted as \({\varvec{Q}}\) as not to be confused with the function basis for NG-RC. For the Lorenz system, the polynomial functions are often chosen as the bases. Similar to the NG-RC method, the whole basis function matrix \({\varvec{Q}}\) is obtained from the observed data \({\varvec{x}}\), where the k-th column \(\varvec{Q_k}\) for time \(t_k\) as:

$$\begin{aligned} \begin{aligned} \varvec{Q_k}&=(1,x(t_k),y(t_k),z(t_k),x^2(t_k),x(t_k)y(t_k),\\&x(t_k)z(t_k),y^2(t_k),y(t_k)z(t_k),z^2(t_k)). \end{aligned} \end{aligned}$$
(9)

It is worth to be noted that the basis function matrix \(\varvec{Q}\) is exactly a part of the function matrix \({\varvec{P}}\) except for the time-delay terms.

The basic assumption of HOCC is also the same as NG-RC, where the function base \({\varvec{Q}}\) is complete for the original dynamical systems, from which the dynamical function \({\varvec{f}}({\varvec{x}})\) in Eq. (1) could be expressed as a linear transformation of \({\varvec{Q}}\) as

$$\begin{aligned} {\varvec{f}}({\varvec{x}}(t))=\varvec{A}_2 \varvec{Q}, \end{aligned}$$
(10)

where \({\varvec{A}}_2\) denotes the coefficient matrix of \({\varvec{Q}}\). Up to this step, the two methods, NG-RC and HOCC, are exactly the same, with only a slightly difference in the choice of function basis. If we use the ridge regression method to get \(\varvec{A}_2\) directly, this is the NG-RC method without time-delay terms. However, in the HOCC method, one more step is applied to remove the noise. Here, one takes the function vector \({\varvec{Q}}^T({\varvec{x}}(t-\tau ))\) with time delay as

$$\begin{aligned} {\varvec{Q}}({\varvec{x}})=(Q_1({\varvec{x}}),Q_2(\varvec{x}),\ldots ,Q_{10}({\varvec{x}}))^T, \end{aligned}$$
(11)

and right multiple it with Eq. (1). Then by taking time averaging to calculate all related correlations, we have

$$\begin{aligned} {\varvec{B}}^T(-\tau )=\varvec{A_2} \varvec{\hat{C}}(-\tau )+< \varvec\Gamma (t) {\varvec{Q}}^T(t-\tau )>, \end{aligned}$$
(12)

with

$$\begin{aligned} \begin{aligned} {\varvec{B}}(-\tau )&=(B_1(-\tau ),B_2(-\tau ),\ldots ,B_{10}(-\tau ))^T,\\ B_\mu (-\tau )&=<{\dot{x}}(t)Q_\mu (t-\tau )>\\&=\frac{1}{L-P}\sum _{k=p+1}^L {\dot{x}}(t_k)Q_\mu (t_{k-p}),\\ {\dot{x}}(t_k)&=\frac{x(t_{k+1})-x(t_k)}{\Delta t},\tau =p\Delta t,\\ \varvec{\hat{C}}(-\tau )&=(C_{\mu \upsilon })\\&=\left( \frac{1}{L-P}\sum _{k=p+1}^L Q_\mu (t_k)Q_\upsilon \left( t_{k-p}\right) \right) , \end{aligned} \end{aligned}$$
(13)

where \(\mu = 1,2,\ldots ,10\), \(<\cdot>\) denotes time averaging. The time delay \(\tau \) is assumed to satisfy the inequality \(0\approx \tau _d \ll \tau \ll 1\), that it is much larger than the correlation time of dynamical noise \(\tau _d\), and much smaller than the characteristic times of deterministic network dynamics, previously assumed to be of order 1. In this case, noises and correlations are decorrelated as

$$\begin{aligned} < \varvec {\Gamma} (t){\varvec{Q}}^T(t-\tau )>\approx 0,\tau >t_d, \end{aligned}$$
(14)

since the fast-changing noise must not be correlated with any variable data of previous times, disregarding any forms of colored noises. Now with the noise-decorrelation of Eqs. (14) and (12) can be reduced to

$$\begin{aligned} {\varvec{B}}^T(-\tau )=\varvec{A}_2\hat{C}, \end{aligned}$$
(15)

which leads to

$$\begin{aligned} \varvec{A}_2={\varvec{B}}^T(-\tau )\varvec{\hat{C}}^{-1}, \end{aligned}$$
(16)

which could be solved directly. This differential-time correlation-based procedure to get \({\varvec{A}}_2\) is the essential part of the HOCC method and also the major difference between the NG-RC method. After getting the coefficient matrix \({\varvec{A}}_2\), one can reconstruct the original dynamic is as

$$\begin{aligned} \varvec{{\dot{x}}}(t)=\varvec{A_2Q}, \end{aligned}$$
(17)

and also iterate the system and obtain the predicted time series \({\varvec{y}}\) similar to NG-RC.

It can be seen that both the NG-RC and HOCC methods use the same idea to fit the original system with function bases that are selected in advance and then solve its coefficient matrix. If both methods choose the same bases, the target matrix for its optimization is the same. The difference is that in the HOCC method, the \(\varvec{\hat{C}}\) in Eq. (15) is composed of the differential-time correlations of the basis vectors, and the coefficient matrix \({\varvec{A}}_2\) is regression solved after the correlations, so that the noise is removed by using the property that the noise and the correlators must be decorrelated. While in the NG-RC method, the matrix \({\varvec{Y}}\) is directly combined by the basis vectors. The ridge regression method is used directly to solve the coefficient matrix \({\varvec{A}}_1\), and by adjusting \(\alpha \) to remove noises while preventing over-fitting.

It is straightforward to notice that these two methods are comparable in theory. In the following, we will use numerical methods to check how well the simple ridge regression method used in NG-RC is for the noise resistance, compared to the HOCC method which has a special designed time difference correlations procedure for noise elimination.

3 The NG-RC method without time-delay function bases

In this paper, the Lorenz system in Eq. (3) is set with \(\sigma =10\), \(\rho =28\), \(\beta =8/3\)(the Lorenz system is chaotic with this parameter), and the sampling interval reads \(h= 0.0002\). The data of the original Lorenz system is generated by the iteration of the Runge–Kutta method, which is noted as \({\varvec{ y}}_{\text {Lorenz}}\). Two types of noise are considered, as the Gaussian white noise and Ornstein–Uhlenbeck colored noise. To show the noise effect, we increase the noise strength gradually, from 0.0001 to 25. The colored noise correlation time is fixed at 25 h. The phase diagrams with either white or colored noise are shown in Fig. 1.

Fig. 1
figure 1

Phase diagrams of the Lorenz system are driven by different intensities of white noise or colored noise. \(h=0.00002\), \(\sigma =10\), \(\rho =28\), \(\beta =8/3\). (a–d) show the Lorenz system driven by white noise with \(D=0.0001\), \(D=0.01\), \(D=5\), and \(D=15\). (e–h) show the Lorenz system driven by colored noise with \(D=0.0001\), \(D=0.01\), \(D=5\), and \(D=15\)

Full size image

It is clear that noises affect the dynamics of the Lorenz system dramatically in Fig. 1. How to get the original system through such data is the challenging problem that we want to solve with NG-RC and HOCC methods.

In Section 2, we know that if the same function bases are selected, i.e., the NG-RC method without time-delay function bases, then the goal matrix of the two methods is the same. But NG-RC and HOCC have different procedures for noise resistance. Hence, in the following, we compare NG-RC and HOCC in two steps. In this section, we only focus on the NG-RC method without time-delay function bases, denoted as NG-RC10 for it only considering the 10 function bases. And in the next section, we will use the full bases introduced in NG-RC.

3.1 White noise-driven system

First, consider the white noise-driven Lorenz system. With HOCC and NG-RC methods, the dynamical system is reconstructed. Compared with the original Lorenz system, We obtain reconstruction errors of these two methods and show them in Table 1.

Table 1 When the white noise-driven system is reconstructed, the standard deviation of the coefficients obtained by the two methods and the mean of the difference correspond to the original Lorenz system
Full size table

When the D is smaller, the standard deviation of the coefficients corresponding to the Lorenz system obtained by the HOCC method is about \(10^{-5}\) to \(10^{-6}\), and the other terms are about \(10^{-2}\). When the D is large, the standard deviation of coefficient terms is about \(10^{-3}\), and other terms are about \(10^{-2}\). It can be found that the reconstruction result of NG-RC10 is close to that of the HOCC method. HOCC method has only slightly better noise resistance ability than NG-RC10 for white noise cases. Here, the train steps L and sampling interval h are chosen as \(L=15\) million and \(h=0.0002\), which are chosen as one of the best parameters for the HOCC method, studied in [37].

To further explore the processing ability of the two methods for noisy data with different parameters, and better understand their noise resistance characteristics, we adopted the control variable method to analyze the noise resistance performance of the NG-RC and HOCC methods from the perspective of the influence of train steps L, sampling interval h and noise strength D on the predicted results respectively. Instead of the reconstructed parameters, here we use a single numerical indicator introduced in [35], \(E_{\text {t}}\), to estimate the reconstruction result, which reads

$$\begin{aligned} E_{\text {t}}=\frac{1}{N}\sum _{k=1}^N(y_{{{\text {Lorenz}}}_k}-y_k)^2, \end{aligned}$$
(18)

as mean square error between reconstructed time series \(\varvec{y}\) and the original one \({\varvec{y}_ \text{Lorenz}}\). The smaller the \(E_{\text {t}}\) is, the better the noise resistance ability of the method. The experimental results of \(E_{\text {t}}\) changes with the above three variables are shown in Fig. 2. Here, considering that the ridge regression parameter \(\alpha \) of the NG-RC method has a certain influence on its noise resistance ability, for each data point in Fig. 2, \(\alpha \) was optimized to obtain the optimal \(E_{\text {t}}\) for display. The optimization process is in Supplementary Note 1.

When the sampling interval is sufficiently small, as shown in Fig. 2a, fixing \(h = 0.00002\) and choosing four different intensities of white noise to drive the system for training, the \(E_{\text {t}}\) of the two methods do not differ much when the amount of training data is small, and both decrease as the number of train steps increases. These results coincide with the one obtained from the reconstructed parameters shown in Table 1 that the NG-RC10 method and HOCC method have almost the same noise resistance in these cases.

However, as shown in Fig. 2b, increasing the sampling interval to \(h = 0.001\), the reconstruction error \(E_{\text {t}}\) of the HOCC method appears to be a “plateau area” when D is small, while \(E_{\text {t}}\) continues decreasing with the increase of L for NG-RC10 method. The simpler NG-RC method works even better than HOCC for time series with large sampling intervals and sufficient large train steps. More details can be found in Fig. 2c, where the training data are the same and large enough (15 million), and the white noise-driven system with three different sampling intervals is selected for training. The reconstruction error \(E_{\text {t}}\) of both methods increases with the increase of D, while \(E_{\text {t}}\) of the HOCC method appears “plateau area” at \(h=0.001\) and \(h=0.0002\). Combined with Fig. 2b, the HOCC method can no longer decrease \(E_{\text {t}}\) when training and predicting data with minor D and greater h, no matter how to reduce D or increase the number of train steps, and this lower limit varies with h. The larger the h, the higher the lower limit.

The above results are corroborated in Fig. 2d. For NG-RC10, \(E_{\text {t}}\) is more affected by D, but the variation of \(E_{\text {t}}\) with h is smaller for the same D system. For the HOCC method, when h is small, the smaller D is, the smaller \(E_{\text {t}}\) is, similar to the NG-RC10 method. But for large sample interval h, the difference between \(E_{\text {t}}\) corresponding to different D decreases until it overlaps when \(h>0.001\). In these cases, a decrease in the noise strength D does not result in the improvement of prediction capacity. The sampling interval defines a minimum value of \(E_{\text {t}}\), increasing with the increase of h. As a result, for time series with large sampling intervals, the NG-RC10 method works better than HOCC, as shown in Fig. 3. Here, the \(\alpha \) is also optimized. When \(h=0.00002\), the noise resistance ability of the two methods is comparable in Fig. 3a. When increasing h to 0.0002 and 0.001, the \(E_{\text {t}}\) of the HOCC methods becomes larger for smaller intensity noise, while the results of NG-RC10 are less affected, as shown in Fig. 3b, c. The appearance of the “plateau area” of the HOCC method is an open question and out of the scope of this paper, but from this phenomenon, the NG-RC10 method could provide a better prediction for the dynamical system with white noise.

Fig. 2
figure 2

Effects of L, D, and h on the \(E_{\text {t}}\) of the two methods. (a–c) the circle line represents the HOCC method and the star line represents NG-RC10. (a, b) the influence of L on two methods: blue, red, green, and rose red represents D = 0.001, \(D=0.01\), \(D=0.1\), and \(D=0.8\) respectively, where \(h=0.0002\) in (a) and \(h=0.001\) in (b). c the effect of D on two methods: fixed \(L=\) 15 million, red, blue and green represents \(h=0.00002\), \(h=0.0002\), \(h=0.001\). d the effect of h on two methods: fixed number of \(L=\) 15 million, the red and blue represent the HOCC and NG-RC10, and the circle, star, and square lines represent the noise intensity of \(D=0.001\), \(D=0.1\), and \(D=0.8\). (Color figure online)

Full size image
Fig. 3
figure 3

Prediction error \(E_{\text {t}}\) of the two methods for different noise strength D with sampling interval h. The black solid line indicates that the \(E_{\text {t}}\) of the two methods are equal. The h used in (a–c) are \(h=0.001\), \(h=0.0002\) and \(h=0.00002\), \(L=\) 15 million, and the dots of different colors represent 20 different D. (Color figure online)

Full size image

In the above results, the prediction error \(E_{\text {t}}\) is used to describe the noise resistance ability of the method. Meanwhile, we noted that other indicators were also used in previous studies to measure the reconstruction or prediction ability of the method. For example, in [16, 17], the results obtained by the reconstruction method are compared with the coefficients of the original dynamic system to measure its reconstruction ability. In [35], the mean square error of the prediction time sequence obtained by the noise resistance method and the training data was calculated to measure the method’s fitting ability to the training data. In [38], the prediction ability of the method was measured by the coincident steps between the prediction sequence and the original noise-free sequence. To understand the two methods in multiple dimensions, we check the noise resistance ability of the two methods in terms of a more refined four-dimensional representation. Other than the prediction error \(E_{\text {t}}\), we consider the training error \(E_{\text {n}}\), prediction time \(T_{\text {p}}\), and auto-correlation prediction error \(E_{\text {a}}\).

(1) The training error \(E_{\text {n}}\), the mean square error of \(\varvec{y}\) and \(\varvec{y_{train}}\), is defined as

$$\begin{aligned} E_{\text {n}}=\frac{1}{N}\sum _{k=1}^N(y_{{train}_k}-y_k)^2. \end{aligned}$$
(19)

It is the objective function of the training phase and is used to measure the learning error with noise.

(2) The prediction time \(T_{\text {p}}\), the coincident steps of \(\varvec{y}\) and \({\varvec{y}_ \text{Lorenz}}\), is defined as the maximum time step k where the square error between the predicted time series and original Lorenz system is smaller than 0.01. It is important to note here that \(T_{\text {p}}\) is correlated with \(E_{\text {t}}\). A Smaller prediction error \(E_{\text {t}}\) results in a larger prediction time \(T_{\text {p}}\). But for different dynamical systems, \(T_{\text {p}}\) also depends on the system’s maximum Lyapunov exponent, where the Lyapunov time is usually used as the unit of \(T_{\text {p}}\).

(3) Auto-correlation prediction error \(E_{\text {a}}\) is defined as the time series auto-correlation coefficient prediction error between \({\varvec{y}}\) and \({\varvec{y}_ \text{Lorenz}}\). To measure the difference between the predicted time series and the original Lorenz system time series long-time evolution behavior of the two methods. The auto-correlation coefficients of the time series \(r_k(k=1,2,\ldots ,N)\) are calculated using the following equation: \(r_k=\frac{c_k}{c_0}\) with \(c_k=\frac{1}{T}\sum _{t=1}^{T-k}(x_t-\bar{x})(x_{t+k}-{\bar{x}})\) and \(c_0=\frac{1}{T}\sum _{t=1}^{T}(x_t-\bar{x})^2\). Here \(\{x_t\}\) represents a set of time series, T represents the length of the time series, and \(\{x_{t+k}\}\) represents the time series after delaying \(\{x_t\}\) by k steps, leading to

$$\begin{aligned} E_a=\frac{1}{N}\sum _{k=1}^N(r_{\text {Lorenz}_k}-r_k)^2. \end{aligned}$$
(20)

The training and prediction results of the two methods using the above four indexes for the white noise-driven system are shown in Fig. 4, where the two methods use the same data set for training, and the size of the training data is selected to be 15 million.

Fig. 4
figure 4

\(E_{\text {n}}\), \(E_{\text {t}}\), \(T_{\text {p}}\), \(E_{\text {a}}\) of the white noise-driven system by NG-RC10 and HOCC methods. The blue line represents the HOCC method, and the red line represents NG-RC10. (Color figure online)

Full size image

It can be seen that the two methods have very different performances in the four indicators. For training error \(E_{\text {n}}\), there two methods have similar performance, satisfying \(E_{\text {n}} = 10^{-5}\) approximately as shown in Fig. 4a, showing that both methods has reached the optimized result as they designed to get. However, such optimized results from these two methods are different, shown as by the prediction error \(E_{\text {t}}\) in Fig. 4b, especially when D is small. Here \(E_{\text {t}}\) of NG-RC10 is smaller than that of the HOCC method, the dynamical system from NG-RC10 is closer to the original Lorenz system than HOCC. This fact results in a longer prediction time \(T_{\text {p}}\) and smaller auto-correlation prediction error \(E_{\text {a}}\) of NG-RC10 in Fig. 4c, d, describing the better prediction ability for the short and long evolution of the system.

Compared with the HOCC method, we can conclude that the NG-RC method with the same function bases has a better noise resistance and prediction ability for white noise. This is from the learning limit of HOCC by large sampling intervals. Studying the mechanism of HOCC is out of the scope of this paper. But for the NG-RC method, it is sufficient to conclude a positive statement for its noise resistance to white noise. We will consider the NG-RC method with time-delay terms in the next section and obtain the same results.

3.2 Colored noise-driven system

The spectrum of noise is an important feature. The HOCC method has developed a full frame to deal with colored noise and shows a good noise resistance ability [37]. Here we take the Ornstein–Uhlenbeck noise and check the noise resistance of the NG-RC10 method with colored noise.

Similar to the analysis of white noise, we first reconstruct the parameters and check the reconstruction errors of HOCC and NG-RC10. The results are shown in Table 2. No matter how small the noise strength D is, the reconstruction errors of NG-RC10 are much larger than HOCC. As the variations of the reconstructed parameters are kept sufficiently small, one can conclude that the reconstructed parameters by NG-RC10 have systematic bias from the original dynamical systems. This error is removed by HOCC through differential-time correlation methods.

Table 2 When the colored noise-driven system is reconstructed, the standard deviation of the coefficients obtained by the two methods and the mean of the difference correspond to the original Lorenz system
Full size table

The training and prediction results of the two methods using the four numerical indicators for the colored noise-driven system are shown in Fig. 5, where the two methods use the same data set for training, and the size of the training data is selected to be 15 million. The optimization process of \(\alpha \) is shown in Supplementary Note 2. Similar to the white noise cases, \(E_{\text {n}}\) of the HOCC method and NG-RC10 are almost the same, but for the prediction error, \(E_{\text {t}}\) of the NG-RC10 method is always larger than \(E_{\text {t}}\) of HOCC. Consequently, HOCC has better prediction ability when dealing with the prediction time \(T_{\text {p}}\) and auto-correlation prediction error \(E_{\text {a}}\). However, it is interesting to note that when the noise strength is sufficiently small as \(D<0.01\), the NG-RC10 and HOCC have almost the same numerical indicators, showing the same prediction capacity, even the reconstructed parameters shown in Table 2 from NG-RC10 have a much larger error compared with the ones of HOCC.

Fig. 5
figure 5

\(E_{\text {n}}\), \(E_{\text {t}}\), \(T_{\text {p}}\), \(E_{\text {a}}\) of the colored noise-driven system by NG-RC10 and HOCC methods. The blue line represents the HOCC method, and the red line represents the NG-RC10. (Color figure online)

Full size image
Fig. 6
figure 6

Relation between \(E_{\text {t}}\) and \(\tau \) of NG-RC10 and HOCC method. The sampling interval is \(h=0.0002\), and the noise correlation length is \(\tau _d=25h\)

Full size image

The power of HOCC to deal with colored noise is from the time delay \(\tau \) in the differential-time correlations. When \(\tau \) is much larger than the correlation length \(\tau _d\) of the noise and much smaller than the characteristic time of the system dynamics, HOCC has a good noise resistance of colored noise [4, 17]. As shown in Fig. 6, the prediction error \(E_{\text {t}}\) decreases with the increase of \(\tau \) to a minimum value after \(\tau >100\). As for the NG-RC10 method, its prediction error \(E_{\text {t}}\) is the same as the HOCC with \(\tau =1\).

The NG-RC10 methods without the differential-time correlations could not reconstruct the original dynamics correctly, as it mixes the dynamics and noise correlations. However, if the noise strength is sufficiently small, the NG-RC10 method could give the same good prediction of the system’s evolution as the ones from the HOCC method, which has good reconstructed parameters. The mechanism of this phenomenon is an open question, and out of the scope of this paper. We will study it in our following work with various types of colored noise.

4 The NG-RC method with time-delay function bases

In the above section, NG-RC10 shows a good effect in antiwhite noise prediction and even performs better than the HOCC method when the sampling interval h is large. However, in colored noise resistance prediction, its noise resistance ability is worse than HOCC, especially when the noise strength D is large. In this section, we further consider the NG-RC method with all 28 function bases and explore the contributions of the additional time-delay terms.

It is worth noting that there are two parameters in the method: k and s. The linear part of the function bases of the method consists of the input vector at the current and at \(k-1\) previous times steps spaced by s, where \(s-1\) is the number of skipped steps between consecutive observations. For the noiseless Lorenz system, \(k=2\) and \(s=1\) are often used. Increasing k means adding more time-delay bases to the linear terms. And the s is similar to the \(\tau \) in the HOCC method, increasing s is to train with data that skip more observations between consecutive observations. This section will optimize both parameters.

4.1 White noise-driven system

To optimize parameters k and s to obtain the optimal prediction results, enough data was used for training. The \(E_{\text {t}}\) under different k and s are obtained by training 20 white noise-driven systems with different D. Figure 7 shows the result when \(D=0.1\).

Fig. 7
figure 7

Relationship between \(E_{\text {t}}\) and k or s of the white noise-driven system by NG-RC method with time-delay function bases. The parameters of the white noise-driven Lorenz system are \(h=0.0002\), \(D=0.1\)

Full size image

As shown in Fig. 7, \(E_{\text {t}}\) increase with the increase of k and s, indicating that increasing the number of time-delay bases in the basis function and using data after skipping more observations between consecutive observations for training are counterproductive to the noise resistance ability of the NG-RC method. Experiments on all the white noise-driven systems with different D show similar results. The k and s that make \(E_{\text {t}}\) reach the minimum are mostly \(k=2\) and \(s=1\), which are often used to predict the noiseless Lorenz system. With optimized parameters of k and s, the results of the four indexes are shown in Fig. 8. See Supplementary Note 3 for the optimization process of \(\alpha \).

Fig. 8
figure 8

\(E_{\text {t}}\),\(E_{\text {n}}\),\(T_{\text {p}}\),\(E_{\text {a}}\) of the white noise-driven system by NG-RC method with time-delay function bases and NG-RC10. The blue line represents the NG-RC method with time-delay function bases, and the red line represents NG-RC10. (Color figure online)

Full size image

Figure 8 shows the prediction results of NG-RC10 and NG-RC after optimized parameter in the white noise-driven system. The difference between NG-RC10 and NG-RC is small in all four numerical indicators. The NG-RC method with time-delay function bases has no significant effect on the prediction performance of the white noise-driven system. Hence both the NG-RC10 and NG-RC methods have a good white noise resistance.

4.2 Colored noise-driven system

As for the colored noise, the k and s are still optimized. Figure 9 shows the change of \(E_{\text {t}}\) with k and s when \(D=0.0001\). For different k, when \(s=1\), \(E_{\text {t}}\) is small, and then with the increase of s, \(E_{\text {t}}\) rapidly peaks, and then gradually decreases. The difference is that the \(E_{\text {t}}\) when \(k=2\) is always smaller than the \(E_{\text {t}}\) corresponding to other k, and presents a U-shaped change with s, and its lowest point is close to the position where \(E_{\text {t}}\) of HOCC method starts to stabilize when it changes with \(\tau \) in Fig. 6. It can be seen that the selection of appropriate k and s in the time-delay bases have a certain effect on the denoising of the NG-RC method. Figure 10 shows the results of four indexes of the NG-RC method optimized after k and s and the NG-RC method without time-delay bases. Each data point in the figure is the result of \(\alpha \) optimization, see Supplementary Note 4 for details.

Fig. 9
figure 9

Relationship between \(E_{\text {t}}\) and k or s of the colored noise-driven system by NG-RC method with time-delay function bases. The parameters of the colored noise-driven Lorenz system are \(h=0.0002\), \(D=0.0001\), and \(\tau _d=25h\)

Full size image
Fig. 10
figure 10

\(E_{\text {n}}\), \(E_{\text {t}}\), \(T_{\text {p}}\), \(E_{\text {a}}\) of the colored noise-driven system by NG-RC method with time-delay function bases and NG-RC10. The blue line represents the NG-RC method with time-delay function bases and the red line represents NG-RC10. (Color figure online)

Full size image

In Fig. 10a, \(E_{\text {n}}\) of the NG-RC method with time-delay bases is very similar to that of the NG-RC method without time-delay bases, indicating that they have similar fitting effects on training data. In Fig. 10b, the NG-RC method with time-delay bases is smaller than that without time-delay bases when the D is relatively large or small. Similarly, for \(T_{\text {p}}\) and \(E_{\text {a}}\) in Fig. 10c, d, except for several data points with moderate D, the \(T_{\text {p}}\) and \(E_{\text {a}}\) of other data points of the NG-RC method with time-delay bases are smaller than those of NG-RC method without time-delay bases. It can be seen from the above results that the resistance ability to colored noise of the NG-RC method optimized with k, s, and \(\alpha \) is improved compared with the NG-RC method without time-delay bases. However, compared with the HOCC method in Fig. 5, there is still a certain gap. Further improving the NG-RC’s resistance ability to colored noise is an open question and a promising approach.

5 Conclusions

In this paper, the noise resistance ability of the NG-RC method is studied from the theoretical as well as numerical experimental, with reference to the HOCC method. Various aspects of these two methods are compared, such as the reconstruction error of parameters, training error \(E_{\text {n}}\), prediction error \(E_{\text {t}}\), prediction time \(T_{\text {p}}\), and the auto-correlation prediction error \(E_{\text {a}}\). The similarity of the NG-RC and HOCC is shown theoretically, from which we study the NG-RC method without time-delay function bases. Such NG-RC10 method share the same function bases with HOCC. With different procedures and algorithms, we find that the NG-RC10 method has a better noise resistance when dealing with white noise than HOCC. Even for colored noise, the NG-RC10 method also shows a good prediction power when the noise strength is small, comparable with HOCC, while it cannot provides the correct reconstructed parameters.

The NG-RC method with time-delay function bases is also discussed. Such additional time-delay terms are helpful in the noise resistance of this method. The NG-RC method with and without time-delay function bases has the same noise resistance capacity for white noise. But for the colored noise, the NG-RC method with time-delay function bases works better by optimizing k and s in some conditions.

Reservoir computing methods, including the NG-RC method we discussed in this paper, is a promising study field of inverse problems of the dynamical system. In this paper, we show the simple ridge regression method in reservoir computing has a relatively strong noise resistance for white noise. But how to improve its noise resistance for colored noise is still an open question and a promising research topic.