Stability and Hopf bifurcation on an immunity delayed HBV/HCV model with intra- and extra-hepatic coinfection and saturation incidence

Abstract

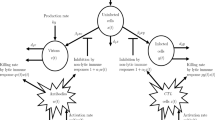
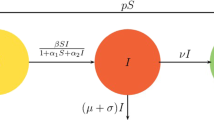
A hepatitis B or C virus (HBV or HCV) epidemic model with intra- and extra-hepatic coinfection, immune delay and saturation incidence, as well as antiviral therapy is proposed in this paper. The existence of equilibria (infection-free, immune-free and immune-activated), the basic reproduction numbers, i.e., $R_{0}$, $R_{1}$, are given respectively, by which the criteria on (local and global) stability of above equilibria are established. Furthermore, if the immune delay $\tau >\tau _{0}$, both the existence of subcritical (supercritical) Hopf bifurcation on the immune-activated equilibrium $E^{*}$, and the stability of bifurcating periodic solutions are obtained. Finally, the theoretical results are demonstrated by numerical simulations. We derive that the immune delay and intra- and extra-hepatic coinfection have significant influence on the transmission of HBV/HCV, could cause more complicated dynamics at $E^{*}$ from stability to unstablity untill bifurcation, which greatly increases the difficulty of disease control. While effective antiviral therapy could evidently decrease the spread of HBV/HCV.

Appendices

Appendix A: The details in Sect. 3.2

$$\begin{aligned} F_{1}=&a_{l}+d_{l}+a_{e}+d_{e}+r+\gamma +\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}},\\ F_{2}=&a_{e}\gamma +(a_{e}+\gamma )\Big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big ) +a_{l}\Big (a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big )\\&+ \Big (d_{l}+\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\Big )\Big (a_{l}+a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big ) \\&-k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{(1)}}{(1+\alpha V^{(1)})^{2}} -k_{e}(1-\epsilon ) \frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})^{2}},\\ F_{3}=&a_{e}\gamma \Big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big )+k_{e}(1-\epsilon ) \frac{\beta _{e}^{2}T_{e}^{(1)}V^{(1)}}{(1+\alpha V^{(1)})^{3}}\\&+a_{l}\Big (a_{e}\gamma + (a_{e}+\gamma )\big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\big )\Big )\\&+ \Big (d_{l}+\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\Big )\Big ((a_{e}+\gamma )\big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{ (1)}}) +a_{l}\big (a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\big )+a_{e}\gamma \Big ) \\&+k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{l}^{*}V^{(1)}}{(1+\alpha V^{(1)})^{3}}-\Big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}+a_{l}\Big ) k_{e}(1-\epsilon ) \frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})^{2}} \\&-k_{l}(1-\epsilon ) \frac{\beta _{l}T_{l}^{(1)}}{(1+\alpha V^{(1)})^{2}}\Big (d_{e}+a_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big )\\&-\Big (d_{l}+\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\Big )\Big (k_{l}(1-\epsilon ) \frac{\beta _{l}T_{l}^{(1)}}{(1+\alpha V^{(1)})^{2}}\\&+k_{e}(1-\epsilon ) \frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})^{2}}\Big ),\\ F_{4}=&a_{l}\Big (\big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\big )a_{e}\gamma + k_{e}(1-\epsilon ) \frac{\beta _{e}^{2}T_{e}^{(1)}V^{(1)}}{(1+\alpha V^{(1)})^{3}}\Big )\\&+k_{l}(1-\epsilon ) \frac{\beta _{l}^{2}T_{l}^{(1)}V^{(1)}}{(1+\alpha V^{(1)})^{3}}\Big (d_{e}+a_{e}\\&+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big )+\Big (d_{l}+\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\Big ) \Big (a_{e}\gamma \big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\big )+ k_{e}(1-\epsilon ) \frac{\beta _{e}^{2}T_{e}^{(1)}V^{(1)}}{(1+\alpha V^{(1)})^{3}}\\&+\big (a_{e}\gamma +(a_{e}+\gamma ) \big (\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}+d_{e}\big )\big )a_{l}\Big )-a_{l}k_{e}(1-\epsilon ) \frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})^{2}}\\&\Big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big ) -a_{e}k_{l}(1-\epsilon ) \frac{\beta _{l}T_{l}^{(1)}}{(1+\alpha V^{(1)})^{2}} \Big (\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}+d_{e}\Big )-\Big (\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\\&+d_{l}\Big )\Big (\frac{k_{e}(1-\epsilon )\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})^{2}} \big (d_{e}+a_{l}+\frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})}\big )+k_{l}(1-\epsilon ) \frac{\beta _{l}T_{l}^{(1)}}{(1+\alpha V^{(1)})^{2}}\big (d_{e}+a_{e}+\frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})}\big )\Big ),\\ F_{5}=&a_{l}\Big (d_{l}+\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\Big )\Big (a_{e}\gamma \big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\big )+ k_{e}(1-\epsilon )\frac{\beta _{e}^{2}T_{e}^{(1)}V^{(1)}}{(1+\alpha V^{(1)})^{3}}\Big )+\Big (\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\\&+d_{e}\Big )a_{e}k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{l}^{(1)}V^{(1)}}{(1+\alpha V^{(1)})^{3}}-\Big (d_{l}+\frac{\beta _{l}V^{(1)}}{1+\alpha V^{(1)}}\Big ) \Big (d_{e}+\frac{\beta _{e}V^{(1)}}{1+\alpha V^{(1)}}\Big )\\&\Big (a_{l}k_{e}(1-\epsilon ) \frac{\beta _{e}T_{e}^{(1)}}{(1+\alpha V^{(1)})^{2}}+a_{e}k_{l}(1-\epsilon ) \frac{\beta _{l}T_{l}^{(1)}}{(1+\alpha V^{(1)})^{2}}\Big ). \end{aligned}$$

Appendix B: The details in Sect. 3.3

$$\begin{aligned}&A_{1}=a_{l}+d_{l}+a_{e}+d_{e}+r+\gamma +pZ^{*}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}},\\&A_{2}=r\Big (a_{l}+d_{l}+a_{e}+d_{e}+\gamma +pZ^{*}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )+\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )(a_{e}+\gamma ) \\&\quad +(a_{l}+pZ^{*})\Big (a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\\&\quad -k_{e}(1-\epsilon )\frac{\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}-k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big (a_{e}+d_{e}+a_{l}+\gamma +pZ^{*}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )+a_{e}\gamma ,\\&A_{3}=r\Big [a_{e}\gamma +\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )(a_{e}+\gamma )+\Big (a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )(a_{l}+pZ^{*})+\Big (d_{l}\\&\quad +\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \Big (a_{e}+d_{e}+a_{l}+\gamma +pZ^{*}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\Big ]+\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )a_{e}\gamma \\&\quad +k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}} +(a_{l}+pZ^{*})\Big (a_{e}\gamma +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )(a_{e}+\gamma )\Big )+\Big (d_{l}\\&\quad +\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big [\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )(a_{e}+\gamma )+a_{e}\gamma +(a_{l}+pZ^{*})\\&\quad \Big (a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\Big ]\\&\quad -\Big (d_{e}+a_{l}+r+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}} +pZ^{*} +\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}+d_{l}\Big )k_{e}(1-\epsilon )\frac{\beta _{e}T_{e}}{(1+\alpha V^{*})^{2}}\\&\quad -\Big (r+d_{e}+a_{e}+d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}}{(1+\alpha V^{*})^{2}},\\&A_{4}=r\Big [\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) a_{e}\gamma +(a_{l}+pZ^{*})\Big (a_{e}\gamma \\&\quad +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )(a_{e}+\gamma )\Big )+\Big (\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\\&\quad +d_{l}\Big )\Big ((a_{l}+pZ^{*})\big (a_{e}+d_{e}+\gamma +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )+a_{e}\gamma +\big (d_{e}\\&\quad +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )(a_{e}+\gamma )\Big ) +k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big ]+k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{1}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big (a_{e}\\&\quad +d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )+\Big (\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\\&\quad +d_{l}\Big )a_{e}\gamma \Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) + \frac{k_{e}(1-\epsilon )\beta _{e}^{2}T_{2}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\\&\quad +(a_{l}+pZ^{*}) \Big (a_{e}\gamma +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )\\&\quad (a_{e}+\gamma )\Big )-r\Big [\Big (d_{e}+a_{e}+d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\\&\quad +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}} +\Big (\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\\&\quad +d_{e}+a_{l}+pZ^{*}+d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \frac{k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\Big ]\\&\quad -(a_{l}+pZ^{*}) \frac{k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )-a_{e}\Big (d_{e}\\&\quad +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )k_{l}(1-\epsilon )\frac{\beta _{l}T_{1}^{*}}{(1+\alpha V^{*})^{2}}-\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \Big [\Big (a_{l}+d_{e}\\&\quad +pZ^{*}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) \frac{k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +\Big (a_{e}+d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) \frac{k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big ], \end{aligned}$$

$$\begin{aligned}&A_{5}=r\Big [(a_{l}+pZ^{*})\Big (\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) a_{e}\gamma +k_{e}(1-\epsilon )\frac{\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big )\\&\quad +\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big (a_{e}\gamma \\&\quad \big (\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}+d_{e}\big )+\frac{k_{e}(1-\epsilon ) \beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}+(a_{l}+pZ^{*})\\&\quad \big (a_{e}\gamma +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )(a_{e}+\gamma )\big )\Big )\\&\quad +k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\big (a_{e}+d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )\Big ]+\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) (a_{l}+pZ^{*}) \Big (a_{e}\gamma \big (d_{e}\\&\quad +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )+k_{e}(1-\epsilon )\frac{\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big )+a_{e}\Big (d_{e}\\&\quad +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) k_{l}(1-\epsilon )\frac{\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\\&\quad -ra_{e}(d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}) k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +(a_{l}+pZ^{*})\frac{ k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\Big (\frac{\beta _{e}V^{*}}{1+\alpha V^{*}} \\&\quad +d_{e}\Big )+\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big ( k_{e}(1-\epsilon )\frac{\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}} \\&\quad \big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}+a_{l}+pZ^{*}\big )\\&\quad +\big (a_{e}+d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big )-\Big (d_{l}\\&\quad +\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big ( \big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )\\&\quad (a_{l}+pZ^{*}) k_{e}(1-\epsilon )\frac{\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}+a_{e}\big (d_{e}\\&\quad +\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big ),\\&A_{6}=r\Big [\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )(a_{l}+pZ^{*}) \Big (\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )a_{e}\gamma \\&\quad + k_{e}(1-\epsilon ) \frac{\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{2}}\Big )\\&\quad + a_{e}\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )k_{l}(1-\epsilon )\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big ]\\&\quad -r \Big [a_{e}\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\frac{ k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )(a_{l}+pZ^{*})\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) k_{e}(1-\epsilon )\frac{\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\Big ], \end{aligned}$$

$$\begin{aligned}&B_{1}=-qI_{l}^{*},\\&B_{2}=qZ^{*}pI_{l}^{*}-qI_{l}^{*}\Big (a_{l}+d_{l}+a_{e}+d_{e}+\gamma +pZ^{*}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}+ \frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ),\\&B_{3}=qZ^{*}pI_{l}^{*}\Big (a_{e}+d_{e}+\gamma +d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}+ \frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\\&\quad +qI_{l}^{*}\Big (k_{e}(1-\epsilon )\frac{\beta _{e}T_{2}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +\frac{k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big ) -qI_{l}^{*}\Big [a_{e}\gamma \\&\quad +\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )(a_{e}+\gamma ) +(a_{l}+pZ^{*})\Big (a_{e}+\gamma \\&\quad +d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )+\Big (a_{e}+\gamma +d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\\&\quad +a_{l}+pZ^{*}\Big )\Big (d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big ],\\&B_{4}=qZ^{*}pI_{l}^{*}\Big [a_{e}\gamma +\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) (a_{e}+\gamma )+\Big (d_{l}\\&\quad +\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big (a_{e}+\gamma + d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\Big ]\\&\quad +qI_{l}^{*}\Big [\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}+a_{l}+pZ^{*}+ d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\\&\quad \frac{ k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}+\Big (a_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\\&\quad +d_{e}+d_{l}+\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \frac{k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big ]-qZ^{*}pI_{l}^{*}\\&\quad \frac{k_{e}(1-\epsilon )\beta _{e}T_{2}^{*}}{(1+\alpha V^{*})^{2}}-qI_{l}^{*}\Big [\Big (\frac{\beta _{e}V^{*}}{1+\alpha V^{*}} \\&+d_{e}\Big )a_{e}\gamma +\frac{ k_{e}(1-\epsilon ) \beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}} +\Big (a_{e}\gamma +(d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}})(a_{e}+\gamma )\Big )(a_{l}+pZ^{*})\\&+\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \Big (a_{e}\gamma +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )(a_{e}+\gamma )+ (a_{l}+pZ^{*})\big (a_{e}+\gamma +d_{e}\\&+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )\Big )+ \frac{k_{l}(1-\epsilon )\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big ], \end{aligned}$$

$$\begin{aligned}&B_{5}=qZ^{*}pI_{l}^{*}\Big [a_{e}\gamma \Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big ) +\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\\&\quad \Big (a_{e}\gamma +(a_{e}+\gamma )\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )\Big )\Big ]\\&\quad +qI_{l}^{*}\Big [(a_{l}+pZ^{*})\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\frac{k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +a_{e}\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\frac{k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big (\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}a_{l}+pZ^{*}\big )\\&\quad \frac{k_{e}(1-\epsilon )\beta _{e}T_{2}^{*}}{(1+\alpha V^{*})^{2}}+\big (a_{e}+d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) \\&\quad \frac{k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big )\Big ]-qZ^{*}pI_{l}^{*}\Big [\Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}+ d_{l}\\&\quad + \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) k_{e}(1-\epsilon )\frac{\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad + \frac{k_{e}(1-\epsilon )\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big ]-qI_{l}^{*}\Big [(a_{l}+pZ^{*})\\&\quad \Big (\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) a_{e}\gamma +\frac{k_{e}(1-\epsilon )\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big ) \\&\quad +\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )\Big ((d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}) a_{e}\gamma \\&\quad +(a_{l}+pZ^{*})\big (a_{e}\gamma +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )(a_{e}+\gamma )\big ) \\&\quad +\frac{k_{e}(1-\epsilon )\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big ) + \frac{k_{l}(1-\epsilon )\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\\&\quad \Big (a_{e}+d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\Big ],\\&B_{6}=qZ^{*}pI_{l}^{*}\Big [\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \Big ( \big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )a_{e}\gamma \\&\quad + \frac{k_{e}(1-\epsilon )\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big )\Big ]+qI_{l}^{*}\Big [\Big (\frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\\&\quad +d_{l} \Big ) \Big ((a_{l}+pZ^{*})\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) \frac{k_{e}(1-\epsilon )\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}\\&\quad +\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big )a_{e} \frac{k_{l}(1-\epsilon )\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}}\Big )\Big ]\\&\quad -q^{*}ZpI_{l}^{*}\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big ) \Big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )\\&\quad \frac{k_{e}(1-\epsilon )\beta _{e}I_{e}^{*}}{(1+\alpha V^{*})^{2}}-qI_{l}^{*}\Big [\frac{a_{e}k_{l}(1-\epsilon )\beta _{l}^{2}T_{l}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big (d_{e} \\&+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\Big )+\Big (d_{l}+ \frac{\beta _{l}V^{*}}{1+\alpha V^{*}}\Big )(a_{l}+pZ^{*})\\&\quad \Big (\big (d_{e}+\frac{\beta _{e}V^{*}}{1+\alpha V^{*}}\big ) a_{e}\gamma +\frac{k_{e}(1-\epsilon )\beta _{e}^{2}T_{e}^{*}V^{*}}{(1+\alpha V^{*})^{3}}\Big )\Big ]. \end{aligned}$$

Appendix C: The details in Sect. 5.1

$$\begin{aligned} C_{1}=&B_{2}-A_{1}B_{1};C_{2}=A_{1}B_{3}+B_{1}A_{3}-B_{2}A_{2}-B_{4};\\ C_{3}=&A_{2}B_{4}+B_{2}A_{4}+B_{4}-A_{1}B_{5}\\&-A_{3}B_{3}-A_{5}B_{1}; C_{4}=A_{3}B_{5}+A_{5}B_{3}-A_{2}B_{6}-A_{6}B_{2}-A_{4}B_{4};\\ C_{5}=&A_{4}B_{6}+A_{6}B_{4} -A_{5}B_{5}; C_{6}=A_{6}B_{6}.\\ D_{1}=&B_{1}; D_{2}=B_{2}A_{1}-A_{2}B_{1}-B_{3};\\ D_{3}=&A_{4}B_{1}+A_{2}B_{3}+B_{5}-A_{2}B_{3}-A_{1}B_{4};\\ D_{4}=&A_{5}B_{2} +A_{1}B_{6}+A_{3}B_{4}-A_{6}B_{1}-A_{4}B_{3}-A_{2}B_{5};\\ D_{5}=&A_{6}B_{3}+A_{4}B_{5}-A_{3}B_{6}-A_{5}B_{4};\\ D_{5}=&A_{5}B_{6}-A_{6}B_{5}.\\ S_{1}=&B_{1}^{2};S_{2}=B_{2}^{2}-2B_{1}B_{3};S_{3}=B_{3}^{2}+2B_{1}B_{5}-2B_{2}B_{4};\\ S_{4}=&B_{4}^{2}+2B_{2}B_{6}-2B_{3}B_{5};\\ S_{5}=&B_{5}^{2}-2B_{4}B_{6};S_{6}=B_{6}^{2}.\\ h_{1}=&A_{1}^{2}-2A_{2}-B_{1}^{2}; h_{2}=A_{2}^{2}+2A_{4}-2A_{1}A_{3}+2B_{1}B_{3}-B_{2}^{2};\\ h_{3}=&2A_{1}A_{5}+A_{3}^{2}-2A_{6}\\&-2A_{2}A_{4}-2B_{1}B_{5}-B_{3}^{2}+2B_{2}B_{4}; \\ h_{4}=&A_{4}^{2}+2A_{2}A_{6}-2A_{3}A_{5}-B_{4}^{2}-2B_{2}B_{6}+2B_{3}B_{5}; \\ h_{5}=&A_{1}^{2}-2A_{4}A_{6}-B_{5}^{2}+2B_{4}B_{6}; h_{6}=A_{6}^{2}-B_{6}^{2}. \end{aligned}$$

Appendix D: The details in Sect. 6

We have obtained that the model (6) experiences Hopf bifurcation at the equilibrium $E^{*}$ for $\tau =\tau _{0}$, and $\pm i\omega _{0}$ is the pure imaginary root corresponding to the characteristic equation at $E^{*}$.

Let $\widetilde{T_{l}}(t)=T_{l}(t)-T_{l}^{*}$, $\widetilde{I_{l}}(t)=I_{l}(t)-I_{l}^{*}$, $\widetilde{T_{e}}(t)=T_{e}(t)-T_{e}^{*}$, $\widetilde{I_{e}}(t)=I_{e}(t)-I_{e}^{*}$, $\widetilde{V}(t)=V(t)-V^{*}$, $\widetilde{Z}(t)=Z(t)-Z^{*}$, and replace $\widetilde{T_{l}}$, $\widetilde{I_{l}}$, $\widetilde{T_{e}}$, $\widetilde{I_{e}}$, $\widetilde{V}$, $\widetilde{Z}$, with $T_{l}$, $I_{l}$, $T_{e}$, $I_{e}$, V, Z.

Then we define $\tau =\tau _{0}+\mu$, $t=s\tau$, $T_{l}(s\tau )=\overline{T_{l}}(s)$, $I_{l}(s\tau )=\overline{I_{l}}(s)$, $T_{e}(s\tau )=\overline{T_{e}}(s)$, $I_{e}(s\tau )=\overline{I_{e}}(s)$, $V(s\tau )=\overline{V}(s)$, $Z(s\tau )=\overline{Z}(s)$, and still denote $\overline{T_{l}}$, $\overline{I_{l}}$, $\overline{T_{e}}$, $\overline{I_{e}}$, $\overline{V}$, $\overline{Z}$ as $T_{l}$, $I_{l}$, $T_{e}$, $I_{e}$, V, Z. The linear term at the right of the transformed model is sorted out through calculation is (D1),

$$\begin{aligned} \left\{ \begin{aligned} \dot{T_{l}}(t)&=(\tau _{0}+\mu )[-d_{l}T_{l}(t)-Q_{1}T_{l}(t)-Q_{2}V(t)],\\ \dot{I_{l}}(t)&=(\tau _{0}+\mu )[ Q_{1}T_{l}(t)-Q_{2}V(t) -a_{l}I_{l}(t) -pI_{l}(t)Z^{*}-pZ(t)I_{l}^{*}],\\ \dot{T_{e}}(t)&=(\tau _{0}+\mu )[-Q_{3}T_{e}(t)-Q_{4}V(t)-d_{e}T_{e}(t)],\\ \dot{I_{e}}(t)&=(\tau _{0}+\mu )[-Q_{3}T_{e}(t)+Q_{4}V(t)- a_{e}I_{e}(t)],\\ \dot{V}(t)&=(\tau _{0}+\mu )[k_{l}(1-\epsilon )I_{l}(t)+k_{e}(1-\epsilon )I_{e}(t)-\gamma V(t)],\\ \dot{Z}(t)&=(\tau _{0}+\mu )[qZ^{*}I_{l}(t-1)+qI_{l}^{*}Z(t-1)-rZ(t)], \end{aligned} \right. \end{aligned}$$

(D1)

where

$$\begin{aligned} Q_{1}&=\frac{\beta _{l}V^{*}}{1+\alpha V^{*}},\\ Q_{2}&=\frac{\beta _{l}T_{l}^{*}}{(1+\alpha V^{*})^{2}},\\ Q_{3}&=\frac{\beta _{e}V^{*}}{1+\alpha V^{*}},\\ Q_{4}&=\frac{\beta _{e}T_{e}^{*}}{(1+\alpha V^{*})^{2}}. \end{aligned}$$

And the nonlinear term at the right of the transformed model is (D2),

$$\begin{aligned} f(\mu , \mu _{t})=(\tau _{0}+\mu ) \left[ \begin{aligned}&K_{1}T_{l_{t}}(0)V_{_{t}}(0)+K_{2}V_{_{t}}(0)V_{_{t}}(0)+\cdots \\&K_{1}T_{l_{t}}(0)V_{_{t}}(0)+K_{2}V_{_{t}}(0)V_{_{t}}(0)-pI_{l_{t}}(0)Z_{_{t}}(0)+\cdots \\&P_{1}T_{e_{t}}(0)V_{_{t}}(0)+P_{2}V_{_{t}}(0)V_{_{t}}(0)+\cdots \\&P_{1}T_{e_{t}}(0)V_{_{t}}(0)+P_{2}V_{_{t}}(0)V_{_{t}}(0)+\cdots \\&0\\&qI_{l_{t}}(-1)V_{_{t}}(-1) \end{aligned} \right] , \end{aligned}$$

(D2)

where

$$\begin{aligned} K_{1}=\frac{\beta _{l}}{(1+\alpha V^{*})^{2}}, K_{2}=\frac{\beta _{l}T_{l}^{*}\alpha }{2(1+\alpha V^{*})^{2}}, P_{1}=\frac{\beta _{e}}{(1+\alpha V^{*})^{2}}, P_{2}=\frac{\beta _{e}T_{e}^{*}\alpha }{2(1+\alpha V^{*})^{2}}, \end{aligned}$$

and

$$\begin{aligned} \mu _{t}(\theta )= \left[ \begin{array}{cccccc} &{}T_{l_{t}}(\theta )\\ &{}I_{l_{t}}(\theta )\\ &{}T_{e_{t}}(\theta )\\ &{}I_{e_{t}}(\theta )\\ &{}V_{_{t}}(\theta )\\ &{}Z_{_{t}}(\theta ) \end{array} \right] = \left[ \begin{array}{cccccc} T_{l_{t}}(t+\theta )\\ I_{l_{t}}(t+\theta )\\ T_{e_{t}}(t+\theta )\\ I_{e_{t}}(t+\theta )\\ V_{_{t}}(t+\theta )\\ Z_{_{t}}(t+\theta ) \end{array} \right] , \theta \in [-1, 0]. \end{aligned}$$

Then the model (6) could be written as a functional differential equation in $C =C([-1, 0],\ R_{+}^{6})$.

For $\phi (\theta )=(\phi _{1}(\theta ), \phi _{2}(\theta ), \phi _{3}(\theta ), \phi _{4}(\theta ), \phi _{5}(\theta ), \phi _{6}(\theta ))^{T}\in C$, define operator $L_{\mu }\phi =(\tau _{0}+\mu )\mathbb {M}_{1}\phi (0)+(\tau _{0}+\mu )\mathbb {M}_{2}\phi (-1)$, where

$$\begin{aligned} \mathbb {M}_{1}= & {} \left( \begin{array}{cccccc} -d_{l}-Q_{1} &{} 0 &{} 0 &{} 0 &{} -Q_{2} &{}0 \\ Q_{1} &{} -a_{l}-pZ^{*} &{} 0 &{} 0 &{} Q_{2} &{} -pI_{l}^{*}\\ 0 &{} 0 &{} -Q_{3}-d_{e} &{} 0 &{} -Q_{4} &{} 0\\ 0 &{} 0 &{} Q_{3} &{}-a_{e} &{} Q_{4} &{} 0\\ 0 &{}k_{l}(1-\epsilon ) &{} 0 &{}k_{e}(1-\epsilon ) &{}-\gamma &{} 0\\ 0 &{}0 &{} 0 &{}0 &{} 0 &{}-r\\ \end{array}\right) ,\\ \mathbb {M}_{2}= & {} \left( \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 0\\ 0 &{}0 &{} 0 &{}0 &{}0 &{} 0\\ 0 &{}qZ^{*} &{} 0 &{}0 &{} 0 &{}qI_{l}^{*} \end{array} \right) . \end{aligned}$$

According to the Riesz representation theorem, there is a matrix value function $\eta (\theta , \mu ):[-1, 0]\rightarrow R^{6}$, such that

$$\begin{aligned} \eta (\theta )\in C([-1, 0],\ R_{+}^{6}), \end{aligned}$$

then we have

$$\begin{aligned} \begin{aligned} L_{\mu }\phi =\int ^{0}_{-1}d\eta (\theta , \mu )\phi (\theta ). \end{aligned} \end{aligned}$$

(D3)

For $\phi \in C([-1, 0],\ R_{+}^{6})$, we define

$$\begin{aligned} A(\mu )\phi = \left\{ \begin{aligned}&\frac{d\phi }{d\theta },~\theta \in [-1,0), \\&\int ^{0}_{-1}d\eta (\mu , s)\phi (s),~\theta =0, \end{aligned} \right. \end{aligned}$$

(D4)

and

$$\begin{aligned} R(\mu )(\phi )= \left\{ \begin{aligned}&0,~\theta \in [-1,0), \\&f(\mu , \phi ),~\theta =0. \end{aligned} \right. \end{aligned}$$

(D5)

Therefore, model (6) is equivalent to abstract differential equation (D6)

$$\begin{aligned} \begin{aligned} \dot{\mu _{t}}=A(\mu )\mu _{t}+R(\mu )\mu _{t}. \end{aligned} \end{aligned}$$

(D6)

Next, we can discuss the Eq. (D6).

For $\varphi \in C^{1}([0,1], (R^{6})^{*})$, we can define the adjoint operator,

$$\begin{aligned} A^{*}\varphi (s)= \left\{ \begin{aligned}&-\frac{d\varphi }{ds},~s\in (0,1], \\&\int ^{0}_{-1}d\eta ^{T}(t, 0)\phi (-t),~s=0, \end{aligned} \right. \end{aligned}$$

(D7)

and define the bilinear inner product as (D8)

$$\begin{aligned} \begin{aligned} \langle \varphi (s),\phi (s)\rangle =\bar{\varphi }(0)\phi (0)-\int ^{0}_{-1}\int ^{\theta }_{\xi =0} \bar{\varphi }(\xi -\theta )d\eta (\theta )\phi (\xi )d\xi , \end{aligned} \end{aligned}$$

(D8)

where $\eta (\theta )=\eta (\theta ,0)$, and the conjugate operator of $A(\mu )$ is $A^{*}$. Based on the above discussion, $\pm i\omega _{0}\tau _{0}$ is the eigenvalue of A(0) and $A^{*}$. Then we will calculate the eigenvectors of A and $A^{*}$ about $i\omega _{0}\tau _{0}$ and $-i\omega _{0}\tau _{0}$.

Suppose that $q(\theta )$ and $q^{*}(s)$ are the eigenvectors of $A(\mu _{0})$ and $A^{*}$ corresponding to $i\omega _{0}\tau _{0}$ and $-i\omega _{0}\tau _{0}$ respectively, and $\langle q^{*}(s), q(\theta )\rangle =1$.

When $\theta \ne 0$, according to the definition of A(0), easily that $q(\theta )=q(0)e^{i\tau _{0}\omega _{0}\theta }$ and q(0) satisfies the following equation,

$$\begin{aligned} (\int ^{0}_{-1}d\eta (0,s)e^{i\tau _{0}\omega _{0}\theta }-i\tau _{0}\omega _{0}I)q(0)=0, \end{aligned}$$

where I is the identity matrix, and $q(0)=(q_{1}, q_{2}, q_{3}, q_{4}, q_{5}, q_{6})^{T}$, calculation shows that

$$\begin{aligned} \left\{ \begin{aligned}&q_{1}=1, q_{2}=\frac{\tau _{0}k_{e}(1-\epsilon )q_{4}-(\tau _{0}\gamma +i\tau _{0} \omega _{0})q_{5}}{\tau _{0}k_{l}(1-\epsilon )}, q_{3}=-\frac{\tau _{0}Q_{4}q_{5}}{\tau _{0}M_{2}+i\tau _{0} \omega _{0}}, \\&q_{4}=\frac{\tau _{0}Q_{3}q_{3}+\tau _{0}Q_{4}q_{5}}{\tau _{0}a_{e}+i\tau _{0} \omega _{0}}, q_{5}=-\frac{\tau _{0}M_{1}+i\tau _{0}\omega _{0}}{ \tau _{0} Q_{2}}, q_{6}=\frac{qZ^{*} \tau _{0} e^{i\tau _{0}\omega _{0}}q_{2}}{\tau _{0}r+i\tau _{0} \omega _{0}-qI_{l}^{*} \tau _{0} e^{i\tau _{0}\omega _{0}}}, \end{aligned} \right. \end{aligned}$$

where $M_{1}=Q_{1}+d_{l}$, $M_{2}=Q_{3}+d_{e}$. Similarly, $q^{*}$ satisfies the following equation

$$\begin{aligned} (i\tau _{0}\omega _{0}I + \int ^{0}_{-1}d\eta ^{T}(0,s)e^{-i\tau _{0}\omega _{0}\theta })q^{*}=0, \end{aligned}$$

we can further get

$$\begin{aligned} \left\{ \begin{aligned}&q_{1}^{*}=1, q_{2}^{*}=\frac{\tau _{0}M_{1}-i\tau _{0}\omega _{0}}{Q_{1}}, q_{3}^{*}=-\frac{ Q_{4}q_{5}^{*}}{\tau _{0}M_{2}-i\tau _{0}\omega _{0}}, q_{4}^{*}=\frac{k_{e}(1-\epsilon )q_{5}^{*}}{\tau _{0}a_{e}-i\tau _{0} \omega _{0}},\\&q_{5}^{*}=\frac{[-\tau _{0}(a_{l}+pZ^{*})+i\tau _{0}\omega _{0}]q_{2}^{*}+qZ^{*}e^{i\tau _{0}\omega _{0}} q_{6}^{*}}{ k_{l}(1-\epsilon )}, q_{6}^{*}=\frac{pI_{l}^{*}(\tau _{0}M_{1}-i\tau _{0} \omega _{0})}{Q_{1}(qI_{l}^{*}e^{i\tau _{0}\omega _{0}}+i\omega _{0}) }. \end{aligned} \right. \end{aligned}$$

Let $q^{*}(s)=Dq^{*}e^{i\tau _{0}\omega _{0}s}$, we demand to use $\langle q^{*}(s), q(\theta )\rangle =1$ to determine the formula of D,

$$\begin{aligned} \langle q^{*}(s), q(\theta )\rangle =\overline{D}[\overline{q^{*}}^{T}q(0)-\overline{q^{*}}^{T}\tau _{0}\mathbb {M}_{2} e^{i\tau _{0}\omega _{0}}q(0)]. \end{aligned}$$

Thus, we can choose D as

$$\begin{aligned} D=\frac{1}{(1+q_{2}^{*}\overline{q}_{2}+q_{3}^{*}\overline{q}_{3}+q_{4}^{*}\overline{q}_{4}+q_{5}^{*}\overline{q}_{5} +q_{6}^{*}\overline{q}_{6})+qq_{6}^{*}\tau _{0}e^{i\tau _{0}\omega _{0}}(Z^{*}\overline{q}_{2}+I_{l}^{*}\overline{q}_{6})}, \end{aligned}$$

at the same time, we can easily obtain $\langle q^{*}(s),\overline{q}(\theta )\rangle =0$.

According to the algorithm in [52] and the similar discussion in [45], we can calculate the corresponding coefficients,

$$\begin{aligned} \begin{aligned} g_{20}=&2\overline{D}\tau _{0}\big \{(\overline{q^{*}_{1}}+\overline{q^{*}_{2}})(K_{1}q_{1}q_{5}+ K_{2}q^{*}_{5})+(\overline{q^{*}_{3}}+\overline{q^{*}_{4}})(P_{1}q_{3}q_{5}+P_{2}q_{5}^{2})\\ {}&-q_{2}q_{6}(\overline{q^{*}_{2}}p +\overline{q^{*}_{6}}qe^{-2i\tau _{0}\omega _{0}}) \big \},\\ g_{02}=&2\overline{D}\tau _{0}\big \{(\overline{q^{*}_{1}}+\overline{q^{*}_{2}})(K_{1}\overline{q}_{1} \overline{q}_{5}+ K_{2}\overline{q}_{5}^{2})+(\overline{q^{*}_{3}}+\overline{q^{*}_{4}})(P_{1} \overline{q}_{3}\overline{q}_{5}+\overline{q}_{3}\overline{q}_{5})\\&+\overline{q^{*}_{6}}q\overline{q}_{2}\overline{q}_{6} e^{2i\tau _{0}\omega _{0}}\big \},\\ g_{11}=&\overline{D}\tau _{0}\big \{(\overline{q^{*}_{1}}+\overline{q^{*}_{2}})[K_{1}(q_{1}\overline{q}_{5} +q_{5}\overline{q}_{1})+2K_{2}q_{5}\overline{q}_{5}]+(\overline{q^{*}_{3}}+\overline{q^{*}_{4}})[ 2P_{2}\overline{q}_{5}\overline{q^{*}_{5}}\\&+P_{1} (q_{3}\overline{q}_{5}+q_{5}\overline{q}_{3})]-(p\overline{q^{*}_{2}}-q\overline{q^{*}_{6}}) (q_{2}\overline{q}_{6}+ q_{6}\overline{q}_{2})\big \},\\ g_{21}=&\overline{D}\tau _{0}\big \{(\overline{q^{*}_{1}}+\overline{q^{*}_{2}})[2K_{1}(q_{5} W^{(1)}_{11}(0)+q_{1}W^{(5)}_{11}(0))+4K_{2}q_{5}W^{(5)}_{11}(0)\\&+K_{1}(W^{(1)}_{20}(0)\overline{q}_{5} +\overline{q}_{1}W^{(5)}_{20}(0))+2K_{2}\overline{q}_{5}W^{(5)}_{20}(0)]+ (\overline{q^{*}_{3}}+\overline{q^{*}_{4}})\\&[2P_{1}(W^{(3)}_{20}(0)q_{5}+ W^{(5)}_{11}(0)q_{3})+4P_{2}q_{5}W^{(5)}_{11}(0)+P_{1}(W^{(3)}_{20}(0)\overline{q}_{5} \\ {}&+\overline{q}_{3}W^{(5)}_{20}(0))+2P_{2}\overline{q}_{5}W^{(5)}_{20}(0)]+2\overline{q^{*}_{6}}q e^{-i\tau _{0}\omega _{0}}(q_{2}W^{(6)}_{11}(-1)\\&+q_{6}W^{(2)}_{11}(-1))+ \overline{q^{*}_{6}}q e^{ i\tau _{0}\omega _{0}}(\overline{q}_{2} W^{(6)}_{20}(-1)+\overline{q}_{6} W^{(2)}_{20}(-1))\big \}. \end{aligned} \end{aligned}$$

Further, we solve the expressions of $W_{20}(\theta )$ and $W_{11}(\theta )$,

$$\begin{aligned} \begin{aligned} W_{20}(\theta )&=\frac{ig_{20}}{\tau _{0}\omega _{0}}q(0)e^{i\tau _{0}\omega _{0}\theta }+\frac{i \overline{g}_{02}}{3\tau _{0}\omega _{0}}\\&\quad \overline{q}(0)e^{-i\tau _{0}\omega _{0}\theta }+ E_{1}e^{2i\tau _{0}\omega _{0}\theta },\\ W_{11}(\theta )&=\frac{ig_{11}}{\tau _{0}\omega _{0}}q(0)e^{i\tau _{0}\omega _{0}\theta }\\&\quad +\frac{i \overline{g}_{11}}{\tau _{0}\omega _{0}}\overline{q}(0)e^{-i\tau _{0}\omega _{0}\theta }+E_{2}, \end{aligned} \end{aligned}$$

and $E_{1}$ $E_{2}$ can be calculated as follows,

$$\begin{aligned} \begin{aligned} E_{1}&=\Big [2i\tau _{0}\omega _{0}I-\int ^{0}_{-1}d_{\theta }\eta (\mu _{0}, \theta )\Big ]^{-1}H_{20}(0), \\ E_{2}&=-\Big [\int ^{0}_{-1}d_{\theta }\eta (\mu _{0}, \theta )\Big ]^{-1}H_{11}(0), \end{aligned} \end{aligned}$$

where $H_{20}(0)=g_{20}(\overline{q^{*}}(0))^{-1}$, $H_{11}(0)=g_{11}(\overline{q^{*}}(0))^{-1}$.