Exact similariton solution families and diverse composite waves in coherently coupled inhomogeneous systems

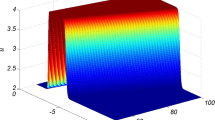
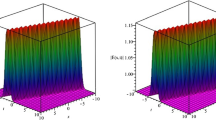
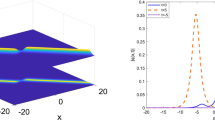
Abstract

Seeking analytical solutions of nonlinear Schrödinger (NLS)-like equations remains an open topic. In this paper, we revisit the general inhomogeneous nonautonomous NLS (inNLS) equation and report on exact similaritons under generic constraint relationships by proposing a novel generic self-similar transformation, which implies that there exist a rich variety of highly controllable solution families for inhomogeneous systems. As typical examples, richly controllable behaviors of the self-similar soliton (SS), self-similar Akhmediev breather (SAB), self-similar Ma breather (SMB), and self-similar rogue wave (SRW) are presented in a periodic distribution nonlinear system. With the aid of a linear transformation, these novel similariton solutions are deployed as a basis for constructing two-component composite solutions to a pair of coherently coupled inNLS equations including four-wave mixing. The diverse composite waves that emerge, including SS–SS, SAB–SMB, and SRW–SRW families, are investigated in some detail. The family of similariton solutions presented here may prove significance for designing the control and transmission of nonlinear waves.

Appendices

Appendix A: Explicit self-similar solutions of Eq. (1)

The explicit solutions of SS, SAB, SMB and SRW for inNLS Eq. (1) can be obtained by combining Eqs. (11)–(16) and the exact solutions of the soliton [22], Akhmediev and Ma breather [23], and rogue wave (RW) [24] of Eq. (8), which are expressed as follows:

(1) Exact SS solution:

$$ u_{SS} = k_{1} \eta_{s} \frac{{r(z)^{{(1{ - 4}\alpha_{r} )/2}} }}{{d(z)^{{(1 + 4\alpha_{d} )/2}} }}{\text{sech}}[\eta_{s} (T - T_{s} + 2\delta_{s} Z)]e^{{i[(\eta_{s}^{2} - \delta_{s}^{2} )Z - \delta_{s} T + \varPhi_{s} + \varphi (z,t)] - 2\alpha_{p} \int {p(z)dz} }} , $$

(A1)

where η_s, δ_s, T_s and ϕ_s represent the amplitude, frequency, initial position and phase of the SS, respectively.

(2) Exact SAB solution

$$ \begin{gathered} u_{SAB} = k_{1} \frac{{r(z)^{{(1{ - 4}\alpha_{r} )/2}} }}{{d(z)^{{(1 + 4\alpha_{d} )/2}} }}\frac{{\cosh [a(Z - Z_{ab} ) - 2i\omega_{ab} ] - \cos (\omega_{ab} )\cos [b(T - T_{ab} )]}}{{\cosh [a(Z - Z_{ab} )] - \cos (\omega_{ab} )\cos [b(T - T_{ab} )]}} e^{{i\left[ {2(Z - Z_{ab} ) + \phi (z,t)} \right] - 2\alpha_{p} \int {p(z)dz} }} , \hfill \\ \end{gathered} $$

(A2)

where a = 2sin(2ω_ab), b = 2sin(ω_ab), ω_ab ∈ ℝ. The parameters Z_ab and T_ab are, respectively, related to the initial position and time-shift of the SAB.

(3) Exact SMB solution

$$ \begin{gathered} u_{SMB} = k_{1} \frac{{r(z)^{{(1{ - 4}\alpha_{r} )/2}} }}{{d(z)^{{(1 + 4\alpha_{d} )/2}} }}\frac{{\cos [m_{a} (Z - Z_{m} ) - 2i\omega_{m} ] - \cosh (\omega_{m} )\cosh [m_{b} (T - T_{m} )]}}{{\cos [m_{a} (Z - Z_{m} )] - \cosh (\omega_{m} )\cosh [m_{b} (T - T_{m} )]}} \, e^{{i\left[ {2(Z - Z_{m} ) + \phi (z,t)} \right] - 2\alpha_{p} \int {p(z)dz} }} , \hfill \\ \end{gathered} $$

(A3)

where m_a = 2sinh(2ω_m), m_b = 2sinh(ω_m), ω_m ∈ ℝ. The parameters Z_m and T_m determine the initial position and time-shift of the SMB, respectively.

(4) Exact SRW solution

$$ u_{SRW} = k_{1} \frac{{r(z)^{{(1{ - 4}\alpha_{r} )/2}} }}{{d(z)^{{(1 + 4\alpha_{d} )/2}} }}\alpha_{g} \times \left[1 - \frac{{4 + i16\left| {\alpha_{g} } \right|^{2} (Z - Z_{g} )}}{{1 + 4\left| {\alpha_{g} } \right|^{2} (T - T_{g} ) + 16\left| {\alpha_{g} } \right|^{4} (Z - Z_{g} )^{2} }}\right]\times e^{{i\left[ {2\left| {\alpha_{g} } \right|^{2} (Z - Z_{g} ) + \phi (z,t)} \right] - 2\alpha_{p} \int {p(z)dz} }}, $$

(A4)

where α_g is related to the background intensity of the SRW. The parameters Z_g and T_g determine the initial position and time-shift of the SRW, respectively. Here, the self-similar variables Z ≡ Z(z) and T ≡ T(z, t) in (A1)–(A4) are given by Eqs. (12) and (13), respectively.

Appendix B: Some special cases of similariton (2)

(1) When α_p = 0, 5α_d = –3α_r, r⁵(z) = d³(z) and Ω₀ = 0, under the constraint conditions Γ(z) = 0 and Ω₂(z) = [–8d_z²(z) + 5d(z)d_zz(z)] /[50d³(z)], the self-similar variables are reduced to those studied in Ref. [11]:

$$ A(z) = k_{1} d^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 5}} \right. \kern-0pt} 5}}} (z), $$

(B1.1)

$$ Z(z) = k_{1}^{2} \int {d^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}} (z)} dz, $$

(B1.2)

$$\begin{aligned} {}&T(z,t) = k_{1} d^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 5}} \right. \kern-0pt} 5}}} (z)t - 2k_{1} \\& \int {d^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}} (z)\left( {k_{2} + \int {d^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} (z)\varOmega_{1} (z)dz} } \right)dz},\end {aligned} $$

(B1.3)

$$ \phi (z,t) = \frac{{d_{z} (z)}}{{10d^{2} (z)}}t^{2} + \frac{{\int {d^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} (z)\varOmega_{1} (z)dz} }}{{d^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} (z)}}t - \int {d^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}} (z)\left( {k_{2} + \int {d^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0pt} 5}}} (z)\varOmega_{1} (z)dz} } \right)^{2} dz}. $$

(B1.4)

(2) When α_p = 0, α_r = 0, α_d = − 1/2 and Ω₀(z) = 0, under the constraint conditions Γ(z) = –d_z(z)/2d(z) and Ω₂(z) = [r(z)r_z(z)d_z(z) + 2d(z)r_z²(z) – d(z)r(z)r_zz(z), the self-similar variables are reduced to the first case reported in Ref. [18]:

$$ A\left( z \right) = k_{1} \left[ {d\left( z \right)r\left( z \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} , $$

(B2.1)

$$ Z(z) = k_{1}^{2} \int {d(z)r^{2} (z)} dz ,$$

(B2.2)

$$ T(z,t) = k_{1} r(z)t - 2k_{1} \int {\left[ {d(z)r^{2} (z)\left( {k_{2} + \int {\frac{{\varOmega_{1} (z)}}{r(z)}dz} } \right)} \right]dz}, $$

(B2.3)

$$ \phi (z,t) = - \frac{{r_{z} (z)}}{4d(z)r(z)}t^{2} + r(z)\left[ {k_{2} + \int {\frac{{\varOmega_{1} (z)}}{r(z)}dz} } \right]t - \int {\left[ {d(z)r^{2} (z)\left( {k_{2} + \int {\frac{{\varOmega_{1} (z)}}{r(z)}dz} } \right)^{2} } \right]} dz. $$

(B2.4)

(3) When α_p = 0, α_r = 1/2, α_d = − 1/2 and Ω₀(z) = 0, under the constraint conditions Ω₂(z) = 0 and Γ(z) = r_z(z)/2r(z) – d_z(z)/2d(z), the self-similar variables are reduced to those reported in Refs. [12, 18]:

$$ A\left( z \right) = k_{1} \left[ {d\left( z \right)/r\left( z \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}, $$

(B3.1)

$$ Z(z) = k_{1}^{2} \int {d(z)} dz ,$$

(B3.2)

$$ T(z,t) = k_{1} t - 2k_{1} \int {d(z)\left( {k_{2} + \int {\varOmega_{1} (z)dz} } \right)dz},$$

(B3.3)

$$ \phi (z,t) = [k_{2} + \int {\varOmega_{1} (z)dz} ]t - \int {[d(z)(k_{2} + \int {\varOmega_{1} (z)} )^{2} ]} dz. $$

(B3.4)

(4) When α_p = 1/2, α_r = 0, α_d = 0, p(z) = w_z(z)/w(z) and d(z) = r(z) = 1, Ω₀(z) = Ω₁(z) = 0, under the constraint conditions Γ(z) = w_z(z)/2w(z) and Ω₂(z) = w_zz(z)/4w(z), the self-similar variables are reduced to those reported in Refs. [33, 34]:

$$ A(z) = \frac{{k_{1} }}{w(z)},$$

(B4.1)

$$ Z(z) = k_{1}^{2} \int {w^{ - 2} (z)} {{d}}z ,$$

(B4.2)

$$ T(z,t) = k_{1} w^{ - 1} (z)t - 2k_{1} k_{2} \int {w^{ - 2} (z){{d}}z}, $$

(B4.3)

$$ \phi (z,t) = \frac{{w_{z} (z)}}{4w(z)}t^{2} + \frac{{k_{2} }}{w(z)}t - k_{2}^{2} \int {\frac{1}{{w^{2} (z)}}} {{d}}z .$$

(B4.4)

It should be pointed out that there is a slight difference among Appendix B and Refs. [11, 12, 18, 33, 34] due to the different coefficients used in the theory.