Resonant interactions between lumps/rogue waves and solitons for the (3+1)-dimensional Yu–Toda–Sasa–Fukuyama equation

Abstract

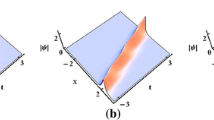
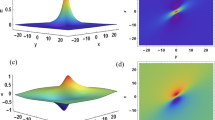
Under investigation in this paper is a (3+1)-dimensional Yu–Toda–Sasa–Fukuyama equation. Employing the Kadomtsev–Petviashvili hierarchy reduction, we obtain the semi-rational solutions which describe the interactions between the lumps/rogue waves and the parallel line solitons. We find that the phase difference of two solitons determines the waves amplitudes and the forms of the interactions. Asymptotic analysis shows that the solitons keep their shapes before and after the interactions, which means the interactions are elastic. On the x-y and $z-y$ planes, the lump waves generate in the middle of solitons, while the line rogue waves only raise on the x–z plane. We show the connection with the general form of multi-soliton solutions mathematically, and analyze the interactions through four characteristic lines, which present the shapes and propagation traces of the localized waves. We find that the amplitudes of lumps affect the interaction patterns, as well as the strength and position of soliton. When $N\ge 3$, interactions among lumps and solitons show more complex phenomena, our analysis summarizes the law of the interaction pattern. The numerical simulations of the nonlinear waves are also given.

Appendix A

In this appendix, we will prove that Solutions (5) satisfy Bilinear Equation (3). Via the idea of Refs. [31, 32], we consider the following coefficient transformation

$$\begin{aligned}{} & {} x_1=\zeta =x-\omega z,~~x_2=i\sqrt{\omega } y,~~x_3=-\omega t, \end{aligned}$$

where $x_i$’s are the same as the variable coefficient defined in Refs. [31, 32].

We consider the $\tau$ functions which meet the KP hierarchy [31,32,33,34,35] and set the Grammian determinant

$$\begin{aligned}{} & {} \tau _{n}(x,y,z,t)=\det _{1\le r,j\le N} \left( m^{(n)}_{rj}\right) , \end{aligned}$$

(A.1)

where $m^{(n)}_{rj}$, $\varphi ^{(n)}_{i}$ and $\psi ^{(n)}_{j}$ are the functions of variables x, y, z and t, satisfying the following differential and difference relations

Using the differential formula of determinant

$$\begin{aligned} \partial _ { x }\det _{1\le r,j\le N} ( a _ { r j } ) = \sum _ { r, j = 1 } ^ { N } A _ { r j } \partial _ { x }a_ { i j } \end{aligned}$$

and the expansion formula of bordered determinant

$$\begin{aligned} \begin{vmatrix} a _ { r j }&{ b _ { r} }\\ { c _ { j } }&{ d } \end{vmatrix} = - \sum A _ { r j } b _ { r } c _ { j } + d \det ( a _ { r j } ) \end{aligned}$$

where $A _ { r j }$ is the $(r,j)-$cofactor of the matrix $(a _ { r j })$, we can verify the derivative of the Tau Function (A.1) as follows:

$$\begin{aligned}{} & {} \partial _{\zeta }\tau _{n}=\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{-\psi _{j}}^{(n)}&{0}\end{vmatrix},\nonumber \\{} & {} \partial _{\zeta }^2\tau _{n}=\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}\\{-\psi _{j}}^{(n)}&{0}\end{vmatrix}+\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-1)}&{0}\end{vmatrix},\nonumber \\{} & {} \partial _{\zeta }^3\tau _{n}=\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+2)}\\ {-\psi _{j}}^{(n)}&{0}\end{vmatrix}+2\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}\\{\psi _{j}}^{(n-1)}&{0} \end{vmatrix}\nonumber \\{} & {} \quad +\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{-\psi _{j}}^{(n-2)}&{0}\end{vmatrix},\nonumber \\{} & {} \partial _{\zeta }^4\tau _{n}=\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+3)}\\ {-\psi _{j}}^{(n)}&{0}\end{vmatrix}\nonumber \\{} & {} \quad +3\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+2)}\\{\psi _{j}}^{(n-1)}&{0}\end{vmatrix}+3\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}\\{-\psi _{j}}^{(n-2)}&{0}\end{vmatrix}\nonumber \\{} & {} \quad +\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-3)}&{0}\end{vmatrix} +2\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-1)}&{0}&{0}\\{-\psi _{j}}^{(n)}&{0}&{0}\end{vmatrix},\nonumber \\{} & {} \partial _{y}\tau _{n}{=}i\sqrt{\omega }\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n{+}1)}\\{{-}\psi _{j}}^{(n)}&{0} \end{vmatrix}{+}i\sqrt{\omega }\begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{{-}\psi _{j}}^{(n{-}1)}&{0}\end{vmatrix}\!\!,\nonumber \\{} & {} \partial _{y}^2\tau _{n}=\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+3)}\\{\psi _{j}}^{(n)}&{0}\end{vmatrix}\nonumber \\{} & {} \quad -\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}\\{\psi _{j}}^{(n-2)}&{0}\end{vmatrix}-\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+2)}\\{-\psi _{j}}^{(n-1)}&{0}\end{vmatrix}\nonumber \\{} & {} \quad -\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-3)}&{0}\end{vmatrix}-2 \omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-1)}&{0}&{0}\\{-\psi _{j}}^{(n)}&{0}&{0}\end{vmatrix},\nonumber \\{} & {} \partial _{t}\tau _{n}=\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+2)}\\{\psi _{j}}^{(n)}&{0}\end{vmatrix}\nonumber \\{} & {} \quad +\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-2)}&{0}\end{vmatrix}+\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}\\{\psi _{j}}^{(n-1)}&{0}\end{vmatrix}\nonumber \\{} & {} \partial _{\zeta }\partial _{t}\tau _{n}=\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+3)}\\ {\psi _{j}}^{(n)}&{0}\end{vmatrix}+\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n)}\\ {\psi _{j}}^{(n-3)}&{0}\end{vmatrix}\nonumber \\{} & {} \quad +\omega \begin{vmatrix}{m_{rj}}^{(n)}&\varphi _r^{(n+1)}&\varphi _r^{(n)}\\{\psi _{j}}^{(n-1)}&{0}&{0}\\{-\psi _{j}}^{(n)}&{0}&{0}\end{vmatrix}.\nonumber \\ \end{aligned}$$

(A.2)

Combined with the definition of the bilinear differential operators, we calculate and simplify Bilinear Equation (3) as follows:

$$\begin{aligned}{} & {} \left( -\omega D_{\zeta }^4-4D_{\zeta } D_t+3 D_y^2\right) \tau _ { n }\cdot \tau _ { n }\\{} & {} \quad =\tau _ { n } \left( -2 \omega \partial _{\zeta }^4\tau _ { n } +6 \partial _{y}^2\tau _ { n }-8 \partial _{\zeta }\tau _ { n }\partial _{t}\tau _ { n }\right) \\{} & {} \quad -6 \omega \left( \partial _{\zeta }^2\tau _ { n }\right) ^2\\{} & {} \quad +8 \omega \partial _{\zeta }\tau _ { n } \partial _{\zeta }^3\tau _ { n }-6 \left( \partial _{y}\tau _ { n }\right) ^2+8 \partial _{t}\tau _ { n } \partial _{\zeta }\tau _ { n }\\{} & {} \quad =-24\omega \begin{vmatrix} { m _ { r j } }^{ ( n ) }\end{vmatrix} \times \begin{vmatrix} { m _ { r j } }^{ ( n ) }&\varphi _r^{ ( n+1 ) }&\varphi _r^{ ( n ) } \\ { \psi _ { j } } ^ { ( n-1 ) }&{ 0 }&{ 0 }\\ { - \psi _ { j } } ^ { ( n ) }&{ 0 }&{ 0 } \end{vmatrix}\\{} & {} \quad +24\omega \begin{vmatrix} { m _ { r j } }^{ ( n ) }&\varphi _r^{ ( n +1) } \\ { - \psi _ { j } } ^ { ( n ) }&{ 0 } \end{vmatrix}\times \begin{vmatrix} { m _ { r j } }^{ ( n ) }&\varphi _r^{ ( n ) } \\ { -\psi _ { j } } ^ { ( n-1 ) }&{ 0 }\end{vmatrix}\\{} & {} \quad -24\omega \begin{vmatrix}{ m _ { r j } }^{ ( n ) }&\varphi _r^{ ( n +1) } \\ { \psi _ { j } } ^ { ( n-1 ) }&{ 0 }\end{vmatrix}\times \begin{vmatrix} { m _ { r j } }^{ ( n ) }&\varphi _r^{ ( n) } \\ { \psi _ { j } } ^ { ( n) }&{ 0 }\end{vmatrix}. \end{aligned}$$

By comparing the Jacobian formula of determinant

$$\begin{aligned}{} & {} \begin{vmatrix} { a _ { rj } }\end{vmatrix}\times \begin{vmatrix} {a _ { rj }}&{b _ { r }}&{c _ { r } }\\ d _ {j }&e&f\\ g _ {j }&h&k \end{vmatrix}=\begin{vmatrix} {a _ { rj }}&{c _ { r } }\\ g _ { j }&k \end{vmatrix}\times \begin{vmatrix} {a _ { rj }}&{b _ { r } }\\ d _ { j }&a _ { e } \end{vmatrix}-\begin{vmatrix} {a _ { rj }}&{c _ { r } }\\ d _ { j }&f \end{vmatrix}\nonumber \\{} & {} \quad \times \begin{vmatrix} {a _ { rj }}&{b _ { r } }\\ g _ { j }&h \end{vmatrix} \end{aligned}$$

(A.3)

we can prove $\tau _{n}$ satisfies Bilinear Equation (3).

We derive the following solutions

$$\begin{aligned}{} & {} \tau _n=\det _{1\le r, j\le N}\left( m_{rj}^{(n)}\right) ,\\{} & {} m_{rj}^{(n)}=\int \phi _r^{(n)}\psi _j^{(n)}dx_1,\\{} & {} \phi _r^{(n)}=A_rp_r^ne^{\xi _r},~~\psi _j^{(n)}=B_j(-q_j)^{-n}e^{\eta _r},\\{} & {} A_r=\sum _{k=0}^{n_r}C_{rk}(\partial _{p_r})^{n_r-k},~~B_j=\sum _{l=0}^{n_j}D_{jl}(\partial _{q_j})^{n_j-l}, \end{aligned}$$

where $\xi _r$’s and $\eta _j$’s are the functions with respect to the variables x, y, z and t, defined as,

$$\begin{aligned}{} & {} \xi _r=p_r(x-\omega z)+i\sqrt{\omega }{p_r}^2y -{p_r}^3 \omega t+\xi _{0 r},\\{} & {} \eta _j=q_j(x-\omega z)-i\sqrt{\omega }{q_j}^2y -{q_j}^3 \omega t+\eta _{0 j}, \end{aligned}$$

with r and j being two integers and $p_r$’s, $q_j$’s, $\xi _{0 r}$’s and $\eta _{0j}$’s being the complex constants. Through some calculations, the element $m_{rj}^{(n)}$ can be written as follows:

$$\begin{aligned}{} & {} m_{rj}^{(n)}=\delta _{rj}+e^{\xi _r+\eta _r}\left( -\frac{p_r}{q_j}\right) ^n\sum _{k=0}^{n_r}C_{rk}\\{} & {} \quad \times \left( \partial _{p_r}+\xi '_r+\frac{n}{p_r}\right) ^{n_r-k}\\{} & {} \quad \times \sum _{l=0}^{n_j}D_{jl}\left( \partial _{q_j}+\eta '_j-\frac{n}{q_j}\right) ^{n_j-l}\frac{1}{p_r+q_j}, \end{aligned}$$

where $\beta _{rj}$’s are real constants. Setting some conditions

$$\begin{aligned}{} & {} p_r=q_j^*,~~C_{rk}=D_{rk}^*,~~\xi _{0 r}=\eta _{0 r}^*,~~\beta _{rj}=\beta _{j r},\\{} & {} x_1=\xi =x-\omega z,~~x_2=i\sqrt{\omega } y,~~x_3=-\omega t, \end{aligned}$$

we get that function.

$$\begin{aligned}{} & {} \xi _{r}=\eta _{r}^*,~~ m_{rj}^{(n)}=m_{j r}^{(-n)*},~~ \tau _n=\tau _{-n}^*, \end{aligned}$$

and $\tau _0$ is a real functions, with “$*$” being the complex conjugate. We can verify that $f(x,y,z,t)=\tau _0$ is a real.