Abstract
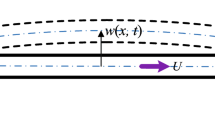
The effectiveness of continuous vibro-impact forcing representations for the cantilevered pipe that conveys fluid is explored and analyzed. The previously accepted forcing model utilizing a smoothened trilinear spring is estimated using three continuous forcing representations, namely, polynomial, rational polynomial, and hyperbolic tangent. The accuracy of the estimated forcing functions is investigated and analyzed by calculating the root mean square error, and bifurcation diagrams are generated and compared to the nominal system. Additionally, the dynamic response of the system is further characterized using Poincare maps, power spectra, and basins of attraction. Once all continuous forcing representations are analyzed and compared to the nominal system, the computational cost of each method is examined, and further limitations of the hyperbolic tangent method are discovered. It is proved that the hyperbolic tangent forcing representation most accurately captures the dynamic response of the pipeline, and the least accurate representation is the rational polynomial representation. Additionally, considerable computational cost is saved when employing the hyperbolic tangent representation compared to the discontinuous representation.
























Similar content being viewed by others
Data availability
Data will be made available on reasonable request.
References
Semler, C., Li, G.X., Paidoussis, M.P.: The non-linear equations of motion of pipes conveying fluid. J. Sound Vib. 169(5), 577–599 (1994)
Paidoussis, M.P., Li, G.X., Rand, R.H.: Chaotic motions of a constrained pipe conveying fluid: comparison between simulation, analysis, and experiment. J. Appl. Mech. 58, 559–565 (1991)
Paidoussis, M.P., Moon, F.: Nonlinear and chaotic fluidelastic vibrations of a flexible pipe conveying fluid. J. Fluids Struct. 2, 567–591 (1988)
Paidoussis, M.P., Semler, C.: Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid: a full nonlinear analysis. Nonlinear Dyn. 4, 655–670 (1993)
Wang, L., Liu, Z.Y., Abdelkefi, A., Wang, Y.K., Dai, H.: Nonlinear dynamics of cantilevered pipes conveying fluid: towards a further understanding of the effect of loose constraints. Int. J. Non-Linear Mech. 95, 19–29 (2017)
Paidoussis, M.P., Semler, C., Wadham-Gagnon, M., Saaid, S.: Dynamics of cantilevered pipes conveying fluid. Part 2: dynamics of the system with intermediate spring support. J. Fluids Struct. 23, 569–587 (2007)
Yoon, J.-Y., Kim, B.: Effect and feasibility analysis of the smoothening functions for clearance-type nonlinearity in a practical driveline system. Nonlinear Dyn. 3(85), 1651–1664 (2016)
Kim, T.C., Rook, T.E., Singh, R.: Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity. J. Sound Vib. 3(263), 665–678 (2003)
Shin, Y., Sass, D., Jendrzejczyk, J.A.: Vibro-impact responses of a tube with tube-baffle interaction. Trans. Can. Soc. Mech. Eng. 5(1), 15–23 (1978)
Whiston, G.: The vibro-impact response of a harmonically excited and preloaded one-dimensional linear oscillator. J. Sound Vib. 115(2), 303–319 (1987)
Jing, H.-S., Young, M.: Random response of a single-degree-of-freedom vibro-impact system with clearance. Earthq. Eng. Struct. Dyn. 19(6), 789–798 (1990)
Saunders, B., Vascancellos, R., Kuether, R., Abdelkefi, A.: Insights on the continuous representations of piecewise-smooth nonlinear systems: limits of applicability and effectiveness. Nonlinear Dyn. 107, 1479–1494 (2022)
Vasconcellos, R., Abdelkefi, A., Marques, F., Hajj, M.: Representation and analysis of control surface freeplay. J. Fluids Struct. 31, 79–91 (2012)
Dai, H., Yue, X., Yuan, J., Xie, D., Alturi, S.: A comparison of classical Runge–Kutta and Henon’s methods for capturing chaos and chaotic transients in an aeroeastic system with freeplay nonlinearity. Nonlinear Dyn. 81, 169–188 (2015)
Wayhs-Lopes, L., Dowell, E., Bueno, D.: Influence of friction and asymmetric freeplay on the limit cycle oscillation in aeroelastic system: an extended Henon’s technique to temporal integration. J. Fluids Struct. 96, 103054 (2020)
Detroux, T., Renson, L., Masset, L., Kerschen, G.: The harmonic balance method for bifurcation analysis of large-scale nonlinear mecanical systems. Comput. Methods Appl. Mech. Eng. 296, 18–38 (2015)
Zhou, K., Dai, H.L., Abdelkefi, A., Ni, Q.: Theroretical modeling and nonlinear analysis of piezoelectric energy harvesters with different stoppers. Int. J. Mech. Sci. 166, 1681–1874 (2020)
Alvis, T., Abelkefi, A.: Effectiveness and nonlinear characterization of vibro-impact energy harvesting absorbers in controlling base-excited systems. Smart Mater. Struct. 30, 9 (2021)
Alvis, T., Abdelkefi, A.: Effective design of vibro-impact energy harvesting absorbers with asymmetric stoppers. Eur. Phys. J. Spec. Top. 231, 1567–1586 (2022)
Lai, Z., Thomson, G., Yurchenko, D., Val, D., Rodgers, E.: On energy harvesting from a vibro-impact oscillator with dielectric membranes. Mech. Syst. Signal Process. 107, 105–121 (2018)
Lai, Z., Wang, S., Zhu, L., Zhang, G., Wang, J., Yang, K., Yurchnko, D.: A hybrid piezo-dielectric wind energy harvester for high-performance vortex-induced-vibration energy harvesting. Mech. Syst. Signal Process. 150, 107212 (2021)
Ostasevicius, V., Dauksevicius, R., Gaidys, R., Palevicius, A.: Numerical analysis of fluid-structure interaction effects on vibrations of cantilever microstructure. J. Sound Vib. 308, 660–673 (2007)
Ostasevicius, V., Gaidys, R., Dauksevicius, R.: Numerical analysis of dynamic effects of a nonlinear vibro-impact process for enhancing the reliability of contact-type MEMS devices. Sensors 9, 10202–10216 (2009)
Li, T., Lamarque, C.-H., Seguy, S., Berlioz, A.: Chaotic characteristic behavior of a linear oscillator coupled with vibro-impact nonlinear energy sink. Nonlinear Dyn. 91, 2319–2330 (2018)
Luo, G.-W., Xie, J.-H.: Hopf Bifurcation of a two-degree-of freedom vibro-impact system. J. Sound Vib. 11(3), 391–408 (1998)
Liu, Y., Pavlovskaia, E., Wiercigroch, M., Peng, Z.: Forward and backward motion control of a vibro-impact capsule system. Int. J. Non-Linear Mech. 70, 30–46 (2015)
Ashley, H., Haviland, G.: Bending vibrations of a pipe line containing flowing fluid. J. Appl. Mech. 17, 229–232 (1950)
Zhou, K., Ni, Q., Dai, H., Wang, L.: Nonlinear forced vibrations of supported pipe conveying fluid. J. Sound Vib. 471, 115189 (2020)
Wang, L.: A further study on the non-linear dynamics of simply supported pipes conveying. Int. J. Non-Linear Mech. 44, 115–121 (2009)
Yi-min, H., Young-shou, L., Bao-hui, L., Yan-jiang, L., Zhu-feng, Y.: Natural frequency analysis of fluid conveying pipeline with different boundary conditions. Nucl. Eng. Des. 240, 461–467 (2010)
Maalawi, K., Ziada, M.: On the static instability of flexible pipes. J. Fluids Struct. 5(16), 685–690 (2002)
Modarres-Sadeghi, Y., Semler, C., Wadham-Gagnon, M., Paidoussis, M.P.: Dynamics of cantilevered pipes conveying fluid. Part 3: three-dimensional dynamics in the presence of an end-mass. J. Fluids Struct. 23(4), 589–603 (2007)
Modarres-Sadeghi, Y., Paidoussis, M.: Nonlinear dynamics of extensible fluid-conveying pipes. J. Fluids Struct. 25, 535–543 (2009)
Mostafa, N.: Effect of a viscoelastic foundation on the dynamic stability. Int. J. Appl. Sci. Eng. 12, 59–74 (2014)
Gregory, R.W., Paidoussis, M.P.: Unstable oscillation of tubular cantilevers conveying fluid II. Experiments. Proc. Roy. Soc. Lond. Ser. A Math. Phys. Sci. 293(1435), 428–542 (1966)
Paidoussis, M.P., Issid, N.T.: Dynamic stability of pipes conveying fluid. J. Sound Vib. 33(3), 267–294 (1974)
Paidoussis, M.P.: Flow-induced instabilities of cylindrical structures. ASME Appl. Mech. Rev. 40(2), 163–175 (1987)
Paidoussis, M.P., Li, G.X., Moon, F.: Chaotic osccillations of the autonomous system of a constrained pipe conveying fluid. J. Sound Vib. 135(1), 1–19 (1989)
Paidoussis, M.P., Semler, C.: Nonlinear dynamics of a fluid-conveying cantilevered pipe with an intermediate spring support. J. Fluids Struct. 7, 269–298 (1993)
Semler, C., Paidoussis, M.P.: Nonlinear analysis of the parametric resonances of a planar fluid-conveying cantilevered pipe. J. Fluids Struct. 10(7), 787–825 (1996)
Paidoussis, M.P., Grinevich, E., Adamovic, D., Semler, C.: Linear and nonlinear dynamics of cantilevered cylinders in axial flow. Part 1: physical dynamics. J. Fluids Struct. 16(6), 691–713 (2002)
Lopes, J.-L., Paidoussis, M.P., Semler, C.: Linear and nonlinear dynamics of cantilevered cylinders in axial flow. Part 2: The equations of motion. J. Fluids Struct. 16(6), 715–737 (2002)
Semler, C., Lopes, J.L., Augu, N., Paidoussis, M.P.: Linear and nonlinear dynamics of cantilevered cylinders in axial flow. Part 3: nonlinear dynamics. J. Fluids Struct. 16(6), 739–759 (2002)
Rinaldi, S., Paidoussis, M.P.: Dynamics of a cantilevered pipe discharging fluid, fitted with a stabilizing end-piece. J. Fluids Struct. 26(3), 517–525 (2010)
Ghayesh, M.H., Païdoussis, M.P.: Three-dimensional dynamics of a cantilevered pipe conveying fluid, additionally supported by an intermediate spring array. Int. J. Non-Linear Mech. 45(5), 507–524 (2010)
Rinaldi, S., Païdoussis, M.P.: Theory and experiments on the dynamics of a free-clamped cylinder in confined axial air-flow. J. Fluids Struct. 28, 167–179 (2012)
Giacobbi, D.B., Semler, C., Paidoussis, M.P.: Dynamics of pipes conveying fluid of axially varying density. J. Sound Vib. 473, 115202 (2020)
Paidoussis, M.P., Abdelbaki, A.R., Faisal, B.M.F.J., Tavallaeinejad, M., Moditis, K., Misra, A.K., Nahon, M., Ratigan, J.L.: Dynamics of a cantilevered pipe subjected to internal and reverse external axial flow: a review. J. Fluids Struct. 106, 103349 (2021)
Butt, M.F.J., Paidoussis, M.P., Nahon, M.: Dynamics of a confined pipe aspirating fluid and concurrently subjected to external axial flow: an experimental investigation. J. Fluids Struct. 104, 103299 (2021)
Saunders, B., Vasconcellos, R., Kuether, R., Abdelkefi, A.: Characterization and interaction of geometric and contact/impact nonlinearities in dynamical systems. Mech. Syst. Signal Process. 167, 108481 (2022)
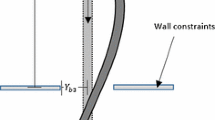
Taylor, G., Ceballes, S., Abdelkefi, A.: Insights on the point of contact analysis and characterization of constrained pipelines conveying fluid. Nonlinear Dyn. 93, 1261–1275 (2018)
Bajaj, A.K., Sethna, P.R., Lundgren, T.S.: Hopf bifurcation phenomena in tubes carrying a fluid. SIAM J. Appl. Math. 2(39), 213–230 (1980)
Alvis, T., Ceballes, S., Abdelkefi, A.: Sensitive parameter identification and uncertainty quantification for the stability of pipeline conveying fluid. Int. J. Mech. Mater. Des. (2021)
Zhu, H., Wang, W., Yin, X.: Spectral element method for vibration analysis of three-dimensional pipes conveying fluid. Int. J. Mech. Mater. Des. 15, 345–360 (2019)
Dai, J., Liu, H., Miao, C., Tong, G.: A parametric study on thermo-mechanical vibration of axially functionally graded material pipe conveying fluid. Int. J. Mech. Mater. Des. 15, 715–726 (2019)
Guo, X., Xiao, C., Ge, H., Ma, H., Li, H., Sun, W., Liu, Z.: Dynamic modeling and experimental study of a complex fluid-conveying pipeline system with series and parallel structures. Appl. Math. Model. 109, 186–208 (2022)
Khudayarov, B., Turaev, F.: Mathematical simulation of nonlinear oscillations of viscoelastic pipelines conveying fluid. Appl. Math. Model. 66, 662–679 (2019)
Wang, Y., Tang, M., Yang, M., Qin, T.: Three-dimensional dynamics of a cantilevered pipe conveying pulsating fluid. Appl. Math. Model. 114, 502–524 (2023)
Askarian, A., Permoon, M., Zahedi, M., Shakouri, M.: Stability analysis of viscoelastic pipes conveying fluid with different boundary conditions described by fractional Zener model. Appl. Math. Model. 103, 750–763 (2022)
Liang, F., Gao, A., Yang, X.: Dynamical analysis of spinning functionally graded pipes conveying fluid with multiple spans. Appl. Math. Model. 83, 454–469 (2020)
Niordson, F.I.: "Vibrations of a Cylindrical Tube Containing Fluid, vol. 73. Kungliga Tekniska Hogskolans Handlingar (1953)
Paidoussis, M.P.: A review of flow-induced vibrations in reactors and reactor components. Nucl. Eng. Des. 74(1), 31–60 (1983)
Lai, Z., Yang, S., Lu, L., Tan, T., Sun, L.: Two-phase flow-induced vibration fatigue damage of tube bundles with clearance restriction. Mech. Syst. Signal Process. 166, 108442 (2022)
Housner, G.W.: Bending vibrations of a pipe when liquid flows through it. J. Appl. Mech. 19, 205–208 (1952)
Benjamin, T.B.: Dynamics of a system of articulated pipes conveying fluid-I. Theory. Proc. Roy. Soc. Lond. Ser. A Math. Phys. Sci. 261(1307), 487–499 (1961)
Paidoussis, M.P., Li, G.X.: Pipes conveying fluid: a model dynamical problem. J. Fluids Struct. 7(2), 137–204 (1993)
Paidoussis, M.P.: Pipes conveying fluid: a fertile dynamics problem. J. Fluids Struct. 114, 103664 (2022)
Ratigan, J.: Underground storage of hydrocarbons in salt formations. In: American Gas Association Conference, Las Vegas (1995)
Askarian, A.R., Haddapour, H., Firouz-Abadi, R., Abtahi, H.: Nonlinear dynamics of extensible visoelastic cantilevered pipes conveying pulsatile flow with an end nozzle. Int. J. Non-Linear Mech. 91, 22–35 (2017)
Wang, L., Hong, Y., Dai, H., Ni, Q.: Natural frequency and stability tuning of cantilevered CNTs conveying fluid in magnetic field. Acta Mech. Solida Sin. 29, 567–576 (2016)
Paidoussis, M.P.: 1992 Calvin Rice Lecture: some curiosity-driven research in fluid structure ineteractions and its current applications. J. Press. Vessel Technol. 115(1), 2–14 (1993)
Ibrahim, R.A.: Mechanics of pipes conveying fluids—part II: applications and fluidelastic problems. J. Press. Vessel Technol. 133, 2 (2011)
Chen, S., Rosenber, G.: Vibration and stability of tube exposed to pulsating parallel flow. Trans. Am. Nucl. Soc. 13, 335–336 (1970)
Ren, Y., Li, L., Jin, Q., Nie, L.P.F.: Vibration and snapthrough of fluid-conveying graphene-reinforced composite pipes under low-velocity impact. AIAA J. 59(12), 5091–5105 (2021)
Li, L., Nie, L., Ren, Y., Jin, Q.: On the impact process and stress field of functionally graded graphene reinforced composite pipes with a viscoelastic interlayer. J. Vib. Control 10775463221095297 (2022)
Ni, Q., Wang, Y., Tang, M., Luo, Y., Yan, H., Wang, L.: Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints. Nonlinear Dyn. 81, 893–906 (2015)
Acknowledgements
The authors T. Alvis and A. Abdelkefi would like to thank Sandia National Laboratories for their funding of this project. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the US Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the US Department of Energy or the United States Government.
Funding
Funding is provided by Sandia National Laboratories.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
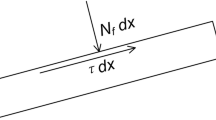
Dimensional equation of motion:
Terms from Eq. (4)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Alvis, T., Saunders, B.E. & Abdelkefi, A. Consequences and benefits of utilizing continuous vibro-impact representations in constrained pipeline conveying fluid systems. Nonlinear Dyn 111, 9095–9125 (2023). https://doi.org/10.1007/s11071-023-08357-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08357-2