Experimental and theoretical investigation of superharmonic resonances in a planar oscillator under angular base excitation

Abstract

This paper explores the complicated dynamic behavior of a mechanical oscillator under harmonic angular excitation. The motivation behind this work comes from the nature of the actuation produced by high-performance dither motors. A lumped-mass model, which captures the primary and the 1 : 2 superharmonic resonances observed on an analogous experimental test setup, is put forward. The equations of motion governing the dynamics of the model are derived and are found to comprise both parametric and direct forcing terms. The governing equations are solved analytically using the generalized harmonic balance method and numerical integration. The method of multiple scales is utilized to obtain closed-form expressions that relate the system parameters to the oscillation amplitudes in the vicinity of the direct and the 1 : 2 superharmonic resonances. It is found that eccentricity plays a vital role in the occurrence of the resonances. Besides, the relationship between the excitation amplitudes and the resulting oscillations for the direct and the superharmonic resonances are dissimilar. A few salient differences between classical (rectilinear) and angular base excitation mechanisms are pointed out.

Appendices

Appendix A: Derivation of the equations of motion

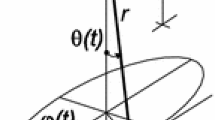
The equations of motion (EoM) governing the system of Fig. 1 are derived as follows. The position vector $\vec {P}$ of mass m is

$$\begin{aligned} \vec {P}=\left( x+x_e\right) {\hat{i}}+\left( y+y_e\right) {\hat{j}} \end{aligned}$$

(56)

where ${\hat{i}}$ and ${\hat{j}}$ are unit vectors along the axes marked X and Y. The time derivative,

$$\begin{aligned} {\frac{d\vec {P}}{dt}}={\vec {P}}'={x}'{\hat{i}}+\left( x+x_e\right) {{\hat{i}}}'+{y}'{\hat{j}}+\left( y+y_e\right) {{\hat{j}}}' \end{aligned}$$

(57)

where $\left( \bullet \right) '$ denotes differentiation with respect to time t. The derivatives of the unit vector are ${{\hat{i}}}'=\Omega \vec {k} \times \vec {i}=\Omega \vec {j}$ and ${{\hat{j}}}'=\Omega \vec {k} \times \vec {j}=-\Omega \vec {i}$. Using these relations, Eq. (57) can be expressed as

$$\begin{aligned} {\vec {P}'}=\left( {x}'-\left( y+y_e\right) \Omega \right) {\hat{i}}+\left( {y}'+\left( x+x_e\right) \Omega \right) {\hat{j}}. \end{aligned}$$

(58)

The quantity $\left( {\vec {P}}'\right) ^2$ is

$$\begin{aligned} \begin{aligned}&\quad {\vec {P}'}\,^2={x'}^2+y^2\Omega ^2+y_e^2\Omega ^2+2yy_e\Omega ^2-2{x'}y\Omega \\&\quad -2{x'}y_e\Omega +{y'}^2+x^2\Omega ^2+x_e^2\Omega ^2\\&\quad +2xx_e\Omega ^2+2x{y'}\Omega +2x_e{\dot{y}}\Omega . \end{aligned} \end{aligned}$$

(59)

The kinetic energy of the mass m is $T=\frac{1}{2}m {\vec {P}'}\,^2$, and the potential energy stored in the springs is $V=\frac{1}{2}k_x x^2+\frac{1}{2}k_y y^2$. This form of potential energy strictly models a linear spring which describes the motion of a small magnitude about the mean position. Note that large amplitude oscillations, where geometric nonlinearities can be significant, are not of interest in this work. The Lagrangian $L=T-V$ of the system is developed, and the damping terms are included in the formulation by employing the Rayleigh dissipation function.

$$\begin{aligned} R=\frac{1}{2} c{x'}^2+\frac{1}{2} c{y'}^2. \end{aligned}$$

(60)

Following the Euler-Lagrange equations,

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial L}{\partial {q_i'}}\right) -\frac{\partial L}{\partial {q_i}}=-\frac{\partial R}{\partial {q_i'}}, \quad i=1,2 \end{aligned}$$

(61)

where $q_1=x$ and $q_2=y$, the EoM are derived as

$$\begin{aligned}{} & {} m{x''}+c{x'}+k_xx=2m{y'}\Omega +m\left( y+y_e\right) {\Omega '}\nonumber \\{} & {} \quad +m\left( x+x_e\right) \Omega ^2 \end{aligned}$$

(62)

and

$$\begin{aligned}{} & {} m{y''}+c{y'}+k_yy=-2m{x'}\Omega -m\left( x+x_e\right) {\Omega '}\nonumber \\{} & {} \quad +m\left( y+y_e\right) \Omega ^2. \end{aligned}$$

(63)

This work explores the effect of angular base excitation, and therefore it is assumed that $\Omega ={\overline{\Omega }}\sin \lambda t$. The following equations can be obtained by substituting this function in Eqs. (62) and (63).

$$\begin{aligned}{} & {} m{x''}+c{x'}+k_xx=2m{y'}{\overline{\Omega }}\sin \lambda t+m\left( y+y_e\right) \nonumber \\{} & {} \quad {{\overline{\Omega }}\lambda \cos \lambda t}+m\left( x+x_e\right) {\overline{\Omega }}^2\sin ^2\lambda t \end{aligned}$$

(64)

$$\begin{aligned}{} & {} m{y''}+c{y'}+k_yy=-2m{x'}{\overline{\Omega }}\sin \lambda t-m\left( x+x_e\right) \nonumber \\{} & {} \quad {{\overline{\Omega }}\lambda \cos \lambda t}+m\left( y+y_e\right) {\overline{\Omega }}^2\sin ^2\lambda t. \end{aligned}$$

(65)

Using the variables, $x^*=\frac{x}{l_0}$, $y^*=\frac{y}{l_0}$, $t^*=\frac{t}{t_0}=\omega t$, and parameters $x_e^*=\frac{x_e}{l_0}$, $y_e^*=\frac{y_e}{l_0}$, $\omega =\sqrt{\frac{k_x}{m}}$, $\omega _{yx}=\sqrt{\frac{k_y}{k_x}}$, $\zeta ^*=\frac{c}{2m\omega }$, $\Omega ^*=\frac{{\overline{\Omega }}}{\omega }$, $\lambda ^*=\frac{\lambda }{\omega }$, Eqs.(64) and (65) can be expressed as

$$\begin{aligned}{} & {} \begin{aligned}&\ddot{x^*}+\zeta ^*\dot{x^*}+x^*=2\dot{y^*}{\Omega ^*}\sin \lambda ^* t^*\\&\quad +\left( y^*+y^*_e\right) {{\Omega ^*}\lambda ^* \cos \lambda ^* t^*}\\&\quad +\left( x^*+x^*_e\right) {\Omega ^*}^2\sin ^2\lambda ^* t^* \end{aligned} \end{aligned}$$

(66)

$$\begin{aligned}{} & {} \begin{aligned}&\ddot{y^*}+\zeta ^*\dot{y^*}+\omega _{yx}^{*2}y^*=-2{\dot{x^* }}{\Omega ^*}\sin \lambda ^*t^*\\&\quad -\left( x^*+x^*_e\right) {{\Omega ^*}\lambda ^*\cos \lambda ^* t^*}\\&\quad +\left( y^*+y^*_e\right) {\Omega ^*}^2\sin ^2\lambda ^* t^* \end{aligned} \end{aligned}$$

(67)

where $\dot{\left( \bullet \right) }$ denotes the differentiation with respect to non-dimensional time, $t^*$. The equations of motion (Eqs. 1) and (2) are obtained by omitting the ‘$*$’ superscripts for brevity, and expressing the $\sin ^2 \lambda t$ in terms of $\cos 2\lambda t$.

Appendix B: Parameter estimation

Parameters are estimated from the experimental setup as described below.

• 1. Natural frequency, $\omega$: The cylindrical specimen is displaced slightly from its rest position. $\omega$ is estimated experimentally from the fast Fourier transform of the response to such an initial configuration. The response obtained resembles that of Fig. 3.

• 2. Damping coefficient, $\zeta$: The ratio of the amplitudes of decaying oscillations are used to estimate $\zeta$. Once the amplitudes $x_0$ and $x_n$ of the initial and the $n^{th}$ vibration amplitudes are obtained from a decaying response such as that of Fig. 3, $\zeta \approxeq \frac{\delta }{2\pi }$ where $\delta =\frac{1}{n}ln\frac{x_0}{x_n}$.

• 3. Eccentricities, $x_e$ and $y_e$: These are measured using a Vernier caliper.

Appendix C: Equivalence between measurements made from the fixed and the oscillating frames.

Measurements made are from the fixed (laboratory) FoR. Therefore, a coordinate transformation from the oscillating FoR to the fixed FoR is required to interpret the results. Figure 15 depicts two FoRs, a fixed frame $X_F Q Y_F$ and a rotating frame $X_R Q Y_R$. The vibrometer measures the displacement $y_f$ of the flexible cylinder from the fixed FoR. The displacement $y_f$ can be expressed as

$$\begin{aligned} y_f=x_r\sin \theta +y_r\cos \theta . \end{aligned}$$

(68)

Fig. 15

Schematic depicting the transformation from a rotating to a stationary frame of reference

If the angular displacement $\theta$ is small, $y_f\approxeq \left( x_r\theta +y_r\right) \approxeq y_r$. This means that for small values of $\theta$, the observations ($x_f$ and $y_f$) made from the fixed FoR and those made from the moving FoR ($x_r$ and $y_r$) are identical. For the experiments, the results presented here, $\theta$, are of the order of $1e-5$ radians, while the orders of magnitude of $x_r$ and $y_r$ are comparable.