Abstract
Research on spinning shafts is mostly restricted to cases of constant rotating speed without examining the dynamics during their spin-up or spin-down operation. In this article, initially the equations of motion for a spinning shaft with non-constant speed are derived, then the system is discretised, and finally a nonlinear dynamic analysis is performed using multiple scales perturbation method. The system in first-order approximation takes the form of two coupled sets of paired equations. The first pair describes the torsional and the rigid body rotation, whilst the second consists of the equations describing the two lateral bending motions. Notably, equations of the lateral bending motions of first-order approximation coincide with the system in case of constant rotating speed, and considering the amplitude modulation equations, as it is shown, there are detuning frequencies from the Campbell diagram. The nonlinear normal modes of the system have been determined analytically up to the second-order approximation. The comparison of the analytical solutions with direct numerical simulations shows good agreement up to the validity of the performed analysis. Finally, it is shown that the Campbell diagram in the case of spin-up or spin-down operation cannot describe the critical situations of the shaft. This work paves the way, for new safe operational ‘modes’ of rotating structures bypassing critical situations, and also it is essential to identify the validity of the tools for defining critical situations in rotating structures with non-constant rotating speeds, which can be applied not only in spinning shafts but in all rotating structures.
Similar content being viewed by others
1 Introduction
Starting about 93 years ago, with the pioneered seminal work by Campbell [1,2,3], the main theory was developed to examine critical situations in vibrations of turbine wheels in constant rotating speeds. This work is the basis of the current examination of critical speeds of rotating structures in steady states using the diagram that indicates how the natural frequencies of the structure vary with the rotating speed (limited to steady states) incorporating the excitation frequency due to rotating speed, which forms the Campbell diagram (CD). Since then, based on CD, plenty of research articles have been reported about rotating structures and spinning shafts but restricted mainly to steady states. Extended literature review on critical speeds on steady states is out of the scope of this work. Only a few articles are related in examining their dynamics during spin-up and spin-down operation, which corresponds to non-constant rotating speed. Plaut and Wauer [4] examined parametric, external and combination resonances in coupled flexural and torsional oscillations of an unbalanced rotating shaft with non-constant rotating speed, but the rigid body equation of motion for non-constant rotating speed was neglected. Suherman and Plaut [5] used flexible internal support in order to mitigate lateral bending vibrations. In [5], a model was developed and dynamics for a spinning shaft with non-constant rotating speed was examined including a flexible internal support considering also the equation of rigid body motion, but the torsional motion was neglected in this treatment. Wauer [6] modelled and formulated equations of motion for cracked beams considering non-constant rotating speed, but without considering the rigid body equation of motion. It should be commented that in [4,5,6] the models are not considering all the motions in order to perform nonlinear dynamic analysis and the results are limited to these models. In [7], the equations of motion of a spinning shaft with dynamic boundary conditions (eccentric sleeves) were derived, since the main work was about the dynamics of the shaft due to the particular dynamic boundary conditions; although non-constant rotating speed was considered, it was not given any special attention.
Further work has been conducted in the so-called non-ideal systems, which correspond to rotating mechanical systems incorporating the electromechanical coupling with the DC motor to examine Sommerfeld effect but limited to discrete systems with the excitation of natural frequencies by the external torque of the motor [8,9,10]. The significance of considering non-ideal systems is discussed in [11], whereas there is comparison in dynamic results between ideal and non-ideal systems. Although in this area of research it is considered in some cases non-constant rotating speed, the work is focused on the effect of external torque through the DC motor in the nonlinear dynamics of these electromechanical systems, and it is also restricted to discrete models. In [12], nonlinear dynamics of rings rotating with variable speed considering small fluctuations from a constant average value were examined.
Noted that since 1960s with the works of Kauderer as mentioned in [13] and Rosenberg [14], the development of the nonlinear normal modes (NNMs) theory in examining dynamics of nonlinear mechanical systems is started, which has been continued about a decade later, for example, in [15,16,17]. Further information can be found in [13, 18, 19] with summaries of the methods used on this field. On this article, the method of multiple scales that has been developed in [20] will be used, and a discussion of the application of this method in examining NNMs is given in [21]. The reason for selecting multiple scales is that the spinning shaft with non-constant rotating speed is a non-natural mechanical system and can be treated relatively easy without the inversion of the mass matrix. As it is discussed herein another reason is that the arising formulation allows straight comparisons with the case of constant rotating speed.
In [22], NNMs of a Jeffcott rotor using multiple scales approach considering discrete model representing geometric nonlinearities of the shaft and constant rotating speed were determined. Invariant manifolds approach for the determination of NNMs has been used in [23] to examine dynamics of a spinning shaft with constant rotating speed including nonlinearities by the supported journal bearings. A combined method based on the invariant manifold with multiharmonic balance technique has been used in [24], to determine the NNMs of an asymmetric disc rotor with constant rotating speeds, considering nonlinearities in bearings. The multiharmonic balance technique has been used in [25], to examine stability and vibrations analysis of a complex flexible rotor bearing system. Based on invariant manifolds approach, in [26] a new method has been developed for the determination of NNMs, incorporating Rausher and harmonic balance methods, and it has been applied to determine the dynamics of a spinning shaft with constant rotating speed with nonlinearities and inertia forces in the supports. It should be noted that in [22,23,24,25,26] the models were considering constant rotating speed and nonlinearities in bearings, without examination of non-constant rotating speed. In [27], non-constant rotating speed for a rotating composite blade was considered, whereas a nonlinear system of partial differential equations (PDEs) coupled with one integro-differential equation (IDE) describing the rigid body angular motion, which is a similar model with the spinning shaft in non-constant rotating speed derived, herein, is derived.
Configuration of the spinning shaft with the considered motions, as a simply supported Euler Bernoulli beam
In this article, the dynamics of the shaft as an elastic continuum with non-constant rotating speed are examined purely and its correlation with the critical situations resulted from the steady-state analysis using the CD. Initially, the equations of motion of a spinning shaft with non-constant rotating speed made of isotropic material and considering Euler–Bernoulli (EB) beam are derived. Then, the nonlinear system of the PDEs has been discretised, and finally the method of multiple scales is used to determine the nonlinear normal modes (NNMs) with the analytical solution for the first- and second-order approximations of the discretised nonlinear system. At the end, in the numerical results section at first, a comparison of the individual multiple scales solution with numerical integration is made. Then, there is a comparison of the CD obtained from commercial finite element analysis (FEA) software with this one obtained from analytical solutions. Finally, the full multiple scales solution is compared with the direct numerical integration of the original system, and also the validity of the critical speeds obtained from the CD, considering also the detuning frequencies, is examined.
2 Equations of motion
On this part of the article, initially, the system of PDEs that describes the motion of a spinning shaft with non-constant rotating speed is derived, and then, it will be discretised with projection to the infinite basis of the associated linear system.
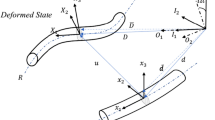
The shaft is considered, as simply supported EB isotropic beam with uniform properties and dimensions in the longitudinal direction, with rigid body \((\theta )\) motion, axial (u), lateral bending motions (v, w) with rotary inertia terms, and torsional motions \((\phi )\). Also in this paper, any non-conservative forces (damping, external forces/torques) and any imbalance are not considered. The Hamilton’s Principle is employed as follows,
with the variation of the kinetic energy of the shaft \((\delta T)\) and the variation of the potential energy of the shaft \(\left( {\delta U} \right) \).
The partial derivatives are designated with a subindex after a comma that shows under which variable is performed the differentiation, e.g. \(f_{,tt}\) means two derivatives of f with respect to time.
The integral of the variation of the kinetic energy is given by,
where \({{\varvec{R}}}\) is the position vector, \(\rho \) is the density of the shaft, and V is the volume of the shaft.
Considering the deformations for EB beam with generalised coordinates axial (u), both lateral bending (v, w) and torsional \((\phi )\) motions are indicated in Fig. 1. The position vector \(({{\varvec{R}}})\) in a fixed coordinate system can be defined as a rigid body rotation \((\theta )\) with respect to x axis applied in the position vector \(({{\varvec{r}}})\) in the rotating frame, and it is given by,
where A is the rigid body rotation matrix with respect to x axis with angle-\(\theta \) as indicated in Fig. 1.
Considering Eq. (3), the acceleration vector is given by,
where the first acceleration term is due to non-constant rotating speed, the second term is the centrifugal acceleration, the third term is the Coriolis acceleration and the last one is the translational acceleration.
In Eq. (2), inside the integral in the variation of kinetic energy, the vector product of the acceleration vector (Eq. 4) and the variation of the position vector are involved. The explicit form of the variation of the position vector based on the involved partial derivatives with respect to the generalised coordinates is derived in “Appendix-A” section. The determination of the vector product in right-hand side of Eq. (2) has been done in “Appendix-A” section, and using equations (A.3), the variation of kinetic energy with respect to the generalised coordinates is a trivial process.
In case of EB isotropic beam with the associated displacement vector including rotary inertia terms, it is trivial to define the variation of potential energy with respect to the generalised coordinates [28].
Finally, considering the variations of kinetic and potential energy with respect to the generalised coordinates and using Hamilton’s principle (Eq. 1), the following equations of motion arise:
-
Axial motion (u),
$$\begin{aligned} \delta J_u =mu_{,tt} -\left( {EAu_{,x} } \right) _{,x} =0. \end{aligned}$$(5a) -
Lateral bending in y-direction (v),
$$\begin{aligned} \delta {J}_{v}= & {} \underline{m\theta _{,tt}w-m\theta _{,t}^{2}v+2m\theta _{,t}w_{,t}}\nonumber \\&+\,mv_{,tt} -\left( {I_{1} v_{,ttx}} \right) _{,x} +\left( {EIv_{,xx}}\right) _{,xx} =0.\nonumber \\ \end{aligned}$$(5b) -
Lateral bending in z-direction (w),
$$\begin{aligned} \delta J_{w}= & {} \underline{-m\theta _{,tt} v-m\theta _{,t}^{2} w-2m\theta _{,t} v_{,t}}\nonumber \\&+\,mw_{,tt} -(I_{1} w_{,ttx})_{,x} +(EIw_{,xx})_{,xx} =0.\nonumber \\ \end{aligned}$$(5c) -
Torsional motion \((\phi )\),
$$\begin{aligned} \delta {J_\phi } {=} - {I_1}{\theta _{,tt}} - \underline{{I_1}\theta _{,t}^2\phi } + {I_1}{\phi _{,tt}} - {\left( {GI{\phi _{,x}}} \right) _{,x}} {=} 0.\nonumber \\ \end{aligned}$$(5d) -
Rigid body rotation \((\theta )\),
$$\begin{aligned} \delta J_\theta= & {} 2I_{1} \theta _{,tt} L+\theta _{,tt} \mathop {\int } \nolimits _0^L \left[ {\underline{mw^{2}+mv^{2}+2I_{1} \phi ^{2}}} \right] \hbox {d}x \nonumber \\&+\,2\theta _{,t} \mathop {\int }_{0}^{L} \left[ \underline{mvv_{,t} +mww_{,t} +2I_{1} \phi _{,t} \phi }\right] \hbox {d}x\nonumber \\&+\, \mathop {\int }_{0}^{L} \left[ \underline{mwv_{,tt} -mvw_{,tt} -2I_{1} \phi _{,tt}}\right] \hbox {d}x=0,\nonumber \\ \end{aligned}$$(5e)
where the nonlinear terms on these equations are underlined and noted that since the angular rigid body position \((\theta )\) is a variable, then the centrifugal and Coriolis are also nonlinear terms.
The distributed mass and the inertia coefficient for the spinning shaft with cyclical cross section as obtained through integration over the area of the cross section are given by,
where \(D_{i} =2r_{i}, D_{o} =2r_{o}\), the internal and external diameters of the shaft’s cross section, respectively (Fig. 1).
Also, it should be noted that Eq. (5a) describing the axial motion is fully decoupled from the rest of the system, and it is the typical equation describing the axial motion of an elastic beam; therefore, there is no reason to be considered any further in the present analysis. The derived equations of motion (Eq. 5) in case of restricted to lateral bending with rigid body rotation motions coincide with those obtained in [5], whereas the torsional motion has been neglected.
Considering also simply supported beam and the Hamilton’s principle, the strong and weak boundary conditions (BCs) are,
-
lateral bending in y-direction (v) (fixed in displacement-free to rotate, in both sides)
$$\begin{aligned} v\left( {0,t} \right)&= v\left( {L,t} \right) =v_{,xx} \ \left( {0,t} \right) = v_{,xx} \left( {L,t} \right) =0, \end{aligned}$$(7a--d) -
lateral bending in z-direction (w) (fixed in displacement-free to rotate, in both sides)
$$\begin{aligned} w\left( {0,t} \right)&=w\left( {L,t} \right) =w_{,xx} \left( {0,t} \right) \\&=w_{,xx} \left( {L,t} \right) =0, \end{aligned}$$(8a--d) -
torsional motion \((\phi )\), in one end that it is associated with the rigid body motion the coordinate system is fixed and the other end is considered as free (depends on the particular configuration of the shaft, e.g. second motor in the other side),
$$\begin{aligned} \phi \left( {0,t} \right) =\phi _{,x} \left( {L,t} \right) =0. \end{aligned}$$(9a--b)In case of constant rotating speed (\(\theta _{,t} =\varOmega =ct,\) therefore \(\theta _{,tt} =0\)), then the system of coupled equations in both lateral bending and torsion is taking the form,
-
Lateral bending in y-direction (v),
$$\begin{aligned}&-\,m\varOmega ^{2}v+2m\varOmega w_{,t} +mv_{,tt} -\left( {I_{1} v_{,ttx} } \right) _{,x}\nonumber \\&\quad +\,\left( {EIv_{,xx} } \right) _{,xx} =0. \end{aligned}$$(10a) -
Lateral bending in z-direction (w),
$$\begin{aligned}&-\,m\varOmega ^{2}w-2m\varOmega v_{,t} +mw_{,tt} -\left( {I_{1} w_{,ttx} } \right) _{,x} \nonumber \\&\quad +\,\left( {EIw_{,xx} } \right) _{,xx} =0. \end{aligned}$$(10b) -
Torsional motion \((\phi )\),
$$\begin{aligned} -I_{1} \varOmega ^{2}\phi +I_{1} \phi _{,tt} -\left( {GI\phi _{,x} } \right) _{,x} =0, \end{aligned}$$(10c)
whereas the torsional equation is decoupled from the rest lateral bending motions, and these both lateral bending equations of motion are typically found in the literature of spinning shafts. Also, it should be commented that the torsional motion \((\phi )\) is not the total distributed angular position \((\varphi \left( {x,t} \right) \), which is defined in the fixed frame with respect to rotation about x axis). Based on the configuration in Fig. 1, the total distributed angular position is given by, \(\varphi \left( {x,t} \right) =-\theta \left( t \right) +\phi \left( {x,t} \right) \), and this transformation lead to free–free boundary conditions for the total distributed angular position of the shaft with respect to the fixed frame.
The system of equations (5) can be projected to the infinite base of the corresponding linear modes of the homogeneous linearised problem of these PDEs (Eq. 5 neglecting the underlined terms). The linearised system is forming decoupled PDEs, whereas considering the B.C.s (Eq. 7–9), it can be shown that the equations are also self-adjoint, since the equations describe the well-known elastic motions in bending and torsion with typical BCs [29]. Therefore, the linear mode shapes are orthogonal to each other and also the linear modal equations decoupled.
The two corresponding PDEs (of Eq. 5b-c) describing the motion in both lateral bending motions including the rotary inertia terms are identical in both directions. The associated boundary value problem (BVP) solution is described in “Appendix-B” section with linear mode shapes and natural frequencies of the k-mode given by,
whereas the mode shapes have been normalised considering only the mass (m) coefficient terms.
The non-homogeneous torsional BVP can be solved using the integral of the Green’s function arising from the homogeneous problem multiplied with angular positions, but the angular acceleration has to be defined explicitly in order to obtain a specific solution. Therefore, we restrict the solutions to the corresponding linear homogeneous PDE describing torsional motion which arises from Eq. (5d) by neglecting terms associated with the rigid body motion. In this case, the linear BVP is similar to this one of a rod in axial vibration with clamped-free B.C.s. The solution of this BVP is having the following mode shapes and natural frequencies of the k-mode [29],
respectively, whereas the mode shapes have been normalised. The notation in frequency is used to designate that corresponds to the fixed-free boundary value problem, and then, the projection of the dynamics to the linear mode shapes is associated with this BVP. Noted that on this BVP local torsional motion is used instead of total angular position which corresponds to the free–free BVP. (And it is associated with the natural frequencies of the rotating shaft in torsion.)
The displacements in bending and the rotational angles due to torsion in equations (5b–d) are expressed in series of the linear mode shapes as follows,
where \(q_{v,k} \left( t \right) \) is the k-mode modal displacement in y-direction of bending, \(q_{w,k} \left( t \right) \) is the k-mode modal displacement in z-direction of bending, \(q_{\phi ,k} \left( t \right) \) is the k-mode modal displacement in torsion.
Equations (5b-c) are multiplied with \(y_j \left( s \right) \) and Eq. (5d) with \(y_j \left( s \right) \), and they are integrated over the length span of the shaft, using the weighted residual approach with Bubnov–GalerkinFootnote 1 approximation. As first attempt, in order to simplify the problem, the discrete system of equations of motion with truncation of series to the first linear mode for each motion is considered, and finally, the discrete equations describing the motion are taking the form,
with the following constants,
and also, the index associated with the number of modes is neglected since the first one in all cases is considered. Restricting equations (14) to the case of constant rotating speed (\(\theta _{,t} =\varOmega =ct,\) therefore \(\theta _{,tt} =0)\) the system of (Eq. 14) is taking the form,
The system of (Eq. 16) has coupled equations only between lateral bending motions through the Coriolis force and the associated CD (with these equations); as it is shown in [30] and herein, it is the same as this one obtained from FEA of a spinning shaft with constant rotating speed.
The multiple scales perturbation method developed by Nayfeh [20] is used, and different time scales are considered as follows,
therefore,
and also, the solutions of the system of the ‘modal’ equations (Eq. 14) are in the following form,
Also, following the multiple scales approach, the system of equations (14) for the various \(\varepsilon \)-scale orders (up to second order) is taking the form:
\(\underline{\varepsilon ^{0}},\)
\(\underline{\varepsilon ^{1}},\)
\(\underline{\varepsilon ^{2}},\)
In the left side of systems of Eqs. (19–20), the equations are coupled in pairs; the first pair is with the equations describing the rigid body angle with torsion and the second pair is with the coupled equations describing the two lateral bending vibrations.
3 Dynamic analysis
In this section, the systems (Eqs. 19 , 20), arising from multiple-scale formulation in different scales, will be solved explicitly.
3.1 Solution of first-order approximation for rigid body with torsional motions
The system of equations of the rigid body with torsional motions for the first-order approximation is described by equations (19a, d). Elimination of the secular terms in Eq. (19a), and taking into consideration Eq. (18), leads to,
Considering (21), the terms in the right-hand side of Eq. (19d) are seen to be eliminated.
To simplify the equations for the rest of the article, over-dot notation will be used instead of \(D_{0}\), and dash notation will be used instead of \(D_{1}\).
The first-order approximation for rigid body rotation (Eq. 19a) with torsion (Eq. 19d), considering equations (18, 21) and the new notation, can be written in the following form,
In the above system (Eq. 22), the angular rigid body position is involved only with its derivative; therefore, this system can be solved with respect to \(\dot{\theta }\). Then, the angular position can be trivially obtained by integration in time of the angular velocity. Using Eq. (22a) in (22b), the system can be decoupled easily, and the solution of these equations is a trivial problem given by [29],
with,
and setting,
then, the amplitudes of (Eq. 23) are given by,
3.2 Solution of first-order approximation for both lateral bending motions
The system of equations for both lateral bending motions of the first-order approximation is described by equations (19b–c). Considering Eq. (18) and the new notation, then the first-order approximation \((\varepsilon ^{1})\) equations of motion for lateral bending (Eq. 19b, c) are taking exactly the same form with equations (16a-b), which corresponds to constant rotating speed. As it is shown in [30], it will be verified in the numerical Sect. 4.2, and the natural frequencies of this system form the CD. The solution of the system (Eq. 16a-b) can be obtained by writing the system as first-order differential equations, and the four roots of the characteristic polynomial are given by,
with,
which, it is true for any \(\Omega \) if,
then the shaft has sufficient large ratio of length with respect to the internal and external radius of the hollow shaft, in which it is the case for most flexible shafts in engineering applications. Also,
Therefore, based on (Eq. 28) and the values of the following parameters defined by (Eq. 29a,c), and condition (Eq. 29b), there are the following three cases for the solutions of the eigenvalue problem.
Case 1 \(\eta _2 >0,\,\eta _{1} +\sqrt{\eta _2 }<0\),
The first condition occurs when,
And the second occurs when,
The eigenvalues are given by,
Case 2 \(\eta _2>0,\, \eta _{1} +\sqrt{\eta _2 }>0\),
In the second case, the eigenvalues are given by,
Case 3 \(\eta _2 <0,\)
In the third case, the eigenvalues are given by,
The first case corresponds to relatively low rotating speeds. The explicit form of the natural frequencies with respect to rotating speed, in first case, is given by,
and, the plot of these frequencies with respect to the rotating speed is used to form the CD for a shaft with constant rotating speed.
It should be noted that in case of neglecting the rotary inertia terms in bending (with \(I_{1} =0\) in Eq. 5b, c, then \(M=0\)), then the evaluation of the parameters in equations (29a,c) indicates that it corresponds to the first case and the natural frequencies are given by,
In case of constant rotating speed, it should be mentioned that based on the latest definition of the normal modes which are the periodic motions [19], not all of these frequencies are associated with the normal modes since the periodicity condition for the angular position must satisfy,
and this is true only when \(\omega _i =n\varOmega \) (with n any integer) which is the case of critical speeds of the shaft in steady states, and these are the frequencies of the associated Normal Modes of the shaft, which justifies the resonances in FRFs whilst varying the rotating speeds, and they occur when the rotating speed is very close (due to damping) to the critical speed. Otherwise stated, the critical speeds in terms of frequencies are the same with the vibration frequencies of the structure which cause resonance, and this terminology is used also on this article arising from the standard definition in the literature, irrespective though, if it is true or not in the case of non-constant rotating speeds which is under examination herein.
The associative, on the eigenvalues, matrix of eigenvectors and its inverse are given by,
Since system (Eq. 16a–b) is a linear system, the solution can be determined easily using the fundamental solution matrix which is given by,
with,
Therefore, the solutions are given by,
with,
3.3 Solution of amplitude modulation equations of first order for rigid body with torsional motions
In order to finalise the first-order approximation solution for rigid body and torsional motions, in this section, the amplitudes in equations (23) with respect to time scale \(T_{1}\) are determined by solving the amplitude modulation equations arising by elimination of the secular terms of \({\varepsilon }^{2}\) in equations (20a,d). Considering equations (18, 21) and elimination of \(T_2 \) secular terms, the right-hand side of equations (20a,d) leads to,
The explicit form of equations (45), considering the first-order solutions (Eqs. 23 , 42) are taking the form,
with,
Elimination of secular terms of Eq. (46) and averaging in constant terms lead to the amplitude modulation equations of first-order approximation given by,
whereas in the derivation of (Eq. 48b) the explicit form of amplitudes defined in equations (26–27) which lead to elimination of the second term in left side was considered. Also, with averaging of the rest secular terms of Eq. (46) and separating real with imaginary parts, the following set of equations lead to,
Using equations (26–27) in (Eqs. 49a, 49c) it can be shown that,
Then, the system of equations (49b,d) is taking the form,
with,
The eigenvalues \(\left( {\lambda _{3,1\div 2} } \right) \) and also the associated eigenvectors are given by,
and the solution of the system (Eq. 49) can be determined using the fundamental solution matrix, which is given by,
which lead to the solution of amplitudes for torsional and rigid body motions in \(T_{1}\)-scale, and in explicit form they are given by,
whereas the last two equations arise from equations (49a,c) considering (Eqs. 50, 55a–b) in conjunction with (Eqs. 26–27).
Combining the solutions in both scales (Eq. 23 with 55), the following final solution in torsional with rigid body motions for first-order approximation leads to,
3.4 Solution of amplitude modulation equations of first order for both lateral bending motions
In this section, the amplitudes in equations (42) with respect to time scale \(T_{1}\) by eliminating the secular terms of \(\varepsilon ^{2}\) in equations (20b–c) are determined. Considering equations (18, 21) and, using the new notation, the right-hand side of equations (20b–c) are taking the form,
Considering the first-order solutions (Eqs. 23 , 42), equations (57) are taking the form,
where the overbar denotes the complex conjugate. In equations (58), the elimination of secular terms and the separation of real with imaginary parts lead to the following two decoupled similar systems of differential equations, which can be written in the following general form,
where \(j=1\) corresponds to the system arising from first frequency \((\omega _{1})\) and \(j=2\) to the system arising from the second frequency \((\omega _2)\).
Setting,
The eigenvalues of this system are given by,
The associated matrix of eigenvectors and its inverse are given by,
With fundamental solution matrix given by,
and,
Then, the solution of system (Eq. 59) is given by,
with amplitudes for:
\(B_{{v1,j}} \left( {T_{1} } \right) \) given by,
\(B_{{ v2,j}} \left( {T_{1} } \right) \) given by,
\(B_{{w1,j}} \left( {T_{1} } \right) \) given by,
\(B_{{w2,j}} \left( {T_{1} } \right) \) given by,
Combining the solutions in both scales (Eq. 42 with 64), the following final solution in both lateral bending motions for first-order approximation leads to,
In equations (66a-b), it is clear that the frequencies \(\omega _{\mathrm{det},1,1} \), \(\omega _{\mathrm{det},1,2} \), \(\omega _{\mathrm{det},2,1} \), \(\omega _{\mathrm{det},2,2} \) are all detuning frequencies from the CD; since it is shown in [30] and in numerical section 4.2 of this article, the first-order solution frequencies \((\omega _{1} ,\omega _2)\) coincide with those in CD.
It should be mentioned that the system (Eq. 59) becomes singular near the first-order critical speeds with the condition of,
and this analysis is no longer valid. Similarly, in the case of neglecting rotary inertia terms with \((M=0)\), then, exactly at the critical speeds of first-order approximation the system (Eq. 59) becomes singular and this analysis is no longer valid.
Also, in case of critical speeds in first-order approximation (which can be obtained also from the CD), then \(\omega _j =\varOmega \), either for \(j=1,2\), and then,
3.5 Solution of second-order approximation for rigid body with torsional motions
In this section, the second-order system of differential equations for the rigid body with torsional motions formed by equations (20a,d) is solved, and considering Eq. (46) after the elimination of secular terms in Sect. 3.3, the following system of differential equations leads to:
with constants in \(T_{0}\)-scale given by (Eq. 47). This system can be decoupled easily to,
with,
The solution of second equation can be derived easily considering the solution of first-order approximation, and using the Duhamel’s integral, it is given by [29],
with,
Finally, considering (Eq. 72) with direct integration of Eq. (70a) the angular velocity in second-order approximation leads to,
with,
3.6 Solution of second-order approximation for both lateral bending motions
In this section, the second-order system of differential equations for both lateral bending motions formed by equations (20b–c) is solved, whereas using new notation, considering (Eq. 58) and neglecting secular terms, leads to the following system of differential equations:
with,
Comparison of the direct numerical simulation with the analytical solution of first-order approximation: a for bending motion in y-direction \((q_{v,1} \left( {T_0 } \right) )\), b for bending motion in z-direction \((q_{w,1} \left( {T_0 } \right) )\)
The solution of the non-homogeneous linear system (Eq. 76), for zero initial conditions, can be determined through integration of the fundamental matrix \({\varvec{\Phi }} _{\mathbf{2}} \left( {\mathbf{T}_{\mathbf{0}} -{{\varvec{s}}}} \right) \) (explicit form is given by Eq. 39) multiplied with the non-homogeneous part; therefore, using also equations (27, 42, 55, 64), it is given by,
with, amplitudes given in equations (C.2-13) in “Appendix-C” section.
It should be noted that considering zero initial conditions in torsion, equation (27b) applied in (Eq. 77) leads to,
Therefore, Eq. (79) means that in case of zero torsional initial conditions the second-order approximation for both lateral bending motions is zero.
4 Numerical results and discussion
A stainless steel shaft with external and internal radius \({r}_{\mathrm{o}} {=0.03\,\hbox {m}}\), and \({r}_\mathrm{i} {=0.028\,\hbox {m}}\) is considered, respectively. The length is \({L=1\,\hbox {m}}\), the density is \(\rho {=7850\,\hbox {kg/m}}^{{3}}\), with the material properties of Young’s and shear modulus are \(E=200\,\hbox {GPa}\), \(G=76.9\,\hbox {GPa}\), respectively. It should be noted that the particular shaft is thin-walled since the ratio of length with thickness is 500 \(({\gg }\, 10)\) and ratio of length with external diameter is 16.67 \(({>}\,10)\); therefore, for the examination of the lower modes of vibration it can be modelled as EB beam by neglecting the shear effects [31].
4.1 Verification of individual analytical solutions
In this section, the shaft with the following initial conditions is considered,
and it is compared, the individual solutions are obtained in Sects. 3.1–3.6 with direct numerical integration of the associated individual systems. It should be mentioned that for this angular velocity (\(\dot{\theta }_{1}(0))\), in order to define the natural frequencies in bending, based on Sect. 3.2 for the first-order approximation analysis, the following parameters have to be specified using equations (32a,c),
which corresponds to the first case and the frequencies in bending for first-order approximation are given by Eq. (35). Also, for this particular shaft \(\eta _2 \le 0\) for \(\dot{\theta }_{1} (0) \ge 15{,}890 \hbox { rad/s } (=151{,}741\,\hbox {R.P.M.})\) in very high rotating speeds which is the third case and can be practically ignored for this shaft.
In Fig. 2a, b, the responses from analytical solution (Eq. 42a–b) and the responses with the direct numerical integration of the system with equations (28a–b) are depicted, which is the first-order approximation for both lateral bending motions. In both figures (2a,b), the numerical simulation with the analytical solutions is in very good agreement.
Comparison of the direct numerical simulation with the analytical solution of amplitude modulation equations for both lateral bending motions: a amplitudes \({B}_{\mathrm{v1,1}} \left( {T_{1} } \right) \) and \({B}_{\mathrm{v2,1}} \left( {T_{1} } \right) \), b amplitudes \({B}_{\mathrm{v1,2}} \left( {T_{1} } \right) \) and \({B}_{\mathrm{v2,2}} \left( {T_{1} } \right) \), c amplitudes \({B}_{\mathrm{w1,1}} \left( {T_{1} } \right) \) and \({B}_{\mathrm{w2,1}} \left( {T_{1} } \right) \), d amplitudes \({B}_{\mathrm{w1,2}} \left( {T_{1} } \right) \) and \({B}_{\mathrm{w2,2}} \left( {T_{1} } \right) \)
The analytical solutions (Eq. 64a–d) of amplitude modulation equations for both lateral bending motions in T1 scale defined by the systems (Eq. 59 for first with \(j=1\) and second mode with \(j=2\)) and those obtained by direct numerical integration, are depicted in Fig. 3a–d. The analytical solutions in both figures are in very good agreement with those obtained from direct numerical integration.
In Fig. 4a–b are depicted the responses for the second-order approximation for torsional and rigid body motions of the system of equations (69) using direct numerical integration and also using the analytical solutions (Eqs. 72, 74). In Fig. 4a, b, the analytical solutions are in very good agreement with those obtained from numerical integration.
Comparison of the direct numerical integration results with the analytical response of second-order approximation: a for torsional modal motion \(\left( {q_{\phi ,2} \left( {T_0 } \right) } \right) \), b for angular velocity \((\dot{\theta }_{2}(T_{0}))\)
In Fig. 5a, b are depicted the second-order approximation responses, from analytical solutions (Eq. 78a, b) for both lateral bending motions and compared with those obtained with direct numerical integration of the system (Eq. 76); they are in very good agreement.
Comparison of the direct numerical integration results with the analytical response of second-order approximation: a for bending motion in y-direction \((q_{v,2} \left( {T_0 } \right) )\), b for bending motion in z-direction (\(q_{w,2} \left( {T_0 } \right) )\).
4.2 Determination of Campbell diagram
In this section, the CD obtained with finite element simulations using commercial software (ANSYS), the analytical frequencies from Sect. 3.2, and the detuning frequencies from Sect. 3.4 is compared. Based on the particular shaft dimensions and material, in Table 1 are listed the different values of the parameters (\(\eta _{1}, \,\eta _2)\) determined by equations (29a, c) for several rotating speeds, whereas it is clear: \(\eta _{1} <0\), \(\eta _2 >0\) and \(\left( {\eta _{1} +\sqrt{\eta _2 }} \right) <0\) which leads to the first case of solutions as described in Sect. 3.2. The natural frequencies are given by Eq. (35). It should be noted that the natural frequencies obtained with Eq. (35) are corresponding to the solution of the first-order approximation without considering the detuning frequencies arising from the amplitude modulation equations.
A solid model of the shaft was created for FEA with the commercial software ANSYS, and linear modal analysis for various rotating speeds was performed. In Fig. 6 are depicted the natural frequencies of the first two modes in bending for five rotating speeds determined with FEA and those obtained from analytical methods of Sects. 3.2 (linear) and 3.4 (detuning frequencies).
It is clear that the two lines associated with the theoretical linear natural frequencies (f1, f2) obtained using Eq. (35) are in very good agreement with those obtained with FEA.
Campbell diagram and the nonlinear first-order solution with detuning frequencies
Even for zero rotating speed, whereas there is one double mode in bending (with different mode shapes), there is a slight discrepancy in frequencies between analytical and FEA with the value of the later to be slightly lower. This can be attributed to the fact that the EB beam theory is neglecting the shear effects, which is not the case in the finite element modelling in ANSYS. The same trend is following the natural frequencies in all the rest rotating speeds. Also, it can be depicted from Fig. 6 that the critical speed based on the linear natural frequencies is at 4878 R.P.M.
Also in Fig. 6, the theoretical natural frequencies for different rotating speeds are depicted using the first-order solution (Eq. 35) incorporating the detuning frequencies from amplitude modulation equations (67a–b) (considering \(\hbox {A}_{\mathrm{11}} ={\varOmega })\) and neglecting the single point that the amplitude modulation equations become singular. In Fig. 6, examining the detuning frequencies from the CD, there are additional three distinct main lines of frequencies (below 5000 R.P.M.).
The first one is below the first linear mode resulting in one more ‘critical speed’ at 3260 R.P.M., which is lower than the linear one. Also, about the other two additional lines of modes; one is in between the two linear modes and one is higher than the second linear mode. The significance of the solutions of the first-order approximation and also of the CD with the associated critical speeds are examined in the next section, whereas it is compared the analytical solutions with direct numerical integration of the original system.
4.3 Comparison of multiple scales solution with direct numerical integration
In this section, a shaft with initial conditions only in lateral bending to restrict the examination in phenomena relevant to the CD is considered. It should be noted that a considered set of initial conditions in lateral bending is not just one. The shaft can have any value of \(\theta \) as initial condition (arbitrary constant); therefore, the selected set of initial conditions for lateral bending motions corresponds to all instances which have the same combined radial amplitude, and it is defined by the two deformations of the lateral bending motions. In this section, the following set of initial conditions is used,
for four different rotating speeds,
-
(a)
\({\dot{\theta }_a}\left( 0 \right) = 104.72\hbox { rad/s }(=1000\hbox { R.P.M.})\),
-
(b)
\({\dot{\theta }_b}\left( 0 \right) = 157.08\hbox { rad/s }(=1500\hbox { R.P.M.})\),
-
(c)
\({\dot{\theta }_c}\left( 0 \right) = 341.39\hbox { rad/s }(=3260\hbox { R.P.M.})\),
-
(d)
\({\dot{\theta }_d}\left( 0 \right) = 510.82\hbox { rad/s }(=4878\hbox { R.P.M.})\),
and the responses obtained from overall multiple scale solution (Eq. 17) using first- and second-order solutions (Eqs. 56 , 66, 72, 74, 78) are compared with those responses obtained with the direct numerical integration of equations (14). It should be commented that for these initial conditions, the second-order approximation for both lateral bending motions is zero (Eq. 79).
The third \((\dot{\theta }_{c}(0)\) and fourth \((\dot{\theta }_{d}(0))\) angular velocities are at the critical speeds as they are obtained from Fig. 6, and it is examined the validity of this first-order approximation analysis.
On each one of the following figures that correspond to the responses of lateral bending motions, three responses are depicted: these ones obtained from direct numerical simulation; the second ones obtained from the full multiple scales analysis; and the third ones obtained from multiple-scale analysis restricted to only \(T_{0}\)-scale of the first-order approximation analysis.
Comparison of the direct numerical integration responses with the multiple scales solution for \(\dot{\theta }_{a}(0)\) rad/s: a bending motion in y-direction \((q_v \left( t \right) )\), b bending motion in z-direction (\(q_w \left( t \right) )\), c torsional modal angle \(\left( {q_\phi \left( t \right) } \right) \), d angular velocity \((\dot{\theta }(t))\)
In Fig. 7a–d are depicted the transient responses from analytical solution and those from direct numerical integration for the first angular velocity \(\dot{\theta }_{a}(0)\). In Fig. 7a, the modal responses are depicted for lateral bending motion in the y-direction \((q_v \left( t \right) )\), obtained from analytical and numerical solutions. The responses of the direct numerical integration with the full multiple scales solution are in very good agreement apart of some small spikes, e.g. in around 0.2, 0.35 s etc. in higher frequencies due to restricted multiple scales analysis to second-order approximation. On the contrary, the first-order solution which corresponds to the restricted T0-scale solution (associated with the CD) is very different from this one obtained from direct numerical integration even in low frequencies, e.g. envelope. In Fig. 7b are depicted the transient modal responses for lateral bending motion in the z-direction \((q_w \left( t \right) )\), which are provide the same qualitative results as those obtained from Fig. 7a for lateral bending motion in the y-direction \((q_v \left( t \right) )\); the numerical with the analytical are in good agreement.
For low angular velocities, the first-order total analytical solution is valid for the estimation of the dominant frequencies as they are obtained including the detuning frequencies from the CD, noted though that the associated solutions with the CD are not describing the dynamics.
In Fig. 7c are depicted the transient modal responses for torsion, obtained from direct numerical integration and the multiple scales solution. They follow the same envelope in lower frequencies but not in higher frequencies. Similar results are concluded from Fig. 7d, with the transient responses of the angular velocity between the solutions obtained from direct numerical integration and multiple scales solutions. In both analytical solutions, for torsional modal angle and angular velocity, the higher-order terms in multiple scales analysis are needed for convergence in higher frequencies.
It should be noted that similar results for torsional and rigid body rotation responses were obtained in all the other cases. Therefore on the subsequent presented results, although there has been comparison between numerical with analytical solutions for all the responses, due to the fact that the torsional with rigid body motions responses have the same information as in Fig. 7c, d, they will be omitted and it will be presented only the results for lateral bending motions.
Figure 8a, b depicts the transient responses of the analytical solution, and the direct numerical integration using the second angular velocity \(\dot{\theta }_{b}(0)\). In Fig. 8a are depicted the modal responses for lateral bending motion in the y-direction (\(q_v \left( t \right) )\), obtained from the direct numerical integration of the original system, and of the analytical solutions. The responses of the direct numerical integration with the multiple scales solution are in very good agreement for a short time interval, e.g. 0–0.3 s, but in later stages some lower frequencies in numerical responses are different from the full analytical solution and this discrepancy can be attributed that the higher-order terms (higher than second-order approximation) are getting significant for this initial angular velocity.
Also, considering the restricted to \(T_{0}\)-scale of first-order approximation solution, the comparison with direct numerical integration solution shows that they are very different.
In Fig. 8b are depicted the transient modal responses for lateral bending motion in the z-direction (\(q_w \left( t \right) )\). The full multiple scales analytical solution is in good agreement with this one obtained from direct numerical integration only for the first 0.04 s and then some different lower frequencies in the numerical solution are playing a dominant role and can be attributed to the need of including higher-order terms in the multiple scales solution. It should be commented that the first-order analytical solution restricted only to \(T_{0}\)-scale is very different from this one obtained from direct numerical integration.
Comparison of the direct numerical integration responses with the multiple scales solution for \(\dot{\theta }_{b}(0)= 157.08\) rad/s: a bending motion in y-direction \((q_{v} \left( t\right) )\), b bending motion in z-direction \((q_{w} \left( t\right) )\)
In Fig. 9 are depicted the transient responses for lateral bending motion in the y-direction \((q_v \left( t \right) )\), of the analytical solutions, and direct numerical integration for the third angular velocity \(\dot{\theta }_{c}(0)\) which is in the critical speed caused by the detuning frequency.
The responses of the direct numerical integration with the multiple scales solution are in very good agreement for a very short time interval, e.g. 0–0.2 s, but in later stages some lower frequencies in numerical responses make them different from the full analytical solution, and this discrepancy can be attributed to the absence of higher-order terms in the multiple scales analytical solution. Also, considering the first-order approximation response restricted to \(T_{0}\)-scale solution, the comparison with direct numerical integration response shows that they are very different, even in lower frequencies.
Considering that the lower extreme values of almost the same amplitude on this time interval, which are indications of the lower frequency, then for the numerical solution they are 13 and for the first-order restricted analytical solution they are 21, which means that the analytical frequency is almost double of this one existing in numerical responses. Similar results were obtained for the responses of lateral bending motion in the z-direction (\(q_w \left( t \right) )\).
Comparison of the direct numerical integration responses with the multiple scales solution for \(\dot{\theta }_{c}(0)= 341.39\) rad/s, corresponding to bending motion in y-direction \((q_v \left( t \right) )\)
Comparison of the direct numerical integration responses with the multiple scales solution for \(\dot{\theta }_{d}(0)=510.82\) rad/s, corresponding to bending motion in y-direction \((q_v \left( t \right) )\)
In Fig. 10 are depicted the transient modal responses for lateral bending motion in the y-direction (\(q_v \left( t \right) )\), of the analytical solutions, and the direct numerical integration for the fourth angular velocity \(\dot{\theta }_{d}(0)\), which is the first critical speed designated by the CD. The responses of the direct numerical integration with the multiple scales solution are very different.
Wavelet spectra of the numerical responses for lateral bending motion in y-direction (\(q_v \left( t \right) )\) at \(\dot{\theta }_{d}(0)=510.82\) rad/s
Also, considering the first-order approximation restricted to \(T_{0}\)-scale solution (CD frequencies), the comparison with direct numerical integration solution shows that they are very different too, even in lower frequencies considering that the lower extreme values of the numerical solution on this time interval are 8, and for the first-order analytical solution they are 16; therefore, the designated by CD frequency is double of this one from numerical simulation. Similar results, without any qualitative difference, were obtained from the comparison of the transient modal responses for lateral bending motion in the z-direction (\(q_w \left( t \right) )\).
The numerical responses in fourth case, for both lateral bending motions, have been further analysed using wavelet transform (with Morlet motherwavelet) with a MATLAB tool developed in University of Liege [32, 33]. In Fig. 11 is depicted the wavelet spectrum of the response in lateral bending in y-direction \((q_v \left( t \right) )\), and it is clear that the dominant lower frequency is about 38 Hz, and also considering the first-order theoretical analysis in \(T_{0}\)-scale, \(f_{1} =81.3 \hbox { Hz}\), (equal to the critical speed) which is about the double size of the main frequency of both lateral bending numerical responses.
Similar results were obtained from the wavelet spectrum of the numerical response for lateral bending in z-direction (\(q_w \left( t \right) )\). Therefore, the ‘critical speed’ arising from the CD in case of non-constant rotating speed is no longer critical since the numerical responses are having different frequencies from this one which corresponds to the critical speed \((f_{1})\).
The critical speeds defined by the CD are no longer valid to describe critical situations in case of non-constant rotating speed.
Also, near the critical speeds the multiple scales, up to second-order solution, are not capturing the dominant lower frequencies. In such cases, higher-order terms have to be included in the multiple scales solution for the determination of NNMs. Noted that the selected method in determining the NNMs (multiple scales) is rather useful to make clear the comparison between the dynamical systems arising with constant rotating speed and the case of non-constant rotating speed, since they coincide in first-order approximation.
Since the system is nonlinear, it should be mentioned that for the selected initial conditions in numerical simulations there is no evidence of chaos, small perturbations led after several circles to very close solutions with the original simulation. Further investigation is needed on this aspect for any case of spinning shaft, by means of examining possible routes to chaos in a spinning shaft with non-constant rotating speed. Also, noted that the Bubnov–Galerkin approximation is truncated to only the first mode, in order to examine nonlinear modal interactions (caused from the modal coupling in rigid body rotation equation) more modes have to be included.
5 Conclusions
In this article, modelling of the spinning shaft with non-constant rotating speed and then discretisation by projecting the dynamics in the basis of infinite modes associated with the linear system have been performed. In the discrete system which arises after truncation to the first mode, the method of multiple scales for nonlinear dynamic analysis is applied. The system’s equations were written up to second-order time scale and their left side showed that the four originally coupled equations were coupled in pairs. The first pair consists of the equations describing rigid body motion coupled with torsion and the first- and second-order approximations have been solved explicitly considering also the amplitude modulation equations arising from the elimination of the secular terms in second-order approximation. The comparison of the individual analytical responses obtained from the second-order approximation for torsional and rigid body motions with those arising from direct numerical integration is in very good agreement.
The second pair of equations, describing the two lateral bending motions in the first order, is coinciding with the case of constant rotating speed, and then, the explicit form of the natural frequencies was derived, which are in very good agreement with the CD obtained with commercial finite element software. The consideration of the amplitude modulation equations arising from the elimination of secular terms in second-order approximation resulted detuning frequencies in the CD. The individual solutions for first- and second-order approximations for both lateral bending motions are in very good agreement with the solutions obtained by direct numerical integration.
Finally, the original system of the discrete modal equations is numerically integrated to get the responses for comparison with the multiple scales analytical solutions. In case of relative low rotating speeds, the full multiple-scale analytical responses for both lateral bending motions are in good agreement with the numerical solution, but the restricted solution to \(T_{0}\)-scale of first-order approximation which is associated with the CD is very different. The analytical torsional and angular velocity responses are very close to numerical solutions only in low frequencies (the envelope). In order to have better agreement, between numerical and analytical results for torsional and rigid body responses the higher-order terms in multiple scales analysis have to be considered.
In higher rotating speeds even close to the critical speeds obtained from the CD, the multiple scales solution up to second order for lateral bending motions, is not describing very well the dynamics, and higher-order terms in multiple scales analysis have to be included. Also, in critical speeds arising from the CD, the original nonlinear system is vibrating in frequencies different than those corresponding to the critical speeds. Therefore, these speeds are not critical for non-constant rotating speed, and therefore, the CD fails to describe the critical situations during spin-up, down operation.
Since it is shown in this work that the CD is no longer describing the critical situations, this work paves the way for new safe operational ‘modes’ of rotating structures with bypassing critical situations defined by the CD using acceleration of the rotating speed and then ‘settle’ in a ‘secure’ higher rotating speed for steady-state operation. Further work is needed on this direction, since the critical situations during spin-up/down operation for the safety of the rotating structure have to be identified.
Also, this work is important to identify the validity of the tools used to describe critical situations in case of spin-up, down operations of all rotating structures not only restricted to spinning shafts but in any other rotating structure, e.g. motors, gearboxes, turbines, wind turbines and helicopter blades.
As a continuation of this work, additional terms in modelling, e.g. non-conservative forces/torques, imbalances etc, subsequent with dynamic analysis have to be considered. Since the system is nonlinear, it is essential to find any possible routes to chaos. Also, nonlinear modal interactions have to be examined, including more terms in Bubnov–Galerkin approximation.
Notes
Based on the remark by Prof. Y. V. Mikhlin.
References
Campbell, W.: The protection of steam turbine disk wheels from axial vibration part I. General Electric Rev. XXVII(6), 352–360 (1924)
Campbell, W.: The protection of steam turbine disk wheels from axial vibration part II—exposition of the nature and theory of vibration in turbine wheels. General Electric Rev. XXVII(7), 459–484 (1924)
Campbell, W.: The protection of steam turbine disk wheels from axial vibration part III—methods of design and testing for the protection of turbine bucket wheels from axial vibration. General Electric Rev. XXVII(8), 511–535 (1924)
Plaut, R.H., Wauer, J.: Parametric, external and combination resonances in coupled flexural and torsional oscillations of an unbalanced shaft. J. Sound Vib. 183, 889–897 (1995)
Suherman, S., Plaut, R.H.: Use of a flexible internal support to suppress vibrations of a rotating shaft passing through a critical speed. J. Vib. Control 3, 213–234 (1997)
Wauer, J.: Modelling and formulation of equations of motion for cracked rotating shafts. Int. J. Solids Struct. 26, 901–914 (1990)
Kirk, A., Georgiades, F., Bingham, C.: Towards determination of critical speeds of a rotating shaft with eccentric sleeves: equations of motion, mech. machine science. In: Proceedings of 9th IFToMM Int. Conf. on Rotor Dynamics, pp. 1809–1822, Milan, 22–25 September, 2014 (2015)
Balthazar, J.M., Mook, D.T., Weber, H.I., Brazil, R.M.L.R.F., Fenili, A., Belato, D., Felix, J.L.P.: An overview on non-ideal vibrations. Meccanica 38, 613–621 (2003)
Warminski, J., Balthasar, J.M., Brasil, R.M.L.R.F.: Virbations of a non-ideal parametrically and self-excited model. J. Sound Vib. 245, 363–374 (2001)
Felix, J.L., Balthazar, J.M., Brazil, R.M.: A short note on transverse vibrations of a shaft carrying two (or one) disk excited by a nonideal motor. J. Comput. Nonlinear Dyn. 4(1), 014501 (2008). https://doi.org/10.1115/1.3007979
Warminski, J., Balthasar, J.M.: Vibrations of a parametrically and self-excited system with ideal and non-ideal energy sources. J. Braz. Soc. Mech. Sci. Eng. (2003). https://doi.org/10.1590/S1678-58782003000400014
Natsiavas, S.: On the dynamics of rings rotating with variable spin speed. Nonlinear Dyn. 7, 345–363 (1995)
Mikhlin, Y.V., Avramov, K.V.: Nonlinear normal for vibrating mechanical systems. Review of theoretical developments. Appl. Mech. Rev. 63, 060802-1:21 (2010)
Rosenberg, R.M.: Normal modes of nonlinear dual-mode systems. J. Appl. Mech. 27, 263–268 (1960)
Rand, R.: Nonlinear normal modes in two-degrees-of-freedom systems. J. Appl. Mech. 38, 561 (1971)
Szemplinska-Stupnicka, W.: Non-linear normal modes and the generalized Ritz method in the problems of vibrations of non-linear elastic continuous systems. Int. J. Nonlinear Mech. 18, 149–165 (1983)
Vakakis, A.F., Manevitch, L.I., Mikhlin, Y.V., Pilipchuk, V.N., Zevin, A.A.: Normal Modes and Localization in Nonlinear Systems. Wiley, New York (1996)
Avramov, K.V., Mikhlin, Y.V.: Review of applications of nonlinear normal modes for vibrating mechanical systems. Appl. Mech. Rev. 65, 020801-1:20 (2013)
Kerschen, G., Peeters, M., Golinval, J.-C., Vakakis, A.F.: Nonlinear normal modes, part I: a useful framework for the structural dynamicist. Mech. Syst. Signal Process. (2009). https://doi.org/10.1016/j.ymssp.2008.04.002
Nayfeh, A.H.: A perturbation method for treating nonlinear oscillation problems. Stud. Appl. Math. (1965). https://doi.org/10.1002/sapm1965441368
Nayfeh, A.H.: On direct methods for constructing nonlinear normal modes of continuous systems. J. Vib. Control 1, 389–430 (1995). https://doi.org/10.1177/107754639500100402
Yabuno, H., Kashimura, T., Inoue, T., Ishida, Y.: Nonlinear normal modes and primary resonance of horizontally supported Jeffcott rotor. Nonlinear Dyn. 66, 377–387 (2011)
Legrand, M., Jiang, D., Pierre, C., Shaw, S.W.: Nonlinear normal modes of a rotating shaft based on the invariant manifold method. Int. J. Rotat. Mach. 10(4), 319–335 (2004)
Avramov, K.V., Borysiuk, O.V.: Nonlinear dynamics of one disk asymmetrical rotor supported by two journal bearings. Mech. Mach. Theory 67, 1201–1219 (2012). https://doi.org/10.1007/s11071-011-0063-x
Villa, C., Sinou, J.-J., Thouverez, F.: Stability and vibration analysis of a complex flexible rotor bearing system. Commun. Nonlinear Sci. Numer. Simul. 13, 804–821 (2008). https://doi.org/10.1016/j.cnsns.2006.06.012
Perepelkin, N.V., Mikhlin, Y.V., Pierre, C.: Non-linear normal forced vibration modes in systems with internal resonance. Int. J. Nonlinear Mech. 57, 102–115 (2013)
Georgiades, F., Latalski, J., Warminski, J.: Equations of motion of rotating composite blades with non-constant rotating speed. Meccanica (2014). https://doi.org/10.1007/s11012-014-9926-9
Nayfeh, A.H., Pai, F.: Linear and Nonlinear Structural Mechanics, 1st edn. Willey, New York (2004)
Meirovitch, L.: Fundamental of Vibrations. Waveleand Press, Long Grove (2001). ISBN: 1577666917, 9781577666912
Georgiades, F.: Towards the determination of a nonlinear Campbell diagram of a spinning shaft with non-constant rotating speed. Euromech 573, 25–27 August 2015, Lyon. http://573.euromech.org/speakers
Librescu, L., Song, O.: Thin-Walled Composite Beams. Springer, Berlin (2006)
Argoul, P., Le, T.-P.: Instantaneous indicators of structural behaviour based on the continuous Cauchy wavelet analysis. Mech. Syst. Signal Process. 17, 243–250 (2003)
Le, T.-P., Argoul, P.: Continuous wavelet transform for modal identification using free decay response. J. Sound Vib. 277, 73–100 (2004)
Acknowledgements
The author would like to thank Prof. Y. V. Mikhlin, for his valuable suggestions on improving the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix-A
In this part of the article, it is determined explicitly the variation of position vector \((\delta {{\varvec{R}}})\) and also the product with the acceleration vector. Considering the generalised coordinates, with all the deformation variables and the rigid body motion (and their derivatives), then the variation of position vector is given by,
The product in right-hand side of Eq. (2), using equations (A.1) and the explicit definition of the partial derivatives of the position vector in fixed frame \(({{\varvec{R}}})\), can be written as follows:
and each term in Eq. A.2 has the explicit form,
Appendix-B
In this Appendix, the BVP for the underlying linear equation of Eq. (5c) is solved, which is given by,
Using separation of variables,
and, considering constant cross section in longitudinal direction lead to,
with the following constants,
and the boundary conditions arising from equation (8) using (Eq. B.2),
The characteristic polynomial of Eq. (B.3) is,
with roots,
Considering the roots (B.7a–b) of the characteristic polynomial, the general solution of Eq. (B.3) after using hyperbolic and trigonometric identities is given by,
Considering the boundary conditions (B.5a–d) lead to,
whereas (B.9c) has the non-trivial solution of,
Using Eq. (B.10), with (Eq. B.7a with B.4) the natural frequencies are given by,
Finally, considering equations (B.9a–b) in Eq. (B.8) the mode shapes are given by,
considering orthonormality condition.
Appendix-C
In this appendix, the amplitudes for second-order approximation of the second-order solution for lateral bending motions will be given explicitly.
Defining the following constants,
then the amplitudes in Eq. (78) are given by,
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Georgiades, F. Nonlinear dynamics of a spinning shaft with non-constant rotating speed. Nonlinear Dyn 93, 89–118 (2018). https://doi.org/10.1007/s11071-017-3888-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-017-3888-0