A torsion-based solution to the hyperbolic regime of the $J_2$-problem

Abstract

A popular intermediary in the theory of artificial satellites is obtained after the elimination of parallactic terms from the $J_2$-problem Hamiltonian. The resulting quasi-Keplerian system is in turn converted into the Kepler problem by a torsion. When this reduction process is applied to unbounded orbits, the solution is made of Keplerian hyperbolae. For this last case, we show that the torsion-based solution provides an effective alternative to the Keplerian approximation customarily used in flyby computations. Also, we check that the extension of the torsion-based solution to higher orders of the oblateness coefficient yields the expected convergence of asymptotic solutions to the true orbit.

1 Introduction

The adoption of techniques for the removal of high-frequency modes of the motion has been common in the study of nonlinear dynamical problems, since the seminal investigations of planetary motions of the 18th and 19th centuries. With these techniques, the solution is decomposed into secular, long-, and short-period perturbations, facilitating the description of the long-term dynamics. Other than ad-hoc procedures for approaching particular problems, Poincaré’s theory of asymptotic expansions built the foundations for the use of perturbation approaches [41] to solve this now decomposed problem. Nevertheless, Poincaré’s method gives the solution in implicit form. This fact notably complicates the computation of high-order terms [11], which are however needed in different applications and, in particular, in the theory of artificial satellites. The generalized method of averaging introduced the concept of near-identity transformation [1, 26] and helped in the automatization of the computation of higher orders, yet effectively reverting the solution series remained a problem to be solved [25, 42].

The theory of Lie transforms provided a possible solution to the inversion problem, yielding explicit solutions [21], and became the reference approach, to this day, because of the efficient and versatile algorithms that it introduces [8, 13, 19]. For the application to the theory of artificial satellites, first-order orbital perturbation solutions suffice in some contexts [5, 39], yet considering at least the second-order term of Earth’s oblateness becomes mandatory in long-term orbit propagation suites [3, 4, 34, 40]. Still, some missions may require the analytical computation of higher orders of orbits of different kinds [27, 31, 33].

The most successful application of perturbation approaches remains the case of conditionally periodic motion, i.e. the common orbits of artificial satellites. On the other hand, the dynamics of interplanetary orbits often features a multi-body environment and, locally, may also be dominantly hyperbolic. These cases normally foresee numerical approaches or simple analytical solutions based on the Keplerian dynamics. However, more accurate analytical solutions would provide clear benefits to the design and planning of close flybys.

The hyperbolic regime of an artificial satellite of an oblate body was solved in closed form by Hori [20], who showed that the perturbation approach may be useful without restriction to the typical case of quasi-periodic motion.¹ However, differently from the classical elliptical regime, the perturbed hyperbolic motion features strict boundary conditions that must be imposed. More precisely, the effect of the oblateness perturbation vanishes when the artificial satellite approaches infinity in its hyperbolic-type motion. Consequently, the transformation between mean and osculating variables that encapsulates the perturbation solution must become the identity, when evaluated at infinity.

In Hori’s first-order approach, the $J_2$-problem Hamiltonian is directly reduced to the Kepler Hamiltonian in (mean) hyperbolic Delaunay variables. Consequently, the solution of the mean-to-osculating transformation that yields the complete Hamiltonian reduction depends on non-periodic terms of the true anomaly. Nonetheless, the explicit appearance of the true anomaly in Hori’s solution is not of concern, since its value is bounded by the asymptotes of a Keplerian hyperbola. Therefore, these non-periodic terms do not play any secular role. After the application of these boundary conditions to Hori’s transformation, these terms appear always like coefficients involving the difference between the instantaneous true anomaly and the constant true anomaly of the asymptote of the Keplerian hyperbola. Despite non-periodic, this type of coefficients resembles the equation of the center, given by the difference between the true and mean anomalies, which comprises essential short-period terms of the elliptic motion. But the resemblance goes beyond a formal likeness, and we find that these terms can be handled advantageously with known techniques, to efficiently deal with the equation of the center.

In particular, the equation of the center does not play any role in the elimination of the parallax simplification, which, conversely, depends only on trigonometric functions of the true anomaly, cf. §6.2.1 of Ref. [30]. This last feature is not exclusively the case of bounded perturbed Keplerian motion, but also applies to unbounded motion. This becomes evident using Deprit’s original formulation of the elimination of the parallax in polar variables [9]. Furthermore, Deprit’s radial intermediary, which is obtained after the elimination of the parallax up to first-order effects of the oblateness coefficient, provides an integrable solution of the $J_2$-problem, also called the main problem in the theory of artificial satellites [2], and is valid for both bounded and unbounded orbits. Nevertheless, the nature of the solution is different in the two regimes. Deprit’s reduction of the main problem to a quasi-Keplerian system must be amended in the second case, in order to consider the boundary conditions that characterize the hyperbolic-like motion.

We compute the additional terms that are needed in the elimination of the parallax, for the transformation of the hyperbolic regime of the main problem into a quasi-Keplerian system, which, in turn, is converted into a pure Keplerian system by the standard torsion transformation [9]. The new transformation provides simpler equations than the Hori’s case, when mapping the mean to the osculating hyperbolic Delaunay variables. Still, the new transformation shares analogous deficiencies to those of Hori’s solution. Namely, it fails in the limit case of parabolic orbits, and the accuracy of the perturbation solution deteriorates for values of the eccentricity close to 1. In this regard, it is worth mentioning that existing perturbation solutions of bounded motion suffer analogous limitations too.

Moreover, we show that the reduction to a quasi-Keplerian hyperbola is easily extended to higher orders, despite the now unavoidable appearance of non-periodic functions of the true anomaly in the transformation. While these higher-order terms may not have relevant effects in practice (for flyby design or gravity assist maneuvers), they dramatically reduce the errors of the perturbation solution nearby the pericenter and help showing how the perturbation approach follows the expected convergence beyond its common application to the case of quasi-periodic motion. Needless to say, analogous improvements are expected if Hori’s perturbation solution was eventually extended beyond the first order of the oblateness coefficient.

Due to the hyperbolic character of the unbounded perturbed Keplerian motion, one might expect high sensitivity of the main problem dynamics with respect to initial conditions. However, for common values of the $J_2$ coefficient of solar system bodies, the perturbation solution succeeds in capturing the dynamics and can even predict the qualitative features of the branches of the classical Newtonian rosetta when the energy becomes positive.² Indeed, high-order terms of the perturbation solution are required in these extreme cases. Certainly, while the perturbation approach is useful in dealing with an ample diversity of nonlinear problems (see Ref. [12], for instance), it is not the only possibility in dealing with differential equations of the kind approached in this paper. Trying alternative methods in the literature specially adapted for dealing formally with nonlinearities of partial differential equations, as, for instance [44,45,46], may motivate future efforts

2 Deprit’s radial intermediary

The main problem of the artificial satellite admits Hamiltonian formulation. When using polar canonical variables, it is written in the form

$$\begin{aligned} \mathcal {M}= & {} \frac{1}{2}\left( R^2+\frac{\varTheta ^2}{r^2}\right) -\frac{\mu }{r} \nonumber \\{} & {} -\frac{1}{4}J_2\frac{\mu }{r}\frac{\alpha ^2}{r^2}\left( 2-3\sin ^2I+3\sin ^2I\cos 2\theta \right) ,\nonumber \\ \end{aligned}$$

(1)

where the physical parameters $\mu$, $\alpha$, and $J_2$ characterize the gravitational field of the attracting body and denote the gravitational parameter, equatorial radius, and oblateness coefficient, respectively. The polar canonical coordinates $(r,\theta )$ stand for the radius and the polar angle, and their conjugate momenta $(R,\varTheta )$ for the radial velocity and the specific angular momentum; $I=\arccos (N/\varTheta )$ is the inclination of the instantaneous orbital plane, and the canonical pair $(\nu ,N)$ represents the right ascension of the ascending node and the third component of the angular momentum vector per mass unit. Because $\nu$ does not appear in the Hamiltonian (1) $\mathcal {M}$, we immediately infer that N is an integral of the main problem dynamics.

Up to first-order effects of $J_2$, $\mathcal {M}$ (1) can be reduced to the integrable quasi-Keplerian Hamiltonian in new prime variables

$$\begin{aligned} \mathcal {M}= & {} \frac{1}{2}\left( R'^2+\frac{\varTheta '^2}{r'^2}\right) -\frac{\mu }{r'} \nonumber \\{} & {} -\frac{1}{2}\frac{\varTheta '^2}{r'^2}\frac{1}{2}J_2\frac{\alpha ^2}{(\varTheta '^2/\mu )^2}\left[ 2-3\sin ^2I(\varTheta ',N)\right] ,\nonumber \\ \end{aligned}$$

(2)

which is known as Deprit’s radial intermediary [9]. In the case of bounded motion, this intermediary has been proposed for different applications [3, 16, 17]. The reduction of the main problem to Deprit’s radial intermediary is achieved by an infinitesimal contact transformation $(r,\theta ,\nu ,R,\varTheta ,N,J_2)\mapsto (r',\theta ',\nu ',R',\varTheta ',N)$ with generating function

$$\begin{aligned} \mathcal {U}_1= & {} -\varTheta \frac{1}{8}\frac{\alpha ^2}{p^2}\left[ \left( 4\kappa +3\right) s^2\sin 2\theta \right. \nonumber \\{} & {} \left. +(4-6s^2-2s^2\cos 2\theta )\sigma \right] +\mathcal {C}_0, \end{aligned}$$

(3)

Here, s abbreviates the sine of the inclination, $p=\varTheta ^2/\mu$ is the parameter of the conic, and the nondimensional functions

$$\begin{aligned} \sigma =\frac{pR}{\varTheta }, \qquad \kappa =\frac{p}{r}-1, \end{aligned}$$

(4)

represent the projections of the eccentricity vector in the orbital frame. Explicitly, $\sigma =e\sin {f}$ and $\kappa =e\cos {f}$, with e and f denoting eccentricity and true anomaly, respectively. Then, from the last of the equalities in Eq. (4), we readily obtain $\lim _{r\rightarrow \infty }\cos {f}=-1/e$.

On one hand, the differences between Eq. (3) and the equivalent term in Ref. [9] are a consequence of a distinct arrangement of the involved functions, and, on the other, of the addition of the “integration constant” $\mathcal {C}_0$. The latter must not explicitly depend on $\theta$, when it is formulated in the specific algebra of the functions

$$\begin{aligned} \begin{array}{rl} C= &{} \left( \kappa \cos \theta +\sigma \sin \theta \right) \varTheta /p, \\ S= &{} \left( \kappa \sin \theta -\sigma \cos \theta \right) \varTheta /p, \end{array} \end{aligned}$$

(5)

used in Ref. [9]. However, their use may hide the real nature of this integration constant, which is nothing but being free from short-period effects [36]. For this reason, and also for simplicity, eliminating the parallax in Delaunay variables is nowadays encouraged, rather than in the set of polar variables [35].

Delaunay variables are denoted with $(\ell ,g,h,L,G,H)$, and represent the mean anomaly, the argument of the periapsis, the longitude of the ascending node, the so-called Delaunay action, the specific angular momentum, and the third component of the angular momentum vector per mass unit, respectively. When the generating function $\mathcal {U}_1$ in Eq. (3) is reformulated in Delaunay variables, one must distinguish between bounded and unbounded motion. The classical set of elliptic Delaunay variables is used [7, 10, 14] in the former, whereas hyperbolic Delaunay variables are used for the latter instead [15, 20]. Nonetheless, in both cases Eq. (3) becomes

$$\begin{aligned} \mathcal {U}_1= & {} -G\frac{1}{8}\frac{\alpha ^2}{p^2}\left\{ s^2[3e\sin (f+2g)+3\sin (2f+2g) \right. \nonumber \\{} & {} \left. +e\sin (3f+2g)]-(6s^2-4)e\sin {f}\right\} \nonumber \\{} & {} +\mathcal {C}_0(g,L,G,H), \end{aligned}$$

(6)

Still, the meaning of the symbols is slightly different, i.e., despite $p=G^2/\mu$ and $I=\arccos {H}/{G}$ have the same meaning in both regimes of motion, the eccentricity is $e=(1-\eta ^2)^{1/2}<1$, with $\eta =G/L$, for bounded motion, whereas $e=(1+\eta ^2)^{1/2}>1$ and $\eta =-G/L$ in the hyperbolic case. The true anomaly f is an implicit function of the mean anomaly and the eccentricity, whose computation requires the preliminary solution of Kepler’s equation. For unbounded motion, Kepler equation takes the form

$$\begin{aligned} \ell =e\sinh {u}-u, \end{aligned}$$

(7)

where the hyperbolic anomaly u is related to the true anomaly by

$$\begin{aligned} \sqrt{e+1}\tanh \left( \frac{1}{2}u\right) =\sqrt{e-1}\tan \left( {\frac{1}{2}}f\right) . \end{aligned}$$

(8)

3 Polar variables mapping to the quasi-Keplerian system

In his approach, Hori chose the new Hamiltonian to simply be the Keplerian part of the perturbation problem. That is, the transformed Hamiltonian in the prime hyperbolic Delaunay variables reads $\mathcal {M}'=+\mu /(2a)$, where $a={L'}^{2}/\mu$ is the semi-major axis of the osculating hyperbola. Because of this choice, non-trigonometric functions of the true anomaly appear in the generating function, which Hori solved up to an integration constant, as we did in Eq. (6). Differently from the elliptical case, the latter is in no way arbitrary, and Hori determined it by imposing the required boundary conditions at infinity to his transformation of the hyperbolic Delaunay variables.³

Hori had not yet invented his perturbation method based on Lie series [21] and relied on von Zeipel’s algorithm for computing his first-order solution [43]. We resort to the method of Lie transforms [8] in following derivations, whose basic equations are summarized in Appendix A for the convenience of interested readers. Moreover, in contrast with Hori’s choice of the Keplerian, we are satisfied with finding the transformation that yields Deprit’s radial intermediary, in this way simplifying the computation of the mapping.

Finally, the quasi-Keplerian system (2) is transformed into a pure Keplerian system by a torsion transformation [9]. Since the torsion is performed in polar variables, we find advantageous to derive the transformation equations of the polar variables, rather than the hyperbolic Delaunay ones, directly from Eq. (6). That is, to the first order

$$\begin{aligned} \xi =\xi '+J_2\xi _{0,1}|_{\xi =\xi '} \end{aligned}$$

(9)

where $\xi \equiv (r,\theta ,\nu ,R,\varTheta ,N)^\tau$, $\tau$ means transposition, $\xi _{0,1}\equiv \{\xi ,\mathcal {U}_1\}$, and the curly braces denote the Poisson bracket operator. Still, since the boundary conditions are naturally formulated in terms of the true anomaly, we find it convenient to write the transformation in terms of the hyperbolic Delaunay variables. Because of this, the partial derivatives of the polar variables with respect to the hyperbolic Delaunay ones are needed. They are listed in Table 1. While mostly analogous to the case of elliptic Delaunay variables, sign changes appear in the partial derivatives with respect to the hyperbolic Delaunay action, cf. Table 5.1 of Ref. [30].

Table 1 Non-vanishing partial derivatives of the polar variables with respect to the hyperbolic Delaunay variables ($\partial \varTheta /\partial {G}=1$)

We readily find that the correction to the radial velocity automatically fulfills the boundary condition $\{R,\mathcal {U}_1\}|_{\infty }\equiv 0$. Next, we compute

$$\begin{aligned} \{\varTheta ,\mathcal {U}_1\}|_{\infty }= & {} G\frac{1}{4}\frac{\alpha ^2}{p^2}\frac{s^2}{e^2} \left[ 2\eta ^3\sin 2g-(3\eta ^2+1)\cos 2g\right] \\{} & {} -\frac{\partial {\mathcal {C}_0}}{\partial {g}}, \end{aligned}$$

from which $\mathcal {C}_0$ is solved to make the right hand of the equation to vanish. We obtain

$$\begin{aligned} \mathcal {C}_0= & {} -G\frac{1}{8}\frac{\alpha ^2}{p^2}\frac{s^2}{e^2}\left[ 2\eta ^3\cos 2g+(3e^2-2)\sin 2g\right] \\{} & {} +\mathcal {C}_1(L,G,H), \end{aligned}$$

This is the same as the function Z computed by Hori except for a sign due to the different convention in the Hamiltonian formulation used by Hori. It follows the computation of

$$\begin{aligned} \{\nu ,\mathcal {U}_1\}|_{\infty }= \frac{3}{2}c\frac{\alpha ^2}{p^2}\eta +\frac{\partial {\mathcal {C}_1}}{\partial {H}}, \end{aligned}$$

where $c=H/G$. The constant $\mathcal {C}_1$ is then solved after imposing the vanishing of the right side. We obtain

$$\begin{aligned} \mathcal {C}_1=-G\frac{3}{4}\frac{\alpha ^2}{p^2}\eta (1-s^2)+\mathcal {C}_2(L,G). \end{aligned}$$

Analogously,

$$\begin{aligned} \{\theta ,\mathcal {U}_1\}|_{\infty }=\frac{1}{2}\eta \frac{\alpha ^2}{p^2}+\frac{\partial {\mathcal {C}_2}}{\partial {G}}, \end{aligned}$$

from which, recalling that $\eta =-G/L$ and $p=G^2/\mu$, we obtain

$$\begin{aligned} \mathcal {C}_2=G\frac{1}{4}\frac{\alpha ^2}{p^2}\eta +\mathcal {C}_3(L). \end{aligned}$$

Finally, we check that the choice $\mathcal {C}_3=0$ fulfills the last condition $\{r,\mathcal {U}_1\}|_{\infty }=0$. In summary,

$$\begin{aligned} \mathcal {C}_0= & {} G\frac{1}{4}\frac{\alpha ^2}{p^2}\Big \{(3s^2-2)\eta \nonumber \\{} & {} -\frac{s^2}{e^2}\Big [\eta ^3\cos 2g+\frac{1}{2}(3e^2-2)\sin 2g\Big ]\Big \}, \end{aligned}$$

(10)

thus making Eq. (6) fully determined.

It is worth noting that Eq. (10) can be rewritten in polar variables using the alternative form

$$\begin{aligned} \mathcal {C}_0= & {} \varTheta \frac{1}{4}\frac{\alpha ^2}{p^2}\Big \{(3s^2-2)\eta \\{} & {} -\frac{p^2s^2}{e^4\varTheta ^2}\left[ \eta ^3\left( C^2-S^2\right) +\left( 3e^2-2\right) CS\right] \Big \}, \end{aligned}$$

with $e=(p/\varTheta )\sqrt{C^2+S^2}$, whereas $C\equiv {C}(r,\theta ,R,\varTheta )$ and $S\equiv {S}(r,\theta ,R,\varTheta )$ are given in Eq. (5). In this way, we show that $\mathcal {C}_0$ is free from the explicit appearance of $\theta$, as it must be when using Deprit’s algebra based on these functions [9].

Once the generating function has been fully determined, we compute the corrections

$$\begin{aligned} r_{0,1}= & {} p\frac{1}{4}\frac{\alpha ^2}{p^2}\Big \{ (3s^2-2)\left( 1+\frac{e}{\eta }\sin {f}\right) +\frac{s^2}{2e^3}\big [ (e^2-4) \nonumber \\{} & {} \times \eta \sin (f-2g) -3e^2\eta \sin (f+2g)+(3e^2-4)\nonumber \\{} & {} \times \cos (f-2g)+3e^2\cos (f+2g) \nonumber \\{} & {} +2e^3\cos (2f+2g) \big ] \Big \} \end{aligned}$$

(11)

$$\begin{aligned} \theta _{0,1}= & {} \frac{1}{16}\frac{\alpha ^2}{p^2}\Big ( \frac{1}{\eta }\big [12(5s^2-4)-6(7s^2-6)e^2 +8e \nonumber \\{} & {} \times (3s^2-2)\cos {f} +2e^2(3s^2-2)\cos 2f \big ]\nonumber \\{} & {} +\frac{\eta }{e^3}\big \{ (e^2-4)es^2\cos (2f-2g) +4(e^2-4)s^2\nonumber \\{} & {} \times \cos (f-2g) +2 e \big [e^2(7s^2-4)-4(4 s^2-1)\big ] \nonumber \\{} & {} \times \cos 2g -12e^2s^2\cos (f+2g) -3e^3s^2 \nonumber \\{} & {} \times \cos (2f+2g) \big \} +\frac{1}{e^3}\big \{ (4-3e^2)es^2\nonumber \\{} & {} \times \sin (2f-2g) -4(3e^2-4)s^2\sin (f-2g) +2e \nonumber \\{} & {} \times \left[ 3e^2(5s^2-2)-4(4s^2-1)\right] \sin 2g -8e^4(6s^2 \nonumber \\{} & {} -5)\sin {f} +4e^2\left[ e^2(5s^2-3)-3s^2\right] \sin (f+2g) \nonumber \\{} & {} +e^3(11s^2-12)\sin (2f+2g) +4e^4(s^2-1) \nonumber \\{} & {} \times \sin (3f+2g) \big \} \Big ) \end{aligned}$$

(12)

$$\begin{aligned} \nu _{0,1}= & {} c\frac{1}{4}\frac{\alpha ^2}{p^2}\Big \{ \frac{1}{e^2}\left[ (3e^2-2)\sin 2g+2\eta ^3\cos 2g\right] -6\eta \nonumber \\{} & {} -6e\sin {f} +3e\sin (f+2g)+3\sin (2f+2g) \nonumber \\{} & {} +e\sin (3f+2g) \Big \} \end{aligned}$$

(13)

$$\begin{aligned} R_{0,1}= & {} \frac{G}{p}\frac{1}{32}\frac{\alpha ^2}{p^2}\Big \{ \frac{e}{\eta }(3s^2-2)\big [2e^2\cos 3f+8e\cos 2f \nonumber \\{} & {} +(6e^2+8)\cos {f}+8e\big ] +\eta \frac{s^2}{e^3}\big [(e^2-4)e^2 \nonumber \\{} & {} \times \cos (3f-2g) +4(e^2-4)e\cos (2f-2g) -(e^4 \nonumber \\{} & {} +4e^2+16)\cos (f-2g) -8(e^2+2)e\cos 2g \nonumber \\{} & {} -(5 e^2+16)e^2\cos (f+2g) \nonumber \\{} & {} -12e^3\cos (2f+2g) -3 e^4\cos (3f+2g) \big ] \nonumber \\{} & {} -\frac{s^2}{e^3}\left[ (3e^2-4)e^2\sin (3f-2g) \right. \nonumber \\{} & {} +4(3e^2-4)e\sin (2f-2g) \nonumber \\{} & {} +(3e^4+4e^2-16) \sin (f-2g) \nonumber \\{} & {} +4(e^4+4) e\sin 2g +(19e^2+16)\nonumber \\{} & {} \times e^2\sin (f+2g) \nonumber \\{} & {} +4(2e^2+7)e^3\sin (2f+2g)\nonumber \\{} & {} \left. +19e^4\sin (3f+2g) +4e^5\sin (4f+2g) \right] \Big \} \end{aligned}$$

(14)

$$\begin{aligned} \varTheta _{0,1}= & {} \varTheta \frac{1}{4}\frac{\alpha ^2}{p^2}s^2\Big \{\frac{1}{e^2}\left[ (3e^2-2)\cos 2g-2\eta ^3\sin 2g\right] \nonumber \\{} & {} +3e\cos (f+2g) +3\cos (2f+2g)\nonumber \\{} & {} +e\cos (3f+2g) \Big \}. \end{aligned}$$

(15)

The appearance of $\eta$ in denominators of $r_{0,1}$, $\theta _{0,1}$ and $R_{0,1}$ deteriorates the accuracy of these corrections for orbits close to parabolic. Note that Eqs. (11)–(15) depend on the true anomaly only through trigonometric functions, opposite to Hori’s corrections [20]. On the other hand, the explicit appearance of f in Hori’s solution is not criticizable, as far as the possible values of the true anomaly are bounded by the values taken by the asymptotes of the Keplerian hyperbola.

We complete the analytical solution by applying a torsion to the quasi-Keplerian Hamiltonian (2). Disregarding the prime notation without risk of confusion, Eq. (2) is rearranged like

$$\begin{aligned} \mathcal {M}=\frac{1}{2}\left( R^2+\frac{\tilde{\varTheta }^2}{r^2}\right) -\frac{\mu }{r}, \end{aligned}$$

(16)

where

$$\begin{aligned} \tilde{\varTheta }^2=\varTheta ^2\left[ 1-\frac{1}{2}J_2\frac{\alpha ^2}{p^2}(3c^2-1)\right] \end{aligned}$$

(17)

is only function of $\varTheta$ and the parameters of the simplified problem, i.e. the integral N and the physical parameters defining the gravitational field. The objective of the torsion is to find a canonical transformation $(\theta ,\nu ,\varTheta ,N)\mapsto (\theta ^*,\nu ^*,\varTheta ^*,N^*)$ such that $\tilde{\varTheta }=\varTheta ^*$ in the new variables. That is, Eq. (16) turns into the Kepler problem Hamiltonian in the asterisk variables.

There is no distinction between bounded or unbounded motion when working with polar variables; thus, the torsion transformation coincides with the elliptic case, originally described in §9 of [9]. Rather, we follow the notation proposed in [17] and denote $\varPhi =\varPhi (\varTheta ,N)\equiv \tilde{\varTheta }/\varTheta$, $\epsilon =\epsilon (\varTheta )\equiv -\frac{1}{2}J_{2}(\alpha /p)^{2}<0$, and define the torsion by the sequence:

$$\begin{aligned} \varTheta ^*= & {} \varTheta \varPhi , \end{aligned}$$

(18)

$$\begin{aligned} \theta ^*= & {} \theta \varPhi \left( \varPhi ^2-2\epsilon \frac{\partial \varPhi ^2}{\partial \epsilon }-\frac{1}{2}c\frac{\partial \varPhi ^2}{\partial {c}}\right) ^{-1}, \end{aligned}$$

(19)

$$\begin{aligned} \nu ^*= & {} \nu -\frac{1}{2}\frac{\theta ^*}{\varPhi }\frac{\partial \varPhi ^2}{\partial {c}}, \end{aligned}$$

(20)

Note that not only N remains unaltered, but r and R as well. The inverse transformation requires first to solve $\varTheta =\varTheta (\varTheta ^*,N)$ from the implicit function (18), which is then replaced in Eqs. (19) and (20) to be trivially solved in $\theta$ and $\nu$. Alternatively to the numerical solution by root-finding procedures, Eq. (18) can be inverted analytically in the form of a power series in $\epsilon$. If we limit to the first order of $J_2$ of the perturbation solution computed hitherto, we obtain

$$\begin{aligned} \varTheta =\varTheta ^*\left[ 1-\frac{1}{2}(3c^2-1)\epsilon \right] , \end{aligned}$$

(21)

where, now, $c=N/\varTheta ^*$, and $p=\varTheta ^{*2}/\mu$ must be replaced in the definition of $\epsilon$.

If written in asterisk variables, Eq. (16) becomes a Kepler Hamiltonian, that is next completely reduced by the exact transformation from polar to hyperbolic Delaunay variables. Thus, $\mathcal {M}=+\mu ^2/(2L^2)$, from which

$$\begin{aligned} \begin{array}{rl} \ell = &{} \ell _0+nt \\ g= &{} g_0 \\ h= &{} h_0 \\ L= &{} L_0 \\ G= &{} G_0 \\ H= &{} H_0 \end{array} \end{aligned}$$

with $n=-\mu ^2/L^3$.

Note that the Keplerian orbit obtained with the torsion may have no physical sense, showing complex values of the inclination. This fact is clearly observed in the limit case obtained when making $\varTheta =N$ in Eq. (21). Namely,

$$\begin{aligned} \frac{N}{\varTheta ^*}\equiv {c}=1-(3c^2-1)\epsilon , \end{aligned}$$

this is a quadratic equation in c that may have real solutions only in the interval $-\frac{1}{2}+\frac{1}{\sqrt{6}}\le \epsilon <0$, in which $c>1$ always. Regardless the meaning that c may have in Eq. (21) in these particular cases, the torsion transformation remains valid.

4 Higher-order extensions

A second-order solution of the main problem based on a quasi-Keplerian Hamiltonian would be harmed by the appearance of secular terms in the transformation equations, in the bounded orbit case. However, this kind of terms are not of concern in the case of unbounded motion, where their variation is limited by the asymptotes of the hyperbola. Therefore, we can safely extend the first-order solution to higher orders following exactly the same approach. In particular, we first compute the mapping that yields a quasi-Keplerian Hamiltonian while accepting the boundary conditions at infinity, and we then apply a torsion to obtain the final Keplerian.

Thus, from the known terms obtained at the second order of the elimination of the parallax, we select the terms that are free from the true anomaly, but also from the argument of the periapsis and the eccentricity. The latter, we recall, is a function of the radius and radial velocity, in addition to the specific angular momentum. We thus obtain

$$\begin{aligned} \mathcal {M}_{0,2}=-\frac{\varTheta ^2}{r^2}\frac{\alpha ^4}{p^4}\frac{1}{16}(21s^4-42s^2+20), \end{aligned}$$

(22)

The simple consideration of this additional term in the reduction of the quasi-Keplerian Hamiltonian $\mathcal {M}=\mathcal {M}_{0,0}+J_2\mathcal {M}_{0,1}+\frac{1}{2}J_2^2\mathcal {M}_{0,2}$ yields additional refinements in the computation of the final Keplerian mean motion, as well as in the solution of the torsion transformation given by Eqs. (18)–(20). Here, now

$$\begin{aligned} \varPhi =\Big [1-\epsilon (3c^2-1)-\frac{1}{4}\epsilon ^2(21c^4-1)\Big ]^{1/2}. \end{aligned}$$

(23)

In addition, the analytical inversion of Eq. (18) provided by Eq. (21) must be replaced by the second-order solution of $J_2$, given by

$$\begin{aligned} \varTheta =\varTheta ^*\Big [1-\frac{\epsilon }{2}(3c^2-1)-\frac{3\epsilon ^2}{4}(2c^2-1)(5c^2-1)\Big ], \end{aligned}$$

(24)

where c, and p are now functions of the asterisk variables.

Major improvements are expected if we complement the analytical solution with the second-order corrections of the elimination of the parallax. That is, Eq. (9) is replaced by

$$\begin{aligned} \xi =\xi '+J_2\xi _{0,1}|_{\xi =\xi '}+\frac{1}{2}J_2^2\xi _{0,2}|_{\xi =\xi '}, \end{aligned}$$

(25)

where $\xi _{0,2}\equiv \{\xi _{0,1},\mathcal {U}_1\}+\{\xi ,\mathcal {U}_2\}$. To do that, we need to compute the generating function term $\mathcal {U}_2$ of the Lie transformation that yields $\mathcal {M}_{0,2}$. This is obtained in the usual way, up to an arbitrary constant, say $Q_0\equiv {Q}_0(g,h,L,G,H)$.

The new corrections need to match the boundary condition at infinity as well. Analogously to the first order, we readily find that $R_{0,2}|_{\infty }\equiv 0$, and hence that the boundary conditions are automatically fulfilled by the corrections to the radial velocity. On the contrary, the equality $\varTheta _{0,2}|_{\infty }=0$ involves the partial derivative $\partial {Q}_0/\partial {g}$, which we solve by indefinite integration to obtain

$$\begin{aligned} Q_0= & {} G\frac{\alpha ^4}{p^4}\frac{1}{256 e^2}\Big \{\! -2s^2\big [ 3e^4(17s^2-18)\\{} & {} + 8e^2(75 s^2 -68)+ 8(s^2+6)\\{} & {} + 96\eta ^3(5s^2-4)(\arctan \eta +\pi ) \big ]\sin 2g \\{} & {} - 3(3e^4+6e^2-16)s^4\sin 4g\\{} & {} +\frac{4s^2}{\eta ^2}\big \{ 6\eta ^2[e^4(15s^2-14)\\{} & {} + 4(3 e^2-2)(5s^2-4)](\arctan \eta +\pi )\\{} & {} +\eta [e^4(278-329s^2)+e^2(298s^2-284)\\{} & {} + 4(s^2+6)]\big \}\cos 2g +6\eta (e^2+8)s^4\cos 4g \Big \}\\{} & {} +Q_1. \end{aligned}$$

We get the new integration constant $Q_1\equiv {Q}_1(L,G,H)$ from $\nu _{0,2}|_{\infty }\!\!=\!0$, which only involves the partial derivative $\partial {Q}_1/\partial {H}$. We obtain

$$\begin{aligned} Q_1= & {} G\frac{\alpha ^4}{p^4}\frac{3}{128\eta }(1-s^2)\big [2e^2\eta (5s^2+13)(\arctan \eta +\pi )\\{} & {} -e^2(11s^2+75)-85s^2+107\big ] +Q_2. \end{aligned}$$

Analogously, the integration constant $Q_2\equiv {Q}_2(L,G)$ is solved from $\theta _{0,2}|_{\infty }=0$, which only involves the partial derivative $\partial {Q}_2/\partial {G}$. We obtain

$$\begin{aligned} Q_2= & {} G\frac{\alpha ^4}{p^4}\frac{1}{128\eta }\left[ 81e^2-30e^2\eta (\arctan \eta +\pi )-49\right] \\{} & {} +Q_3. \end{aligned}$$

We take $Q_3\equiv {Q}_3(L)=0$ for simplicity, and finally obtain

$$\begin{aligned} \mathcal {U}_2= & {} G\frac{\alpha ^4}{p^4}\frac{3}{64e^2}\big \{ [2e^4(15s^2-14)+8(3e^2-2)(5s^2-4)]\nonumber \\{} & {} \times {s}^2\cos 2g -16\eta ^3(5s^2-4)s^2\sin 2g \nonumber \\{} & {} -e^4(5s^4+8s^2 -8) \big \}\psi \nonumber \\{} & {} +G\frac{\alpha ^4}{p^4}\frac{1}{256e^3\eta }\sum _{k=0}^2s^{2k} \bigg \{\sum _{j=j_0}^5\sum _{i=0}^3q_{k,i,j} \nonumber \\{} & {} \times e^{2i+1-(j\bmod 2)}\cos (jf+2kg)\nonumber \\{} & {} +\eta \sum _{j=j_0}^{j_1}\sum _{i=0}^2p_{k,i,j} e^{2i+1-(j\bmod 2)}\sin (jf+2kg) \bigg \},\nonumber \\ \end{aligned}$$

(26)

where $j_0=-2 (k \bmod 2)-1$, $j_1=6-2 (k \bmod 2)$, $\psi =\pi -f+\arctan \eta$, and the inclination polynomials $p_{k,i,j}$ and $q_{k,i,j}$ are listed in Tables 2 and 3. The second-order corrections $\xi _{0,2}$ to the polar variables are then obtained from the straightforward evaluation of the corresponding Poisson brackets.

Note that the appearance of the function $\psi$, which also exists in Hori’s first-order solution, was only delayed to the second order of our approach. This postponement resembles analogous effect in the case of bounded motion, where the elimination of the parallax delays by one order the need of integrating by parts the terms involving the equation of the center, in the computation of the generating function [18, 29].

Table 2 Inclination polynomials $q_{k,i,j}$ in Eq. (26)

Table 3 Inclination polynomials $p_{k,i,j}$ in Eq. (26)

5 Performance of the analytical solution

We choose the physical parameters of the Earth ($\mu =398600.44$ $\mathrm {km^3/s^2}$, $\alpha =6378.1363$ km, $J_2=0.001082634$) in the first two examples. For Earth gravity assists, the flyby altitude typically ranges from about 300 km, as in the case of NASA’s Galileo mission,⁴ to the more common several thousands of km, as for instance for NASA’s Stardust mission.⁵ Accordingly, we choose a perigee altitude of 1000 km over the Earth’s surface, low enough to experience the oblateness perturbing effect.

We test first a high-eccentricity hyperbolic-type orbit, where the flyby happens in a relatively short time. Both the Kepler approach and the first order of the perturbation solution are expected to provide acceptable results in this case. The second example deals with a quasi-parabolic orbit, where the spacecraft remains longer in the close vicinity of Earth. We expect this case to be a more challenging benchmark for the analytical solution.

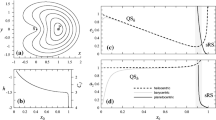
In the first case, we choose the following initial orbital elements: $a=2459.38$ km, $e=4$, $I=23.5^\circ$, $\varOmega =60^\circ$, $\omega =90^\circ$, $M=-21400^\circ$. They correspond, approximately, to the entrance of a test satellite into Earth’s sphere of influence (SOI). We obtain The “true” reference solution from the numerical simulation of these initial conditions in the main problem dynamics, ensuring the preservation of both the energy integral and the third component of the angular momentum, within at least 14 digits along the 36 h propagation interval. The reference orbit is shown in Fig. 1.

Fig. 1

Earth’s flyby with $e=4$ and 1000 km periapsis distance. Top: true orbit. Bottom: magnification on the closest approach. Distance in km

Then, we analytically propagate the initial conditions: first in the Keplerian dynamics, next in the “common” interpretation of Deprit’s radial intermediary (abbreviated DRI in the following). Here, Eqs. (16)–(17) are assumed to remain valid in osculating elements. Finally, we propagate them in the “natural” interpretation of DRI [9], i.e., in the approximation of the main problem dynamics provided by the new perturbation solution. We show the Root Sum Square (RSS) errors of each analytical solution with respect to the true orbit in Fig. 2. The Keplerian propagation starts with zero error and, because the disturbing effect of $J_2$ is very small at the SOI entrance, then grows slowly, reaching the one-meter level at a distance of approximately 25 Earth’s radii, just a few hours before the closest approach. The RSS error grows notably during the perigee passage and, due to the different mean Keplerian and $J_2$-perturbed motions, increases almost linearly after that. At the end of the propagation, the RSS error of the Keplerian approximation reaches several hundreds of km.

Fig. 2

RSS position error of the flyby in Fig. 1 when using the Keplerian dynamics, DRI-common, and the first order of the perturbation solution. Note the logarithmic scale

When using the “common” version of DRI, we get closer to the $J_2$ dynamics, although of a slightly different orbit, because of the lack of transformation between original and prime variables. For this reason, the errors in the arrival branch of the predicted orbit grow faster than the Keplerian approximation, until the accumulation of nonlinear effects due to the $J_2$ perturbation is significant enough (which happens at about 1.5 Earth’s radius for this orbit). Then, the better representation of the main problem dynamics by DRI results in clearly smaller errors than the Keplerian approximation during the flyby, and also in the departure branch of the orbit, as illustrated with the dashed gray lines in both plots of Fig. 2. The computational burden of DRI is notably alleviated when the root-finding procedure needed in the solution of the implicit function Eq. (18) is replaced by the direct evaluation of Eq. (21). In this case, the analytical propagation starts with an initial error of half a meter, which is however negligible at the precision of the analytical propagation.

The accuracy notably improves when using the natural version of DRI, labelled “first order” in Fig. 2. Here, we unavoidably deal with the mandatory transformation of the initial osculating state to the mean elements that initialize the constants of the perturbation solution, using the corrections in Eqs. (11)–(15) with opposite signs, and the consequent recovery of osculating elements using Eqs. (11)–(15) in order to compute the RSS error.⁶ Errors provided by the first-order solution grow fast at perigee passage, but their following almost linear increase is, approximately, $J_2$ times smaller than in the Keplerian and DRI cases due to the much better approximation provided by the perturbation solution, and barely reaches 100 m at the end of the propagation.

For the second case, we choose the quasi-parabolic orbit $a=1.47563\times 10^6$ km, $e=1.005$, $I=23.5^\circ$, $\varOmega =60^\circ$, $\omega =90^\circ$, $M=-1^\circ$, which flies about 1000 km over Earth’s surface, but for a longer time compared to the previous example. The reference orbit, shown in Fig. 3, has been numerically integrated in the main problem dynamics for a 24 h interval. On one hand, we compare it with the equivalent solutions provided by the Keplerian approximation, and, on the other, the torsion-based solution of the main problem, both in the common and natural versions.

Fig. 3

Quasi-parabolic flyby 1000 km above Earth’s surface. Distance in km

Now the spacecraft undergoes the disturbing effects of the oblateness perturbation for a much longer time than in the previous flyby, and hence, the improvements of DRI over the Keplerian approximation are much more evident in this example, as shown in Fig. 4—where the approximate inversion in Eq. (21) has been used and hence the apparent initial error of the torsion-based solution. Also, analogous improvements to the previous example are also obtained by the first-order perturbation solution in this case, for which the errors remain $\mathcal {O}(J_2)$ with respect to corresponding ones of the Keplerian approximation. However, as shown in Fig. 4, the errors of the first-order solution now clearly peak along the close visit to Earth reaching a RSS error of about 700 m at perigee (about 10% of the minimum distance to the Earth’s surface), which immediately falls by one order of magnitude, finally reaching about 200 m at the end of the propagation. The latter figure means a $\mathcal {O}(J_2)$ improvement when compared to about the same number of km, instead of m, provided by the Keplerian approach. The peak, we recall, is due to the appearance of $\eta$ in denominators of some of the first-order corrections, which in this more challenging case takes the value $\eta \approx 0.1$. On the other hand, it deserves mentioning that the fact that the errors of the first-order solution decrease form the initial 10 m level to just a few meters when approaching Earth is just an apparent paradox that is easily explained by the approximate truncation of the inversion of the torsion to the first order of $J_2$, and the decreasing value of $\theta$ in Eq. (19). Eventually, errors in the dynamical modeling provided by the natural version of DRI overcome those due to the approximation in Eq. (21) and grow again irrespective of the $\theta$ value.

Fig. 4

RSS position errors of the flyby in Fig. 3 when using the Keplerian dynamics and the first order of the perturbation solution. Note the logarithmic scale

As in the case of bounded motion, a general improvement of the first-order solution is obtained when including second-order terms in the mean elements propagation, a strategy that negligibly increases the computational burden [2, 3]. In our case, this means including the term in Eq. (22) in the quasi-Keplerian Hamiltonian, as well as Eqs. (23) and (24) in the solution of the torsion transformation. As shown in Fig. 5, while these additional terms generally reduce the errors of the analytical propagation (labelled “first order +”), they do not show improvements during the close approach to the Earth. Certainly, computing the second-order corrections derived from Eq. (26) makes a full second-order solution that, as expected, generally improves the accuracy to $\mathcal {O}(J_2^2)$, as we also show in Fig. 5 (black-dashed curve labelled “second order”). The fact that the expected improvement does not happen at perigee to the whole extent, is due to the appearance in denominators of the second-order corrections of higher powers of $\eta$ than in the first-order approach, which now reach the fourth power in the case of $\theta _{0,2}$ and $R_{0,2}$. Still, the error of the second-order solution at perigee passage remains at least 20 times smaller than those of the first-order solution. Finally, the RSS error curve labelled “second order +” includes third-order secular terms obtained from the elimination of the parallax in the perturbation solution. Like in the first-order case, these additional terms slightly improve the computation of the “mean” mean motion—the mean motion of the quasi-Keplerian Hamiltonian—yet their effects are only noted in the departure branch of the orbit.

Fig. 5

RSS position errors of the flyby in Fig. 3 when using higher orders of the perturbation solution. Note the logarithmic scale

Because perturbation theories of this kind are rather uncommon, the final example is intended to show that the convergence of the successive orders of the perturbation solution, commonly observed in the case of bounded perturbed Keplerian motion (see [28, 32], for instance), also happens in the current case of perturbed hyperbolic Keplerian motion. To do that, we test our solution with the challenging case of a fish-type orbit [38]. However, since parabolic orbits are necessarily excluded from the current perturbation solution due to the $\eta$ divisor that affects the elimination of the parallax transformation, we rather base our tests on an equivalent hyperbolic branch of the Newtonian rosetta.

Thus, for the gravitational parameters of Jupiter ($\mu =1.268\times 10^8\,\mathrm {km^3/s^2}$, $\alpha =71492$ km, $J_2=0.01475$), we choose the initial conditions of an equatorial orbit with $a=724920$ km, $e=1.1$, $g=270^\circ$, and $\ell =-120^\circ$. The fact that this orbit would impact Jupiter is not of concern for our validation purposes. The results are summarized in Fig. 6, where the true orbit, computed numerically, is represented by a black curve, approaching Jupiter from the top-left corner, surrounding the attraction center by a more than $180^\circ$ angle, to first cross the approaching branch of the orbit, and then leave the scene by the left side of the picture. The Keplerian approximation (gray curve in Fig. 6) only mimics the true trajectory in the approaching part and then takes a clearly divergent path. DRI (gray-dashed curve) is able to turn the departure branch toward the true solution, a result that is clearly improved by the first-order theory (gray dotted curve), yet not enough enhanced to produce the crossing between the approaching and departing branches of the orbit. This intersection is obtained with the second-order solution (black dotted curve of Fig. 6), yet it happens out of the frame of Fig. 6, clearly far away from the true event. The third-order approximation (black dot-dashed curve of Fig. 6) notably improves the results, and the crossing now occurs inside the displayed area in Fig. 6. Finally, the black-dashed curve, which was computed with a fifth-order truncation of the elimination of the parallax complemented with additional secular terms coming from a sixth-order truncation of the quasi-Keplerian Hamiltonian, reasonably approximates the true orbit. We expect that higher-order truncations would continue to converge slowly to the true solution, yet we did not compute them due to the important growth in the size of the perturbation series and the corresponding exponential increase in the computational burden. We are satisfied with these results, which show the correctness of Hori’s approach for dealing with unbounded perturbed Keplerian motion.

Fig. 6

True hyperbolic rosetta branch (black curve) and successive approximations of the perturbation solution truncated to the zeroth (Keplerian, gray), first (gray, dotted), second (black, dotted), third (black, dot-dashed) and fifth order (black, dashed) of Jupiter’s main problem. The gray-dashed curve was generated with the “common” version of DRI. Distances are km

6 Remarks on the boundary condition: the third-body perturbation case

Similarly to Hori’s approach, the transformation that yields Deprit’s radial intermediary depends on the choice made for the integration constant. The main problem straightforwardly suggests to impose null perturbing effects at infinity, as at great distances from the primary the non-uniform gravity field of the planet flown by is negligible.

Yet, in practical examples for the Solar or a planetary system, the great distances from the flyby body are characterized by stronger effects of the main attractor of the whole system. We therefore proceed at assessing whether perturbation approaches of this kind, with Keplerian boundary condition, are suitable to study the perturbed hyperbolic Kepler problem with third-body effects only.

Identifying with the subscript B the perturbing body, the full Hamiltonian of the third-body perturbation case is

$$\begin{aligned} \mathcal {M} = \mathcal {M}_0 + \mathcal {M}_B = -\frac{\mu }{2a} - \mu _B \bigg (\frac{1}{|\textbf{r}-\textbf{r}_B|}-\frac{\textbf{r}\cdot \textbf{r}_B}{r_B^3}\bigg ). \end{aligned}$$

(27)

Following Lidov and Kozai [24, 37], we replace $\textbf{r}\cdot \textbf{r}_B = r r_B\cos \psi$ and model the perturbing potential $\mathcal {M}_B$ as a series expansion on the Legendre polynomials of $\cos \psi$:

$$\begin{aligned} \mathcal {M}_B = -\frac{\mu _B}{r_B} \sum _{j=2}^{+\infty } \frac{\varepsilon ^j}{j!} j! \, \frac{r^j}{r_B^j} P_j(\cos \psi ). \end{aligned}$$

(28)

For instance, $P_0(x)=1$, $P_1(x)=x$, $P_2(x)=\frac{1}{2}(3x^2-1)$, $P_3(x)=\frac{1}{2}(5x^3-3x)$, and so on. The small parameter $\varepsilon$ is just a token to identify the strength of the perturbation effects with the ratio $r/r_B$, that is, retaining few orders only provides an accurate approximation if $r\ll {r}_B$. More generally, the series converges if $r<r_B$. Note the absence of the first two orders, consequence of $P_0$ leading to the constant expression $\mu _B/r_B$ and the first-order term canceling with the tidal part of the perturbing potential.

Following the same principle of Hori’s approach for the main problem, we seek a condition where the third-body perturbation vanishes by itself. We approximate

$$\begin{aligned} \mathcal {M}_B \approx -\frac{\mu _B}{r_B} 2 \, \frac{r^2}{r_B^2} \frac{1}{2}\big (3\cos ^2\psi -1\big ), \end{aligned}$$

(29)

and observe that $\cos ^2\psi =1/3$ makes the second term vanish. We could be tempted to use this particular point to set the Keplerian boundary condition, however, this unique setting corresponds to the second-order term only being null, rather than the full original potential. In addition, trajectories such that $\cos ^2\psi =1/3$ is never verified may exist. Considering the higher-order terms, we do not find a value of $\cos \psi$ that makes all terms in the expansion vanish.

These considerations suggest that the boundary condition derived from a Keplerian hyperbola may not be suitable for the third-body perturbation case. This aspect remarks that this method remains valid for the main problem only or more in general for vanishing perturbations at infinity. We strengthen our claim with a numerical proof of the just mentioned observation, whose analytical equations of motion in prime variables we obtained with the help of a symbolic processor, following the same steps of Hori’s approach but applying the Lie transform method. We do not include them in this article for the sake of brevity. We study the case of a planetary flyby of Venus modeling the third-body perturbation of the Sun, within Venus’ SOI. We consider the SOI entrance state, with position $\textbf{r}^T=[-104551.25,-597237.74,-110314.51]$, km, and velocity $\textbf{v}^T=[3.25,17.76,3.67]$, km/s, at the time $t_0 = 8119.84$ MJD2000, in the Ecliptic J2000 reference frame centered on Venus. We simulate the flyby motion using an ephemeris model that includes the Solar System planets, the Moon and general relativity effects up to the “critical” point where $\cos \psi =-1/\sqrt{3}$. Then, we compare in Fig. 7 the consequent forward simulations, starting from this critical point and up to the SOI exit, of the Lie transform-based approach, the numerical simulation of the second-order term only of the third-body potential, the Keplerian integration, and the full third-body effect (not expanded).

Fig. 7

Evolution of the error for the third-body models, relative to the ephemeris solution

In clear contrast with the improvements obtained for the main problem case, we observe from Fig. 7 the divergent behavior of the analytical perturbation solution. Setting the boundary condition as the Keplerian solution where the perturbing potential vanishes, in analogy with Hori’s approach, the so obtained analytical solution provides even worse predictions than the Keplerian only case, without converging toward the numerically simulated trajectory for the same physical model. Other types of boundary conditions should be explored in dedicated works, for instance the magnitude difference between the perturbation and the Keplerian term in specific regions of the hyperbolic trajectory.

7 Conclusions

Most main problem intermediaries in the theory of artificial satellites were originally computed in polar variables and, hence, are not constrained to the case of bounded orbits. Therefore, the improvements they provide in their common realization over the Keplerian approximation encompass the case of unbounded motion as well and are clearly leveraged in their naturalized versions. However, in the latter case, the integration “constant” on which the perturbation theory depends upon can no longer remain arbitrary. On the contrary, it must be determined in such a way that the perturbation solution fulfills the boundary conditions at infinity derived from the Keplerian hyperbola.

In particular, we have shown that Deprit’s radial intermediary provides an efficient alternative to the Keplerian approximation commonly used in flyby design. Moreover, because the appearance of secular terms is not at all of concern for hyperbolic-type motion, higher-order refinements of Deprit’s quasi-Keplerian approach are readily computed. Because of that, the analytical computation of unbounded perturbed Keplerian motion can take full advantage of the convergence to the true solution provided by the computation of consecutive higher orders of the perturbation approach, where the accuracy of the analytical solution is notably increased.

Inclusion of the third-body perturbation in the analytical solution is under study in order to apply it to real scenarios.

A Deprit’s perturbation algorithm. Basic formulas

A Lie canonical transformation $({\varvec{x}},{\varvec{X}})\mapsto ({\varvec{y}},{\varvec{Y}};\epsilon )$, where ${\varvec{x}}$, ${\varvec{y}}$, are canonical coordinates, ${\varvec{X}}$, ${\varvec{Y}}$, their conjugate momenta, respectively, and $\epsilon$ is a small parameter, is defined as the solution of the differential system

$$\begin{aligned} \frac{\textrm{d}{\varvec{x}}}{\textrm{d}\epsilon }=\frac{\partial {W}}{\partial {\varvec{X}}}, \quad \frac{\textrm{d}{\varvec{X}}}{\textrm{d}\epsilon }=-\frac{\partial {W}}{\partial {\varvec{x}}}, \end{aligned}$$

(30)

for the initial conditions ${\varvec{x}}({\varvec{y}},{\varvec{Y}};0)={\varvec{y}}$, ${\varvec{X}}({\varvec{y}},{\varvec{Y}};0)={\varvec{Y}}$. The scalar function $W=\sum _{m\ge 0}(\epsilon ^m/m!)W_{m+1}({\varvec{x}},{\varvec{X}})$, is the generator of the Lie transformation.

For an analytic function $F=F({\varvec{x}},{\varvec{X}},\epsilon )$ given by its Taylor series expansion

$$\begin{aligned} F=\sum _{m\ge 0}\frac{\epsilon ^m}{m!}F_{m,0}({\varvec{x}},{\varvec{X}}), \end{aligned}$$

(31)

Deprit [8] devised an efficient algorithm for the direct computation of the Taylor series expansion of F in the new variables. Namely,

$$\begin{aligned} F^*=F({\varvec{x}}({\varvec{y}},{\varvec{Y}}\epsilon ),{\varvec{x}}({\varvec{y}},{\varvec{Y}}\epsilon ),\epsilon )\equiv \sum _{m\ge 0}\frac{\epsilon ^m}{m!}F_{0,m}({\varvec{y}},{\varvec{Y}}), \end{aligned}$$

where the coefficients $F_{0,m}$ are iteratively computed from the recursion

$$\begin{aligned} F_{m,q+1}=F_{m+1,q}+\sum _{i=0}^m{m\atopwithdelims (){i}}\{F_{m-i,q},W_{i+1}\}, \end{aligned}$$

(32)

in which curly brackets denote the Poisson bracket operator.

When $F=\mathcal {H}\equiv \mathcal {H}_0+\mathcal {D}$ is a perturbation Hamiltonian, in which $\mathcal {H}_0$ is integrable and the magnitude of the disturbing function $\mathcal {D}$ is small compared to $\mathcal {H}_0$, Eq. (32) is definitively useful in computing a perturbation solution to $\mathcal {H}$. Indeed, after arranging the perturbation Hamiltonian in the form of Eq. (31), the coefficients $\mathcal {H}_{0,m}$ of a transformed Hamiltonian with some desired characteristics are computed from Eq. (32) starting from $\mathcal {H}_{0,m}=\mathcal {H}_{1,m-1}+\{\mathcal {H}_{0,m-1},W_{1}\}$. Repeated iterations of Deprit’s recursion yield the homological equation

$$\begin{aligned} \{W_{m},\mathcal {H}_{0,0}\}=\tilde{\mathcal {H}}_{0,m}-\mathcal {H}_{0,m}, \end{aligned}$$

(33)

where terms $\tilde{\mathcal {H}}_{0,m}$ are known from previous computations, terms $\mathcal {H}_{0,m}$ are selected according to some simplification criterion (commonly making cyclic one of the canonical variables), and terms $W_{m}$, from which the perturbation solution arises, must be solved from a partial differential equation. Complete solutions of the homological equation depend on arbitrary functions of the variables, which we normally can choose at our convenience. However, when boundary conditions apply to the perturbation problem, these arbitrary functions must be fixed to determine the particular solution of the homological equation that strictly adheres to the dynamics of the problem. This is precisely the case of hyperbolic-type motion dealt with in this paper.

The usefulness of Deprit’s recursion and Deprit’s perturbation approach is not constrained to Hamiltonian perturbation problems. Quite on the contrary, they apply to the much more general case of perturbations of vectorial flows after minor modifications of the algorithms [19, 23].