On the global dynamics of path-following control of automated passenger vehicles

Abstract

The nonlinear dynamics of the path-following control of passenger cars is analyzed in this paper. The effect of specific modeling aspects, such as tire deformation, steering dynamics, feedback delay and controller saturation, is considered. Possible equilibrium points and singularities in the state space are uncovered and analyzed for different vehicle model and controller designs. The equilibrium of stable path following is then analyzed in greater detail: The domains of stabilizing control gains are presented in stability charts and the basin of attraction of the equilibrium along the stable domain is approximated with the help of numerical continuation. Unsafe zones of control gains are highlighted, where the stable equilibrium is surrounded by low-amplitude unstable limit cycles. Finally, it is shown how specific modifications of the control law can remove unwanted equilibrium points and increase the basin of attraction of stable path following, resulting in safer and more reliable control of the vehicle.

1 Introduction

Automated driving functions have the potential to significantly reduce the risk and severity of road traffic accidents [31, 46]. However, in order to ensure reliable and safe operation under all potential circumstances, it is vital to understand the possible dynamics that the controlled vehicle might exhibit. This paper aims to provide a comprehensive global picture of the nonlinear dynamics of path-following control with feedback delay.

The first nontrivial question during the control design process is the choice of vehicle model. The most commonly used modeling approach for describing the lateral and yaw dynamics of the vehicle is the use of the so-called single-track vehicle model (sometimes also referred to as bicycle model) [20, 40]. Depending on the specific use-case and the accuracy needed, there exist many variations of this model [34, 39]: The simplest vehicle models assume rigid wheels with no tire deformation [19, 26], but a wide range of tire models are also available in the literature to describe the tire-road interaction [33]. The arising side forces and self-aligning moments are commonly considered as different linear and nonlinear functions of the side slip angles [21, 45], but more involved tire models can also be applied [5]. Additional modeling aspects include the consideration of geometrical nonlinearities [10, 30, 45], the drive type of the vehicle [30], the inertia of the steering system [49] and the caster length of the steered wheel [48]. When selecting the appropriate vehicle model, a balance needs to be found between model complexity and fidelity. More complex models might provide more accurate results at the expense of computational time, but it also needs to be kept in mind that the additional parameters of complex vehicle and tire models might not be known accurately in practice.

The second important issue is related to the control law. In general, the desired steering angle or the steering torque is generated based on the feedback signal of the lateral distance from the reference path and the misalignment between the path direction and the longitudinal axis of the vehicle. The earliest control algorithms were proposed in the 1950 s [43] and since then a large variety of different controllers have been put forward using sophisticated control design techniques like model predictive control [7, 8, 13, 23], Lyapunov-based control [42, 47], sliding mode control [9], look-ahead/preview control [1, 53], and machine learning-based control [2, 4], just to mention a few. See [35] for a comparative analysis of the different control methods. Recent efforts also included developing controllers which can drive at the handling limits, for example, in the case of emergency maneuvers [14, 23, 52]. In such scenarios, to take full advantage of the abilities of the vehicle, it is essential to have a clear understanding of the dynamics of the controlled vehicle and tune the controllers accordingly.

It is also important to take into consideration the time delay in the control loop during the control design process. The total time delay consists of components such as sensor delays, the delay caused by computation and communication within the vehicle by the various electronic control units, and the actuation delay in the steering system. Together, these effects can add up to several hundred milliseconds: For example, in [6], the delay of the entire control loop was experimentally determined to be in the range of 0.7$-$0.9 s. In [16], the actuation delay in the steering system was observed to be around 0.4 s. Similarly, in [53], a delay of 0.4 s was found between the steering command and the actual steering angle, while in [36], the measured steering system delay was 0.5 s.

Typically, the essence of most path-following controllers can be reduced to a nonlinear feedback law which may be expressed in an explicit or implicit function of the lateral displacement and the misalignment. For small lateral distance and small misalignment all of these nonlinear laws simplify to a linear control law with two tunable gains. In this paper we utilize this simple linear controller to distill the most important features of path following. After the detailed analysis of the controlled vehicle with the linear control law, we also propose a specific nonlinear modification and show how it can improve the path-following performance of automated vehicles.

The nonlinear analysis of the controlled vehicle has mostly been covered in the literature with the consideration of a human driver [10, 17, 24, 25, 28]. Driver models are often based on some kind of feedback controller with reaction time delay; for a comprehensive overview see [37] and [27]. Depending on the objective of the calculations, the nonlinear analysis of the system can be performed using a number of different methods: A more analytical approach is to perform the normal form transformation and center manifold reduction of the system to predict the nonlinear behavior of the vehicle in the vicinity of the linear stability limits [17, 24, 48]. In order to cover a wider range of system parameters, bifurcation diagrams can also be constructed using a series of numerical simulations [25, 32] or by applying numerical continuation methods [10, 28, 49]. In addition, phase portraits can be used to analyze the possible equilibrium points of the system and the trajectories between them [10, 22, 32, 48, 54].

The contributions of this paper are twofold: On the one hand, a comprehensive nonlinear analysis of the dynamics of the controlled vehicle is provided, including the location of equilibrium points and singularities, numerical continuation of periodic orbits and quantifying the basin of attraction along the entire stable domain of control gains. Three different variations of the single-track model are considered, in order to demonstrate the importance of considering tire dynamics and the often neglected effects of the steering system. In addition, the entire analysis is performed with the explicit consideration of the feedback delay in the controller, instead of the common simplification of approximating it with a first-order lag term [10, 24, 28]. Based on the results of this analysis, sensitivity to disturbances can directly be taken into account when tuning the controller and unsafe control gains, which might lead to high performance in the linear sense but are vulnerable to perturbations, can be avoided.

As the second main contribution of the paper, we explore how the dynamics can be significantly improved by some specific modifications of the control law. This way the domain of attraction of stable path following can be increased, leading to a safer and more robust control performance, while also removing unwanted equilibrium points from the state space. This may ensure that the controlled vehicle can safely handle a variety of unexpected changes in road conditions and other disturbances, from emergency obstacle avoidance to hitting an ice patch.

The rest of the paper is organized as follows: The vehicle models with different modeling considerations are presented in Sect. 2. A linear and a nonlinear path-following controller is introduced in Sect. 3 with two different saturation functions to prevent unreasonably strong control actions. Section 4 presents the possible equilibrium points and singularities of the controlled vehicle. The following two sections focus on the most important equilibrium (i.e., the straight-line motion): The domains of stabilizing control gains of the linearized system are calculated in Sect. 5, while the dynamics of the nonlinear system are analyzed in detail in Sect. 6. To further illustrate the results of our analysis, some representative numerical simulations are presented in Sect. 7. The results are then concluded in Sect. 8.

2 Vehicle models

Three variations of the in-plane single-track model of passenger cars are presented in this section, with increasing complexity. The main modeling assumptions of the single-track model apply to all three variations, i.e., the front and the rear wheels are both merged into a single wheel, respectively, while no pitch and roll motions are considered.

Fig. 1

Vehicle models: (a) kinematic model with assigned steering angle, (b) dynamic model with assigned steering angle, (c) dynamic model with torque steering

2.1 Kinematic model with assigned steering angle

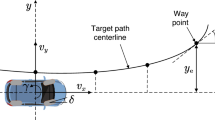
The simplest version of the single-track model of passenger cars (see Fig. 1a) assumes rigid wheels, which means that the side slip of the tires are neglected. This assumption is valid for lower lateral accelerations. Furthermore, the rotational degree of freedom of the wheels are not considered, either, leading to the so-called skate model of the wheels [39, 41]. The configurational coordinates of the vehicle include the rear axle center position coordinates $x_\textrm{R}$ and $y_\textrm{R}$ in the global coordinate system and the yaw angle $\psi$. Selecting the coordinates of point R as configurational coordinates greatly simplifies the resulting equations. The steering angle $\delta _{\textrm{s}}$ is directly assigned by the controller without considering the dynamics of the steering system. The vehicle parameters include the wheelbase f and the longitudinal velocity V, which is assumed to be constant. Since the parameter V determines the velocity component of point R pointing into the rolling direction of the rear wheels, this modeling choice corresponds to a rear wheel drive vehicle.

The constant longitudinal velocity and the no side slip conditions at the front (point F) and rear (point R) wheels can be described by the following three kinematic constraints:

$$\begin{aligned}&{\dot{x}}_\textrm{R}\sin (\psi +\delta _{\textrm{s}}) - {\dot{y}}_\textrm{R}\cos (\psi +\delta _{\textrm{s}}) - f{\dot{\psi }}\cos \delta _{\textrm{s}}= 0 , \end{aligned}$$

(1)

$$\begin{aligned}&\quad -{\dot{x}}_\textrm{R} \sin \psi + {\dot{y}}_\textrm{R} \cos \psi = 0 ,\end{aligned}$$

(2)

$$\begin{aligned}&\quad {\dot{x}}_\textrm{R} \cos \psi + {\dot{y}}_\textrm{R} \sin \psi = V . \end{aligned}$$

(3)

These constraint equations can be directly solved for the state derivatives, leading to the equations of motion

$$\begin{aligned} {\dot{x}}_\textrm{R}&= V \cos \psi , \end{aligned}$$

(4)

$$\begin{aligned} {\dot{y}}_\textrm{R}&= V \sin \psi , \end{aligned}$$

(5)

$$\begin{aligned} {\dot{\psi }}&= \frac{V}{f} \tan \delta _{\textrm{s}}\, . \end{aligned}$$

(6)

2.2 Dynamic model with assigned steering angle

As a next modeling step, the vehicle model is extended with the inclusion of elastic tires (see Fig. 1b). The deformation of the tires generates active forces, therefore the vehicle mass m and yaw moment of inertia $J_z$ also need to be considered. The distance of the center of gravity C from the rear axle is denoted by d.

The configurational coordinates $x_\textrm{R}$, $y_\textrm{R}$ and $\psi$ are the same as in the case of the kinematic model of Sect. 2.1. However, since the direction of the velocity vectors at the front and rear axles are now determined by the side slip angles $\alpha _\textrm{F}$ and $\alpha _\textrm{R}$, only the kinematic constraint (Eq. 3) of constant longitudinal velocity remains.

By using the lateral velocity $\sigma _1$ of point R and the yaw rate $\sigma _2$ as so-called pseudovelocities, the equations of motions of the vehicle can be derived using the Appell–Gibbs method [15], as detailed in [51]. The governing equations consist of the formulas of the generalized velocities

$$\begin{aligned}{} & {} {\dot{x}}_\textrm{R} = V \cos \psi - \sigma _1 \sin \psi , \end{aligned}$$

(7)

$$\begin{aligned}{} & {} {\dot{y}}_\textrm{R} = V \sin \psi + \sigma _1 \cos \psi , \end{aligned}$$

(8)

$$\begin{aligned}{} & {} {\dot{\psi }} = \sigma _2, \end{aligned}$$

(9)

and the Appell–Gibbs equations

$$\begin{aligned} \begin{bmatrix} m &{} md\\ md &{} J_\textrm{C}+md^2\\ \end{bmatrix} \begin{bmatrix} {\dot{\sigma }}_1 \\ {\dot{\sigma }}_2 \end{bmatrix} = \begin{bmatrix} f_1 \\ f_2 \end{bmatrix} , \end{aligned}$$

(10)

where the right-hand side is

$$\begin{aligned} f_1= & {} -F_\textrm{R} -F_\textrm{F} \cos \delta _{\textrm{s}}-m V \sigma _2, \end{aligned}$$

(11)

$$\begin{aligned} f_2= & {} -M_\textrm{F} -M_\textrm{R}- F_\textrm{F} f \cos \delta _{\textrm{s}}- m d V \sigma _2. \end{aligned}$$

(12)

The lateral tire forces $F_\textrm{F}$ and $F_\textrm{R}$, as well as the self-aligning moments $M_\textrm{F}$ and $M_\textrm{R}$ are calculated using the nonlinear brush tire model (see Appendix A.1 for details) as functions of the side slip angles

$$\begin{aligned} \alpha _{\textrm{R}} = \arctan \left( \frac{\sigma _1}{V}\right) , \quad \alpha _{\textrm{F}} = \arctan \left( \frac{v_{\textrm{F},\perp }}{v_{\textrm{F},\parallel }} \right) , \end{aligned}$$

(13)

where the perpendicular and parallel velocity components (with respect to the rolling direction) at the front wheel are

$$\begin{aligned} v_{\textrm{F},\perp }&= \left( \sigma _1 + f \sigma _2 \right) \cos \delta _{\textrm{s}}- V \sin \delta _{\textrm{s}}\, , \end{aligned}$$

(14)

$$\begin{aligned} v_{\textrm{F},\parallel }&= \left( \sigma _1 + f \sigma _2 \right) \sin \delta _{\textrm{s}}+ V \cos \delta _{\textrm{s}}\, . \end{aligned}$$

(15)

The kinematic trail from the suspension system is not considered when calculating the self-aligning moment.

We note that the analysis in the subsequent sections includes equilibrium points where the rolling direction of the steered wheel changes, i.e., it starts rolling backward. Although these points carry little practical relevance, they help us gain a deeper understanding of the global dynamics of the controlled vehicle. In order to accurately determine the direction of the tire side force in such cases too, a modified side slip angle ${\tilde{\alpha }}_{\textrm{F}} = \alpha _{\textrm{F}} \, \textrm{sign} ( v_{\textrm{F},\parallel } )$ was used during the calculation of $F_{\textrm{F}}$ (for the self-aligning moment $M_{\textrm{F}}$, the original definition of $\alpha _{\textrm{F}}$ can be used).

2.3 Dynamic model with torque steering

In the previous models, the steering angle $\delta _\textrm{s}$ was used as the system input. Since the input signal is generated by the controller, this means that the desired steering angle instantaneously appears at the wheels, and a sudden change in the reference signal will cause the steered wheels to jump instantaneously from one angle to another.

In order to overcome this limitation, the single-track vehicle model from Sect. 2.2 is extended with the dynamics of the actuation (see Fig. 1c). This means that the path-following controller only determines the desired steering angle $\delta _{\textrm{s}}^\textrm{des}$, and an additional lower-level controller is used to generate a steering torque $M_\textrm{s}$ that aims to minimize the error between the desired and the actual steering angle. This steering torque acts against the moment of inertia $J_\textrm{F}$ of the steering system and the self-aligning moment at the front wheels $M_\textrm{F}$.

In order to extend the vehicle model with the above considerations, the steering angle $\delta _{\textrm{s}}$ is used as an additional generalized coordinate, alongside $x_\textrm{R}$, $y_\textrm{R}$ and $\psi$. Since the kinematic constraint of constant longitudinal speed in Eq. (3) still applies, the difference between the number of generalized coordinates (four) and kinematic constraints (one) increases to three, therefore a third pseudovelocity $\sigma _3$ needs to be defined. A suitable choice is to define it as the steering rate, i.e., $\sigma _3:= {\dot{\delta }}_\textrm{s}$.

The resulting equations of motion consist of the time derivatives of the generalized coordinates

$$\begin{aligned}{} & {} {\dot{x}}_\textrm{R} = V \cos \psi -\sigma _1 \sin \psi , \end{aligned}$$

(16)

$$\begin{aligned}{} & {} {\dot{y}}_\textrm{R} = V \sin \psi +\sigma _1 \cos \psi , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} {\dot{\psi }} = \sigma _2,\end{aligned}$$

(18)

$$\begin{aligned}{} & {} {\dot{\delta }}_\textrm{s} = \sigma _3, \end{aligned}$$

(19)

as well as the three Appell–Gibbs equations

$$\begin{aligned} \begin{bmatrix} m &{} md &{} 0\\ md &{} J_\textrm{C}+md^2 + J_\textrm{F}&{} J_\textrm{F}\\ 0 &{} J_\textrm{F} &{} J_\textrm{F} \\ \end{bmatrix} \begin{bmatrix} {\dot{\sigma }}_1 \\ {\dot{\sigma }}_2 \\ {\dot{\sigma }}_3 \end{bmatrix} = \begin{bmatrix} f_1 \\ f_2 \\ f_3 \end{bmatrix} , \end{aligned}$$

(20)

with

$$\begin{aligned} f_1= & {} -F_\textrm{R} -F_\textrm{F} \cos \delta _{\textrm{s}}-m V \sigma _2, \end{aligned}$$

(21)

$$\begin{aligned} f_2= & {} -M_\textrm{F} -M_\textrm{R}- F_\textrm{F} f \cos \delta _{\textrm{s}}- m d V \sigma _2, \end{aligned}$$

(22)

$$\begin{aligned} f_3= & {} - M_\textrm{F} + M_\textrm{s}. \end{aligned}$$

(23)

The steering torque $M_\textrm{s}$ is generated by the lower-level proportional-derivative controller as follows:

$$\begin{aligned} M_\textrm{s} = -k_\textrm{p} \left( \delta _{\textrm{s}}- \delta _{\textrm{s}}^\textrm{des} \right) - k_\textrm{d} \sigma _3 , \end{aligned}$$

(24)

where $k_\textrm{p}$ and $k_\textrm{d}$ denote the lower-level control gains.

3 Path-following controller

In this section, the path-following problem of the vehicle is established. Our goal is to drive the rear axle center point R along the path by feeding back the lateral deviation and the yaw angle error. We select point R for tracking the reference path, since this will lead to the simplest form of the control law. Furthermore, it was shown in [39] that achieving zero displacement and angle error at the same time during path following is only possible for tracking the rear axle center point (assuming the simplest, kinematic vehicle model). Further analysis regarding the effect of sensor location (i.e., which point is used for feedback) can be found in [38].

In order to simplify our analysis, a straight reference path along the x-axis is considered. This way the vehicle state $y_\textrm{R}$ directly corresponds to the lateral position error and the yaw angle error is equal to $\psi$. Two controller variations are considered, first, a simple linear feedback controller, then a modified nonlinear version. In addition, the saturation of the control input will also be considered.

In the case of the kinematic vehicle model and the dynamic model with assigned steering angle, the output of the controllers detailed in this section directly generate the steering angle, i.e., ${\delta _{\textrm{s}}= \delta _{\textrm{s}}^\textrm{des}}$. In the vehicle model with torque steering, however, $\delta _{\textrm{s}}^\textrm{des}$ is only used as the reference of the lower-level controller in Eq. (24).

3.1 Linear control law

The simplest linear control law generates the desired steering angle as

$$\begin{aligned} \delta _{\textrm{s}}^\textrm{des}(t) = -P_y y_\textrm{R}(t-\tau ) - P_{\psi } \psi (t-\tau ) , \end{aligned}$$

(25)

where $P_y$ and $P_\psi$ are the control gains and $\tau$ denotes the feedback delay. The delay term includes sensor and communication delays, processing time as well as actuator delays.

3.2 Nonlinear control law

As a variation of the linear control law in Eq. (25), the nonlinear control law

$$\begin{aligned} \delta _{\textrm{s}}^\textrm{des}(t) = -P_\psi \left( \psi (t-\tau ) + \arctan \left( \frac{P_y}{P_\psi } y_\textrm{R}(t-\tau ) \right) \right) \end{aligned}$$

(26)

is considered, which was originally proposed in [39]. When linearized around small errors, Eq. (26) leads to the linear controller in Eq. (25), therefore close to the reference path, the two controllers behave similarly. However, the arctangent function in Eq. (26) limits the effect of large lateral errors: notice that the second term in the control law acts as the reference yaw angle

$$\begin{aligned} \psi _\textrm{des} = - \arctan \left( \frac{P_y}{P_\psi } y_\textrm{R}(t-\tau ) \right) , \end{aligned}$$

(27)

therefore if the vehicle is far from the reference path ($y_\textrm{R} \rightarrow \pm \infty$), the controller will steer directly toward it $\left( \psi _\textrm{des} \rightarrow \mp \pi /2 \right)$.

Fig. 2

Saturation functions

Table 1 List of vehicle parameters

3.3 Controller saturation

In order to prevent unreasonably large steering angles, the control signal can be limited by a saturation function. The simplest approach is to use

$$\begin{aligned} \textrm{sat} (\delta _{\textrm{s}}^\textrm{des}) = {\left\{ \begin{array}{ll} -\delta _\textrm{sat} &{} \textrm{if} \quad \delta _{\textrm{s}}^\textrm{des} < -\delta _\textrm{sat} , \\ \delta _{\textrm{s}}^\textrm{des} &{} \textrm{if} \quad -\delta _\textrm{sat} \le \delta _{\textrm{s}}^\textrm{des} \le \delta _\textrm{sat} , \\ \delta _\textrm{sat} &{} \textrm{if} \quad \delta _{\textrm{s}}^\textrm{des} > \delta _\textrm{sat} , \\ \end{array}\right. } \end{aligned}$$

(28)

which simply ensures that the control signal does not go below the lower saturation limit $-\delta _\textrm{sat}$ or above the upper limit $\delta _\textrm{sat}$. Between these two threshold levels, the original value is unchanged (see Fig. 2a).

An alternative option is to use a continuous wrapper function such as

$$\begin{aligned} g(\delta _{\textrm{s}}^\textrm{des}) = \frac{2 \delta _\textrm{sat}}{\pi } \arctan \left( \frac{\pi }{2 \delta _\textrm{sat}} \delta _{\textrm{s}}^\textrm{des} \right) \end{aligned}$$

(29)

(originally introduced in [39]). This function is bounded by $\pm \delta _\textrm{sat}$, but it also affects the input signal between the limits, as shown in Fig. 2b. This allows the use of larger control gains, which improves tracking performance for small errors, while the shape of the saturation function mitigates the control action for larger errors, which may help to avoid unwanted oscillations and overshoots.

Calculating the saturation thresholds, i.e., the maximum allowable steering angle can be based on the current vehicle speed, in order to limit the lateral acceleration of the vehicle during the maneuver and thus ensure passenger comfort. The lateral acceleration at the rear axle is

$$\begin{aligned} a_\textrm{R}^\textrm{lat} = - \ddot{x}_\textrm{R} \sin \psi + \ddot{y}_\textrm{R} \cos \psi , \end{aligned}$$

(30)

which, using the equations of motion of the kinematic vehicle model in Eqs. (4–6), can be written as

$$\begin{aligned} a_\textrm{R}^\textrm{lat} = \frac{V^2}{f} \tan \delta _{\textrm{s}}\,. \end{aligned}$$

(31)

From this, the steering angle limit corresponding to a given maximum allowable lateral acceleration is

$$\begin{aligned} \delta _\textrm{sat} = \arctan \left( \frac{f a_\textrm{R,max}^\textrm{lat}}{V^2} \right) . \end{aligned}$$

(32)

Throughout this paper, we consider a maximum lateral acceleration of 8 m/s$^2$, which, using the parameters in Table 1, corresponds to a saturation level of $\delta _\textrm{sat}=0.0539$ rad ($\approx 3.09$ deg) at ${V=20}$ m/s.

4 Equilibria and singularities

In order to gain a deeper understanding of the global dynamics of the controlled vehicle, first, the possible equilibrium points of the system have to be uncovered. The simplicity of the kinematic vehicle model allows us to reach some analytical results, which can then be used to better understand and verify the results of the more complicated vehicle models.

4.1 Kinematic model with linear controller

The closed loop system of the kinematic vehicle model and the linear controller in Eq. (25) is the following:

$$\begin{aligned} {\dot{y}}_\textrm{R}= & {} V \sin \psi , \end{aligned}$$

(33)

$$\begin{aligned} {\dot{\psi }}= & {} \frac{V}{f} \tan \left( -P_y y_\textrm{R}(t-\tau ) - P_{\psi } \psi (t-\tau ) \right) . \end{aligned}$$

(34)

Note that the equation of ${\dot{x}}_\textrm{R}$ (Eq. 4) can be decoupled from the rest, because the position of the vehicle along the x-axis does not influence its lateral dynamics.

In an equilibrium point defined by ${y_\textrm{R}(t) \equiv y_\textrm{R,0}}$ and ${\psi (t) \equiv \psi _0}$, the following system of algebraic equations is satisfied:

$$\begin{aligned} 0= & {} V \sin \psi _0, \end{aligned}$$

(35)

$$\begin{aligned} 0= & {} \frac{V}{f} \tan \underbrace{ \left( -P_y y_\textrm{R,0} - P_{\psi } \psi _0 \right) }_{=\delta _{\textrm{s},0}}. \end{aligned}$$

(36)

From Eq. (35), it can be seen that the possible equilibria in terms of $\psi$ are located at

$$\begin{aligned} \psi _0 = k \pi , \quad k \in {\mathbb {Z}}, \end{aligned}$$

(37)

which means that the stationary motion of the vehicle will always be parallel to the x-axis, either in the positive or in the negative direction. Since there is no tire deformation included in the kinematic model, this can only be achieved if the steered wheels point parallel to the vehicle body, i.e., ${\delta _{\textrm{s},0} = n \pi }$, ${n \in {\mathbb {Z}}}$ (see Eq. 36). Using the control law in Eq. (25), this corresponds to

$$\begin{aligned} -P_y y_\textrm{R,0} - P_\psi \psi _0 = n \pi , \end{aligned}$$

(38)

which leads to

$$\begin{aligned} y_\textrm{R,0} = \frac{1}{P_y}(P_\psi k + n). \end{aligned}$$

(39)

Therefore, there exist infinitely many stationary solutions parallel to the x-axis at different values of y, where the corresponding vehicle orientation $\psi _0$ and steering angle $\delta _{\textrm{s},0}$ are determined by the integers k and n. Note that at this point, there is no limit imposed on the steering angles and the front wheels can be turned around arbitrarily many times.

Fig. 3

Equilibrium points and singularities in the kinematic vehicle model for ${P_y=0.3 \, \textrm{m}^{-1}}$ and ${P_\psi =1}$. (a) Phase portrait in the ${(y_\textrm{R},\psi )}$ plane. (b) The location of the equilibria as the control gain $P_y$ is increased. (c) Illustration of the steady state trajectories. Vehicle parameters are listed in Table 1

Fig. 4

Equilibrium points and singularities of the dynamic vehicle models using the different controller variations. Gray contour lines show the steering angle values along the phase portraits. In the shaded areas, the steering angle exceeds the saturation limit. The control gains are ${P_y=0.015 \, \textrm{m}^{-1}}$ and ${P_\psi =0.6}$, the rest of the vehicle parameters are listed in Table 1. The stability of the equilibrium points correspond to the dynamic vehicle model with torque steering

An example of the location of these equilibria (green circles and red crosses) in the ${(y_\textrm{R},\psi )}$ phase portrait can be seen in Fig. 3a with the corresponding stationary steering angles that are also highlighted by the gray isolines. As $P_y$ is increased, the equilibrium points move closer to each other in terms of $y_\textrm{R}$ according to Eq. (39), as shown in Fig. 3b. The sketches in panel (c) illustrate the steady state vehicle trajectories corresponding to the different equilibrium points marked by roman numbers in panel (a).

Singularities may also occur in the kinematic model, when the tangent function in Eq. (6) becomes singular. This occurs if ${\delta _{\textrm{s},0}=\frac{\pi }{2}+l \pi }$, ${l \in {\mathbb {Z}}}$, which corresponds to configurations when the direction of the steered wheel is perpendicular to the vehicle body. In such scenarios, the kinematic constraint at the front wheel (Eq. 1) would result in a zero velocity component in the longitudinal direction of the vehicle. This obviously contradicts the kinematic constraint in Eq. (3), which prescribes a constant (nonzero) longitudinal speed V. Therefore, the kinematic model becomes singular at these values of $\delta _{\textrm{s}}$. If the steering angle is generated according to the linear controller in Eq. (25), these singularities can be described by

$$\begin{aligned} \psi = -\frac{1}{P_\psi } \left( \frac{\pi }{2} + l \pi + P_y y_\textrm{R} \right) , \end{aligned}$$

(40)

as shown by the black dashed lines in the ${(y_\textrm{R},\psi )}$-plane in Fig. 3a).

4.2 Dynamic vehicle models

In case of the more complicated vehicle models and controllers, the equilibrium points can only be identified numerically. However, some considerations can be used to reduce the dimension of the corresponding system of nonlinear algebraic equations that needs to be solved. On the one hand, the equation of $x_\textrm{R}$ can be decoupled in case of the other vehicle models too. In addition, Eqs. (8) and (17) can be used to directly express the value of $\sigma _1$ in an equilibrium (where ${\dot{y}}_\textrm{R} \equiv 0$) as

$$\begin{aligned} \sigma _{1,0} = -V \tan \psi _0. \end{aligned}$$

(41)

Moreover, $\sigma _2$ and (in case of the third vehicle model) $\sigma _3$ can only be zeros in an equilibrium, since these state variables are by definition directly equal to the state derivatives ${\dot{\psi }}$ and ${\dot{\delta }}_\textrm{s}$. As a result, finding the equilibria of the dynamic vehicle model with assigned steering angle reduces to a two dimensional problem (with unknowns $y_\textrm{R,0}$ and $\psi _0$), while for the dynamic vehicle model with torque steering, three unknowns remain ($y_\textrm{R,0}$, $\psi _0$ and $\delta _{\textrm{s},0}$). The possible solutions of the resulting system of nonlinear algebraic equations were calculated numerically using the multi-dimensional bisection method [3]. This way both equilibrium points and singularities of the system can be identified.

The two vehicle models with tire dynamics lead to the same phase portraits, as seen in Fig. 4. When using the linear controller (Fig. 4a), a similar periodicity of equilibrium points (green circles and red crosses) can be observed as in the case of the kinematic model in Fig. 3a. The stationary values of $\psi$ and $\delta _{\textrm{s}}$ are once again integer multiples of $\pi$, while the distance of the equilibria in terms of $y_\textrm{R}$ depends on the control gains.

When the vehicle model includes the lateral tire dynamics, singularities may occur if the longitudinal (with respect to the wheel) velocity component of the steered wheel becomes zero. This occurs if the direction of the wheel is perpendicular to the vehicle body (${\delta _{\textrm{s}}=p \pi /2}$, ${p \in {\mathbb {Z}}}$), where the wheel is on the verge of changing its rolling direction. This leads to the signum function in ${\tilde{\alpha }}_{\textrm{F}}$ (see the end of Sect. 2.2) becoming singular, thus the side slip angle is not defined properly in these points. This is similar to the common problem of tire models becoming singular at low speeds because of the vehicle speed in the denominator of the side slip angle [21]. These singular points are depicted in Fig. 4a by black circles.

When a saturation function is used to limit the applied steering angles (Fig. 4b), the equilibrium points with steering angle values outside of the saturation limits (corresponding to the gray areas in the figure) disappear. The nonlinear controller in Eq. (26) has a similar effect (see Fig. 4c), where the atan function limits the effect of $y_\textrm{R}$ (i.e., the distance from the reference path) on the input signal. Therefore the steering angle is much more limited along the phase portrait, which has the effect of removing a large number of equilibrium points (see how the linear isolines of $\delta _{\textrm{s}}$ along the phase portrait in Fig. 4a are replaced by the nonlinear curves in Fig. 4c). However, large values of $\psi$ can still lead to unreasonably large steering angles, therefore it is still possible that the vehicle will follow a different path parallel to the x-axis.

Notice how the saturation function in Fig. 4b and the nonlinear controller in Fig. 4c remove unwanted equilibria from different regions of the phase portrait. If the two is combined (i.e., the nonlinear control law is used with a saturation function, Fig. 4d), all the unwanted stationary motions can be avoided: the nonlinearity in the control law mitigates the effect of large lateral errors, while the saturation function prevents reaching any additional equilibrium points with large steering angles. The only remaining equilibrium of the system is the origin, which corresponds to stationary straight-line motion along the x-axis as intended.

We note that the choice of saturation function has no effect on the stationary motions of the vehicle, i.e., Eqs. (28) and (29) lead to the same results in this section. In addition, the stability of the individual equilibrium points depends on the choice of parameters (which can of course affect the location of the equilibria too) as well as the vehicle model. In Fig. 4, the stability of the equilibria were evaluated using the vehicle model with torque steering, for the parameter values listed in Table 1. In the next section, the stability properties of the origin will be explored in greater detail.

5 Linear stability analysis of the straight-line motion

Here, the equilibrium of straight-line motion along the x-axis is analyzed in detail. The state variables are all zeros in this stationary motion apart from ${x_\textrm{R}=Vt}$, but as previously, the corresponding equation can be decoupled from the rest. The reduced state vectors consisting of the remaining state variables are

$$\begin{aligned} {\textbf{x}}_\textrm{kin}= \begin{bmatrix} y_\textrm{R}&\psi \end{bmatrix} ^\textrm{T} \end{aligned}$$

(42)

in case of the kinematic vehicle model,

$$\begin{aligned} {\textbf{x}}_\textrm{dyn}= \begin{bmatrix} y_\textrm{R}&\psi&\sigma _1&\sigma _2 \end{bmatrix} ^\textrm{T} \end{aligned}$$

(43)

for the dynamic vehicle model with assigned steering angle, and

$$\begin{aligned} {\textbf{x}}_\textrm{servo}= \begin{bmatrix} y_\textrm{R}&\psi&\delta _{\textrm{s}}&\sigma _1&\sigma _2&\sigma _3 \end{bmatrix} ^\textrm{T} \end{aligned}$$

(44)

for the dynamic model with torque steering. Linearizing the corresponding equations of motion around the origin leads to the linear state space model

$$\begin{aligned} \dot{{\textbf{x}}}_i={\textbf{A}}_i {\textbf{x}}_i + {\textbf{B}}_i u_i, \quad i \in \{ \textrm{kin}, \, \textrm{dyn}, \, \textrm{servo} \}, \end{aligned}$$

(45)

where the state matrices ${\textbf{A}}_i$ and input matrices ${\textbf{B}}_i$ are listed in Appendix A.2. In the vehicle models with directly assigned steering angle, the system input is ${u_\textrm{kin}=u_\textrm{dyn}=\delta _{\textrm{s}}}$, while in case of torque steering, the desired steering angle is considered as the input of the system (${u_\textrm{servo} = \delta _{\textrm{s}}^\textrm{des}}$). The steering torque $M_\textrm{s}$ is regarded as part of the system dynamics in the matrices ${\textbf{A}}_\textrm{servo}$ and ${\textbf{B}}_\textrm{servo}$.

Linearizing the control law in Eq. (26) leads to the linear controller in Eq. (25), therefore the choice of controller does not affect the local stability of the system. Introducing the appropriately sized gain vector ${\textbf{K}}_i$, where the only nonzero elements are $-P_y$ and $-P_\psi$ in the first and second place, respectively, the linearized system input can be written as $u_i = {\textbf{K}}_i {\textbf{x}}_i (t-\tau )$.

Thus, the characteristic equation of the system becomes

$$\begin{aligned} D_i(\lambda ) := \det \left( \lambda {\textbf{I}}_i - {\textbf{A}}_i - {\textbf{B}}_i {\textbf{K}}_i \textrm{e}^{-\lambda \tau } \right) = 0 , \end{aligned}$$

(46)

where ${\lambda \in {\mathbb {C}}}$ is the characteristic exponent and ${\textbf{I}}_i$ is the identity matrix of appropriate size. Because of the time delay in the control loop, the characteristic equation is transcendental with infinitely many roots in the complex plane. The asymptotic stability of the linearized system is ensured if all of these characteristic roots have negative real parts. At the boundaries of stability, there exist characteristic exponents whose real part is zero. If a characteristic exponent moves to the right half plane at ${\lambda = 0}$, static stability loss occurs, where the state variables diverge without oscillation. This may correspond to a saddle-node bifurcation of the nonlinear system. Conversely, if a complex conjugate pair of characteristic exponents crosses the imaginary axis (i.e., ${\lambda = \pm \textrm{i} \omega }$), dynamic stability loss occurs, where the vehicle loses its stability with oscillations at the vibration frequency $\omega$. The nonlinear system in this case may undergo a Hopf-bifurcation.

The effects of the control gains $P_y$ and $P_\psi$ on the stability of the system can be showcased using stability charts, as in Fig. 5. Substituting ${\lambda = 0}$ into the characteristic equation in Eq. (46) leads to the boundary of static stability loss at ${P_y=0}$ for all three vehicle models. Conversely, the boundaries of dynamic stability loss can be determined using the D-subdivision method [18, 29], by evaluating ${D_i(\textrm{i}\omega )=0}$. The resulting complex equation can be separated into its real and imaginary part, then the two equations can be solved for two arbitrary system parameters, leading to the curves of the stability boundaries parameterized by $\omega$.

Fig. 5

Stability maps of the three vehicle models in the delay-free case (top three panels) and with a feedback delay of ${\tau =0.5}$ s (bottom three panels). The rest of the vehicle parameters are listed in Table 1

The top three panels of Fig. 5 show the stability charts of the controlled vehicle in the delay-free case. When the steering system dynamics are neglected (panels a and b), the stable domain is unbounded, while in the torque steering model (panel c) the delay-free stable domain has a similar D shape to the delayed cases in the bottom three panels. This shows that the inertia of the steering system acts as a filtering mechanism on the higher-level controller, which affects the overall dynamics similarly to a feedback delay. The time delay, however, significantly reduces the stable domain, as indicated by the different scaling of the stability charts in panels (d–f). Here, the consideration of the steering dynamics seems to have a beneficial effect in terms of stability, but the nonlinear analysis in the following section will show that the majority of the additional stable area can be unsafe to use in practice.

6 Nonlinear analysis of the straight-line motion

The stability charts in the previous section only provide information about the local dynamics of the system near the equilibrium point corresponding to the straight-line motion. The boundaries of dynamic stability loss, however, correspond to Hopf bifurcations in the nonlinear system. This means that there exist limit cycles in the state space and the quality of the solution can largely depend on the initial conditions. The vehicle might also react differently to different sizes of perturbations, and it is possible that stable straight-line motion is not achieved even if the control gains are selected from the linearly stable parameter domain.

In order to gain a clear picture of these nonlinear phenomena, we performed numerical continuation with the help of the DDE-Biftool [11, 12, 44] software package. The results in this section are based on the most realistic vehicle model, where the tire dynamics and the steering torque are both considered. By following the limit cycles emerging from the bifurcation points at the stability boundary, it can be uncovered which regions of the stable parameter domain are more susceptible to perturbations. For control gain combinations where the limit cycle amplitude is lower, the system can leave the basin of attraction of the stable equilibrium even for smaller perturbations.

Since the state space of the system is infinite dimensional due to the time delay in the control loop, we can only show sections of the basin of attraction along the control parameters: In the bifurcation diagrams in Fig. 6, the oscillation amplitude in terms of $y_\textrm{R}$ is used to represent the periodic solutions.

Fig. 6

Nonlinear analysis of the four controller variations. Panels (a–p): bifurcation diagrams along different sections of the stability charts. Panels (q–t): stability charts with the colormap indicating the amplitude of unstable limit cycles inside the stable domain. Red plus sign denotes the optimal control gains of the linear closed-loop system

The four columns in Fig. 6 correspond to the four controller variations: the first column shows the nonlinear behavior of the linear controller in Eq. (25) without any saturation function. The panels of the second column correspond to the nonlinear control law in Eq. (26) still without saturation. In the third column, the nonlinear control law is wrapped into the saturation function sat$(\delta _{\textrm{s}}^\textrm{des})$ in Eq. (28) and in the last column, the saturation function $g(\delta _{\textrm{s}}^\textrm{des})$ in Eq. (29) is used with the nonlinear control law. The bifurcation diagrams in panels (a)-(p) show the limit cycle amplitudes of the four controller variations in terms of $y_\textrm{R}$ as a function of the control gain $P_y$, for different fixed values of $P_\psi$. The corresponding sections of $P_\psi$ are indicated by dashed lines in the stability charts in panels (q)-(t).

In addition, the color maps in the stability charts show how the unstable limit cycle amplitudes change along the stable domain of control gains. We consider the regions of stabilizing control gains where the limit cycle amplitude is below 3.5 m (representing the width of one lane) as unsafe from a practical point of view. The so-called safe zone, where the amplitudes are above this limit and therefore the vehicle is more robust against perturbations, is shaded gray in Fig. 6q–t.

When using the linear controller in Eq. (25) (first column in Fig. 6), a large part of the linearly stable domain of control gains is enclosed by a low-amplitude unstable limit cycle, and the safety condition is only met for smaller control gains. Based on the linearized system, a pair of optimal control parameters can be identified, which results in the fastest decay of the solution near the equilibrium. This optimal gain combination is denoted by a red plus sign in panel (q). Even though the best performance of the linearized system can be achieved in this point, the nonlinear analysis indicates that the vehicle will be susceptible to perturbations if the controller is tuned this way. This shows that relying only on the results of linear analysis can be misleading and it can result in serious safety issues in practice.

The nonlinear control law in Eq. (26) was already shown (in Sect. 4.2) to be able to remove a number of unwanted equilibrium points, but based on the bifurcation diagrams (in the second column in Fig. 6), it has practically no effect on the nonlinear dynamics near the equilibrium of straight-line motion. Namely, the branches of unstable limit cycles in the bifurcation diagrams (a), (e), (i) and (m) are very similar to the branches of panels (b), (f), (j) and (n), respectively. Accordingly, the coloring of the unsafe zones in panels (q) and (r) concur.

The saturation of the input signal, however, can significantly increase the size of the safe zone. If the basic threshold function in Eq. (28) is used (third column in Fig. 6), where the input signal is cut off above a predetermined threshold, the branches of the limit cycles sharply change direction once the saturation level is reached, see panels (g) and (k). This leads to a significant increase in the size of the safe zone, while the rest of the limit cycles, where the saturation is not active, remain unchanged.

Although the local bifurcations of the system are not influenced by the saturation, fold bifurcations of periodic orbits occur and stable periodic orbits with amplitudes below 3.5 m appear for control gains inside the stable domain (see panel c). This means that the vehicle will start oscillating around the lane centerline when sufficiently perturbed. It is also possible that multiple fold points occur along the same branch, leading to two different unstable periodic orbits (with different amplitudes) for the same control gains (see panel g). The coloring of the stable domain, however, always corresponds to the lowest amplitude unstable limit cycle, indicating the basin of attraction of the equilibrium. We note that in order to avoid numerical problems during the continuation process, the saturation function sat$(\delta _{\textrm{s}}^\textrm{des})$ was smoothed according to Appendix A.3.

The continuous saturation function $g(\delta _{\textrm{s}}^\textrm{des})$ modifies the input signal even for small steering angles, therefore it affects the limit cycles at lower amplitudes, leading to a further increase in the safe zone of control parameters (see the panels in the fourth column of Fig. 6). Although locally, the Hopf-bifurcations still remain subcritical, the emerging unstable limit cycles surround only a small part of the stable domain and nearly all stabilizing control gains become sufficiently robust against perturbations.

Fig. 7

Bifurcation diagrams of the four controller variations for ${P_\psi =0.6}$. The vertical axes show the amplitude of the lateral position $y_\textrm{R}$ (a), the desired steering angle (b), and the actual steering angle (c) along the periodic orbits

Figure 7 shows the bifurcation diagrams at ${P_\psi =0.6}$ not only in terms of $y_\textrm{R}$ (as in panels (e)-(h) in Fig. 6), but also in terms of the desired steering angle $\delta _{\textrm{s}}^\textrm{des}$ and the realized steering angle $\delta _{\textrm{s}}$. It can be seen that even if there is no saturation function wrapped around the control law, the actual steering angle remains smaller than $\delta _{\textrm{s}}^\textrm{des}$ due to the steering system dynamics. When the simpler saturation function sat$(\delta _{\textrm{s}}^\textrm{des})$ is applied, the fold of periodic orbits occurs when the desired steering angle reaches the saturation level. Until that point, the saturation function has no effect, and the limit cycle branch follows exactly the non-saturated cases. On the other hand, since the continuous saturation function $g(\delta _{\textrm{s}}^\textrm{des})$ becomes active for small steering angles too, the corresponding branches do not follow the others. It can also be seen in panel (b) that while the sat$(\delta _{\textrm{s}}^\textrm{des})$ function sharply cuts off the desired steering angle once the saturation threshold is reached, in case of the $g(\delta _{\textrm{s}}^\textrm{des})$ function, the desired steering angle smoothly converges toward the limit value $\delta _\textrm{sat}$.

As previously, the limit cycles in panel (a) are considered up to a maximum oscillation amplitude of $y_\textrm{R}=3.5$ m. In panels (b) and (c), the branches are plotted in color until this limit is reached, while the rest of the branches are colored in gray. Since the corresponding limit cycles are rapidly increasing in amplitude beyond this point, numerical issues start to occur and the results become less reliable.

Fig. 8

Simulation results using the control gains of points A, B and C in Fig. 6 with two different initial conditions. Vehicle parameters are listed in Table 1

7 Numerical simulations

In order to illustrate the effect of the above nonlinear phenomena, a series of numerical simulations were performed. Three pairs of control gains were selected (see points A to C in Fig. 6) to demonstrate the sensitivity of the system to initial conditions in different parts of the stable domain. Point A (${P_y = 0.005 \, \textrm{m}^{-1}}$, ${P_\psi =0.2}$) is inside the safe zone using all four controller variations, i.e., there is no unstable limit cycle with amplitude lower than 3.5 m around the stable equilibrium if these control gains are used. In point B (${P_y =0.015 \, \textrm{m}^{-1}}$, ${P_\psi =0.6}$), the limit cycle amplitudes are lower when no saturation function is used, while point C (${P_y = 0.025 \, \textrm{m}^{-1}}$, ${P_\psi =0.8}$) is only part of the safe zone when using the continuous saturation function $g(\delta _{\textrm{s}}^\textrm{des})$. In addition, the red plus signs in the stability charts in Fig. 6 indicate the optimal control gains in terms of the fastest decay of the linearized system (${P_y =0.0093 \, \textrm{m}^{-1}}$, ${P_\psi =0.548}$).

The simulations were performed using two different initial conditions in terms of $y_\textrm{R}$ (the rest of the state variables were set to zero): On the one hand, $y_\textrm{R}(t\le 0) = 3.5$ m was used to represent a regular lane-change maneuver, while a larger initial condition was considered as $y_\textrm{R}(t\le 0) = 7$ m, as if the automated vehicle wants to change two lanes at once.

The simulation results in Fig. 8 show that when the control gains are selected from the safe zone (panels a and d), the vehicle can safely perform both maneuvers regardless of which controller is used. However, since the control gains used in point A are relatively small, the evolution of the lateral position is not ideal: some unwanted oscillations can be observed, with large settling time and significant overshoot.

The performance of the controller can be improved by selecting larger control gains (see panels b and e using the control gains in point B). Since point B is the closest to the optimal control gains of the linearized system, a smoother, more dynamic lane change can be observed in panel (b). However, because of the unstable limit cycle, the larger initial condition leads to instability in panel (e) if no controller saturation is used. This shows that relying only on the linear analysis of the system can lead to safety issues in practice.

Finally, the control gains in point C are selected from the part of the stable domain where the limit cycle amplitude is dangerously low in all controller variations, except when the saturation function $g(\delta _{\textrm{s}}^\textrm{des})$ is used. Therefore, only this controller variation results in a stable lane-change maneuver (regardless of initial conditions). When the simpler saturation function is used, the system leaves the basin of attraction of the stable equilibrium and converges to a stable periodic solution instead (this stable limit cycle can be observed in Fig. 6c). If no saturation function is used, the vehicle loses its stability in both simulation scenarios, even though the control gains are selected from the linearly stable domain.

Fig. 9

Numerical simulations in the unstable domain

Two additional simulation setups can be seen in Fig. 9, where the control gains are selected from the linearly unstable domain. In panel (a), the stable domain is left by selecting a too large value for $P_\psi$. In this case, the saturation functions in the controller mitigate the negative effects of stability loss, as the vehicle will move according to a small amplitude stable limit cycle instead of swerving off the road. Stable limit cycle solutions can be similarly observed in panel (b), where the stable domain is left in the direction of $P_y$. However, the amplitude of the oscillations is significantly larger in this case, therefore the saturation functions provide no additional safety benefit here.

8 Conclusion

A comprehensive dynamical analysis of the path-following control of automated vehicles was presented in this paper. By comparing three variations of the single-track vehicle model, we showed the importance of including the tire-ground interaction and the often neglected steering system dynamics in the vehicle model. The consideration of these modeling aspects can largely influence the domain of stabilizing control gains of the path-following controller. As an additional modeling step, the kinematic trail of the suspension system could potentially also affect the dynamics of the steered wheel.

The possible steady states and singularities of the controlled vehicle have also been explored. We showed that there exist steady state motions parallel to the reference path for all vehicle models. However, by limiting the applicable steering angles using some simple nonlinearities in the control law, these undesirable equilibrium points can be removed from the state space.

A comprehensive bifurcation analysis of the entire stable domain of control gains has also been performed. The amplitudes of the uncovered unstable limit cycles around the stable equilibrium are good indicators of the robustness of the system against perturbations. Based on the limit cycle amplitudes, a safe zone could be identified inside the stable domain, where no unstable limit cycle exists with oscillation amplitude below a certain limit. This safe zone of control parameters can be extended using the nonlinearities in the control law. This allows the use of larger control gains, which leads to faster control action without compromising the safety of the controller. This is especially important in case of emergency obstacle avoidance, where the controller must be able to handle larger perturbations in a fast and accurate way, without significant overshoot.

We showed that the nonlinear behavior of the vehicle can further be improved by using a continuous wrapper function to limit the control action. In addition, a series of numerical simulations have been performed to illustrate the sensitivity of the system to perturbations depending on the controller selection. Although the calculations have been performed based on an oversteering vehicle configuration, the main results apply to understeering vehicles too. Such a scenario is analyzed in detail in [50]. It is also worth noting that smaller delay values do not affect the main results, either: Although the linearly stable domain of control gains increases for smaller values of $\tau$, the nonlinear behavior of the system qualitatively remains the same.

Table 2 List of tire parameters

Overall, the results presented in this paper provide a detailed overview of what kinds of local and global dynamics can be expected from the controlled vehicle, and how these dynamics can be improved by some modifications of the control law. Additionally, the stability charts with the results of the bifurcation analysis provide further insight for the designer compared to the toolset of traditional linear analysis, which can be used as guidelines for tuning the controller in order to achieve reliable and robust lateral control of the vehicle. In future research, the analysis could be extended for the case of non-zero path curvature, and investigating the use of a preview or lookahead control law to compensate the effects of feedback delay.

Appendix

1.1 A.1 Brush tire model

The tire side force and self-aligning moment characteristics in this paper are modeled using the nonlinear brush tire model. This model assumes a parabolic pressure distribution along the tire-ground contact patch due to the vertical wheel load, leading to the lateral force characteristics

$$\begin{aligned} F(\alpha ) = {\left\{ \begin{array}{ll} \phi _1 \tan \alpha + \phi _2 \textrm{sgn}\, \alpha \tan ^2 \alpha +\\ + \phi _3 \tan ^3 \alpha , &{} 0 \le |\alpha |< \alpha _\textrm{crit} , \\ \mu F_z \textrm{sgn}\, \alpha , &{} \alpha _\textrm{crit} < |\alpha | , \end{array}\right. } \end{aligned}$$

(47)

where the coefficients are

$$\begin{aligned} \begin{aligned} \phi _1&= C , \\ \phi _2&= -\frac{C^2}{3 \mu _0 F_z}\left( 2 - \frac{\mu }{\mu _0} \right) , \\ \phi _3&= \frac{C^3}{9 \mu _0^2 F_z^2}\left( 1 - \frac{2\mu }{3\mu _0} \right) . \end{aligned} \end{aligned}$$

(48)

The parameters of the brush model include the vertical wheel load $F_z$, the sliding and rolling coefficients of friction $\mu$ and $\mu _0$ between the tire and the ground, as well as the so-called cornering stiffness ${C=2a^2k}$, where a is the half-length of the contact patch and k is the distributed lateral stiffness of the tire. The critical side slip angle $\alpha _\textrm{crit}$ denotes the state where the entire contact patch begins sliding. This is calculated as $\alpha _\textrm{crit}= \frac{3 \mu _0 F_z}{2 a^2 k}$.

The self-aligning moment characteristic of the brush tire model is

$$\begin{aligned} M(\alpha ) = {\left\{ \begin{array}{ll} \mu _1 \tan \alpha + \mu _2 \textrm{sgn}\, \alpha \tan ^2 \alpha +\\ + \mu _3 \tan ^3 \alpha + \mu _4 \textrm{sgn}\, \alpha \tan ^4 \alpha , &{}0 \le |\alpha |< \alpha _\textrm{crit} , \\ 0 , &{}\alpha _\textrm{crit} < |\alpha | , \end{array}\right. } \end{aligned}$$

(49)

where

$$\begin{aligned} \begin{aligned} \mu _1&= -\frac{a}{3} \phi _1 , \\ \mu _2&= -a \phi _2, \\ \mu _3&= -3 a \phi _3, \\ \mu _4&= \frac{a C^4}{27 \mu _0^3 F_z^3}\left( \frac{4}{3} - \frac{\mu }{\mu _0} \right) . \end{aligned} \end{aligned}$$

(50)

When linearized around zero side slip angle, the tire model simplifies to ${F=C \alpha }$ and ${M=-{\tilde{C}} \alpha }$, where ${{\tilde{C}}=-\frac{a}{3}C}$.

The tire parameter values used in the paper are listed in Table 2.

1.2 A.2 Coefficient matrices of the linearized vehicle models

The linearized version of the kinematic vehicle model introduced in Sect. 2.1 includes the system and input matrix

$$\begin{aligned} {\textbf{A}}_\textrm{kin}=\begin{bmatrix} 0 &{} V \\ 0 &{} 0 \\ \end{bmatrix}, \quad {\textbf{B}}_\textrm{kin}=\begin{bmatrix} 0 \\ V/f \\ \end{bmatrix}. \end{aligned}$$

(51)

The dynamic vehicle model with assigned steering angle from Sect. 2.2 leads to the coefficient matrices

$$\begin{aligned} {\textbf{A}}_\textrm{dyn}=\begin{bmatrix} 0 &{} V &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} A_{33} &{} A_{34} \\ 0 &{} 0 &{} A_{43} &{} A_{44} \\ \end{bmatrix}, \quad {\textbf{B}}_\textrm{dyn}=\begin{bmatrix} 0 \\ 0 \\ B_{3} \\ B_{4} \\ \end{bmatrix}, \end{aligned}$$

(52)

with elements

$$\begin{aligned} \begin{aligned}&A_{33} = \frac{ (C_\textrm{F} (f-d) - C_\textrm{R} d - {\tilde{C}}_\textrm{F} - {\tilde{C}}_\textrm{R} ) d m - (C_\textrm{F} + C_\textrm{R}) J_\textrm{C} }{ m V J_\textrm{C} }, \\&A_{34} = \frac{ C_\textrm{F} f ( m d (f-d) - J_\textrm{C}) -{\tilde{C}}_\textrm{F} m d f }{m V J_\textrm{C}} -V, \\&A_{43} = \frac{ d C_\textrm{R} - (f-d) C_\textrm{F} + {\tilde{C}}_\textrm{F} + {\tilde{C}}_\textrm{R} }{ V J_\textrm{C} }, \\&A_{44} = \frac{{\tilde{C}}_\textrm{F} - C_\textrm{F} (f-d) f}{ V J_\textrm{C} }, \end{aligned} \end{aligned}$$

(53)

and

$$\begin{aligned} \begin{aligned}&B_{3} = \frac{C_{\textrm{F}} (J_\textrm{C} - m d (f-d) ) + md {\tilde{C}}_\textrm{F}}{m J_\textrm{C} }, \\&B_{4} = \frac{C_{\textrm{F}} (f-d) - {\tilde{C}}_\textrm{F} }{J_\textrm{C} }. \end{aligned} \end{aligned}$$

(54)

Finally, the linearization of the dynamic vehicle model with torque steering (Sect. 2.3) results in

$$\begin{aligned}{} & {} {\textbf{A}}_\textrm{servo}= \begin{bmatrix} 0 &{} V &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} {\tilde{A}}_{43} &{} {\tilde{A}}_{44} &{} {\tilde{A}}_{45} &{} {\tilde{A}}_{46} \\ 0 &{} 0 &{} {\tilde{A}}_{53} &{} {\tilde{A}}_{54} &{} {\tilde{A}}_{55} &{} {\tilde{A}}_{56} \\ 0 &{} 0 &{} {\tilde{A}}_{63} &{} {\tilde{A}}_{64} &{} {\tilde{A}}_{65} &{} {\tilde{A}}_{66} \end{bmatrix} , \end{aligned}$$

(55)

$$\begin{aligned}{} & {} \quad {\textbf{B}}_\textrm{servo}= \begin{bmatrix} 0&0&0&{\tilde{B}}_{4}&{\tilde{B}}_{5}&{\tilde{B}}_{6} \end{bmatrix}^{\textrm{T}}, \end{aligned}$$

(56)

where the elements of the system matrix ${\textbf{A}}_\textrm{servo}$ are

$$\begin{aligned}&{\tilde{A}}_{43} = \frac{C_\textrm{F} (m d (d-f) +J_\textrm{C}) -m d k_\textrm{p}}{m J_\textrm{C}}, \nonumber \\&{\tilde{A}}_{44} = \frac{(-{\tilde{C}}_\textrm{R}-(C_\textrm{F}+C_\textrm{R}) d + C_\textrm{F} f) d m - (C_\textrm{F}+C_\textrm{R}) J_\textrm{C}}{m V J_\textrm{C}} ,\nonumber \\&{\tilde{A}}_{45} = \frac{C_\textrm{F} f (m d (f-d)-J_\textrm{C})}{m V J_\textrm{C}} - V, \nonumber \\&{\tilde{A}}_{46} = - \frac{d k_\textrm{d}}{J_\textrm{C}}, \nonumber \\&{\tilde{A}}_{53} = \frac{C_\textrm{F} (f-d)+k_\textrm{p}}{J_\textrm{C}}, \nonumber \\&{\tilde{A}}_{54} = \frac{(C_\textrm{F}+C_\textrm{R}) d-C_\textrm{F} f +{\tilde{C}}_\textrm{R} }{V J_\textrm{C}}, \nonumber \\&{\tilde{A}}_{55} = -\frac{C_\textrm{F} f (f-d) }{V J_\textrm{C}} , \nonumber \\&{\tilde{A}}_{56} = \frac{k_\textrm{d}}{J_\textrm{C}}, \nonumber \\&{\tilde{A}}_{63} = \frac{-{\tilde{C}}_\textrm{F} J_\textrm{C} - C_\textrm{F} (f-d) J_\textrm{F} - k_\textrm{p} (J_\textrm{F}+J_\textrm{C})}{J_\textrm{F} J_\textrm{C}}, \nonumber \\&{\tilde{A}}_{64} = \frac{ \left( -{\tilde{C}}_\textrm{R}-(C_\textrm{F}+C_\textrm{R}) d + C_\textrm{F} f \right) J_\textrm{F} + {\tilde{C}}_\textrm{F} J_\textrm{C}}{J_\textrm{F} J_\textrm{C} V}, \nonumber \\&{\tilde{A}}_{65} = \frac{f \left( C_\textrm{F} J_\textrm{F} (f-d) + {\tilde{C}}_\textrm{F} J_\textrm{C} \right) }{J_\textrm{F} J_\textrm{C} V}, \nonumber \\&{\tilde{A}}_{66} = -k_\textrm{d} \frac{J_\textrm{F}+J_\textrm{C}}{J_\textrm{F} J_\textrm{C}}, \end{aligned}$$

(57)

and the input matrix ${\textbf{B}}_\textrm{servo}$ consists of

$$\begin{aligned} {\tilde{B}}_4 = \frac{d k_\textrm{p}}{J_\textrm{C}}, \quad {\tilde{B}}_5 = -\frac{k_\textrm{p}}{J_\textrm{C}}, \quad {\tilde{B}}_6 = k_\textrm{p} \frac{J_\textrm{F} + J_\textrm{C}}{J_\textrm{F} J_\textrm{C}}. \end{aligned}$$

(58)

1.3 A.3 Controller saturation

In order to avoid numerical issues during the continuation process, the saturation function in Eq. (28) was smoothed out using second-order polynomials as follows:

$$\begin{aligned} \textrm{sat} (\delta _{\textrm{s}}^\textrm{des}) = {\left\{ \begin{array}{ll} -\delta _\textrm{sat}, \quad \quad \quad \quad \quad \textrm{if} \quad \delta _{\textrm{s}}^\textrm{des} \le -\delta _\textrm{sat} - c , \\ \delta _{\textrm{s}}^\textrm{des} + \frac{(-\delta _\textrm{sat} - \delta _{\textrm{s}}^\textrm{des} + c)^2}{4c}, \\ \quad \quad \quad \textrm{if} \quad -\delta _\textrm{sat}-c< \delta _{\textrm{s}}^\textrm{des}< -\delta _\textrm{sat}+c , \\ \delta _{\textrm{s}}^\textrm{des}, \quad \quad \textrm{if} \quad -\delta _\textrm{sat}+c \le \delta _{\textrm{s}}^\textrm{des} \le \delta _\textrm{sat}-c , \\ \delta _{\textrm{s}}^\textrm{des} - \frac{(\delta _\textrm{sat} - \delta _{\textrm{s}}^\textrm{des} - c)^2}{4c}, \\ \quad \quad \quad \textrm{if} \quad \delta _\textrm{sat}-c< \delta _{\textrm{s}}^\textrm{des} < \delta _\textrm{sat}+c , \\ \delta _\textrm{sat}, \quad \quad \quad \quad \quad \textrm{if} \quad \delta _{\textrm{s}}^\textrm{des} \ge \delta _\textrm{sat} + c , \\ \end{array}\right. } \end{aligned}$$

(59)

The value of parameter c was set to $5 \cdot 10^{-5}$.