1 Introduction

The presented work is a continuation of previous works by authors dealing with the system of three degrees of freedom with a spherical pendulum [1,2,3]. In this work, a system consisting of a mass element and a spherical pendulum swung from the mass element is examined. The mass element is suspended from a linear spring and a damper. It is assumed that the damping in the system studied is described by the fractional Riemann–Liouville derivative [4] and this damping occurs in the damper and at the pivot point of the spherical pendulum. The considered system with a spherical pendulum can be used as a model of a real machine or its components, which operates in an energy-dissipating environment. In many scientific works, the systems containing a spherical pendulum are used to model the dynamics of certain types of structures, such as cranes [5,6,7,8,9,10], vibration absorbers [11,12,13], energy harvesters [14]. Thus, the dynamics of systems with a spherical pendulum is an absorbing issue of scientific research and has been studied in a number of researches [15]. A brief review of publications dealing with this issue is presented in the paper by Han et al. [16].

In previous works, the authors studied autoparametric systems containing a spherical pendulum with a viscous and magnetorheological energy dissipation system. Sado et al. [1] analyzed the influence of initial conditions on energy transfer between vibrating elements and the existence of chaotic motion in a system with a spherical pendulum. Sado and Freundlich [2] studied a dynamical behavior of a three-degree-of-freedom system having a spherical pendulum. This system was controlled by a magnetorheological damper. The analyzed system consisted of a spherical pendulum suspended from a mass block which was suspended from a vertical linear spring and a magnetorheological damper. They investigated the influence of magnetorheological damper parameters on the system vibration close to internal and external resonances. These studies revealed that in addition to the regular behavior of the spherical pendulum, chaotic oscillations for all coordinates can arise near internal and external resonant regions. In all above-mentioned authors’ works, the obtained equations of motion were solved using numerical methods.

It is well known that energy dissipation can have a significant impact on the dynamic behavior of a structure or its components. For this reason, various advanced methods for modeling damping in mechanical systems are being developed. One of these methods is the use of fractional derivatives to model energy dissipation. The use of fractional derivatives to model energy dissipation has increased very significantly over the past few decades [17,18,19]. Fractional derivatives are used to describe viscous damping because these derivatives allow a more accurate description of the damping phenomenon over a wider frequency range [20, 21]. These derivatives have also been employed in modeling processes of energy dissipation in systems having pendulums [22,23,24,25]. Thus far, however, there has been small number of publications investigating dynamical systems with pendulum and fractional damping, especially with a spherical pendulum.

Rossikhin and Shitikova [22] investigated damped oscillations of two-degree-of-freedom system with a plane pendulum suspended from a mass element which was attached to a spring. They assumed that the system oscillates in a viscous medium whose damping properties are described by fractional derivatives. Additionally, the authors assumed small finite amplitudes of vibrations which allowed the use of multiple-scale method to solve the problem. They studied the impact of the damping described by the fractional derivative on damped free vibrations and the energy transfer in the system.

Seredyńska and Hanyga [23] studied damped vibrations of a planar, inextensible and extensible pendulums in which the damping was described by a fractional derivative. This analysis was an example of the presented method for solving nonlinear differential equations with fractional damping. They determined the conditions of existence, uniqueness and dissipativity for a certain class of nonlinear dynamical systems including systems with fractional damping.

Hedrih [24] analyzed multi-pendulum systems with fractional-order creep elements. In this study, parallel pendulums were joined with creep elements, which were modeled using fractional-order derivatives. The governing equations of the system and its analytical solution for selected cases of the pendulum system were presented. The vibration modes of the systems with one and two pendulums having creep fractional elements were analyzed. The authors concluded that there is a mathematical analogy in descriptions between multi-pendulum systems and chain dynamical systems.

To the our knowledge, thus far only by the authors have performed the study of vibrations of a spherical pendulum with fractional damping [3]. In the aforementioned work, the authors assumed fractional damping only in the damper attached to the mass element [3]. The effect of a fractional-order derivative on the system vibrations was analyzed using numerical calculations. The impact of the fractional damping on the system vibrations waveforms and on the energy transfer in the system was shown. Thus, this study is a continuation of the authors’ earlier work.

2 Description of the analyzed system

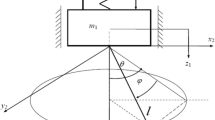
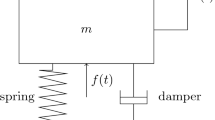
In this study, we consider a system with a spherical pendulum suspended from an oscillator excited harmonically by a force \(F_z(t)=P_1 \cos (\nu _1 t)\) acting in the vertical direction (Fig. 1). Additionally, the pendulum is excited harmonically in horizontal direction by forces \(F_x(t)=P_2 \cos (\nu _2 t)\), \(F_y(t)=P_3 \cos (\nu _2 t)\). The oscillator consists a linear spring and a fractional damper. Furthermore, it is assumed that there is also fractional damping in the pendulum pivot point. This damping is expressed by moments proportional to fractional derivative of order \(\alpha \). Thus, the analyzed system has three degrees of freedom. The motion of the spherical pendulum can be analyzed using various coordinate systems [9, 26,27,28,29]. In this study, the spherical coordinates presented by Leung and Kuang [9], and Aston [28] are employed to describe the motion of the pendulum. The following generalized coordinates z, \(\theta \), \(\phi \) are assumed (Fig. 1). The position of the mass element \(m_1\) is defined by coordinate z, whereas the position of the pendulum of mass \(m_2\) and length l is defined by the coordinates: z, \(\theta \), \(\phi \). The coordinate z is the vertical displacement of the body of mass \(m_1\) measured from the static position of equilibrium. The angle \(\theta \) is the angle between the vertical axis and the deflection of the pendulum in the plane xz. The angle \(\phi \) is the angle between the deflections of the pendulum in the plane xz and pendulum. The selected coordinates are useful in the dynamic analysis of the spherical pendulum [28, 29] and enable more interesting results to be obtained than using the classical spherical coordinates [1,2,3].

Fig. 1
figure 1

Schematic diagram of the system analyzed

Full size image

The position of a pendulum bob of mass \(m_2\) in Cartesian coordinates is determined as follows (see Appendix A)

$$\begin{aligned} \begin{aligned}&x_2=l\cos \phi \sin \theta \\&y_2=l\sin \phi \\&z_2=l\cos \phi \cos \theta +z_1 \\&z_1=z+z_{st} \end{aligned} \end{aligned}$$
(1)

where \(z_{st}\) is the static deflection determined as follows

$$\begin{aligned} z_{st}=\frac{(m_1+m_2)g}{k} \end{aligned}$$
(2)

where g is gravitational acceleration

The kinetic energy T of the system can be expressed as

$$\begin{aligned} \begin{aligned} T&= \frac{1}{2}{\dot{z}}_1^2(m_1+m_2 )+\frac{1}{2}m_2 l^2{\dot{\phi }}^2+\frac{1}{2}m_2 l^2{\dot{\theta }}^2\cos ^2\phi \\&\quad -m_2 l{\dot{z}}_1 {\dot{\phi }} \sin \phi \cos \theta -m_2 l{\dot{z}}_1 {\dot{\theta }} \cos \phi \cos \theta \end{aligned} \end{aligned}$$
(3)

The potential energy V of the system is expressed as

$$\begin{aligned} V\!=-(m_1+m_2 )z_{1}g-m_2 gl\cos \phi \cos \theta +\frac{1}{2} k(z_{1})^2 \end{aligned}$$
(4)

In this study, a fractional damping characterized by the damping coefficient \(c_{\alpha _1}\) and the order of the fractional derivative \(\alpha _1\) is assumed in the damper, while for the coordinates \(\theta \) and \(\phi \) the damping at the pendulum pivot point is described by the damping coefficient \(c_{\alpha _2}\) and the order of the fractional derivative \(\alpha _2\). Thus, the dissipation force \(R({\dot{z}}^{(\alpha )})\), moments \(M({\dot{\theta }}^{(\alpha )})\) and \(M({\dot{\phi }}^{(\alpha )})\) (Fig. 1) are determined by following expressions

$$\begin{aligned} \begin{aligned}&R({\dot{z}}^{(\alpha )})=c_{\alpha _1} \frac{d^{\alpha _1}}{dt^{\alpha _1}}\left( z(t)\right) ,\; M({\dot{\theta }}^{(\alpha )})=c_{\alpha _2} \frac{d^{\alpha _2}}{dt^{\alpha _2}}\left( \theta (t)\right) , \\&M({\dot{\phi }}^{(\alpha )})=c_{\alpha _2} \frac{d^{\alpha _2}}{dt^{\alpha _2}}\left( \phi (t)\right) \end{aligned} \end{aligned}$$
(5)

where z(t), \(\theta (t)\) and \(\phi (t)\) are the generalized coordinates, \( c_{\alpha _{1,2}} \) are damping coefficients and \( \frac{d^\alpha }{dt^\alpha } \) is a fractional derivative of the order \( \alpha _{1,2}\).

In this analysis, the fractional Riemann–Liouville derivative [4] is used, which it is defined as

$$\begin{aligned} \begin{aligned}&\frac{d^\alpha }{dt^\alpha }f(t)\equiv D_0^\alpha (f(t))\equiv {\dot{f}}^{(\alpha )}(t) \\&\quad \quad \equiv \frac{1}{\varGamma (m-\alpha )}\frac{d^m}{dt^m }\int \limits _0^t\frac{f(\tau )}{(t-\tau )^{\alpha +1-m}}d\tau \end{aligned} \end{aligned}$$
(6)

where \({\varGamma (m-\alpha )}\) is the Euler gamma function [4], m is a positive integer number satisfying inequality \({m-1< \alpha < m}\) and \(t > 0\). The fractional derivative order is assumed to be in a range of \(0 < \alpha \le 1\).

Using the fractional dissipation function \( D = \frac{1}{2}c_\alpha (D_t^\alpha (z))^2\) [30], the equations of motion of the system can be written as

$$\begin{aligned} \begin{aligned}&\ddot{z}(m_1+m_2)-m_2l\ddot{\theta }\cos \phi \sin \theta -m_2l\ddot{\phi }\sin \phi \cos \theta \\&\qquad \quad + 2m_2 l {\dot{\phi }} {\dot{\theta }}\sin \phi \sin \theta -m_2 l{\dot{\theta }}^2\cos \phi \cos \theta \\&\qquad \quad -m_2 l{\dot{\phi }}^2\cos \phi \cos \theta +c_{\alpha _1} {\dot{z}}^{(\alpha _1)}\\&\qquad \quad +k z = P_1 \cos \nu _1 t ,\\&\qquad \quad -m_2 l\ddot{z} \cos \phi \sin \theta \\&\qquad \quad +m_2l^2\ddot{\theta }\cos ^2 \phi - 2m_2 l {\dot{\phi }} {\dot{\theta }}\cos \phi \sin \phi \\&\qquad \quad + m_2 gl\cos \phi \sin \theta +c_{\alpha _2}{\dot{\theta }}^{(\alpha _2)}\\&\quad \quad =P_2 l \cos \phi \cos \theta \cos \nu _2 t , \\&\qquad \quad -m_2 l\ddot{z} \sin \phi cos\theta +m_2l^2\ddot{\phi }\\&\qquad \quad +m_2 l^2 {\dot{\theta }}^2 \cos \phi \sin \phi \\&\qquad \quad +m_2 g l \sin \phi \cos \phi +c_{\alpha _2} {\dot{\phi }}^{(\alpha _2)}\\&\quad \quad =-P_2 l \sin \phi \sin \theta \cos \nu _2 t +P_3 l \cos \phi \cos \nu _2 t \end{aligned} \end{aligned}$$
(7)

The dimensionless equations can be obtained by introducing the dimensionless time \(\tau = \omega _1 t \) and defining the following parameters

$$\begin{aligned} \begin{aligned}&\omega _1^2=\frac{k}{m_1+m_2}, \quad \omega _2^2=\frac{g}{l},\quad \beta =\frac{\omega _2}{\omega _1},\quad {\bar{z}}=\frac{z}{l}, \\&\mu _1=\frac{\nu _1}{\omega _1}, \quad \mu _2=\frac{\nu _2}{\omega _1} \\&\gamma _1=\frac{c_{\alpha _1} \omega _1^{\alpha _1}}{(m_1+m_2 ) \omega ^2_1}, \quad \gamma _2=\frac{c_{\alpha _2} \omega _1^{\alpha _2}}{m_2 \omega ^2_1 l^2}, \quad a=\frac{m_2}{m_1+m_2 } \\&p_1=\frac{P_1}{(m_1+m_2 ) \omega _1^2 l}, \quad p_2=\frac{P_2}{m_2 l \omega _1^2 l}, \quad p_3=\frac{P_3}{m_2 l \omega _1^2 l} \end{aligned} \end{aligned}$$
(8)

Using parameters defined in Eq. (8), the equations of motion (7) can be transformed into a dimensionless form (where the overbars are omitted for convenience)

$$\begin{aligned} \begin{aligned}&\ddot{z}-a\ddot{\phi }\sin \phi \cos \theta +2a{\dot{\phi }}{\dot{\theta }}\sin \phi sin\theta -a\ddot{\theta }\cos \phi \sin \theta \\&\quad -a{\dot{\theta }}^2 \cos \phi \cos \theta -a{\dot{\phi }}^2 \cos \phi \cos \theta +\gamma _1 {\dot{z}}^{(\alpha _1)}+z \\&\quad = p_1 \cos (\mu _1 \tau ) ,\\&\ddot{\theta } \cos ^2\phi -\ddot{z}\cos \phi \sin \theta - 2{\dot{\theta }} {\dot{\phi }}\cos \phi \sin \phi \\&\quad +\beta ^2 \cos \phi \sin \theta +\gamma _2 {\dot{\theta }}^{(\alpha _2)}\\&\quad = p_2 \cos \phi \cos \theta \cos (\mu _2 \tau ), \\&\ddot{\phi }-\ddot{z}\sin \phi \cos \theta +{\dot{\theta }}^2 \cos \phi \sin \phi +\beta ^2 \sin \phi \cos \theta \\&\quad +\gamma _2 {\dot{\phi }}^{(\alpha _2)}=-p_2 \sin \phi \sin \theta \cos (\mu _2 \tau ) \\&\quad \quad + p_3 \cos \phi \cos (\mu _2 \tau ) \end{aligned} \end{aligned}$$
(9)

3 Method of solution

An approximate solution to Eq. (9) can be obtained using the multiple-scale method [31]. For small osculations in the vicinity of equilibrium position, trigonometrical functions can be expanded into Maclaurin series; thus,

$$\begin{aligned} \begin{aligned}&\sin \phi =\phi -\frac{\phi ^3}{6},\ \cos \phi =1-\frac{\phi ^2}{2}, \\&\sin \theta =\theta -\frac{\theta ^3}{6}, \ \cos \theta =1-\frac{\theta ^2}{2} \end{aligned} \end{aligned}$$
(10)

Substituting the approximated trigonometrical functions Eq. (10) into Eq. (9), the following system of equations is obtained

$$\begin{aligned} \begin{aligned}&\ddot{z}-a\ddot{\theta }\theta -a\ddot{\phi }\phi =p_1\cos \left( \mu _1\tau \right) +a\left( {{\dot{\phi }}}^2+{{\dot{\theta }}}^2\right) \\&\ -\gamma _1{{\dot{z}}}^{(\alpha _1)}-z \\&\ -\ddot{z}\theta +\ddot{\theta }\left( 1-\phi ^2\right) =p_2\cos \left( \mu _2\tau \right) -\beta ^2\theta -\gamma _2{{\dot{\theta }}}^{(\alpha _2)} \\&\ -\ddot{z}\phi +\ddot{\phi }=p_3\cos {\left( \mu _2\tau \right) }-{{\dot{\theta }}}^2\phi -\beta ^2\phi - \gamma _2{{\dot{\phi }}}^{\left( \alpha _2\right) } \end{aligned} \end{aligned}$$
(11)

The approximate solution of Eq. (11) for small vibrations can be expressed by expansion with different timescales as shown below [31,32,33]

$$\begin{aligned} \begin{aligned} z\left( t\right)&=\varepsilon z_1\left( T_0,T_1,T_2, \ldots \right) +\varepsilon ^2z_2\left( T_0,T_1,T_2, \ldots \right) \\&\quad +\varepsilon ^3z_3\left( T_0,T_1,T_2, \ldots \right) +\ldots \\ \theta \left( t\right)&=\varepsilon \theta _1\left( T_0,T_1,T_2, \ldots \right) +\varepsilon ^2\theta _2\left( T_0,T_1,T_2, \ldots \right) \\&\quad +\varepsilon ^3\theta _3\left( T_0,T_1,T_2, \ldots \right) +\ldots \\ \phi \left( t\right)&=\varepsilon \phi _1\left( T_0,T_1,T_2, \ldots \right) +\varepsilon ^2\phi _2\left( T_0,T_1,T_2, \ldots \right) \\&\quad +\varepsilon ^3\phi _3\left( T_0,T_1,T_2, \ldots \right) +\ldots \end{aligned} \end{aligned}$$
(12)

where

$$\begin{aligned} T_n=\varepsilon ^n \tau \quad (n=0,1,2,3 \ldots ) \end{aligned}$$
(13)

are new independent variables, \(\varepsilon \) is a formal small parameter, \(T_0 = \tau \) is the fast timescale and \(T_1\), \(T_2\) are slow timescale [31, 32].

Using the chain rule, the integer-order derivatives can be expanded in series of a small parameter \(\varepsilon \)

$$\begin{aligned} \begin{aligned}&\frac{d}{d\tau }=D_0+\varepsilon D_1+\varepsilon ^2D_2+\ldots \\&\frac{d^2}{d\tau ^2}=D_0^2+2\varepsilon {D_0D}_1+\varepsilon ^2(D_1^2+2D_0D_2)+\ldots \end{aligned} \end{aligned}$$
(14)

where \(D_n = \frac{\partial }{\partial T_n}\)

A fractional-order derivative can be expanded in series of a small parameter as shown Rossikhin and Shitikova [18, 34]

$$\begin{aligned} \begin{aligned} D^\alpha&=\left( \frac{d}{dt}\right) ^\alpha =\left( D_0+\varepsilon D_1+\varepsilon ^2D_2+\ldots \right) ^\alpha =D_0^\alpha \\&\quad +\varepsilon \alpha D_0^{\alpha -1}D_1\\&\quad +{\frac{1}{2}\varepsilon }^2\alpha \left[ \left( \alpha -1\right) D_0^{\alpha -2}D_1^2+2D_0^{\alpha -1}D_2\right] \end{aligned} \end{aligned}$$
(15)

where \(D_0^{\alpha }\), \(D_0^{\alpha -1}\) and \(D_0^{\alpha -2}\) are the Riemann–Liouville fractional derivatives with respect time \(T_0\).

Introducing additional small parameters [33],

$$\begin{aligned} \begin{aligned}&\gamma _1=\varepsilon {\widetilde{\gamma }}_1,\; \gamma _2=\varepsilon {\widetilde{\gamma }}_2,\; \gamma _2=\varepsilon {\widetilde{\gamma }}_2, \\&p_1=\varepsilon ^2{\widetilde{p}}_1, \; p_2=\varepsilon ^2{\widetilde{p}}_2,\; p_3=\varepsilon ^2{\widetilde{p}}_3 \end{aligned} \end{aligned}$$
(16)

Substituting expression (12)-(16) into (11) and equating terms standing at the equal powers of a small parameter \(\varepsilon \) and limiting the approximate solution by terms of \(\varepsilon ^2\), a following system of recurrent equations can be obtained

for \(\varepsilon ^1\)

$$\begin{aligned} \begin{aligned}&D_0^2\left( z_1\right) +z_1=0 \\&D_0^2\left( \theta _1\right) +\beta ^2\theta _1=0 \\&D_0^2\left( \phi _1\right) +\beta ^2\phi _1=0 \end{aligned} \end{aligned}$$
(17)

for \(\varepsilon ^2\)

$$\begin{aligned} D_0^2{(z}_2)+z_2= & {} -2{D_0D}_1\left( z_1\right) +\ aD_0^2\left( \theta _1\right) \cdot \theta _1 \nonumber \\{} & {} +\ aD_0^2\left( \phi _1\right) \cdot \phi _1 +{\widetilde{p}}_1cos\left( \mu _1\tau \right) \nonumber \\{} & {} \quad -{\widetilde{\gamma }}_1D_0^{\alpha _1} \left( z_1\right) \nonumber \\{} & {} +a\left( \left( D_0^2\left( \phi _1\right) \right) ^2+\left( D_0^2\left( \theta _1\right) \right) ^2\right) \nonumber \\ D_0^2{(\theta }_2)+\beta ^2\theta _2= & {} {\widetilde{p}}_2\cos {\left( \mu _2\tau \right) }-2{D_0D}_1\left( \theta _1\right) \nonumber \\{} & {} -D_0^2\left( z_1\right) \theta _1-{\widetilde{\gamma }}_2D_0^{\alpha _2}\left( \theta _1\right) \nonumber \\ D_0^2{(\phi }_2)+\beta ^2\phi _2= & {} {\widetilde{p}}_3\cos {\left( \mu _2\tau \right) }-2{D_0D}_1\left( \phi _1\right) \nonumber \\{} & {} -D_0^2\left( z_1\right) \phi _1-{\widetilde{\gamma }}_2D_0^{\alpha _2}\left( \phi _1\right) \end{aligned}$$
(18)

Since further in the present analysis the expansions for displacements are limited by the expressions (18) of order \(\epsilon ^2\), we assume that the amplitudes \(A_{z1}\), \(A_{\theta 1}\) and \(A_{\phi 1}\) are functions of time \(T_1\) only. Therefore, the sought solutions to Eq. (17) are as below

$$\begin{aligned} \begin{aligned}&z_1=A_{z1}(T_1)e^{iT_0}+{{\bar{A}}}_{z1}(T_1)e^{-iT_0} \\&\theta _1=A_{\theta 1}(T_1)e^{i{\beta T}_0}+{{\bar{A}}}_{\theta 1}(T_1)e^{-i{\beta T}_0} \\&\phi _1=A_{\phi 1}(T_1)e^{i\beta T_0}+{{\bar{A}}}_{\phi 1}(T_1)e^{-i\beta T_0} \end{aligned} \end{aligned}$$
(19)

where \(A_{z1}\), \(A_{\theta 1}\) and \(A_{\phi 1}\) are arbitrary complex functions of the timescale \(T_1\), and overbars denote complex conjugate functions.

In general, the Riemann–Liouville fractional derivative of the exponential function may be calculated according with method presented by Rossikhin and Shitikova [34, 35], namely

$$\begin{aligned} D_0^\alpha \left( e^{i\omega t}\right) =\left( i\omega \right) ^\alpha e^{i\omega t}+\frac{sin\pi \alpha }{\pi }\int _{0}^{\infty }{\frac{u^\alpha }{u+i\omega }e^{-ut}du} \end{aligned}$$
(20)

It can be shown that if the lower limit of the integral in the definition Eq. (6) is \(-\infty \;\) then the Riemann–Liouville fractional derivative of the exponential function has a form [4, 35]

$$\begin{aligned} D_{\ +}^\alpha \left( e^{i\omega t}\right) =\left( i\omega \right) ^\alpha e^{i\omega t} \end{aligned}$$
(21)

where \(D_{\ +}^\alpha \) is defined as [4, 35]

$$\begin{aligned} D_+^\alpha \ f\left( t\right) \equiv \frac{1}{\varGamma \left( 1-\alpha \right) }\frac{d}{dt}\int _{-\infty }^{t} {\frac{f\left( \tau \right) d\tau }{\left( t-\alpha \right) ^\alpha },\quad 0<}\alpha <1\ \end{aligned}$$
(22)

The improper integral in Eq. (20) may be omitted under certain circumstances, which are justified in the papers by Roshikhin and Shitikova [18, 35]. Furthermore, Roshikhin and Shitikova [34] have shown that the improper integral in Eq. (20) does not affect the solution obtained by the method of multiple timescales when it is limited to the first- and second-order approximations. Thus, in further analysis the simplified derivative of the exponential function Eq. (21) is used.

Substituting solution to the fist approximation Eq. (19) into equations for the second approximation Eq. (18), the following system of equations is obtained

$$\begin{aligned} \begin{aligned}&D_0^2{(z}_2)+z_2={\widetilde{p}}_1\frac{1}{2}e^{i\mu _1T_0}-2{A^\prime }_{z1}\left( T_1\right) ie^{iT_0} \\&\quad -a\beta ^2\left( A_{\theta 1}^2{\left( T_1\right) e}^{i{2\beta T}_0}+A_{\theta 1}\left( T_1\right) {{\bar{A}}}_{\theta 1}\left( T_1\right) \right) \\&\quad -a\beta ^2\left( A_{\phi 1}^2{\left( T_1\right) e}^{i2\beta T_0}+A_{\phi 1}\left( T_1\right) {{\bar{A}}}_{\phi 1}\left( T_1\right) \right) \\&\quad +a\beta ^4\left( A_{\phi 1}^2\left( T_1\right) e^{i2\beta T_0}+A_{\phi 1}\left( T_1\right) {{\bar{A}}}_{\phi 1}\left( T_1\right) \right) \\&\quad +a\beta ^4\left( A_{\theta 1}^2{\left( T_1\right) e}^{i{2\beta T}_0}+A_{\theta 1}\left( T_1\right) {{\bar{A}}}_{\theta 1}\left( T_1\right) \right) \\&\quad -{\widetilde{\gamma }}_1A_{z1}{\left( T_1\right) i^{\alpha _1}e}^{iT_0}+cc.\\&D_0^2{(\theta }_2)+\beta ^2\theta _2={\widetilde{p}}_2\frac{1}{2}e^{i\mu _2T_0}-2{A^\prime }_{\theta 1}{\left( T_1\right) i\beta e}^{i{\beta T}_0} \\&+A_{z1}\left( T_1\right) {{\bar{A}}}_{\theta 1}{\left( T_1\right) e}^{iT_0\left( 1-\beta \right) }\\&\quad +A_{z1} \left( T_1\right) A_{\theta 1}{\left( T_1\right) e}^{iT_0\left( \beta +1\right) }\\&\quad -{\widetilde{\gamma }}_2A_{\theta 1}{\left( T_1\right) i^{\alpha _2}\beta e}^{i{\beta T}_0}+cc. \\&D_0^2{(\phi }_2)+\beta ^2\phi _2={\widetilde{p}}_3\frac{1}{2}e^{i\mu _2T_0}-2{A^\prime }_{\phi 1}{\left( T_1\right) i\beta e}^{i\beta T_0} \\&\quad +A_{z1}\left( T_1\right) {{\bar{A}}}_{\phi 1}\left( T_1\right) e^{iT_0\left( 1-\beta \right) }\\&\quad {+A}_{z1} \left( T_1\right) A_{\phi 1}{\left( T_1\right) e}^{iT_0\left( \beta +1\right) }\\&\quad -{\widetilde{\gamma }}_2A_{\phi 1}\left( T_1\right) i^{\alpha _2}\beta e^{i{\beta T}_0}+cc. \end{aligned} \end{aligned}$$
(23)

where cc. stands for complex conjugate terms.

Then, in order to eliminate the expressions that result in secular terms, we need to distinguish the following cases \(2\beta =1 \;\), \(\mu _1=1 \;\), \(1-\beta =\beta \;\), \(\mu _2 =\beta \;\), \(\mu _3 = \beta \;\). In the analyzed system, the internal resonance occurs for \(\beta = 0.5\), whereas the external resonances occur for \(\mu _1=1 \;\), \(\mu _2 =\beta \;\) and \(\mu _3 = \beta \;\). All resonances should be analyzed separately.

4 A case of the internal resonance for \(\beta =0.5\) and the external resonance for \(\mu _1=1\)

We are considering the internal resonance for \(\beta =0.5 \;\) and the external resonance for \(\mu _1=1 \;\). Introducing detuning parameters \(\sigma _1\) and \(\sigma _2\), we assume that \(p_2 = p_3 = 0\) and

$$\begin{aligned} \begin{aligned}&1-\beta =\beta -\varepsilon \sigma _2\\&\mu _1=1-\varepsilon \sigma _1 \end{aligned} \end{aligned}$$
(24)

The secular terms in Eq. (23) may be eliminated if

$$\begin{aligned} \begin{aligned}&\frac{1}{2}{\widetilde{p}}_1e^{i\sigma _1T_1}-\left( 2i{A^\prime }_{z1}\left( T_1\right) +{\widetilde{\gamma }}_1{i^{\alpha _1}A}_{z1}\left( T_1\right) \right) \\&\qquad -a\beta ^2\left( A_{\theta 1}^2\left( T_1\right) +A_{\phi 1}^2\left( T_1\right) \right) e^{-i\sigma _2T_1} \\&\quad +a\beta ^4\left( A_{\phi 1}^2\left( T_1\right) e^{-i\sigma _2T_1} +A_{\theta 1}^2\left( T_1\right) e^{-i\sigma _2T_1}\right) =0 \\ \\&\qquad -2{A^\prime }_{\theta 1}\left( T_1\right) i\beta +A_{z1}\left( T_1\right) {{\bar{A}}}_{\theta 1}\left( T_1\right) e^{i\sigma _2T_1} \\&\qquad -{\widetilde{\gamma }}_2A_{\theta 1}\left( T_1\right) i^{\alpha _2}\beta =0 \\ \\&\qquad -2{A^\prime }_{\phi 1}\left( T_1\right) i\beta +A_{z1}\left( T_1\right) {{\bar{A}}}_{\phi 1}\left( T_1\right) e^{i\sigma _2T_1} \\&\qquad -{\widetilde{\gamma }}_2A_{\phi 1}\left( T_1\right) i^{\alpha _2}\beta =0 \end{aligned} \end{aligned}$$
(25)

Assuming that

$$\begin{aligned} \begin{aligned}&A_{z1}=\frac{1}{2}a_{z1}e^{i\psi _1},\ \ {{\bar{A}}}_{z1}=\frac{1}{2}a_{z1}e^{-i\psi _1},\\&A_{\theta 1}=\ \frac{1}{2}a_{\theta 1}e^{i\psi _2}\ ,\ \ {{\bar{A}}}_{\theta 1}=\ \frac{1}{2}a_{\theta 1}e^{-i\psi _2},\\&A_{\phi 1}=\frac{1}{2}a_{\phi 1}e^{i\psi _3},\ \ {\ {\bar{A}}}_{\phi 1}=\frac{1}{2}a_{\phi 1}e^{-i\psi _3} \end{aligned} \end{aligned}$$
(26)

Noting that the amplitudes \(a_{z1}\), \(a_{\theta 1}\) and \(a_{\phi 1}\) are the functions of time \(T_1\), and considering that \(T_1 = \varepsilon T_0\), then substituting expressions (26) into system of Eq. (25) and separating real and imaginary parts of Eq. (25), we obtain the following equations

$$\begin{aligned}{} & {} -a_{z1}{\psi ^\prime }_1-\frac{1}{2}{\widetilde{\gamma }}_1a_{z1}\cos \left( \frac{\pi \alpha _1}{2}\right) \nonumber \\{} & {} \quad +\frac{1}{4}a a_{\theta 1}^2\beta ^2\left( \beta ^2-1\right) \cos \left( \varTheta _1\right) \nonumber \\{} & {} \quad +\frac{1}{4}a a_{\phi 1}^2\beta ^2\left( \beta ^2-1\right) \cos {\left( \varTheta _{2\ }\right) } +\frac{1}{2}{\widetilde{p}}_1\cos {\left( {\ \varTheta }_3\right) } \nonumber \\{} & {} \quad =0 \nonumber \\{} & {} \quad {a^\prime }_{z1}-\frac{1}{2}{\widetilde{\gamma }}_1a_{z1}\sin \left( \frac{\pi \alpha _1}{2}\right) \nonumber \\{} & {} \quad +\frac{1}{4} a a_{\theta 1}^2\beta ^2\left( \beta ^2-1\right) \sin \left( \varTheta _1\right) \nonumber \\{} & {} \quad +\frac{1}{4}a a_{\phi 1}^2\beta ^2\left( \beta ^2-1\right) \sin \left( \varTheta _{2\ }\right) +\frac{1}{2}{\widetilde{p}}_1\sin \left( {\ \varTheta }_3\right) \nonumber \\{} & {} \quad =0 \nonumber \\{} & {} \quad \beta a_{\theta 1}\psi _2^\prime -\frac{1}{4}a_{z1}a_{\theta 1}\cos \left( \varTheta _1\right) \nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_2\frac{1}{2}a_{\theta 1}\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\{} & {} \quad \beta \psi _2^\prime -\frac{1}{4}a_{z1}\cos \left( -\varTheta _1\right) -{\widetilde{\gamma }}_2\frac{1}{2}\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\{} & {} \quad {\beta a}_{\phi 1}{\psi ^\prime }_3-\frac{1}{4}a_{z1}a_{\phi 1}\cos \left( -\varTheta _{2\ }\right) \nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_2\frac{1}{2}a_{\phi 1}\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\{} & {} \quad \beta {a^\prime }_{\phi 1}-\frac{1}{4}a_{z1}a_{\phi 1}sin\left( {\varTheta }_{2\ }\right) \nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_2\frac{1}{2}a_{\phi 1}\beta \sin {\left( \frac{\pi \alpha _2}{2}\right) }=0 \end{aligned}$$
(27)

where

$$\begin{aligned} \begin{aligned}&\varTheta _1=2\psi _2-\sigma _2T_1-\psi _1,\; \varTheta _2={{2\psi }_3-\sigma }_2T_1-\psi _1,\\&\varTheta _3=\sigma _1T_1-\psi _1, \; {\varTheta ^\prime }_1=2{\psi ^\prime }_2-\sigma _2-{\psi ^\prime }_1, \\&{\ \varTheta ^\prime }_2={{2\psi ^\prime }_3-\sigma }_2-{\psi ^\prime }_1, \; {\varTheta ^\prime }_3=\sigma _1-{\psi ^\prime }_1 \end{aligned} \end{aligned}$$
(28)

We assume for steady-state solution that

$$\begin{aligned} \begin{aligned}&{a^\prime }_{z1}=0,\quad {a^\prime }_{\theta 1}=0, \quad {a^\prime }_{\phi 1}=0, \\&{\varTheta ^\prime }_1=0, \quad {\varTheta ^\prime }_2=0, \quad {\varTheta ^\prime }_3=0 \end{aligned} \end{aligned}$$
(29)

Noticing that

$$\begin{aligned} {\psi ^\prime }_1=\sigma _1,\ \ {\psi ^\prime }_2=\frac{1}{2}\left( \sigma _2+\sigma _1\right) ,\ \ {\psi ^\prime }_3=\frac{1}{2}\left( \sigma _2+\sigma _1\right) \end{aligned}$$
(30)

and substituting Eqs. (29) and (30) into Eqs. (27) and (27) have the form

$$\begin{aligned} \begin{aligned}&2a_{z1}\left( \sigma _1-{\widetilde{\gamma }}_1cos\left( \frac{\pi \alpha _1}{2}\right) \right) +\frac{1}{2}a\beta ^2\left( \beta ^2-1\right) \\&\quad \cdot \left( a_{\theta 1}^2cos\left( \varTheta _1\right) {+a_{\phi 1}^2}\cos {\left( \varTheta _{2\ }\right) }\right) +{\widetilde{p}}_1\cos {\left( {\ \varTheta }_3\right) }=0 \\&\qquad -{\widetilde{\gamma }}_1a_{z1}sin\left( \frac{\pi \alpha _1}{2}\right) +\frac{1}{2}a\beta ^2\left( \beta ^2-1\right) \\&\quad \cdot \left( a_{\theta 1}^2sin\left( \varTheta _1\right) +a_{\phi 1}^2sin \left( \varTheta _{2\ }\right) \right) +{\widetilde{p}}_1sin\left( {\ \varTheta }_3\right) =0\\&\quad a_{\theta 1}\left( 2\beta \left( \sigma _2+\sigma _1\right) -a_{z1} \cos {\left( \varTheta _1\right) -2{\widetilde{\gamma }}_2\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }}\right) =0 \\ \\&\quad a_{\theta 1}\left( a_{z1}sin\left( \varTheta _1\right) -2{\widetilde{\gamma }}_2 \beta \sin {\left( \frac{\pi \alpha _2}{2}\right) }\right) =0 \\&\quad a_{\phi 1}\left( 2\beta \left( \sigma _2+\sigma _1\right) -a_{z1}\cos {\left( \varTheta _{2 }\right) -{2\widetilde{\gamma }}_2\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }}\right) =0 \\&\quad a_{\phi 1}\left( a_{z1}sin\left( \varTheta _{2}\right) -{2\widetilde{\gamma }}_2\beta \sin {\left( \frac{\pi \alpha _2}{2}\right) }\right) =0\end{aligned} \end{aligned}$$
(31)

It can be concluded that according to the assumptions made previously, four cases of the steady-state solution are possible.

4.1 The case with amplitudes \(a_{\theta 1}=0\) and \(a_{\phi 1}=0\)

The first case is if amplitudes \(a_{\theta 1}=0\) and \(a_{\phi 1}=0\), in this case the pendulum does not vibrate. The system corresponds to a one-degree-of-freedom oscillator with the mass \(m=m_1+m_2\) and the amplitude \(a_{z1}\) is

$$\begin{aligned} \begin{aligned}&a_{z1}\left( {\widetilde{\gamma }}_1\cos {\left( \frac{\pi \alpha _1}{2}\right) } +2\sigma _1\right) ={\widetilde{p}}_1\cos {\left( { \varTheta }_3\right) } \\&{\widetilde{\gamma }}_1a_{z1}sin\left( \frac{\pi \alpha _1}{2}\right) ={\widetilde{p}}_1sin\left( {\varTheta }_3\right) \end{aligned} \end{aligned}$$
(32)

Thus, solving Eq. (32), the amplitude \(a_{z1}\) and the phase angle \(\varTheta _3\) can be calculated, namely

$$\begin{aligned}{} & {} \begin{aligned}&a_{z1}=\sqrt{\frac{{\widetilde{p}}_1^2}{{\widetilde{\gamma }}_1^2 +4{\widetilde{\gamma }}_1\cos {\left( \frac{\pi \alpha _1}{2}\right) }\sigma _1+4\sigma _1^2}} \end{aligned} \end{aligned}$$
(33)
$$\begin{aligned}{} & {} \begin{aligned}&\tan \left( \varTheta _3\right) =\frac{{\widetilde{\gamma }}_1sin\left( \frac{\pi \alpha _1}{2}\right) }{\left( {\widetilde{\gamma }}_1\cos {\left( \frac{\pi \alpha _1}{2}\right) }-2\sigma _1\right) } \end{aligned} \end{aligned}$$
(34)

Equation (33) shows that for parameter \(\sigma _1=0\), amplitude \(a_{z1}\) does not depend on the order of the fractional derivative \({\alpha _1}\). This dependency for small values of damping coefficient \({\widetilde{\gamma }}_1\) and for \(\sigma _1 \ne 0\) is weak.

4.2 The case with amplitudes \(a_{\theta 1}=0\) and \(a_{\phi 1} \ne 0\)

The second case is if the amplitudes \(a_{\theta 1}=0\) and \(a_{\phi 1} \ne 0\), thus a following system of equations may be formulated

$$\begin{aligned}{} & {} 2a_{z1}\left( \sigma _1-{\widetilde{\gamma }}_1cos\left( \frac{\pi \alpha _1}{2}\right) \right) +\frac{1}{2}a\beta ^2\left( \beta ^2-1\right) a_{\phi 1}^2\cos {\left( \varTheta _{2 }\right) } \nonumber \\{} & {} \qquad +{\widetilde{p}}_1\cos {\left( {\varTheta }_3\right) }=0 \nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_1a_{z1}sin\left( \frac{\pi \alpha _1}{2}\right) +\frac{1}{2}a\beta ^2\left( \beta ^2-1\right) a_{\phi 1}^2sin\left( \varTheta _{2\ }\right) \nonumber \\{} & {} \qquad +{\widetilde{p}}_1sin\left( {\ \varTheta }_3\right) =0 \nonumber \\{} & {} \quad 2\beta \left( \sigma _2+\sigma _1\right) -a_{z1}\cos {\left( \varTheta _{2\ }\right) } -2{\widetilde{\gamma }}_2\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\{} & {} \quad a_{z1}sin\left( \varTheta _{2\ }\right) -2{\widetilde{\gamma }}_2 \beta \sin \left( \frac{\pi \alpha _2}{2}\right) =0 \end{aligned}$$
(35)

Solving Eq. (35), the amplitude \(a_{z1}\) and the phase angle \(\varTheta _2\) can be obtained, viz

$$\begin{aligned}{} & {} \begin{aligned} a_{z1}=2\beta \sqrt{\left( \sigma _2+\sigma _1\right) ^2-2{\widetilde{\gamma }}_2 \left( \sigma _2+\sigma _1\right) \cos {\left( \frac{\pi \alpha _2}{2}\right) +{\widetilde{\gamma }}_2^2}} \end{aligned}\nonumber \\ \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \begin{aligned} \tan \left( \varTheta _2\right) =\frac{{\widetilde{\gamma }}_2\sin {\left( \frac{\pi \alpha _2}{2}\right) }}{\left( \sigma _2+\sigma _1\right) -{\widetilde{\gamma }}_2\cos {\left( \frac{\pi \alpha _2}{2}\right) }} \end{aligned} \end{aligned}$$
(37)

Similarly, the amplitude \(a_{\phi 1}\) and the phase angle \(\varTheta _3\) can be calculated using the equations (35)

Equation (36) shows that if \(\sigma _1=-\sigma 2\), amplitude \(a_{z1}\) does not depend on the order of the fractional derivative \({\alpha _2}\). This dependency for \(\sigma _1 \ne -\sigma 2\) and for small values of damping coefficient \({\widetilde{\gamma }}_2\) is weak.

4.3 The case with amplitudes \(a_{\theta 1} \ne 0\) and \(a_{\phi 1}=0\)

The third case is if the amplitude \(a_{\theta 1} \ne 0\) and \(a_{\phi 1}=0\), then

$$\begin{aligned} \begin{aligned}&2a_{z1}\left( \sigma _1-{\widetilde{\gamma }}_1\cos \left( \frac{\pi \alpha _1}{2}\right) \right) +\frac{1}{2}a\beta ^2\left( \beta ^2-1\right) a_{\theta 1}^2\cos \left( \varTheta _1\right) \\&\qquad +{\widetilde{p}}_1\cos {\left( { \varTheta }_3\right) }=0 \\&\qquad -{\widetilde{\gamma }}_1a_{z1}\sin \left( \frac{\pi \alpha _1}{2}\right) +\frac{1}{2}a \beta ^2\left( \beta ^2-1\right) a_{\theta 1}^2\sin \left( \varTheta _1\right) \\&\qquad +{\widetilde{p}}_1\sin \left( {\ \varTheta }_3\right) =0 \\&\quad 2\beta \left( \sigma _2+\sigma _1\right) -a_{z1}\cos {\left( \varTheta _{1}\right) } -2{\widetilde{\gamma }}_2\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \\&\quad a_{z1}\sin \left( \varTheta _{1}\right) -2{\widetilde{\gamma }}_2 \beta \sin \left( \frac{\pi \alpha _2}{2}\right) =0 \end{aligned} \end{aligned}$$
(38)

The amplitude \(a_{z1}\) and the phase angle \(\varTheta _1\) can be calculated, namely

$$\begin{aligned}{} & {} \begin{aligned}&a_{z1}= \\&2\beta \sqrt{\left( \sigma _2+\sigma _1\right) ^2+{\widetilde{\gamma }}_2^2-2 \left( \sigma _2+\sigma _1\right) {\widetilde{\gamma }}_2\cos {\left( \frac{\pi \alpha _2}{2}\right) }}\\ \end{aligned}\nonumber \\ \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \begin{aligned} \tan \left( \varTheta _1\right) =\frac{{\widetilde{\gamma }}_2\sin {\left( \frac{\pi \alpha _2}{2}\right) }}{\left( \sigma _2+\sigma _1\right) -{\widetilde{\gamma }}_2\cos {\left( \frac{\pi \alpha _2}{2}\right) }} \end{aligned} \end{aligned}$$
(40)

The amplitude \(a_{\theta 1}\) and the phase angle \(\varTheta _3\) can be calculated using Eq. (38)

Similarly as in the previous case, if \(\sigma _1=-\sigma 2\), amplitude \(a_{z1}\) does not depend on the order of the fractional derivative \({\alpha _2}\). This dependency for \(\sigma _1 \ne -\sigma 2\) and for small values of damping coefficient \({\widetilde{\gamma }}_2\) is weak.

4.4 The case with amplitudes \(a_{\theta 1} \ne 0\) and \(a_{\phi 1} \ne 0\)

The forth case is if the amplitudes \(a_{\theta 1} \ne 0\) and \(a_{\phi 1} \ne 0\), then solving Eq. (29), amplitude \(a_{z1}\) and angle \(\varTheta _2\) can be derived, namely

$$\begin{aligned} \begin{aligned}&a_{z1}= \\&2\beta \sqrt{\left( \sigma _2+\sigma _1\right) ^2-2{\widetilde{\gamma }}_2\cos { \left( \frac{\pi \alpha _2}{2}\right) }\left( \sigma _2+\sigma _1\right) +{\widetilde{\gamma }}_2^2} \end{aligned} \end{aligned}$$
(41)

and

$$\begin{aligned} \tan \left( \varTheta _2\right) =\frac{{\widetilde{\gamma }}_2sin{\left( \frac{\pi \alpha _2}{2}\right) }}{\left( \sigma _2+\sigma _1\right) -{\widetilde{\gamma }}_2cos{\left( \frac{\pi \alpha _2}{2}\right) }} \end{aligned}$$
(42)

Equation (29) shows that \(\cos \varTheta _2=\cos \varTheta _1\) and \(\sin \varTheta _2=\sin \varTheta _1\). Taking this into account, after some mathematical transformations, we can find that

$$\begin{aligned} \begin{aligned}&a_{\theta 1}^4a^2\beta ^4\left( \beta ^2-1\right) ^2 \\&\qquad -2a_{\theta 1}^2a\cdot a_{z1}\beta ^2\left( \beta ^2-1\right) ^2 \cdot \\&\quad \left( {\widetilde{\gamma }}_1\cos {\left( \frac{\pi \alpha _1}{2}-\varTheta _{1\ }\right) }+2\sigma _1 \cos {\left( \frac{\pi \alpha _1}{2}\right) }\right) \\&\qquad +a_{z1}^2\left( {\widetilde{\gamma }}_1^2+4\sigma _1^2+4{\widetilde{\gamma }}_1\sigma _1 \cos {\left( \frac{\pi \alpha _1}{2}\right) }\right) -{\widetilde{p}}_1^2=0 \end{aligned} \end{aligned}$$
(43)

Having expression for \(a_{z1}\) and \(\tan \left( \varTheta _2\right) \), we can derive expressions for amplitudes \(a_{\theta 1}\) and \(a_{\phi 1}\) by solving Eq. (43).

In this case, amplitude \(a_{z1}\) does not depend on the order of the fractional derivative \({\alpha _2}\). This dependency for \(\sigma _1 \ne -\sigma _2\) and for small values of damping coefficient \({\widetilde{\gamma }}_2\) is weak.

5 A case of the internal resonance for \(\beta =0.5 \;\) and the external resonance for \(\mu _2=\beta \;\)

We are considering the internal resonance for \(\beta =0.5 \;\) and the external resonance for \(\mu _2=\beta \;\). Introducing detuning parameters \(\sigma _1\) and \(\sigma _3\), and assuming that \(p_1=0\) whereas \(p_2\ne 0\) and \(p_3 \ne 0\)

$$\begin{aligned} \begin{aligned}&1-\beta =\beta -\varepsilon \sigma _2\\&\mu _2=1+\varepsilon \sigma _3 \end{aligned} \end{aligned}$$
(44)

The secular terms in Eq. (23) may be eliminated if

$$\begin{aligned}{} & {} -2{A^\prime }_{z1}\left( T_1\right) i-a\beta ^2\left( A_{\theta 1}^2\left( T_1\right) +A_{\phi 1}^2\left( T_1\right) \right) e^{-i\sigma _2T_1} \nonumber \\{} & {} \qquad +a\beta ^4\left( A_{\phi 1}^2\left( T_1\right) e^{-i\varepsilon \sigma _2T_0} +A_{\theta 1}^2\left( T_1\right) e^{-i\sigma _2T_1}\right) \nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_1A_{z1}\left( T_1\right) i^{\alpha _1}=0 \nonumber \\{} & {} \quad {\widetilde{p}}_3\frac{1}{2}e^{i\sigma _3T_1}-2{A^\prime }_{\theta 1}\left( T_1\right) i\beta +A_{z1}\left( T_1\right) {{\bar{A}}}_{\theta 1}\left( T_1\right) e^{i\sigma _2T_1} \nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_2A_{\theta 1}\left( T_1\right) i^{\alpha _2}\beta =0 \nonumber \\{} & {} \quad {\widetilde{p}}_3\frac{1}{2}e^{i\varepsilon \sigma _3T_1}-2{A^\prime }_{\phi 1}\left( T_1\right) i\beta \nonumber \\{} & {} \qquad +A_{z1}\left( T_1\right) {{\bar{A}}}_{\phi 1}\left( T_1\right) e^{-i\sigma _2T_1}\nonumber \\{} & {} \qquad -{\widetilde{\gamma }}_2A_{\phi 1}\left( T_1\right) i^{\alpha _2}\beta =0 \end{aligned}$$
(45)

Assuming that the amplitudes have the same form as in section 4 Eq. (26) and noting that the amplitudes \(a_{z1}\), \(a_{\theta 1}\) and \(a_{\phi 1}\) are functions of time \(T_1\), and considering that \(T_1 = \varepsilon T_0\), then substituting expressions (26) into system of Eq. (45), and separating real and imaginary parts of Eq. (45), the following equations can be obtained

$$\begin{aligned}&4a_{z1}{\psi ^\prime }_1+a a_{\theta 1}^2\beta ^2\left( \beta ^2-1\right) \cos {\left( \varPhi _1\right) } \nonumber \\&\qquad +a a_{\phi 1}^2\beta ^2\left( \beta ^2-1\right) \cos {\left( \varPhi _2\right) }-2{\widetilde{\gamma }}_1a_{z1} \cos {\left( \frac{\pi \alpha _1}{2}\right) }=0 \nonumber \\&\qquad -4{a^\prime }_{z1}+aa_{\theta 1}^2\beta ^2\left( \beta ^2-1\right) sin\left( \varPhi _1\right) \nonumber \\&\qquad +a a_{\phi 1}^2\beta ^2\left( \beta ^2-1\right) sin\left( \varPhi _2\right) -2{\widetilde{\gamma }}_1a_{z1}sin \left( \frac{\pi \alpha _1}{2}\right) =0 \nonumber \\&\quad {\widetilde{p}}_2\cos {\left( \varPhi _4\right) }+2\beta \ a_{\theta 1}\left( \frac{1}{2} \left( \varPhi _1^\prime -\varPhi _2^\prime \right) +\sigma _3-\varPhi _3^\prime \right) \nonumber \\&\qquad -\frac{1}{2}a_{z1}a_{\theta 1}\cos {\left( \varPhi _1\right) }-{\widetilde{\gamma }}_2 \beta a_{\theta 1}\cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\&\quad {\widetilde{p}}_2\sin {\left( \varPhi _4\right) }-2{{\beta a}^\prime }_{\theta 1} +\frac{1}{2}a_{z1}a_{\theta 1}sin\left( \varPhi _1\right) \nonumber \\&\qquad -{\widetilde{\gamma }}_2\beta \ a_{\theta 1}sin\left( \frac{\pi \alpha _2}{2}\right) =0 \nonumber \\&\quad {\widetilde{p}}_3\cos {\left( \varPhi _3\right) }+{\beta a}_{\phi 1}(\sigma _3-{\psi \prime }_3) -\frac{1}{2}a_{z1}a_{\phi 1}\cos {\left( \varPhi _{2\ }\right) } \nonumber \\&\qquad -{\widetilde{\gamma }}_2\beta \ a_{\theta 1}\cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\&\quad {\widetilde{p}}_3\sin {\left( \varPhi _3\right) }-2\beta {a^\prime }_{\phi 1} +\frac{1}{2}a_{z1}a_{\theta 1}sin\left( \varPhi _{2\ }\right) \nonumber \\&\qquad -{\widetilde{\gamma }}_2\beta \ a_{\phi 1}sin\left( \frac{\pi \alpha _2}{2}\right) =0 \end{aligned}$$
(46)

where

$$\begin{aligned}{} & {} \varPhi _1=2\psi _2-\sigma _2T_1-\psi _1,\ \ \varPhi _{2\ }=2\psi _3-\sigma _2T_1-\psi _1, \nonumber \\{} & {} \varPhi _3=\sigma _3T_1-\psi _3,\ \ {\ \varPhi ^\prime }_1=2{\psi ^\prime }_2-\sigma _2-{\psi ^\prime }_1, \nonumber \\{} & {} {\varPhi ^\prime }_{2\ }={{2\psi ^\prime }_3-\sigma }_2-{\psi ^\prime }_1,\ \ {\varPhi ^\prime }_3=\sigma _1-{\psi ^\prime }_3, \nonumber \\{} & {} \varPhi _{4\ }=\varPhi _3-\frac{1}{2}\left( \varPhi _1-\varPhi _{2\ }\right) \end{aligned}$$
(47)

We assume for steady-state solution that

$$\begin{aligned}{} & {} {a^\prime }_{z1}=0,\quad {a^\prime }_{\theta 1}=0, \quad {a^\prime }_{\phi 1}=0, \nonumber \\{} & {} {\varPhi ^\prime }_1=0, \quad {\varPhi ^\prime }_2=0, \quad {\varPhi ^\prime }_3=0 \end{aligned}$$
(48)

Noticing that

$$\begin{aligned} \begin{aligned}&{\psi ^\prime }_1=2\sigma _3-\sigma _2-2{\varPhi \prime }_3-\varPhi _2^\prime , \\&{\psi ^\prime }_3=\sigma _3-{\ \varPhi ^\prime }_3,\ \ {\psi ^\prime }_2= \frac{1}{2}\left( \varPhi _1^\prime -\varPhi _2^\prime \right) +\sigma _3-\varPhi _3^\prime \end{aligned} \end{aligned}$$
(49)

and substituting Eqs. (48) and (49) into Eq. (46), we obtain following expressions

$$\begin{aligned}&2a_{z1}\left( 2\left( 2\sigma _3-\sigma _2\right) -{\widetilde{\gamma }}_1a_{z1} \cos {\left( \frac{\pi \alpha _1}{2}\right) }\right) \nonumber \\&\qquad +a\beta ^2\left( \beta ^2-1\right) (a_{\theta 1}^2\cos {\left( \varPhi _1\right) } \nonumber \\&\quad +a_{\phi 1}^2\cos {\left( \varPhi _2\right) })=0\nonumber \\&\quad a\beta ^2\left( \beta ^2-1\right) \left( a_{\theta 1}^2sin\left( \varPhi _1\right) +a_{\phi 1}^2sin\left( \varPhi _2\right) \right) \nonumber \\&\qquad -2{\widetilde{\gamma }}_1a_{z1}sin\left( \frac{\pi \alpha _1}{2}\right) =0 \nonumber \\&\quad {\widetilde{p}}_2\cos {\left( \varPhi _4\right) }+2\beta \ a_{\theta 1}\sigma _3 -\frac{1}{2}a_{z1}a_{\theta 1}\cos {\left( \varPhi _1\right) } \nonumber \\&\qquad -{\widetilde{\gamma }}_2\beta \ a_{\theta 1}\cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\&\quad {\widetilde{p}}_2\sin {\left( \varPhi _4\right) } +\frac{1}{2}a_{z1}a_{\theta 1}sin\left( \varPhi _1\right) \nonumber \\&\quad -{\widetilde{\gamma }}_2\beta \ a_{\theta 1}sin\left( \frac{\pi \alpha _2}{2}\right) =0 \nonumber \\&\quad {\widetilde{p}}_3\cos {\left( \varPhi _3\right) } +{\beta a}_{\phi 1}\sigma _3-\frac{1}{2}a_{z1}a_{\phi 1}\cos {\left( \varPhi _{2\ }\right) } \nonumber \\&\qquad -{\widetilde{\gamma }}_2\beta \ a_{\theta 1}\cos {\left( \frac{\pi \alpha _2}{2}\right) }=0 \nonumber \\&\quad {\widetilde{p}}_3\sin {\left( \varPhi _3\right) } +\frac{1}{2}a_{z1}a_{\phi 1}sin\left( \varPhi _{2\ }\right) \nonumber \\&\quad -{\widetilde{\gamma }}_2\beta \ a_{\phi 1}sin\left( \frac{\pi \alpha _2}{2}\right) =0 \end{aligned}$$
(50)

Equation (50) shows that several cases of the steady-state solution are possible. The first case is if amplitude \(a_{z 1}=0\), in this case the mass element does not vibrate. Amplitudes \(a_{\theta 1}\), \(a_{\phi 1} \) are equal and

$$\begin{aligned} a_{\theta 1}\!=\!a_{\phi 1}\!=\!\frac{{\widetilde{p}}_2}{\beta \sqrt{4\sigma _3^2 \!+\!{\widetilde{\gamma }}_2^2\beta ^2-4{\widetilde{\gamma }}_2\sigma _3\cos {\left( \frac{\pi \alpha _2}{2}\right) }}}\qquad \end{aligned}$$
(51)

The second case is when all amplitudes are not equal zero. In this case, the relationship between amplitude \(a_{\theta 1}\) and \(a_{z 1}\) is as below

$$\begin{aligned} \begin{aligned}&a_{\theta 1}= \\&\frac{{\widetilde{p}}_2}{\sqrt{\beta ^2\sigma _3^2+\frac{1}{4}a_{z1}^2 +{\widetilde{\gamma }}_2^2\beta ^2-2\beta \sigma _3w_\theta -a_{z1}{\widetilde{\gamma }}_2 \beta \left( \cos {\left( \varPhi _1+\frac{\pi \alpha _2}{2}\right) }\right) }} \end{aligned} \end{aligned}$$
(52)

where

$$\begin{aligned} w_\theta =a_{z1}\cos {\left( \varPhi _1\right) }+2{\widetilde{\gamma }}_2 \beta \cos {\left( \frac{\pi \alpha _2}{2}\right) } \end{aligned}$$

The relationship between amplitude \(a_{\phi 1}\) and \(a_{z 1}\) is expressed as

$$\begin{aligned} \begin{aligned}&a_{\phi 1}= \\&\frac{{\widetilde{p}}_3}{\sqrt{\beta ^2\sigma _3^2+\frac{1}{4}a_{z1}^2 +{\widetilde{\gamma }}_2^2\beta ^2-2\beta \sigma _3w_\phi -a_{z1}{\widetilde{\gamma }}_2 \beta \left( \cos {\left( \varPhi _2+\frac{\pi \alpha _2}{2}\right) }\right) }} \end{aligned} \end{aligned}$$
(53)

where

$$\begin{aligned} w_\phi =a_{z1}\cos {\left( \varPhi _2\right) }+2{\widetilde{\gamma }}_2\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) } \end{aligned}$$

The next two cases occur when one of the amplitudes \(a_{\theta 1}=a_{\phi 1}=0\). Equation (50) shows that this case is possible when amplitudes \(\widetilde{p}_2=\widetilde{p}_3=0\); thus, the pendulum does not vibrate. Another cases occur when \(a_{\theta 1}=0\) and \(a_{\phi 1}\ne 0\) or \(a_{\theta 1} \ne 0\) and \(a_{\phi 1}=0\). In these cases, one of the amplitudes \(\widetilde{p}_2=0\) or \(\widetilde{p}_3=0\) correspondingly, and the movement of the pendulum is in one plane.

The dynamic behavior of the system can be also analyzed when one of the forces \(\widetilde{p}_2, \widetilde{p}_3\) is zero. For example, if \(\widetilde{p}_2=0\) then Eq. (50) shows that the amplitude \(a_{z 1}\) is expressed as

$$\begin{aligned} \begin{aligned} a_{z1}=2\beta \sqrt{2\sigma _3^2+{\widetilde{\gamma }}_2^2-\sigma _3\cos {\left( \frac{\pi \alpha _2}{2}\right) }} \end{aligned} \end{aligned}$$
(54)

The amplitude \(a_{\phi 1}\) can be calculated using Eq. (53) and phase angle \(\varPhi _1\) may be calculated from

$$\begin{aligned} \begin{aligned} \tan {\left( \varPhi _1\right) }=\frac{{\widetilde{\gamma }}_2\beta sin\left( \frac{\pi \alpha _2}{2}\right) }{\left( 2\beta \sigma _3 -{\widetilde{\gamma }}_2\beta \cos {\left( \frac{\pi \alpha _2}{2}\right) }\right) } \end{aligned} \end{aligned}$$
(55)

Having calculated \(a_{z 1}\), \(a_{\phi 1}\) and \(\varPhi _1\), amplitude \(a_{\phi 1}\) and phase angle \(\varPhi _2\) can be determined using Eq. (50).

Equation (54) shows that amplitude \(a_{z1}\) does not depend on damping coefficient \({\widetilde{\gamma }}_1\) but it depends on damping coefficient \({\widetilde{\gamma }}_2\) and detuning parameters \(\sigma _3\). If \(\sigma _3=0\), amplitude \(a_{z1}\) does not depend on the order of the fractional derivative \({\alpha _2}\). This relationship for \(\sigma _3 \ne 0\) and for small values of damping coefficient \({\widetilde{\gamma }}_2\) is weak.

6 Numerical calculations

Example calculations are made for the case of the internal resonance for \(\beta =0.5\) and the external resonance for \(\mu _1=1\) and the subcase presented in subsection 4.4, namely for \(a_{\theta 1} \ne 0\) and \(a_{\phi 1} \ne 0\). The amplitudes \(a_{z1}\) and \(a_{\theta 1}\) as a function of the detuning parameter \(\sigma _1\) are computed using Eqs. (41), (42) and (43). The calculations are performed for the following system parameters: \(\sigma _2 = 1.0\), \(a =0.5\), \(\beta = 0.5\), \(\gamma _2 = 0.002\), \(\gamma _2 = 0.004\), \(p_1=0.001\) and orders of fractional derivative \(\alpha _2 = 0.25\), \(\alpha _2 =.50\), \(\alpha _2 = 0.75\), \(\alpha _2 = 1.00\). The calculations are made using the “Mathematica” package. The obtained relationships for amplitude \(a_{z1}\) are presented in Fig. 2, whereas for the amplitude \(a_{\theta 1}\) are presented in Fig. 3.

Fig. 2
figure 2

Amplitude \(a_{z1}\) as a function of the detuning parameter \(\sigma _1\), \(\sigma _2 =1.0\), \( a = 0.5\), \(\beta =0.5\), \(p_1=0.001\), a) \(\gamma _2 = 0.002 \), b) \(\gamma _2 = 0.004 \)

Full size image
Fig. 3
figure 3

Amplitude \(a_{\theta 1}\) as a function of the detuning parameter \(\sigma _1\), \(\sigma _2 = 1.0\), \( a = 0.5\), \(\beta =0.5\), \(p_1=0.001\), a) \(\gamma _2 = 0.002 \), b) \(\gamma _2 = 0.004 \)

Full size image

Figure 2 shows that the amplitude \(a_{z1}\) depends weakly on the order of the fractional derivative, as well on the damping coefficient \(\gamma _2\). Moreover, we can see that the amplitude \(a_{z1} = \widetilde{\gamma }_2\) for \(\sigma _1 = -1.0\).

The graph shown in Fig. 3 shows that the amplitude \(a_{\theta 1}\) also depends weakly on the order of the fractional derivative, virtually all curves coincide. The graphs presented in Fig. 3 show that the order of the fractional derivative effects on the range of existing real solution of Eq. (43) for amplitude \(a_{\theta 1}\), namely an increase in the order of the fractional derivative, decreases the range of the solution. The decrease in the range of the solution is more noticeable for a higher damping coefficient \(\gamma _2\).

7 Conclusions

In this paper, analysis of a nonlinear three-degree-of-freedom system with a spherical pendulum is performed. A fractional damping is assumed in the damper and in the spherical pendulum pivot point. The approximate analytical solution is obtained using the multiple-scale method. Steady-state solutions for different combinations of external and internal resonances are studied. The analysis is performed for two types of excitation. The first excitation case assumes only excitation by a vertical force acting on the oscillator and for an internal resonance for \(\beta =0.5\) and an external resonance for \(\mu _1=1.0\), while the second case assumes excitation with a force acting on the pendulum in the horizontal direction (Fig. 1) and an internal resonance for \(\beta =0.5\) and an external resonance for \(\mu _2=\beta \).

It is shown that the amplitude \(a_{z1}\) depends weakly on the order of the fractional derivative, as well on the damping coefficient. Similarly, the amplitudes \(a_{\theta 1}\) and \(a_{\phi 1}\) depend weakly on the order of the fractional derivative. The study can be extended to a transient analysis and analysis of other external and internal resonances.