Fundamental competition of smooth and non-smooth bifurcations and their ghosts in vibro-impact pairs

Abstract

A combined analysis of smooth and non-smooth bifurcations captures the interplay of different qualitative transitions in a canonical model of an impact pair, a forced capsule in which a ball moves freely between impacts on either end of the capsule. The analysis, generic for the impact pair context, is also relevant for applications. It is applied to a model of an inclined vibro-impact energy harvester device, where the energy is generated via impacts of the ball with a dielectric polymer on the capsule ends. While sequences of bifurcations have been studied extensively in single- degree-of-freedom impacting models, there are limited results for two-degree-of-freedom impacting systems such as the impact pair. Using an analytical characterization of impacting solutions and their stability based on the maps between impacts, we obtain sequences of period doubling and fold bifurcations together with grazing bifurcations, a particular focus here. Grazing occurs when a sequence of impacts on either end of the capsule are augmented by a zero-velocity impact, a transition that is fundamentally different from the smooth bifurcations that are instead characterized by eigenvalues of the local behavior. The combined analyses allow identification of bifurcations also on unstable or unphysical solutions branches, which we term ghost bifurcations. While these ghost bifurcations are not observed experimentally or via simple numerical integration of the model, nevertheless they can influence the birth or death of complex behaviors and additional grazing transitions, as confirmed by comparisons with the numerical results. The competition between the different bifurcations and their ghosts influences the parameter ranges for favorable energy output; thus, the analyses of bifurcation sequences yield important design information.

1 Introduction

Vibro-impact (VI) systems present a remarkable class of nonlinear systems where impacts drive the interaction between the system components. A classical VI system is comprised of a forced mass and motionless rigid barrier(s) or a pair of moving impacting masses, either of which can be forced. Some examples of VI systems are shown in Fig. 1. The simplest VI models include both that of a ball bouncing on a harmonically moving surface, studied in [1, 2] and a pendulum impacting a barrier [3]. A complete dynamical model includes equations governing behavior both between impacts and at the impacts. Thus the dynamics fall into the general class of non-smooth dynamics [4,5,6]. Even when a linear system governs the dynamics between impacts, the VI system exhibits nonlinear behavior that necessarily follows from these non-smooth interactions.

Modeling the impact dynamics can take on different levels of complexity. Using a restitution coefficient r, defined as the ratio between the mass velocity immediately after and before impact, implies that it happens instantaneously or on a negligibly short time scale as compared to the overall system. Typically $0\le r\le 1$, depending on the material, shape and contact surfaces of the impacting bodies. Systems with instantaneous impacts are strongly nonlinear, given the discontinuous velocities of the impacting bodies before and after any non-elastic impact, since the velocity is reduced for $r<1$ and changes direction for $r>0$.

The specific type of non-smooth nonlinearity, due to the instantaneous impact approximation in the VI systems, can facilitate analysis in some cases. Indeed, when the energy losses due to impacts ($r\!<\!1$) dominate other damping mechanisms, the latter are neglected, yielding a conservative system between impacts that can be studied analytically. Complementing the system response with the impact condition(s) for its velocity allows one to derive an explicit analytical solution for its periodic motion, as in [7], and to study the dynamical dependence on system parameters, including the classical nonlinear analyses of smooth bifurcations observed in VI systems. Such analytical results cannot capture the non-smooth behavior explicitly, so that complementary numerical simulations or semi-analytical methods are generally required. One type of non-smooth bifurcation, first reported in [8], is a grazing bifurcation characterized by a zero-velocity impact. Later, in [9, 10] gave a global bifurcation analysis, indicating the importance of the grazing phenomenon on the global dynamics of VI systems. In the context of a spring-mass system colliding against a motionless barrier [11], A. Nordmark introduced the term grazing impact associated with the flow tangential to the impacting surface. It is treated as a bifurcation, separating non-impacting and vibro-impacting motions. The near-grazing two-dimensional map was also derived in [11], demonstrating the continuity of the bifurcating branch with the square root singularity of the corresponding Jacobian at the grazing point.

Fig. 1

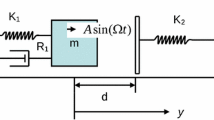
Examples for different VI systems. Sketch of a a two-degree-of-freedom (TDOF) impact pair subject to base excitation $y_2$ and a force $y_1$ applied to the mass [12], b a single-degree-of-freedom (SDOF) system [13], here $k_b$ indicates the spring constant for the barrier, so that as $k_b\rightarrow \infty$, we recover instantaneous impact. c TDOF impact oscillators with motion limiting constraints for both masses [14], d two oscillators coupled only by impact [15]

These earlier analyses of grazing and related maps generated deep interest in obtaining a better understanding of non-smooth dynamics in related SDOFs. In [16] the authors compared bifurcations in instantaneous and soft impact models, hypothesizing the grazing as a limiting case of either a fold ($F\!B$) or a period doubling ($P\!D$) bifurcation. Three bifurcation scenarios in the Nordmark map were discovered in [17], depending on the values of the bifurcation parameter. In [18] the author compared a grazing transition of a stable periodic orbit with $F\!B$s, also considering coalescing stable and unstable orbits of the impacting solution. Transitions via grazing to either chaotic attractors or periodic behavior have been studied in terms of generic bifurcation parameters in [19] and in terms of increased excitation amplitude in [18]. Banerjee et al. [20] discussed the grazing for unstable trajectories in an experimental SDOF system, also calling the phenomenon “invisible” grazing, since this grazing phenomenon was not possible to observe in the physical system. Other grazing-related features studied in SDOF VI systems include a dramatic increase in eigenvalues of unstable solutions near grazing, in [18], vanishing singularities of the Jacobian matrix in [21], sufficient conditions for periodic orbits that branch off of the grazing bifurcation [22], and comparisons of Nordmark and Poincaré maps to study grazing born from high-amplitude chaotic attractors [13]. In addition to the above-mentioned studies there are others, including [23,24,25,26] SDOF systems with linear dynamics between one-sided impacts, linear SDOFs with two-sided impacts [27,28,29,30,31,32,33,34] and oblique impacts [35], as well as multi-DOF systems with impacts [14, 15, 36,37,38,39,40]. Relevant information and references for the dynamics and bifurcations in non-smooth systems and related analytical methods can be found in books [4,5,6, 41, 42] and in the review paper [43].

In this paper we focus on the analysis of grazing and its interplay with smooth bifurcations, such as period doubling and saddle node or fold bifurcations (FB), in the two-sided vibro-impact pair. The term impact pair is used to clearly distinguish a category of VI systems where the barriers are moving with respect to the main impacting mass. In [12], and also in [16], the authors discussed the different sequences of bifurcation scenarios, including $P\!D$, $F\!B$, and grazing, in a two-degree-of-freedom (TDOF) impact pair, with an additional forcing on the mass. In [37] the authors considered a vibro-impact pair with a barrier and showed the cases when the $P\!D$ bifurcation preceded grazing bifurcation in a vibro-impact-slider pair. The authors of [44, 45] focused on gear VI dynamics, whose motion resembles that of a system with two moving barriers.

They demonstrated that grazing-grazing and $P\!D$-grazing trajectories can appear simultaneously in co-dimension 2-bifurcation scenarios, creating or destroying the gaps of periodic motion that separate chaotic regions in the bifurcation structure [44], and that chaos may die by grazing or by boundary crisis [45]. Combined analytical and numerical studies in [41] illustrate the potential for complex behaviors and transition, with various sequences of smooth bifurcations, coexisting periodic behaviors, and grazing bifurcations for the horizontal impact pair. Existence and stability conditions for different types of periodic solutions for the impact pair are given in [46] and [47], while sticking and grazing conditions for individual trajectories are discussed in [48]. For complex bifurcation sequences in SDOF systems, [49] find three scenarios of co-dimension 2 bifurcations (amplitude and frequency of the excitation) in cases where grazing may lead to a stable impacting solution and [50] considers degenerate bifurcations, where $F\!B$ and/or $P\!D$ bifurcations coincide with the grazing point. The variety of different options observed and reported in the above-mentioned publications has been a source of inspiration for this work, where we consider the phenomenon of grazing in a wide range of transitions.

A goal of this paper is to develop analytical results for the impact pair, in particular related to the interplay of smooth bifurcations such as $P\!D$ and $F\!B$ and discontinuity-induced grazing bifurcations. The sequence of different types of bifurcations, as well as the settings in which both types of bifurcations occur, has clear implications for the types of solutions that can and cannot be observed in different parameter contexts. In contrast to SDOF systems for which there is a wealth of analyses, as described above, that consider the appearance of both grazing and $F\!B$ or $P\!D$ bifurcations, TDOF systems—and in particular the impact pair—have not undergone a systematic study. In the majority of the SDOF studies mentioned above, the grazing corresponds to the transition between non-impacting and impacting scenarios only. In contrast, in the context of the impact pair, the grazing trajectories separate different types of impacting trajectories and consequently can appear in different sequences that include smooth bifurcations.

The model we consider in this paper takes the form of the “canonical” impact pair, where there is simple unimodal forcing on the motion of the barriers without a separate forcing on the mass. Our analysis provides a framework for studying the general structure that underpins the sequences and “competition” between smooth and non-smooth bifurcations in the impact pair. A formulation in terms of relative displacements facilitates handling the impact as a fixed switching manifold, a valuable viewpoint commonly used throughout studies of non-smooth dynamics. This flexibility allows a thorough analysis of these sequences without the tendency toward more complex behavior that is specific to other impact pair type models with additional inputs and forcing, as in [12, 44, 45]. At the same time, our framework provides a foundation for studying these other scenarios.

While we focus much on the general question of non-smooth and smooth bifurcations in an impact pair, we are simultaneously motivated by the relevance of our analysis in the energy harvesting context. We apply the results to describe the dynamics and energy harvesting (EH) capabilities of a VI-EH device whose dynamics follow that of an impact pair. The device is comprised of a capsule, both ends of which are covered with flexible membranes made out of dielectric elastomer (DE) material [51], in which a ball moves freely without any friction. The capsule is excited externally, and the ball is excited by impacting one of the membranes, at the same time deforming the membranes and changing their capacitance. Thus, this concept falls directly into a category of a vibro-impact pair, since both the ball and the membranes, serving as barriers to the ball, move with respect to each other. The collection of work utilizing VI dynamics for energy harvesting before 2017 can be found in [52]. As the research in this area continues, new ideas and concepts have been emerging [53,54,55,56,57].

The paper is structured as follows: In Sect. 2 we provide a framework for studying the relationship between smooth and non-smooth grazing bifurcations, including the context of the VI-EH model and a notation for tracking different behaviors on both stable and unstable or unphysical branches. In Sect. 3.2 we give the analytical results for both smooth and grazing bifurcations. In Sect. 4 we compare the analytical results to numerical simulations, demonstrating how the analytical approach provides insight into the sequences of smooth and non-smooth bifurcations and into additional complex behaviors.

2 Context and framework

In this section we provide the context of the VI-EH model in which we develop our analysis of the impact pair. We also give a framework and notation for studying different families of bifurcations in the general impact pair system. The approach is then demonstrated using this framework in the context of the VI-EH model throughout the paper.

2.1 The VI-EH model

We demonstrate the dynamical analyses in the context of an inclined VI-EH system. Figure 2a shows a schematic of the device, consisting of a cylinder of mass M moving under the influence of harmonic excitation ${\mathcal {F}}(\omega \tau + \varphi )$ with period $\frac{2\pi }{\omega }$ and a ball of mass m freely moving inside the cylinder under the influence of gravity $g = 9.8 \; \mathrm{m/s}^2$. The motion of this system is described by two equations for the acceleration of the cylinder and the ball between impacts

$$\begin{aligned}{} & {} {\ddot{X}}=\frac{{\mathcal {F}}(\omega \tau + \varphi )}{M}, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \ddot{x} = -g\sin \beta \, , \end{aligned}$$

(2)

for X the position of the center of the cylinder, and x the position of the ball.

Fig. 2

a Model sketch for the vibro-impact energy harvester, adapted from [58]. Set of parameters: $\beta$ angle of incline, $\partial B$ (bottom) $\partial T$ (top) cylinder DE membranes, s distance between membranes, M (cylinder) and m (ball) masses. b Illustration of typical motion of the ball (solid red line) within the capsule (dash-dotted blue lines) with forcing ${\mathcal {F}}(\omega \tau + \phi )$ for different values of $\beta$: one impact on $\partial B$ and $\partial T$ per period for smaller $\beta$ ($\pi /9$); with two (one) impact(s) on $\partial B$ ($\partial T$) per period for larger $\beta$ ($4\pi /9$)

We denote $\tau = \tau _j$ as the $j{\textrm{th}}$ impact with either of the DE membranes located on the top $\partial T$ or bottom $\partial B$ of the cylinder. Then the ball velocity ${\dot{x}}(\tau _j) \equiv {\dot{x}}_j$ and displacement $x(\tau _j) \equiv x_j$ at the $j{\textrm{th}}$ impact follow the impact condition

$$\begin{aligned}{} & {} {\dot{x}}_j^+=-r {\dot{x}}_j^- + (r+1) {\dot{X}}_j,\nonumber \\{} & {} x_j=X_j \pm \frac{s}{2} \hbox { for } x_j \in \partial B (+)\hbox { or }\partial T (-), \end{aligned}$$

(3)

where r is the coefficient of restitution and superscripts ${\ }^-$/${\ }^+$ denote the ball velocities just before/after each impact. This impact condition reflects the fact that the velocity of the cylinder does not change upon impact, based on our assumption that m is negligible compared to M. Periodic behaviors with different sequences of impacts are shown in Fig. 2b, alternating $\partial T$ and $\partial B$ (upper) and periodic behavior with three impacts per forcing period, two on $\partial B$ and one on $\partial T$ (lower).

Non-dimensionalization of (1) and (2) with (3) allows us to streamline the analysis, by reducing the number of parameters to some key dimensionless quantities. Furthermore, we introduce a relative position Z(t) in terms of the difference of the non-dimensional displacements of the cylinder $X^*$ and of the ball $x^*$ as in [58, 59],

$$\begin{aligned}{} & {} \tau =\frac{\pi }{\omega }t, \qquad {X(\tau )}= \frac{ A \pi ^{2}}{ M \omega ^2} X^*(t),\nonumber \\{} & {} x(\tau )=\frac{A \pi ^{2}}{M \omega ^2}x^*(t), \qquad A\equiv \parallel {\mathcal {F}} \parallel , \end{aligned}$$

(4)

$$\begin{aligned}{} & {} {Z(t)}={X^*(t)}-{x^*(t)}, \nonumber \\{} & {} {\ddot{Z}}(t)= F(\pi t+ \varphi )+ \dfrac{M g \sin \beta }{A}=f(t)+\bar{g},\nonumber \\{} & {} {\parallel F \parallel } = 1. \end{aligned}$$

(5)

In (5) A is an appropriate norm of the strength of the forcing ${\mathcal {F}}$, so that in the dimensionless setting the forcing has the unit norm. Then the impact condition (3) at the dimensionless time $t=t_j$ of the $j^{\textrm{th}}$ impact is given by

$$\begin{aligned}&{\dot{Z}}_j^+=-r {\dot{Z}}_j^-, \quad Z_j=\pm \frac{d}{2}, \quad d = \frac{M \omega ^{2}}{A\pi ^{2}} s, \end{aligned}$$

(6)

where d is dimensionless capsule length. Throughout our study we fix the parameters $M = 124.5$ g, $\omega = 5 \pi$ Hz, allowing us to focus on variability of the non-dimensional capsule length d as it varies with dimensional capsule length s or forcing strength A.

The formulation in terms of the relative variable Z facilitates tracking the dynamics between impacts, which take place on the fixed switching manifolds $Z= \pm d/2$. It is straightforward to find Z between impacts, by integrating (5) over $t\in (t_j, t_{j+1})$ with initial conditions ${\dot{Z}}_j^+$ and ${Z}_j^+$ following the impact at $t_{j}$, yielding equations for the relative velocity ${\dot{Z}}(t)$ and displacement Z(t) at times between two impacts. Replacing ${\dot{Z}}_j^+$ with ${\dot{Z}}_j^-$ via (6), using continuity of the displacement ${Z}_j^+ ={Z}_j^-$, and dropping the superscripts yields

$$\begin{aligned} {\dot{Z}}(t)&=-r {\dot{Z}}_{j} + \bar{g}(t-t_{j}) + F_1(t)-F_1(t_{j}), \end{aligned}$$

(7)

$$\begin{aligned} Z(t)&=Z_{j}-r {\dot{Z}}_{j}(t-t_{j}) +\frac{\bar{g}}{2}(t-t_{j})^2\nonumber \\&\quad +F_2(t)-F_2(t_{j})-F_1(t_{j})(t-t_{j}), \end{aligned}$$

(8)

where $F_1(t)=\int f(t)dt$, $F_2(t)=\int F_1(t)dt$. These equations form the basis of our analysis, as we evaluate them at $t=t_{j+1}$ to get maps for the relative velocity and displacement between two impacts, as described in detail in Sect. 3.1.

While our focus is on the analysis of the general bifurcation structure, it is valuable to track the influence of this structure on the energy output for the VI-EH device with DE membranes on both ends of the capsule. Typically DE membranes are made out of acrylic or silicon-based polymers, which are highly stretchable (300–700%), light, and non-conductive, with the dielectric permittivity coefficient $\epsilon$ being 2–12 times higher than that of air. Both sides of the membranes are covered with compliant electrodes, i.e., electrodes, which can stretch the same amount as the membranes. Thus, each membrane becomes a variable capacitance capacitor. Having applied bias voltage at the point of the maximum membrane deformation, corresponding to the maximum value of the capacitance, the excessive voltage can be harvested from the membrane as it returns to its undeformed state, corresponding to its minimum capacitance value. Thus, the amount of harvested energy is proportional to the difference in the capacitance between the deformed and undeformed states, $C=\epsilon _0 \epsilon A_m/h$, where the $A_m$ and h are the areas and the thickness of the membrane at each state. Note that the features of the proposed concept align with Fig. 2a and are thus consistent with the relative motion formulation in terms of Z.

To calculate the electrical power generated by the device, we use two quantities: the average output voltage per impact ${\overline{U}}_I$ and average voltage over a time interval ${\overline{U}}_T$. These depend nonlinearly on the relative dimensional velocity ${\dot{Z}}$ at impact. This nonlinear relationship arises from the deformation of the DE membrane upon impact and involves geometric deflection quantities and mechanical properties of the material. These average quantities are calculated by the formulas

$$\begin{aligned}&U_k=U_k^{\textrm{imp}}-U_{\textrm{in}}, \qquad {\overline{U}}_I =\frac{1}{N}\sum _{k=1}^N U_k, \nonumber \\&{\overline{U}}_T =\frac{1}{t_f - t_0}\sum _{k=1}^N U_k\, , \end{aligned}$$

(9)

where $U_k$ is the net output voltage at the $k{\textrm{th}}$ impact representing the difference between the generated voltage $U_k^{\textrm{imp}}$ and constant input voltage $U_{\textrm{in}}=2000$ V applied to the membranes, N is the number of impacts over a time $[t_0,t_f]$ and $t_f - t_0 = \frac{\omega }{\pi }(\tau _f-\tau _0)$ is the corresponding dimensionless time interval. Details on the energy harvesting parameters are given in Appendix A.

2.2 A framework for dynamics of the impact pair

Both TDOF and SDOF systems experience discontinuity-induced bifurcations, such as grazing, and traditional bifurcations such as $P\!D$ and $F\!B$. But the TDOF impact pair, as in the VI-EH model, has fundamentally different sequences of periodic solutions and bifurcations as compared with SDOF systems that are based on a mass impacting a fixed barrier. In SDOF systems, it is common to study bifurcations from a smooth periodic solution to a non-smooth periodic solution via grazing with the barrier. However, for the TDOF impact pair, the simplest periodic solution by definition must involve impact with at least one side of the capsule, similar to the bouncing ball. Furthermore, the sequence of bifurcations in the TDOF impact pair includes a wider range of possibilities, including grazing bifurcations generated via an additional impact per forcing period with either end of the cylinder, as well as smooth bifurcations such as $P\!D$ appearing without additional impacts.

In order to track the different types of qualitative behavior in the TDOF impact pair, we employ a notation that captures different types of impacting behavior. For example, increasing the forcing amplitude A in the impact pair yields a basic sequence of bifurcations from a low amplitude state, starting with an impact on only one end per forcing period T, to a single impact on each end or to combinations of multiple impacts on each end that may or may not have period T. To differentiate across the range of impacting solutions, we use the notation n:m/pT to categorize different periodic motions for an impact pair with a T-periodic external excitation, as in [59]. The integers n and m indicate the number of impacts against the bottom and top, respectively, of the capsule per period T, simplified to n:m for the cases where $p=1$. This notation also captures sequences of period doubling sequences, such as transitions from 1:1 to 1:1/pT for $p=2,4,\ldots$, as well as non-smooth bifurcations via grazing. Grazing occurs for the critical parameter value where the trajectory has a zero relative velocity at impact, so that beyond this critical value the system dynamics includes an additional impact (with nonzero impact velocity). The notation reflects this as we observe transitions from n:m behavior to $(n+1)$:m or n:$(m+1)$ behavior in the impact pair. For example, as an impact pair, the VI-EH system exhibits favorable energy output following a grazing transition from 1:0 to 1:1 behavior, that is, where the system moves from impact on only one end of the capsule to alternating impacts on both ends. This transition is achieved, e.g., through increased forcing amplitude, with further increases driving transitions from 1:1 to either 2:1 or 1:2 behavior via what we term first-order grazing on the bottom or top of the capsule. Alternatively, it may undergo a period doubling transition to 1:1/2T prior to any grazing bifurcation. For completeness, we also include the notation n:m/C, indicating complex, aperiodic behavior, where over long time periods the typical number of impacts against the bottom (top) of the capsule is n(m). Our computational results capture the n:m/C behaviors, but we do not study them analytically in this paper.

Fig. 3

Bifurcation diagrams for the relative impact velocity ${\dot{Z}}_k$. Black circles indicate the results from attracting behavior obtained by numerical simulation of the full system (1)–(3). Solid (dotted) lines indicate stable (unstable or unphysical) analytical results for impact velocities ${\dot{Z}}_k$ for 1:1 and 2:1 solutions. Blue (green) lines correspond to impacts on $\partial B$ ($\partial T$). a $\beta = \pi /9$, $r=.3$, $A=5$ N, decreasing s, $0.16<s<0.64$ m; b $\beta = \pi /4$, $r=.5$, $s=0.5$ m, increasing A, $3.1<A< 14.5$; c $\beta = \pi /3$, $r=.5$, $A=5$ N, decreasing s, $0.19<s<0.72$ m; d $\beta = \pi /2$, $r=.7$, $s=0.5$ m, for increasing A, $1.4<A< 14.5$. Labels of red dots for different bifurcations as given in Table 1

Figure 3 provides motivating examples of different sequences of bifurcations that commonly appear for the impact pair (5)–(6) for both smooth and grazing bifurcations. Here and throughout the paper we take ${{\mathcal {F}}}= A\cos (\omega \tau + \phi )$ in (4)–(5). The markers on the bifurcation diagrams give values for the impact velocities ${\dot{Z}}_j$ obtained numerically for large t, that is, for the attracting or stable behavior. These numerical results are obtained by a continuation-type method for d decreasing, choosing a value of d, computing over a sufficiently long time to reach the attracting behavior, from which we obtain the sequence of values of ${\dot{Z}}_j$ at that value of d. This attracting behavior provides the initial condition for computing the attractor at the next value of decreasing d, usually chosen close to the previous value of d. From (6), d varies linearly with dimensional capsule length s and is inversely proportional to forcing amplitude A. Then Fig. 3 shows the results for d decreasing in the continuation-like method, with either decreasing s or increasing A. The notation from Table 1 is used to highlight different types of transitions. Some select analytical results, specifically stable and unstable 1:1 and 2:1 solutions and the $P\!D$ and $G_{n:m}^{\nu :\mu }$ bifurcations, are shown in Fig. 3 to provide a more complete picture of the motivating examples. These analyses leading to these results are discussed in detail in Sect. 3.

We note that the detailed structure of the bifurcation diagram follows from the choice to graph relative impact velocity vs. a bifurcation parameter. This choice fits naturally with the expressions for ${\dot{Z}}_j$ and $Z_j$ in (7)–(8) which form the basis of the maps between impacts defined in Sect. 3.1. One could also choose to use a stroboscopic (Poincaré) map, as in [60] where it is shown to yield a similar bifurcation structure for the VI-EH model as shown in this paper. One difference is that there may be additional discontinuities in the 1:1 branches in the stroboscopic map, resulting from the shift in the asymmetry of the 1:1 solution. That is, the phase of the impacts relative to the periodicity of the stroboscopic map may result in additional discontinuities in the bifurcation diagram besides those associated with grazing or other bifurcations.

Figure 3a shows grazing bifurcations for decreasing s, with transitions from 1:1 to 2:1 and 2:1 to 3:1 solutions, denoted by $G_{1:1}^{2:1}$ and $G_{2:1}^{3:1}$, respectively. Panel (b) shows a period doubling bifurcation from 1:1 to 1:1/2T, labeled $P\!D$, with the transition labeled $P\!D_G$ from 1:1/pT to 2:1 behavior following additional period doubling, and finally $G_{2:1}^{3:1}$. Panel (c) shows $P\!D$ transitions from 1:1 solutions to 1:1/2T and from 2:1 to 2:1/2T for smaller d, followed by $P\!D_G$ from 2:1/pT to 3:1. In between there is a sequence of period doublings of 1:1/pT behavior, then a window of n:m/C which terminates in 2:1 periodic behavior. Panel (d) is qualitatively similar to Panel (c) for $d<.4$, but there are two separate regions of stability for the 1:1 solution. For $d>.8$, the 1:1 solution is stable, followed by a sequence of $P\!D$ to reach 1:1/pT and eventually chaotic behavior as d decreases, until a second stability region for the 1:1 solution is reached for $d<.4$.

Furthermore, the results in Panels (a)–(d) illustrate several types of transitions to 2:1 behavior, where the low velocity branch of the stable 2:1 solution does not reach ${\dot{Z}}_j = 0$. In Panel (a) at the critical point $G_{1:1}^{2:1}$, the 1:1 solution meets an unstable 2:1 branch (not shown in Fig. 3), which in turn meets the stable 2:1 solution at a fold bifurcation ($F\!B$). A similar transition was observed for a SDOF system in [50]. Figure 3 illustrates that the TDOF impact pair exhibits a variety of transitions in which the $F\!B$ structure plays a role. In addition to the 1:1 to 2:1 transition in Panel (a), it is present in the transition to 2:1 behavior via $P\!D_G$ in Panel (b), and following n:m/C in Panel (c) via a transient grazing TG defined in Table 1. For simplicity we do not label $F\!B$ and TG in Fig. 3; the mechanisms and significance of these features in the context of grazing transitions are discussed in detail in Sect. 4, and labeled in the figures there.

Table 1 Notation for different types of state transitions for the impact pair

Table 1 gives the notation to identify and distinguish first-order grazing transitions $G_{n:m}^{\nu :\mu }$, period doubling $P\!D$, and grazing from period doubled $P\!D_G$, as shown in Fig. 3. These are all transitions from a stable solution to a different stable state, motivating the analytical study of critical transitions as demonstrated in Sect. 3. In Table 1 we introduce the term first-order grazing, since in the impact pair setting, different types of grazing typically yield transitions that add one impact per forcing period. We also introduce the term higher- order grazing generically for a collection of different types of transitions that can add multiple impacts per forcing period, usually limited to the larger n and/or m settings. While we do not study higher-order grazing analytically, we point out some occurrences observed numerically in Sect. 4.

Beyond $G_{n:m}^{\nu :\mu }$ and $P\!D$, the analysis allows identification of critical parameter values on unstable or unphysical branches. Specifically, we identify first-order ghost grazing, ${\tilde{G}}_{n:m}^{\nu :\mu }$ that is, grazing of unstable solutions, typically those that have lost stability via $P\!D$. Furthermore, we identify ghost period doubling ${\widetilde{P\!D}}$ on unphysical branches, occurring on the dotted branches following grazing, e.g., on the dotted line for the unphysical 1:1 solution shown in Panel (a) for d below $G_{1:1}^{2:1}$. We refer to these as unphysical solutions since they violate the containment condition, which is $\mid Z(t)\mid \ < d/2$. Similar terminology was used in [32, 50] in a SDOF system, and we discuss it further in Sect. 3.2. These ghost bifurcations are defined in Table 1, and their significance in the dynamical behavior and energy output of the VI-EH device implications are discussed in Sect. 4. One delicate difference to note: The value $G_{n:m}^{\nu :\mu }$ may correspond to a bifurcation to an unstable $\nu$:$\mu$ solution, which generically coexists with a stable $\nu$:$\mu$ solution, so that the transition observed numerically is from a stable n:m to the stable $\nu$:$\mu$ solution. This was mentioned above in the context of $F\!B$ for the critical point $G_{1:1}^{2:1}$ in Fig. 3a. This $G_{n:m}^{\nu :\mu }$ transition contrasts with ghost grazing, which corresponds to grazing of an unstable n:m solution, as discussed in detail in Sect. 4.1.

Comparisons of the values of $\beta$ and r for the different examples shown in Fig. 3 suggest trends that we confirm in the next section with the analytical results. For example, grazing transitions are more likely to be observed for smaller r and $\beta$ and decreasing s, while $P\!D$ is observed more often for larger r and $\beta$, and increasing A. Panel (b) illustrates that for smaller and intermediate ranges of $\beta$ and r, and increasing A, $P\!D$ of 1:1 solutions precedes transitions to 2:1 solutions, but grazing occurs for other n:m transitions. Panel (d) shows separate intervals with different 1:1 solutions followed by separate $P\!D$ transitions. Such sequences are observed for other values of larger $\beta$ and r, in the case of A increasing.

In the following we develop a systematic approach based on the (semi)-analytical results for studying transitions between n:m/pT solutions for an impact pair. The analytical approach provides a new structure for studying sequences of different solutions on stable and unstable branches, filling a gap in the study of TDOF impact pair-type systems. The new notation provides a framework for tracking the bifurcation sequences of grazing, period doubling, and fold bifurcations, even for the unstable or unphysical solutions, since these bifurcation ghosts contribute to the routes to complex dynamics, as discussed in Sect. 4.2. The added value of our general semi-analytical study of the dynamics is its applicability to explain and predict energy output in the VI-EH system. For example, transitions from n:m/pT to $(n+1)$:m solutions frequently appear via grazing bifurcations, with changes in average energy output resulting from the additional impact per forcing period. With the VI-EH system as a motivation for our analysis, we focus on smaller values of n and m, for which that system exhibits larger parameter ranges of higher energy outputs.

3 Analytical results for bifurcations

We outline the analytical approaches for identifying smooth bifurcations for n:m periodic solutions for the impact pair, with explicit equations for 1:1 and 2:1 solutions as in [59]. We also provide the analytical approach for identifying first-order grazing transitions. Then these results are combined to capture sequences of the different $P\!D$ and grazing bifurcations, including their corresponding ghost bifurcations. All results are illustrated in the context of the VI-EH model (7) and (8). We note that similar analyses were applied to a slowly varying subsystem in a vibro-impact nonlinear energy sink, based on an impact pair (see [40] and references therein.)

3.1 Maps for periodic solutions

Fig. 4

Schematics illustrating the composition of maps and corresponding sequence of impacts for a 1:1, 2:1 and n:1 T-periodic solutions; b 2:2 and n:m T-periodic solutions

In [58, 59] analytical descriptions of n:1 periodic solutions were obtained, based on compositions of maps from impact to impact. There are four basic nonlinear maps $P_\ell , \; \ell =1, 2, 3, 4$ for the corresponding transitions between impacts,

$$\begin{aligned}&P_{1} : (Z_j\in \partial B, {\dot{Z}}_j, t_j) \mapsto (Z_{j+1}\in \partial B, {\dot{Z}}_{j+1}, t_{j+1}),\nonumber \\&P_{2} : (Z_j\in \partial B, {\dot{Z}}_j, t_j) \mapsto (Z_{j+1}\in \partial T, {\dot{Z}}_{j+1}, t_{j+1}),\nonumber \\&P_{3} : (Z_j\in \partial T, {\dot{Z}}_j, t_j) \mapsto (Z_{j+1}\in \partial B, {\dot{Z}}_{j+1}, t_{j+1}),\nonumber \\&P_{4} : (Z_j\in \partial T, {\dot{Z}}_j, t_j) \mapsto (Z_{j+1}\in \partial T\, , {\dot{Z}}_{j+1}, t_{j+1})\, . \end{aligned}$$

(10)

The mathematical expressions for these maps take different forms depending on whether $Z_j$ and $Z_{j+1}$ are located on either $\partial B$ or $\partial T$. Specifically, we take $t=t_{j+1}$ in (7)–(8) to get the equations for ${\dot{Z}}_j^-$ and $Z_j^-$, and dropping ${}^-$ as above, we obtain the maps for $P_\ell$, $\ell = 1, 2, 3, 4$,

$$\begin{aligned} {\dot{Z}}_{j+1}&=-r {\dot{Z}}_j + \bar{g} (t_{j+1}-t_j) + F_1(t_{j+1})-F_1(t_j), \end{aligned}$$

(11)

$$\begin{aligned} D_\ell&=-r {\dot{Z}}_j (t_{j+1}-t_j) +\frac{\bar{g}}{2} (t_{j+1}-t_j)^2 \nonumber \\&\quad +F_2(t_{j+1})-F_2(t_j)-F_1(t_j) (t_{j+1}-t_j) \, , \end{aligned}$$

(12)

where $D_1=D_4 =0$, $D_2 = -d$ and $D_3 = d$.

A n:m periodic solution is then composed of the sequence of $n+m$ maps $P_1^{n-1}\circ P_2\circ P_4^{m-1}\circ P_3$ that are completed during one forcing period of length T. The sequence involves a transition from $\partial B$ and $\partial T$ ($P_2$) and vice versa ($P_3$), as well as consecutive impacts on either $\partial B$ ($P_1$) and $\partial T$ ($P_4$). A diagram of such sequences is shown in Fig. 4.

Given the inclination angle $\beta >0$, it is not difficult to imagine that (4)–(6) regularly generate n:1 solutions for $n\ge 1$ of the specific form $P_1^{n-1}\circ P_2 \circ P_3$, which we focus on here. The maps form the basis for deriving an analytical form of the periodic motion in terms of several quantities: the impact velocities ${\dot{Z}}_{k+\ell }$, $\ell = 0\ldots , n$, the time intervals between impacts $\Delta t_{k+\ell -1}=t_{k+\ell }-t_{k+\ell -1}$ for the $n+1$ maps, and the phase difference at the initial impact $\varphi _{k} = \textrm{mod}(\pi t_{k} + \varphi , 2\pi )$. The approaches used in [58, 59] determine the $n+2$-tuple

$$\begin{aligned} ({\dot{Z}}_{k},\varphi _{k},\Delta t_{k}, \ldots , \Delta t_{k+n-1}), \end{aligned}$$

(13)

which define the n:1 periodic solution. The $n+2$ equations for (13) are obtained through the steps i) summing the equations for ${\dot{Z}}_j$ for all $P_j$; ii) summing the equations for the $Z_j$ for all $P_j$; iii) $n-1$ pairwise combinations of the equation for ${\dot{Z}}_{k+j}$ with that of the impact position $Z_{k+j+1}$, applied successively for $j = 1,\ldots ,n-1$; and iv) ${\dot{Z}}_k$ from the equation for position $Z_{k+1}$ in $P_1$. These $n+2$ equations take the form ${\dot{Z}}_k= h_\ell (\varphi _{k},\Delta t_{k}, \ldots , \Delta t_{k+n-1})$, and the remaining ${\dot{Z}}_j$ for $j=k+1,\ldots , k+n$ and $\Delta t_{k+n}$ are determined, respectively, from combining (13) with (11) for the $P_j$’s, and with the periodicity conditions $\sum _{\ell =1}^{n+1} \Delta t_{k+\ell -1} = T$ and ${\dot{Z}}_{k+n+1}={\dot{Z}}_k$. Note that for this formulation, the analytical solution for the $n+2$-tuple yields the initial impact velocity ${\dot{Z}}_k$ and phase shift $\varphi _k$ for the first map in the sequence $P_1^{n-1}\circ P_2 \circ P_3$, which is $P_1$ for $n>1$, and $P_2$ for $n=1$.

We focus primarily on transitions from either 1:1 or 2:1 periodic solutions and recall the analytical results that define these two types of periodic solutions for the forcing ${{\mathcal {F}}} = A\cos (\omega t +\phi )$. The three equations for the triple ${\mathcal {K}} _3^*\equiv ({\dot{Z}}_{k},\varphi _{k},\Delta t_{k})$ that determine the 1:1 periodic solution are [58],

$$\begin{aligned}&{\dot{Z}}_{k}=\frac{1}{(r-1)} [F_1(t_{k+1})-F_1(t_{k})] \nonumber \\&\qquad -\frac{\bar{g}}{(r-1)} \left( \frac{T}{1+r}-\Delta t_k \right) , \end{aligned}$$

(14)

$$\begin{aligned}&{\dot{Z}}_{k}=\frac{T}{r \Delta t_k-\Delta t_{k+1}}\cdot \left[ \frac{{\overline{g}}}{2}(\Delta t_k-\Delta t_{k+1})-F_1(t_{k})\right] , \end{aligned}$$

(15)

$$\begin{aligned}&[F_1(t_{k+1})-F_1(t_{k})]^2 + [F_2(t_{k+1})-F_2(t_{k}]^2\nonumber \\&=\left[ {\dot{Z}}_{k}(r-1)+\bar{g} \left( \frac{T}{1+r}-\Delta t_k \right) \right] ^2\nonumber \\&\qquad +\left[ -d+\frac{\Delta t_k \Delta t_{k+1}}{2T}\cdot [2(r+1) {\dot{Z}}_{k}- \bar{g}T]\right] ^2. \end{aligned}$$

(16)

The four equations for the quadruple ${{\mathcal {K}}}_4 \equiv ({\dot{Z}}_{k},\varphi _{k},\Delta t_{k}, \Delta t_{k+1})$ that determine the 2:1 periodic solution are [59],

$$\begin{aligned} {\dot{Z}}_k&=\dfrac{1}{1-r+r^2} \left[ (r-1)\bar{g} \Delta t_k -\bar{g}\Delta t_{k+1} + (1-r)F_1(t_k)+ r F_1(t_{k+1})-F_1(t_{k+2}) + \dfrac{T\bar{g}}{r+1} \right] . \end{aligned}$$

(17)

$$\begin{aligned} {\dot{Z}}_k&= \dfrac{1}{r \Delta t_k} \left[ F_2(t_{k+1})-F_2(t_k)\right] + \dfrac{1}{2 r} \left[ \bar{g} \Delta t_k - 2 F_1(t_k) \right] . \end{aligned}$$

(18)

$$\begin{aligned} {\dot{Z}}_{k}&=\dfrac{1}{r} \left[ \bar{g}\Delta t_k + F_1(t_{k+1})-F_1(t_k) \right] -\dfrac{1}{r^2 \Delta t_{k+1}} \left[ d + F_2(t_{k+2})-F_2(t_{k+1}) \right] \nonumber \\&\quad -\dfrac{1}{2 r^2} \left[ \bar{g} \Delta t_{k+1} - 2 F_1(t_{k+1}) \right] . \end{aligned}$$

(19)

$$\begin{aligned} {\dot{Z}}_k&=\dfrac{\left[ \dfrac{\bar{g}}{2} (\Delta t_k^2+\Delta t_{k+1}^2+\Delta t_{k+2}^2)+F_1(t_k)(-r^2 \Delta t_{k+2}+r\Delta t_{k+1}-\Delta t_{k})\right] }{r^3 \Delta t_{k+2} - r^2 \Delta t_{k+1} + r \Delta t_k} + \end{aligned}$$

(20)

$$\begin{aligned}&\quad + \dfrac{F_1(t_{k+1})(r^2 \Delta t_{k+2}-r \Delta t_{k+1} +r \Delta t_{k+2}-\Delta t_{k+1})}{r^3 \Delta t_{k+2} - r^2 \Delta t_{k+1} + r \Delta t_{k}} + \nonumber \\&\quad + \dfrac{ r^2 \bar{g} \Delta t_{k} \Delta t_{k+2}-r \bar{g} \Delta t_{k} \Delta t_{k+1}- r \bar{g} \Delta t_{k+1} \Delta t_{k+2} - (1+r) \Delta t_{k+2} F_1(t_{k+2})}{r^3 \Delta t_{k+2} - r^2 \Delta t_{k+1} + r \Delta t_{k}} . \end{aligned}$$

(21)

The linear stability analysis of the n:1 periodic solution defined by the $n+2$-tuple (13) is based on the linear techniques of [8, 41, 61]. The analysis provides a linear equation for the small perturbation $\delta {\textbf{H}}_{k}$ to the fixed point ${\textbf{H}}^*_{k} = (t_{k},{\dot{Z}}_{k})$ of the n:1 periodic solution, $\delta {\textbf{H}}_{k+(n+1)} = {\textbf{J}}_{n+1} ({\textbf{H}}^*_{k+i, i=1,\ldots n}) \delta {\textbf{H}}_{k}$. The matrix ${\textbf{J}}_{n+1}$ is based on the product of Jacobians from the composition of maps $P_j$ evaluated at the appropriate fixed values $H_\ell ^*$ that define the n:1 solution.

The details for computing ${\textbf{J}} _{n+1}$ are given in [58, 59] for the 1:1 and 2:1 periodic solutions. The eigenvalues $\lambda _i, i=1,2$ of ${\textbf{J}} _{n+1}$ then give the linear (in)stability of the n:1 solution, as well as indicating the nature of the (loss of) stability. For example, $\vert \lambda _i \vert =1$ yields a $P\!D$ bifurcation (specifically, $\lambda _i = -1$), resulting in a transition from 1:1 to 1:1/2T periodic solutions. Figure 6 shows the values $d=d_{\mathrm{P\!D}}$ for transitions to 1:1/2T and 2:1/2T behavior. Depending on the parameter values, there can be additional period doublings to 1:1/pT and 2:1/pT solutions for $p\ge 2$. We do not study these analytically, but they are observed in the numerical simulations of (5)–(6) shown below.

3.2 Analytical results for grazing bifurcations

In order to compare the prevalence of transitions from 1:1 to 1:1/pT solutions via $P\!D$ vs. transitions from 1:1 to 2:1 solutions via grazing, we give analytical conditions for determining first-order grazing bifurcations. The linear stability analysis [58, 59] based on the eigenvalues for the linearized map composition does not apply in this case, since it assumes the composition of smooth trajectories. In contrast, grazing is a discontinuity-induced bifurcation, corresponding to the critical parameter value at which a smooth trajectory is tangent to the switching surface. Then the location of the grazing bifurcation is obtained by using the maps $P_j$ above, combined with conditions for intersection of a trajectory with a switching surface.

As discussed above, analytical studies of grazing in SDOF impacting systems usually consider the first instance of grazing with a single barrier. Then the focus is on the transition from a non-impacting smooth periodic behavior to one that has a zero-velocity impact on the barrier. In contrast, for the TDOF impact pair system, our focus is on the transition between different energy producing n:m/pT behaviors, for $n,m\ge 1$. Therefore we study $G_{n:m}^{\nu :\mu }$ and ${\tilde{G}}_{n:m}^{\nu :\mu }$ for $n,m\ge 1$ as described in Table 1 above. We restrict our analysis to first-order grazing as defined there, where one additional impact per period T follows from the grazing.

In particular, we seek the value $d_G$ corresponding to grazing of n:m periodic solutions. We apply a condition based on (7), which gives an analytical expression for the behavior of ${\dot{Z}}$ between impacts on the 1:1 trajectories. In this paper we focus on the condition for the specific type of grazing that occurs when there is a zero-velocity contact on the same surface as that of the previous impact. Then $d_G$ is obtained from the generic condition,

$$\begin{aligned} d_G&=[d \mid {\dot{Z}}(t_G)= -r {\dot{Z}}_j +\bar{g}(t_G-t_j)\nonumber \\&\quad + F_1(t_G)-F_1(t_{j})=0], \end{aligned}$$

(22)

$$\begin{aligned}&\quad \hbox {for } t_j<t_G<t_{j+1}, \ {\dot{Z}}_j\ne 0, \ {\dot{Z}}_{j+1} \ne 0,\nonumber \\ Z_j&= Z(t_G)=\pm \frac{d}{2}. \end{aligned}$$

(23)

Fig. 5

a Grazing flow maps $P_2$, $P_3$, contrasting 1:1 periodic solution with $P_2$ given by the dashed line, versus grazing shown for $P_2$ given by the solid line. b Analytical 1:1 solutions (red) and attracting numerical solutions (blue dotted) in the phase plane. Green vertical lines indicate $\pm d/2$. Top to bottom: stable 1:1 solutions for $||F|| = 6.8$, $r=.4$; period doubling instability for 1:1, with stable 1:1/2T behavior $||F|| = 7.35$, $r=.4$; unphysical 1:1 solution (trajectory outside of capsule) following grazing bifurcation to 2:1 behavior for $||F|| = 7.8$, $r=.25$. Other parameters are $\beta = \pi /6$, $s= .5$m

This definition of $d_G$ states that, following an impact on $\partial B$ ($\partial T$) at $t_j$, the ball returns to the same end of the cylinder at $t_G$ with zero impact velocity ${\dot{Z}}(t_G)$ and then continues to the next impact $t_{j+1}$ with nonzero impact velocity. The condition (22) follows from evaluating (7) at $t=t_G$ and combining with the requirement that ${\dot{Z}}(t_G)=0$. The conditions in (23) ensure that the remainder of the trajectory starts and ends with nonzero impact velocities on either end of the capsule.

An example of a grazing flow map decomposition is shown in Fig. 5a. The complete orbit for the 1:1 solution is given by the composition $P_2\circ P_3$. The dashed line shows the map $P_2$ for $d>d_G$, describing the motion of the ball from point D on $\partial B$ to point A on $\partial T$ (no grazing). For $d=d_G$, the solid line shows $P_2$ that connects points D and A and includes point G where ${\dot{Z}}(t_G)=0, Z(t_G) = -d/2$. This example corresponds to the first-order grazing transition $G_{1:1}^{2:1}$, for example, as observed in Fig. 3a. Calculating $d_G$ from (22)–(23) for this case uses the triple ${{\mathcal {K}}_3} =({\dot{Z}}_k,\varphi _k,\Delta t_k)$ from (14)–(16), which defines the 1:1 solution composed of $P_2\circ P_3$. Then $d_G$ is determined by using this triple in (22). That is, in (22), ${\dot{Z}}_j = {\dot{Z}}_k$, $\varphi _j= \varphi _k$ is used in the definition of $F_1$, $t_{j+1} = t_j + \Delta t_k$, and the ”$+$“ sign is chosen since grazing occurs on the $P_2$ map, with $Z_j = Z(t_G) = d/2$ on $\partial B$. In the calculation we take $t_k=0$ without loss of generality, since the calculation is based on the 1:1 periodic solution. Then we integrate (7) with these values to obtain $d=d_G$ from (22). Values $d_G$ for $G_{1:1}^{2:1}$ and ${\tilde{G}}_{1:1}^{2:1}$ are shown for different values of r and $\beta$ in Fig. 6a, b.

We also obtain analytical results for first-order (ghost) grazing transitions from 2:1 solutions, of which there are two types: $G_{2:1}^{3:1}$ (${\tilde{G}}_{2:1}^{3:1}$) as shown in Figs. 3a, b and 7 and $G_{2:1}^{2:2}$ (${\tilde{G}}_{2:1}^{2:2}$), as shown in Fig. 8. To compute $d_G$ from (22), we use the values from the quadruple ${{\mathcal {K}}_4} =({\dot{Z}}_k,\varphi _k,\Delta t_k,\Delta t_{k+1})$, obtained by solving (17)–(21), which defines the 2:1 solution given by the composition $P_1\circ P_2 \circ P_3$. Specifically, for $G_{2:1}^{3:1}$, grazing occurs when the $P_2$ map reaches $\partial B$ with vanishing ${\dot{Z}}_j$. To compute $d_G$ for $G_{2:1}^{3:1}$, in (22) we set ${\dot{Z}}_j = {\dot{Z}}_{k+1}$, obtained from ${{\mathcal {K}}_4}$ and the appropriate map to get ${\dot{Z}}_{k+1}$. The phase $\varphi _{k}$ from ${{\mathcal {K}}_4}$ is used in the definition of $F_1$, $t_j = \Delta t_{k+1}$ and $t_{j+1} = \Delta t_{k+1} +\Delta t_{k+2}$, with $t_k=0$, based on the T-periodic 2:1 solution. The ”$+$“ is chosen for $Z(t_j) = Z(t_G) = d/2$ on $\partial B$. For $G_{2:1}^{2:2}$, grazing occurs when the $P_3$ map reaches $\partial T$ with ${\dot{Z}}_j=0$ . To compute $d_G$ for $G_{2:1}^{2:2}$, in (22) we set ${\dot{Z}}_j = {\dot{Z}}_{k+2}$ obtained from ${{\mathcal {K}}_4}$ and the appropriate maps to find ${\dot{Z}}_{k+2}$. The phase $\varphi _{k}$ from ${{\mathcal {K}}_4}$ is used in the definition of $F_1$, $t_j = \Delta t_{k+1}+\Delta t_{k+2}$ and $t_{j+1} = T$, with $t_k=0$. The ”-“ sign is chosen for $Z(t_j) = Z(t_G) = -d/2$ on $\partial T$. The analytical results for $d_G$ corresponding to $G_{2:1}^{3:1}$, ${\tilde{G}}_{2:1}^{3:1}$, $G_{2:1}^{2:2}$, and ${\tilde{G}}_{2:1}^{2:2}$ are shown for different values of r and $\beta$ in Fig. 6c, d. While in theory $G_{1:2}^{1:3}$ and $G_{1:2}^{2:2}$ are also possible, in general we do not observe these for the parameter ranges of this study, where $\beta >0$ and where the restitution coefficient is the same for both ends of the capsule. The grazing transitions $G_{1:2}^{1:3}$ and $G_{1:2}^{2:2}$ are observed, for example, when the ratio of the restitution coefficients of $\partial T$ to $\partial B$ is less than unity [62].

The analytical calculations for smooth bifurcations and for grazing allow us to follow unstable or unphysical n:m solutions, determining G or $P\!D$ transitions on these branches. Figure 5b illustrates these types of solutions, showing stable 1:1 behavior, an unstable 1:1 solution following a $P\!D$ bifurcation, and an unphysical 1:1 solution violating containment, following $G_{1:1}^{2:1}$. Even though these critical points are on unstable or unphysical solutions, they have implications for the impact pair dynamics and energy output of the VI-EH device.

3.3 Comparisons of grazing versus period doubling bifurcations

Based on the results obtained from the analytical approaches described above, we compare the sequences of the grazing and $P\!D$ bifurcations. In Fig. 6a, b, for different values of r, we compare values $d_{G}$ at which there is a first-order grazing transition $G_{1:1}^{2:1}$ with the values $d_{P\!D}$ for the $P\!D$ bifurcation from 1:1 to 1:1/2T. In Fig. 6c, d we compare values $d_G$ for which we have a first-order grazing transition from a 2:1 solution, either $G_{2:1}^{3:1}$ or $G_{2:1}^{2:2}$, vs. $d_{P\!D}$ for the $P\!D$ bifurcation from 2:1 to 2:1/2T.

The analytical results are shown in the d vs. r plane for different values of $\beta$, illustrating the relative location of the grazing and period doubling bifurcations, and their ghost counterparts. For example, if $d_G > d_{P\!D}$ for a given value of r in Fig. 6a, b, then as we decrease d, the stable 1:1 solution undergoes a $G_{1:1}^{2:1}$ at $d_G$, while the $P\!D$ bifurcation of 1:1 to 1:1/2T is not observed, thus leading to a ghost ${\widetilde{P\!D}}$. If $d_G < d_{P\!D}$ in Fig. 6a, b, then $P\!D$ from stable 1:1 to 1:1/2T behavior is observed, while the analytical grazing result occurs on the unstable portion of the 1:1 branch, corresponding to a first- order grazing ghost ${\tilde{G}}_{1:1}^{2:1}$. Similar conclusions follow from Fig. 6c, d for the 2:1 solution.

Fig. 6

Bifurcations of the 1:1 periodic motion in a, b: blue markers indicate $P\!D$ and green markers indicate $G_{1:1}^{2:1}$ for a $A = 5$ N, $0.05<d<0.5$, $0.08<s<0.8$ m; b $1.24<A<15.56$ N, $s=0.5$ m. Legends for a and b given in panel b. Bifurcations of 2:1 periodic motion in c, d: blue markers indicate $P\!D$ and green/black markers indicate $G_{2:1}^{3:1}$/$_{2:1}^{2:2}$ for c $A = 5$ N, $0.04<d<0.3$, $0.06<s<0.48$ m; d $5.19<A<38.96$ N, $s=0.5$ m. Legends for c and d given in panel c

Combinations of the Panels (a)–(b) with (c)–(d) in Fig. 6 show the analytical results for the bifurcations observed in Fig. 3, which we recall here.

Figure 3a: For small $\beta$, r, and

decreasing s, grazing rather than $P\!D$ is observed: ${G}_{1:1}^{2:1}$ and ${G}_{2:1}^{3:1}$ are observed, consistent with Fig. 6a, c where $d_{P\!D}<d_{G}$ for both 1:1 and 2:1 periodic solutions.

Figure 3b: For small and mid-range values of $\beta$, r, and increasing A, we see $P\!D$ transitions from 1:1 to 1:1/2T and ${G}_{2:1}^{3:1}$ consistent with Fig. 6b, d where $d_{P\!D}>d_{G}$ for 1:1 solutions and $d_{G}>d_{P\!D}$ for 2:1 periodic solutions.

Figure 3c: For larger values of $\beta$ and mid-range r with decreasing s, we see $P\!D$ transitions from 1:1 to 1:1/2T and for 1:2 to 1:2/2T consistent with Fig. 6a, c where $d_{P\!D}>d_{G}$ for both 1:1 and 2:1 periodic solutions.

Figure 3d: For larger values of both $\beta$ and r and increasing A, there is a large range of d over which there is a sequence of $P\!D$ corresponding to two different parameter ranges of stable 1:1 solutions, leading to a sequence of 1:1/pT solutions and to 1:1/C solutions with TG in some cases. Figure 6b shows the largest d in the sequence of $d_{P\!D}$ from 1:1 to 1:1/2T, where we see that this range is substantially larger for $\beta = 7\pi /18, \pi /2$ than for smaller $\beta$. While not shown in Fig. 6a or b, there are ranges of d for which there are separate sequences of 1:1 solutions, followed by 1:1/pT and in some cases 1:1/C, for larger values of r and other values of $\beta$, as discussed further in Fig. 10 where the analytical results are compared with numerical transitions to 2:1. The complex behavior observed in Fig. 3d is consistent with the multiple 1:1 periodic solutions and larger ranges of bi-stability between different types of periodic solutions that generically appear for larger values of r [62]. We do not pursue a detailed analysis of these here, given that larger values of r are less common for the VI-EH device of interest. However, for decreasing s there is no sequence of different 1:1/pT bifurcations, as observed for increasing A.

The relative location of the curves in Fig. 6 indicates that for some values of parameters we cannot observe first-order grazing at all, for decreasing d, while for other parameters, grazing dominates the transitions. For larger $\beta$ and r and decreasing s shown in Fig. 6a, c, $P\!D$ bifurcations are generally observed, rather than first-order grazing. Then the grazing transitions shown correspond to ghost grazing. For smaller values of $\beta$, the grazing bifurcations of periodic 2:1 solutions tend to be ${\tilde{G}}_{2:1}^{2:2}$ or ${G}_{2:1}^{2:2}$, which follows from the inclination angle closer to the symmetric case of $\beta =0$. The prominence of $P\!D$ and ${\tilde{G}}$ for larger values of $\beta$ has been observed in other studies [62], also showing G and ${\widetilde{P\!D}}$ for certain combinations of asymmetric r (different r on $\partial B$ and $\partial T$) not shown here. In addition to the influence of $\beta$, results in [59] demonstrated that changes in s for the varying A case can shift the $P\!D$ curves as shown in Fig. 6b, d.

We highlight a number of subtle points that are discussed in detail in the next section. The grazing bifurcation $G_{n:m}^{\nu :\mu }$ may correspond to an unstable $\nu$:$\mu$ branch which coexists with a stable $\nu$:$\mu$ branch via a $F\!B$, as shown in Figs. 7 and 8 for $\nu = n+1$ and $\mu = m$. In that case the low velocity impact ${\dot{Z}}_k$ may be bounded away from zero. These transitions may also be associated with bi-stability of the n:m and $\nu$:$\mu$ branches. In that case, hysteresis may be observed numerically, i.e., the observed transitions may be shifted relative to the fixed analytical results for $G_{n:m}^{\nu :\mu }$ and $P\!D$ shown in Fig. 6. That is, using a continuation-type method for decreasing d, the n:m branch is followed until the $G_{n:m}^{\nu :\mu }$ transition is reached, while for increasing d, the $\nu$:$\mu$ branch may be followed until it loses stability, e.g., at an $F\!B$ above that of the $G_{n:m}^{\nu :\mu }$. This hysteresis is not shown in Figs. 3, 7, and 8, since the numerical continuation-type method is focused on decreasing d. A final observation from Fig. 6 is that the analytical results for $G_{n:m}^{\nu :\mu }$ rely on a geometric analysis, in contrast to the analytical results for smooth bifurcations, based on the eigenvalues. This difference is typical of non-smooth bifurcations, which in general cannot be obtained via the techniques for smooth bifurcations.

Fig. 7

a Bifurcation diagram for the relative impact velocity ${\dot{Z}}_k$ for $\beta =\pi /6$, $\omega =5\pi$ Hz, $r=0.3$, $0.2217<s<0.4016$ m, $A=5$ N, s decreasing. Solid (dashed) lines indicate the stable (unstable) analytical results for impact velocities ${\dot{Z}}_k$ for 1:1 and 2:1 solutions. Blue (green) lines correspond to impacts on $\partial B$ ($\partial T$). Magenta lines indicate the unstable 2:1 (subcritical) branch, initiating at $G_{1:1}^{2:1}$. Dotted lines for d below $G_{1:1}^{2:1}$ and $G_{2:1}^{3:1}$ indicate n:1 analytical solutions that violate containment. Black open circles show attracting numerical solutions for decreasing d. Period doubling (grazing) bifurcations are labeled according to the notation in Table 1. b Phase portrait, c time series of periodic 1:1 solution for $d=0.242$, $s=0.389$ m, ${\dot{Z}}(t)=0.686178$, $\varphi =0.447012$. d Phase portrait, e time series of $P\!D$ 1:1/2T solution for $d=0.233$, $s=0.374$, ${\dot{Z}}(t)=0.686668$, $\varphi =0.507226$. g Phase portrait of ghost ${\widetilde{G}}_{1:1}^{2:1}$ for $d=0.205$, $s=0.329$ m, ${\dot{Z}}(t)=0.63746$, $\varphi =0.351488$. Red curve shows initial behavior for one period with time series in f, starting on the unstable 2:1 branch; blue curve is attracting 2:1 solution, time series shown in (h). i Phase portrait and j time series of TG for $d=0.226$, $s=0.363$, ${\dot{Z}}(t)=0.6799$, $\varphi =0.5209$. k Phase portrait of $G_{2:1}^{3:1}$, with inset zoomed to show ${\dot{Z}}_k=0$, with l time series for $d=0.174$, $s=0.28$ m, ${\dot{Z}}(t)=0.54359$, $\varphi =0.0966201$

4 Comparison to numerical simulations

Figures 7 and 8 show the analytically derived bifurcation diagrams and stability results, in terms of ${\dot{Z}}_k$ with d as the bifurcation parameter, compared to the bifurcation diagrams generated numerically via the continuation-type method discussed above for Fig. 3. Panel (a) of Figs. 7 and 8 shows sequences with a combination of transitions, as shown in Fig. 3a–c and listed in Table 1. The numerical results capture complementary behavior, such as the n:m/pT periodic solutions, as well as n:m/C behavior, TG, and higher-order grazing. The phase plane and time series of certain periodic solutions are shown, corresponding to critical points in the bifurcation diagram: n:m/pT periodic solutions and the $P\!D$, G, TG, ${\tilde{G}}$ and ${\widetilde{P\!D}}$ bifurcations for these solutions, labeled as in Table 1. Here we discuss the sequence of these critical points and transitions, as is consistent with Fig. 6. Below (Sects. 4.1 and 4.2) we compare and contrast the multiple routes to grazing and the implications of these critical points.

Fig. 8

a Bifurcation diagram for the relative impact velocity ${\dot{Z}}_k$ for $\beta = \pi /6$, $r=0.25$, $5.986<A<22.23$ N, $\omega = 5 \pi$ Hz, $s=0.5$ m. Lines and symbols as in Fig. 7. b Phase portrait, c time series of $G_{1:1}^{2:1}$ for $d=0.216567$ m, ${\dot{Z}}(t)=0.63741$, $\varphi =0.448723$, $A=7.186$. d Phase portrait for ${\widetilde{P\!D}}$ behavior for $d=0.194872$, ${\dot{Z}}(t)=0.603884$, $\varphi =0.376322$, $A=7.986$. Red curve shows unphysical trajectory that violates containment; blue curve shows stable 2:1 solution with time series shown in (e). f Phase portrait and g time series of 2:1/2T solution for $d=0.12484$, ${\dot{Z}}(t)=0.485267$, $\varphi =0.533536$, $A=12.466$. h and j Time series, i phase portrait of ghost ${\widetilde{G}}_{2:1}^{2:2}$ for $d=0.1132$, ${\dot{Z}}(t)=0.4722$, $\varphi =0.5473$, $A=13.7478$. Red curve shows unstable trajectory initial behavior of unstable 2:2 trajectory for one period with time series in (h); blue curve shows attracting solution, with alternating 2:1 and 2:2 over 2T with time series shown in (j)

As shown in Fig. 7a the $P\!D$ transition from 1:1 to 1:1/2T occurs for larger d than for ${\tilde{G}}_{1:1}^{2:1}$ ghost grazing. Figure 7b–e shows phase planes and time series for values of d just above and below the $P\!D$ transition. As d decreases we observe numerically the sequence of 1:1/2T followed by transient grazing (TG), characterized by irregular small impact velocities ${\dot{Z}}_k$ on $\partial B$, as shown in Fig. 7i, j. For smaller d, there is a stable 2:1 branch, born at a fold bifurcation ($F\!B$), as confirmed by the analytical results for unstable 2:1 (magenta dashed lines) and stable 2:1 (blue solid line) solutions that meet at $F\!B$. The ghost grazing value ${\tilde{G}}_{1:1}^{2:1}$ is not observed in the long time periodic behavior since this grazing point corresponds to the birth of the unstable subcritical branch of 2:1 solutions. This unstable behavior is illustrated in Panels (f)–(h): Panel (f) and the red curve in Panel (g) show the unstable 2:1 solution at ${\tilde{G}}_{1:1}^{2:1}$ for a short time. The blue lines in Panel (g) indicate the subsequent behavior in time, as the solution moves from the unstable 2:1 solution to the stable 2:1 solution. Panel (h) shows the time series for the stable 2:1 solution, to which the system relaxes after a brief transient. Figure 9a shows the eigenvalues for the two 2:1 solutions that exist for d between ${\tilde{G}}_{1:1}^{2:1}$ and FB. The unstable 2:1 solution has eigenvalues $\vert \lambda _i \vert >1$, while for the second stable 2:1 solution, both eigenvalues $\vert \lambda _i \vert <1$ for values of d between $F\!B$ and ${\widetilde{P\!D}}$.

Decreasing d below ${\tilde{G}}_{1:1}^{2:1}$ in Fig. 7a, the system follows the stable 2:1 solution, until it undergoes an additional grazing at $G_{2:1}^{3:1}$. Thus, even though the eigenvalues of the 2:1 solution $\vert \lambda _i \vert <1$ between $G_{2:1}^{3:1}$ and ${\widetilde{P\!D}}$ (see Fig. 9a), that solution is unphysical as it violates containment following grazing, analogous to Fig. 5. Figure 7a indicates that the resulting 3:1 solution is stable at $G_{2:1}^{3:1}$, with the fourth branch of this solution emerging from ${\dot{Z}}_k=0$ at this point. The stability of the 3:1 solution is also illustrated in the phase plane and time series in Panels (k) and (l).

In contrast to Fig. 7a, in which s decreases, there is a different sequence of $P\!D$ and G bifurcations (and other transitions) in Fig. 8a, in which A increases for decreasing d with slightly smaller r. Figures 8b, c illustrate ${G}_{1:1}^{2:1}$, which, as d decreases, is reached before $P\!D$. Then the ghost ${\widetilde{P\!D}}$ of the 1:1 solution occurs for smaller d and is not observed in the dynamics. At the grazing point ${G}_{1:1}^{2:1}$ there is an unstable 2:1 solution (magenta dashed line) that bifurcates subcritically from the 1:1 solution, and there is a $F\!B$ at which a stable 2:1 solution meets the unstable one. Corresponding to this subcritical bifurcation, the value of d for $F\!B$ is greater than that for ${G}_{1:1}^{2:1}$. For d below ${G}_{1:1}^{2:1}$ the 1:1 solution is unphysical (red trajectory in Panel (d)) and the solution moves to the stable 2:1 solution (blue trajectory in Panel (d), time series in (e)). Figure 9b shows the eigenvalues for the two 2:1 solutions that exist for d between ${G}_{1:1}^{2:1}$ and $F\!B$. The unstable branch of 2:1 solutions has an eigenvalue $\vert \lambda _i \vert >1$, while for the second branch both eigenvalues $\vert \lambda _i \vert <1$ for values of d between $F\!B$ and $P\!D$. Following $P\!D$ there is a loss of stability from 2:1 to 2:1/2T behavior, as shown in Panels (f)–(g). Consistent with Fig. 6 for smaller $\beta$, we observe ${\tilde{G}}_{2:1}^{2:2}$ in Fig. 8h–j, in contrast with $G_{2:1}^{3:1}$ (or ${\tilde{G}}_{2:1}^{3:1}$) solutions determined for larger $\beta$. Since $P\!D$ for 2:1 precedes the grazing for decreasing d, then the ghost grazing ${\tilde{G}}_{2:1}^{2:2}$ (red trajectory in Panel (i), with time series in (h)) is obtained theoretically, while the dynamics attract to a more complex alternating 2:1 and 2:2 solution with period 2T (blue trajectory in Panel (i), time series in Panel (j)).

Fig. 9

Graphs of eigenvalues $\vert \lambda _{1,2} \vert$ to confirm the (in)stability of the two different 2:1 solutions, with a corresponding to Fig. 7 and b corresponding to Fig. 8. Blue triangles and black circles correspond to the branch born at $F\!B$, stable for a range of d below $F\!B$, with $\vert \lambda _{1,2} \vert <1$ between $F\!B$ and $P\!D$ or ${\widetilde{P\!D}}$. Red stars and magenta crosses are for unstable 2:1 solutions indicated by the magenta dashed lines in Figs. 7, 8

4.1 Multiple routes to first-order transitions

Comparison of Figs. 7a and 8a illustrates four different mechanisms of first-order transitions that increase the number of impacts per forcing period by one, e.g., n:m/pT to $(n+1)$:m or n:$(m+1)$. Note that these transitions may occur via different types of transitions, not only by either $G_{n:m}^{(n+1):m}$ or $G_{n:m}^{n:(m+1)}$. These all involve grazing or ghost grazing bifurcations, and we list the different signature for each that is apparent in the bifurcation diagram. Some of these types of non-smooth bifurcations have been observed in other studies, and we highlight these connections as well.

• 1. The stable n:m solution experiences first-order grazing at $G_{n:m}^{n+1:m}$ or $G_{n:m}^{n:m+1}$, at which an additional impact with ${\dot{Z}}_k=0$ occurs. If this solution is stable, then an additional low velocity bifurcation branch, initiated at ${\dot{Z}}_k=0$, is also observed in the numerics, e.g., as in $G_{2:1}^{3:1}$ in Fig. 7a, k, and l.

• 2. In contrast to the previous item 1., it is also possible that an unstable $(n+1)$:m (or n:$(m+1)$) solution follows from the first-order grazing of a stable n:m solution, yielding ${G}_{n:m}^{n+1:m}$ or $G_{n:m}^{n:m+1}$. This type of grazing bifurcation has been called “invisible” grazing in the experimental context in [20], since the grazing was predicted analytically but not observable, presumably because of the instability. That case commonly yields a scenario where both a subcritical unstable bifurcating branch and a stable branch meet at a $F\!B$ point. Then there is a range of bi-stability of the n:m solution with the bifurcating $(n+1)$:m or n:$(m+1)$ solution, discussed further under Sect. 4.2. The $G_{1:1}^{2:1}$ transition shown in Fig. 8a–c illustrates this type of grazing transition.

• 3. A third type of grazing transition occurs in the more complex $P\!D_G$ transition, where $P\!D$ or a sequence of $P\!D$’s yield a n:m/pT solution. Examples are shown in Figs. 3b, c for transitions to 2:1 and 3:1 periodic solutions, respectively. By following the unstable n:m branch, we may reach a ghost grazing ${\tilde{G}}_{n:m}^{\nu :\mu }$, leading to an unstable branch of the $\nu$:$\mu$ solution. In Sect. 4.2, we describe the relationship between ghost grazing and $P\!D_G$ or TG, namely, that a transition via some type of grazing transition occurs generally at a value of d between the $P\!D$ transition to n:m/2T and ${\tilde{G}}_{n:m}^{\nu :\mu }$.

• 4. There may also be sequences of transient grazing TG that occur within n:m/C, that eventually disappear when a stable $(n+1)$:m or n:$(m+1)$ solution branch is available. Such a transition is shown in Fig. 7, where the $F\!B$, corresponding to the birth of a stable 2:1, quenches the 1:1/C behavior. A similar transition to a 2:1 solution following 1:1/C appears in Fig. 3c. Similar transitions were observed in [44], explaining some of the gaps in chaotic behavior for a model of gear dynamics. This model is similar to that of the impact pair, but it includes additional forcing frequencies that facilitate larger windows of chaos.

4.2 Implications for bi-stability, transient behavior, and complex dynamics

The analytical approach provides knowledge about the sequence of smooth bifurcations, e.g., $P\!D$ and $F\!B$, and non-smooth grazing bifurcations. While this analysis does not provide exact results for the more complex bifurcations, it nevertheless provides insight into the birth and death of these more complex dynamics. We highlight this insight in a few specific contexts.

Ghost grazing: As mentioned above in the context of different routes to grazing, in instances where there is $P\!D$ of the stable solution and ${\tilde{G}}$ of the unstable solution, typically $P\!D_G$ or TG leads to a transition from n:m to $(n+1)$:m or n:$(m+1)$ for values of d above ${\tilde{G}}$. The basis for this conclusion is illustrated in the phase planes where we observe that a trajectory for the n:m/pT solution is naturally closer to grazing than the n:m trajectory. This follows from the “loops” in the phase plane trajectories as shown in Figs. 5 and 7d. For example, in the map $P_2$ from $\partial B \rightarrow \partial T$, these loops correspond to intervals of increased Z as the bottom of the capsule approaches the ball. Since $P\!D$ leads to multiple loops in the phase plane trajectory, one of these loops on the n:m/2T solution must take values of Z(t) closer to d/2 ($\partial B$) than the values of Z(t) on the $P_2$ map for the n:m solution (compare Fig. 7b, d). Then, the resulting loops from n:m/pT or from n:m/C yield $P\!D_G$ or TG, respectively, at a larger value of d than for ghost grazing ${\tilde{G}}_{n:m}^{\nu :\mu }$ of n:m solutions. Thus being able to locate ghost grazing analytically provides a lower bound on the critical parameter value at which the n:m-type solution transitions to one with an additional impact per period. Figure 10 illustrates this for different parameter combinations as d decreases, e.g., $P\!D_G$ or TG transitions to 2:1 behavior occur at or before ${\tilde{G}}_{1:1}^{2:1}$, and transitions to 3:1 or 2:2 periodic solutions precede ${\tilde{G}}_{2:1}^{3:1}$ and ${\tilde{G}}_{2:1}^{2:2}$, respectively.

Fig. 10

a Combining Fig. 6a and c with numerically obtained transitions to 2:1 and 3:1 behavior for $\beta =\pi /3$; b Combining Fig. 6b and d with numerically obtained transitions to 2:1 and 3:1 behavior for $\beta =\pi /3$; c Combining Fig. 6b and d with numerically obtained transitions to 2:1, 3:1 and 2:2 behavior for $\beta =\pi /6$

Fold bifurcations and bi-stability: The analysis allows the calculation of both unstable and stable branches of n:m solutions, and with the corresponding stability analysis we can identify any $F\!B$ points. The location of $F\!B$ indicates the potential for either intermediate regions of TG or bi-stability between different periodic solutions.

Regions of bi-stability occur for grazing transitions to unstable (subcritical) solutions, as shown in Fig. 8a. A typical signature in a computationally or experimentally observed transition from n:m or n:m/pT to $(n+1)$:m is that the additional impact has nonzero impact velocity at the transition. This feature suggests an underlying grazing bifurcation to an unstable subcritical $(n+1)$:m, which in turn meets the stable $(n+1)$:m solution at $F\!B$. These transitions, in the context of bi-stability, may occur from G or from $P\!D_G$ as shown in Fig. 3a, b. An example of such a grazing point is given by ${G}_{1:1}^{2:1}$ in Fig. 8a. While the location of ${G}_{1:1}^{2:1}$ is a fixed value determined analytically, the transition between 1:1 and 2:1 solutions observed numerically may occur at a different value due to the bi-stability. For example, one could use the numerical continuation-type method to follow the stable 2:1 branch for increasing d starting below ${G}_{1:1}^{2:1}$. Then it is possible to follow this branch to $F\!B$ rather than reaching the 1:1 solution at ${G}_{1:1}^{2:1}$, as was observed for decreasing d. This hysteresis in the numerical results illustrates how the analytical results are necessary to provide the full picture, independent of increasing or decreasing d.

In contrast to the bi-stable case, TG tends to occur in the absence of bi-stability, i.e., when there is no overlap of stable n:m/pT and $(n+1)$:m/pT behavior. Then grazing may follow the sequence of $P\!D$’s leading to n:m/C, so that the grazing occurs intermittently on a complex trajectory, without a sustained first-order grazing transition. The contrast can be seen by comparing transitions from 1:1/pT to 2:1 behavior in Fig. 3b and from 1:1/C to 2:1 in Fig. 3c, as well as transitions from 1:1/C to 2:1 in Fig. 7 and from 1:1 to 2:1 in Fig. 8. Larger ranges of bi-stability are prevalent for certain combinations of larger r and $\beta$, with other factors such as increasing A also playing a role. These aspects have been observed in other studies [58, 62], but we do not explore them here.

Ghost period doubling: For smaller r, we observe ranges of $\beta$ in Fig. 6 where ${\widetilde{P\!D}}$ of the n:m solutions occur well below $G_{n:m}^{\nu :\mu }$, possibly with $P\!D$ following $G_{n:m}^{\nu :\mu }$ yielding $\nu$:$\mu$/pT. In this setting ${\widetilde{P\!D}}$ of n:m does not influence the $\nu$:$\mu$ behavior, since the n:m and $\nu$:$\mu$ are different periodic solutions with different dynamics. This separation follows from the dynamical route to grazing, where the bifurcation is induced purely by the discontinuity of impact rather than by eigenvalues or other smooth parametric variation.

The mechanism of a ${\widetilde{P\!D}}$, as an unphysical solution, suggests changes in the device design to avoid (or facilitate) G occurring before the ${\widetilde{P\!D}}$. This is particularly relevant for parameter ranges where the ${\widetilde{P\!D}}$ and $G_{n:m}^{\nu :\mu }$ are in close proximity to each other, near the intersection of different colored curves as shown in Fig. 6. Increased r or $\beta$ near these intersections could yield a $P\!D$ rather than ${\widetilde{P\!D}}$, which may or may not be desirable. In cases where ${\widetilde{P\!D}}$ and $G_{n:m}^{\nu :\mu }$ (nearly) coincide, there may be complex transients or chaotic behavior. For example, in Fig. 10c, where the $P\!D$ of the 2:1 solution and $G_{2:1}^{2:2}$ occur in close proximity, there are complex higher- order grazing transitions for small windows of r near these bifurcations. Figure 6 shows that the proximity of $P\!D$ and G depends on how d changes with its underlying dimensional quantities (s and A), indicating multiple scenarios where small variation in these parameters can advance $P\!D$ ahead of the $G_{n:m}^{\nu :\mu }$.

Figure 10 combines the analytical results from Fig. 6 together with numerically obtained transitions. As described above, we see that $P\!D_G$ and TG transitions are bounded below by the analytically determined ghost grazing ${\tilde{G}}$. These transitions do not necessarily depend on r continuously, as seen for the $P\!D_G/\textit{TG}$ transitions to 2:1 solutions in Panels (b) and (c). Recall that for larger $\beta$ and r with decreasing A, there are two separate ranges of d with stable 1:1 solutions, as discussed for Fig. 3d. In these cases there is a larger range of d over which 1:1, 1:1/pT, or 1:1/C solutions are sustained, so that the $P\!D_G$ or TG transition to 2:1 behavior is shifted to smaller values of d as discussed in the contexts of Figs. 3 and 6. Similarly, in Fig. 10c there is a range of d below the $P\!D$ of the 1:1 curve for which 1:1/pT and 2:1 solutions are bi-stable. In the figures we give the $P\!D_G/\textit{TG}$ curve for decreasing d, indicating quenching of 1:1/pT or 1:1/C in this setting. Furthermore in Panel (c) for larger r, fluctuations in the $P\!D_G$ transition to 2:2 correspond to some narrow windows of bi-stable 3:1 transitions, apparent with slight variation in initial conditions but not shown in these figures. As discussed above, here we focus on the case of decreasing d, but in the case of bi-stability, the numerically obtained transitions may shift for increasing d due to hysteresis. Other influences of complexity appear in Fig. 10a, where larger r and $\beta$ contribute to fluctuations in transitions to 3:1 from 2:1/pT via $P\!D_G$ or from 2:1/C following TG, indicating dependence on initial conditions and numerical sensitivities in the simulations. Additional irregularities appear in Panel (c), near the transition from $G_{2:1}^{3:1}$ to $P\!D$ of 2:1 and $P\!D_G$ to 2:2 values (near $r= .2$). These follow from the coincidence of $P\!D$ of the 2:1 solution and $G_{2:1}^{2:2}$, discussed above in the context of ${\widetilde{P\!D}}$. Indeed, a closer examination of the solution near this transition indicates a narrow region that takes values very close to that of 3:1 behavior, but in fact is of the form of alternating 3:1 and 2:1 behavior over a 2T period.

4.3 Implications for the VI-EH device

The $P\!D$, $G_{n:m}^{\nu :\mu }$, $P\!D_G$ and TG transitions all have implications for energy output in the VI-EH device. In general, we see that any function dependent on the relative impact velocity ${\dot{Z}}_k$ is influenced by these transitions, e.g., any type of energy measure that is dependent on ${\dot{Z}}_k$, as shown in A. Each of these types of grazing bifurcations yields abrupt changes in ${\dot{Z}}_k$ directly, as well as changes in the underlying dynamics. In addition, the stability or complexity properties of these solutions influence the robustness of the behavior.

Figures 7a and 8a give the bifurcations of ${\dot{Z}}_k$ in terms of d in two different settings: for decreasing s, and increasing A. We emphasize that this is not just a matter of d increasing with s or decreasing with A, but rather the locations of the bifurcations are different in these two cases; this follows from the fact that increasing A not only reduces d, but also reduces the influence of gravity, as evidenced from the non-dimensional gravity term $\bar{g}$ in (5). Likewise the energy output has different sequences in the two different scenarios, following from the different bifurcations which indicate critical parameters at which the energy output may change abruptly.

Fig. 11

Numerically obtained output voltage $U_{k}$ (black circles), average value of output voltage per impact ${\overline{U}}_I$ (red circles) and per time ${\overline{U}}_T$ (magenta stars). Solid (dotted) lines correspond to stable (unstable/unphysical) analytical results for $U_{k}$ from 1:1 and 2:1 periodic solutions, with blue (green) indicating $U_{k}$ from impact on $\partial B$ ($\partial T$). The results based on ${\dot{Z}}(t_k)$ in a Fig. 7a for $\beta =\pi /6$, $r=0.3$, $0.223<s<0.4$ m, $A=5$ N, s decreasing; b Fig. 8a for $\beta = \pi /6$, $r=0.25$, $5.986<A<22.23$ N, $s=0.5$ m

Figure 11 shows the energy output corresponding to the bifurcations in Figs. 7a and 8a in terms of the average output voltages per impact ${\overline{U}}_I$ and per time interval ${\overline{U}}_T$, both of which exhibit abrupt changes at parameter values corresponding to different grazing transitions. These changes follow directly from the definitions of ${\overline{U}}_I$ and ${\overline{U}}_T$ in (9), since via each grazing transition, an additional low velocity impact is added per forcing period. In the transitions from n:m to $(n+1)$:m or n:$(m+1)$ behavior, typically the impact velocity for the additional impact decreases with n, m, leading to larger drops in ${\overline{U}}_I$, while the ${\overline{U}}_T$ increases with successively smaller jumps. In contrast, following the $P\!D$ of the 1:1 solution shown in Fig. 7a, the corresponding ${\overline{U}}_I$ and ${\overline{U}}_T$ shown in Fig. 11a change gradually for successive $P\!D$ solutions, since the branches for ${\dot{Z}}_k$ of the 1:1/pT solutions are changing gradually. Likewise for a sequence of $P\!D$ leading to complex behavior, as in Fig. 8a for small $d<0.12$, there is a gradual drop in ${\overline{U}}_I$ for complex behavior that includes several impacts with small ${\dot{Z}}_k$. Then there is a discontinuous decrease in ${\overline{U}}_I$, shown numerically in Fig. 11b, following the subsequent higher- order grazing transitions to 3:2, 4:2, and eventually n:m behavior with large n with frequent ${\dot{Z}}_k$ near zero.

Figure 12 compares the influence of the different types of bifurcations on the energy output, for smaller and larger values of r. Figure 6 indicates that the sequence of bifurcations in terms of d can be completely different for smaller or larger r. These differences influence the sequence of energy output. For decreasing s shown in Fig. 12a, for smaller r the transitions $G_{n:m}^{n+1:m}$ occur for larger values of d in contrast to larger r. The grazing via $P\!D_G$ or TG are postponed to smaller d for larger r, yielding larger ranges of d for which ${\overline{U}}_I$ (${\overline{U}}_T$) takes larger (smaller) values for decreasing s. For increasing A, shown in Fig. 12b this ordering is different, as follows from the relative positions of G, $P\!D$, and $P\!D_G$ transitions shown in Figs. 6 and 10. The $G_{1:1}^{2:1}$ transition for smaller r occurs for smaller d than the $P\!D_G$ transition from 1:1/pT to 2:1 for larger r, while the $P\!D_G$ transition to 2:2 behavior for smaller r occurs for larger d than for the $P\!D_G$ with larger r. Furthermore, increasing A (smaller d) drives sequences of $P\!D$ and more complex solutions, particularly for larger r. As shown in Fig. 12b for smaller d, ${\overline{U}}_I$ increases for complex solutions where larger r expands the range of ${\dot{Z}}_k$, while for smaller r these complex solutions add more frequent ${\dot{Z}}_k$ near 0, so that ${\overline{U}}_I$ decreases.

While the differences in ${\overline{U}}_{I}$ and ${\overline{U}}_T$ follow naturally in regions where different values of r yield different n:m/pT solutions for the same value of d, it may seem counterintuitive that the energy output for the different values of r is comparable for the same type of n:m behavior, or in some cases larger for smaller r. This observation, apparent in ${\overline{U}}_T$ in Fig. 12a and in both ${\overline{U}}_T$ and ${\overline{U}}_I$ in Fig. 12b, follows directly from the phase differences $\phi _k$ of impacts, relative to minima of the capsule trajectory, as shown in Fig. 2b. Impacts that occur away from the minima, where the capsule and ball move in opposite directions, generate larger ${\dot{Z}}_k$. In contrast, for impacts that occur closer to these minima, with smaller differences in the capsule and ball velocities, the relative impact velocities ${\dot{Z}}_k$ are smaller. Typically larger r favors solutions where the impact is near the minima of the capsule trajectory, thus yielding reduced energy output.

Fig. 12

Average value of output voltage per impact ${\overline{U}}_I$ and over time ${\overline{U}}_T$ with $\beta =\pi /6$, and $0.1<d<0.28$, for two cases: a $A = 5$ N, $0.16<s<0.45$ m; b $5.56<A<15.56$, $s=0.5$ m

We recall the analytical results for $P\!D$, $G_{1:1}^{2:1}$ and $G_{2:1}^{3:1}$ from Fig. 6 highlighting their connection to the influence of device features, such as its length s, the angle $\beta$ and the restitution coefficient r. Since in a real application the excitation amplitude is given, the device and its energy performance should be designed using the three parameters mentioned above. Obviously the 1:1 response is the most beneficial EH option, thus where possible, the device should be designed to sustain this response under a given excitation. Small values of the angle $\beta$ reduce the asymmetry of the device, thereby expanding the range of a 1:1 response in a shorter device. The value of the restitution coefficient, which can be controlled by the thickness of the DE membranes, can also influence the device performance. This may be especially helpful when the transition to 2:1 motion is inevitable, as demonstrated in Fig. 12.

For larger values of $\beta$ with s (and thus d) decreasing, the $P\!D$ transition from 1:1 to 1:1/2T is observed, with transitions to 2:1 behavior via $P\!D_G$ or TG occurring for s above that for ghost grazing ${\tilde{G}}_{1:1}^{2:1}$, as shown in Fig. 10a. Comparing with Fig. 6a, as $\beta$ decreases, the value of $d_{P\!D}$ decreases until it is below $d_G$ given by $G_{1:1}^{2:1}$ for a range of r. This trade-off between the variation of $\beta$, s and r is then captured by the intersection of the analytically provided curves for $d_{P\!D}$ and $d_{G}$, indicating parameter combinations that limit the potential for different types of grazing transitions that yield additional impacts per forcing period.

5 Conclusions

A combined analysis of smooth and non-smooth bifurcations provides new insight into the interplay of smooth and non-smooth bifurcations. The novel approach is developed in the context of a canonical model of an impact pair, a forced capsule in which a ball moves freely between impacts on either end of the capsule. The results provide a systematic approach to study the interplay of different qualitative transitions in TDOF systems, which have received limited attention as compared with SDOF systems.

The integrated analytical approach provides sequences of bifurcations on stable branches as well as complementary ghost bifurcations on unstable or unphysical branches. The foundation of the results is an analytical characterization of impacting solutions and their stability based on the maps between impacts. In the language of non-smooth dynamics, we use compositions of maps based on the smooth dynamics between intersections with switching manifolds. This foundation provides two different bifurcation analyses, one traditionally based on eigenvalues as is used widely for smooth bifurcations, and a second based on the geometry of the intersection of trajectories with the impacting surface, yielding grazing for zero-velocity impacts. Combining these two approaches, we obtain sequences of period doubling and fold bifurcations together with grazing bifurcations, the type of non-smooth bifurcation naturally occurring in impacting systems. With this analytical basis, we are also able to identify ghost bifurcations for both smooth and non-smooth bifurcations which can occur on unstable or unphysical solutions.

Even though they cannot be observed numerically or experimentally, ghost bifurcations influence the birth or quenching of complex behaviors and additional grazing transitions. For example, the ghost grazing bifurcation provides a lower bound on a variety of transitions in which an additional impact is added per forcing period. Tracking stable and unstable—sometimes termed “invisible”—branches allows the identification of fold bifurcations, which are critical mechanisms in multiple types of grazing transitions. The proximity of ghost period doubling bifurcations to grazing bifurcations can yield different transition scenarios with complex quasi-periodic behavior, where a small variation in the parameters can replace the grazing with period doubling in the observed dynamics. Transient grazing, which can occur following sequences of period doubling that culminate in chaotic windows, can eventually lead to a quenching of the complex behavior when it reaches a branch from a grazing bifurcation, typically at a fold point. All of these influences, indicated by the analytical results, are confirmed by comparisons with numerical results.

While the analysis is developed with broader TDOF systems in mind, we demonstrate that it is also relevant for applications. It is applied to a model of inclined vibro-impact energy harvesting (VI-EH) device, where the energy is generated by the variable capacitance principle via impacts of the ball with a dielectric polymer on the capsule ends. The desire for new sustainable and renewable power technologies as alternatives to conventional batteries has generated strong interest in energy harvesting, usually characterized by energy scavenging from vibrations occurring in manmade machines and structures. As is typical for an energy harvesting system, the VI-EH system considered here includes both a mechanical system to absorb the energy of vibrations, and a transduction mechanism to convert it to electrical energy. The saturation of ideas in the linear theory of energy harvesting, i.e., using linear mechanical and electrical systems, has shifted the focus of scientists to nonlinear systems, exploiting their relatively broad bandwidth that allows efficient energy absorption over a wide range of the excitation frequency. VI systems, as a class of strongly nonlinear system, can provide this preferred wide bandwidth once the mass is engaged in the vibro-impact regime.

Table 2 The output voltage calculation of the VI-EH device through the membrane deformation upon impact from [51]

The competition between the different bifurcations and their ghosts influences the parameter ranges for favorable energy output of the VI-EH. The analyses of the bifurcation sequences provide their parametric dependencies, indicating the types of transitions that are more likely for given parameter combinations. For small restitution coefficients r and small inclined angle $\beta$, first- order grazing bifurcations dominate the lower-order transitions, i.e., with a small number of impacts per forcing period being increased by one with a small relative impact velocity. Then we observe jumps in the energy output, increasing for output averaged over time, and decreasing for output averaged per impact. In contrast, for larger values of r and $\beta$, sequences of period doubling bifurcations are more prevalent, which can result in aperiodic or chaotic dynamics. In that case the change in energy output is more gradual during these sequences, but there are still opportunities for complex grazing-type transitions which can generate additional impacts per period with small relative impact velocities. Then the ghost grazing bifurcation gives a lower bound on these transitions, grazing period doubled solutions $P\!D_G$ and transient grazing TG, at which there are abrupt changes in energy output. These transitions are often affiliated with fold bifurcations, near which there is the potential for bi-stability of behaviors with different energy outputs. By capturing the different sequences of various types of bifurcations, the analysis provides direction on how to avoid undesirable behavior that may occur via grazing or period doubling.

In addition to the valuable insights provided by this analysis, it also indicates several areas of future study that are needed, related to bi-stability, global stability analyses, and aperiodic behavior. Furthermore, given the important role of the restitution coefficient, the results point to the need for more realistic models that take into account interactions of the ball with the membrane.

Appendix A

In the following Table 2, we present the details of calculating harvested energy versus impact velocity.