Dynamics of a weakly nonlinear string on an elastic foundation with a partly prescribed discrete spectrum

Abstract

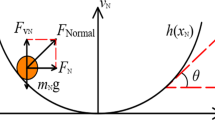
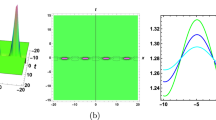
In this paper the dynamics of a weakly nonlinear elastic string on a Winkler elastic foundation is studied. The foundation may be spatially heterogeneous. At one end of the string a mass-spring system is attached, and the other end of the string is fixed. The string is assumed to be long, and the lower part of the spectrum of the string is prescribed. It is shown that localized modes exist and that the dynamics of the string for large times is determined by these localized modes. The frequencies of these localized modes can be controlled by special choices for the spatial heterogeneities in the elastic foundation. Analytical and numerical results are presented to illustrate the findings.

Appendix

In this “Appendix”, we derive formula (38). Let us consider first the case $W(x,x_0) =0$. Then the solution of the spectral problem (15) has the form $\psi _k=A \sin (kx) + B \cos (kx),$ where the boundary conditions (13) imply that

$$\begin{aligned} A \sin kL + B\cos kL&=0, \end{aligned}$$

(75)

$$\begin{aligned} (K-\lambda _k M) B&=b_0 k A \end{aligned}$$

(76)

and $\lambda _k=a^2 - c^2 k^2$. This system reduces to the following equation for the unknown wave number k:

$$\begin{aligned} \tan (kL)= \frac{ b_0 k}{K + M c^2 k^2 - M a^2}. \end{aligned}$$

To find an asymptotical solution k for this equation for large L, we introduce the variable $z=kL$. Then, one obtains

$$\begin{aligned} \tan z = \frac{ b_0 z}{L(\mu + M c^2 (z/L)^2}, \quad \mu =K- Ma^2. \end{aligned}$$

For large L one has $z=n \pi + O(L^{-1})$, where n are non-negative integers. This relation gives us (38) for $W=0$. To estimate the effect of the localized perturbations to $\lambda _k$ and $\omega _k$, we apply the standard perturbation theory. The perturbation $\tilde{\lambda }$ of $\lambda$ is

$$\begin{aligned} \tilde{\lambda }= \frac{ \int _0^{L} W(x,x_0) \psi _k(x) ^2 \mathrm{{d}}x }{ \int _0^{L} \psi _k(x) ^2 \mathrm{{d}}x}. \end{aligned}$$

For large L the denominator of this fraction is of order L, while the numerator has the order 1 (because W is not zero on part of the interval). Therefore, we conclude that $\tilde{\lambda }=O(L^{-1})$, which finally proves (38).

For a localized mode at $x=0$ (induced by the oscillator) one can show, by an analogous estimate, that $\tilde{\lambda }=O(\exp (-c L))$, where $c>0$ is a constant.