Skip to main content
SpringerLink
Log in

On the periodic orbits around the collinear libration points in the SCR4BP with non-spherical primaries

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

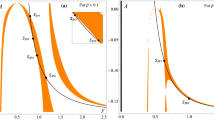
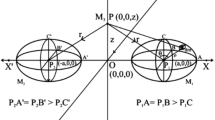
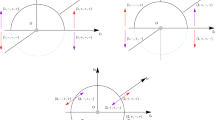
In this paper, we have drawn the periodic orbits in the restricted four-body problem. The fourth body of infinitesimal mass moves under the Newtonian gravitational law due to three mass points (known as primaries) in the collinear Euler’s configuration. We have studied the dynamics of the fourth body in the spatial collinear restricted four-body problem (SCR4BP) with non-spherical primaries. We have determined the periodic orbits by using the Fourier series method only around collinear libration points in SCR4BP with non-spherical primaries. The effects of the orbital parameter \(\varepsilon \) (\(0<\varepsilon <1\)), which controls the size of the orbit, on the periodic orbits and their period are investigated. In order to study the effect of this parameter, we have retained the terms up to third order with respect to the orbital dimensions. We have also drawn the variational graphs to determine the variation in the time period T of the periodic orbits. Moreover, we have unveiled that how oblateness and mass parameters influence the shape, size, and period of the periodic orbits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data availability

All the incorporated data that support the findings of this study are available in the article and in its supplementary material files.

References

  1. Alvarez-Ramírez, M., Barrabés, E., Medina, M., Ollé, M.: Ejection–collision orbits in the symmetric collinear four-body problem. Commun. Nonlinear Sci. Numer. Simul. 71, 82–100 (2019). https://doi.org/10.1016/j.cnsns.2018.10.026

    Article  MathSciNet  MATH  Google Scholar 

  2. Arribas, M., Abad, A., Elipe, A., Palacios, M.: Equilibria of the symmetric collinear restricted four-body problem with radiation pressure. Astrophys. Space Sci. 361, 84 (2016). https://doi.org/10.1007/s10509-016-2671-x

    Article  MathSciNet  Google Scholar 

  3. Baltagiannis, A.N., Papadakis, K.E.: Equilibrium points and their stability in the restricted four-body problem. Int. J. Bifurc. Chaos 21, 2179–2193 (2011). https://doi.org/10.1142/S0218127411029707

    Article  MathSciNet  MATH  Google Scholar 

  4. Baltagiannis, A.N., Papadakis, K.E.: Families of periodic orbits in the restricted four-body problem. Astrophys. Space Sci. 336, 357–367 (2011). https://doi.org/10.1007/s10509-011-0778-7

    Article  MATH  Google Scholar 

  5. Baltagiannis, A.N., Papadakis, K.E.: Periodic solutions in the Sun–Jupiter–Trojan Asteroid–Spacecraft system. Planet. Space Sci. 75, 148–157 (2013). https://doi.org/10.1016/j.pss.2012.11.006

    Article  Google Scholar 

  6. Bhatnagar, K.B., Chawla, J.M.: The effect of oblateness of the bigger primary on collinear libration points in the restricted problem of three bodies. Celest. Mech. 16, 129–136 (1977)

    Article  MATH  Google Scholar 

  7. Brown, E.W.: On the oscillating orbits about the triangular equilibrium points in the problem of three bodies. Mon. Not. R. Astron. Soc. 71, 492–502 (1911)

    Article  MATH  Google Scholar 

  8. Burgos-García, J., Delgado, J.: Periodic orbits in the restricted four-body problem with two equal masses. Astrophys. Space Sci. 345, 247–263 (2013). https://doi.org/10.1007/s10509-012-1118-2

    Article  MATH  Google Scholar 

  9. Burgos-García, J.: Families of periodic orbits in the planar Hill’s four-body problem. Astrophys. Space Sci. 361, 353 (2016). https://doi.org/10.1007/s10509-016-2943-5

    Article  MathSciNet  Google Scholar 

  10. Burgos-García, J., Lessard, Jean-P., Mireles James, J.D.: Spatial periodic orbits in the equilateral circular restricted four-body problem: computer-assisted proofs of existence. Celest. Mech. Dyn. Astron. 131, 2 (2019). https://doi.org/10.1007/s10569-018-9879-8

    Article  MathSciNet  MATH  Google Scholar 

  11. Elipe, A.: On the restricted three-body problem with generalized forces. Astrophys. Space Sci. 188, 257–269 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  12. Elipe, A., Ferrer, S.: On the equilibrium solutions in the circular planar restricted three rigid bodies problem. Celest. Mech. 37(1), 59–70 (1985). https://doi.org/10.1007/BF01230341

    Article  Google Scholar 

  13. Elipe, A., Lara, M.: Periodic orbits in the restricted three body problem with radiation pressure. Celest. Mech. Dyn. Astron. 68, 1–11 (1997). https://doi.org/10.1023/A:1008233828923

    Article  MathSciNet  MATH  Google Scholar 

  14. Elipe, A., Abad, A., Arribas, M., Ferreira, A.F.S., de Moraes, R.V.: Symmetric periodic orbits in the dipole-segment problem for two equal masses. Astron. J. 161, 274 (2021). https://doi.org/10.3847/1538-3881/abf353

    Article  Google Scholar 

  15. Farquhar, R.W.: The control and use of libration-point satellites. Ph.D. thesis, Stanford University, Stanford, California (1968)

  16. Giacaglia, G.E.O.: Regularization of the restricted problem of four bodies. Astron. J. 69, 165 (1967). https://doi.org/10.1086/110291

    Article  MathSciNet  Google Scholar 

  17. Hénon, M.: Families of periodic orbits in the three-body problem. Celest. Mech. 10, 375–388 (1974)

    Article  MATH  Google Scholar 

  18. Kalvouridis, T., Arribas, M., Elipe, A.: Parametric evolution of periodic orbits in the restricted four-body problem with radiation pressure. Planet. Space Sci. 55(4), 475–493 (2007). https://doi.org/10.1016/j.pss.2006.07.005

    Article  Google Scholar 

  19. Llibre, J., Saeed, T., Zotos, E.E.: Periodic orbits and equilibria for a seventh-order generalized Hénon–Heiles Hamiltonian system. J. Geom. Phys. 167, 104290 (2021). https://doi.org/10.1016/j.geomphys.2021.104290

    Article  MATH  Google Scholar 

  20. Llibre, J., Paşca, D., Valls, C.: The circular restricted four-body problem with three equal primaries in the collinear central configuration of the three-body problem. Celest. Mech. Dyn. Astron. 133, 53 (2021). https://doi.org/10.1007/s10569-021-10052-6

    Article  MATH  Google Scholar 

  21. Majorana, A.: On a four-body problem. Celest. Mech. 25, 267–270 (1981). https://doi.org/10.1007/BF01228963

    Article  MATH  Google Scholar 

  22. Michalodimitrakis, M.: The circular restricted four-body problem. Astrophys. Space Sci. 75, 289–305 (1981). https://doi.org/10.1007/BF00648643

    Article  Google Scholar 

  23. Mittal, A., Ahmad, I., Bhatnagar, K.B.: Periodic orbits in the photogravitational restricted problem with the smaller primary an oblate body. Astrophys. Space Sci. 323, 65–73 (2009). https://doi.org/10.1007/s10509-009-0038-2

    Article  MATH  Google Scholar 

  24. Palacios, M., Arribas, M., Abad, A., Elipe, A.: Symmetric periodic orbits in the Moulton–Copenhagen problem. Celest. Mech. Dyn. Astron. 131, 16 (2019). https://doi.org/10.1007/s10569-019-9893-5

    Article  MathSciNet  MATH  Google Scholar 

  25. Papadakis, K.E.: Families of periodic orbits in the photogravitational three-body problem. Astrophys. Space Sci. 245, 1–13 (1996). https://doi.org/10.1007/BF00637799

    Article  MATH  Google Scholar 

  26. Papadakis, K.E.: Homoclinic and heteroclinic orbits in the photogravitational restricted three-body problem. Astrophys. Space Sci. 302, 67–82 (2006). https://doi.org/10.1007/s10509-005-9007-6

    Article  MATH  Google Scholar 

  27. Papadakis, K.E.: Asymptotic orbits in the restricted four-body problem. Planet. Space Sci. 55, 1368–1379 (2007). https://doi.org/10.1016/j.pss.2007.02.005

    Article  Google Scholar 

  28. Papadakis, K.E., Ragos, O., Litzerinos, C.: Asymmetric periodic orbits in the photogravitational Copenhagen problem. J. Comput. Appl. Math. 227(1), 102–114 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  29. Papadakis, K.E.: Families of three-dimensional periodic solutions in the circular restricted four-body problem. Astrophys. Space Sci. 361, 129 (2016). https://doi.org/10.1007/s10509-016-2713-4

    Article  MathSciNet  Google Scholar 

  30. Papadouris, J.P., Papadakis, K.E.: Periodic solutions in the photogravitational restricted four-body problem. Mon. Not. R. Astron. Soc. 442, 1628–1639 (2014). https://doi.org/10.1093/mnras/stu981

    Article  Google Scholar 

  31. Pedersen, P.: On the periodic orbits in the neighbourhood of the triangular equilibrium points in the restricted problem of three bodies. Mon. Not. R. Astron. Soc. 94, 167–184 (1933). https://doi.org/10.1093/mnras/94.2.167

    Article  MATH  Google Scholar 

  32. Pedersen, P.: Fourier series for the periodic orbits around the triangular libration points. Mon. Not. R. Astron. Soc. 95, 482–495 (1935)

  33. Qian, Y.J., Liu, Y., Zhang, W., Yang, X.D., Yao, M.H.: Stationkeeping strategy for quasi-periodic orbit around Earth–Moon \(L_2\) point. J. Aerosp. Eng. 230(4), 760–775 (2016). https://doi.org/10.1177/0954410015597257

    Article  Google Scholar 

  34. Qian, Y.J., Zhang, W., Yang, X.D., Yao, M.H.: Energy analysis and trajectory design for low-energy escaping orbit in Earth–Moon system. Nonlinear Dyn. 85(1), 463–478 (2016). https://doi.org/10.1007/s11071-016-2699-z

    Article  MathSciNet  Google Scholar 

  35. Qian, Y.J., Yang, X.D., Zhang, W., Zhai, G.Q.: Periodic motion analysis around the libration points by polynomial expansion method in planar circular restricted three-body problem. Nonlinear Dyn. 91, 39–54 (2018). https://doi.org/10.1007/s11071-017-3818-1

    Article  Google Scholar 

  36. Rabe, E.: Determination and survey of periodic trojan orbits in the restricted problem of three bodies. Astron. J. 66, 500 (1961). https://doi.org/10.1086/108451

    Article  MathSciNet  Google Scholar 

  37. Rabe, E., Schanzle, A.: Periodic librations about the triangular solutions of the restricted Earth–Moon problem and their orbital stabilities. Astron. J. 67, 10 (1962). https://doi.org/10.1086/108802

    Article  Google Scholar 

  38. Roy, A.E.: Orbital Motion. Adam Hilger Ltd., Bristol (1982)

    MATH  Google Scholar 

  39. Schuerman, D.W.: The restricted three-body problem including radiation pressure. Astrophys. J. 238, 337–342 (1980)

    Article  MathSciNet  Google Scholar 

  40. Simmons, J.F.L., McDonald, A.J.C., Brown, J.C.: The restricted 3-body problem with radiation pressure. Celest. Mech. 35, 145–187 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  41. Strömgren, E.: Connaissance actuelle des orbites dans le problme des trois. corps. Bull. Astron 9, 87–130 (1933)

    MATH  Google Scholar 

  42. Suraj, M.S., Aggarwal, R., Mittal, A., Meena, O.P., Asique, M.C.: On the spatial collinear restricted four-body problem with non-spherical primaries. Chaos Solitons Fractals 133, 109609 (2020). https://doi.org/10.1016/j.chaos.2020.109609

    Article  MathSciNet  MATH  Google Scholar 

  43. Verrier, P.E., McInnes, C.R.: Periodic orbits for three and four co-orbital bodies. Mon. Not. R. Astron. Soc. 442, 3179–3191 (2014). https://doi.org/10.1093/mnras/stu1056

    Article  Google Scholar 

  44. Zhou, Y., Zhang, W.: Analysis on nonlinear dynamics of two first-order resonances in a three-body system. Eur. Phys. J. Spec. Top. 231, 2289–2306 (2022). https://doi.org/10.1140/epjs/s11734-022-00428-6

    Article  Google Scholar 

  45. Zotos, E.E.: Classifying orbits in the restricted three-body problem. Nonlinear Dyn. 82, 1233 (2015). https://doi.org/10.1007/s11071-015-2229-4

    Article  MathSciNet  MATH  Google Scholar 

  46. Zotos, E.E.: Revealing the escape mechanism of three-dimensional orbits in a tidally limited star cluster. Mon. Not. R. Astron. Soc. 446, 770–792 (2015). https://doi.org/10.1093/mnras/stu2129

    Article  Google Scholar 

  47. Zotos, E.E.: Comparing the escape dynamics in tidally limited star cluster models. Mon. Not. R. Astron. Soc. 452(1), 193–209 (2015). https://doi.org/10.1093/mnras/stv1307

    Article  MathSciNet  Google Scholar 

  48. Zotos, E.E.: Crash test for the Copenhagen problem with oblateness. Celest. Mech. Dyn. Astron. 122, 75–99 (2015). https://doi.org/10.1007/s10569-015-9611-x

  49. Zotos, E.E.: How does the oblateness coefficient influence the nature of orbits in the restricted three-body problem? Astrophys. Space Sci. 358, 33 (2015). https://doi.org/10.1007/s10509-015-2435-z

    Article  Google Scholar 

  50. Zotos, E.E.: Orbital dynamics in the planar Saturn-Titan system. Astrophys. Space Sci. 358(1), 1–12 (2015). https://doi.org/10.1007/s10509-015-2403-7

  51. Zotos, E.E., Dubeibe, F.L., González, G.A.: Orbit classification in an equal-mass non-spinning binary black hole pseudo-Newtonian system. Mon. Not. R. Astron. Soc. 477(4), 5388–5405 (2018). https://doi.org/10.1093/mnras/sty946

    Article  Google Scholar 

  52. Zotos, E.E., Jung, C.: Orbital and escape dynamics in barred galaxies-III. The 3D system: correlations between the basins of escape and the NHIMs. Mon. Not. R. Astron. Soc. 473(1), 806–825 (2018). https://doi.org/10.1093/mnras/stx2398

  53. Zotos, E.E., Nagler, J.: On the classification of orbits in the three-dimensional Copenhagen problem with oblate primaries. Int. J. Non-Linear Mech. 108, 55–71 (2019). https://doi.org/10.1016/j.ijnonlinmec.2018.10.009

  54. Zotos, E.E., Jung, C., Papadakis, K.E.: Families of periodic orbits in a double-barred galaxy model. Commun. Nonlinear Sci. Numer. Simul. 89, 105283 (2020). https://doi.org/10.1016/j.cnsns.2020.105283

    Article  MathSciNet  MATH  Google Scholar 

  55. Zotos, E.E., Erdi, B., Saeed, T., Alhodaly, M.S.: Orbit classification in exoplanetary systems. Astron. Astrophys. 634, A60 (2020). https://doi.org/10.1051/0004-6361/201937224

    Article  Google Scholar 

  56. Zotos, E.E., Erdi, B., Saeed, T.: Classification of orbits in three-dimensional exoplanetary systems. Astron. Astrophys. 645, A128 (2021). https://doi.org/10.1051/0004-6361/202039690

    Article  Google Scholar 

  57. Zotos, E.E., Papadakis, K.E., Wageh, T.: Mapping exomoon trajectories around Earth-like exoplanets. Mon. Not. R. Astron. Soc. 502, 5292–5301 (2021). https://doi.org/10.1093/mnras/stab421

    Article  Google Scholar 

Download references

Acknowledgements

Authors are thankful to the two anonymous reviewers, whose comments and suggestions are very useful in improving the manuscript.

Funding

The authors state that they have not received any funding.

Author information

Authors and Affiliations

  1. Department of Mathematics, Sri Aurobindo College, University of Delhi, New Delhi, Delhi, 110017, India

    Md Sanam Suraj

  2. Department of Mathematics, Hansraj College, University of Delhi, Delhi, 110007, India

    Om Prakash Meena

  3. Department of Mathematics, Deshbandhu College, University of Delhi, New Delhi, Delhi, 110019, India

    Rajiv Aggarwal

  4. Department of Mathematics, ARSD College, University of Delhi, New Delhi, Delhi, 110021, India

    Amit Mittal

  5. Department of Physics, Deshbandhu College, University of Delhi, New Delhi, Delhi, 110019, India

    Md Chand Asique

Authors
  1. Md Sanam Suraj
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Om Prakash Meena
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rajiv Aggarwal
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Amit Mittal
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Md Chand Asique
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Om Prakash Meena.

Ethics declarations

Conflict of interest

The authors state that they have not received any research grants and have no known competing personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

A The values of various coefficients in Eq. 11a

$$\begin{aligned} \rho _{00}&= \frac{1}{\sqrt{k}}\\ \rho _{01}&=-\frac{L}{k^{3/2}} \\ \rho _{02}&= \frac{3 L^2-k}{2 k^{5/2}}\\ \rho _{03}&= -\frac{1}{2 k^{3/2}}\\ \rho _{04}&= \frac{L \left( 3 k-5 L^2\right) }{2 k^{7/2}}\\ \rho _{05}&= \frac{3 L}{2 k^{5/2}}\\ \rho _{06}&= \frac{3 k^2-30 k L^2+35 L^4}{8 k^{9/2}}\\ \rho _{07}&= \frac{3 \left( k-5 L^2\right) }{4 k^{7/2}}\\ \rho _{08}&= \frac{3}{8 k^{5/2}}\\ \rho _{10}&= \frac{2}{\sqrt{4 k-4 L+1}}\\ \rho _{11}&= \frac{4 (1-2 L)}{(4 k-4 L+1)^{3/2}} \\ \rho _{12}&= \frac{8 \left( 6 L^2-2 k-4 L+1\right) }{(4 k-4 L+1)^{5/2}} \\ \rho _{13}&= -\frac{4}{(4 k-4 L+1)^{3/2}}\\ \rho _{14}&= \frac{16 (2 L-1) \left( 6 k-10 L^2+4 L-1\right) }{(4 k-4 L+1)^{7/2}}\\ \rho _{15}&= \frac{24 (2 L-1)}{(4 k-4 L+1)^{5/2}}\\ \rho _{16}&= \frac{32 \left( 6 k^2-60 k L^2+48 k L-12 k+70 L^4-80 L^3\right) }{(4 k-4 L+1)^{9/2}}\\&\quad +\,\frac{32(36 L^2-8 L+1)}{(4 k-4 L+1)^{9/2}} \\ \rho _{17}&= \frac{96 \left( k-5 L^2+4 L-1\right) }{(4 k-4 L+1)^{7/2}}\\ \rho _{18}&= \frac{12}{(4 k-4 L+1)^{5/2}}\\ \rho _{20}&= \frac{2}{\sqrt{4 k+4 L+1}}\\ \rho _{21}&= -\frac{4 (2 L+1)}{(4 k+4 L+1)^{3/2}}\\ \rho _{22}&= \frac{8 \left( 6 L^2-2 k+4 L+1\right) }{(4 k+4 L+1)^{5/2}}\\ \rho _{23}&= -\frac{4}{(4 k+4 L+1)^{3/2}}\\ \rho _{24}&= \frac{16 (2 L+1) \left( 6 k-10 L^2-4 L-1\right) }{(4 k+4 L+1)^{7/2}} \end{aligned}$$
$$\begin{aligned} \rho _{25}&= \frac{24 (2 L+1)}{(4 k+4 L+1)^{5/2}}\\ \rho _{26}&= \frac{32 \left( 6 k^2-60 k L^2-48 k L-12 k+70 L^4\right) }{(4 k+4 L+1)^{9/2}}\\&+\frac{32(80 L^3+36 L^2+8 L+1)}{(4 k+4 L+1)^{9/2}}\\ \rho _{27}&= \frac{96 \left( k-5 L^2-4 L-1\right) }{(4 k+4 L+1)^{7/2}}\\ \rho _{28}&=\frac{12}{(4 k+4 L+1)^{5/2}} \end{aligned}$$

B The values of various coefficients in Eq. 11b

$$\begin{aligned} \rho _{10}^*&= \frac{8}{(4 k-4 L+1)^{3/2}}\\ \rho _{11}^*&= \frac{48 (1-2 L)}{(4 k-4 L+1)^{7/2}} \\ \rho _{12}^*&= \frac{192 \left( 5 L^2-4 L-k+1\right) }{(4 k-4 L+1)^{7/2}} \\ \rho _{13}^*&=-\frac{48}{(4 k-4 L+1)^{5/2}}\\ \rho _{14}^*&= \frac{640 (2 L-1) \left( 3 k-7 L^2+4 L-1\right) }{(4 k-4 L+1)^{9/2}}\\ \rho _{15}^*&= \frac{480 (2 L-1)}{(4 k-4 L+1)^{7/2}}\\ \rho _{16}^*&= \frac{1920 \left( 2 k^2-6 k-28 k L^2+24 k L+42 L^4-56 L^3\right) }{(4 k-4 L+1)^{11/2}}\\&\quad +\,\frac{1920(30 L^2-8 L+1)}{(4 k-4 L+1)^{11/2}}\\ \rho _{17}^*&= \frac{960 \left( 2 k-14 L^2+12 L-3\right) }{(4 k-4 L+1)^{9/2}} \\ \rho _{18}^*&= \frac{240}{(4 k-4 L+1)^{7/2}}\\ \rho _{20}^*&= \frac{8}{(4 k+4 L+1)^{3/2}}\\ \rho _{21}^*&= -\frac{48 (2 L+1)}{(4 k+4 L+1)^{5/2}}\\ \rho _{22}^*&= \frac{192 \left( 5 L^2+4 L-k+1\right) }{(4 k+4 L+1)^{7/2}}\\ \rho _{23}^*&= -\frac{48}{(4 k+4 L+1)^{5/2}}\\ \rho _{24}^*&= \frac{640 (2 L+1) \left( 3 k-7 L^2-4 L-1\right) }{(4 k+4 L+1)^{9/2}}\\ \rho _{25}^*&= \frac{480 (2 L+1)}{(4 k+4 L+1)^{7/2}} \end{aligned}$$
$$\begin{aligned} \rho _{26}^*&= \frac{1920 \left( 2 k^2-6 k-28 k L^2-24 k L+42 L^4+56 L^3\right) }{(4 k+4 L+1)^{11/2}}\\&\quad +\,\frac{1920(30 L^2+8 L+1)}{(4 k+4 L+1)^{11/2}}\\ \rho _{27}^*&= \frac{960 \left( 2 k-14 L^2-12 L-3\right) }{(4 k+4 L+1)^{9/2}}\\ \rho _{28}^*&= \frac{240}{(4 k+4 L+1)^{7/2}} \end{aligned}$$

C The values of various coefficients in the expansion of potential function U

$$\begin{aligned} U_{0}^*&=\frac{A \left( \rho _{10}^*+\rho _{20}^*\right) +2 (\beta \rho _{00}+\rho _{10}+\rho _{20})}{2 \varLambda }\\ U_{1}^*&=\frac{A \left( \rho _{11}^*+\rho _{21}^*\right) +2 (\beta \rho _{01}+\rho _{11}+\rho _{21})}{2 \varLambda }\\ U_{2}^*&=\frac{A \left( \rho _{12}^*+\rho _{22}^*\right) +2 (\beta \rho _{02}+\rho _{12}+\rho _{22})}{2 \varLambda }\\ U_{3}^*&=\frac{A \left( \rho _{13}^*+\rho _{23}^*\right) +2 (\beta \rho _{03}+\rho _{13}+\rho _{23})}{2 \varLambda }\\ U_{4}^*&=\frac{A \left( \rho _{14}^*+\rho _{24}^*\right) +2 (\beta \rho _{04}+\rho _{14}+\rho _{24})}{2 \varLambda }\\ U_{5}^*&=\frac{A \left( \rho _{15}^*+\rho _{25}^*\right) +2 (\beta \rho _{05}+\rho _{15}+\rho _{25})}{2 \varLambda }\\ U_{6}^*&= \frac{A \left( \rho _{16}^*+\rho _{26}^*\right) +2 (\beta \rho _{06}+\rho _{16}+\rho _{26})}{2 \varLambda }\\ U_{7}^*&=\frac{A \left( \rho _{17}^*+\rho _{27}^*\right) +2 (\beta \rho _{07}+\rho _{17}+\rho _{27})}{2 \varLambda }\\ U_{8}^*&=\frac{A \left( \rho _{18}^*+\rho _{28}^*\right) +2 (\beta \rho _{08}+\rho _{18}+\rho _{28})}{2 \varLambda } \end{aligned}$$

D The values of various coefficients in the coefficient scheme Table 3

$$\begin{aligned} A_{01}&=\frac{1}{2}a_1^2+\frac{1}{2}a_{-1}^2\\ A_{02}&=2 a_0a_1+a_1 a_2+a_{-1}a_{-2}\\ A_{03}&=2a_0a_{-1}+a_1a_{-2}-a_{-1}a_{2}\\ A_{04}&=\frac{1}{2}a_1^2-\frac{1}{2}a_{-1}^2\\ A_{05}&= a_1 a_{-1}\\ A_{06}&=a_1a_2-a_{-1}a_{-2}\\ A_{07}&=a_1a_{-2}+a_{-1}a_{2}\\ B_{01}&=\frac{1}{2}a_1 b_1+\frac{1}{2}a_{-1}b_{-1}\\ B_{02}&=\frac{1}{2} (a_1b_2+a_2b_1)+\frac{1}{2}(a_{-1}b_{-2} \\&\quad +\,a_{-2}b_{-1})+a_1b_0+a_0b_1\\ B_{03}&=\frac{1}{2}(a_1b_{-2}+a_{-2}b_1)-\frac{1}{2}(a_{-1}b_{2}\\&\quad +\,a_{2}b_{-1})+a_{-1}b_{0}+a_0 b_{-1}\\ B_{04}&=\frac{1}{2}a_1 b_1-\frac{1}{2}a_{-1}b_{-1}\\ B_{05}&=\frac{1}{2}a_1 b_{-1}+\frac{1}{2}a_{-1}b_{1}\\ B_{06}&=\frac{1}{2} (a_1b_2+a_{2}b_{1})-\frac{1}{2}(a_{-1}b_{-2}+a_{-2}b_{-1})\\ B_{07}&=\frac{1}{2}(a_1b_{-2}+a_{-2}b_{1})+\frac{1}{2}(a_{-1}b_2+a_2b_{-1})\\ C_{01}&=\frac{1}{2}b_1^2+\frac{1}{2}b_{-1}^2\\ C_{02}&=2b_0b_1+b_1b_2+b_{-1}b_{-2}\\ C_{03}&=2b_0b_{-1}+b_1b_{-2}-b_{-1}b_{2}\\ C_{04}&=\frac{1}{2}b_1^2-\frac{1}{2}b_{-1}^2\\ C_{05}&= b_1 b_{-1}\\ C_{06}&=b_1b_2-b_{-1}b_{-2}\\ C_{07}&=b_1b_{-2}+b_{-1}b_{2}\\ D_{01}&=0\\ D_{02}&=\frac{3}{4}a_1^3+\frac{3}{4}a_1 a_{-1}^2\\ D_{03}&=\frac{3}{4}a_{-1}^3+\frac{3}{4}a_1^2a_{-1}\\ D_{04}&=0\\ D_{05}&=0\\ D_{06}&=\frac{1}{4} a_1^3-\frac{3}{4} a_{1}a_{-1}^2\\ D_{07}&=-\frac{1}{4} a_{-1}^3+\frac{3}{4} a_{1}^2a_{-1}\\ E_{01}&=0\\ E_{02}&=\frac{3}{4}a_1^2b_1+\frac{1}{4}a_{-1}^2b_1+\frac{1}{2}a_1 a_{-1}b_{-1}\\ E_{03}&=\frac{3}{4}a_{-1}^2b_{-1}+\frac{1}{4}a_1^2b_{-1}+\frac{1}{2}a_1 a_{-1}b_{1}\\ E_{04}&=0\\ E_{05}&=0\\ E_{06}&=\frac{1}{4}a_1^2b_1-\frac{1}{4}a_{-1}^2b_1-\frac{1}{2}a_1 a_{-1}b_{-1}\\ E_{07}&=\frac{1}{4}a_1^2b_{-1}-\frac{1}{4}a_{-1}^2b_{-1}+\frac{1}{2}a_1 a_{-1}b_{1}\\ F_{01}&=0\\ F_{02}&=\frac{3}{4}a_1b_1^2+\frac{1}{4}a_{1}b_{-1}^2+\frac{1}{2}a_{-1} b_1b_{-1}\\ F_{03}&=\frac{3}{4}a_{-1}b_{-1}^2+\frac{1}{4}a_{-1}b_1^2+\frac{1}{2}a_1 b_1 b_{-1}\\ F_{04}&=0\\ F_{05}&=0\\ F_{06}&=\frac{1}{4}a_1b_1^2-\frac{1}{4}a_{1}b_{-1}^2-\frac{1}{2}a_{-1} b_1b_{-1}\\ F_{07}&=\frac{1}{4}a_{-1}b_1^2-\frac{1}{4}a_{-1}b_{-1}^2+\frac{1}{2}a_1 b_1 b_{-1}\\ G_{01}&=0\\ G_{02}&=\frac{3}{4} b_1^3+\frac{3}{4} b_{1}b_{-1}^2\\ G_{03}&=\frac{3}{4} b_{-1}^3+\frac{3}{4} b_{1}^2b_{-1}\\ G_{04}&=0\\ G_{05}&=0\\ G_{06}&=\frac{1}{4} b_1^3-\frac{3}{4} b_{1}b_{-1}^2\\ G_{07}&=-\frac{1}{4} b_{-1}^3+\frac{3}{4} b_{1}^2b_{-1} \end{aligned}$$

E The values of various coefficients in the second-order terms \(a_0, b_0, a_{\pm 2} \, \text {and}\, b_{\pm 2} \)

$$\begin{aligned} \sigma _{1}&=\varPi _{1}^2 U^*_{5}\\ \sigma _{2}&=12 {U^*_4}+2 \varPi _{1} {U^*_5}\\ \sigma _{3}&={U^*_5}\\ \sigma _{4}&=4 \varPi _{1}+\varPi _{2}-16\\ \sigma _{5}&=8 \varPi _{1}+\varPi _{2}-16\\ \sigma _{6}&=\varPi _{1}^2 \varPi _{2} {U^*_5}\\ \sigma _{7}&={U^*_5} (\varPi _{1} \varPi _{2}+\varPi _{1} \sigma _{4})-12 \varPi _{2} {U^*_4}\\ \sigma _{8}&=\sigma _{5} {U^*_5}-48 {U^*_4}\\ \sigma _{9}&=4 {U^*_5}\\ \sigma _{10}&=3 (4 {U^*_4}+\varPi _{1} {U^*_5})\\ \sigma _{11}&=3 {U^*_5} \end{aligned}$$

F The values of various coefficients in the third-order terms \(a_{\pm 3}\) and \(b_{\pm 3}\)

$$\begin{aligned} \varPi _{3}&=4-\varPi _{1}-\varPi _{2}\\ \sigma _{12}&=-27 \sigma _{6} {U^*_4}-2 \varPi _{1} \varPi _{2} \sigma _{10} {U^*_5}-3 \sigma _{6} {U^*_5}\\ \sigma _{13}&=\sigma _{12}-3 \varPi _{1}^2 \varPi _{2} \varPi _{3} {U^*_7}-18 \varPi _{1}^3 \varPi _{3} {U^*_8}\\ \sigma _{14}&=9 (-3 \sigma _{7} {U^*_4}-2 \varPi _{1} \sigma _{10} {U^*_5}-3 \varPi _{1}^2 \varPi _{3} {U^*_7})\\ \sigma _{15}&=24 \varPi _{3} {U^*_6}+15 \varPi _{1}^2 {U^*_7}-6 \varPi _{1} \varPi _{3} {U^*_7}\\ \sigma _{16}&=\sigma _{15}-3 \sigma _{8} {U^*_4}-2 \varPi _{1} \sigma _{11} {U^*_5}-2 \sigma _{10} {U^*_5}\\ \sigma _{17}&=6 {U^*_8} (3 \varPi _{1}^2 \varPi _{3}-5 \varPi _{1}^3)-12 \varPi _{1} \varPi _{3} {U^*_7}\\ \sigma _{18}&=\sigma _{17}+{U^*_5} (\varPi _{1} \sigma _{8}+\sigma _{7})-8 \sigma _{10} {U^*_5}\\ \sigma _{19}&=24 \varPi _{3} {U^*_6}+15 \varPi _{1}^2 {U^*_7}-6 \varPi _{1} \varPi _{3} {U^*_7}\\ \sigma _{20}&=\sigma _{19}-3 \sigma _{8} {U^*_4}-2 \varPi _{1} \sigma _{11} {U^*_5}-2 \sigma _{10} {U^*_5}\\ \sigma _{21}&=3 {U^*_7} (10 \varPi _{1}-\varPi _{3})-2 \sigma _{11} {U^*_5}\\ \sigma _{22}&=9 \sigma _{20}+\varPi _{2} (\sigma _{21}-3 \sigma _{9} {U^*_4}-120 {U^*_6})\\ \sigma _{23}&=6 {U^*_8} (3 \varPi _{1} \varPi _{3}-15 \varPi _{1}^2)-8 \sigma _{11} {U^*_5}\\ \sigma _{24}&=\sigma _{23}+{U^*_5} (\varPi _{1} \sigma _{9}+\sigma _{8})\\ \sigma _{25}&=-3 \sigma _{9} {U^*_4}-2 \sigma _{11} {U^*_5}+3 {U^*_7} (10 \varPi _{1}-\varPi _{3})\\ \sigma _{26}&=\sigma _{9} {U^*_5}+60 {U^*_7}+6 {U^*_8} (\varPi _{3}-15 \varPi _{1})\\ \sigma _{27}&=-3 \varPi _{2} \sigma _{6} {U^*_4}-3 \varPi _{1} \sigma _{6} {U^*_5}\\ \sigma _{28}&=\sigma _{13}-3 \varPi _{2} \sigma _{7} {U^*_4}-3 \varPi _{1} \sigma _{7} {U^*_5}\\ \sigma _{29}&=\varPi _{2} \sigma _{16}+\sigma _{14}-3 \sigma _{18}\\ \sigma _{30}&=\sigma _{22}-3 (\sigma _{24}-12 {U^*_7} (\varPi _{3}-5 \varPi _{1}))\\ \sigma _{31}&=-3 \sigma _{26}+9 (\sigma _{25}-120 {U^*_6})+15 \varPi _{2} {U^*_7}\\ \sigma _{32}&=135 {U^*_7}+90 {U^*_8}\\ \sigma _{33}&=36 \sigma _{6} {U^*_4}+10 \varPi _{1} \sigma _{6} {U^*_5}+6 \varPi _{1}^4 \varPi _{3} {U^*_8}\\ \sigma _{34}&=6 \sigma _{7} {U^*_4}+4 \varPi _{1}^2 \varPi _{3} {U^*_7}+12 \varPi _{1}^3 \varPi _{3} {U^*_8}\\ \sigma _{35}&=\varPi _{1} (\varPi _{1} \sigma _{8}+16 \sigma _{10}+10 \sigma _{7})+9 \sigma _{6}\\ \sigma _{36}&=12 \varPi _{3} {U^*_6}+5 \varPi _{1}^2 {U^*_7}+2 \varPi _{1} \varPi _{3} {U^*_7}\\ \sigma _{37}&=6 \sigma _{8} {U^*_4}+{U^*_8} (30 \varPi _{1}^2 \varPi _{3}-60 \varPi _{1}^3)\\ \sigma _{38}&=\varPi _{1} (\varPi _{1} \sigma _{9}+16 \sigma _{11}+10 \sigma _{8})+9 \sigma _{7}\\ \sigma _{39}&=-5 (-12 {U^*_6}-2 \varPi _{1} {U^*_7})-3 \varPi _{3} {U^*_7}\\ \sigma _{40}&=9 (3 \varPi _{1} \varPi _{3}-15 \varPi _{1}^2)+\varPi _{1} (\varPi _{3}-15 \varPi _{1})\\ \sigma _{41}&={U^*_5} (10 \varPi _{1} \sigma _{9}-48 \sigma _{11}+9 \sigma _{8}) \end{aligned}$$
$$\begin{aligned} \sigma _{42}&=60 {U^*_7}+{U^*_8} (9 (\varPi _{3}-15 \varPi _{1})-5 \varPi _{1})\\ \sigma _{43}&={U^*_5} (\sigma _{38}-48 \sigma _{10})\\ \sigma _{44}&=4 \sigma _{39}+6 \sigma _{9} {U^*_4}+\sigma _{40} {U^*_8}\\ \sigma _{45}&=\varPi _{1}^2 \sigma _{6} {U^*_5}\\ \sigma _{46}&=\sigma _{33}+\varPi _{1}^2 \sigma _{7} {U^*_5}\\ \sigma _{47}&=\sigma _{35} {U^*_5}+6 (\sigma _{34}-5 \varPi _{1}^4 {U^*_8})\\ \sigma _{48}&=6 (\sigma _{37}-4 \sigma _{36})+\sigma _{43}\\ \sigma _{49}&=\sigma _{41}+6 \sigma _{44}\\ \sigma _{50}&=6 \sigma _{42}+9 \sigma _{9} {U^*_5}\\ \sigma _{51}&=-270 {U^*_8}\\ \end{aligned}$$

G The values of various coefficients in \(q_1, q_2,\) \(q_3\) and \(q_4\)

$$\begin{aligned} \sigma _{52}&=3 \varPi _{1}^3 \varPi _{3} {U^*_7}-18 \varPi _{3} \sigma _{1} {U^*_4}\\ \sigma _{53}&=2 \varPi _{1} \sigma _{11} {U^*_5}+2 \sigma _{10} {U^*_5}+6 \varPi _{1} \varPi _{3} {U^*_7}\\ \sigma _{54}&=\varPi _{1} (\sigma _{53}+72 \varPi _{3} {U^*_6}-15 \varPi _{1}^2 {U^*_7})\\ \sigma _{55}&=3 {U^*_4} (\varPi _{1} \sigma _{9}+6 (\varPi _{3} \sigma _{3}-5 \sigma _{2}))\\ \sigma _{56}&=3 {U^*_7} (\varPi _{3}-10 \varPi _{1})-360 {U^*_6}\\ \sigma _{57}&=-3 \varPi _{1} \sigma _{6} {U^*_4}\\ \sigma _{58}&=\sigma _{52}-3 \varPi _{1} \sigma _{7} {U^*_4}+2 \varPi _{1}^2 \sigma _{10} {U^*_5}\\ \sigma _{59}&=\sigma _{54}-3 {U^*_4} (\varPi _{1} \sigma _{8}+6 (\varPi _{3} \sigma _{2}-5 \sigma _{1}))\\ \sigma _{60}&=\varPi _{1} (\sigma _{56}+2 \sigma _{11} {U^*_5})-\sigma _{55}\\ \sigma _{61}&=90 \sigma _{3} {U^*_4}-15 \varPi _{1} {U^*_7}\\ \sigma _{62}&={U^*_5} (6 \varPi _{1} \varPi _{3} \sigma _{1}-\varPi _{1} (\varPi _{1} \sigma _{7}+\sigma _{6}))\\ \sigma _{63}&=6 (\sigma _{1} (\varPi _{3}-5 \varPi _{1})+\varPi _{1} \varPi _{3} \sigma _{2})-8 \varPi _{1} \sigma _{10}\\ \sigma _{64}&={U^*_5} (\sigma _{63}-\varPi _{1} (\varPi _{1} \sigma _{8}+\sigma _{7}))-12 \varPi _{1}^2 \varPi _{3} {U^*_7}\\ \sigma _{65}&=6 (\sigma _{2} (\varPi _{3}-5 \varPi _{1})+\varPi _{1} \varPi _{3} \sigma _{3}-5 \sigma _{1})\\ \sigma _{66}&={U^*_5} (-8 \varPi _{1} \sigma _{11}-\varPi _{1} (\varPi _{1} \sigma _{9}+\sigma _{8})+\sigma _{65})\\ \sigma _{67}&=\sigma _{66}-12 \varPi _{1} {U^*_7} (\varPi _{3}-5 \varPi _{1})\\ \sigma _{68}&=60 \varPi _{1} {U^*_7}+18 \varPi _{1} {U^*_8} (15 \varPi _{1}-\varPi _{3})\\ \sigma _{69}&=\sigma _{3} (\varPi _{3}-5 \varPi _{1})-5 \sigma _{2}\\ \sigma _{70}&=-\varPi _{1}^2 \sigma _{6} {U^*_5}\\ \sigma _{71}&=\sigma _{62}-18 \varPi _{1}^4 \varPi _{3} {U^*_8}\\ \sigma _{72}&=\sigma _{64}-18 \varPi _{1} {U^*_8} (3 \varPi _{1}^2 \varPi _{3}-5 \varPi _{1}^3)\\ \sigma _{73}&=\sigma _{67}-18 \varPi _{1} {U^*_8} (3 \varPi _{1} \varPi _{3}-15 \varPi _{1}^2)\\ \sigma _{74}&=\sigma _{68}+{U^*_5} (6 \sigma _{69}-\varPi _{1} \sigma _{9})\\ \sigma _{75}&=90 \varPi _{1} {U^*_8}-30 \sigma _{3} {U^*_5} \end{aligned}$$

H The values of various coefficients in the expression of E

$$\begin{aligned} \sigma _{76}&=\varPi _{2} \sigma _{57}-\sigma _{70}\\ \sigma _{77}&=\varPi _{2} \sigma _{58}+\sigma _{57}-\sigma _{71}\\ \sigma _{78}&=\varPi _{2} \sigma _{59}+\sigma _{58}-\sigma _{72}\\ \sigma _{79}&=\varPi _{2} \sigma _{60}+\sigma _{59}-\sigma _{73}\\ \sigma _{80}&=\varPi _{2} \sigma _{61}+\sigma _{60}-\sigma _{74}\\ \sigma _{81}&=\sigma _{61}-\sigma _{75} \end{aligned}$$

I The values of various coefficients in the first-order terms \(a_{-1} \, \text {and}\, b_{-1}\)

$$\begin{aligned} \sigma _{82}&=\varPi _1 \sigma _{76}\\ \sigma _{83}&= \varPi _1 \sigma _{77}-2 \varPi _3 \sigma _{57}-\sigma _{76}\\ \sigma _{84}&=4 \sigma _{57}-2 \varPi _3 \sigma _{58}-\sigma _{77}+\varPi _1 \sigma _{78}\\ \sigma _{85}&=4 \sigma _{58}-2 \varPi _3 \sigma _{59}-\sigma _{78}+\varPi _1 \sigma _{79}\\ \sigma _{86}&=4 \sigma _{59}-2 \varPi _3 \sigma _{60}-\sigma _{79}+\varPi _1 \sigma _{80}\\ \sigma _{87}&=4 \sigma _{60}-2 \varPi _3 \sigma _{61}-\sigma _{80}+\varPi _1 \sigma _{81}\\ \sigma _{88}&=4 \sigma _{61}-\sigma _{81}\\ \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Suraj, M.S., Meena, O.P., Aggarwal, R. et al. On the periodic orbits around the collinear libration points in the SCR4BP with non-spherical primaries. Nonlinear Dyn 111, 5547–5577 (2023). https://doi.org/10.1007/s11071-022-08131-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-08131-w

Keywords

Search

Navigation