Discontinuous dynamics of a 3-DOF oblique-impact system with dry friction and single pendulum device

Abstract

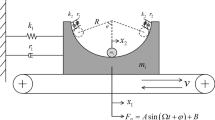
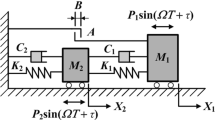
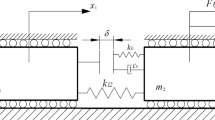
Based on the high-dimensional flow switchability theory in discontinuous dynamical systems, this paper aims at investigating the dynamical behaviors of a 3-DOF (three degree-of-freedom) oblique-impact system with dry friction and single pendulum device. The oblique impact system considered in this paper consists of elastic contact model and Coulomb friction model; meanwhile, the unequal kinetic and static friction coefficients result in the flow barriers. Firstly, according to two factors that cause discontinuity, namely friction and impact, different regions, boundaries and edges are delineated in four- and two-dimensional phase spaces. Secondly, the conditions of motion transformation at separation boundaries are developed. Thirdly, the switching criteria of motion at the edges in four-dimensional phase space are deduced, which is a further extension and enrichment of flow switching theory in higher-dimensional space. Finally, some typical motions are visually demonstrated by numerical simulations, and the sliding bifurcation scenarios are presented. Compared with low-dimensional flow switchability theory, this method can more systematically study the dynamic behaviors of multiple degree-of-freedom system under the simultaneous action of multiple objects and give more convenient analytical conditions. The study on the complex motion mechanism of such a 3-DOF oblique-impact system provides a reference for the parameter selection of single pendulum shock absorbers, which is useful in exploring how to suppress the vibration/noise of friction/impact system in mechanical engineering field.

Appendices

Appendix A

When the elastic constraint $k _{3}$ is not compressed, the system M and the mass $m _2$ are independent of each other. The phase space of the system M is divided into ten 4-dimensional domains, seventeen 3-dimensional boundaries, ten 2-dimensional edges and two 1-dimensional edges as follows.

The ten domains are defined as:

$$\begin{aligned} \Omega _{1}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\;|z ^{(3)}|<l\sin \theta _0,\dot{z }^{(3)}\in (-\infty ,+\infty )\},\nonumber \\ \Omega _{2}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\;|z ^{(3)}|<l\sin \theta _0,\dot{z }^{(3)}\in (-\infty ,+\infty )\},\nonumber \\ \Omega _{3}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\;z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{4}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\;z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{5}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\;z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}<0\},\nonumber \\ \Omega _{6}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\;z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}<0\},\nonumber \\ \Omega _{7}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\;z ^{(3)}<-l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{8}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\;z ^{(3)}<-l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{9}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\;z ^{(3)}<-l\sin \theta _0,\;\dot{z }^{(3)}<0\},\nonumber \\ \Omega _{a}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\;z ^{(3)}<-l\sin \theta _0,\dot{z }^{(3)}<0\}; \end{aligned}$$

(A.1)

and the corresponding three-dimensional boundaries are defined by $\partial \Omega _{\alpha _1\alpha _2}^{(ns)}=\bar{\Omega }_{\alpha _1}^{(ns)}\cap \bar{\Omega }_{\alpha _2}^{(ns)}$ for ($\alpha _{i }\in \{1,2,\ldots ,9,a\}, i =1,2;\,\,\alpha _1\ne \alpha _2$ without repeating), i.e.,

$$\begin{aligned} \partial \Omega _{12}^{(ns)}= & {} \partial \Omega _{21}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{12}^{(ns)}= & {} \varphi _{21}^{(ns)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,|z ^{(3)}|\le l\sin \theta _0,\,\dot{z }^{(3)}\in (-\infty ,+\infty )\bigr \},\nonumber \\ \partial \Omega _{13}^{(ns)}= & {} \partial \Omega _{31}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{13}^{(ns)}= & {} \varphi _{31}^{(ns)}\equiv z ^{(3)}-l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{15}^{(ns)}= & {} \partial \Omega _{51}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{15}^{(ns)}= & {} \varphi _{51}^{(ns)}\equiv z ^{(3)}-l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{24}^{(ns)}= & {} \partial \Omega _{42}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{24}^{(ns)}= & {} \varphi _{42}^{(ns)}\equiv z ^{(3)}-l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{26}^{(ns)}= & {} \partial \Omega _{62}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{26}^{(ns)}= & {} \varphi _{62}^{(ns)}\equiv z ^{(3)}-l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{34}^{(ns)}= & {} \partial \Omega _{43}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{34}^{(ns)}= & {} \varphi _{43}^{(ns)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,z ^{(3)}\ge l\sin \theta _0,\,\dot{z }^{(3)}\ge 0\bigr \}, \end{aligned}$$

$$\begin{aligned} \partial \Omega _{56}^{(ns)}= & {} \partial \Omega _{65}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{56}^{(ns)}= & {} \varphi _{65}^{(ns)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,z ^{(3)}\ge l\sin \theta _0,\,\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{35}^{(ns)}= & {} \partial \Omega _{53}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{35}^{(ns)}= & {} \varphi _{53}^{(ns)}\equiv \dot{z }^{(3)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\dot{x }^{(1)}\ge 0,\;z ^{(3)}\ge l\sin \theta _0\bigr \},\nonumber \\ \partial \Omega _{46}^{(ns)}= & {} \partial \Omega _{64}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{46}^{(ns)}= & {} \varphi _{64}^{(ns)}\equiv \dot{z }^{(3)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\dot{x }^{(1)}\le 0,\;z ^{(3)}\ge l\sin \theta _0\bigr \},\nonumber \\ \partial \Omega _{17}^{(ns)}= & {} \partial \Omega _{71}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{17}^{(ns)}= & {} \varphi _{71}^{(ns)}\equiv z ^{(3)}+l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{19}^{(ns)}= & {} \partial \Omega _{91}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{19}^{(ns)}= & {} \varphi _{91}^{(ns)}\equiv z ^{(3)}+l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{28}^{(ns)}= & {} \partial \Omega _{82}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{28}^{(ns)}= & {} \varphi _{82}^{(ns)}\equiv z ^{(3)}+l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{2a}^{(ns)}= & {} \partial \Omega _{a2}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{2a}^{(ns)}= & {} \varphi _{a2}^{(ns)}\equiv z ^{(3)}+l\sin {\theta }_0=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{78}^{(ns)}= & {} \partial \Omega _{87}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{78}^{(ns)}= & {} \varphi _{87}^{(ns)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,z ^{(3)}\le -l\sin \theta _0,\,\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{9a}^{(ns)}= & {} \partial \Omega _{a9}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{9a}^{(ns)}= & {} \varphi _{a9}^{(ns)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,z ^{(3)}\le -l\sin \theta _0,\,\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{79}^{(ns)}= & {} \partial \Omega _{97}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{79}^{(ns)}= & {} \varphi _{97}^{(ns)}\equiv \dot{z }^{(3)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\dot{x }^{(1)}\ge 0,\;z ^{(3)}\le -l\sin \theta _0\bigr \},\nonumber \\ \partial \Omega _{8a}^{(ns)}= & {} \partial \Omega _{a8}^{(ns)} =\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\nonumber \\ \varphi _{8a}^{(ns)}= & {} \varphi _{a8}^{(ns)}\equiv \dot{z }^{(3)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\dot{x }^{(1)}\le 0,\;z ^{(3)}\le -l\sin \theta _0\bigr \}. \end{aligned}$$

(A.2)

Finally, the two-dimensional edges of the three-dimensional boundaries are defined by $\angle \Omega _{\alpha _1\alpha _2\alpha _3}^{(ns)}=\partial \Omega _{\alpha _1\alpha _2}^{(ns)}\cap \partial \Omega _{\alpha _2\alpha _3}^{(ns)}=\cap _{i =1}^{3}\bar{\Omega }_{\alpha _{i }}^{(ns)}$ for ($\alpha _{i }\in \{1,2,\ldots ,9,a\},\,\,i =1,2,3;\,\,\alpha _1\ne \alpha _2\ne \alpha _3$ without repeating), i.e.,

$$\begin{aligned} \angle \Omega _{135}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{13}^{(ns)}=\varphi _{15}^{(ns)}\equiv z ^{(3)}-l\sin \theta _0=0,\nonumber \\ \;\varphi _{35}^{(ns)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{246}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{24}^{(ns)}=\varphi _{26}^{(ns)}\equiv z ^{(3)}-l\sin \theta _0=0,\;\nonumber \\ \varphi _{46}^{(ns)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0\bigr \}, \end{aligned}$$

$$\begin{aligned} \angle \Omega _{1234}^{(ns)}= & {} \angle \Omega _{213}^{(ns)}=\angle \Omega _{134}^{(ns)}=\angle \Omega _{124}^{(ns)}=\angle \Omega _{243}^{(ns)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{13}^{(ns)}=\varphi _{24}^{(ns)} \equiv z ^{(3)}-l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(ns)}= & {} \varphi _{34}^{(ns)} \equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{1256}^{(ns)}= & {} \angle \Omega _{215}^{(ns)}=\angle \Omega _{126}^{(ns)} =\angle \Omega _{156}^{(ns)}=\angle \Omega _{265}^{(ns)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{15}^{(ns)}=\varphi _{26}^{(ns)} \equiv z ^{(3)}-l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(ns)}= & {} \varphi _{56}^{(ns)} \equiv \dot{x }^{(1)}=0,\;x ^{(1)} \le x ^{(2)}+d ,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \angle \Omega _{3456}^{(ns)}= & {} \angle \Omega _{435}^{(ns)}=\angle \Omega _{346}^{(ns)} =\angle \Omega _{356}^{(ns)}=\angle \Omega _{465}^{(ns)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)}) \;|\;\varphi _{34}^{(ns)}=\varphi _{56}^{(ns)}\equiv \dot{x }^{(1)}=0,\nonumber \\ \varphi _{35}^{(ns)}= & {} \varphi _{46}^{(ns)}\equiv \dot{z }^{(3)}=0,x ^{(1)}\le x ^{(2)}+d ,\;z ^{(3)}\ge l\sin \theta _0\bigr \},\nonumber \\ \angle \Omega _{179}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{17}^{(ns)}=\varphi _{19}^{(ns)} \equiv z ^{(3)} +l\sin \theta _0=0,\;\nonumber \\ \varphi _{79}^{(ns)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)} \le x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{28a}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{28}^{(ns)}=\varphi _{2a}^{(ns)}\equiv z ^{(3)}+l\sin \theta _0=0,\;\nonumber \\ \varphi _{8a}^{(ns)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)}\le x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0\bigr \},\nonumber \\ \angle \Omega _{1278}^{(ns)}= & {} \angle \Omega _{217}^{(ns)}=\angle \Omega _{128}^{(ns)}=\angle \Omega _{178}^{(ns)}=\angle \Omega _{287}^{(ns)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{17}^{(ns)}=\varphi _{28}^{(ns)}\equiv z ^{(3)}+l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(ns)}= & {} \varphi _{78}^{(ns)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{129a}^{(ns)}= & {} \angle \Omega _{219}^{(ns)}=\angle \Omega _{12a}^{(ns)} =\angle \Omega _{19a}^{(ns)}=\angle \Omega _{2a9}^{(ns)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{19}^{(ns)}=\varphi _{2a}^{(ns)}\equiv z ^{(3)}+l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(ns)}= & {} \varphi _{9a}^{(ns)} \equiv \dot{x }^{(1)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \angle \Omega _{789a}^{(ns)}= & {} \angle \Omega _{879}^{(ns)}=\angle \Omega _{78a}^{(ns)}=\angle \Omega _{79a}^{(ns)} =\angle \Omega _{8a9}^{(ns)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{78}^{(ns)} =\varphi _{9a}^{(ns)} \equiv \dot{x }^{(1)}=0,\nonumber \\ \varphi _{79}^{(ns)}= & {} \varphi _{8a}^{(ns)}\equiv \dot{z }^{(3)}=0,\;x ^{(1)}\le x ^{(2)}+d ,\;z ^{(3)}\le -l\sin \theta _0\bigr \}; \end{aligned}$$

(A.3)

and the one-dimensional edges formed by the intersection of two-dimensional edges are defined by

$$\begin{aligned} \angle \Omega _{123456}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{13}^{(ns)}=\varphi _{15}^{(ns)}=\varphi _{24}^{(ns)}\nonumber \\= & {} \varphi _{26}^{(ns)}\equiv z ^{(3)}-l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(ns)}= & {} \varphi _{34}^{(ns)}=\varphi _{56}^{(ns)}\equiv \dot{x }^{(1)}=0, \varphi _{35}^{(ns)}=\varphi _{46}^{(ns)}\equiv \dot{z }^{(3)}=0,\nonumber \\ x ^{(1)}\le & {} x ^{(2)}+d \bigr \},\nonumber \\ \angle \Omega _{12789a}^{(ns)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{17}^{(ns)}=\varphi _{19}^{(ns)}\nonumber \\= & {} \varphi _{28}^{(ns)}=\varphi _{2a}^{(ns)}\equiv z ^{(3)}+l\sin \theta _0=0, \nonumber \\ \end{aligned}$$

$$\begin{aligned} \varphi _{12}^{(ns)}= & {} \varphi _{78}^{(ns)}=\varphi _{9a}^{(ns)}\equiv \dot{x }^{(1)}=0,\nonumber \\ \varphi _{79}^{(ns)}= & {} \varphi _{8a}^{(ns)}\equiv \dot{z }^{(3)}=0,\;x ^{(1)}\le x ^{(2)}+d \bigr \}. \end{aligned}$$

(A.4)

Fig. 16

Domains, boundaries and edges of system M in four-dimensional coordinates where the stick motion between masses $m _1$ and $m _2$ does not occur

The two-dimensional phase space of mass $m _2$ is divided into two domains and three boundaries. The two domains are defined as:

$$\begin{aligned} \Omega _{1}^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\; |\;x ^{(2)}>x ^{(1)}-d ,\;\dot{x }^{(2)}<0\},\nonumber \\ \Omega _{2}^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\; |\;x ^{(2)}>x ^{(1)}-d ,\;\dot{x }^{(2)}>0\}; \end{aligned}$$

(A.5)

and the corresponding boundaries are defined by

$$\begin{aligned} \partial \Omega _{12}^{(2)}= & {} \partial \Omega _{21}^{(2)}=\bigl \{(x ^{(2)},\dot{x }^{(2)})\;|\;\varphi _{12}^{(2)}=\varphi _{21}^{(2)}\equiv \dot{x }^{(2)}=0,\;\nonumber \\ {}{} & {} {x}^{(2)}>x ^{(1)}-d \bigr \},\nonumber \\ ^{1}\partial \Omega _{1\infty }^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\;|\;^{1}\varphi _{1\infty }^{(2)}\equiv x ^{(2)}-x ^{(1)}+d =0,\;\dot{x }^{(2)}<0\bigr \},\nonumber \\ ^{1}\partial \Omega _{2\infty }^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\;|\;^{1}\varphi _{2\infty }^{(2)}\equiv x ^{(2)}-x ^{(1)}+d =0,\;\dot{x }^{(2)}>0\bigr \}. \nonumber \\ \end{aligned}$$

(A.6)

Fig. 17

Domains and boundaries of mass $m _2$ in two-dimensional coordinates where the stick motion between masses $m _1$ and $m _2$ does not occur

The region division, where the elastic constraint $k _{3}$ does not function (i.e., $x ^{(1)}-x ^{(2)}<d$), is depicted in Figs. 16 and 17. In Fig. 16, the domain partition of system M with a certain value of $x ^{(1)}$ is given. The intersection of the closures of any two domains $\Omega _{\lambda }^{(ns)}$ $(\lambda =1,2,\ldots ,9,a)$ forms the corresponding boundary. The velocity boundary $\partial \Omega _{\alpha _1\alpha _2}^{(ns)}$ $((\alpha _1,\alpha _2)\in \{(1,2),(3,4),(5,6),(7,8),(9,a)\})$, which is expressed in the green plane, means that the velocity of $m _1$ is zero. The velocity boundary $\partial \Omega _{\alpha _3\alpha _4}^{(ns)}$ $((\alpha _3,\alpha _4)\in \{(3,5),(4,6),(7,9),(8,a)\})$, which is expressed in the gray plane, means that the relative velocity between the pendulum ball $m _3$ and the mass $m _1$ is zero. The displacement boundaries $\partial \Omega _{\alpha _5\alpha _6}^{(ns)}$ $((\alpha _5,\alpha _6)\in \{(1,3),(1,5),(2,4),(2,6)\})$ and $\partial \Omega _{\alpha _7\alpha _8}^{(ns)}$ $((\alpha _7,\alpha _8)\in \{(1,7),(1,9),(2,8),(2,a)\})$, which represent the displacement difference between the pendulum ball $m _3$ and the mass $m _1$ as $l\sin \theta _0$ and $-l\sin \theta _0$, are shown in dark blue and steel blue planes, respectively. The intersection of the boundaries forms the edges represented by the red solid lines and the red dots. In Fig. 17, the domains $\Omega _{\sigma }^{(2)}$ $(\sigma =1,2)$ of mass $m _2$, in which the stick motion does not occur, are represented in pink and orange, respectively. The velocity boundary $\partial \Omega _{12}^{(2)}$ is depicted by the red dashed line; and the elastic impact boundaries $^{1}\partial \Omega _{1\infty }^{(2)}$ and $^{1}\partial \Omega _{2\infty }^{(2)}$ are depicted by the black dotted-dashed curves.

When the elastic constraint $k _{3}$ is in action, the masses $m _1$ and $m _2$ will have stick motion. The domains, boundaries and edges of the system M in the stick motion can be expressed as:

$$\begin{aligned} \Omega _{1}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\;| z ^{(3)}|<l\sin \theta _0,\;\dot{z }^{(3)}\in (-\infty ,+\infty )\},\nonumber \\ \Omega _{2}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; | \;x ^{(1)}>x ^{(2)}+d ,\; \dot{x }^{(1)}<0,\;| z ^{(3)}|<l\sin \theta _0,\;\dot{z }^{(3)}\in (-\infty ,+\infty )\},\nonumber \\ \Omega _{3}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\; z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{4}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\; z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{5}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\; z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}<0\},\nonumber \\ \Omega _{6}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\; z ^{(3)}>l\sin \theta _0,\;\dot{z }^{(3)}<0\},\nonumber \\ \Omega _{7}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\; z ^{(3)}<-l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{8}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\; z ^{(3)}<-l\sin \theta _0,\;\dot{z }^{(3)}>0\},\nonumber \\ \Omega _{9}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}>0,\; z ^{(3)}<l\sin \theta _0,\;\dot{z }^{(3)}<0\},\nonumber \\ \Omega _{a}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}<0,\; z ^{(3)}<-l\sin \theta _0,\;\dot{z }^{(3)}<0\}; \end{aligned}$$

(A.7)

$$\begin{aligned} \partial \Omega _{12}^{(s)}= & {} \partial \Omega _{21}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)}, z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{12}^{(s)}=\varphi _{21}^{(s)}\equiv \dot{x }^{(1)}=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,|z ^{(3)}|\le l\sin \theta _0,\,\dot{z }^{(3)}\in (-\infty ,+\infty )\bigr \},\nonumber \\ \partial \Omega _{13}^{(s)}= & {} \partial \Omega _{31}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{13}^{(s)}=\varphi _{31}^{(s)}\equiv z ^{(3)}-l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{15}^{(s)}= & {} \partial \Omega _{51}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{15}^{(s)}=\varphi _{51}^{(s)}\equiv z ^{(3)}-l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{24}^{(s)}= & {} \partial \Omega _{42}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{24}^{(s)}=\varphi _{42}^{(s)}\equiv z ^{(3)}-l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{26}^{(s)}= & {} \partial \Omega _{62}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{26}^{(s)}=\varphi _{62}^{(s)}\equiv z ^{(3)}-l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{34}^{(s)}= & {} \partial \Omega _{43}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{34}^{(s)}=\varphi _{43}^{(s)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,z ^{(3)}\ge l\sin \theta _0,\,\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{56}^{(s)}= & {} \partial \Omega _{65}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{56}^{(s)}=\varphi _{65}^{(s)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,z ^{(3)}\ge l\sin \theta _0,\,\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{35}^{(s)}= & {} \partial \Omega _{53}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{35}^{(s)}=\varphi _{53}^{(s)}\equiv \dot{z }^{(3)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\dot{x }^{(1)}\ge 0,\;z ^{(3)}\ge l\sin \theta _0\bigr \},\nonumber \\ \partial \Omega _{46}^{(s)}= & {} \partial \Omega _{64}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{46}^{(s)}=\varphi _{64}^{(s)}\equiv \dot{z }^{(3)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\dot{x }^{(1)}\le 0,\;z ^{(3)}\ge l\sin \theta _0\bigr \}, \end{aligned}$$

$$\begin{aligned} \partial \Omega _{17}^{(s)}= & {} \partial \Omega _{71}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{17}^{(s)}=\varphi _{71}^{(s)}\equiv z ^{(3)}+l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{19}^{(s)}= & {} \partial \Omega _{91}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{19}^{(s)}=\varphi _{91}^{(s)}\equiv z ^{(3)}+l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{28}^{(s)}= & {} \partial \Omega _{82}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{28}^{(s)}=\varphi _{82}^{(s)}\equiv z ^{(3)}+l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{2a}^{(s)}= & {} \partial \Omega _{a2}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{2a}^{(s)}=\varphi _{a2}^{(s)}\equiv z ^{(3)}+l\sin {\theta }_0=0,\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{78}^{(s)}= & {} \partial \Omega _{87}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{78}^{(s)}=\varphi _{87}^{(s)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,z ^{(3)}\le -l\sin \theta _0,\,\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \partial \Omega _{9a}^{(s)}= & {} \partial \Omega _{a9}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{9a}^{(s)}=\varphi _{a9}^{(s)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,z ^{(3)}\le -l\sin \theta _0,\,\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \partial \Omega _{79}^{(s)}= & {} \partial \Omega _{97}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{79}^{(s)}=\varphi _{97}^{(s)}\equiv \dot{z }^{(3)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\dot{x }^{(1)}\ge 0,\;z ^{(3)}\le -l\sin \theta _0\bigr \},\nonumber \\ \partial \Omega _{8a}^{(s)}= & {} \partial \Omega _{a8}^{(s)}=\bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\;\varphi _{8a}^{(s)}=\varphi _{a8}^{(s)}\equiv \dot{z }^{(3)}=0,\;\nonumber \\ x ^{(1)}\ge & {} x ^{(2)}+d ,\dot{x }^{(1)}\le 0,\;z ^{(3)}\le -l\sin \theta _0\bigr \}; \end{aligned}$$

(A.8)

$$\begin{aligned} \angle \Omega _{135}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{13}^{(s)}=\varphi _{15}^{(s)}\equiv z ^{(3)}-l\sin \theta _0=0,\;\nonumber \\ \varphi _{35}^{(s)}\equiv & {} \dot{z }^{(3)}=0, x ^{(1)}\ge x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{246}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{24}^{(s)}=\varphi _{26}^{(s)} \equiv z ^{(3)}-l\sin \theta _0=0,\;\nonumber \\ \varphi _{46}^{(s)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)}\ge x ^{(2)}+d ,\;\dot{x }^{(1)}\le 0\bigr \},\nonumber \\ \angle \Omega _{1234}^{(s)}= & {} \angle \Omega _{213}^{(s)}=\angle \Omega _{134}^{(s)}=\angle \Omega _{124}^{(s)}=\angle \Omega _{243}^{(s)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{13}^{(s)}=\varphi _{24}^{(s)}\equiv z ^{(3)}-l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(s)}= & {} \varphi _{34}^{(s)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\ge x ^{(2)}+d ,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{1256}^{(s)}= & {} \angle \Omega _{215}^{(s)}=\angle \Omega _{126}^{(s)}=\angle \Omega _{156}^{(s)} =\angle \Omega _{265}^{(s)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{15}^{(s)}=\varphi _{26}^{(s)}\equiv z ^{(3)}-l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(s)}= & {} \varphi _{56}^{(s)}\equiv \dot{x }^{(1)}=0,\; x ^{(1)}\ge x ^{(2)}+d ,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \angle \Omega _{3456}^{(s)}= & {} \angle \Omega _{435}^{(s)}=\angle \Omega _{346}^{(s)}=\angle \Omega _{356}^{(s)}=\angle \Omega _{465}^{(s)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{34}^{(s)}=\varphi _{56}^{(s)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ \varphi _{35}^{(s)}= & {} \varphi _{46}^{(s)}\equiv \dot{z }^{(3)}=0,x ^{(1)}\ge x ^{(2)}+d ,\;z ^{(3)}\ge l\sin \theta _0\bigr \},\nonumber \\ \angle \Omega _{179}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{17}^{(s)}=\varphi _{19}^{(s)}\equiv z ^{(3)}+l\sin \theta _0=0,\;\nonumber \\ \varphi _{79}^{(s)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)}\ge x ^{(2)}+d ,\;\dot{x }^{(1)}\ge 0\bigr \}, \end{aligned}$$

$$\begin{aligned} \angle \Omega _{28a}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{28}^{(s)}=\varphi _{2a}^{(s)}\equiv z ^{(3)}+l\sin \theta _0=0,\nonumber \\ \;\varphi _{8a}^{(s)}\equiv & {} \dot{z }^{(3)}=0,x ^{(1)}\ge x ^{(2)} +d ,\;\dot{x }^{(1)}\le 0\bigr \},\nonumber \\ \angle \Omega _{1278}^{(s)}= & {} \angle \Omega _{217}^{(s)}=\angle \Omega _{128}^{(s)}=\angle \Omega _{178}^{(s)}=\angle \Omega _{287}^{(s)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{17}^{(s)}=\varphi _{28}^{(s)}\equiv z ^{(3)}+l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(s)}= & {} \varphi _{78}^{(s)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\ge x ^{(2)}+d ,\;\dot{z }^{(3)}\ge 0\bigr \},\nonumber \\ \angle \Omega _{129a}^{(s)}= & {} \angle \Omega _{219}^{(s)}=\angle \Omega _{12a}^{(s)}=\angle \Omega _{19a}^{(s)}=\angle \Omega _{2a9}^{(s)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{19}^{(s)}=\varphi _{2a}^{(s)}\equiv z ^{(3)}+l\sin \theta _0=0,\nonumber \\ \varphi _{12}^{(s)}= & {} \varphi _{9a}^{(s)}\equiv \dot{x }^{(1)}=0,\;x ^{(1)}\ge x ^{(2)}+d ,\;\dot{z }^{(3)}\le 0\bigr \},\nonumber \\ \angle \Omega _{789a}^{(s)}= & {} \angle \Omega _{879}^{(s)}=\angle \Omega _{78a}^{(s)}=\angle \Omega _{79a}^{(s)}=\angle \Omega _{8a9}^{(s)}\nonumber \\= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)},\dot{z }^{(3)})\;|\; \varphi _{78}^{(s)}=\varphi _{9a}^{(s)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ \varphi _{79}^{(s)}= & {} \varphi _{8a}^{(s)}\equiv \dot{z }^{(3)}=0,x ^{(1)}\ge x ^{(2)}+d ,\;z ^{(3)}\le -l\sin \theta _0\bigr \},\nonumber \\ \angle \Omega _{123456}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{13}^{(s)}=\varphi _{15}^{(s)}=\varphi _{24}^{(s)} =\varphi _{26}^{(s)} \equiv z ^{(3)}-l\sin \theta _0=0, \nonumber \\{} & {} \varphi _{12}^{(s)}=\varphi _{34}^{(s)}=\varphi _{56}^{(s)}\equiv \dot{x }^{(1)}=0, \varphi _{35}^{(s)}=\varphi _{46}^{(s)}\equiv \dot{z }^{(3)}=0,\; x ^{(1)}\ge x ^{(2)}+d \bigr \},\nonumber \\ \angle \Omega _{12789a}^{(s)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)},z ^{(3)}, \dot{z }^{(3)})\;|\;\varphi _{17}^{(s)}=\varphi _{19}^{(s)}=\varphi _{28}^{(s)} =\varphi _{2a}^{(s)} \equiv z ^{(3)}+l\sin \theta _0=0,\nonumber \\{} & {} \varphi _{12}^{(s)}=\varphi _{78}^{(s)}=\varphi _{9a}^{(s)}\equiv \dot{x }^{(1)}=0, \varphi _{79}^{(s)}=\varphi _{8a}^{(s)} \equiv \dot{z }^{(3)}=0,\;x ^{(1)}\ge x ^{(2)}+d \bigr \}. \end{aligned}$$

(A.9)

Fig. 18

Domains, boundaries and edges of system M in four-dimensional coordinates where the stick motion between masses $m _1$ and $m _2$ occurs

With stick motion, the domains and boundaries of the mass $m _2$ are defined as:

$$\begin{aligned} \Omega _{1}^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\; |\;x ^{(2)}>x ^{(1)}-d ,\;\dot{x }^{(2)}<0\},\nonumber \\ \Omega _{2}^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\; |\;x ^{(2)}>x ^{(1)}-d ,\;\dot{x }^{(2)}>0\},\nonumber \\ \Omega _{3}^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\; |\;x ^{(2)}<x ^{(1)}-d ,\;\dot{x }^{(2)}<0\},\nonumber \\ \Omega _{4}^{(2)}= & {} \bigl \{(x ^{(2)},\dot{x }^{(2)})\; |\;x ^{(2)}<x ^{(1)}-d ,\;\dot{x }^{(2)}>0\}; \end{aligned}$$

(A.10)

$$\begin{aligned} \partial \Omega _{12}^{(2)}= & {} \partial \Omega _{21}^{(2)}=\bigl \{(x ^{(2)}, \dot{x }^{(2)})\;|\;\varphi _{12}^{(2)}=\varphi _{21}^{(2)}\equiv \dot{x }^{(2)}=0,\;\nonumber \\ x ^{(2)}> & {} x ^{(1)}-d \bigr \},\nonumber \\ \partial \Omega _{34}^{(2)}= & {} \partial \Omega _{43}^{(2)}=\bigl \{(x ^{(2)},\dot{x }^{(2)})\;|\; \varphi _{34}^{(2)}=\varphi _{43}^{(2)}\equiv \dot{x }^{(2)}=0,\;\nonumber \\ x ^{(2)}< & {} x ^{(1)}-d \bigr \},\nonumber \\ \partial \Omega _{13}^{(2)}= & {} \partial \Omega _{31}^{(2)}=\bigl \{(x ^{(2)},\dot{x }^{(2)})\;|\;\varphi _{13}^{(2)}=\varphi _{31}^{(2)}\nonumber \\\equiv & {} x ^{(2)}-x ^{(1)}+d =0,\;\dot{x }^{(2)}<0\bigr \},\nonumber \\ \partial \Omega _{24}^{(2)}= & {} \partial \Omega _{42}^{(2)}=\bigl \{(x ^{(2)},\dot{x }^{(2)})\;|\;\varphi _{24}^{(2)}=\varphi _{42}^{(2)}\nonumber \\\equiv & {} x ^{(2)}-x ^{(1)}+d =0,\;\dot{x }^{(2)}>0\bigr \}. \end{aligned}$$

(A.11)

The above regional division is depicted in Figs. 18 and 19. When the displacement difference between the masses $m _1$ and $m _2$ is greater than $d$, the domains, boundaries and edges of system M are shown in Fig. 18. In Fig. 19, the stick domains $\Omega _{3}^{(2)}$ and $\Omega _{4}^{(2)}$ of mass $m _2$ are represented by light blue and light gray, respectively. The velocity boundary $\partial \Omega _{34}^{(2)}$ with stick motion is represented by yellow dashed line; and the displacement boundaries $\partial \Omega _{13}^{(2)}$ and $\partial \Omega _{24}^{(2)}$ are also represented by black dotted-dashed curves.

Appendix B

The regions and boundaries of mass $m _1$ in two-dimensional coordinates are represented by Eqs. (B.1) and (B.2).

$$\begin{aligned} \Omega _{1}^{(1)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}>0\},\nonumber \\ \Omega _{2}^{(1)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)})\; |\;x ^{(1)}<x ^{(2)}+d ,\;\dot{x }^{(1)}<0\},\nonumber \\ \Omega _{3}^{(1)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}>0\},\nonumber \\ \Omega _{4}^{(1)}= & {} \bigl \{(x ^{(1)},\dot{x }^{(1)})\; |\;x ^{(1)}>x ^{(2)}+d ,\;\dot{x }^{(1)}<0\}; \end{aligned}$$

(B.1)

$$\begin{aligned} \partial \Omega _{12}^{(1)}= & {} \partial \Omega _{21}^{(1)}=\bigl \{(x ^{(1)},\dot{x }^{(1)})\;|\;\varphi _{12}^{(1)}=\varphi _{21}^{(1)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ x ^{(1)}< & {} x ^{(2)}+d \bigr \},\nonumber \\ \partial \Omega _{34}^{(1)}= & {} \partial \Omega _{43}^{(1)}=\bigl \{(x ^{(1)},\dot{x }^{(1)})\;|\;\varphi _{34}^{(1)}=\varphi _{43}^{(1)}\equiv \dot{x }^{(1)}=0,\;\nonumber \\ x ^{(1)}> & {} x ^{(2)}+d \bigr \},\nonumber \\ \partial \Omega _{13}^{(1)}= & {} \partial \Omega _{31}^{(1)}=\bigl \{(x ^{(1)},\dot{x }^{(1)})\;|\;\varphi _{13}^{(1)}=\varphi _{31}^{(1)}\nonumber \\\equiv & {} x ^{(1)}-x ^{(2)}-d =0,\;\dot{x }^{(1)}>0\bigr \},\nonumber \\ \partial \Omega _{24}^{(1)}= & {} \partial \Omega _{42}^{(1)}=\bigl \{(x ^{(1)},\dot{x }^{(1)})\;|\;\varphi _{24}^{(1)}=\varphi _{42}^{(1)}\nonumber \\\equiv & {} x ^{(1)}-x ^{(2)}-d =0,\;\dot{x }^{(1)}<0\bigr \}. \end{aligned}$$

(B.2)

Fig. 19

Domains and boundaries of mass $m _2$ in two-dimensional coordinates where the stick motion between masses $m _1$ and $m _2$ occurs

Fig. 20

Domains and boundaries of mass $m _1$ in two-dimensional absolute coordinates

Fig. 21

Relative domains and boundaries with stick motion for the two masses: a $m _1$ and b $m _2$

In Fig. 20, the free domains $\Omega _{1}^{(1)}$ and $\Omega _{2}^{(1)}$ are, respectively, shown in pink and orange, and the stick domains $\Omega _{3}^{(1)}$ and $\Omega _{4}^{(1)}$ are, respectively, painted as light blue and light gray. The velocity boundaries $\partial \Omega _{12}^{(1)}$ and $\partial \Omega _{34}^{(1)}$ are painted as red and yellow dashed lines, respectively. The black dotted-dashed curves indicate the displacement boundaries $\partial \Omega _{13}^{(1)}$ and $\partial \Omega _{24}^{(1)}$.

The relative domains and boundaries of mass $m _{i }$ $(i \ne \bar{i }\in \{1,2\})$ are expressed by

$$\begin{aligned} \Omega _{1}^{({i })}= & {} \bigl \{(z ^{({i })},\dot{z }^{({i })})\; |\;(-1)^{{i }}{} z ^{({i })}>-d ,\;(-1)^{{i }}\dot{z }^{(i )}<-(-1)^{{i }}\dot{x }^{(\bar{i })}\bigr \},\nonumber \\ \Omega _{2}^{({i })}= & {} \bigl \{(z ^{({i })},\dot{z }^{({i })})\; |\;(-1)^{{i }}{} z ^{({i })}>-d ,\;(-1)^{{i }}\dot{z }^{(i )}>-(-1)^{{i }}\dot{x }^{(\bar{i })}\bigr \},\nonumber \\ \Omega _{3}^{({i })}= & {} \bigl \{(z ^{({i })},\dot{z }^{({i })})\; |\;(-1)^{{i }}{} z ^{({i })}<-d ,\;(-1)^{{i }}\dot{z }^{(i )}<-(-1)^{{i }}\dot{x }^{(\bar{i })}\bigr \},\nonumber \\ \Omega _{4}^{({i })}= & {} \bigl \{(z ^{({i })},\dot{z }^{({i })})\; |\;(-1)^{{i }}{} z ^{({i })}<-d ,\;(-1)^{{i }}\dot{z }^{(i )}>-(-1)^{{i }}\dot{x }^{(\bar{i })}\bigr \}; \nonumber \\ \end{aligned}$$

(B.3)

$$\begin{aligned} \partial \Omega _{12}^{(i )}= & {} \partial \Omega _{21}^{(i )} =\bigl \{(z ^{(i )},\dot{z }^{(i )})\;|\;\varphi _{12}^{(i )} =\varphi _{21}^{(i )}\nonumber \\\equiv & {} \dot{z }^{(i )} +\dot{x }^{(\bar{i })}=0,\;(-1)^{i }{} z ^{({i })}>-d \bigr \},\nonumber \\ \partial \Omega _{34}^{(i )}= & {} \partial \Omega _{43}^{(i )}=\bigl \{(z ^{(i )}, \dot{z }^{(i )})\;|\;\varphi _{34}^{(i )}=\varphi _{43}^{(i )}\nonumber \\\equiv & {} \dot{z }^{(i )}+\dot{x }^{(\bar{i })}=0,\;(-1)^{i }{} z ^{({i })}<-d \bigr \},\nonumber \\ \partial \Omega _{13}^{(i )}= & {} \partial \Omega _{31}^{(i )}=\bigl \{(z ^{(i )}, \dot{z }^{(i )})\;|\;\varphi _{13}^{(i )}=\varphi _{31}^{(i )}\nonumber \\\equiv & {} z ^{(i )}+(-1)^{i }{} d =0,\;(-1)^{i }\dot{z }^{({i })}<0\bigr \},\nonumber \\ \partial \Omega _{24}^{(i )}= & {} \partial \Omega _{42}^{(i )}=\bigl \{(z ^{(i )}, \dot{z }^{(i )})\;|\;\varphi _{24}^{(i )}=\varphi _{42}^{(i )}\nonumber \\\equiv & {} z ^{(i )}+(-1)^{i }{} d =0,\;(-1)^{i }\dot{z }^{({i })}>0\bigr \}. \end{aligned}$$

(B.4)

As shown in Fig. 21, the time-independent displacement boundaries $\partial \Omega _{13}^{(i )}$ and $\partial \Omega _{24}^{(i )}$ $(i \in \{1,2\})$ become black straight lines.