Study the bifurcations of a 2DoF mechanical impacting system

Abstract

Impacting mechanical systems with suitable parameter settings exhibit a large amplitude chaotic oscillation close to the grazing with the impacting surface. The cause behind this uncertainty is the square root singularity and the occurrence of dangerous border collision bifurcation. In the case of one-degree-of-freedom mechanical systems, it has already been shown that this phenomenon occurs under certain conditions. This paper proposes the same uncertainty of a two-degree freedom mechanical impacting system under specific requirements. This paper shows that the phenomena earlier reported in the case of one-degree-of-freedom mechanical systems (like narrow band chaos, finger-shaped attractor, etc.) also occur in the two-degrees-of-freedom mechanical impacting system. We have numerically predicted that the narrowband chaos ensues under specific parameter settings. We have also shown that narrowband chaos can be avoided under some parameter settings. At last, we demonstrate the numerical predictions experimentally by constructing an equivalent electronic circuit of the mechanical rig.

1 Introduction

Various dynamical systems with impact phenomena have been observed and studied extensively in diverse scientific and engineering fields. These systems exhibit a wide range of dynamic behaviors, particularly when grazing occurs within specific parameter regions. Some of the notable phenomena observed in these systems include transitions between different periodic attractors, the occurrence of chaotic orbits at grazing, and the presence of finger-shaped chaotic attractors in the Poincaré section at the bifurcation point.

Over the past three decades, researchers have extensively investigated practical and engineering systems that involve impacts, especially focusing on one-degree-of-freedom mechanical impacting systems under various configurations. These studies have contributed valuable insights into the dynamics of these systems and have been documented in numerous research works [2, 5, 11, 12, 19, 20, 23, 25, 27].

These systems’ rich dynamics and complex behaviors have practical implications and find applications in diverse engineering and scientific disciplines. As research in this area continues, further advancements in understanding and controlling the behaviors of impacting systems are anticipated, offering potential applications in a wide array of fields.

The bifurcation structure of impact oscillators was investigated by Feigin [9]. Whiston [26] provided a numerical approach to study the dynamics, such as the steady-state analysis, phase-space diagrams, domains of attraction, etc., of a one-degree-of-freedom vibro-mechanical impacting system with and without excitations. Nordmark [18] showed the characteristics ‘Square root singularity’ at the grazing condition where one of the Jacobian elements of the Poincaré map goes to infinity, which leads to infinite local stretching in the state space. Peterka et al. [21], Ivanov [13], and Lenci et al. [15] showed the transition to chaos, its stabilization, and reduction of chaos at the grazing condition of a mechanical impacting system. Blazejczyk-Okolewska et al. have shown the co-existing attractors in impacting systems having dry friction under the influence of system noise [4]. Dankowicz et al. [6] have discussed the stability analysis and the bifurcations of a periodic orbit associated with the stick–slip oscillations. Bernardo et al. [7, 8] presented the unified framework of local analysis of grazing and sliding bifurcations. They showed that this leads to a normal map form under some general conditions, which contains a lower order square-root singularity or a $\frac{3}{2}$–singularity. Awrejcewicz et al. [1] studied numerically the dynamics of a triple pendulum having an impact and showed that under certain conditions, periodic, quasi-periodic, and chaotic motions were detected. Ma et al. [16] have studied the occurrence of large amplitude chaos of a soft impacting system and showed that in the case of a discrete map, during the bifurcation, the determinant of the Jacobian matrix remains invariant, and the trace shows a singularity at the grazing point. They have also shown how the character of a soft impacting system’s zero time discontinuity map changes over a range of parameters as the system is driven from a non-impacting orbit to an impacting orbit [17]. Ing et al. [11, 12] showed the bifurcation scenarios close to grazing experimentally for a nearly symmetrical piecewise linear mechanical impacting oscillator. They also have experimentally studied the bifurcations of an impact oscillator with a one-sided elastic constraint. Banerjee et al. [3] have discovered a narrow band of chaos close to the grazing condition for a simple soft impact oscillator experimentally for a range of system parameters. Also, numerical stability analysis shows that this abrupt onset of chaos is caused by a dangerous bifurcation where two unstable period-3 orbits take part at grazings. Kundu et al. [14] have numerically investigated the character of the normal form map in the neighborhood of a grazing orbit for four possible configurations of soft impacting systems. They have shown the conditions when there is an onset of chaos and under which this onset of chaos can be avoided for the one degree of freedom mechanical impacting systems. Suda and Banerjee [24] have shown that for one degree of freedom mechanical impacting system, one can avoid the narrow band chaos not just for singular parameter values but for a range of parameter values. They have demonstrated its mechanism by computing the interplay between stable and unstable periodic orbits in the bifurcation diagram. George et al. [10] showed some typical behaviors, such as finite-time transient behavior of the orbit before settling to a long-time behavior of an impacting mechanical system. Witkowski et al. [27] have studied the dynamics of a mechanical one-degree-of-freedom oscillator with harmonic forcing and impacts both numerically and experimentally. They have shown the bifurcation diagram obtained experimentally where a transition of chaos occurs from a periodic orbit under the variation of a parameter. Seth and Banerjee [22] have proposed an electronic switching circuit that can act as an analog of a one-degree-of-freedom mechanical impacting system. They have shown that the phenomena reported earlier through numerical simulation (like narrow-band chaos, finger-shaped attractor, etc.) also occur in the circuit. They have experimentally obtained the evolution of the chaotic attractor at grazing as the stiffness ratio varies, which is very hard to perform in mechanical rigs. They also have confirmed experimentally that the theoretical prediction of the occurrence of narrow-band chaos can be avoided for some discrete values of parameters.

While most of the earlier works have focused on theoretical investigations and experimental studies of one-degree-of-freedom mechanical impacting systems, there is a need to explore whether phenomena like narrow-band chaos and finger-shaped attractors can also occur in two-degree-of-freedom mechanical impacting systems. Further research in this direction is essential to deepen our understanding of the dynamics of such systems and their potential applications in various fields of science and engineering.

The primary objective of this paper is to propose a forced two-degree-of-freedom mechanical system incorporating compliant impact. Through various parameter configurations, we have demonstrated the occurrence of chaos in the bifurcation diagram when the amplitude of the externally applied periodic signal is varied. Moreover, we have established that a specific relationship between the externally applied signal’s frequency and the system’s natural frequencies can prevent the emergence of chaotic attractors, similar to observations made in one-degree-of-freedom mechanical impacting systems.

To further validate our findings, we have constructed an electronic circuit that closely mimics the behavior of the mechanical oscillator. Through numerical simulations and experimental investigations, we have confirmed that the dynamical phenomena observed in the one-degree-of-freedom mechanical system are also present in the two-degree-of-freedom system.

This paper showcases the intriguing dynamics and complexity that can arise in mechanical systems subjected to compliant impact, providing valuable insights into the behavior of such systems and their analogous electronic circuits.

2 Mechanical system under investigation

2.1 System description

Fig. 1

The schematic representation of a two-degree-of-freedom mechanical impacting system

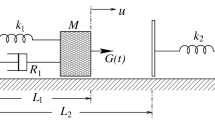
Figure 1 illustrates a schematic diagram of the two-degree-of-freedom mechanical system under investigation. The system is a forced, damped oscillator comprising two masses, $m_1$ and $m_2$, with a massless compliant obstacle that $m_1$ can impact. The compliant obstacle is connected to $m_2$ through a spring with spring constant $k_o$ and a damper with damping coefficient $c_o$. $m_1$ is attached to a fixed support by a spring with spring constant $k_1$ and a damper with damping coefficient $c_1$. $m_2$ is connected to the fixed support with a damper having a damping coefficient $c_2$. The two masses, $m_1$ and $m_2$, are connected with a spring having spring constant $k_\textrm{12}$.

The system is subjected to an external periodic forcing function F(t) applied to $m_2$; as a result of this external force, both $m_1$ and $m_2$ start to oscillate from their respective equilibrium positions. At equilibrium, when no external force is acting on $m_2$, there is a linear distance $\delta$ between the compliant obstacle and $m_1$.

Depending on the conditions, two situations can arise when a force is applied to $m_2$. First, there may be no impact, and in this scenario, both masses, $m_1$ and $m_2$, will oscillate under the influence of the force F(t). The second possibility is the occurrence of an impact between $m_1$ and the compliant wall. In between, a condition happens when $m_1$ touches the impacting surface attached to $m_2$, and the system reaches the grazing condition.

In our analysis, the friction terms related to the movements of the two masses with the hard surface have been neglected to simplify the system.

2.2 Mathematical equations of the model

The equations of motion for the considered system, taking into account the negligible effect of dry friction between the masses and the hard surface, can be expressed as follows:

For $(x_2 - x_1) < \delta$,

$$\begin{aligned} \begin{aligned} m_1\ddot{x}_1&= - c_1\dot{x}_1 - k_1x_1 - k_\textrm{12}(x_1-x_2) \\ m_2\ddot{x}_2&= - c_2\dot{x}_2 + k_\textrm{12}(x_1-x_2) + F(t) \end{aligned} \end{aligned}$$

(1)

and, for $(x_2 - x_1) \ge \delta$

$$\begin{aligned} \begin{aligned} m_1\ddot{x}_1 =&- c_1\dot{x}_1 - k_1 x_1 - k_\textrm{12}(x_1-x_2) - c_0 (\dot{x}_1 - \dot{x}_2) \\&- k_0 (x_1 - x_2 - \delta ) \\ m_2\ddot{x}_2 =&- c_2\dot{x}_2 + k_\textrm{12}(x_1-x_2) + c_0 (\dot{x}_1 - \dot{x}_2) \\&+ k_0 (x_1 - x_2 - \delta ) + F(t) \end{aligned} \end{aligned}$$

(2)

where $F(t) = F_o \sin (\varOmega t)$ represents the external excitation applied to mass $m_2$. In these equations, $m_1$ and $m_2$ denote the masses, $x_1$ and $x_2$ represent their displacements from equilibrium positions, $\dot{x}_1$ and $\dot{x}_2$ are their corresponding velocities, and $\ddot{x}_1$ and $\ddot{x}_2$ are their respective accelerations. The parameters $c_1$, $c_2$, $k_1$, $k_\textrm{12}$, $c_0$, $k_0$, $F_o$, and $\varOmega$ are the damping coefficients, spring constants, amplitude, and angular frequency of the external excitation, respectively. The parameter $\delta$ represents the linear distance between the compliant obstacle and $m_1$ at equilibrium, and $c_0$ and $k_0$ are the damping coefficient and spring constant of the compliant obstacle, respectively.

2.3 Non-dimensional form of the system

To simplify the analysis and study the dynamics numerically, we transform the dimensional Eqs. (1) and (2) into non-dimensional ones. We introduce the non-dimensional time $\tau = \omega _n t$, where $\omega _n = \sqrt{\frac{K_1}{m_1}}$ is the natural angular frequency of the mass $m_1$ attached to the fixed support. Next, we define the non-dimensional forcing frequency as $\omega = \frac{\varOmega }{\omega _n}$.

The non-dimensional state variables are defined as $y_i = \frac{x_i}{\delta }$ for $i = 1,2$. We then express the derivatives in terms of the non-dimensional time $\tau$ as follows: $\dot{x_i} = \frac{dx_i}{dt} = \frac{dx_i}{d\tau } \cdot \frac{d\tau }{dt} = \omega _n \delta y_i'$, and $\ddot{x}_i = \frac{d^2x_i}{dt^2} = \frac{d^2x_i}{d\tau ^2} \cdot \frac{d\tau ^2}{dt^2} = \omega _n^2 \delta y_i''$.

After going through some mathematical calculations, we obtain the non-dimensional equations as follows:

For $(y_2 - y_1) < 1$,

$$\begin{aligned} \begin{aligned} y^{\prime \prime }_1 =&- 2\xi _1 y^{\prime }_1 - y_1 - \beta (y_1 - y_2)\\ y^{\prime \prime }_2 =&- 2 \xi _2 y^{\prime }_2 + \frac{\beta }{\mu } (y_1-y_2) + f_0 \sin (\omega \tau ) \end{aligned} \end{aligned}$$

(3)

and, for $(y_2 - y_1) \ge 1$,

$$\begin{aligned} \begin{aligned} y^{\prime \prime }_1 =&- 2 \xi _1 y^{\prime }_1 - y_1 - \beta (y_1 - y_2) - 2 \xi _0 (y^{\prime }_1 - y^{\prime }_2) \\&- \beta _0 (y_1 - y_2 - 1) \\ y^{\prime \prime }_2 =&- 2\xi _2 y^{\prime }_2 + \frac{\beta }{\mu }(y_1 - y_2) + \frac{2 \xi _0}{\mu } (y^{\prime }_1 - y^{\prime }_2) \\&+ \frac{\beta _0}{\mu } (y_1 - y_2 - 1) + f_0 \sin (\omega \tau ) \end{aligned} \end{aligned}$$

(4)

where, $\xi _1 = \frac{c_1}{2 m_1 \omega _n}$, $\xi _2 = \frac{c_2}{2 m_2 \omega _n}$, $\xi _0 = \frac{c_0}{2 m_1 \omega _n}$, $\beta = \frac{k_{12}}{k_1}$, $\beta _0 = \frac{k_0}{k_1}$, $\mu = \frac{m_2}{m_1}$, $f_0 = \frac{F_0}{m_2 {\omega _n}^2 \delta }$, and $\omega _n = \sqrt{\frac{k_1}{m_1}}$. These non-dimensional equations describe the dynamics of the two-degree-of-freedom mechanical system under study.

2.4 Expressions of the natural frequencies

Given that our analyzed system exhibits a two-dimensional configuration, it manifests two discernible normal modes of vibration, each corresponding to its respective natural frequency. Utilizing Eq. (3), we are able to calculate these natural frequencies denoted as $\omega _\mathrm{+}$ and $\omega _\mathrm{-}$. During the process of examining the system’s free vibration behavior, we assume specific conditions where the damping coefficients ($\xi _1$ and $\xi _2$) and the external forcing function ($f_0$) are all equal to zero. As a result, the equations of motion undergo a simplification in this scenario.

$$\begin{aligned} \omega _\mathrm{\pm }{} & {} = \pm \frac{1}{\sqrt{2}}\Bigg [\Big \{\beta \Big (1 + \frac{1}{\mu }\Big ) + 1\Big \}\nonumber \\{} & {} \quad \pm \sqrt{\Big \{\beta \Big (1 + \frac{1}{\mu } \Big ) +1\Big \}^{2} - \frac{4\beta }{\mu }}\Bigg ]^\frac{1}{2} \end{aligned}$$

(5)

To obtain the natural frequencies, we need to specify the values of the parameters $\beta$ and $\mu$.

In the context of a one-degree-of-freedom mechanical impacting system, it has been noted that large amplitude chaotic oscillations emerge at the bifurcation point when the excitation frequency is a non-integer multiple of the system’s natural frequency. However, this onset of chaos can be mitigated by establishing a definite relationship between the external excitation frequency and the system’s natural frequency, as reported in previous studies [3, 14].

In our research, we shall investigate the occurrence of large amplitude chaotic oscillations at the bifurcation point under the condition that the externally applied signal’s frequency is not related to an integer multiple of some relations with the two natural frequencies. Similarly to previous observations, we aim to explore whether this chaotic behavior can be suppressed when the frequency relation approaches an integer multiple. Here, we note down that the average value of the system’s natural frequencies is given by:

$$\begin{aligned} \omega _\textrm{avg} = \frac{(\omega _\mathrm{+} + \omega _\mathrm{-})}{2} \end{aligned}$$

(6)

3 Numerical results from non-dimensional equations

To elucidate the distinctive dynamics of the analyzed mechanical system (1), we have opted to express the mathematical equations in non-dimensional forms, as represented by Eqs. (3) and (4). For our investigation, we have selected $f_0$ as a variable non-dimensional parameter while maintaining the remaining parameters constant. By incrementally increasing $f_0$ from lower to higher values, we have observed diverse system dynamics, leading to various orbital patterns. Our study has been focused on two specific conditions: (i) $\frac{\omega }{\omega _\textrm{avg}} = \frac{2}{m}$, where m is a non-integer, and (ii) m being an integer. The conditions are chosen in such a way as to make an analogy with the one-degree-of-freedom system and higher-degree-of-freedom systems.

3.1 $m = 2.5106$, i.e., the non-integer condition

The non-dimensional parameters are chosen as $\xi _1 = 0.014$, $\xi _2 = 0.018$, $\xi _0 = 6.6296 \times 10^{-4}$, $\beta = \frac{1}{10.4}$, $\beta _0 = 25.02$, and $\mu = \frac{1}{9.8}$. $f_0$ is considered to be varied. Using those parameter values, $\omega _{+}$ and $\omega _{-}$ are 1.1528 and 0.8420, respectively, which makes $\omega _\textrm{avg}$ 0.9974. For the simplicity of the calculation, we have approximated the $\omega _\textrm{avg}$ value to be unity. So, $\omega = \frac{2}{m}$.

Fig. 2

Time-series waveforms and the corresponding frequency spectra for different values of $f_0$. a Before impact for $f_0 = 0.1$, Period-1 orbit, b Close to the grazing condition for $f_0 = 0.17$, Chaotic orbit, c After bifurcation for $f_0 = 0.22$, period-1 orbit. In each subfigure, the upper trace is the time-series waveforms, The x-axis is the non-dimensional time, and the y-axis is the non-dimensional displacement ($y_2 - y_1$) (in blue color) compared with a constant value, 1 (in red color). The lower trace is the frequency spectra, where the x-axis is the nondimensional linear frequency and the y-axis is the Power spectrum. The initial condition is chosen at $(-\,0.5,-\,0.1,-\,0.01,1)$. (Color online)

Figure 2 illustrates distinct time-series waveforms corresponding to different values of the non-dimensional parameter $f_0$. In Fig. 2a, a period-1 waveform is depicted, accompanied by its corresponding frequency spectra. The presence of a single peak at the externally applied non-dimensional frequency, 0.1268, verifies the periodic nature of the orbit. Notably, the state-variable $(y_2 - y_1)$ does not reach a value of 1 in this case, indicating the system’s behavior before the occurrence of border collision. During this phase, both masses oscillate freely without experiencing an impact.

As the value of $f_0$ increases, grazing takes place between mass $m_1$ and the massless wall attached to mass $m_2$. Figure 2b showcases the existence of a chaotic orbit where $(y_2 - y_1)$ touches the value of 1, indicating proximity to the bifurcation point. At this juncture, the waveform becomes irregular, and the power spectrum spans a wide range across the frequency axis, though a peak remains at 0.1268 due to the periodic forcing applied.

Further increasing $f_0$ leads to the emergence of a period-1 orbit, characterized by conditions far from after the bifurcation. Figure 2c demonstrates the time-series waveform and corresponding frequency spectra of this period-1 orbit after the impact event.

Fig. 3

Phase-Space trajectories for different values of $f_0$. a Before impact for $f_0 = 0.1$, Period-1 orbit, b Close to the grazing condition for $f_0 = 0.17$, Chaotic orbit, c After bifurcation for $f_0 = 0.22$, Period-1 orbit. The x-axis is the non-dimensional velocity $y^{\prime }_2$ and the y-axis is the non-dimensional displacement $(y_2 - y_1)$. The initial condition is chosen at $(-\,0.5, -\,0.1, -\,0.01, 1)$. (Color online)

Fig. 3 displays different phase-space trajectories corresponding to various values of the non-dimensional parameter $f_0$, corresponding to the time-series waveforms shown in Fig. 2. The non-dimensional parameter values utilized are the same as those previously specified.

In Fig. 3a, a period-1 orbit is depicted for $f_0 = 0.1$. The orbit exhibits a single loop in the phase space, resulting in its periodic nature. This represents the situation before any impact occurs. As $f_0$ is increased further in the forward direction, grazing conditions emerge. For $f_0 = 0.17$, the orbit becomes chaotic, as evident from the erratic behavior exhibited in the phase space. This chaotic nature of the orbit persists over a range of $f_0$ values.

Figure 3c shows the phase-space diagram after the bifurcation. In this case, the orbit displays one loop in the phase-space, indicating a period-1 behavior.

Fig. 4

Poincaré section of the chaotic attractor close to grazing ($f_0 = 0.17$) for $m = 2.5106$ showing the large amplitude chaotic oscillation at the bifurcation. The x-axis is the non-dimensional velocity $y^{\prime }_2$ and the y-axis are the non-dimensional displacement $(y_2 - y_1)$. (Color Online)

In Fig. 4, a discrete-time phase-space attractor is presented, representing a state close to the grazing condition. The phase space is discretized based on the synchronization of the period of the input forcing sine wave function, which means the state variable is observed at regular intervals of T time, where $T = \frac{\omega }{2\pi }$.

The chaotic attractor observed at the bifurcation point exhibits a distinctive finger-shaped structure, reminiscent of what is commonly observed in one-degree-of-freedom mechanical impacting systems [3]. This structure confirms that the proposed two-degrees-of-freedom mechanical impacting system, with the specified parameter values, demonstrates similar phenomena to those observed in soft impacting one-degree-of-freedom systems near the grazing value.

The presence of fuzzy dots in the finger-shaped attractor is a result of the impacting wall being attached to mass $m_2$, causing it to move back and forth during the grazing process. These characteristics collectively contribute to the intricate dynamics of the system in the vicinity of the grazing condition.

Fig. 5

a Bifurcation diagram (Blue color) and b the maximal Lyapunov Exponent (red color) plot in non-dimensional parameter space of the system (1) for $m = 2.5106$ showing the large amplitude chaotic oscillation in the bifurcation diagram around the bifurcation point when the bifurcation parameter $f_0$ is varied smoothly from 0.08 to 0.28. (Color online)

In Fig. 5a, the numerically obtained bifurcation diagram of the system (1) is presented. In this diagram, the bifurcation parameter is represented by $f_0$, while the remaining parameters are held constant (as indicated at the beginning of this section). As $f_0$ increases, a border collision bifurcation occurs, wherein a period-1 orbit undergoes a transformation into other periodic orbits with different periodicities through chaotic oscillations around the bifurcation point. This specific phenomenon is observed when the parameter m takes on a non-integer value (in our case, $m = 2.5106$).

Figure 5b illustrates the corresponding maximal Lyapunov Exponent within the parameter space of $f_0$. The maximal Lyapunov Exponent exhibits positive values when chaos occurs in the bifurcation diagram, while it shows negative values for periodic orbits. Similar behavior has been previously reported in the equivalent one-degree-of-freedom mechanical impacting system [24]. This characterization of the maximal Lyapunov Exponent serves as an important indicator of the presence of chaos and periodicity within the system dynamics.

3.2 $m = 2.1$, i.e., close to integer value

Fig. 6

a Bifurcation diagram (in blue color) and b the corresponding maximal Lyapunov Expoent (in red color) in the non-dimensional parameter space of the system (1) at close to an integer value of m. The parameter $f_0$ of both the figures varied smoothly from 0.4 to 1.4. (Color Online)

In Fig. 6a, the numerically obtained bifurcation diagram is presented for the case when $m = 2.1$, which is close to an integer value of m. The other parameters have been kept fixed as in the previous case. When varying the bifurcation parameter $f_0$ in the forward direction, i.e., from low to high values, a period-1 orbit emerges after bifurcation from another period-1 orbit. Notably, no chaotic orbits are observed close to the bifurcation point, as was the case when m was a non-integer value.

In Fig. 6a, the bifurcation point represents a situation where a period-1 attractor transforms into another period-1 attractor with distinct amplitude and frequency. This bifurcation diagram indicates that the occurrence of large amplitude chaos in a two-degree-of-freedom mechanical impacting system can be avoided when m is an integer or close to an integer value. Similar observations have been reported in the context of a schematic representation of a one-degree-of-freedom mechanical impacting system [24].

Figure 6b shows the corresponding maximal Lyapunov Exponent, which consistently displays negative values throughout the parameter range. This confirms the absence of a chaotic attractor in the bifurcation diagram, further supporting the notion that large amplitude chaos can be mitigated in the system when m is an integer or close to an integer value.

Fig. 7

Time-series waveforms and the corresponding frequency spectra for different values of $f_0$ at $m=2.1$. a Before impact for $f_0 = 0.6$, Period-1 orbit, b After the bifurcation for $f_0 = 1.2$, also a periodic orbit. In the upper trace of each figure, the x-axis is the non-dimensional velocity $y^{\prime }_2$, and the y-axis is the non-dimensional displacement $(y_2 - y_1)$ with blue color compared with a constant value 1 with the red color. In the case of the lower trace, the x-axis is the nondimensional frequency, and the y-axis is the normalized power spectra. (Color online)

Fig. 8

Phase-Space trajectories for different values of $f_0$ at $m=2.1$. a Before impact for $f_0 = 0.6$, Period-1 orbit, b After the bifurcation for $f_0 = 1.2$, also a periodic orbit having different amplitude. The x-axis is the non-dimensional velocity $y^{\prime }_2$ and the y-axis is the non-dimensional displacement $(y_2 - y_1)$. (Color online)

Figure 7 depicts various time-series waveforms of the displacement $(y_2 - y_1)$ compared to a constant value of 1, corresponding to different values of $f_0$ when $m = 2.1$. In Fig. 7a, a period-1 waveform is shown before the bifurcation. The waveform of $(y_2 - y_1)$ does not reach the constant value of 1 during this period-1 attractor. The corresponding phase-space diagram, Fig. 8a, shows the state of the system in the period-1 orbit before the bifurcation, with no points touching the reference level.

The bifurcation occurs when $(y_2 - y_1)$ touches the value of 1. Following the bifurcation, Fig. 7b displays the time-series waveform of a period-2 attractor. Figure 8b represents the corresponding phase-space diagram of the period-2 orbit after the bifurcation. Here, one loop in the phase space touches the reference level (the impacting surface) while the other loop does not.

An important note to consider is that although the time series and phase-space diagrams reveal two loops in the periodic orbit, the bifurcation diagram shows only one point on the Poincaré plane corresponding to that orbit. This discrepancy arises because the considered rig is a non-autonomous dynamical system, and we are observing points on the phase space at intervals of $\tau$, which is the non-dimensional time period of the externally applied periodic forcing. Consequently, despite having two loops in the orbit due to the different frequencies, we obtain one value of the state variable at each sample with a $\tau$-time period, resulting in a single point in the Poincaré section.

To investigate the behavior of the system when $m = 2.21$, close to an integer value, we examined the bifurcation diagram. For a one-degree-of-freedom mechanical impacting system, it has been reported that there is no chaos in the bifurcation diagram for a soft impacting system under similar conditions [24].

Fig. 9

Bifurcation diagram in non-dimensional parameter space for $m = 2.21$, i.e., close to the integer condition. (Color online)

The numerically obtained bifurcation diagram of the system for $m = 2.21$ is presented in Fig. 9. Strikingly, this diagram bears resemblance to the figure depicted in Fig. 6. As the bifurcation parameter $f_0$ undergoes a smooth increment, a border collision bifurcation occurs, whereby a period-1 orbit transitions into another type of period-1 orbit. However, the noteworthy observation is that at the point of this bifurcation, where the period-1 orbit with a frequency emerges from a period-1 orbit having a frequency equal to the frequency of the external forcing function frequency, there is an absence of large amplitude chaotic oscillations. This finding unequivocally confirms that when the value of m approaches an integer, the occurrence of large amplitude oscillations can be effectively circumvented.

The analysis of the bifurcation diagram for $m = 2.21$ in our two-degree-of-freedom mechanical impacting system confirms the absence of narrow band chaos close to the bifurcation point, just as observed in the equivalent one-degree-of-freedom system. This suggests that the disappearance of narrow-band chaos near the bifurcation point is consistent when the value of m is close to an integer, regardless of the system’s degree of freedom. This observation further supports the notion that certain parameter configurations, specifically when m is close to an integer, can lead to a more predictable and stable behavior in impacting systems.

4 Equivalent electronic circuit of the considered mechanical system

4.1 Schematic representation

Fig. 10

a The switching circuit under consideration. b Switch ON instant: The subsystem for $V_\textrm{C2} < V_\textrm{ref}$, c Switch OFF Instant: The subsystem for $V_\textrm{C2} \ge V_\textrm{ref}$

The electronic analog circuit representing the considered mechanical system (1) introduced in this paper is depicted in Fig. 10a. We assume that the equivalent mechanical impacting system possesses low damping and high stiffness. In this scenario, we set the separation between the impacting wall and the mass $m_1$ to zero, simplifying the circuit without significantly altering its dynamics.

The electronic circuit system consists of two LCR circuits with an input voltage $V_\textrm{in}$, which is a sinusoidal wave with an amplitude $V_\textrm{amp}$ and a linear frequency f. The system incorporates an analog switch S, controlled by an op-amp-based comparator. When the voltage across capacitor $C_2$, denoted as $V_\textrm{C2}$, falls below a reference voltage $V_\textrm{ref}$, the switch is in the ‘ON’ state, resulting in the circuit configuration shown in Fig. 10b. Conversely, when $V_\textrm{C2} \ge V_\textrm{ref}$, the switch turns ‘OFF,’ connecting the series capacitor $C_0$ and resistor $R_0$ in parallel across the switch with the circuit, as illustrated in Fig. 10c.

Let $i_2$ represent the current flowing through the inductor $L_2$ and resistance $R_2$, where $i_2 = \frac{dq_2}{dt}$. In this context, $q_2$ signifies the charge stored in capacitor $C_\textrm{2}$ due to the current $i_2$. Similarly, let $i_1$ denote the current flowing through the inductor $L_1$, with $i_1 = \frac{dq_1}{dt}$, and $q_1$ representing the charge stored in capacitor $C_1$ due to the current flow $i_1$. These variables, namely $i_1$, $i_2$, $q_1$, and $q_2$, constitute the system’s state variables, resulting in a four-dimensional system representation.

The system parameters encompass $R_1$, $R_2$, $R_0$, $L_1$, $L_2$, $C_\textrm{1}$, $C_\textrm{2}$, $C_0$, $V_\textrm{ref}$, the driving frequency $f = \frac{\varOmega _e}{2\pi }$, and $V_\textrm{amp}$, where $\varOmega _e$ denotes the angular frequency of the input sinusoidal signal. Notably, $V_\textrm{amp}$ is employed as the bifurcation parameter while keeping the remaining parameters at constant values.

4.2 Mathematical model

When considering all the circuit components to be ideal, the system can be described by a set of second-order ordinary differential equations (ODEs) that constitute a 4D piecewise smooth model, given as follows:

For $(q_2 - q_1) < q_\textrm{ref}$:

$$\begin{aligned} \begin{aligned} L_1\ddot{q}_1&= - R_1\dot{q}_1 - \frac{q_1}{C_1} - \frac{q_1-q_2}{C_2} \\ L_2\ddot{q}_2&= - R_2\dot{q}_2 - \frac{q_2 - q_1}{C_2} + V_\textrm{amp} \sin (\varOmega _e t) \end{aligned} \end{aligned}$$

(7)

and, for $(q_2 - q_1) \ge q_\textrm{ref}$:

$$\begin{aligned} \begin{aligned} L_1\ddot{q}_1 =&- R_1\dot{q}_1 - \frac{q_1}{C_1} - \frac{q_1 -q_2}{C_2} - R_0 (\dot{q}_1 - \dot{q}_2) \\&- \frac{q_1 - q_2}{C_0}\\ L_2\ddot{q}_2 =&- R_2\dot{q}_2 + \frac{q_1 - q_2}{C_2} + R_0 (\dot{q}_1 - \dot{q}_2) \\&+ \frac{q_1 - q_2}{C_0} + V_\textrm{amp} \sin (\varOmega _e t) \end{aligned} \end{aligned}$$

(8)

Here, $q_\textrm{ref}$ is defined as $V_\textrm{ref}\cdot C_\textrm{2}$. It is important to note that in this system, when the switch is in the ‘ON’ state (Fig. 10b), the system follows Eq. (7). Conversely, when the switch is in the ‘OFF’ state (Fig. 10c), the system follows Eq. (8). Consequently, the system can be represented in a discrete-time realization through a 4D piecewise smooth map with two compartments separated by a border. The condition represents the borderline between the two compartments where the value of $(q_2 -q_1)$ reaches $q_\textrm{ref}$ precisely at the Poincaré observation instants (maximum positive amplitude of the input sine wave).

4.3 Non-dimensional equations of the circuit equations

To obtain the non-dimensional equations for the analog electronic circuit, we follow a similar procedure as described in Sect. 2.3. By reformulating the dimensional Eqs. (7) and (8), we arrive at the non-dimensional equations as follows:

For $(z_2 - z_1) < e$:

$$\begin{aligned} \begin{aligned} z^{\prime \prime }_1 =&- 2\xi _1 z^{\prime }_1 - z_1 - \beta (z_1 - z_2)\\ z^{\prime \prime }_2 =&- 2 \xi _2 z^{\prime }_2 + \frac{\beta }{\mu } (z_1 - z_2) + v_0 \sin (\omega \tau ) \end{aligned} \end{aligned}$$

(9)

and, for $(z_2 - z_1) \ge e$:

$$\begin{aligned} \begin{aligned} z^{\prime \prime }_1 =&- 2 \xi _1 z^{\prime }_1 - z_1 - \beta (z_1 - z_2) - 2 \xi _0 (z^{\prime }_1 - z^{\prime }_2) \\&- \beta _0 (z_1 - z_2) \\ z^{\prime \prime }_2 =&- 2\xi _2 z^{\prime }_2 + \frac{\beta }{\mu }(z_1 - z_2) + \frac{2 \xi _0}{\mu } (z^{\prime }_1 - z^{\prime }_2) \\&+ \frac{\beta _0}{\mu } (z_1 - z_2) + v_0 \sin (\omega \tau ) \end{aligned} \end{aligned}$$

(10)

In these equations, the non-dimensional displacement is represented as $z_i = \frac{q_i}{q_0}$, where $q_0$ is the characteristic displacement. The non-dimensional time is denoted as $\tau = \omega _n t$, with $\omega _n = \sqrt{\frac{1}{L_1C_1}}$ being the natural frequency. The dimensionless parameters are defined as follows: $\xi _1 = \frac{R_1}{2 L_1 \omega _n}$, $\xi _2 = \frac{R_2}{2 L_2 \omega _n}$, $\xi _0 = \frac{R_0}{2 L_1 \omega _n}$, $e = \frac{C_2 V_\textrm{ref}}{q_0}$, $\beta = \frac{C_\textrm{1}}{C_2}$, $\beta _0 = \frac{C_1}{C_0}$, $\mu = \frac{L_2}{L_1}$, and $v_0 = \frac{V_\textrm{amp}}{L_2 {\omega _n}^2 q_0}$.

Upon comparison of Eqs. (3), (4), and Eqs. (9), (10), we observe that the pairs of equations are equivalent to each other. The only difference between them lies in the presence of two additional terms in Eq. (4), namely $\beta _0 e$ and $- \frac{\beta _0 e}{\mu }$. However, these terms are constant values and do not significantly impact the system’s dynamics. They merely cause a positive shift in the bifurcation point for Eqs. (3) and  (4). This subsection will correspond to the conversion of a mechanical impacting system to an equivalent analog electronic circuit.

In the next section, we will present the numerical results of Eqs. (3) and (4).

4.4 Numerical results from the circuit equations

To set up the electronic circuit and appropriately consider the parameter values in a real experimental environment, we first plot the time-series waveforms of the circuit numerically in Fig. 10a under suitable parameter settings. The purpose of this section is to observe whether the electronic circuit, under a specific parameter configuration, accurately emulates the behavior of the mechanical impacting system (1) or not.

We present the time-series waveforms of the electronic circuit shown in Fig. 10a, obtained through numerical simulations, ensuring that the chosen parameter values are well-suited for simulating the mechanical impacting system. This investigation allows us to assess the circuit’s ability to mimic and replicate the dynamics exhibited by the mechanical impacting system (1).

Fig. 11

Time-Series waveforms of the circuit from simulation. a Period-1 orbit for $V_\textrm{amp} = 0.3$ V before reaching the reference voltage, $q_\textrm{ref}$, b Chaotic orbit for $V_\textrm{amp} = 0.57$ V when $(q_2-q_1)$ touches $q_\textrm{ref}$, c Period-1 orbit at $V_\textrm{amp} = 0.71$ V after the bifurcation. In each subfigure, the upper trace (blue color) is the charge stored in capacitor $C_2$ compared with $q_\textrm{ref} = V_\textrm{ref} \cdot C_2$ and the lower trace (green color) is the normalized comparator output. The initial condition is chosen at $(-\,0.5\,V, -\,0.1\,V, -\,0.01\,V, 1\,V, 0.001\,V)$. (Color online)

Figure 11 presents several numerically obtained time-series waveforms for the considered equivalent electronic circuit under specific parameter values of $V_\textrm{amp}$. The constant parameter values used are: $L_1 = 100.4$ mH, $L_2 = 10.21$ mH, $R_1 = 230$ $\varOmega$, $R_2 = 29.7$ $\varOmega$, $C_1 = 1.601$ nF, $C_2 = 16.680$ nF, $R_0 = 10.5$ $\varOmega$, $C_0 = 64.0$ pF, $V_\textrm{ref} = 3.0$ V, and $f = 10$ kHz. The amplitude of the applied sine voltage, $V_\textrm{amp}$, is varied to explore different dynamical behaviors.

When the charge stored in the capacitor $C_2$, $(q_2 - q_1)$, remains below the reference charge $q_\textrm{ref}$, the comparator output remains high, i.e., 1. This situation represents the condition before border collision, and the circuit exhibits a period-1 waveform, as shown in Fig. 11a. As $V_\textrm{amp}$ is increased to a point where $(q_2 - q_1)$ touches $q_\textrm{ref}$, at the bifurcation point, the dynamics of the state variable becomes chaotic in nature, as demonstrated in Fig. 11b. The comparator output becomes erratic during this chaotic behavior.

For higher values of $V_\textrm{amp}$, $(q_2 - q_1)$ returns to a periodic behavior, although it hits the switching condition $q_\textrm{ref}$. The corresponding time-series waveform and the comparator output are shown in Fig. 11c. Therefore, it is evident that the system exhibits a chaotic attractor within a small range of the parameter space, specifically during the grazing condition. Before and after the grazing conditions, the orbits remain periodic. The same phenomena have been reported in the equivalent electronic circuit of a one-degree-of-freedom mechanical impacting system [22].

This observation highlights the circuit’s capability to reproduce various dynamic behaviors, including periodic and chaotic states, similar to what was observed in the mechanical impacting system, validating its equivalence for certain parameter settings.

We shall now observe the discrete-time representation of the chaotic attractor from the circuit close to the bifurcation to check the attractor’s shape as obtained in the case of the considered mechanical impacting system as shown in Fig. 4.

Fig. 12

a Phase space diagram and b Poincaré section of the chaotic attractor close to grazing for m non-integer condition. The x-axis is the value of the current flowing through the inductor $L_2$, $\dot{q}_2$, and the y-axis is the charge of the capacitor $C_2$, $(q_2-q_1)$, in F. (Color online)

Figure 12a shows the phase-space diagram of the circuit for m non-integer condition. The amplitude of the externally applied sine wave is $V_\textrm{amp} = 0.57$ V. The remaining fixed parameter is shown earlier in this section. The attractor is chaotic during the bifurcation. Figure 12b depicts the Poincaré section of that chaotic attractor at grazing. Here also, the discrete-time representation of the chaotic attractor is finger-shaped. This finger-shaped attractor was discussed earlier in [3]. This confirms that the proposed circuit can be used to validate the numerical prediction of the considered mechanical system (1).

Fig. 13

Bifurcation diagrams of the equivalent circuit when input voltage amplitude $V_\textrm{amp}$ is used as varying parameter for (a) m is non-integer and (b) m is close to an integer value. For (a) $f = 10$ kHz and for (b) $f = 11.96$ kHz. The x-axis is the amplitude of the externally applied sinusoidal signal, $V_\textrm{amp}$ in V and the y-axis is the charge stored in the capacitor $C_2$ in F

In Fig. 13a, the numerically obtained bifurcation diagram of the considered electronic circuit is presented when m is a non-integer value. In this diagram, $V_\textrm{amp}$ is taken as the bifurcation parameter, while the remaining parameters are kept fixed (as stated earlier in this section). When m is a non-integer value, the bifurcation diagram displays a border collision bifurcation from a periodic orbit to another periodic orbit with different periodicities, characterized by large amplitude chaotic oscillations around the bifurcation point. This observation aligns with the findings presented in Fig. 5 for the mechanical impacting system.

Figure 13b shows the bifurcation diagram when m is close to an integer value. In this case, no chaotic attractor is observed at the bifurcation. This corresponds to the same phenomena observed in the equivalent circuit of a one-degree-of-freedom mechanical impacting system [22].

Overall, these results support the notion that the electronic circuit behaves analogously to the mechanical impacting system under certain parameter configurations, exhibiting similar bifurcation patterns and dynamics. The absence of chaotic attractors when m is close to an integer value further supports the hypothesis that specific parameter settings can avoid chaotic behavior, making the system more predictable and stable.

5 Experimental results

Fig. 14

Circuit diagram of the experimental system. LM324 is an Op-Amp, LM311P is a comparator, and CD4053BE is a CMOS single 8-channel analog multiplexer/demultiplexer with logic-level conversion. The parameter values are: $L_1 = 100.4$ mH (internal impedence 71.7 $\varOmega$), $L_2 = 10.21$ mH (internal impedence 13.6 $\varOmega$), $R_1 = 158.3$ $\varOmega$, $R_2 = 16.1$ $\varOmega$, $C_1 = 1.601$ nF, $C_2 = 16.680$ nF, $R_0 = 10.5$ $\varOmega$, $C_0 = 64.0$ pF, $f = 10$ kHz, and $V_\textrm{ref} = 3.0$ V. The supply voltages have been taken as $\pm V_\textrm{CC} = \pm 12$ V. (Color Online)

Figure 14 showcases the circuit diagram used for the experimental setup, developed to validate the numerically predicted results with the same parameter values. For minimizing the loading effect of the signal generator, a quad LM324 op-amp is utilized as a unity gain buffer. The LM311P serves as a comparator to compare the voltage $V_\textrm{C2}$, which corresponds to the voltage across capacitor $C_2$, with the constant reference voltage $V_\textrm{ref}$. When $V_\textrm{C2} < V_\textrm{ref}$, the comparator output remains in the on state, while it switches to the off state otherwise. To achieve the desired functionality, CD4053BE is used as an analog switch.

In the experimental setup, the amplitude value of the input voltage, denoted as $V_\textrm{amp}$, is chosen from a signal generator. This setup allows for conducting real-world experiments, enabling the validation of the theoretical predictions and the agreement of the circuit’s behavior with the numerically obtained results.

Fig. 15

Time-Series waveforms of the circuit from experiment: x-axis is the time and y-axis is the voltage in V. a Period-1 waveform for $V_\textrm{amp} = 0.3$ V (Grid division: 1.00 V), b Chaotic waveform for $V_\textrm{amp} = 0.57$ V (Grid division: 1.00 V), c Period-1 waveform after the bifurcation at $V_\textrm{amp} = 0.72$ V (Grid division: 2.00 V). In each subfigure, the upper trace is the voltage across the capacitor $C_2$. The lower trace is the Spread spectrum characteristics. FFT sample rate 2.50 MSa/s, span 25.00 kHz, center 216.0 kHz, scale 20 dB. (Color online)

Figure 15 presents the CRO traced time-series waveforms obtained experimentally for the circuit (10). At $V_\textrm{amp} = 0.3$ V, the waveform exhibits a period-1 orbit, as shown in Fig. 15a. The presence of a single peak in the frequency spectrum confirms the periodic nature of the orbit.

As the parameter $V_\textrm{amp}$ is varied, a chaotic waveform is generated at $V_\textrm{amp} = 0.57$ V. The corresponding frequency spectra confirm the chaotic behavior of the orbit, as shown in Fig. 15b. This is the condition during the border collision bifurcation, where the system undergoes a transition from a periodic orbit to a chaotic one.

After the bifurcation, the voltage across capacitor $C_2$, denoted as $V_\textrm{C2}$, becomes periodic, as illustrated in Fig. 15c. The corresponding frequency spectra are presented alongside the waveform.

Fig. 16

Phase-space diagrams for different attractors obtained from experiment: x-axis is the voltage across resistance $R_2$, i.e., $V_\textrm{R2}$ in V and y-axis is the voltage across the capacitor $C_2$, $V_\textrm{C2}$ in V. a Period-1 orbit for $V_\textrm{amp} = 0.3$ V, b Chaotic orbit for $V_\textrm{amp} = 0.57$ V, c Period-1 orbit after bifurcation at $V_\textrm{amp} = 0.72$ V. In each subfigure, the grid divisions are: along the x-axis 50 mV and along the y-axis 2.00 V. (Color online)

Figure 16 displays the experimentally obtained phase-space trajectories for different values of $V_\textrm{amp}$ in the equivalent electronic circuit (10). In Fig. 16a, a period-1 orbit is observed for $V_\textrm{amp} = 0.3$ V. The presence of a single loop in the phase space confirms that the orbit is periodic. This represents the condition before the bifurcation. Figure 16b illustrates the erratic and complex nature of the orbit in the phase space at $V_\textrm{amp} = 0.57$ V, indicative of chaotic behavior. This condition occurs during the bifurcation. Figure 16c reveals the existence of a period-1 attractor after the bifurcation, where the phase-space trajectory forms a single loop.

The experimental results consistently support the theoretical findings, demonstrating that when the forced frequency is a non-integer multiple of twice the average value of the two natural frequencies, the system exhibits chaos in the bifurcation diagram around the grazing of the equivalent circuit, mimicking the behavior of the mechanical oscillator. The agreement between the experimental and theoretical results reinforces the circuit’s equivalence to the mechanical impacting system and its ability to reproduce similar bifurcation patterns and dynamics.

Fig. 17

Time-Series waveforms of the circuit from experiment: x-axis is the time and y-axis is the voltage in V. (a) Period-1 waveform for $V_\textrm{amp} = 2.50$ V (Grid division: 1.00 V), (b) Period-1 waveform after the bifurcation at $V_\textrm{amp} = 3.10$ V (Grid division: 1.00 V). In each subfigure, the upper trace is the voltage across the capacitor $C_2$. The lower trace is the Spread spectrum characteristics. FFT sample rate 2.50 MSa/s, span 25.00 kHz, center 216.0 kHz, scale 20 dB. (Color online)

Figure 17 presents the experimentally obtained time-series waveforms when the externally applied frequency is close to an integer multiple of the average of the two natural frequencies. Figure 17a shows the period-1 waveform before the bifurcation at $V_\textrm{amp} = 2.50$ V. The presence of a single peak in the frequency spectra confirms the periodic nature of the waveform. At this point, the maximum amplitude of $V_\textrm{C2}$ does not cross the DC reference voltage, i.e., $V_\textrm{ref} = 3.0$ V. Figure 17b depicts the waveform of $V_\textrm{C2}$ after the bifurcation at $V_\textrm{amp} = 3.10$ V. This waveform is also period-1 in nature. At this stage, the voltage $V_\textrm{C2}$ has crossed the DC voltage $V_\textrm{ref} = 3.0$ V.

It is worth noting that the experimentally obtained time-series waveform after the bifurcation at $V_\textrm{amp} = 3.10$ V does not perfectly match the numerical prediction. The discrepancy arises due to various unavoidable factors in the experimental circuit implementation, such as the resistance of connecting wires, the tolerance level of capacitors and inductors, ICs’ time delay of propagation, etc. These uncertainties contribute to the slight change in the waveform compared to the numerical prediction. However, despite these differences, the overall dynamics remain the same, demonstrating the robustness of the circuit’s equivalence.

The experimental investigation was extended to examine other parameter values in the bifurcation diagram. In the entire parameter range, no chaotic waveform was observed, and the chaotic attractor was absent, confirming that chaotic oscillation can be avoided when m is either an integer or close to an integer. The experimental results effectively validate and corroborate the numerically predicted outcomes.

In conclusion, the experimental results provide strong support for the numerical predictions, further validating the circuit’s equivalence to the mechanical impacting system and confirming the avoidance of chaotic behavior when m is close to an integer value. The small discrepancies between the experimental and numerical results highlight the real-world challenges in circuit implementation but do not compromise the fundamental dynamics and overall agreement between theory and experiment.

6 Conclusions

In this study, we have presented a schematic representation of a two-degree-of-freedom forced damped mechanical impacting oscillator. Our findings reveal that when the externally applied frequency deviates from an integer multiple of the summation of the two natural frequencies, chaos emerges in the bifurcation diagram. The chaotic attractor at the bifurcation point demonstrates a distinct finger-shaped discrete-time representation. Analogous behavior has been observed in a one-degree-of-freedom mechanical impacting system. Additionally, we have demonstrated that when the forcing frequency closely aligns with an integer multiple of the summation of the two natural frequencies, chaos can be avoided.

By non-dimensionalizing the equations governing the system and establishing a one-to-one correspondence between the mechanical and electronic equivalent circuit, we have demonstrated that the considered system exhibits similar dynamic phenomena as reported in one-degree-of-freedom mechanical impact oscillators. Notably, this includes the occurrence of narrowband chaos, the appearance of a finger-shaped attractor near the grazing parameter value, and the disappearance of chaotic oscillations within specific parameter ranges.

To facilitate experimental investigations on impacting systems, we have introduced an electronic analog of the mechanical impacting system. The electronic equivalent circuit provides a convenient and direct platform for practical explorations. We have successfully validated our numerical predictions through experimental circuit results.

Overall, our study offers valuable insights into the occurrence and avoidance of narrow-band chaos in two-degree-of-freedom mechanical impacting systems. In future research, we plan to conduct more comprehensive analytical and numerical investigations on other types of two-degree-of-freedom mechanical impacting systems to make this claim more robust.