Frequency combs in a MEMS resonator featuring 1:2 internal resonance: ab initio reduced order modelling and experimental validation

Abstract

This paper is devoted to a detailed analysis of the appearance of frequency combs in the dynamics of a micro-electro-mechanical systems (MEMS) resonator featuring 1:2 internal resonance. To that purpose, both experiments and numerical predictions are reported and analysed to predict and follow the appearance of the phononic frequency comb arising as a quasi-periodic regime between two Neimark-Sacker bifurcations. Numerical predictions are based on a reduced-order model built thanks to an implicit condensation method, where both mechanical nonlinearities and electrostatic forces are taken into account. The reduced order model is able to predict a priori, i.e. without the need of experimental calibration of parameters, and in real time, i.e. by solving one or two degrees-of-freedom system of equations, the nonlinear behaviour of the MEMS resonator. Numerical predictions show a good agreement with experiments under different operating conditions, thus proving the great potentiality of the proposed simulation tool. In particular, the bifurcation points and frequency content of the frequency comb are carefully predicted by the model, and the main features of the periodic and quasi-periodic regimes are given with accuracy, underlining that the complex dynamics of such MEMS device is effectively driven by the characteristics of the 1:2 internal resonance.

1 Introduction

The spread of MEMS in the consumer market is rapidly increasing thanks to their small dimensions, high performances and low costs. At the same time, new application fields for MEMS devices are emerging and rapidly evolving, e.g. Internet of Things, Aerospace, high-end applications, virtual or augmented reality. This is posing an important challenge to MEMS designers that have to simultaneously improve the effectiveness of actual devices and find innovative working principles that go beyond the actual state of the art mainly limited to linear dynamic behaviours of mechanical components. In this context, nonlinear phenomena usually avoided by design [28, 68] are starting to emerge as promising solutions to improve performances of existing MEMS devices [4, 61] and/or to design a new generation of sensors and actuators [37, 73].

Among other nonlinear phenomena, phononic frequency combs, which are the mechanical counterparts of photonic frequency combs largely studied in the literature with specific reference to optic metrology [85], are attracting interest from the MEMS community since they can be employed as efficient sensing mechanisms [23] or promising solutions for vibration energy harvesting [6].

Phononic frequency combs can be generated through contact mechanisms [29], mutual synchronization of resonators [56, 94] or internal resonance [10]. Internal resonance is defined in nonlinear vibration theory as an existing commensurate frequency relationship, which, in turn, gives rise to important coupling and energy exchange between the internally resonant modes. It is also known as favouring the appearance of phononic frequency combs, see e.g. [11, 72].

In [22], the first experimental evidence for a phononic frequency comb is reported. In particular, through the intrinsic coupling of the driven phonon mode with a subharmonic mode, the authors generated a phononic frequency comb. Other works in the same direction confirmed the finding; for example, in [64, 65], focusing on a piezoelectric resonator, a frequency comb based on non-degenerate parametric pumping is studied in depth. Furthermore, in [7] a tunable resonator using a suspended $\text {MoS}_2$ monolayer is employed to generate frequency combs.

Although several works present experimental evidences of phononic frequency combs in MEMS devices, only few contributions focus on the modelling of these and other nonlinear phenomena [33, 34, 44, 49, 67, 80]. Most of these works utilize structural theories for beams and analytical expressions for electrostatics. However, it has been recently shown [92] that even for simple beam-like structures a quantitative agreement with experiments is difficult to achieve. As a consequence, the main aim of this investigation is to propose a general technique, applicable also to complex and realistic MEMS, for which simplified theories are not applicable.

To simulate a full order model, i.e. finite element models, a number of numerical methods are available. These approaches represent an appealing alternative to analytical models that exploit simplified beams and shells structural theories, whose applicability to complex MEMS devices is limited [53, 62]. Despite the versatility of full order models, the computational burden remains the major drawback even using highly efficient methods like harmonic balance techniques or shooting procedures[69]. Consequently, the creation of fast, a-priori, reliable and nonlinear multiphysics tools for dynamic simulation would represent a ground-breaking milestone in MEMS design and testing [37, 43, 77].

MOR techniques allow in principle to reduce the full-order model to a few degrees of freedom system, thus significantly lowering the computational cost. Different strategies that make use of linear normal modes as an optimal projection basis upon which the equations of motion can be reduced are actually routinely applied in linear problems arising from vibratory systems like MEMS. However, their extension to nonlinear dynamic problems is still an open issue that is attracting an increasing attention from the scientific community. In general and as done, for example, in [26, 84], one can distinguish between linear and nonlinear techniques for model order reduction.

Linear ROMs are typically Galerkin projections onto low-dimensional linear subspaces. Among this class of methods, one of the simplest solutions is provided by the STiffness Evaluation Procedure (STEP) [58], which uses a selection of linear eigenmodes to compute the coupling coefficients. In order to determine all the coupling terms, the STEP method requires identifying and considering all the high-frequency modes [24, 87], e.g. axial and lateral contraction in beams, thus making its application to 3D FEM models very critical. Such modes are indeed difficult to identify and compute without a deep a-priori knowledge of the structural behaviour of the system under study. Nevertheless, among Linear ROMs, the system eigenmodes are not the only choice for the identification of subspace bases. A valid alternative is represented by proper orthogonal decomposition (POD) methods that generates the linear basis through a data-driven approach. Subspace bases are built from data obtained through simulations of a limited amount of configurations of the system by optimizing their orientation to better fit the curvatures of the nonlinear manifold underlying the dynamics [2, 3, 45].

Among the nonlinear ROMs available so far in the literature, one can mention the quadratic manifold built from modal derivatives [42, 71], that takes into account the amplitude dependence of mode shapes and eigenfrequencies. However, since the nonlinear mapping defined in that case is by definition velocity-independent, this approach is limited to moderate transformations and apply only in the presence of sufficient slow/fast separation between the slave and master coordinates [39, 84, 88]. Another class of nonlinear ROMs that deserves attention is represented by the methods based on the concept of nonlinear normal mode (NNM) firstly proposed by Rosenberg [70]. A NNM has been firstly defined as a synchronous vibration of the system and then generalized by the notion of invariant manifold [75, 81,82,83] and spectral submanifold [38, 66]. Despite the generation of ROMs based on the concept of NNM has been proposed for both small systems with few degrees of freedom (dofs) and complex structures involving inertia and geometrical nonlinearities [63, 89], its extension to multiphysic problems (e.g. electromechanics in MEMS) has not been addressed yet and poses important computational challenges.

The implicit condensation (IC) approach is a versatile method that can be used in a non-intrusive manner to derive efficiently accurate ROMs when a small number of master modes are needed [21, 41, 60]. It is a nonlinear method in the sense that the nonlinear relationship between the coordinates is deduced from a stress manifold built by applying series of static loads. This method has been recently tailored for MEMS structures exhibiting damping, geometric and electrostatic nonlinearities. In particular, a very good agreement between experiments and numerical predictions has been shown in [92] for two double-ended-tuning-fork resonators electrostatically actuated according to their first bending mode and in [27] for a MEMS gyroscope test structure exhibiting 1:2 internal resonance.

In this work, we take a step further by applying the proposed simulation technique to design a MEMS arch resonator exhibiting a 1:2 internal resonance leading to a phononic frequency comb.

MEMS Arch resonators have been extensively studied in the literature, e.g. [1, 35, 36] and theoretical and experimental analyses on 1:2 internal resonance are available as well [25, 32, 51, 74, 90]. Nevertheless, only few applications target their numerical simulation and focus on the 1:2 internal resonance as a way to generate a frequency comb [44]. In particular, the analytical results presented in [27] and the preliminary numerical experiences reported in [25] are deepened to demonstrate that the proposed ab initio simulation process allows predicting in real-time the complex nonlinear dynamics of MEMS resonators and at the same time guides the electro-mechanical design. Interestingly, the ROM is obtained directly from the FE model in a non-intrusive manner, without any tuned parameter fitted from the experiments, and provides excellent predictions when compared to experiments, underlying the accuracy of the method.

The paper is organized as follows: in Sect. 2, the MEMS arch resonator mechanical design is discussed together with the electrostatic actuation/readout scheme, while the electromechanical IC ROM is introduced in Sect. 3. Experimental data measured on the fabricated MEMS arch resonator are reported in Sect. 4 in comparison with numerical results obtained by solving the IC ROM through different techniques. Conclusions are finally reported in Sect. 5.

2 Arch resonators

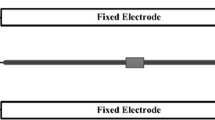
To guarantee the activation of the 1:2 internal resonance able to generate phononic frequency combs by design, we optimized the geometry of a MEMS resonator starting from the topology reported in Fig. 1. An electrostatically actuated MEMS arch resonator is indeed chosen as a very promising candidate thanks to the simple geometry and the strong nonlinear dynamic behaviour. In particular, the asymmetric shape of the arch guarantees non-vanishing quadratic contributions in the elastic force, the clamped–clamped condition is responsible of cubic terms, while the parallel-plate scheme employed for the electrostatic actuation and readout provides electrostatic nonlinearities (see Sect. 3.3).

Fig. 1

a Scanning electron microscopy (SEM) image of the MEMS arch resonator fabricated through the Thelma process of STMicroelectronics. b Schematic view of the electrostatic actuation/detection electrodes: (1) resonator ($V_{\text {DC}}$), (2) tuning electrodes ($V_{\text {T}}$), (3) driving electrodes ($V_{\text {AC}}$), (4) sensing electrodes (ground) and (5) dummy electrodes ($V_{\text {DC}}$)

The arch resonator has been fabricated with the Thelma process of STMicroelectronics [9] and is made of polysilicon, with $E = 167$ GPa, $\nu = 0.22$ and $\rho = 2330$ $\text {kg/m}^3$. It consists of two curved parallel clamped–clamped beams coupled through a vertical rigid connection of length $27\,\upmu \text {m}$ and in-plane thickness of 10 $\upmu \text {m}$. Each beam has a cross section of $5\,\upmu \hbox {m}$ x $24\,\upmu \text {m}$, a rectified length of $532\,\upmu \text {m}$ and is suspended with respect to the substrate through the two lateral anchors.

To guarantee electrostatic actuation and readout, fixed electrodes are also properly designed, as shown in Fig. 1. At rest, the distance between the MEMS arch resonator and the fixed electrodes is equal to 1.8 $\upmu \text {m}$ according to fabrication constraints. When a voltage difference is applied between the MEMS resonator and the fixed electrodes, an electrostatic force is generated. Depending on the frequency of the applied voltage and on the employed polarization scheme, it is possible to actuate the arch mechanical modes reported in Fig. 2.

As an example, the polarization scheme reported in Fig. 1b is used to actuate the first flexural mode of the resonator (Fig. 2a). A time-varying bias voltage $V_{\text {AC}}\sin \omega t$ is imposed on the drive electrodes (coloured in green in Fig. 1b), while the mechanical structure (coloured in blue in Fig. 1b) is kept at a constant $V_{\text {DC}}$ voltage. Sense electrodes (coloured in red in Fig. 1b) are grounded to allow for the readout, while tuning electrodes (coloured in light blue in Fig. 1b) are kept at voltage $V_{\text {T}}$ to shift the resonance frequency of the excited mechanical mode through the electrostatic softening effect [8]. Finally, dummy electrodes (coloured in orange in Fig. 1b) are kept at the same DC voltage of the MEMS arch resonator. The numbering associated with the different coloured portions in Fig. 1b will be utilized in Sect. 3.3 to define electrostatic forces.

In the following, we will focus on the first (Fig. 2a) and sixth (Fig. 2f) eigenmodes of the arch resonator whose natural frequencies are estimated through a finite element method (FEM) modal analysis performed in COMSOL Multiphysics and read 416.66 kHz and 834.15 kHz, respectively. We will refer to these modes as the first and second in-plane flexural modes of the MEMS, while the mode shown in Fig. 2c is an out-of-plane flexural mode and the modes reported in Fig. 2b, d, e are all related to localised bending modes of the curved half-beams. It is worth mentioning that the central clamp between the curved beams has shifted the anti-symmetric bending mode to much higher frequencies.

Fig. 2

Eigenmodes of the MEMS arch resonator shown in Fig. 1. The contour of the normalized displacement field is shown in colour. Eigenmodes (a) and (f) have frequency ratio close to 2 and are coupled through the internal resonance of interest in this investigation

Since the natural frequencies of the first and second bending modes of the resonator are in a ratio close to 1:2 by design and tuning electrodes can be exploited to slightly modify the ratio as desired through the electrostatic softening effect, the 1:2 internal resonance between the first and the second bending modes can be easily activated for reasonable amplitudes of the drive voltage as demonstrated by the authors in [93]. Differently from [93], we are here able to activate the phononic frequency comb for specific combinations of the actuation voltages, thanks to the proper design of the MEMS arch resonator and guided by the proposed ROM technique.

3 Modelling strategy

In order to develop and validate a general ab initio procedure, we start from a fully 3D FEM discretization of the MEMS without resorting to structural theories or semi-analytical approximations. The proposed method is a specific form of the implicit condensation (IC) approach [54, 55] which has been recently validated for MEMS applications in [21, 27, 92]. The underlying assumption is that it is possible to describe the steady-state nonlinear oscillation of a resonator as a combination of few low-frequency master modes. In the case under study, the two master modes are the first and second bending modes previously discussed.

The specific limitations of the IC technique have been deeply analysed in [76, 84] and are twofold. First, only moderate transformations can be addressed, meaning that inertia nonlinearities cannot be included. This implies, for instance, that IC in the proposed form cannot be applied, for example, to micromirrors in large rotations [63], nor to cantilevers with large tip deflections. Secondly, a slow/fast decomposition of the system is required, which means that the active slave coordinates should have eigenfrequencies well above those of the master coordinates. If these assumptions are respected, the IC technique is powerful and can be readily generalised to multiphysics problems, as discussed in the following sections. Interestingly, it can be used in a non-intrusive manner with any finite element code, and it gives good results when a small subset of master modes are selected (typically one or two). On the other hand, the generalization of the method to larger number of master modes comes with computational and accuracy issues.

3.1 Training phase

Let $\varvec{\psi }_i(\textbf{x})$ denote the non-dimensional linear modal shape functions of the master modes, mass normalized according to:

$$\begin{aligned} \int _{\varOmega _0}\rho \varvec{\psi }_i(\textbf{x})\cdot \varvec{\psi }_j(\textbf{x})\,{\text {d}}\varOmega = \mathcal{M}\delta _{ij}, \end{aligned}$$

(1)

where $\mathcal{M}$ denotes a reference mass that is set to unity in all the numerical experiments but helps making explicit the consistency of units.

In a first training phase, a stress manifold is built by statically forcing the structure with body forces per unit volume $\rho \textbf{F}(\textbf{x})=\rho (\beta ^{(1)}\varvec{\psi }_1(\textbf{x}) + \beta ^{(2)}\varvec{\psi }_2(\textbf{x}))$ where $\beta ^{(i)}$ are load multipliers (with the dimensions of an acceleration) of the i-th mode, similarly to what proposed in [54]. It is worth stressing that the space of these body forces represents a notable approximation of the space of inertia forces that near resonance are essentially in equilibrium with elastic internal stresses. For this specific reason, the resulting stress manifold, as discussed next, proves very accurate near the resonance peak.

Once the body forces are defined, several static non-intrusive nonlinear analyses are run with any FEM code to sample the $(\beta ^{(1)},\beta ^{(2)})$ space through:

$$\begin{aligned}&\int _{\varOmega _0}\textbf{P}[\textbf{u}]:\nabla ^T\textbf{w}\,{\text {d}}\varOmega \nonumber \\&\quad = \int _{\varOmega _0}\rho \beta ^{(j)}\varvec{\psi }_j(\textbf{x})\cdot \textbf{w}\,{\text {d}}\varOmega , \qquad \forall \textbf{w}\in \mathcal{C}(0), \end{aligned}$$

(2)

where $\textbf{P}$ is the first Piola–Kirchhoff stress and equilibrium is imposed in the reference configuration. The range of the load-multipliers $\beta ^{(j)}$ is suitably prescribed so as to cover a predefined range of expected displacements in the structure. For instance, considering the resonator shown in Fig. 1, a fraction of the gap between the resonator beams and the electrodes will be covered.

Let $\textbf{u}(\varvec{\beta },\textbf{x})$ denote the solution to Eq. (2) for a given $\varvec{\beta }= (\beta ^{(1)},\beta ^{(2)})$. In the linear limit $\textbf{u}(\varvec{\beta },\textbf{x})$ is only a combination of the modal shapes, but as the load increases, it also contains contributions from other modes, typically high-frequency axial or striction modes which relax significantly the elastic energy. The computed stresses $\textbf{P}[\textbf{u}]$ define a manifold $\mathcal{P}$. We remark that, setting $\textbf{w}=\varvec{\psi }_i$ in (2), we have:

$$\begin{aligned} \mathcal{M}\beta ^{(i)}= \int _{\varOmega _0}\textbf{P}[\textbf{u}(\varvec{\beta },\textbf{x})]:\nabla ^T\varvec{\psi }_i(\textbf{x}) \,{\text {d}}\varOmega , \end{aligned}$$

(3)

thanks to the ortho-normality properties of the linear modal basis. In order to set up the necessary tools for the weak form of equilibrium, we first define the generalized modal coordinates $q_i$, with the dimensions of a displacement, as:

$$\begin{aligned} \mathcal{M}q_i(\varvec{\beta })&=\int _{\varOmega _0}\rho \textbf{u}(\varvec{\beta },\textbf{x})\cdot \varvec{\psi }_i(\textbf{x})\,{\text {d}}\varOmega \qquad i=1,2, \end{aligned}$$

(4)

and invert the map $\textbf{q}(\varvec{\beta })$ sampling the $\varvec{\beta }$ space to obtain a discrete version of the function $\varvec{\beta }(\textbf{q})$. Invertibility is a reasonable assumption with mild nonlinearities and, practically, the inversion is performed numerically through fitting procedures. Consequently a continuous version of the stress manifold can be defined. In our case, we adopt a cubic interpolation for $\beta ^{(i)}$ as follows:

$$\begin{aligned} \beta ^{(i)}(q_1,q_2)&= c_0^{(i)}+c_1^{(i)} q_1+c_2^{(i)} q_2+c_3^{(i)} q_1^2+c_4^{(i)} q_1 q_2 \nonumber \\&\quad +c_5^{(i)} q_2^2+ c_6^{(i)} q_1^3+c_7^{(i)} q_1^2 q_2\nonumber \\&\quad +c_8^{(i)} q_1 q_2^2+c_9^{(i)} q_2^3, \end{aligned}$$

(5)

Table 1 Coefficients of the mechanical nonlinear manifold numerically computed for the two master modes

where the coefficients are collected in Table 1 and a visualization of the modelled manifolds is presented in Fig. 3. In particular, the linear and constant components of the $\beta ^{(i)}(q_1,q_2)$ are removed in Fig. 3b and d in order to provide a clear view of the nonlinear contributions $\beta ^{(i)}_{\text {NL}}$.

Fig. 3

Nonlinear $\beta ^{(i)}$ manifolds for the two master modes. (a) and (c) plot the complete manifolds while in (b) and (d) only the nonlinear contributions are highlighted, setting $c^{(i)}_0=c^{(i)}_1=c^{(i)}_2=0$

Coefficients in Table 1 reveal some interesting properties of the structure under study. First, important quadratic coefficients are present, as a consequence of the curvature of the structure. Second, these nonlinear coefficients arise from the mechanical part of the structure which should derive from an elastic potential, such that for example, the quadratic coefficients should fulfil the two following relationships: $c_4^{(1)}=2 c_3^{(2)}$, $c_4^{(2)}=2 c_5^{(1)}$, and the cubic coefficients should be related through: $c_7^{(1)}=3 c_6^{(2)}$, $c_7^{(2)}= c_8^{(1)}$ and $c_8^{(2)}=3 c_9^{(1)}$ [58, 87]. One can notice that these five relationships are almost perfectly verified by the IC procedure, despite not being imposed directly, highlighting that the method recovers important features of the internal forces. Finally, it is important to remark that between the six quadratic coefficients, two of them—namely $c_4^{(1)}$ and $c_3^{(2)}$—are particularly relevant in the case of 1:2 resonance, since being related to second-order resonant monomials [25, 83]. It is interesting to remark in particular that $c_3^{(2)}$ has not a large value; however, as it will be shown next, this value is absolutely non-negligible and plays a fundamental role in the dynamics of the 1:2 internally resonant system.

It should be remarked that functions $\beta ^{(i)}(q_1,q_2)$ could be fitted with other interpolating function like splines. Furthermore, the polynomial only has cubic order because the displacement levels, limited by the electrostatic pull-in effects, see Sect. 3.3, make higher-order contributions negligible. It is hence apparent that the IC method works at best and in great efficiency when only few clearly identified master modes are interacting. In the presence of several master modes, the IC method might rapidly lose its appeal.

3.2 Generation of the ROM

At this point, following a standard practice, we impose the weak form of the equilibrium condition (Principle of Virtual Power) for two specific choices of the test velocity field, i.e. $\textbf{w}=\varvec{\psi }_i$:

$$\begin{aligned}&\int _{\varOmega _0}\rho \ddot{\textbf{u}}\!\cdot \!\varvec{\psi }_i\,{\text {d}}\varOmega + \int _{\varOmega _0}\textbf{P}[\textbf{u}]\!:\!\nabla ^T\varvec{\psi }_i \,{\text {d}}\varOmega \nonumber \\&\quad = \int _{S_0}\textbf{f}_e\!\cdot \!\varvec{\psi }_i \,{\text {d}}S, \quad i=1,2, \end{aligned}$$

(6)

where $\textbf{f}_e$ are electrostatic forces.

In order to express all the terms as a function of the master coordinates $\textbf{q}$, we now introduce several simplifications.

• We assume that the tensor $\textbf{P}[\textbf{u}]$ is constrained to evolve, during the oscillations, over the stress manifold $\mathcal{P}$ as a function of $\varvec{\beta }$ and hence of $\textbf{q}$. Using Eq. (3) the second term in Eq. (6) simplifies to $\beta _i(\textbf{q})$.

• Inertia forces are taken as a combination of linear modes:

  $$\begin{aligned} \rho \ddot{\textbf{u}}(\textbf{x})=\rho \varvec{\psi }_1(\textbf{x})\ddot{q}_1(t)+\rho \varvec{\psi }_2(\textbf{x})\ddot{q}_2(t). \end{aligned}$$

  It is worth stressing that this statement limits the applicability of the approach to moderate transformations, as it rules out the possibility to describe, for example, large rotations (micromirrors) or large deflections of cantilever beams.

• We finally assume that also the electrostatic forces can be expressed in terms of $\textbf{q}$, as commented in detail in the next section, and we introduce the load participation factors:

  $$\begin{aligned} F_i(\textbf{q})=\int _{S_0}\textbf{f}_e(\textbf{q})\cdot \varvec{\psi }_i \,{\text {d}}S. \end{aligned}$$

  (7)

As a consequence, Eq. (6) yields a ROM in the form of a system of two nonlinear differential equations:

$$\begin{aligned} \mathcal{M}\ddot{q}_i+\mathcal{M}\beta _i(\textbf{q})= F_i(\textbf{q}), \qquad i=1,2. \end{aligned}$$

(8)

As anticipated, the reference mass $\mathcal{M}$ is only needed to correctly specify the dimensions of all the terms, and it will henceforth set to unity.

3.3 Electrostatic forces

Since we aim at developing a numerical technique for moderate transformations, similarly to what proposed for inertia forces, we compute the manifold of electrostatic forces assuming that, for this specific task, the displacement field can be approximated by a linear combination of modes:

$$\begin{aligned} \textbf{u}\simeq \varvec{\psi }_1(\textbf{x})q_1(t)+\varvec{\psi }_2(\textbf{x})q_2(t), \end{aligned}$$

i.e. we assume that the error will have a minor impact on the electrostatic forces despite being critical for the stress field. The efficient generation of the manifold still remains a complex task. At present, the most performing numerical tool is represented by integral equations suitably accelerated, e.g. with fast multipole methods that have been intensively investigated in the last decades [19].

In our applications, the potentials of the conductors $\varOmega _i$ are imposed. According to the numbering of conductors introduced in Fig. 1, $\varPhi _1=\varPhi _5=V_{\text {DC}}$, $\varPhi _2=V_{\text {T}}$, $\varPhi _3=V_{\text {AC}}\sin \omega t$, $\varPhi _4=0$ and the distribution of charge surface density $\sigma$ on the conductors is obtained solving the first-kind integral equation:

$$\begin{aligned} \varPhi (\textbf{x})=\int _{S}\frac{1}{4\pi } \frac{1}{r}\frac{\sigma (\textbf{y})}{\varepsilon _0}{\text {d}}S, \qquad \forall \textbf{x}\in S, \end{aligned}$$

(9)

where $\sigma$ denotes the unknown surface charge density, S is the collection of the surfaces $S_i$ and the data $\varPhi$ has been defined such that $\varPhi =\varPhi _i$ on $S_i$. It is worth recalling that the electrostatic force per unit surface $\textbf{f}_e$ exerted on the conductor at point $\textbf{x}$ of unit normal vector $\textbf{n}$ is directly associated to the main unknown of the problem:

$$\begin{aligned} \textbf{f}_e = \sigma ^2/(2\varepsilon _0) \textbf{n}. \end{aligned}$$

(10)

The second major benefit of the approach is that since only the conductor surfaces need to be discretized, it is straightforward to repeat the analysis following the motion of the device, assuming that the dynamics of electromagnetic forces is much faster than the frequency of oscillation of the resonators.

For a given $\textbf{q}$, let $\tilde{\sigma }_i(\textbf{x},\textbf{q})$ denote the charge distribution corresponding to a fictitious problem where a unit potential is imposed only on $\varOmega _i$: $\varPhi _i=1$ and $\varPhi _j=0$, $j\not = i$. Each field $\tilde{\sigma }_i(\textbf{x},\textbf{q})$ is the solution of (9) with the specified potentials. Thanks to the linearity of Eq. (9) at fixed $\textbf{q}$, the total charge on every conductor can be expressed as:

$$\begin{aligned} \sigma (\textbf{x},q)=\sum _{i=1}^5 \tilde{\sigma }_i(\textbf{x},q) \varPhi _i. \end{aligned}$$

(11)

The nonlinear load participation factor (7) is thus:

$$\begin{aligned} F_i(q)=&\int _{S_1}\frac{\sigma ^2}{2\varepsilon _0} \varvec{\psi }_i\cdot \textbf{n}{\text {d}}S\nonumber \\ =&\sum _{m,n=1}^{5}\left( \int _{S_1}\frac{\tilde{\sigma }_m\tilde{\sigma }_n}{2\varepsilon _0} \varvec{\psi }_i\cdot \textbf{n}{\text {d}}S\right) \varPhi _m \varPhi _n, \; i=1,2, \end{aligned}$$

(12)

where the integration is limited to the surface of the resonator as $\varvec{\psi }_i$ vanishes elsewhere.

Since typically $V_{\text {AC}}$ is much smaller than $V_{\text {DC}}$ and $V_{\text {T}}$, terms in $V^2_{\text {AC}}$ are neglected and hence

$$\begin{aligned} F_i(\textbf{q}) =&f^{(i)}_{\text {DD}}(\textbf{q})V_{\text {DC}}^2 + f^{(i)}_{\text {TT}}(\textbf{q})V_{\text {T}}^2 \nonumber \\&+ 2f^{(i)}_{\text {DT}}(\textbf{q})V_{\text {DC}}V_{\text {T}}+ 2f^{(i)}_{\text {DA}}(\textbf{q})V_{\text {DC}}V_{\text {AC}}\sin \omega t, \end{aligned}$$

(13)

where also the term $f^{(i)}_{\text {AT}}V_{\text {AC}}V_{\text {T}}$ has been considered negligible due to the specific topology of the resonator. In the present case, a cubic interpolation for $f^{(i)}_{\alpha \beta }(\textbf{q})$ is selected and the computed coefficients, with the same ordering as in Eq. (5), are collected in Table 2, while the corresponding manifolds are illustrated in Fig. 4. Also in this case, due to the limited displacements at hand, we opted for a polynomial expression truncated at third order.

Table 2 Coefficients of the electrostatic nonlinear manifold numerically computed for the two modes under study

Fig. 4

Nonlinear electrostatic force manifolds for the two master modes, first bending modes in column 1 and second bending mode in column 2

3.4 Current equation

The IC ROM allows computing the displacements of the structure under given loading conditions. Nevertheless, the MEMS device here considered is near-vacuum encapsulated and direct displacement measurements are not available. Experimental data are on the contrary provided in the form of current I flowing out of the sense electrodes ($\varOmega _4$). However, following [92], the current can be expressed in terms of modal coordinates as:

$$\begin{aligned} I(\textbf{q}) = \sum _{i=1}^2\sum _{n=1}^3\left( \int _{S_1}\frac{\tilde{\sigma }_4\tilde{\sigma }_n}{2\varepsilon _0} \varvec{\psi }_i\cdot \textbf{n}{\text {d}}S\right) \varPhi _n\,\dot{q}_i, \end{aligned}$$

(14)

which can be simplified retaining the only meaningful contribution from $V_{\text {DC}}$:

$$\begin{aligned} I(\textbf{q})=&\sum _{i=1}^2\left( \int _{S_1}\frac{\tilde{\sigma }_4\tilde{\sigma }_1}{2\varepsilon _0} \varvec{\psi }_i\cdot \textbf{n}{\text {d}}S\right) V_{\text {DC}} \,\dot{q}_i \nonumber \\&\simeq \sum _{i=1}^2 f^{(i)}_{\text {DA}}(\textbf{q})V_{\text {DC}} \,\dot{q}_i. \end{aligned}$$

(15)

Equation (15), known as current equation, will thus be used in the following sections to transform the output of the IC ROM simulations and perform direct comparisons with experimental data.

3.5 Quality factor

Dissipation has been neglected in the derivation of Eq. (8) and is now added at the level of the reduced order model considering different sources [46, 91].

In slender MEMS with minimum thickness in the order of few microns the spread of elastic energy through the anchors (i.e. anchor losses) and surface effects can be safely neglected [5, 18] and only two major independent contributions need to be accounted for: thermoelastic dissipation and fluid damping. The overall quality factor Q, related to the ratio of the maximum stored energy over the dissipation in one cycle, is thus expressed as the summation of two independent contributions:

$$\begin{aligned} \frac{1}{Q}=\frac{1}{Q_{\text {fluid}}}+\frac{1}{Q_{\text {TED}}}, \end{aligned}$$

(16)

where $Q_{\text {fluid}}$ refers to the dissipation introduced by the interaction of the gas with the MEMS moving parts, while $Q_{\text {TED}}$ refers to the frequency-dependent thermoelastic quality factor. In our application, the device is encapsulated in near vacuum at a nominal pressure of 70 mbar in Argon, yet fluid damping cannot be neglected. In these conditions, the gas flow develops in the so-called free-molecule regime and its effects can be computed through the integral equation model proposed in [20] and extended in [17] to the high working frequencies typical of the resonators of interest herein. The resulting quality factor values are reported in Table 3. It is worth stressing that in the free molecule flow $Q_{\text {fluid}}$ is proportional to the inverse of the package pressure which in principle is fixed by the fabrication process at the bonding level, but in practice is strongly affected by technological spreads. Since the displacements of the resonator are limited, we ignore here the dependence of $Q_{\text {fluid}}$ on the actual configuration. See, however, [92] for further comments on this issue.

Table 3 Quality factor numerical predictions and experimental estimates

The frequency-dependent thermoelastic quality factor $Q_{\text {TED}}$ refers to damping induced by the process in which part of the vibration energy of the resonator is dissipated into thermal energy, through irreversible heat conduction induced by elastic vibrations [5, 40]. This contribution is broadly studied in the literature on MEMS and can be evaluated using standard numerical approaches [5] implemented in several commercial codes and will not be discussed herein. The thermal properties considered in the calculations are reported in Table 4, and the quality factor is reported in Table 3 for the two master modes. It can be appreciated, in particular, that thermoelastic damping has non-negligible effect on the second bending mode.

Table 4 Thermal properties of the polysilicon

The aforementioned values can be compared with experimental estimates of the quality factors of the system. This can be done resorting to the approximate method developed in [13] for nonlinear frequency response functions (FRFs) with Duffing-like behaviour. Performing this procedure on different points of the FRF reported in Fig. 5 (see Sect. 4 for the experimental setup details), one obtains the values reported in the last column of Table 3. Considering all the uncertainties affecting the encapsulation pressure and the material properties, in the following we adopt the intermediate values 2800 and 5200 for the first and the second master modes, respectively.

3.6 Integration of the final ROM

The resulting nonlinear system describing the dynamics of the arch resonator biased at $V_{\text {DC}}$ and tuned with a potential $V_{\text {T}}$ eventually reads:

$$\begin{aligned}&\ddot{q}_1+\frac{\omega _{01}}{Q_1}\dot{q}_1+\beta _1(\textbf{q})-f^{(1)}_{\text {DD}} (\textbf{q})V_{\text {DC}}^2\nonumber \\&\quad -2f^{(1)}_{\text {DT}}(\textbf{q})V_{\text {DC}}V_{\text {T}} -f^{(1)}_{\text {TT}}(\textbf{q})V_{\text {T}}^2\nonumber \\&\quad =2V_{\text {DC}}V_{\text {AC}}f^{(1)}_{\text {AC}}(\textbf{q}) \sin (\omega t), \end{aligned}$$

(17)

$$\begin{aligned}&\ddot{q}_2+\frac{\omega _{02}}{Q_2}\dot{q}_2+\beta _2(\textbf{q})- f^{(2)}_{\text {DD}}(\textbf{q})V_{\text {DC}}^2\nonumber \\&\quad -2 f^{(2)}_{\text {DT}}(\textbf{q})V_{\text {DC}}V_{\text {T}} -f^{(2)}_{\text {TT}}(\textbf{q})V_{\text {T}}^2= 0, \end{aligned}$$

(18)

where some simplifications of the electrostatic load are included. The $V_{\text {DC}}V_{\text {AC}}$ term is only meaningful for the lowest frequency oscillator, as $\omega \approx \omega _{01}$, while it is neglected in Eq. (18) since $\omega _{02}\approx 2\omega$. Furthermore, the $V_{\text {AC}}^2$ terms are neglected as $V_{\text {DC}}\gg V_{\text {AC}}$ in the applications. The only exception is represented by the preliminary uncoupled simulation of the FRF of the second mode in Fig. 5c, d where $\omega \approx \omega _{02}$ and the $2V_{\text {DC}}V_{\text {AC}}f^{(2)}_{\text {AC}}(\textbf{q}) \sin (\omega t)$ forcing term must be included in Eq. (18). The aforementioned simplifications are customary for MEMS as they are characterized by sharp peaks in the FRFs due to the high quality factors involved.

To enable a direct comparison with the output of experiments, the response obtained from Eqs. (17)-(18) in terms of modal coordinates is transformed in terms of current flowing out of the sense electrodes, using Eq. (15).

In standard operating conditions, we are interested in the steady-state periodic solutions and a number of available numerical packages can be fruitfully applied to generate a rich portrait of the dynamics performing continuation of solutions with bifurcation analysis. Alongside the well-established Auto07p [16], a Fortran package that uses collocation methods, an alternative common choice is Matcont, a Matlab numerical continuation tool for the interactive bifurcation analysis of dynamical systems [15]. Among others, one can mention: Manlab, a Matlab package that implements an Harmonic Balance (HB) technique coupled with the Asymptotic Numerical Method developed in [30, 31]; Nlvib that also exploits HB methods [48]; COCO based on collocation approaches [12]. Another excellent package is BifurcationKit [86], an emerging toolkit for continuation methods in ODEs and PDEs. These packages usually provide the ability to distinguish between stable and unstable branches, locate bifurcation points and follow alternative branches of the solution. We stress that the same versatility is difficult to achieve with a FOM. Indeed, even if a HB formulation with continuation has been recently proposed in [14, 62] for large-scale problems, computing times are not compatible with their application at the design or prototyping levels. In the upcoming sections, unless differently specified, the analysis of the steady-state periodic solutions and their stability is performed with Manlab.

Fig. 5

Frequency response of the MEMS arch resonator around the frequency of the first flexural mode in terms of a amplitude and b phase for $V_{\text {DC}} = 2,3,4$ V, $V_{\text {T}}= 0$ V and $V_{\text {AC}}= 177.8$ mV. Frequency response of the MEMS arch resonator around the frequency of the second bending mode in terms of c amplitude and (d) phase for $V_{\text {DC}}=4$ V, $V_{\text {T}}=4$ V and $V_{\text {AC}}=79.4$ mV. Experiments are reported in dotted lines and numerical predictions in continuous lines

Fig. 6

Typical pattern of the frequency response in presence of a 1:2 IR. Upward and downward sweeps in frequency control can only follow stable branches and are superposed to the complete frequency response. Saddle-node (SN) bifurcations delimit the unstable branches which are plotted in thin lines. Upward (orange) and downward (blue) sweeps have been slightly shifted to improve readability

4 Experimental campaign and simulations

This section is devoted to the comparison between the a-priori predictions provided by the IC method and experiments. Since the design aims at controlling both internal resonance and quasi-periodic regimes, the two aspects are investigated separately using dedicated experimental setups.

4.1 Periodic response and internal resonance

A standard probe station has been employed to perform the experiments. The resonator is excited through an AC signal generated by the Network Analyzer Agilent 4395A while DC voltages ($V_{\text {DC}}, V_{\text {T}}$) are provided by two power suppliers: Yokogawa GS 610 and Agilent E3631A. The output current, measured through the probe connected to the sensing electrodes, is amplified and converted to voltage through the Stanford Current Pre-Amplifier SR570, and it is readout by the network analyser. Finally, the data are post-processed in Matlab.

Fig. 7

Frequency response in terms of amplitude and phase for $V_{\text {DC}}=7$ V,$V_{\text {T}}=5$ V and variable $V_{\text {AC}}$. The NS bifurcation regions are zoomed in the insets

Fig. 8

Frequency response in terms of amplitude and phase for $V_{\text {DC}}=10$ V, $V_{\text {AC}}=316.2$ mV and variable $V_{\text {T}}$

Fig. 9

Frequency response in terms of amplitude and phase for $V_{\text {T}}=5$ V,$V_{\text {AC}}=316.2$ mV and variable $V_{\text {DC}}$

A preliminary characterisation of the MEMS arch resonator is performed by analysing the frequency response of the first and second bending modes (Fig. 5) for limited actuation levels, calibrated in order not to activate the internal resonance. The dynamic response of the arch resonator around the natural frequency of the first mode is reported in Fig. 5a, b in terms of amplitude and phase for $V_{\text {T}}= 0$ V, $V_{\text {AC}}= 177.8$ mV and $V_{\text {DC}} = 2, 3, 4$ V. A standard softening response is obtained, as expected, with an increasing frequency shift at larger $V_{\text {DC}}$.

It is worth stressing that in these tests the intensity of the measured output current is very limited, i.e. in the order of few nA, and a large noise level due to wires, instrument limitations and non-ideal connection between probes and MEMS-pads is expected. In particular, the response for $V_{\text {DC}}=2$ V is very noisy far from resonance, as the oscillation amplitudes are low and the noise of the experimental setup overcomes the system sensitivity.

For this reason, the phase has been plotted only near resonance which is the frequency range of interest. Numerical predictions obtained by solving Eqs. (17)-(18) for the aforementioned voltages levels are also reported in Fig. 5 using continuous lines. A very good agreement between experiments and numerical predictions is found thus providing a strong preliminary validation of ROM adopted. Figure 5c, d displays the response of the MEMS resonator when excited near the second bending mode, for $V_{\text {DC}}$ = 4V, $V_{\text {T}}$ = 4V and $V_{\text {AC}}$ = 79.4mV.

A second phase of the experimental campaign has been devoted to investigate the 1:2 internal resonance between the two bending modes. This is achieved by: (i) selecting a proper combination of the tuning voltage $V_{\text {T}}$ and of the bias voltage $V_{\text {DC}}$ applied on the resonator and (ii) increasing the AC signal applied on the driving electrodes. The former acts on the ratio between the natural frequencies of the two modes under study in order to bring it sufficiently close to 2. The latter activates the nonlinear behaviour of the arch resonator, thus promoting the coupling between the two modes of the structure. In order to allow a better understanding of the plots, in Fig. 6 we first present a typical pattern of the FRF for the amplitude of the first mode in presence of a 1:2 IR.

The shape of the frequency response is typical when the 1:2 internal resonance is excited, and is organized around two peaks corresponding to two different coupled solutions, as highlighted for example in [25]. Each peak corresponds to the contribution of one of the two existing coupled solutions. The two backbones that underlie the dynamics of the FRF reported in Fig. 6 onset from the frequency $\omega _{01}$ and $\omega _{02}/2$. In this campaign, experiments are run in frequency control with an upward sweep and cannot follow the unstable branches delimited by Saddle Node (SN) bifurcations.

When considering the left-hand part of the curve, i.e. the softening peak, the measurement point follows the lower part of the branch and jumps to the upper part at the SN point. When considering the right-hand part of the curve, i.e. the hardening peak, the forward frequency sweep should in principle allow to travel on the upper part of the bifurcated branch up to the peak. Nevertheless, the expected experimental jump is always found before the theoretical SN point. This is a classical feature in such problems, which is due to the fact that the basin of attraction of the upper solution is dramatically shrinking when approaching the SN point. Consequently, the system is very sensitive to non-idealities, e.g. noise or parasitic capacitances coming from the set-up, e.g. wires or instruments, are always present and hardly controllable in a deterministic way with the standard set-up utilized.

Tracking the response beyond the critical bifurcation regime is in principle possible through variable-phase feedback loop similar to the one proposed in [92], but the implementation of such a control scheme is outside the scope of the present work. On the contrary, the numerical solution of the ROM is performed with continuation techniques allowing to reproduce both stable and unstable branches.

Figures 7, 8, 9 present, in terms of both current amplitude and phase, the frequency response of the arch resonator measured for different combinations of $V_{\text {DC}}$, $V_{\text {T}}$ and $V_{\text {AC}}$. Note that only the upward frequency sweep is reported for the sake of clarity. As anticipated, starting from low frequencies and following the upward sweep, the experimental data present a jump to the upper branch at the first SN point, while they should follow the second peak before falling to the lower branch. Continuous lines illustrate numerical predictions showing a remarkable accuracy. In Fig. 7, the actuation level $V_{\text {AC}}$ is varied while keeping $V_{\text {DC}}=7$ V and $V_{\text {T}}=5$ V fixed. In these conditions, the amplitude of the motion increases and the frequency peaks become sharper and clearly visible. Regarding the bifurcation portrait, both simulations and experiments highlight the existence of the different stable and unstable branches delimited by the saddle-node points. Furthermore, with a $V_{\text {AC}}>446.7$ mV, Neimark-Sacker bifurcation points appear in between the two peaks. Here, the system response becomes quasi-periodic and further insight will be provided in what follows. The experimental measurements with the current setup cannot display the QP regime because the output signal is filtered assuming that only the forcing frequency is present. An accurate investigation of the QP regime is performed in Sect. 4.2 recording the output signal in time. It is also worth noticing that for $V_{\text {AC}}=446.7$ mV four NS points are identified, while on the $V_{\text {AC}}=562.3$ mV curves only two exist. This is a consequence of the peculiar shape of the so-called NS boundary region, analysed in [25] and shown in Fig. 16 of Appendix A, having two local minima.

In Fig. 8$V_{\text {DC}}=10$ V and $V_{\text {AC}}=316.2$ mV are kept fixed while $V_{\text {T}}$ is varied highlighting the effect of the tuning electrode that is here used to control the frequency ratio of the coupled modes. In fact, as one may infer from Eqs. (17) and (18), tuning electrodes allow controlling the eigenfrequency mismatch through the variation of the bias difference $|V_{\text {T}}-V_{\text {DC}}|$ with respect to the resonator. When $V_{\text {T}}=0$ V the frequencies have a mismatch that reduces the interaction. With $V_{\text {T}}=9$ V, i.e. $V_{\text {DC}}-V_{\text {T}}=1$ V, frequencies are close enough to provide a strong IR and small NS regions are detected by the numerical approximation. Finally, for $V_{\text {T}}=15$ V, i.e. $V_{\text {T}}-V_{\text {DC}}= 5$ V, the frequency mismatch starts increasing again; the IR effects are still present, but the NS regions disappear. An analysis of the evolution of the ratio between the eigenfrequencies as a function of the bias and tuning potentials is reported in Appendix B.

In Fig. 9$V_{\text {T}}=5$ V and $V_{\text {AC}}=316.2$ mV are kept fixed while $V_{\text {DC}}$ is varied. The $V_{\text {DC}}$ parameter strongly affects the response as it directly controls the forcing and induces an electrostatic shift on both modes. The results reported highlight the outstanding capabilities of the IC method as a tool to design devices tailored to display internal resonance behaviour.

4.2 Quasi-periodicity and frequency combs

As mentioned in previous sections, the system considered might encounter Neimark-Sacker bifurcations along the FRF and, more specifically, due to the 1:2 internal resonance a quasi-periodic (QP) regime can be observed under certain conditions. As well known from classical nonlinear dynamics [59], and as recently investigated, e.g. in [25], when the 1:2 internal resonance is present and proper conditions of forcing, damping and frequency mismatch are verified, Neimark-Sacker (NS) bifurcations can be observed in between the two frequency peaks of the response. As a consequence, the periodic response becomes unstable. Thanks to the design of the arch resonators and the IC ROM Eqs. (17), (18), such regime can be predicted and some of its features reproduced.

Fig. 10

FRF for the mid-span displacement $u_{\text {MID}}$. Numerical solution of the IC model for $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V and $V_{\text {AC}}=0.562$ V. The red line denotes the IC model continuation of periodic solutions. Bifurcation points of this solution are highlighted by the green star markers for saddle Node bifurcations and by green square markers for NS bifurcations. Time-marching solutions of the IC model are reported as dot markers in terms of stroboscopic maps at different frequencies. Inside the NS bifurcation region the continuation of periodic orbits solution and the time marching solution depart from each other. This is due to the QP regime that onset in such regions as highlighted by the cloud of points given by the stroboscopic maps

Fig. 11

Poincaré sections of the IC model mid-span displacement time histories for $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V, $V_{\text {AC}}=0.562$ V for different frequency values

Fig. 12

Experimental (a) and simulated (b) time history of the normalised signal output considering $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V, $V_{\text {AC}}=0.562$ V and $\varOmega =416.90$ kHz

Fig. 13

Frequency spectra of the experimental time histories for $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V, $V_{\text {AC}}=0.562$ V and different excitation frequencies. For each spectrum the forcing frequency as well as the comb spacing (if present) is reported. Frequency peaks are highlighted with bullet markers

Fig. 14

Frequency spectra of the simulated time histories for $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V, $V_{\text {AC}}=0.562$ V and different frequencies. For each spectrum the forcing frequency as well as the comb spacing (if present) is reported. Frequency peaks are highlighted with circle markers

Fig. 15

a FFT heatmap with varying excitation frequency. The power spectral density (PSD) of each FFT is normalized with respect to its maximum so that all the peaks correspond to red regions. The comb spacing tends to shrink inside the QP region enriching with more than one incommensurate frequency after a certain value. b Plot of the incommensurate frequency trend estimated from the FFTs using the average value encountered (red line). The comb spacing is decreasing along the path. Along the path some dispersion on the estimated values can be observed and is highlighted by the grey shaded region

Let us consider the FRF of the mid-span displacement $u_{\text {MID}}$ plotted in Fig. 10. The bifurcation analysis performed on the IC model reveals two NS bifurcation points. Specific algorithms and packages could be in principle used to perform continuation of different branches [15]. Nevertheless, we opt herein for a more straightforward time-marching solution, obtained with a Runge–Kutta scheme of order 4 and 5..

In Fig. 10, the Poincaré map of the midspan displacement $u_{\text {MID}}$ is plotted with black dots. Numerical data are generated by recording the system response, after a transient, at equally spaced time instants $t_k=t_0+kT$ with $k=1,2...n$, where T is the external forcing period and $t_0$ is a reference time corresponding, for example, to a maximum in the periodic response. Before and after the NS bifurcation points, the time marching solution is perfectly overlapped with the one obtained using the approaches detailed in the previous section, while inside the QP region the stroboscopic map provides a cloud of points as expected from a non-periodic regime.

The NS bifurcation, sometimes also called secondary Hopf bifurcation, is met when a limit cycle loses stability with a pair of Floquet multipliers crossing simultaneously the unit circle [50]. In these conditions, the system dynamics bifurcates to a QP regime where the forcing frequency $\varOmega$ is paired with an incommensurate frequency $\omega _{\text {NS}}$ that modulates the system time response. Furthermore, the frequency spectrum of the system is altered and, instead of presenting only isolated peaks corresponding to the multiples of $\varOmega$, also displays secondary, equally spaced peaks placed around the main ones. This spacing is a consequence of the combination of $\varOmega$ with the $\omega _{\text {NS}}$ multiples. More insight is provided by the 3D stroboscopic map of the numerical solution represented in Fig. 11, where f is the forcing frequency and $u_{\text {MID}},\dot{u}_{\text {MID}}$ are the mid-span displacement and velocity. The result is a collection of points that can be used to characterise the system regime: for a fixed f, a single point in the phase space corresponds to a periodic motion; a closed curve corresponds to a quasi-periodic regime with a single incommensurate frequency; more complex patterns denote the coexistence of several incommensurate frequencies and a route to chaos [79].

To provide an insight into the behaviour of the system in such regions, we recorded the output signal in time using an oscilloscope Tektronix MSO 454. An example of experimental measurements of the signal performed inside the predicted QP region is reported in Fig. 12a. Due to the measurement noise in the signal, the typical amplitude modulation expected for a QP regime, and predicted by the IC model in Fig. 12b, is not clearly visible and a post-processing is required.

To better analyse these data, we perform a spectrum analysis of experimental data obtained at various forcing frequencies spanning the region of interest setting $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V, $V_{\text {AC}}=0.562$ V, corresponding to the FRFs of Figs. 7 and 10. The results are collected in Fig. 13. Even though the time signal is noisy, using sufficiently long time windows to operate the Fourier transform allows us to recover a good accuracy in the spectrum and to put in evidence the structure of the frequency combs. We notice that, for points lying outside the NS region predicted by the IC simulation, the response has a sharp peak at the forcing frequency. Entering into the predicted QP region, frequency combs appear in the spectrum. The spacing between the peaks varies depending on the forcing frequency and ranges from 103 Hz up to 725 Hz.

Following the branch of QP solutions, the second frequency of the torus $\omega _{\text {NS}}$ is known to vary with the parameters (here the forcing frequency), see e.g. [25]. Even though $\omega _{\text {NS}}$ should change smoothly in the frequency window, we detect experimentally an irregular pattern, as a consequence of the stability of the QP solution [52]. This aspect has not been deeply investigated during our experiments as the analysis of alternative states as a consequence of the torus stability is out of the scope of this work.

Numerical frequency combs obtained by solving the IC model through time marching techniques are reported in Fig. 14. The clear transition from a periodic response with a single sharp peak in the spectrum to a QP regime with FCs obtained experimentally is indeed well predicted by the ROM model here proposed. The numerical FC spacing ranges from 125 to 500 Hz and tends to change along the frequency path till becoming almost chaotic, in satisfactory agreement with experimental data. This behaviour is compatible with what observed in Fig. 11 where, in a certain range of the forcing frequency, the Poincaré map changes from a pattern with simple closed curves towards a more complicate one denoting the presence of several incommensurate frequencies.

Results are further elaborated in Fig. 15. Here, we consider the 40 numerical output-signal time histories used to generate Fig. 11, corresponding to equally spaced forcing frequencies. Their spectral amplitudes are plotted in Fig. 15a as a heatmap in the $(f_{\text {FFT}},f)$ plane, where $f_{\text {FFT}}$ denotes the FFT component and f the forcing frequency. Colours correspond to the FFT amplitude values. One can identify the same pattern as in Fig. 11. Below $f\approx 416.75$kHz, the spectrum is characterised by one single peak typical of a periodic regime. After the onset of the NS bifurcation, the incommensurate frequency adds equally spaced peaks around the forcing frequency value. Initially, the peak spacing is quite large and clear peaks can be identified. Proceeding further, for $f\approx 416.85\!:\!416.95$ kHz, some peaks disappear and the spacing progressively reduces. After $f\approx 416.95$ kHz the portrait changes abruptly and additional peaks arise suggesting a more complicate behaviour possibly associated with the appearance of several incommensurate frequencies.

Such representation allows estimating the trend of the incommensurate frequency $f_{\text {NS}}$ reported in Fig. 15b. Since the FFT resolution is limited by the simulated time-series to $\varDelta f \approx 20.8\hbox {Hz}$ and due to difficulties in identifying peaks position, we plot an average peak value (thick red line) and the maximum–minimum frequency spacing range (grey shaded region). The global trend shows a decrease of the incommensurate frequency value compatible with the experimental data and a spread after $f\approx 416.95\hbox {kHz}$, as previously highlighted.

5 Conclusions

This paper presents an electromechanical reduced order model based on the implicit condensation approach, that is able to describe the complex nonlinear dynamics of a MEMS resonator. Importantly, this is an ab initio approach in the sense that, starting from general principles, it takes into account the mechanics of the arch resonator, the electrostatic actuation/readout schemes and the different dissipation mechanisms without resorting to simplified and problem-dependent semi-analytical approximations. The ROM has thus been generated from an a priori modelization, without any need to resort to a fitting procedure to tune some of its parameter on the basis of experimental measurements.

By comparing numerical simulations and experiments performed on a MEMS arch resonator fabricated by STMicroelectronics under different operating conditions, we have demonstrated that the ROM model is able to correctly reproduce the 1:2 internal resonance arising from the interaction of the first and second bending modes of the arch resonator. Moreover, we have brought the simulation technique to an unprecedented level of complexity by reproducing the phononic frequency comb observed experimentally. The location of the Neimark-Sacker bifurcations points has been accurately predicted and an in-depth analysis of the quasi-periodic regime arising from these points has been indeed carried out. Also the simulation of the spacing between the secondary peaks of the comb has been addressed, showing that the correct trend and range can be reproduced.

The technique is fairly general and can be applied to a broad family of resonating microstructures experiencing moderate transformations. It only requires the a-priori identification of the master modes and can be applied with reasonable computing cost provided that the number of interacting modes is limited.

Fig. 16

Comparison between the analytical model and experiments for $V_{\text {DC}}=7$ V, $V_{\text {T}}=5$ V and $V_{\text {AC}}=0.562$ V. a experimental FRF compared with the analytical one and NS boundary. b enlarged view of the QP region and the NS boundary crossing points. c incommensurate frequency predicted by the analytical model along the NS boundary

Thanks to its ab initio and reduced order nature, the proposed simulation approach represents a powerful tool to support the design process of a new class of complex nonlinear MEMS devices. The intricate nonlinear dynamics phenomena of such sensors/actuators are indeed very difficult to predict without simple ROM models and consequently were avoided by design. The development of refined numerical tools is thus expected to be a key enabling technology for a new family of MEMS devices built with and for nonlinearities that could potentially revolutionise their applications.

Appendices

A Comparison with an analytical approach

All the results presented in Sect. 4 show the potential of the IC method in predicting QP states in MEMS systems. Nevertheless, an analytical model might be helpful in obtaining a direct control on the nonlinear parameters. In the literature many contributions have addressed the topic of internal resonances from an analytical perspective, including e.g. 1:3 [47] 1:1:2 [78] and 1:2:4 [57] cases. In particular, we discuss herein the analytical model for 1:2 internal resonance discussed in [25] and we compare its results with the experiments. The model is given by a set of two nonlinear ODEs representing the two eigenmodes as coupled oscillators:

$$\begin{aligned}&\ddot{q}_1+\frac{\omega _{01}}{Q_1}\dot{q}_1+k_1 q_1+k_3 q_1 q_2 =f_1 \sin (\omega t), \end{aligned}$$

(19)

$$\begin{aligned}&\ddot{q}_2+\frac{\omega _{02}}{Q_2}\dot{q}_2+k_2q_2+k_4q_1^2 =0, \end{aligned}$$

(20)

with $q_i,\,i=1,2$ modal coordinates and the coefficients $k_i$ defined as a combination of the coefficients in Tables 1 and 2. Referring to the $c_j$ coefficient of each table by means of the notation $\square _{c_j}$ the values in Eqs. (19) and (20) are taken as:

$$\begin{aligned} k_1&=\beta ^{(1)}_{c_1}-f^{(1)}_{\text {DD},c_1}V_{\text {DC}}^2, \\ k_2&=\beta ^{(2)}_{c_2}-f^{(2)}_{\text {DD},c_2} V_{\text {DC}}^2, \\ k_3&=\beta ^{(1)}_{c_4}-f^{(1)}_{\text {DD},c_4} V_{\text {DC}}^2-2 f^{(1)}_{\text {DT},c_4} V_{\text {DC}} V_T-f^{(1)}_{\text {TT},c_4} V_{\text {T}}^2, \\ k_4&=\beta ^{(2)}_{c_3}-f^{(2)}_{\text {DD},c_3} V_{\text {DC}}^2-2 f^{(2)}_{\text {DT},c_3} V_{\text {DC}} V_T-f^{(2)}_{\text {TT},c_3} V_{\text {T}}^2\\ f_1&=2V_{\text {DC}}V_{\text {AC}} f^{(1)}_{\text {DA},c_0}. \end{aligned}$$

The analysis of Eqs. (19) and (20) allows tracing the FRCs, but also to address the stability of the system through the inspection of the Jacobian of the modulation equation. In particular, the NS bifurcation points can be identified and their envelope, i.e. the NS boundary curve, can be defined, see [25] for the analytical expressions. Along such a curve, it is possible to provide an estimate of the incommensurate frequency. Such a value can be expressed as [25]:

Fig. 17

Behaviour of the ratio $\omega _2/\omega _1$ of the eigenfrequencies, with respect to the applied potentials $(V_{\text {T}},V_{\text {DC}})$. a Behaviour of the $\omega _2/\omega _1$ ratio as a function of $V_{\text {T}}$ with given values of $V_{\text {DC}}$. In these conditions the minimum frequency mismatch is reached for $V_{\text {T}}=V_{\text {DC}}$. b contour plot of the function $\omega _2/\omega _1$ in a $(V_{\text {T}},V_{\text {DC}})$ plane

$$\begin{aligned} \omega _{\text {NS}}^2= & {} \frac{1}{2(\mu _1+\mu _2)}\bigg (\frac{q_2 k_3}{k_1} (\mu _1+\mu _2)\nonumber \\{} & {} \sqrt{\mu _2^2+(k_2-2\omega )^2} -\frac{q_2^2 k_3^2\mu _2}{8k_1^2}\nonumber \\{} & {} \quad +2\mu _1(\mu _2^2+(\omega _{02}-2\omega )^2)\nonumber \\{} & {} +2\mu _2(\omega -k_1)^2+2\mu _2\mu _1^2\bigg ), \end{aligned}$$

(21)

with $\mu _1=\omega _{01}/(2Q_1)$ and $\mu _2=\omega _{02}/(2Q_2)$ and $q_2$ corresponding to the values predicted for the NS bifurcation point [25]. The results of the analytical model, compared with the experiments, are reported in Fig. 16. The FRF is almost superimposed with the experiments. For the frequencies corresponding to the NS bifurcations on the FRC, the model predicts a spacing between 500 and 350 Hz. These values are compatible with the ones of the IC model and the experiments.

B Effect of the bias and tuning voltages on the resonance frequencies

The crucial role played by $V_{\text {DC}}$ and $V_{\text {T}}$ has been highlighted in experiments and simulations. They generally induce a negative shift of the eigenfrequencies, and the arch resonator is designed to provide a certain level of flexibility in the frequency match between the coupled bending modes by suitably tuning $V_{\text {DC}}$ and $V_{\text {T}}$. Indeed, data reported in Figs. 7,8 and 9 clearly show that certain combinations of $V_{\text {DC}}$ and $V_{\text {T}}$ allow for a better frequency match. This can be easily justified on the basis of Eqs. (17) and (18). Performing a linearization with respect to the reduced coordinate $q_1$ and $q_2$ in Eqs. (17) and (18), respectively, an analytical expression for $\omega _1$ and $\omega _2$ can be readily obtained:

$$\begin{aligned} \omega _1^2&=c_1^{(1)} -c^{(1)}_{1\text {DD}}V_{\text {DC}}^2 - c^{(1)}_{1\text {TT}}V_{\text {T}}^2 - 2 c^{(1)}_{1\text {DT}}V_{\text {DC}}V_{\text {T}}\nonumber \\ \omega _2^2&=c_2^{(2)} -c^{(2)}_{2\text {DD}}V_{\text {DC}}^2 - c^{(2)}_{2\text {TT}}V_{\text {T}}^2 - 2 c^{(2)}_{2\text {DT}}V_{\text {DC}}V_{\text {T}} \end{aligned}$$

(22)

The ratio between the two frequencies $\omega _2/\omega _1$ with varying $V_{\text {DC}}$ and $V_{\text {T}}$ is plotted in Fig. 17. These plots highlight how the ideal ratio of 2 between the two resonance frequencies cannot be reached exactly. Nevertheless, a value of $V_{\text {T}}$ close to $V_{\text {DC}}$ allows reducing the mismatch, see the marker point in Fig. 17a.