Escape of two-DOF dynamical system from the potential well

Abstract

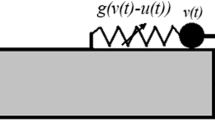
We consider the escape of an initially excited dynamical system with two degrees of freedom from a potential well. Three different benchmark well potentials with different topologies are explored. The main challenge is to reveal the basic mechanisms that govern the escape in different regions of the parametric space and to construct appropriate asymptotic approximations for the analytic treatment of these mechanisms. In this study, numerical and analytical tools are used to classify and map the different escape mechanisms for various initial conditions and to offer the analytic criteria predicting the system’s behavior for those cases.

Appendix

1.1 The lower boundary of the escape energy level

The escape of a dynamical system from a potential well is impossible if the initial energy is less than the value of the potential at its saddle points ($E_{{{\text{sp}}}}$). For any initial energy $E_{0} < E_{{{\text{sp}}}}$ the iso-potential curves are closed, and the is bounded, while for the exact $E_{0} = E_{{{\text{sp}}}}$ the closed counters of the iso-potential curves are broken, and escape channels are formed (cf. Fig. 7). Therefore, the lower limit of the escape energy level can be derived from the analysis of the total potential of the system.

$$ \det \left( {\left. H \right|_{{\overline{q}^{0} }} } \right) < 0 $$

(61)

For the cubic and biquadratic potentials, one can easily find the stationary point as a function of stiffness by setting the gradient of the total potential to zero. Further analysis shows that both potentials exhibit a saddle-node bifurcation for the control parameter-$\varepsilon$, the different system structures present in Fig. 14. With the help of the second partial derivative test, one can classify the saddle point which satisfies the following requirement.

Fig. 14

Iso-potential curves of the total effective potential, in red, the saddle point energy (a) &(b) biquadratic potential (c)&(d) cubic potential. a stiffness 0.25, b stiffness 1.01, c stiffness 0.25, d stiffness 0.51

Hence, the lower boundary of the escape energy for each IC is determined by the following form for the biquadratic potential and the cubic potential, respectively

$$ E_{b}^{{\min }} = \left\{ {\begin{array}{*{20}c} \begin{gathered} - \frac{{\varepsilon ^{2} }}{4} + \frac{\varepsilon }{2} + \frac{1}{4} \hfill \\ \frac{1}{2} \hfill \\ \end{gathered} & \begin{gathered} \varepsilon < 1 \hfill \\ \varepsilon \ge 1 \hfill \\ \end{gathered} \\ \end{array} } \right.$$

(62)

$$ E_{c}^{{\min }} = \left\{ {\begin{array}{*{20}c} \begin{gathered} - \frac{{2\varepsilon ^{3} }}{3} + \frac{\varepsilon }{2} + \frac{1}{6} \hfill \\ \frac{1}{3} \hfill \\ \end{gathered} & \begin{gathered} \varepsilon < \frac{1}{2} \hfill \\ \varepsilon \ge \frac{1}{2} \hfill \\ \end{gathered} \\ \end{array} } \right. $$

(63)