Skip to main content
SpringerLink
Log in

Singular-loop rogue wave and mixed interaction solutions with location control parameters for Wadati–Konno–Ichikawa equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

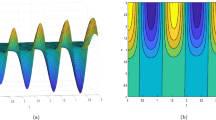
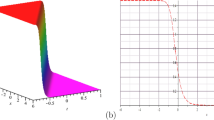
This paper is devoted to studying the complete integrable Wadati–Konno–Ichikawa equation, which is an important integrable model with physical background. Based on the known hodograph transformation, we give an alternative two-component nonlinear system of this equation. By constructing its special generalized \((m, N-m)\)-fold Darboux transformation, we obtain various location-manageable localized wave solutions, like higher-order rogue wave and periodic wave solutions with smooth, singular and singular-loop structures. It is found that the rogue wave can show a singular-loop structure when the special parameters are selected. For the first-order exact solutions, we analyze and summarize the reasons for singular structures when the plane wave amplitude reaches a certain value. Furthermore, we also discuss and summarize mixed interaction structures of diverse localized waves. In particular, these abundant structures can be managed to an arbitrary location by adjusting some control parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Porsezian, K., Nithyanandan, K., VasanthaJayakanthaRaja, R., Shukla, P.K.: Modulational instability at the proximity of zero dispersion wavelength in the relaxing saturable nonlinear system. J. Opt. Soc. Am. B 29, 2803–2813 (2012)

    Article  Google Scholar 

  2. Xiang, Y.J., Dai, X.Y., Wen, S.C., Fan, D.Y.: Modulation instability in metamaterials with saturable nonlinearity. J. Opt. Soc. Am. B 28, 908–916 (2011)

    Article  Google Scholar 

  3. Herrmann, S.G.J.: Soliton propagation in materials with saturable nonlinearity. J. Opt. Soc. Am. B 8, 2296–2302 (1991)

    Article  Google Scholar 

  4. Melvin, T.R.O., Champneys, A.R., Kevrekidis, P.G., et al.: Travelling solitary waves in the discrete Schrödinger equation with saturable nonlinearity: existence, stability and dynamics. Phys. D 237, 551–567 (2008)

    Article  MATH  Google Scholar 

  5. Herrmann, J.: Propagation of ultrashort light pulses in fibers with saturable nonlinearity in the normal-dispersion region. J. Opt. Soc. Am. B 8, 1507–1511 (1991)

    Article  Google Scholar 

  6. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  7. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, New York (2004)

    Book  MATH  Google Scholar 

  8. Ablowitz, M.J., Clarkson, P.A.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  9. Wadati, M., Konno, K., Ichikawa, Y.: New integrable nonlinear evolution equations. J. Phys. Soc. Jpn. 47, 1698–1700 (1979)

    Article  MATH  Google Scholar 

  10. Konno, K., Ichikawa, Y., Wadati, M.: A loop soliton propagation along a stretched rope. J. Phys. Soc. Jpn. 50, 1025–1026 (1981)

    Article  Google Scholar 

  11. Ichikawa, Y., Konno, K., Wadati, M.: Nonlinear transverse oscillation of elastic beams under tension. J. Phys. Soc. Jpn. 50, 1799–1802 (1981)

  12. Boiti, M., Pempinelli, F., Tu, G.Z.: The nonlinear evolution equations related to the Wadati\(--\)Konno\(--\)Ichikawa spectral problem. Prog. Theor. Phys. 69, 48–64 (1983)

    Article  MATH  Google Scholar 

  13. Shen, S.F., Wang, G.F., Jin, Y.Y., Hu, X.R.: Some Wadati\(-\)Konno\(-\)Ichikawa type integrable systems and their constructions. arXiv:2202.10900v1 (2022)

  14. Liu, H.F., Shimabukuro, Y.: N-soliton formula and blow-up result of the Wadati\(-\)Konno\(-\)Ichikawa equation. J. Phys. A 50, 315204 (2017)

    Article  MATH  Google Scholar 

  15. Zhang, Y.S., Rao, J.G., Cheng, Y., He, J.S.: Riemann–hilbert method for the Wadati\(--\)Konno\(--\)Ichikawa equation: N simple poles and one higher-order pole. Phys. D 399, 173–185 (2019)

    Article  MATH  Google Scholar 

  16. Li, Z.Q., Tian, S.F., Yang, J.J.: Soliton resolution for the Wadati\(-\)Konno\(-\)Ichikawa equation with weighted sobolev initial data. Ann. Henri Poincaré (2022). https://doi.org/10.1007/s00023-021-01143-z

  17. Wadati, M., Sogo, M.: Gauge transformations in soliton theory. J. Phys. Soc. Jpn. 52, 394–38 (1983)

    Article  Google Scholar 

  18. Zhang, Y.S., Qiu, D.Q., Cheng, Y., He, J.S.: The Darboux transformation for the Wadati\(-\)Konno\(-\)Ichikawa system. Theor. Math. Phys. 191, 710–724 (2017)

    Article  MATH  Google Scholar 

  19. Wang, G.H., Zhang, Y.S., He, J.S.: Dynamics of the smooth positons of the Wadati\(-\)Konno\(-\)Ichikawa Equation. Commun. Theor. Phys. 69, 227–232 (2018)

    Article  MATH  Google Scholar 

  20. Zhang, Y.S., Qiu, D.Q., Mihalache, D., He, J.S.: The loop rogue wave solutions for the Wadati\(-\)Konno\(-\)Ichikawa equation. Chaos 28, 103108 (2018)

    Article  MATH  Google Scholar 

  21. Wen, X.Y., Yan, Z.: Generalized perturbation \((n, M)\)-fold Darboux transformations and multi-rogue-wave structures for the modified self-steepening nonlinear Schrödinger equation. Phys. Rev. E 92, 012917 (2015)

    Article  Google Scholar 

  22. Wen, X.Y., Yan, Z., Yang, Y.: Dynamics of higher-order rational solitons for the nonlocal nonlinear Schrödinger equation with the self-induced parity-time-symmetric potential. Chaos 26, 063123 (2016)

    Article  Google Scholar 

  23. Wen, X.Y., Yan, Z.: Higher-order rational solitons and rogue-like wave solutions of the (2+1)-dimensional nonlinear fluid mechanics equations. Commun. Nonlinear. Sci. Numer. Simulat. 43, 311–329 (2017)

    Article  MATH  Google Scholar 

  24. Lin, Z., Wen, X.Y.: Dynamical analysis of position-controllable loop rogue wave and mixed interaction phenomena for the complex short pulse equation in optical fiber. Nonlinear Dyn. 108, 2573–2593 (2022)

    Article  Google Scholar 

  25. Li, L., Yu, F.J., Duan, C.N.: A generalized nonlocal Gross-Pitaevskii (NGP) equation with an arbitrary time-dependent linear potential. Appl. Math. Lett. 110, 106584 (2020)

    Article  MATH  Google Scholar 

  26. Yu, F.J., Liu, C.P., Li, L.: Broken and unbroken solutions and dynamic behaviors for the mixed local-nonlocal Schrödinger equation. Appl. Math. Lett. 117, 107075 (2021)

    Article  MATH  Google Scholar 

  27. Li, L., Liu, Y.Y., Yu, F.J.: Some reverse space (RS) rational solutions for the nonlocal coupled nonlinear Schrödinger equations on the plane wave backgrounds Appl. Math. Lett. 129, 107976 (2022)

    MATH  Google Scholar 

  28. Schäfer, T., Wayne, C.E.: Propagation of ultra-short optical pulses in cubic nonlinear media. Phys. D 196, 90–105 (2004)

    Article  MATH  Google Scholar 

  29. Feng, B.F., Maruno, K.I., Ohta, Y.: Integrable discretizations of the short pulse equation. J. Phys. A 43, 085203 (2010)

    Article  MATH  Google Scholar 

  30. Hanif, Y., Sarfraz, H., Saleem, U.: Dynamics of loop soliton solutions of PT-symmetric nonlocal short pulse equation. Nonlinear Dyn. 100, 1559–1569 (2020)

    Article  Google Scholar 

  31. Gupta, R.K., Kumar, V., Jiwari, R.: Exact and numerical solutions of coupled short pulse equation with timedependent coefficients. Nonlinear Dyn. 79, 455–464 (2015)

  32. Gao, B., He, C.F.: Analysis of a coupled short pulse system via symmetry method. Nonlinear Dyn. 90, 2627–2636 (2017)

    Article  MATH  Google Scholar 

  33. Feng, B.F., Ling, L., Zhu, Z.: Multi-soliton, multi-breather and higher order rogue wave solutions to the complex short pulse equation. Phys. D 327, 13–29 (2016)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work has been partially supported by National Natural Science Foundation of China under Grant No. 12071042 and Beijing Natural Science Foundation under Grant No. 1202006.

Author information

Authors and Affiliations

  1. School of Applied Science, Beijing Information Science and Technology University, Beijing, 100192, China

    Zhe Lin & Xiao-Yong Wen

Authors
  1. Zhe Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiao-Yong Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiao-Yong Wen.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The expressions of \(E_0...E_3, F_0...F_4\) in the solutions(19):

$$\begin{aligned} E_0&=-16\, \left( {c}^{2}+1 \right) ^{3} \bigg [ -\frac{1}{2}+2\,{a}^{2}{c}^{5}e_{{0}}d_{{0 }}\\&\quad + {a}^{2}{c}^{4}\left( -3\,{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) -2\,{a}^{2}{c}^{3}e_{{0}}d_{{0}}\\&\quad -{a}^{2}{c}^{2} \left( {d_{{0}}}^{2}+{e_{{0}}}^{2} \right) + acd_{{0}} \left( {c}^{2}+1 \right) ^{3/2} \bigg ] \\&\quad -32c\,\textrm{i} \left( {c}^{2}+1 \right) ^{3} \bigg [ a \sqrt{{c}^{2}+1} \\&\quad \times \left( {a}^{3}{c}^{3}d _{{0}}^{3} +{a}^{3}{c}^{3}e_{0}^{2}d_{{0}} +{a}^{2}{c}^{2}e_{{0}}{d_{{0}}}^{2}+{a}^{2}{c}^{2}e_{{0}}^{3}+\frac{1}{2}\,e_{{0}} \right) \\&\quad +{a}^{2}{c}^{3}e_{{0}}d_{{0}}+{a}^{2}{c}^{2} \left( -{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) -{a}^{2}ce_{{0 }}d_{{0}} +\frac{1}{4}\bigg ] ,\\ E_1&=16\,ac \left( {c}^{2}+1 \right) ^{2} \left( ac^2\sqrt{{c}^{2}+1}+a\sqrt{{c}^{2}+1}\right. \\&\quad \left. +{a}^{2}{c}^{5}d_{{0}}+3\,{a}^{2}{c}^{4}e_{ {0}}-7\,{a}^{2}{c}^{3}d_{{0}}-3\,{a}^{2}{c}^{2}e_{{0}}-2\,{a}^{2}cd_{{0 }} \right) T\\&\quad +16\,a \left( {c}^{2}+1 \right) ^{2}c \left[ a\sqrt{ {c}^{2}+1} \left( 3\,{c}^{3}d_{{0}}+{c}^{2}e_{{0}}+cd_{{0}}\right. \right. \\&\quad \left. \left. -{c} ^{4}e_{{0}}\right) -\frac{1}{2}\,{c}^{4}-{c}^{2}-\frac{1}{2} \right] y\\&\quad +\textrm{i}\Bigg \{ 8\,{a}^{2}{c}^{2} \left( {c}^{2}+1 \right) ^{2}\bigg [ \left( 4\,{a}^ {2}{c}^{3}e_{{0}}d_{{0}}+14{a}^{2}{c}^{2}{d_{{0}}}^{2}\right. \\&\quad \left. +10{a}^{2}{c}^{2}{e_{{0}}}^{2} +4\,{a}^{2}ce_{{0}}d_{{0}}+1 \right) \sqrt{{c} ^{2}+1}\\&\quad +a \left( {c}^{3}d_{{0}}+4\,{c}^{2}e_{{0}}-5\,cd_{{0}}-2\,e_{{0 }} \right) \bigg ] T \\&\quad +16\,{a}^{2}{c}^{2} \left( {c}^{2}+1 \right) ^{2} \bigg [ \left( -{c}^{2}e_{{0}}+2\,cd_{{0}}+e_{{0}} \right) \sqrt{{c} ^{2}+1}\\&\quad -a{c}^{4} \left( 3\,{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) \\&\quad -2a\,{c}^{3}d_{{0}}e_{{0}}-a{c}^{2} \left( 3\,{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) \\&\quad -2ac\,e_{{0}}d_{{0}} \bigg ] y\Bigg \}, \\ E_2&=-4\,{a}^{2}{c}^{2} \left( {c}^{2}+1 \right) \left( 5\,{a}^{2}{c}^{4}- 17\,{a}^{2}{c}^{2}-4\,{a}^{2} \right) {T}^{2}\\&\quad +8\,{a}^{3}{c}^{2} \left( {c}^{2 }+1 \right) ^{3/2}\left( {c}^{4}-7\,{c}^{2}-2 \right) Ty \\&\quad +4\,{a }^{2}{c}^{2} \left( {c}^{2}+1 \right) \\&\left( 3\,{c}^{4}+4\,{c}^{2}+1 \right) {y}^{2}+\textrm{i} \bigg \{ -8\,{a}^{2} \left( {c}^{2}+1 \right) {c}^{3} \left[ {a}^{3}\sqrt{{c}^{2}+1} \right. \\&\quad \left. \left( {c}^{3}d_{{0}}+7\,{c}^{2}e_{{0}}+16\,cd_{{0}}+4\,e_{{0 }} \right) - \left( -3\,{c}^{2}+6 \right) {a}^ {2} \right] {T}^{2}\\&\quad -8\,{a}^{2} \left( {c}^{2}+1 \right) {c}^{3} \left[ a \left( -{c}^{2}+5 \right) \sqrt{{c}^{2}+1}\right. \\&\quad \left. -2{a}^{2}\, \left( {c}^{ 4}e_{{0}}+7\,{c}^{3}d_{{0}}+3\,{c}^{2}e_{{0}}+7\,cd_{{0}}+2\,e_{{0}} \right) \right] Ty\\&\quad -8\,{a}^{2} \left( {c}^{2}+1 \right) \\&\quad {c}^{3} \left[ a \left( 3\,{c}^{3}d_{{0}}+{c}^{2}e_{{0}}+3\,cd_{{0}}+e_{{0}} \right) \sqrt{{c}^{2}+1}-{c}^{2}-1 \right] {y}^{2} \bigg \},\\ E_3&=\textrm{i} \left[ 12{a}^{6}{c}^{4}\, \left( {c}^{2}+4 \right) \sqrt{{c}^{2}+1} {T}^{3}\right. \\&\quad \left. -4{a}^{5}{c}^{4}\, \left( {c}^{2}+1 \right) \left( {c}^{2}+16 \right) y{T}^{2}\right. \\&\quad \left. +28\,{a}^{4} {c}^{4}\left( {c}^{2}+1 \right) ^{3/2}{y}^{2}T-4{a}^{3}{c}^{4}\, \left( {c}^{2}+1 \right) ^{2}{y}^{3}\right] ,\\ F_0&=4 \left( {c}^{2}+1 \right) ^{3}\, \Bigg \{ 4\,ac\sqrt{{c}^{2}+1} \\&\quad \left[ 2\,{a}^{2}{c}^{3}e_{{0}} \left( {d_{{0}}}^{2}+{e_{{0} }}^{2} \right) \right. \\&\quad \left. - \left( 2{a}^{2}{c}^{2}{d_{{0}}}^{3} +2{a}^{2}{c}^{2}{e_{{0}}}^{2}d_{{0}} +d_{{0}} \right) +ce_{{0}}-d_{{0}} \right] + \left( {c}^{2}+1 \right) \\&\quad \left[ 1+4\,{a}^{4} \left( {d_{{0}}}^{2}+{e_{{0}}}^{2} \right) ^{2}{c}^{4}-8\,{a}^{2}{c}^{3}d_{{0}}e_{{0}}\right. \\&\quad \left. +4\,{a}^{2} \left( 2\,{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) {c}^{2} \right] \Bigg \} , \end{aligned}$$
$$\begin{aligned} F_1&=-8\,ac\left( {c}^{2}+1 \right) ^{2} \bigg \{ a\sqrt{{c}^{2}+1} \Big [ 2\, \left( {d_{{0}}}^{2}+3\,{e_{{0}}}^{2} \right) {a}^{2}{c}^{4}\\&\quad +4\,{a}^{2}{c}^{3}d_{{0}}e_{{0}}- \left( 12\,{a}^{2}{c}^{2}{d_{{0}}}^{2} +4\,{a}^{2}{c}^{2} {e_{{0}}}^{2} +1 \right) -2 \Big ] \\&\quad +\Big [ 4\,{a}^{4}{c}^{4}e_{{0}} \left( {c}^{2}+1 \right) \left( {d_{{0}}}^{2}+{e_{{0}}}^{2} \right) \\&\quad +2{a}^{2}{c}^{3}d_{{0}}\, \left( 4{a}^{2}{d_{{0}}}^{2}+4{a}^{2}{e_{{0}}}^{2} -1 \right) -2\,{a}^{2}{c}^{2}e_{{0}}\\&\quad +8\,{a}^{2}cd_{{0}} \Big ] \bigg \} T+8\,ac\left( {c}^{2}+1 \right) ^2 \\&\quad \bigg \{ a\sqrt{{c}^{2}+1} \Big [ 4\,{a}^{2}{c}^{5}d_{{0}} \left( {d_{{0}}}^{2}+{e_{{0}}}^{2} \right) \\&\quad -2\,{c}^{4}e_{{0}}+4d_{{0}}{c}^{3}\, \left( {a}^{2}e_0^{2}+{a}^{2}d_0^{2} +1 \right) \\&\quad -2\,{c}^{2}e_{{0}}+4\,cd_{{0}} \Big ] + \Big [ -4\,{a}^{2}{c}^{3}d_{{0}}e_{{0}}\\&\quad +{c}^{2}\left( 6a^2\,{d_{{0}}}^{2}+a^2{e_{{0}}}^{2}+1\right) +1 \Big ] \left( {c}^{2}+1 \right) \bigg \}y, \\ F_2&=4\,{a}^{4} {c}^{2} \left( {c}^{2}+1 \right) \bigg [ 2{a}^{2} {c}^{2}\left( {c}^{2}+1 \right) \, \left( 3\,{c}^{2}{e_{{0}}}^{2}\right. \\&\quad \left. +4{e_{{0}}}^{2} +8\,d_{{0}}ce_{{0}}+{d_{{0}}}^{2}{c}^{2}+12{d_{{0}}}^{2} \right) \\&\quad +6\,ac\sqrt{{c}^{2}+1} \left( {c}^{3}e_{{0}}+{c}^{2}d_{{0}}-4\,d_{{0}} \right) \\&-3\,{c}^{4}+5\,{c}^{2}+8 \bigg ] {T}^{2}-8\,{a}^{3}\left( {c}^{2}+1 \right) ^{2}{c}^{2} \bigg [ 4{a}^{2}{c}^{2}\,\sqrt{{c}^{2}+1}\\&\quad \left( d_{{0}}ce_{{0}}+3\,{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) + 2a\,{c}^{2}e_{{0}}+2ac^3\,d_{{0}}-12acd_{{0}}\\&\quad -\sqrt{{c}^{2}+1} \left( {c}^{2}-4 \right) \bigg ] yT+8\,{a}^{2}{c}^{2} \left( {c}^{2}+1 \right) ^{2} \\&\quad \left[ {a}^{2}{c}^{2} \left( {c}^{2}+1 \right) \left( 3\,{d_{{0}}}^{2}+{e_{{0}}}^{2} \right) \right. \\&\quad \left. + ac\left( ce_{{0}}-3\,d_{{0}} \right) \sqrt{{c}^{2}+1}+{c}^{2}+1 \right] {y}^{2}, \\ F_3&=-4\,{a}^{3}{c}^{3} \bigg [ {a}^{3}\left( {c}^{4}+2\,{c}^{2}-8 \right) \sqrt{{c}^{2}+1}\\&\quad +2\, {a}^{4}c \left( {c}^{2}+1 \right) \left( {c}^{2}+4\right) \left( ce_{{0}}+2\,d_{{0}} \right) \bigg ] {T}^{3}\\&\quad -4\,{a}^{3}{c}^{3} \bigg [ -2\,{a}^{3} \left( {c}^{5}d_{{0}}+4\,{c}^{4}e_{{0}}\right. \\&\quad \left. +13\,{c}^{3}d_{{0}}+4\,{c}^{2}e_{{0}}+12\,cd_{{0}} \right) \sqrt{{c}^{2}+1}\\&\quad +{a}^{2} \left( {c}^{2}+1 \right) \left( -3\,{c}^{2}+12\right) \bigg ] {T}^{2}y-4\,{a}^{3}{c}^{3}\\ {}&\quad \times \bigg [ -a \left( {c}^{2}+1 \right) ^{3/2} \left( -{c}^{2}+6 \right) \\&\quad +2\,{a}^{2} \left( {c}^{2}+1 \right) \left( {c}^{4}e_{{0}}+6\,{c}^{3}d_{{0}}+{c}^{2}e_{{0}}+6\,c d_{{0}} \right) \bigg ] T{y}^{2}\\&\quad -4\,{a}^{3}{c}^{3}\bigg [ -2\, a \left( {c}^{2}+1 \right) ^{3/2} \left( {c}^{3}d_{{0}}+cd_{{0}} \right) + \left( {c}^{2}+1 \right) ^{2} \bigg ] {y}^{3}, \\ F_4&={a}^{8}{c}^{4}\left( {c}^{2}+4 \right) ^{2}{T}^{4} -8\,{a}^{7}{c}^{4} \left( {c}^{2}+4 \right) \sqrt{{c}^{2}+1}y{T}^{3}\\&\quad +2\,{a}^{6}{c}^{4} \left( {c}^{2}+12 \right) \left( {c}^{2}+1 \right) {y}^{2}{T}^{2}\\ {}&\quad -8 \,{a}^{5}{c}^{4} \left( {c}^{2}+1 \right) ^{3/2}{y}^{3}T\\&\quad +{a}^{4}{c}^{4} \left( {c}^{2}+1 \right) ^{2}{y}^{4}. \end{aligned}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, Z., Wen, XY. Singular-loop rogue wave and mixed interaction solutions with location control parameters for Wadati–Konno–Ichikawa equation. Nonlinear Dyn 111, 3633–3651 (2023). https://doi.org/10.1007/s11071-022-07984-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07984-5

Keywords

Search

Navigation